ЖЭТФ, 2023, том 163, вып. 3, стр. 297-308

АТТОСЕКУНДНАЯ ИНТЕРФЕРОМЕТРИЯ ПРИ УЧАСТИИ

ДИСКРЕТНЫХ СОСТОЯНИЙ

М. М. Попова^a,b*, С. Н. Юдин^b, Е. В. Грызлова^b, М. Д. Киселев^a,b,c,d,

А. Н. Грум-Гржимайло^b,d

^a Московский государственный университет им. М. В. Ломоносова,

Физический факультет

119991, Москва, Россия

^b Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына,

Московский государственный университет им. М.В. Ломоносова

119991, Москва, Россия

^c Лаборатория моделирования квантовых процессов,

Тихоокеанский государственный университет

680035, Хабаровск, Россия

^d Университет ИТМО, Физический факультет

197101, Санкт-Петербург, Россия

Поступила в редакцию 4 октября 2022 г.,

после переработки 4 октября 2022 г.

Принята к публикации 20 октября 2022 г.

Теоретически рассматриваются особенности RABBITT (Reconstruction of Attosecond Beating By

Interference of Two-photon Transitions) спектроскопии в условиях, когда существенную роль играют пе-

реходы через состояния дискретного спектра. Применяется два подхода: численное решение скоростных

уравнений с дискретизацией континуума и теория возмущений в третьем порядке по амплитуде. Оба

подхода используют матричные элементы переходов и амплитуды фотоионизации, полученные высоко-

точным методом R-матрицы. В рамках этих подходов получены фотоэлектронные спектры, амплитуда и

фаза RABBITT-осцилляций, изучено влияние интенсивности затравочного оптического поля и отстройки

от резонанса при возбуждении дискретных состояний.

DOI: 10.31857/S004445102303001X

Методы аттосекундной интерферометрии,

ос-

EDN: QDEOHW

нованные на фотоэмиссии, можно разделить

на

streaking-спектроскопию [12-15] с использованием

1. ВВЕДЕНИЕ

единичного аттосекундного импульса и RABBITT,

Изучение динамики малых квантовых систем в

где используется последовательность импульсов [4,

сверхбыстром масштабе активно развивается в свя-

16,17]. Сравнительные преимущества и недостатки

зи с появлением интенсивных и ультракоротких им-

RABBITT- и streaking-спектроскопии обсуждаются

пульсных источников света в вакуумном ультрафи-

в [18].

олетовом (ВУФ) и рентгеновском режимах. Разви-

Метод RABBITT (Reconstruction of Attosecond

тие источников излучения, основанных на генера-

Beating By Interference of Two-photon Transitions) ос-

ции гармоник высокого порядка (HHG) [1,2], приве-

нован на использовании последовательности ВУФ-

ло к возникновению аттосекундной метрологии, что

импульсов для ионизации мишени совместно с за-

позволило исследовать динамику электронов в ато-

травочным ИК- или оптическим импульсом [19] и

мах, молекулах и твердых телах в естественной вре-

варьировании времени его задержки относительно

менной шкале

[3-7]. Прогресс в технике генерации

ВУФ для извлечения информации об относитель-

позволяет получать импульсы короче 100 ас [8-11].

ных фазах амплитуд переходов. Поскольку ВУФ-

компоненты ω_N являются (как правило, нечетны-

^* E-mail: mm.popova@physics.msu.ru

ми) гармониками оптического/ИК лазера ω_ir , то

297

М. М. Попова, С. Н. Юдин, Е. В. Грызлова и др.

ЖЭТФ, том 163, вып. 3, 2023

ω_N = Nω_ir . Высокочастотный импульс переводит

электрон в состояние непрерывного спектра, назы-

ваемое основная линия (mainline ML), а интен-

сивное низкочастотное поле создает боковые линии

(sidebands

SB) [20] при энергиях, соответствую-

щих дополнительному поглощению или испусканию

n низкочастотных фотонов ω_N ±nω_ir (рис. 1). В низ-

шем порядке теории возмущений можно показать,

что интерференция между переходами, вызванными

поглощением фотона с частотой ω_N с последующим

поглощением фотона с частотой ω_ir и поглощением

фотона ω_N+2 с испусканием ω_ir , приводит к тому,

что величина SB осциллирует на удвоенной частоте

ИК-поля ω_ir при изменении времени его задержки

τ относительно ВУФ:

SB(τ) = a + b cos(2ω_ir τ - φ_max ).

(1)

Для импульсов, содержащих большое число оптиче-

ских циклов, изменение задержки импульса эквива-

лентно изменению фазы ИК-поля φ_ir = ω_ir τ отно-

Рис.

1. Схема многочастотной ¾ВУФ+ИК¿-ионизации

сительно ВУФ.

атома неона при несущей длине волны λ ≈ 800 нм и ВУФ-

Обзор ограничений, накладываемых на

поле, состоящем из 13, 15 и 17 ее гармоник

RABBITT-спектроскопию длиной импульса, фа-

Особенность этой области, привлекшей в послед-

зовыми флуктуациями и статистикой измерений,

нее время усиленное внимание как теоретиков, так

представлен в [21].

и экспериментаторов [27,35-37], участие в форми-

Для описания и интерпретации RABBITT ис-

ровании спектра переходов через дискретные состо-

пользовались подходы, основанные на различных

яния. Вклад последних доминирует в припороговой

вариациях теории возмущений [22-24], в том числе

области, т.е. в нижайших основной и боковой ли-

и при учете релятивистских поправок, приближе-

ниях. Ранее подобное усиление некоторых перехо-

нии сильного поля [25], решении нестационарного

дов отмечалось в области автоионизационных, или

уравнения Шредингера

[26-30] и, наконец, неста-

квазидискретных, состояний [38-42].

ционарной версии R-матрицы [31]. Два последних

Везде, где не отмечено иное, используется атом-

метода, несомненно, эффективны для моделирова-

ная система единиц.

ния, но практически не позволяют анализировать

вклады различных процессов, т. е. являются, по су-

ти, разновидностью численного эксперимента.

2. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

В настоящей работе мы предлагаем и тестируем

Поле представляет собой сумму инфракрасного

подход, основанный на решении скоростных урав-

поля (обозначаемого как ¾ir¿) и нескольких гармо-

нений с использованием полученных с необходимой

ник N-го порядка в ВУФ-диапазоне (обозначаемых

спектроскопической точностью дипольных матрич-

¾N¿):

ных элементов переходов. Мы применяем метод ста-

∑

ционарной R-матрицы [32] для описания переходов

E(t) =

cos²(t/σ_N )n_λg^NλE_N cos(ω_N t + φ_N ) +

между состояниями дискретного спектра и конти-

нуума; метод устранения расходимости [33, 34] для

+ n_λgirλ E_ir cos²(t/σ_ir)cos(ω_irt + φ_ir).

(2)

описания переходов между состояниями континуу-

ма. Для проверки и анализа результатов решения

Здесь n_λg_λ вектор поляризации, представленный

скоростных уравнений мы проводим сравнение с ре-

в виде разложения по ортам в циклическом ба-

зультатами, полученными в рамках теории возму-

зисе n_λ [43]. Если ось z совпадает с направлени-

щений. Развиваемый нами метод применен к иссле-

ем распространения гармоники, то λ = ±1, ина-

дованию RABBITT осцилляций в примыкающей к

че допускается компонента λ

= 0 (в частности,

порогу области непрерывного спектра атома неона

для линейно поляризованного вдоль оси z поля су-

(рис. 1).

ществует только компонента λ = 0). E_N,ir

на-

298

ЖЭТФ, том 163, вып. 3, 2023

Аттосекундная интерферометрия при участии дискретных состояний

пряженность соответствующей гармоники. В каче-

мильтониан и гамильтониан взаимодействия с элек-

стве огибающей мы используем полупериод коси-

тромагнитным полем. Тогда многочастичная волно-

нуса, так как он обладает необходимыми услови-

вая функция электронов в атоме подчиняется урав-

ями гладкости поля и его первой производной в

нению Шредингера:

начале и конце импульса. Отметим, что для гаус-

(

)

∂

совского импульса exp(-x²/2σ^2Γ) ≈ 1 - x²/2σ^2Γ, а

Ψ(r, t) =

Ĥ_at +

Ĥ_int (t) Ψ(r, t).

(7)

∂t

для косинуса cos²(x/σ)

≈ 1 - x²/σ², т.е., что-

В электрическом дипольном приближении Га-

бы иметь такое же поведение в максимуме, как и

мильтониан взаимодействия имеет вид [44]

при гауссовской огибающей, должно удовлетворять-

√

ся соотношение σ =

2σ_Γ. При генерации HHG

Ĥ_int (t) =

A(t)p.

(8)

ширина ВУФ-импульса σ_Γ,N не зависит от номе-

ра гармоники и связана с шириной затравочного

Разложим Ψ(r, t) по собственным функциям

импульса как σ_Γ,N

= σ_Γ,ir/2. Типичная длитель-

φ_n(ǫ)(r) невозмущенного гамильтониана

Ĥ_at :

ность HHG-импульса составляет порядка 10-20 фс,

Ĥ_at φ_n,ǫ(r) = ε_n(ǫ)φ_n(ǫ)(r),

(9)

т. е. в нем укладываются десятки или даже сот-

∑

ни оптических циклов. ИК-импульс начинается в

Ψ(r, t) =

a_n(t)φ_n(r)e-iεnt +

момент -tir = -π/2σir , а ВУФ соответственно в

∫

−t_N = -π/2σ_N.

+ dε_ǫ a_ǫ(t)φ_ǫ(r)e-iεǫ t.

(10)

Векторный потенциал получается из напряжен-

Здесь индекс n(ǫ) обозначает полный набор кван-

ности (2) как

∫^t

товых чисел, необходимых для описания состояний

∑

A(t) = -c E(t^′)dt^′ =

A_h(t).

(3)

дискретного и непрерывного спектров: угловые мо-

менты в соответствующей схеме связи, их проекции

−∞

и энергию состояния. Далее для краткости, если спе-

Векторный потенциал каждой из гармоник

циально не оговорено иное, один индекс будет ис-

(h = N, ir ) электромагнитного поля A_h(t) представ-

пользоваться для обозначения состояний как дис-

лен в виде разложения:

кретного, так и непрерывного спектра.

∑

A_h(t) = c n_λg^hλA^+h(t)e-i(ωht+φh) +

Для коэффициентов разложения a(t) можно по-

лучить систему дифференциальных уравнений пер-

вого порядка, определяющих эволюцию заселен-

+ (-1)^(1-λ)n_-λg^h∗-λA-h (t)ei(ωht+φh),

(4)

ности атомных состояний (каналов непрерывного

где A^±h(t)

коэффициент при exp(∓i(ω_ht + φ_h)),

спектра) во времени:

определяемый как

∫

da_f (t)

∑

= -i ei(εf-εi)t〈φ_f |

Ĥ_int (t)| φ_i〉a_i(t).

(11)

A^±h(t)exp(∓iω_ht) =

∫

Мы используем матричные элементы перехода в

cos²(t^′/σ_h)E_h exp(∓iω_ht^′)dt^′ ≈

форме скорости

-t_h

E_h

〈φ_f |

Ĥ_int (t)| φ_i〉 =

〈φ_f | A(t)p | φ_i〉=

≈ cos²(t/σ_h)

exp(∓iω_ht),

(5)

∑

∓2iω_h

= (g^hλA^+h(t)e-iωht + g^h∗-λA^-h(t)eiωht) ×

т. е. в рассматриваемом случае длинного импуль-

h,λ^h

са огибающая векторного потенциала практически

(J_iM_i, 1λ | J_f M_f )

〈φ_n || p || φ_i〉,

(12)

неотличима от огибающей напряженности поля.

где 〈φ_f || p || φ_i〉 приведенный матричный элемент

3. РЕШЕНИЕ СКОРОСТНЫХ УРАВНЕНИЙ

перехода, (J_iM_i, 1λ | J_f M_f )

коэффициент Клеб-

(РСУ)

ша - Гордана,

J =

√2J + 1.

Представим полный гамильтониан

Ĥ атома в по-

Система уравнений (11) решалась численно с ис-

ле электромагнитного излучения как

пользованием приведенных матричных элементов,

Ĥ= Ĥ_at +

Ĥ_int (t),

(6)

полученных методами, описанными в разд. 5.

Для описания состояний непрерывного спектра в

где

Ĥ_at и

Ĥ_int (t)

атомный (невозмущенный) га-

(11) применялся метод дискретизации континуума,

299

М. М. Попова, С. Н. Юдин, Е. В. Грызлова и др.

ЖЭТФ, том 163, вып. 3, 2023

в котором интегрирование заменяется суммировани-

гаемое в (12), можно записать формальное решение

ем,

уравнения (18) в виде

∫

∑

a(ǫ) dǫ →

a(ǫ_i) dǫ,

(13)

a^(1)f(t) = -i√

〈φ_f || p || φ_i〉 ×

а возникающий при суммировании множитель dǫ

∫

∑

включается в коэффициенты разложения и матрич-

A_N (t)e-i(ωN t+φN )ei(εf -εi)t dt.

(19)

ные элементы:

-tN

√

В первом порядке ТВ есть только однофотонные

a_ǫ

dǫ → aǫi,

(14)

√

переходы под действием ВУФ-излучения, поэто-

〈φ_n |

Ĥ_int (t)| φ_ǫ〉

dǫ → 〈φ_n |

Ĥ_int (t)| φǫi 〉,

(15)

му в фотоэлектронном спектре наблюдаются толь-

〈φ_ǫ |

Ĥ_int (t)| φ_ǫ′ 〉dǫ → 〈φ_ǫ |

Ĥ_int (t)| φ_ǫ′ 〉.

(16)

ко основные линии (ML) при энергиях электронов

ε_f = Nω_ir - ε_i (ε_i энергия атома в основном со-

Тогда |aǫi |² вероятность найти электрон с энерги-

стоянии), а какие-либо осцилляции отсутствуют.

ей в окрестности dǫ точки ǫ_i.

Во втором порядке ТВ присутствуют двухфотон-

Код реализован и зарегистрирован авторами ста-

ные переходы через дискретные возбужденные со-

тьи [45]. При расчетах диапазон энергий электро-

стояния и состояния непрерывного спектра, связан-

нов непрерывного спектра составлял (0, 0.36) ат. ед.,

ные со взаимодействием системы с ИК-полем. Фор-

что позволяло исследовать боковые линии до SB18.

мально решение (19) является начальным условием

Эффект от обрезания области интегрирования в

для (18), и для a^(2)f(t) имеем

представленной части спектра составляет поряд-

∫

ка 1%. Вычисления проводились с равномерным ша-

da^(2)f(t)

∑

= -i ei(εf-εn)t〈φ_k |

Ĥ_int (t)| φ_n〉a⁽¹⁾ⁿ(t),

гом разбиения по энергии dǫ, величины этих шагов

варьировались (dǫ = 0.002 ÷ 0.004 ат.ед.) для ис-

следования сходимости. В реализованной програм-

(20)

ме изначально была заложена возможность изучать

(-i)²

a^(2)f(t) =

√

(10, 10 |J0)〈φ_f || p || φ_n〉〈φ_n || p || φ_i〉 ×

произвольные поляризации излучения, поэтому со-

стояния континуума могли иметь любые возмож-

∫

tir

ные при данном моменте проекции. Размерность си-

× A^± (t)e±i(ωirt+φir)ei(ε-εn)t ×_ω

стемы дифференциальных уравнений была поряд-

-tir

ка 10 000.

∫

∑

A_N (t^′)e-i(ωN t^′+φN )ei(εn-εi)t′ dt^′dt.

4. ТЕОРИЯ ВОЗМУЩЕНИЙ (ТВ)

-tN

(21)

Формулы, представленные в этом разделе, при-

Здесь знак ± отвечает за удержание значимого чле-

менимы для линейно поляризованных в одном на-

на в разложении несущей cos(ω_ir t + φ_ir ) при расче-

правлении гармоник в системе координат, где ось z

те переходов с поглощением (-) и испусканием (+)

сонаправлена с вектором поляризации.

фотона. В дальнейшем будем обозначать первый ка-

В рамках нестационарной теории возмущений

нал как (N) + 1, а второй как (N) - 1, где число в

коэффициенты a_k(t) в уравнении (11) раскладыва-

скобках номер ВУФ-гармоники, а знак определяет

ются в ряд

поглощение или испускание ИК-фотона. Амплитуда

¾(N) + 1¿ зависит от фазы ИК-поля как exp(-iφ_ir ),

a_f (t) = a^(0)f(t) + a^(1)f(t) + a^(2)f(t) + . . .,

(17)

а амплитуда ¾(N +2)-1¿, приводящая к состояниям

той же энергии, как exp(iφ_ir ). Их интерференция

где a^(0)f(t) = δ_fi

решение в отсутствие возмуще-

приводит к тому, что величина SB осциллирует на

ния. В первом порядке ТВ в уравнении (11) остается

удвоенной частоте ω_ir .

только одно слагаемое

Так как в ТВ вероятность обнаружить фотоэлек-

трон в основной фотолинии и в боковых полосах

da^(1)f(t)

= -iei(εf -εi)t〈φ_f |

Ĥ_int (t)| φ_i〉.

(18)

описывается квадратом суммы переходов с участи-

ем нечетного и четного числа фотонов n, соответ-

Дополнив ТВ приближением вращающейся волны,

ственно, второй порядок теории возмущений не вли-

т. е. оставив только близкое к резонансу первое сла-

яет на основные линии ML.

300

ЖЭТФ, том 163, вып. 3, 2023

Аттосекундная интерферометрия при участии дискретных состояний

Таблица 1. Нижние дипольно-разрешенные возбужденные состояния атома неона, их энергия, приведенный матричный

элемент возбуждения из основного состояния (RME) и лидирующие конфигурации

Состояние E, эВ RME

Лидирующие конфигурации

2p⁵(²P_3/2)3s[³²]

16.67

-0.25

-0.92|2p⁵3s³P〉 - 0.39|2p⁵3s¹P〉

2p⁵(²P_1/2)3s[¹²]

16.85

0.60

-0.38|2p⁵3s³P〉 + 0.92|2p⁵3s¹P〉

2p⁵(²P_3/2)4s[³²]

19.69

-0.19

-0.69|2p⁵4s³P〉 - 0.71|2p⁵4s¹P〉

2p⁵(²P_1/2)4s[¹²]

19.78

-0.18

0.71|2p⁵4s³P 〉 - 0.69|2p⁵4s¹P 〉

2p⁵(²P_3/2)3d[¹² ]

20.03

0.10

0.89|2p⁵3d³P 〉 - 0.43|2p⁵3d¹P 〉 - 0.12|2p⁵3d³D〉

2p⁵(²P_3/2)3d[³² ]

20.04

-0.17

0.27|2p⁵3d³P 〉 + 0.72|2p⁵3d¹P 〉 - 0.64|2p⁵3d³D〉

2p⁵(²P_1/2)3d[³² ]

20.14

0.13

-0.36|2p⁵3d³P〉 - 0.54|2p⁵3d¹P〉 - 0.76|2p⁵3d³D〉

2p⁵(²P_3/2)5s[³²]

20.57

-0.12

-0.62|2p⁵5s³P〉 - 0.78|2p⁵5s¹P〉

2p⁵(²P_1/2)5s[¹²]

20.66

0.08

-0.76|2p⁵5s³P〉 + 0.60|2p⁵5s¹P〉

Второй порядок по амплитуде соответствует

интерференцию амплитуд первого и третьего поряд-

четвертому порядку по сечению. Следователь-

ков.

но, для основных линий ML для достижения

Амплитуда в третьем порядке теории возмуще-

того же уровня точности мы должны учесть ний равна

∫

∑

(-i)

a^(3)f(t) =

√

(10, 10 | J^′n0)(10, J^′n0 | J^′0)〈φ_f || p || φ_k〉〈φ_k || p || φ_n〉〈φ_n || p || φ_i〉 ×

J_nkJ

∫tir

∫

× A^± (t)e±i(ωirt+φir)ei(εf-εk)tω

A^± (t^′)e±i(ωir t^′+φir )ei(εk-εn)t′ ×_ω

−tir

-tir

∫

∑

A_n(t^′′)e-i(ωN t^′′+φN )ei(εk-εi)t′′ dt^′′ dt^′ dt.

(22)

-tN

Амплитуды ¾(N)+ 1 - 1¿ и ¾(N)- 1 + 1¿, очевид-

5. СПЕКТРОСКОПИЧЕСКАЯ МОДЕЛЬ

но, как и первый порядок ТВ, не зависят от фазы

ИК-поля; амплитуды ¾(N +2)-2¿ и ¾(N -2)+2¿ ве-

Дипольные матричные элементы переходов меж-

дут себя как exp(±2iφ_ir ). Вероятность обнаружить

ду дискретными состояниями и между дискретными

фотоэлектрон в основной линии ML

состояниями и состояниями континуума были по-

[

]

лучены в Jκ-схеме связи методом R-матрицы [32].

|a^(1+3)f|² ≈ |a^(1)f|² + 2 Re a^(1)fa^(3)∗

(23)

Таким образом, квантовыми числами, характеризу-

ющими состояние, были полный момент J_f ионно-

Слагаемые, отвечающие за интерференцию первого

го остова 2p⁵²P_J

, орбитальный момент электрона

¾(N)¿ и третьего ¾(N ±2)∓2¿ порядков, как и в SB,

дискретной nl или непрерывной εl части спектра,

осциллируют на удвоенной частоте ИК-поля 2ω_ir .

промежуточное квантовое число κ результат их

При ионизации инертного газа (J_i = 0) линей-

векторного сложения, κ = J_f + l, и, наконец, пол-

но поляризованными в одном направлении гармо-

ный момент системы J = κ + 1/2, где 1/2 спин

никами для переходов, вызванных четным числом

электрона. Выбор Jκ-схемы связан с необходимо-

фотонов, возможны только четные полные моменты

стью аккуратного учета переходов из состояний дис-

J, вызванных нечетным числом фотонов только

кретного спектра в состояния непрерывного спектра

нечетные J.

с различным полным моментом конечного иона J_f

301

М. М. Попова, С. Н. Юдин, Е. В. Грызлова и др.

ЖЭТФ, том 163, вып. 3, 2023

(расщепленным на 0.1 эВ) в низкоэнергетической об-

3s-орбитали, остальные состояния описываются

ласти спектра.

скорее в Jκ-схеме связи. Энергии возбуждения

В расчетах использовалась та же спек-

дискретных состояний таковы, что для нашей

троскопическая модель, что и в

[46]: учиты-

цели исследования роли дискретных состояний

вались все возможные термы конфигураций

разумно выбрать область 3d-состояний, так как, в

1s²2s²2p⁵ns (n = 3, 4, 5, 6), 1s²2s²2p⁵nd (n = 3, 4, 5),

отличие от 3s и 4s, они могут быть ионизованы од-

1s²2s²2p⁴3s3p, 3p4s, и 1s²2s¹2p⁵3s3d и использова-

ним фотоном 800 нм и эффективно возбуждены его

лись экспериментальные энергии порогов [47].

гармоникой N = 13, и при этом неплохо отделены

по энергии от ближайших состояний 4s и 5s.

На рис.2 представлены суммы квадратов моду-

лей матричных элементов переходов из основного

состояния в каналы с участием s- и d-волны (a) и

из состояний 2p⁵3d в каналы с участием p- и f-вол-

ны (b). В то время как для переходов из основного

состояния оба канала сопоставимы по величине, для

переходов из возбужденных состояний каналы с f-

волной превосходят каналы с участием p-волны на

два порядка.

Вычисление матричных элементов перехода

между состояниями непрерывного спектра (конти-

нуум - континуум) проводилось в предположении,

что для этих состояний можно пренебречь любыми

корреляциями фотоэлектрона и электронов оста-

точного иона. Сначала c помощью программного

пакета MCHF [48] была найдена самосогласован-

ная волновая функция иона 2p52P, а затем

волновые функции электронов в поле этого иона

P_εl. Затем методом, описанным в работах [33, 34],

вычислялись радиальные матричные элементы

континуум - континуум R_εl,ε′_l′ . Необходимо отме-

тить, что матричные элементы связи состояний

непрерывного спектра R_εl,ε′_l′ имеют полюс при

ε → ε^′, который в подходе [33] выделяется в явном

виде как

√

δ(ε_i -ε_j)

2εsign(l_i-l_j) cos(σli +δli -σlj -δlj ).

(24)

Здесь δ_l и σ_l кулоновская фаза и фаза рассеяния.

Рис. 2. a) Сумма квадратов приведенных матричных эле-

Связь R_εl,ε′_l′ и приведенных матричных элемен-

ментов перехода в s-волны (синяя штриховая линия) и

d-волны (черная сплошная линия) при ионизации из ос-

тов в Jκ-схеме связи можно получить, используя

новного состояния. Серые вертикальные полосы обознача-

квантовую теорию углового момента [49]:

ют положение основных линий (ML19 участвует в образо-

вании SB18, но не показана на спектрах). b) Сумма квад-

〈ε^′, (J_f l^′)k^′,¹² : J^′ ||

D || (J_f l)k, ε, ¹² : J〉 =

ратов матричных элементов ионизации из возбужденных

= 〈ε^′, l^′ ||

D || ε, l〉 ×

состояний в каналы с участием p-волны (штриховые ли-

{

}{

}

нии) и f-волны (сплошные линии)

J_f l k

J k

× (-1)Jf+l-J-1/2kk′JˆJˆ^′

(25)

В табл. 1 приведены дискретные состояния,

1 k^′ l^′

1k^′ J^′

включенные в расчеты, их энергии, приведенные

дипольные матричные элементы перехода из основ-

〈ε^′, l^′ ||

D || ε, l〉 =

l(l0, 10 | l0)R_εl,ε′_l′ .

(26)

ного состояния и лидирующие конфигурации. По

коэффициентам смешивания видно, что, за исклю-

Конструкция в фигурных скобках это 6j-символ

чением нижайшей конфигурации с возбуждением

Вигнера.

302

ЖЭТФ, том 163, вып. 3, 2023

Аттосекундная интерферометрия при участии дискретных состояний

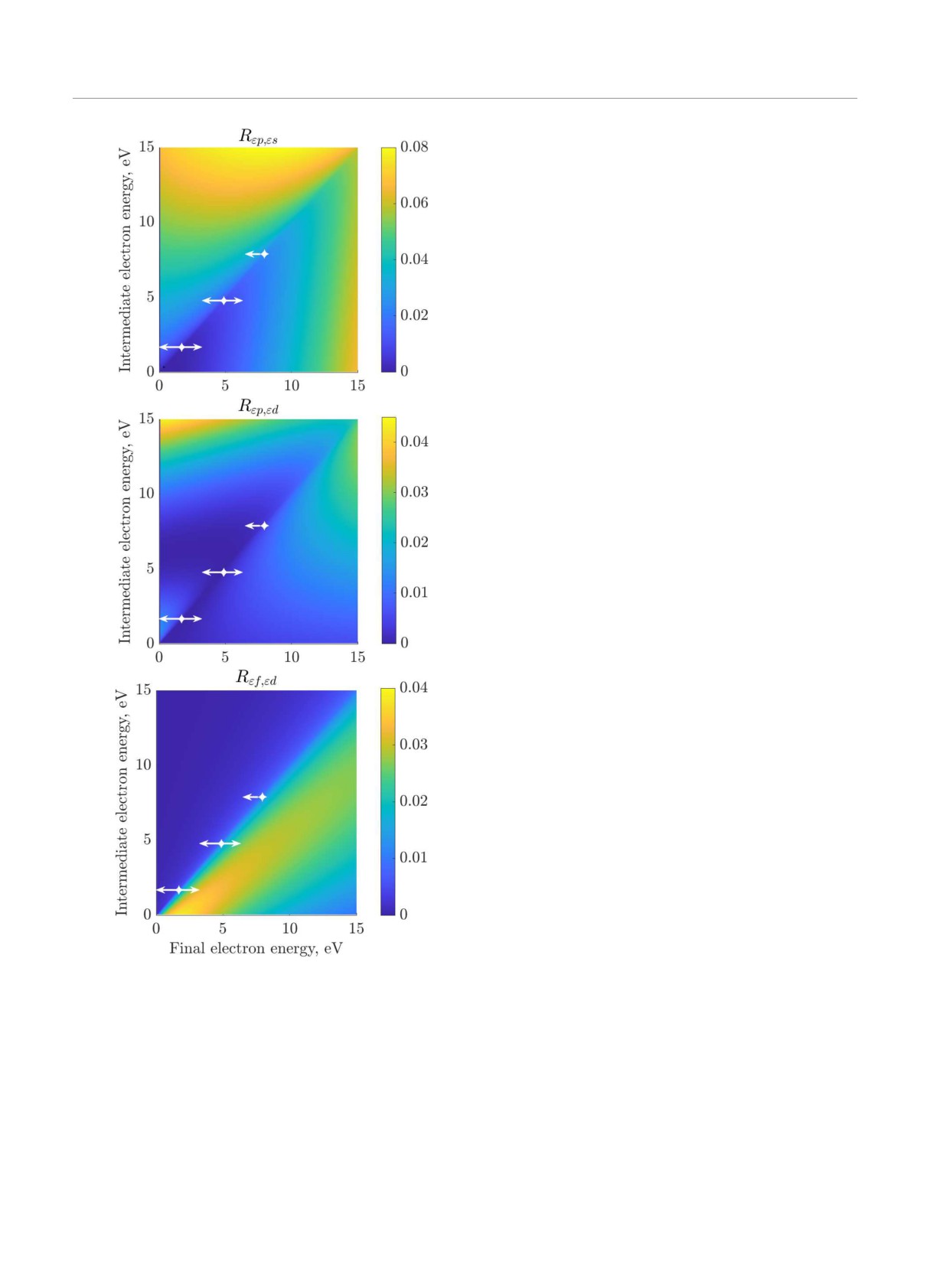
ного интеграла (19). Переходы в p-волну с погло-

щением и испусканием фотона сопоставимы по ве-

личине и в области низких энергий (до 5 эВ) неве-

лики. Переходы из d-волны в f-волну с точностью

до двух-трех процентов совпадают с формулой Гор-

дона [50, 51] и существенно асимметричны: идут в

основном с поглощением фотона и дают определя-

ющий вклад в низкоэнергетической части спектра.

6. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для расчетов мы выбрали параметры по-

ля в соответствии с реализуемыми сейчас на

установках HHG; поле включает в себя нечет-

ные гармоники с

по

с напряженностью

E_N = 10^-4 ат.ед. и длительностью Γ_N = 10 фс, и

инфракрасное поле с напряженностью в диапазоне

E_ir = (2.5-10)·10^-3 ат.ед. и в два раза большей дли-

тельностью Γ_ir = 20 фс. Фазы гармоник являются

изменяемыми параметрами, и здесь мы положи-

ли их нулевыми. В этой работе мы исследуем

окрестность 3d-резонанса и будем изменять несу-

щую частоту ω_ir . Разумный диапазон перестройки

длины волны ИК-гармоники: 798, 800, 802, 804 и

806 нм, этому соответствуют частоты ω_ir : 1.5537,

1.5498, 1.5459, 1.5421, 1.5383 эВ, и соответственно

частоты 13-й гармоники 13ω_ir : 20.20, 20.15, 20.10,

20.05, 20.00 эВ. Подчеркнем, что изменение частоты

ИК-поля автоматически означает изменение часто-

ты всех гармоник, так как это поле является для

них затравочным.

На рис.4a представлены результаты расчетов

при длине волны затравочного поля 800 нм по тео-

рии возмущений и методом решения скоростных

уравнений. Пики при 1.8 и 4.8 эВ это основные ли-

нии, результат ионизации 15-й и 17-й гармониками

(ML15, ML17); пики при 0.2, 3.2 и 6.2 эВ это боко-

вые частоты (SB14, SB16, SB18). Подчеркнем, что,

хотя в расчетах учитывалась 19-я гармоника, спектр

обрезан при энергии, соответствующей боковой ли-

нии SB18, так как диапазон релевантных данных на

2ω_ir меньше, чем диапазон энергий, учитываемых в

Рис. 3. Квадраты радиальной части матричных элементов

расчетах. Положения пиков, полученных РСУ, от-

переходов между состояниями континуума: (a) из s-волны

личаются для различных интенсивностей ИК-поля

в p-волну; (b) из d в p; (c) из d в f. Точками отмечены

из-за динамического штарковского сдвига и прибли-

энергии основных линий, а стрелочками влево (вправо)

жается к положениям по ТВ для меньшей напря-

боковые частоты, соответствующие переходам с испуска-

женности E_ir = 2.5 · 10^-3 ат. ед. Вероятности генера-

нием (поглощением) фотона

ции боковых линий SB16 и SB18 для напряженно-

На рис.3 приведены квадраты радиальных ча-

стей E_ir = 2.5 · 10^-3, 5 · 10^-3, 10^-2 ат.ед. относятся

стей (26), точками отмечены энергии основных ли-

как 1 : 4 : 16, т. е. для них сохраняется пертурбатив-

ний, а стрелочками энергии боковых линий, т. е.

ный режим. Для частоты SB14, где сильную роль

части, дающие максимальный вклад за счет времен-

играют переходы через дискретные состояния, пер-

303

М. М. Попова, С. Н. Юдин, Е. В. Грызлова и др.

ЖЭТФ, том 163, вып. 3, 2023

2.0

·¹²

1.5

ML17

ML15

1.0

SB14

0.5

SB16

SB18

0.0

-0.5

Elect

ron energy, eV

SB18

SB16

ML15

Рис. 4. a) Усредненный по фазе спектр фотоэлектронов

при длине волны затравочного поля 800 нм, полученный

РСУ для напряженности ИК-поля Eir = 2.5 · 10^-3 ат. ед.

(синяя линия), 5 · 10^-3 ат. ед. (черная), 10^-2 ат. ед. (крас-

ная). Тонкая серая линия

результат ТВ для

Рис. 5. a) Усредненный по фазе ИК-поля спектр при 800 нм

Eir

= 5 · 10^-3 ат.ед. b) Усредненный спектр (черная

и Eir = 5 · 10^-3 ат. ед., полученный по теории возмуще-

линия

ТВ, черные точки

РСУ), максимальная и

ний. Жирная черная линия обозначает итоговый спектр;

минимальная величины фотоэлектронных пиков (серая

серая штриховая первый порядок ТВ; красная штрих-

линия

ТВ, серые точки

РСУ) для напряженности

пунктирная

второй порядок ТВ, происходящий с ис-

Eir

= 5 · 10^-3 ат.ед. Разница между максимальной и

пусканием ИК-фотона; синяя штриховая

второй по-

минимальной величинами фотоэлектронных пиков в

рядок ТВ с поглощением ИК-фотона; сиреневая штрих-

ТВ окрашена серым цветом. Для удобства сравнения

пунктирная

вклад интерференции первого и третьего

результаты РСУ здесь и далее сдвинуты по энергии к

порядков; голубыми точками отмечен вклад от третьего

положениям по ТВ

порядка ТВ. b) Осцилляции (RABBITT traces) как функ-

ции задержки ИК-импульса и энергии фотоэлектронов. Ве-

турбативный режим нарушается.

личина осцилляций в SB14 представлена с фактором 5

На рис.4b представлены результаты расчетов

усредненного спектра и максимальной и мини-

На рис.5a показаны вклады отдельных перехо-

мальной величин фотоэлектронных пиков для

дов в итоговый спектр. Ожидаемо, что интерферен-

E_ir = 5 · 10^-3 ат.ед. Для удобства сравнения здесь

ция первого и третьего порядков (сиреневая штрих-

и далее результаты, полученные РСУ, сдвинуты

пунктирная линия в области ML) должна иметь

по энергии к положениям по ТВ. Как спектры,

тот же порядок малости, что и боковые линии SB.

так и амплитуда осцилляций, за исключением

Величина SB растет с ростом энергии, и переходы

ближайших к порогу SB14 и ML15 линий, по-

между состояниями непрерывного спектра, происхо-

лученные обоими методами, совпадают. Разница

дящие с испусканием ИК-фотона (красная штрих-

в первых двух является результатом эффектов

пунктирная линия) систематически ниже, чем пе-

высшего порядка и будет предметом дальнейшего

реходы, происходящие с поглощением ИК-фотона

исследования.

(синяя штриховая линия). Роль переходов из состо-

304

ЖЭТФ, том 163, вып. 3, 2023

Аттосекундная интерферометрия при участии дискретных состояний

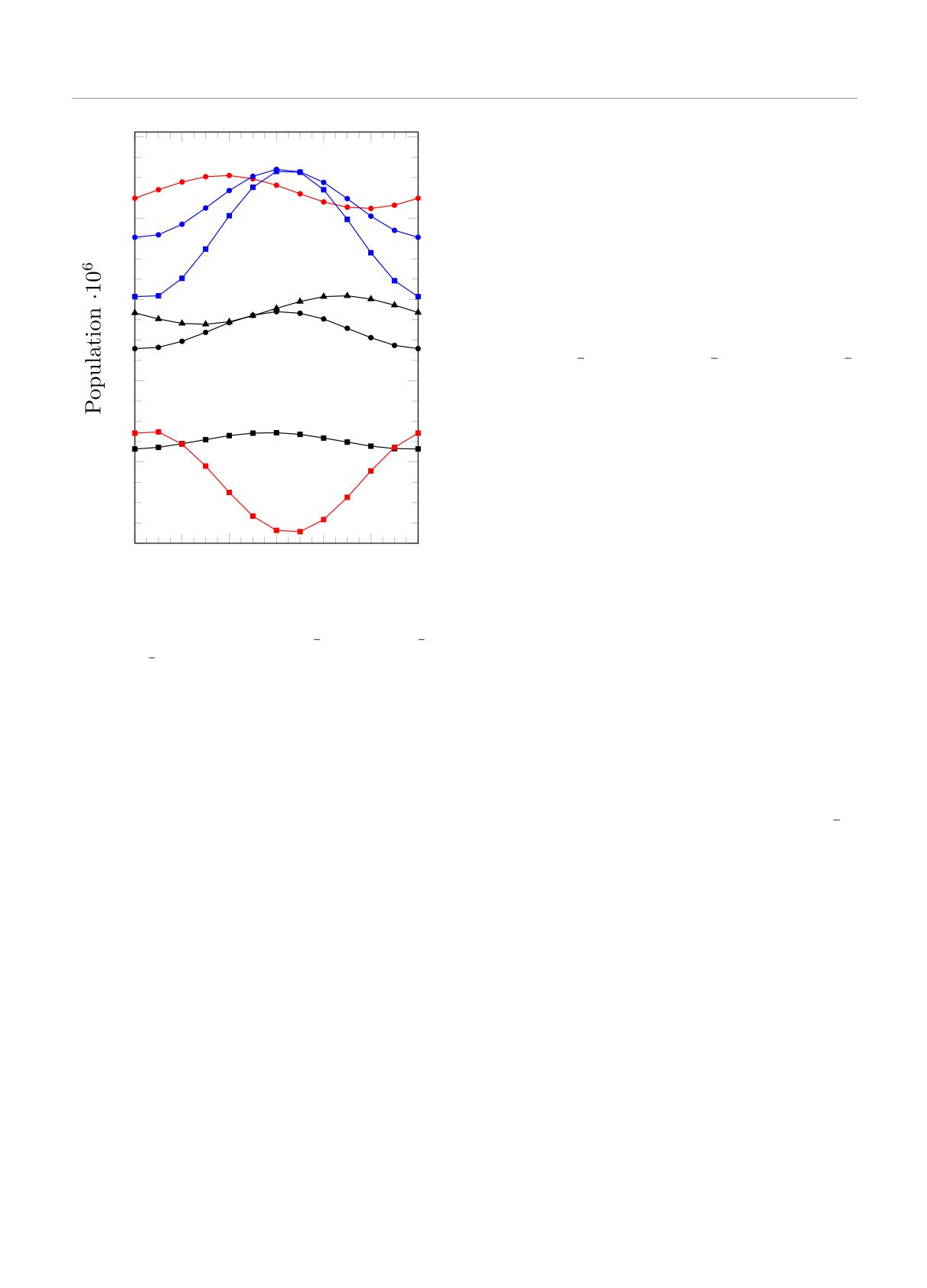
что осцилляции в SB14 будут незначительны (на

рис. 4b они представлены с увеличением в 5 раз).

Вероятность эмиссии электрона при каждой

SB14

энергии зависят от φ_ir как cos(φ_max - φ_ir ), где

φ_max фаза, при которой величина боковой линии

максимальна. Для расчетов по ТВ эта зависимость

ML15

следует из

(18)-(23). Для РСУ это необходимо

проверить, так как высшие порядки могут давать

вклады, осциллирующие в два, четыре и более

ML17

раз быстрее. На рис. 6 приведены зависимости

3d3D

от фазы для заселенности дискретных состояний

3d1P

2p⁵²(P_3/2)3d[¹² ],

2p⁵²(P_3/2)3d[³² ],

2p⁵²(P_1/2)3d[³² ]

и различных линий (SB14, ML15, SB16) в непре-

рывном спектре, интегрированных по энергии.

SB16

Видно, что при данной интенсивности ИК-поля

зависимость от фазы хорошо аппроксимируется

3d3P

косинусом. Анализ методом наименьших квадратов

показал, что аппроксимация расчетов косинусом

осуществляется с относительной точностью вы-

ше, чем 10-2, кроме линии SB14, где точность

порядка 0.1.

120 150 180

Поскольку при любой фиксированной энергии

зависимость от фазы ИК-поля φ_ir представляется

φ_ir, deg

косинусом, двумерный рис. 3b сводится к одномер-

Рис.

6. Зависимости от фазы ИК-поля заселенности

ному, т. е. зависимости амплитуды осцилляций и их

дискретных состояний

2p⁵²P_3/23d[¹

2p⁵²P_3/23d[³

] и

фазы от энергии. На рис.7 эти зависимости приве-

2p⁵²P_1/23d[³

], обозначенных по лидирующей конфигура-

дены для пяти разных длин волн затравочного ИК-

ции как³P,¹P и³D соответственно, и состояний непре-

поля: поскольку изменение длины волны проявля-

рывного спектра SB14, ML15, SB16, проинтегрированных

ется только для нижних линий SB14 и ML15, весь

по энергии (площадь соответствующего пика). Символами

спектр приведен только для энергии ИК-фотона

отмечены значения фаз, при которых проводился расчет

800 нм. Некоторый намек на дублетную структуру,

яний непрерывного спектра в припороговую боко-

особенно заметный при λ = 798 и 800 нм, является

вую линию SB14 крайне мала. Для двухфотонных

проявлением тонкого расщепления порога иониза-

переходов, идущих с поглощением ИК-фотона, до-

ции 2p⁵²P_3/2,1/2 при ионизации, идущей преимуще-

минируют амплитуды перехода в f-волну, для иду-

ственно через верхнюю компоненту 2p⁵(²P_1/2)3d[³² ]₁;

щих с испусканием в p-волну (см. рис. 3) в со-

при увеличении длины волны начинают эффектив-

ответствии с обобщением тенденции Фано (Fano’s

но возбуждаться и компоненты 2p⁵(²P_3/2)3d[k]₁, ко-

Propensity Rule) [52].

торые преимущественно ионизуются на нижний по-

На рис.5b показано традиционное для

рог 2p⁵²P_3/2. Из-за совпадения величины расщеп-

RABBITT-спектроскопии представление дан-

ления компонент 3d-состояния и порога ионизации

ных: двумерная зависимость величины осцилляций

в спектре остается одна линия. ТВ систематически

от задержки ИК-импульса (фазовый сдвиг) и

недооценивает переходы через континуум в ниж-

энергии фотоэлектрона (спектр при данной вели-

нюю ML15 при любой энергии затравочного ИК-

чине задержки с вычетом усредненного по фазе

поля и в меньшей степени в нижнюю SB14. Величи-

ИК-импульса спектра). Амплитуда осцилляций

на и форма последнего, очевидно, оказывается наи-

растет с ростом энергии фотоэлектрона, а фазы

более чувствительной к небольшим изменениям час-

отличаются для различных линий, причем в ML

тоты и является максимальной для 802 нм. В ТВ

и SB практически противоположны. Поскольку

фаза осцилляций резко меняется для разных ком-

для эффективной интерференции и значительных

понент резонанса, что является одним из проявле-

осцилляций необходим сопоставимый вклад от

ний теоремы Левинсона о связи асимптотического

переходов, происходящих с поглощением (N) + 1 и

поведения амплитуды с числом связанных состоя-

испусканием (N + 2) - 1 ИК-фотонов, то ожидаемо,

ний [53, 54].

305

М. М. Попова, С. Н. Юдин, Е. В. Грызлова и др.

ЖЭТФ, том 163, вып. 3, 2023

798 nm

800 nm

802 nm

804 nm

806 nm

1.5

3.0

1.0

0.5

2.0

ML17

0.0

B18

1.0

-0.5

SB14

SB1

L15

-1.0

0.0

2 0

Electron energy, eV

Рис. 7. Величины осцилляций (синие линии и точки) и их фазы (черные линии и точки), рассчитанные по ТВ и РСУ

для Eir = 5 · 10^-3 ат. ед., для различных длин волн затравочного ИК-поля. Результаты ТВ представлены сплошными

кривыми, результаты РСУ точками

7. ЗАКЛЮЧЕНИЕ

вания Российской Федерации (проект №0818-2020-

0005) с использованием вычислительных ресурсов

В работе представлены два подхода для описа-

ЦКП ¾Центр данных ДВО РАН¿. Исследования в

ния ионизации атомов комбинированным многоча-

разд. 5 выполнены при финансовой поддержке Рос-

стотным полем ИК-лазера и его высших гармоник:

сийского научного фонда (проект № 21-42-04412).

основанный на нестационарной теории возмущений

по третий порядок включительно и основанный на

решении системы скоростных уравнений.

ЛИТЕРАТУРА

Проведены демонстрационные расчеты для

ионизации атома неона при параметрах полей, ти-

1. M. Lewenstein, Ph. Balcou, M.Yu. Ivanov et al.,

пичных для современной RABBITT-спектроскопии.

Phys. Rev. A 49, 2117 (1994).

Получены спектры фотоэлектронов для различ-

ных времен задержки (фазового сдвига) ИК-поля

2. А.Ф.Стержантов,М.Ю.Рябикин,В.В.Стрел-

относительно ВУФ-гармоник. Определены вели-

ков, В. Т. Платоненко, УФН 186, 449 (2016).

чины и фазы осцилляций RABBITT для энергий

3. F. Krausz and M. Ivanov, Rev.Mod.Phys. 81,

электронов от порога до 7 эВ.

163 (2009).

Показано, что при современных интенсивностях

полей теория возмущений применима для описания

4. P.M. Paul, E.S. Toma, P. Breger et al., Science

фотоэлектронных спектров в области гладкого кон-

292, 1689 (2001).

тинуума, но гораздо хуже воспроизводит поведение

5. R. Pazourek, S. Nagele, and J. Burgdörfer,

примыкающих к порогу основной и боковой линий.

Faraday Discuss 163, 353 (2013).

Показано, что возбуждение дискретных состоя-

ний с последующей ионизацией механизм, ответ-

6. J. Vos, L. Cattaneo, S. Patchkovskii et al.,

ственный за формирование припороговой боковой

Science 360, 1326 (2018).

линии приводит к ее резкому отличию от осталь-

7. M. Ossiander, J. Riemensberger, S. Neppl et al.,

ных. Резонансный механизм обусловливает сильную

Nature 361, 374 (2018).

зависимость припороговой линии от частоты ИК-по-

ля, проявляющуюся как в формировании и измене-

8. G. Sansone, E. Benedetti, F. Calegari et al.,

нии ее структуры, так и в скачкообразном измене-

Science 314, 443 (2006).

нии фазы осцилляций.

9. E. Goulielmakis, M. Schultze, M. Hofstetter

Финансирование. Работы в разд. 2-4 выполне-

et al., Science 320, 1614 (2008).

ны при финансовой поддержке Российского фон-

да фундаментальных исследований (проект № 20-

10. R. López-Martens, K. Varjú, P. Johnsson et al.,

52-12023) и Министерства науки и высшего образо-

Phys. Rev. Lett. 94, 033001 (2005).

306

ЖЭТФ, том 163, вып. 3, 2023

Аттосекундная интерферометрия при участии дискретных состояний

11.

V. V. Strelkov, E. Mével, and E. Constant, New

31.

B.I. Schneider, K.R. Hamilton, and K. Barts-

J.Phys. 10, 083040 (2008).

chat, Atoms 10, 26 (2022).

12.

E. Constant, V. D. Taranukhin, A. Stolow, and

32.

O. Zatsarinny, Comput.Phys.Commun. 174, 273

P. B. Corkum, Phys. Rev. A 56, 3870 (1997).

(2006).

13.

M. Hentschel, R. Kienberger, Ch. Spielmann

33.

T. Mercouris, Y. Komninos, S. Dionissopoulou,

et al., Nature 414, 509 (2001).

and C. A. Nicolaides, J. Phys. B 29, 13 (1996).

14.

J. Itatani,

F. Quéré, G. L. Yudin et al.,

34.

S. A. Novikov and A. N. Hopersky, J. Phys. B 44,

Phys. Rev. Lett. 88, 173903 (2002).

235001 (2011).

15.

M. Schultze, M. Fieß, N. Karpowicz et al., Science

35.

M. Swoboda, T. Fordell, K. Klünder et al.,

328, 1658 (2010).

Phys. Rev. Lett. 104, 103003 (2010).

16.

Y. Mairesse, A. de Bohan, L. J. Frasinski et al.,

36.

D. M. Villeneuve, P. Hockett, M. J. J. Vrakking,

Science 302, 1540 (2003).

and H. Niikura, Science 356, 1150 (2017).

17.

K. Klünder, J.M. Dahlström, M. Gisselbrecht

et al., Phys.Rev.Lett. 106, 143002 (2011).

37.

K.R. Hamilton, K. Bartschat, M. Moioli et al.,

in MPS-2022 International Conference on Many

18.

L. Cattaneo, J. Vos, M. Lucchini et al.,

Particle Spectroscopy of Atoms, Molecules,

Opt. Express 24, 29060 (2016).

Clusters and Surfaces, Book of Abstracts, 13,

Turku, Finland (2022).

19.

V. Véniard, R. Ta¨ıeb, and A. Maquet, Phys.

Rev. A 54, 721 (1996).

38.

M. Kotur, D. Guenot,

Á. Jiménez-Galán et al.,

20.

Н. Б. Делоне, В. П. Крайнов, Нелинейная

Nature Comm. 7, 10566 (2016).

ионизация атомов лазерным излучением, Физ-

39.

V. Gruson, L. Barreau,

Á. Jiménez-Galan et al.,

матлит, Москва (2001).

Science 354, 734 (2016).

21.

M. Isinger, D. Busto, S. Mikaelsson et al., Phil.

Trans. Roy. Soc. A: Math. Phys. Eng. Sci.

377,

40.

M. A. Fareed, V. V. Strelkov, M. Singh et al.,

20170475 (2019).

Phys. Rev. Lett. 121, 023201 (2018).

22.

J. Benda, Z. Maš´ın, and J. D. Gorfinkiel, Phys.

41.

Á. Jiménez-Galán, L. Argenti, and F. Martın,

Rev. A 105, 053101 (2022).

Phys. Rev. Lett. 113, 263001 (2014).

23.

E. Lindroth and J.M. Dahlström, Phys. Rev. A

42.

B. Ghomashi, N. Douguet, and L. Argenti, Phys.

96, 013420 (2017).

Rev. A 99, 053407 (2019).

24.

J. Vinbladh, J.M. Dahlström, and E. Lindroth,

43.

Д.А. Варшалович, В.К. Херсонский, Е.В. Ор-

Phys. Rev. A 100, 043424 (2019).

ленко, А. Н. Москалев, Квантовая теория уг-

лового момента и ее приложения, т. 1, Физ-

25.

P. K. Maroju, C. Grazioli, M. D. Fraia et al.,

матлит, Москва (2017).

Nature 578, 386 (2020).

26.

A. Harth, N. Douguet, K. Bartschat et al.,

44.

I. I. Sobelman, Atomic Spectra and Radiative

Phys. Rev. A 99, 023410 (2019).

Transitions, Springer, Berlin-Heidelberg (1992).

27.

A. S. Kheifets and A. W. Bray, Phys. Rev. A 103,

45.

С. Н. Юдин, С. М. Бурков, А. Н. Грум-Гржи-

L011101 (2021).

майло, М. Д. Киселев, В. И. Севериненко, Сви-

детельство о государственной регистра-

28.

D. Bharti, D. Atri-Schuller, G. Menning et al.,

ции программы для ЭВМ,

№2021681060 от

Phys. Rev. A 103, 022834 (2021).

17.12.2021 г.

29.

A. Kheifets, Atoms 9, 66 (2021).

46.

M. M. Popova, E. V. Gryzlova, M. D. Kiselev, and

30.

J.M. Dahlström, A. L’Huillier, and J. Maurits-

A. N. Grum-Grzhimailo, Symmetry

13,

1015

son, J.Phys.B 44, 095602 (2011).

(2021).

307