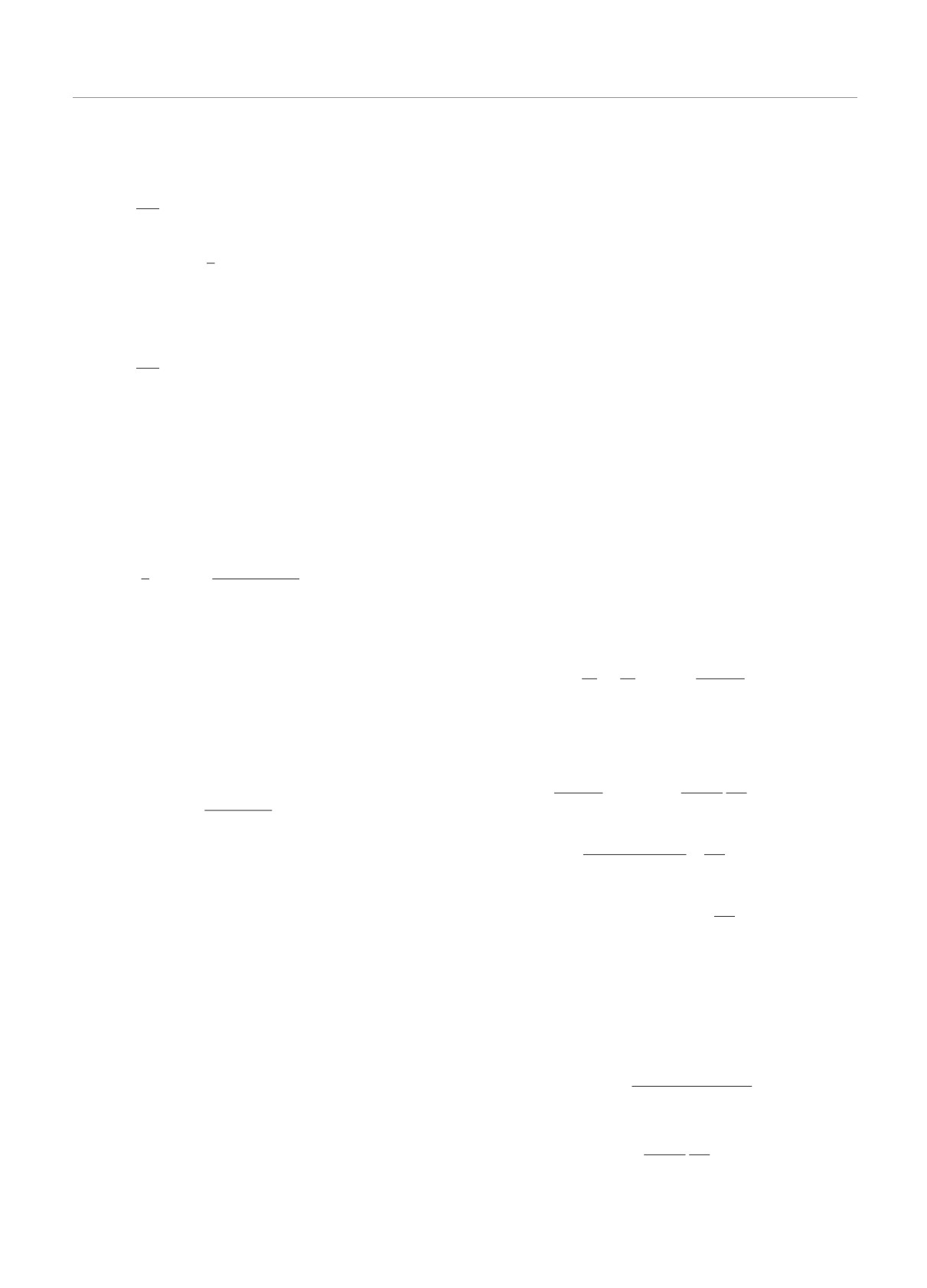ЖЭТФ, 2023, том 163, вып. 3, стр. 321-334

ВЗАИМОДЕЙСТВИЕ ДВУХ ЗАРЯЖЕННЫХ

ДИЭЛЕКТРИЧЕСКИХ ШАРОВ С ТОЧЕЧНЫМ ЗАРЯДОМ

М. М. Родин, А. В. Филиппов^*

Московский физико-технический институт (национальный исследовательский университет)

141701, Долгопрудный, Московская обл., Россия

ГНЦ РФ Троицкий институт инновационных и термоядерных исследований

108840, Троицк, Москва, Россия

Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

Поступила в редакцию 11 октября 2022 г.,

после переработки 2 ноября 2022 г.

Принята к публикации 4 ноября 2022 г.

Рассмотрена задача о взаимодействии трех заряженных частиц, размером одной из которых можно пре-

небречь. Методом разложения по шаровым гармоникам найдены уравнения для коэффициентов разложе-

ния потенциала электрического поля. Получены выражения для декартовых компонент силы и момента

силы взаимодействия. Показано, что несмотря на нарушение аксиальной симметрии при добавлении тре-

тьей частицы, при равномерной зарядке частицы сферической формы все компоненты вектора момента

силы, действующей на нее, равны нулю. Путем выделения вкладов зарядов-изображений в явном виде

получены формулы для поверхностной плотности заряда и силы взаимодействия частиц. Исследованы

условия возникновения притяжения между одноименно заряженными сферическими частицами в зави-

симости от положения точечной.

DOI: 10.31857/S0044451023030033

заряженных тел, а также распределение связанных

EDN: QDIKKL

зарядов на поверхностях диэлектриков. Это позво-

ляет, в частности, определить условия возникнове-

ния притяжения между одноименно заряженными

1. ВВЕДЕНИЕ

объектами [16], что является существенным для опи-

сания эволюции таких систем и объяснения наблю-

В природе и технике существует множество при-

даемых в эксперименте эффектов [17].

меров, когда в механизме взаимодействия заряжен-

Во многих работах, посвященных теоретическо-

ных макроскопических объектов электростатиче-

му исследованию взаимодействия двух диэлектри-

ская сила играет главенствующую роль. К таким

ческих частиц, поставленная задача решалась в

системам относятся заряженные пылевые частицы в

бисферической системе координат (см., например,

космосе [1], заряженные аэрозоли в атмосферах пла-

[7, 9, 16, 18-20]). Известны также результаты рас-

нет и спутников [2-4], частицы конденсированной

четов в сферической системе координат методом

дисперсной фазы в плазме и электролитах [5], части-

переразложения [11, 18, 19, 21], методом изображе-

цы порошковых красок [6] и ряд других. В качестве

ний [18,19] и численные решения методом конечных

модели чаще всего рассматриваются пары проводя-

элементов Галеркина [6]. В последние годы начаты

щих [7,8] или диэлектрических шаров [9-11], части-

исследования электростатического взаимодействия

цы сфероидальной формы [12, 13], системы, вклю-

многих сферических частиц методом интегральных

чающие в себя точечные частицы [14] или неогра-

уравнений [22-25].

ниченные плоскости [15]. Для выбранной геометрии

В настоящей работе исследуется влияние сосед-

рассчитываются сила и потенциал взаимодействия

них частиц на взаимодействие пары заряженных ди-

электрических частиц. В сферической системе ко-

^* E-mail: fav@triniti.ru

ординат рассматривается система из трех частиц,

321

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

одна из которых для упрощения задачи полагает-

поэтому для разложения достаточно использо-

ся точечной (неполяризуемой). Это означает, что

вать четные по азимутальному углу функции

распределение связанных зарядов на поверхностях

r^-n-1P^mn (cosθ) cosmϕ и rⁿP^mn (cosθ) cosmϕ. Обо-

частиц конечного размера возмущено присутстви-

значив µ = cos θ и µ₂ = cos θ₂, запишем представ-

ем третьей частицы, но перераспределением заря-

ление потенциала внутри диэлектрических частиц:

да на поверхности самой этой частицы можно пре-

∑

небречь, т. е. самосогласованное перераспределение

φ_I(r, µ, ϕ) =

α^m1,nrⁿP^mn(µ)cosmϕ,

плотности заряда затрагивает только две частицы

n=0 m=0

(1)

из трех. Эта упрощенная модель приводит, однако,

∑

φ_II(r₂, µ₂, ϕ) =

α^m2,nrⁿ²P^mn(µ₂)cosmϕ,

к существенным вычислительным трудностям, свя-

n=0 m=0

занным с крайне медленной сходимостью рядов для

электростатического потенциала вблизи поверхно-

где α^m1,n, α^m2,n

коэффициенты разложения. Здесь

стей сферических частиц при малых межчастичных

учтено, что в центрах сферических частиц потен-

расстояниях. В данной работе предлагается метод

циал должен быть конечным. Аналогично, в силу

преодоления этих трудностей на основе аналитиче-

обращения в нуль на бесконечности, разложение по-

ских преобразований рядов, входящих в выражение

тенциала каждой из частиц во внешнем простран-

для электростатического потенциала.

стве имеет вид

∑

P^mn(µ)

φ₁(r, µ, ϕ) =

A^m

n,1

cosmϕ,

(2)

rⁿ⁺¹

2. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ В

n=0 m=0

СФЕРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ

∑

P^mn (µ₂)

φ₂(r₂,µ₂,ϕ) =

B^m

n,2

cosmϕ.

(3)

rⁿ⁺¹

2.1. Электростатический потенциал системы

n=0 m=0

Введем сферическую систему координат (r, θ, ϕ)

Второй нижний индекс коэффициентов указывает

с началом в центре первого диэлектрического ша-

на систему координат, в которой проведено разло-

ра радиусом a₁, полярную ось z направим к цен-

жение.

тру второго шара (его радиус a₂, расстояние меж-

Переразложение потенциалов φ₁, φ₂ во взаимных

ду центрами шаров R), а плоскость xz, соответству-

системах координат реализуется с помощью взаим-

ющую нулю азимутального угла ϕ, проведем через

ного представления шаровых функций, отнесенных

третью точечную частицу (см. рис. 1). На рисунке

к соответствующей системе координат. При r < R

точка наблюдения P определена также через ко-

справедлива формула [26]

ординаты (r₂, θ₂, ϕ₂), связанные со вторым шаром

(в дальнейшем введенные системы координат бу-

P^mn(µ₂)

(-1)^n-m

дем для краткости обозначать соответственно СК1

rⁿ⁺¹²

Rⁿ⁺¹

и СК2); отметим, что СК2 получена из СК1 сдвигом

∑

)_k

(n +k)!

вдоль оси z без изменения ориентации осей, поэто-

P^mk(µ),

(4)

(n -m)! (k +m)! R

му ϕ = ϕ₂. Полные заряды частиц обозначим q₁,

k=m

q₂ и q₀; последняя, точечная, частица имеет коорди-

следовательно, потенциал второй сферической час-

наты (r₀₁, θ₀, ϕ = 0) в СК1 и (r₀₂, θ₀₂, ϕ = 0) в СК2.

тицы в системе координат, связанной с первой, мож-

Положение точки наблюдения P относительно то-

но представить в виде

чечной частицы определяется вектором r₀, который

∑

из центра первого шара виден под углом γ.

φ₂(r, µ, ϕ) =

B^mn,1rⁿP^mn(µ)cosmϕ,

(5)

Для определения электростатического потенци-

n=0 m=0

ала системы воспользуемся методом разложения

где

потенциалов сферических частиц по шаровым

функциям в собственных системах координат

∑

(-1)^k-m (k + n)! B^k,2

B^mn,1 =

(6)

с последующим переразложением для удобства

Rⁿ

(k - m)! (n + m)! R^k+1

k=m

подстановки в граничные условия. Данный ме-

тод использовался, например, в работах [11, 16],

Аналогично, при r₂ < R

в которых решалась аксиально-симметричная

∑

задача. В рассматриваемой нами геометрии име-

φ₁(r₂, µ₂, ϕ) =

A^mn,2rⁿ²P^mn(µ₂)cosmϕ,

(7)

ет место симметрия относительно плоскости xz,

n=0 m=0

322

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

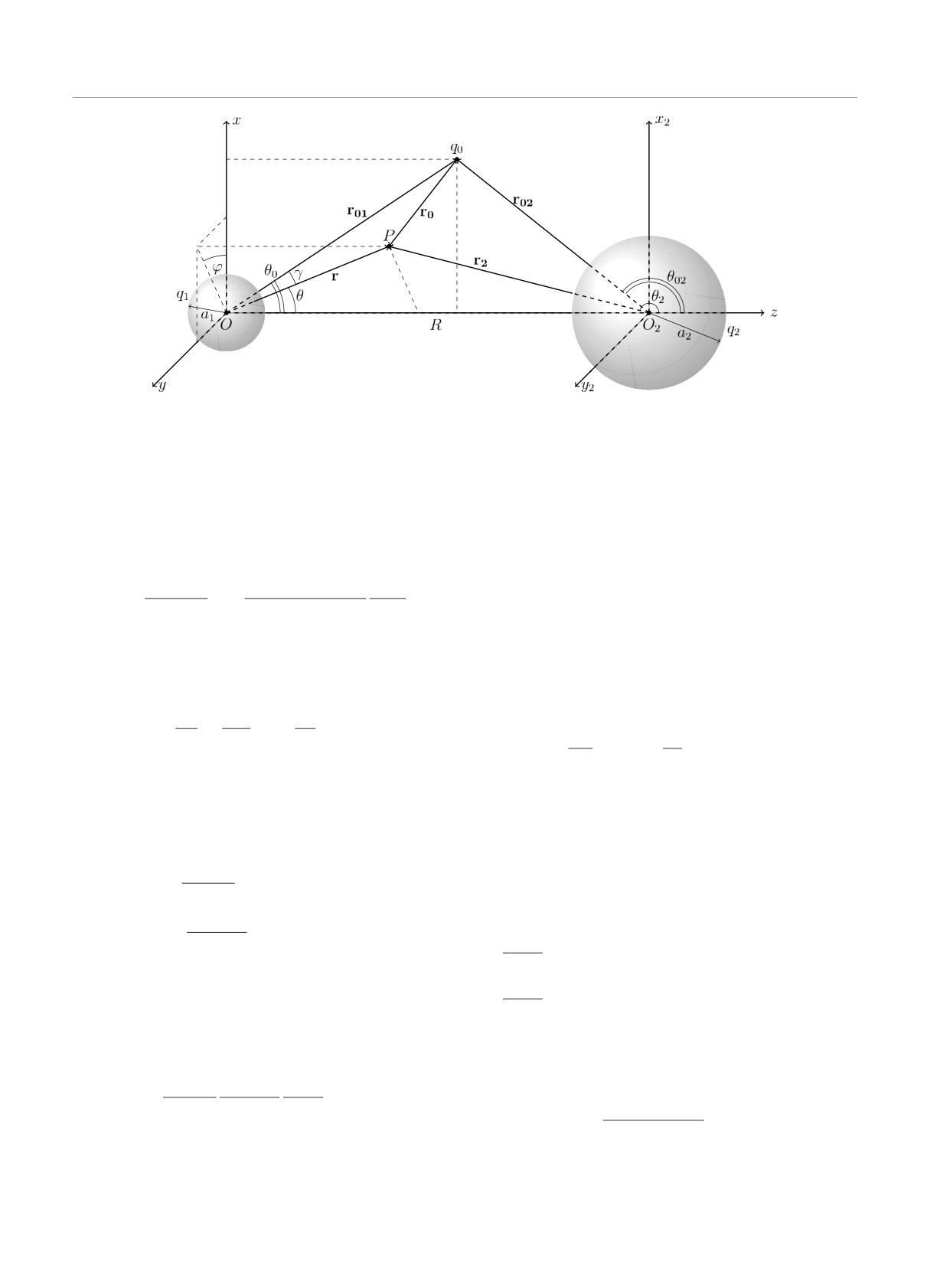
Рис. 1. Геометрия задачи о взаимодействии двух сферических шаров с точечным зарядом q0; O центр первой мак-

рочастицы с радиусом a1 и зарядом q1, O2 центр второй макрочастицы с радиусом a2 и зарядом q2; r, θ и r01, θ0

радиус-вектор, полярный угол точки наблюдения P и координаты точечного заряда в сферической системе координат с

полюсом в точке O и с осью, направленной к O2; r2, θ2 и r02, θ02 радиус-вектор, полярный угол точки наблюдения

P и координаты точечного заряда в сферической системе координат с полюсом в центре второй макрочастицы; R

расстояние между центрами макрочастиц, r0 расстояние между точечным зарядом и точкой наблюдения

где

Суммарный потенциал φ, полученный как супер-

позиция (2), (5) и (11),

n-m

∑

A^mk,1

(-1)

(k + n)!

A^mn,2 =

(8)

Rⁿ

(k - m)! (n + m)! R^k+1

φ=φ₀ +φ₁ +φ₂,

(13)

k=m

Наконец, найдем выражение для потенциала

и потенциал φ_I из (1) должны удовлетворять гра-

третьей частицы в системах координат, связанных

ничным условиям, которые на границе однородных

с первыми двумя. При r < r₀₁ имеем

диэлектриков имеют вид

(

)_n

∑

φ_I|_r=a

= φ|

q₀

r=a1

φ₀ ≡

P_n(ν) .

(9)



(14)

εr₀

εr₀₁

r₀₁

∂φ_I

∂φ

n=0



ε₁

-ε

= 4πσ_1,f .



∂r

r=a1

Здесь мы воспользовались производящей функци-

ей многочленов Лежандра; ν = cosγ, ε диэлек-

Здесь ε₁

диэлектрическая проницаемость мате-

трическая проницаемость среды. Согласно теореме

риала первого шара, σ_1,f

плотность свободного

сложения [27],

заряда на его поверхности. Считая, что свободный

заряд на сферических частицах распределен равно-

∑

мерно, из уравнений (14), дополненных аналогичны-

P_n(ν) =

1+δ_m0

ми для второй частицы, получаем систему уравне-

m=0

ний (n = 0, 1, . . ., m = 0, 1, . . . , n):

(n - m)!

P^mn(µ₀)P^mn(µ)cosmϕ,

(10)

(n + m)!

n,1

+ β_1,nB^mn,1 = 4πσ_1,fa₁δ_n0 - β_1,nC^mn,1,

a²ⁿ⁺¹

где δ_m0

символ Кронекера. Следовательно, в СК1

(15)

B^mn,2

∑

+ β_2,nA^mn,2 = 4πσ_2,fa₂δ_n0 - β_2,nC^mn,2,

2n+1

φ₀(r, µ, ϕ) =

C^mn,1rⁿP^mn(µ)cosmϕ,

(11)

n=0 m=0

где C^mn,2

коэффициенты разложения φ₀ в СК2,

где

аналогичные (12); β_1,n, β_2,n коэффициенты, опре-

деленные соотношениями

(n - m)! q₀

C^mn,1 =

P^mn(µ₀).

(12)

1 + δ_m0 (n + m)! εrⁿ⁺¹

n (ε_i - ε)

β_i,n =

i = 1,2;

(16)

nε_i + (n + 1)ε

Выражение для φ₀(r₂, µ₂, ϕ) будет отличаться толь-

ко индексами.

ε_i

проницаемость i-го диэлектрического шара.

323

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

(

)

Из системы (15) с учетом (6), (8) можно найти

f_1y =

sin θ sin ϕ

E^2r - E^2θ - E^2ϕ

коэффициенты разложения A^mn,1, B^mn,2 потенциалов

4π

шаров в собственных системах координат. При этом

]



для монопольных членов из (15) следуют явные ре-

+ cosθ sinϕE_rE_θ + cosϕE_rE_ϕ



(21)



шения:

r=a1

4πσ_1,f a²¹

q₁

A_0,1 =

≡

(

)

(17)

f_1z =

cosθ

E^2r - E^2θ - E^2ϕ

4πσ_2,f a²²

q₂

4π

B_0,2 =

≡

]



- sinθE_rE_θ

(22)



r=a1

2.2. Плотность поверхностного заряда

Здесь E_r, E_θ, E_ϕ компоненты электрического по-

В ряде работ [11, 16] было показано, что одно-

ля E = -∇φ вдоль ортов СК1.

именно заряженные тела на близких расстояниях

Полную силу получим интегрированием выра-

могут испытывать притяжение вследствие перерас-

жений (20)-(22) по поверхности первой сферы. Ис-

пределения заряда на их поверхностях. При этом

пользуя известные интегралы от выражений, содер-

вклад в отталкивание всегда дает свободный заряд,

жащих присоединенные функции Лежандра, прихо-

распределение которого σ_i,f (i = 1, 2) мы считаем

дим к следующим формулам для компонент силы:

равномерным. Получим выражение для плотности

связанных зарядов σ_i,b = σ_i -σ_i,f , возмущение кото-

∑

(n + m + 2)!

F_1x = -

(1 + δ_m0)

рой может вызвать притяжение. Плотность полного

(n - m)!

n=0 m=0

заряда σ₁ на поверхности диэлектрика определяется

[

(

)

скачком напряженности электрического поля:

× A^mn,1

B^m+1n+1,1 + C^m+1n+1,1



∂φ_I

∂φ

4πσ₁



(18)

(

)]



∂r

−A^m+1n+1,1

B^mn+2,1 + C^mn+2,1

r=a1

(23)

В итоге из выражений (14) и (18) имеем

F_1y = 0,

∑

A^mn,1

σ_1,b =

(2n + 1)

P^mn(µ)cosmϕ.

(19)

∑

∑1+δ

(n + m + 1)!

4π

aⁿ⁺²¹

n=1 m=0

F_1z = -ε

(n - m)!

n=0 m=0

Отметим, что, подставив в эту формулу A^mn,1 из

(

)

первого уравнения системы (15), можно разделить

×A^mn,1

B^mn+1,1 + C^mn+1,1

вклады второй сферической и точечной частиц в

плотность заряда на первой (они будут выражаться

Полученные выражения позволяют рассмотреть

рядами с общим членом, пропорциональным соот-

вклады второго шара и точечной частицы независи-

ветственно B^mn,1 и C^mn,1). Для второго шара справед-

мо. Последний мы бы могли найти, взяв с обратным

ливы аналогичные соображения.

знаком величину проекции силы, с которой первая

сферическая частица действует на точечную:

2.3. Сила взаимодействия

F⁽¹⁾⁰ = -q₀ ∇φ₁|

(24)

r=r01

Найдем теперь составляющие силы, действую-

щей на первый диэлектрический шар. На элемент

поверхности частицы действует сила, определяемая

2.4. Момент силы взаимодействия

максвелловским тензором натяжений [28], проекции

В ряде работ (см., например, [29-37]) было экспе-

которой в декартовой системе координат имеют вид

риментально обнаружено собственное вращение пы-

(

)

левых частиц в пылевой плазме. В работе [14] бы-

f_1x =

sin θ cos ϕ

E^2r - E^2θ - E^2ϕ

4π

ло показано, что к этому может приводить неодно-

]

родное распределение свободного заряда на поверх-



ности пылевой частицы. Поэтому получим выраже-

+ cosθ cosϕE_rE_θ - sinϕE_rE_ϕ

(20)



r=a1

ние для момента силы электростатического взаимо-

324

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

действия, действующей на первую частицу, который

на сферической поверхности возникают чередующи-

определяется выражением [28]

еся области противоположных знаков, тем более яв-

ные, чем меньше число учитываемых членов в ря-

∫

∫π{

εa²¹

дах и чем мельче сетка, в точках которой вычисля-

M₁ =

[r × E] (n · E) -

4π

ется плотность заряда. Для решения этой пробле-

0 0

мы ряды, содержащие коэффициенты разложения

}



потенциала точечной частицы C^mn,1, преобразуем та-

E² [r × n]

sin θ dθ dϕ,

(25)



ким образом, чтобы под знаком суммы не оставалось

r=a1

медленно сходящихся членов.

где n вектор нормали к поверхности первой сфе-

ры. Отсюда с учетом того, что n = e_r, находим

∫



3. ВЗАИМОДЕЙСТВИЕ

εa³¹



M₁ =

E_r [E_θe_ϕ - E_ϕe_θ]

ДИЭЛЕКТРИЧЕСКОГО ШАРА И

4π

r=a1

ТОЧЕЧНОГО ЗАРЯДА: ПРОЦЕДУРА

0 0

УСКОРЕНИЯ СХОДИМОСТИ

× sinθ dθ dϕ.

(26)

Интегрируя (26) (интегралы от произведений

Как подчеркивалось выше, выражения

(19)

шаровых функций см. в [38]), для рассматриваемой

и (23) позволяют выделить вклад точечной части-

здесь задачи, симметричной относительно плоско-

цы, вызывающий ухудшение сходимости входящих

сти xz, находим

в них рядов. Покажем, как можно преобразовать

исходные формулы, для чего рассмотрим систему

M_1,x = 0, M_1,z = 0,

(27)

из двух частиц: сферической и точечной.

Будем придерживаться обозначений, принятых в

∑

∑ (n + m + 1)![

(

M_1y =

A^m+1n,1

B^mn,1 +

разд. 2. Исключим из рассмотрения вторую сферу и

(n - m - 1)!

n=1 m=0

положим µ₀ = 1. Известно [18,19], что электростати-

]

)

(

)

ческий потенциал первой диэлектрической частицы

+C^mn,1

-A^mn,1

B^m+1n,1 + C^m+1n,1

(28)

равен

Обращение в нуль x- и z-составляющих момента си-

∑

q₁

q₀

a²ⁿ⁺¹¹

лы в нашей задаче вызвано тем, что плоскость xz

φ₁ =

β_1,n

P_n(µ).

(29)

εr

rⁿ⁺¹⁰¹rⁿ

является плоскостью симметрии и ось вращения мо-

n=1

жет быть только перпендикулярной этой плоскости.

Входящий в это выражение ряд преобразуем следу-

В случае равномерной зарядки первой частицы

ющим образом:

из первого уравнения системы (15) следует равен-

ство

∑

a²ⁿ⁺¹¹

ε₁ - ε a₁

β_1,n

P_n(µ) = -

rⁿ⁺¹⁰¹rⁿ

ε₁ + ε r₀₁

B^mn,1 + C^mn,1 = -

A^mn,1,

n=1

a²ⁿ⁺¹β1,n

[_∞∑

(r^′01)

n ≥ 1,

0 ≤ m ≤ n,

P_n(µ) +

nε₁ + (n + 1)ε rⁿ

n=1

подстановка которого в выражение (28) приводит

]

к обнулению и y-составляющей момента: M_1,y = 0.

∑

(r^′01)ⁿ

Следовательно, при равномерной зарядке рассмат-

+1-

P_n(µ) ,

(30)

rⁿ

n=0

риваемой частицы присутствие третьей точечной

частицы, нарушающей аксиальную симметрию за-

где r^′01

расстояние, определяющее инверсный об-

дачи, не может приводить к возникновению ее соб-

раз точки, в которой находится заряд q₀, относи-

ственного вращения.

тельно поверхности сферы: r^′01 = a²¹/r₀₁. Тогда, по

В заключение данного раздела отметим, что

определению производящей функции, ряд в послед-

непосредственное использование формул (19), (23),

нем слагаемом при r > r^′01 равен 1/r^′0, где r^′0 рас-

как показали расчеты, в области малых межча-

стояние от образа до точки наблюдения (см. рис.2):

стичных расстояний приводит к сильному сниже-

√

нию точности. Особенно это заметно при визуали-

r^′0 = r² + r^′201 - 2rr^′01µ.

зации распределения заряда по поверхности сфери-

Обозначив

ческой частицы, где из-за близости точечного заря-

ε₁ - ε a

q^′0 =

q₀,

(31)

да и вызванного им дельтообразного пика плотности

ε₁ + ε r₀₁

325

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

Рис. 2. Положение зарядов-изображений, возникающих

при взаимодействии сферической и точечной частиц

Рис. 3. Потенциал шара при r = a1 + 0.5L в зависимости

из (29), (30) получим

от полярного угла θ, найденный по формулам (29) и (32)

(кривые 1 и 2 соответственно) при a1 = 1 мкм, q1 = 10²e,

q₁

q^′0

ε1 = 25, q0 = 50e

φ₁ =

εr

εr^′

мулу для силы, которая, как ожидается, будет да-

∑

q^′0

(r^′01)ⁿ

P_n(µ).

(32)

вать лучшую сходимость:

εr

nε₁ + (n + 1)ε r

n=1

q₀q₁

q₀q^′0

F =

Таким образом, из ряда в (29) мы в явном виде выде-

εr²⁰¹

ε (r₀₁ - r^′01)²

лили вклады двух зарядов-изображений: +q^′0 в цен-

тре сферы и -q^′0 на расстоянии r^′01 от него. Отметим,

q₀q^′0

∑

(n + 1) ε

(a₁ )²ⁿ.

(34)

что общий член ряда в преобразованном выражении

εr²

nε₁ + (n + 1)ε r₀₁

01 n=1

(32) при r₀₁ ≃ a₁ убывает на порядок быстрее по

сравнению с исходным (29).

Второе и третье слагаемые в (34) соответствуют ку-

лоновскому взаимодействию точечного заряда q₀ с

Преимущество в скорости сходимости потенциа-

двумя его изображениями, причем третье слагае-

ла, рассчитанного по новой формуле, продемонстри-

мое быстро растет по абсолютной величине по мере

ровано на рис. 3. Здесь L расстояние между по-

сближения сферической и точечной частиц, что на

верхностью диэлектрического шара и точечным за-

достаточно малых межчастичных расстояниях при-

рядом: L = r₀₁ - a₁. На рис. 3 дана угловая зави-

водит к переходу от отталкивания одноименных за-

симость потенциала при r = a₁ + L/2. Видно, что

рядов к их притяжению.

модифицированная формула для потенциала обес-

Из табл.1 видно, что расчеты по формуле (34)

печивает большую устойчивость, особенно в обла-

с учетом всего нескольких первых членов ряда уже

сти, близкой к полярной оси.

приводят к результату, отличающемуся от оконча-

Из выражения (29) можно получить известную

тельного только в третьей-четвертой значащей циф-

формулу для силы взаимодействия [18]:

ре. Для достижения такой точности при расчетах

с использованием исходной формулы (33), если L

q₀q₁

F =

достаточно мало, может потребоваться вплоть до

εr²

нескольких тысяч членов.

q²⁰

∑

n (n + 1) (ε₁ - ε)

(a₁ )²ⁿ⁺¹

Отметим, что задача, поставленная в данной

(33)

εr²⁰¹

nε₁ + (n + 1)ε r₀₁

n=1

работе, предполагает решение системы линейных

уравнений (15) с матрицей порядка (N -m)×(N -m)

(положительное значение силы соответствует оттал-

для каждого m = 0, 1, . . . , M (в силу отсутствия

киванию, отрицательное притяжению). Исполь-

аксиальной симметрии), причем максимальное зна-

зуя выражение (32), находим альтернативную фор-

чение M ≤ N определяется скоростью убывания

326

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

Таблица 1. Сравнение расчетов по формулам (33) и (34) для силы взаимодействия сферической и точечной частиц при

q1 = 10²e, a1 = 1 мкм, ε1 = 25, q0 = 50e для межчастичных расстояний L1 = 1 нм, L2 = 10² нм и L3 = 10⁴ нм

100

1000

7000

L = 1нм

Из (33) в 10^-7 Н

-3.26 · 10^-4

-2.39 · 10^-2

-0.79122

-1.33087

Из (34) в 10^-8 Н

-1.33099

-1.33097

-1.33090

-1.33089

100

L = 100нм Из (33) в 10-11 Н

-4.88 · 10^-2

-0.32216

-1.07034

-1.18280

Из (34) в 10^-11 Н

-1.18865

-1.18592

-1.18297

-1.18280

L = 104 нм Из (33) в 10-15 Н

9.52701

9.52693

Из (34) в 10^-15 Н

9.52693

коэффициентов (12). Это накладывает определен-

4. СИЛА ВЗАИМОДЕЙСТВИЯ ПРИ a2/R ≪ 1

ные ограничения на количество учитываемых чле-

Рассмотрим случай, когда в поляризацию по-

нов разложения N; в финальных расчетах мы по-

верхностного заряда первой частицы основной

ложили N = 40. Как видно из полученных в этом

вклад от второй частицы вносит монопольный

разделе данных, этого вполне достаточно для дости-

член разложения потенциала этой частицы, а

жения приемлемой точности при вычислении вкла-

вкладом более высоких мультипольных моментов

да точечного заряда в силу взаимодействия.

можно пренебречь. Такой случай реализуется при

Получим теперь выражение для плотности свя-

a₂/R ≪ 1. В этом случае в разложении (6) коэф-

занных зарядов на поверхности сферической части-

фициента B^mn,1 остается только B_0,2, поэтому все

цы, находящейся в поле точечного заряда. Выраже-

коэффициенты с m ≥

1 исчезают: Bmn,1 = 0, а

ние (19) с учетом вида потенциала (29) в данном

коэффициенты для m = 0 с учетом (17) принимают

случае переходит в следующее:

вид

q₂

)n+1

q₀

∑

(a₁

B_n,1 =

(36)

σ_1,b = -

(2n + 1) β_1,n

P_n(µ).

εRⁿ⁺¹

4πa²¹

r₀₁

n=1

Теперь из первого уравнения системы (15) находим

(

)

Проделав преобразования с общим членом ряда,

A^mn,1 = -a²ⁿ⁺¹¹β_1,n

B_n,1δ_m0 + C^mn,1

аналогичные выполненным при получении (30), по-

n = 1,2,...,∞, m = 0,2,...,n.

(37)

сле некоторых алгебраических преобразований фор-

мулы для производящей функции приходим к сле-

На основе найденного приближенного решения, для

дующему выражению:

составляющих силы взаимодействия из (23) полу-

[

(

)

чим выражения

q^′0

r₀₁

r²⁰¹ - a²

σ_1,b =

q₀q₁

4πa²¹

(a²¹ + r²⁰¹ - 2a₁r₀₁µ)^3/2

F_1x ≈ -

P¹¹ (µ₀) -

εr²⁰¹

]

(

)

∑

(2n + 1) ε

(aⁿ¹ )ⁿ

q₀

(ε₁ - ε)

a³¹

a³

P_n(µ)

(35)

P¹¹ (µ₀)

P₂ (µ₀)

nε₁ + (n + 1)ε r₀₁

εr²⁰¹

ε₁

+ 2ε

q₂ R3+q0 r3

n=1

(

)

∑

q₀q₂

a²ⁿ⁺¹¹

a²¹

Здесь q^′0 по-прежнему обозначает величину зарядов-

P¹ⁿ⁺¹ (µ₀)

β_1,n -

β_1,n+1

2εr²

rⁿ⁰¹Rⁿ⁺¹

R²

изображений (31). Выражение в знаменателе второ-

01 n=1

го слагаемого в квадратных скобках это рассто-

ε q²⁰

∑a²ⁿ⁺¹¹

яние от q₀ до точки на сфере, задаваемой перемен-

P^m+1n+1 (µ₀) ×

4 εr²

ной µ. Ясно, что при µ = 1 это расстояние тем мень-

01 n=1 m=0 r01+1

ше отличается от нуля, чем ближе точечная частица

[(n - m)!

β_1,nP^mn (µ₀) -

к поверхности сферической. Как показывают расче-

(n + m)!

ты, после выделения этой сингулярности ряд в по-

]

a²¹

(n - m + 2)!

следнем слагаемом (35) сходится достаточно быст-

−

β_1,n+1

P^mn+2 (µ₀) ,

(38)

r²⁰¹

(n + m + 2)!

ро.

327

ЖЭТФ, вып. 3

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

q₁q₂

q₁q₀

действует вторая, будем находить согласно (23) по

F_1z ≈ -

P₁ (µ₀) +

εR²

εr²

формуле

∑

q²²

a²ⁿ⁺¹¹

∑

∑ 1 + δ_m0 (n + m + 1)!

(n + 1) β_1,n

F^(2)1z = -ε

εR²

R²ⁿ⁺¹

n=1

(n - m)!

n=0 m=0

q₀q₂

∑

aⁿ¹

×A^mn,1B^mn+1,1.

(41)

(n + 1) β_1,n

εr₀₁R

rⁿ

Rⁿ

n=1

Вклад точечной частицы вычислим по формуле

[

]

(24). Для этого в потенциал (2) подставим A^mn,1 из

a₁

P_n (µ₀) +

P_n+1 (µ₀)

первого уравнения системы (15), раскроем скобки и

r₀₁

преобразуем ряд, содержащий коэффициенты C^mn,1,

∑

q²⁰

(n + 1 - m)!

для которых мы имеем явные формулы (12). Это

(1 + δ_m0)β_1,n

2εr²

(n + m)!

приведет нас к выражению, аналогичному (32) и пе-

01 n=1 m=0

реходящему в него при m = 0, µ₀ = 1 и B^mn,1 = 0.

a²ⁿ⁺¹¹

Соответствующая сила (взятая с обратным зна-

P^mn (µ₀)P^mn+1 (µ₀).

(39)

r2n+101

ком, чтобы отражать действие точечной частицы на

первую сферическую) оказывается равной

В выражении (38) первый член соответствует x-

составляющей силы взаимодействия “точечных” за-

q₀q^′0

F^(0)1z = -q0q¹µ0 -

µ₀ +

µ₀ -

рядов q₀ и q₁, z-составляющая этой силы второй

εr²⁰¹

ε (r₀₁ - r^′01)²

член в правой части (39). Из (38) видно, что F_1x пря-

∑

мо пропорциональна q₀ и исчезнет, если удалить то-

q₀q^′0

(n - m + 1)!

−

чечную частицу. Отметим, что ценность выражений

εr²

1+δ_m0

(n + m)!

01 n=1 m=0

(38) и (39) заключается в том, что они справедливы

при любом положении третьей точечной частицы,

( a₁ )2n Pmn (µ₀)Pmn+1(µ₀) +

требуется только выполнение условия a₂/R ≪ 1. В

nε₁ + (n + 1)ε r₀₁

этих формулах можно также выделить расходящу-

∑

q₀

юся при малых значениях L₀₁ = r₀₁ - a₁ часть силы

(n - m + 1) βⁿ¹B^mn,1 ×

r²

01 n=1 m=0

взаимодействия, как это было сделано в разд.3.

Рассмотрим более простой случай расположе-

a²ⁿ⁺¹¹

P^mn+1(µ₀).

(42)

ния зарядов, когда точечный заряд лежит на оси z

rⁿ

и задача становится аксиально-симметричной. При

Полная сила, действующая на первый диэлектриче-

этом θ = 0 или π и µ₀ = ±1. В этом случае x-

ский шар вдоль оси z, есть сумма (41) и (42).

составляющая сила станет равной нулю: F_1x = 0.

Вклад второго шара в силу, действующую на

Для z-составляющей с учетом того, что P_n(1) = 1,

первый вдоль оси x, выделим из выражения (23):

P_n(-1) = (-1)ⁿ, из (39) находим

∑

(n + m + 2)!

(2)

q₁q₂

q₁q₀

F₁

(1 + δ_m0)

F_1z =

µ₀ +

(n - m)!

n=0 m=0

εR²

εr²

(

)

∑

A^mn,1B^m+1n+1,1 - A^m+1n+1,1B^mn+2,1

(43)

(n + 1) β_1,nΨ_nΨ_n+1,

(40)

εa²

Для силы, действующей на первый шар со стороны

1 n=1

точечной частицы вдоль оси x, имеем модифициро-

где величина Ψ_n определена соотношением

ванную формулу:

[

]

aⁿ⁺¹¹

q₀q₁

q₀q^′0

Ψ_n = q₂

+q₀

µⁿ⁰.

F^(0)1x = -

P¹¹ (µ₀) -

Rⁿ⁺¹

rⁿ⁺¹

εr²⁰¹

ε (r₀₁ - r^′01)2

q₀

∑

aⁿ¹

[ (n - m)!

q^′0

aⁿ¹

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

− r²

rⁿ

(n + m)! nε₁ + (n + 1) ε rⁿ

01 n=1 m=0

5.1. Сила взаимодействия

][

1+δ

× P^mn(µ₀) -

βⁿ¹aⁿ⁺¹¹B^mn,1

P^m+1n+1 (µ₀) -

Применим теперь описанную в разд. 3 процеду-

ру к задаче, поставленной в статье. Проекцию силы

]

- (n - m + 1) (n - m + 2) P^m-1n+1 (µ₀)

(44)

на ось z, с которой на первую сферическую частицу

328

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

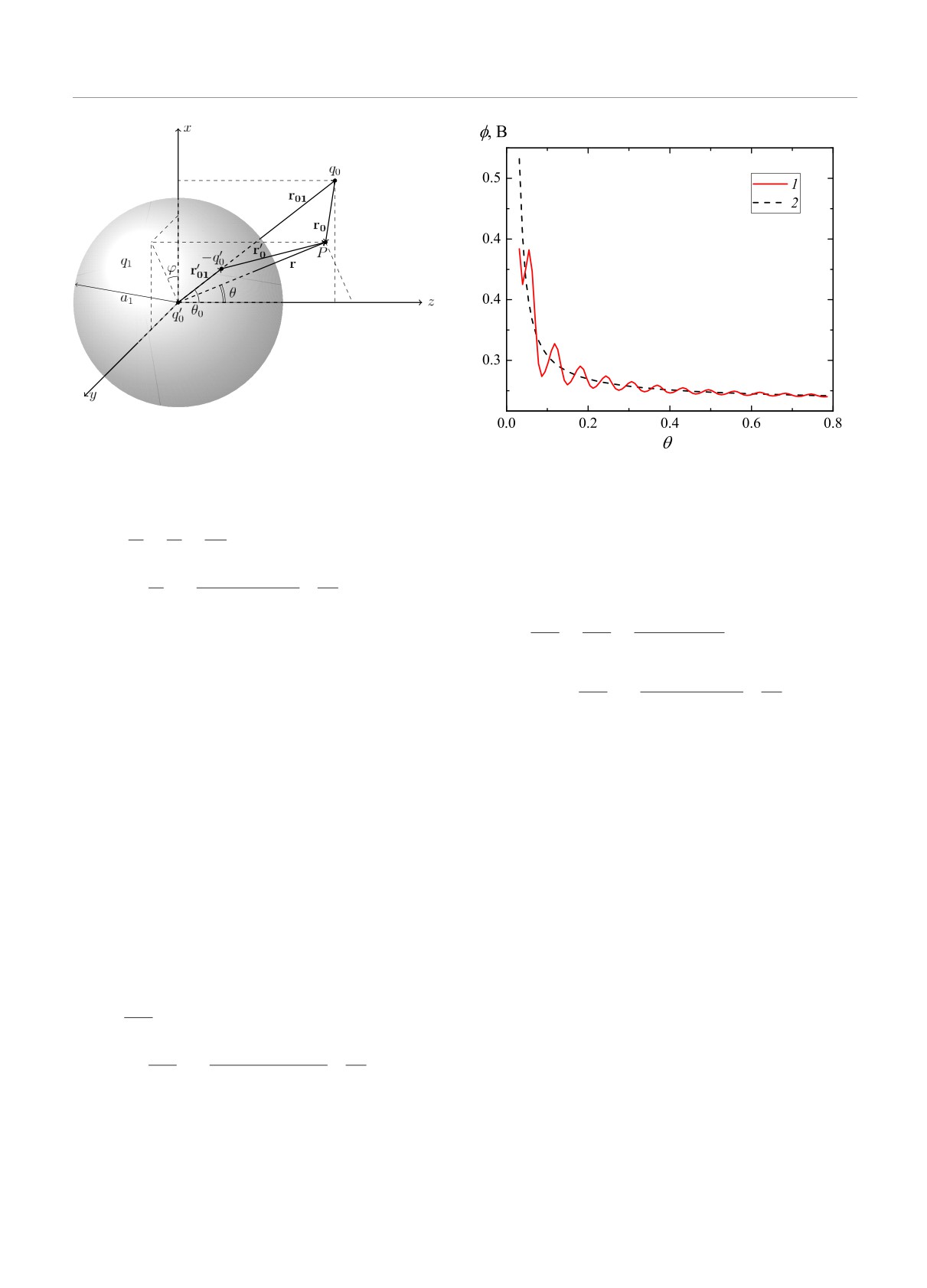
В работах [11,16] исследовался вопрос о том, при

каких соотношениях размеров, зарядов и значениях

диэлектрических проницаемостей две одноименно-

заряженные сферические частицы по мере сближе-

ния могут начать притягиваться друг к другу. Про-

анализируем влияние третьей частицы на этот пере-

ход. Рассмотрим сначала пару одинаковых диэлек-

трических шаров, которые при равных зарядах со-

гласно [16] ни на каких расстояниях притяжения не

испытывают. Расчеты показывают, что присутствие

третьей частицы приводит к изменению характера

их взаимодействия только при малых расстояниях

между их поверхностями, причем сам точечный за-

ряд должен находиться в очень ограниченной обла-

сти между ними. При этом понятно, что смена знака

проекции силы, действующей на каждую из сфер,

происходит вследствие притяжения к точечной ча-

стице, обусловленного третьим слагаемым в форму-

ле (42), на малых расстояниях преобладающим над

(a)

остальными.

Рассмотрим теперь сферические частицы с та-

ким соотношением размеров и зарядов, при кото-

рых притяжение между ними возможно (мы выбра-

ли параметры, соответствующие кривой 2 рисунка 5

в статье [16]), и расположим их на расстоянии чуть

большем и чуть меньшем переходного. Как и следо-

вало ожидать, в этом случае влияние третьей части-

цы качественно заметнее и проявляется в более ши-

роком диапазоне изменения ее координат. На рис. 4a

сферические частицы в отсутствие точечной оттал-

киваются друг от друга и продолжают отталки-

ваться (область 1), если последняя находится в пра-

вой полуплоскости (т.е. при z₀ > 0), не считая об-

ласти вблизи поверхностей шаров при 0 < z₀ < R.

Притяжение (область 2) возникает, когда точечный

заряд расположен в кольцевидной области вокруг

большей из сфер, за исключением тонких участ-

ков (область 3) внутри при z₀

< 0 и снаружи

(b)

при z₀ > 0. В этих участках, а также у поверхности

Рис. 4. Области притяжения

и отталкивания сфериче-

второй частицы со стороны, обращенной к первой

ских частиц в зависимости от положения точечной при

(т. е. при z₀ < L), знаки обеих сил отрицательные, а

a1 = 1.3a2, a2 = 10 мкм, q0 = 50e, q1 = 3q2, q2 = 10³e,

в довольно широкой области за большей из частиц,

ε1 = ε2 = 25 при межчастичном расстоянии L = 100 нм

наоборот, положительные (область 4). В этих слу-

(a) и L = 70 нм (b). Область 1

имеет место отталки-

чаях нельзя говорить о взаимном притяжении или

вание сферических частиц, 2

притяжение, 3

знаки

обеих сил отрицательные, 4

знаки обеих сил положи-

отталкивании сферических частиц.

тельные; на рис. 4a заштрихована область отталкивания, а

На рис.4b показано, как положение неполяризу-

на рис. 4b область притяжения

емой частицы влияет на режим взаимодействия ди-

электрических шаров с теми же параметрами, но на-

не меняет характер их взаимодействия, но теперь

ходящихся на чуть меньшем расстоянии, когда для

та область, где ее влияние приводит к смене знаков

изолированной пары отталкивание уже перешло в

обеих сил (область 1), находится за меньшей из них

притяжение. В основной части пространства, окру-

и становится тем шире по x, чем ближе q₀ к q₁, в

жающего сферы, точечная частица, как и раньше,

отличие от предыдущего случая. Кроме того, пере-

329

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

хода от притяжения к отталкиванию не возникает,

когда точечный заряд располагается в промежутке

между сферическими поверхностями; как мы виде-

ли, в этой зоне при изначальном отталкивании при-

тяжение возникает в первую очередь. Отметим сход-

ство с ранее рассмотренным случаем чуть большего

межчастичного расстояния: здесь мы также видим

отрицательные знаки сил в областях у сферических

поверхностей при π/2 < θ_1,2 < 3π/2 (область 3). Од-

нако основной участок, где обе силы обращены про-

тив оси z, окружает меньшую из сфер и по форме

-10

напоминает область положительных F_1z и F_2z (об-

ласть 4) вокруг большей из них, которую мы видели

в предыдущей конфигурации. При этом в рассмат-

-20

риваемом случае такого режима не наблюдается во-

все.

-30

Дадим несколько более общую картину зависи-

мости сил, действующих на сферические частицы,

-20

-10

от положения точечной. На рис.5 приведены дан-

(a)

ные для векторов F₁, F₂ как функций (x₀, z₀) , по-

лученные с использованием формул (43), (44) для x-

компоненты и аналогичных выражений для второй

макрочастицы. На данном рисунке длины векторов

не согласованы с абсолютным значением сил взаи-

модействия, за счет чего анализ становится проще,

но имеет качественный характер. Однако, в отличие

от еще более упрощенного и наглядного рис.4, дан-

ные на рис. 5 позволяют определить, в каких участ-

ках критических областей (т. е. тех, где характер

взаимодействия сфер противоположен невозмущен-

-10

ному) действительно имеет место ¾чистое¿ притя-

жение или отталкивание. Это можно сделать исхо-

дя из отклонения изображенных векторов от оси z:

-20

мы говорим об относительно ¾чистом¿ притяжении,

если F₁ · ez ≈ |F1| и F2 · ez ≈ - |F2| ; аналогич-

-30

ное определение можно сформулировать для оттал-

кивания. Так, в случае макрочастиц, находящихся

-20

-10

на границе перехода от отталкивания к притяже-

(b)

нию (рис. 4a), описанная ситуация возникает, толь-

Рис. 5. Поле сил F1

(тонкие стрелки) и F2

(жирные стрел-

ко когда точечный заряд находится за большей из

ки) в зависимости от координат точечной частицы. Пара-

сфер (см. рис.5a). Если же переход уже совершен

метры частиц и межчастичные расстояния, как на рис. 4

(рис. 4b), отталкивание скорее будет вызвано тре-

тьей частицей, находящейся вблизи меньшей из них

выбрано таким, каким бы оно было в отсутствие то-

возле оси x₂, что видно из рис.5b.

чечного заряда.

Представленные рисунки указывают только на

В первую очередь внимание на себя обращает об-

знаки сил F_1z и F_2z и описывают взаимодействие

ласть вблизи первой сферической частицы, где ка-

частиц лишь качественно. Для получения количе-

сательная плоскость к графику почти вертикальна.

ственной картины рассмотрим зависимость вели-

В этой области (см., например, рис.4) вне зависимо-

чины z-компоненты силы, действующей на первый

сти от параметров сферических частиц, возможно-

шар при L = 100 нм (что соответствует рис.4a), от

сти возникновения притяжения между ними и ре-

положения третьей частицы (см. рис. 6). В участках,

ализованности этого перехода та или иная части-

занятых сферами, значение силы для наглядности

ца испытывает силу, z-проекция которой имеет тот

330

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

0.1

-0.1

-0.2

(a)

Рис. 6. Зависимость z-компоненты полной силы, дей-

ствующей на первый диэлектрический шар, от положе-

ния точечного заряда. Параметры частиц соответству-

ют рис. 4, расстояние между сферическими поверхностя-

ми L = 100 нм. В отсутствие третьей частицы сферы от-

талкиваются с силой 2.84 · 10^-14 Н

же знак, что z-координата точечного заряда в соот-

ветствующей системе координат. Учитывая рис.6 и

аналогичные ему картины для второго шара, мож-

но говорить, что при различных параметрах систе-

мы не меняется не только знак проекции силы, но и

то, как резко ее абсолютная величина отличается от

таковой на некотором отдалении от сфер. Как уже

говорилось выше, причину следует искать в тре-

(b)

тьем слагаемом в формуле (42): даваемый им вклад

при малых r₀₁ многократно превышает вклады дру-

гих слагаемых, равно как и само значение проекции

силы при больших расстояниях между точечной и

сферической частицами.

Рассмотрим более детально влияние точечной

Рис. 7. Зависимости z-проекции полной силы, действую-

частицы на направление силы, действующей на шар,

щей на первую частицу, от положения точечного заряда на

когда расстояние между ними мало. На рис. 7 при-

оси z. Данные для кривых 1, 3 и 5 получены из решения

ведены зависимости z-проекции полной силы, дей-

системы (15), 2, 4 и 6 по приближенной формуле (40).

ствующей на первую частицу, от положения точеч-

Расчеты проведены при q1 = q2 = 10³e, a1 = 10 мкм,

ного заряда на оси z, полученные из решения си-

a2 = 10 (1, 2), 1 (3, 4), 0.1 (5, 6) мкм, ε1 = ε2 = 25,

стемы (15) и по приближенной формуле (40). Для

q0 = 50e, L = 10 (a), 1 (b) мкм. Здесь Fz1 сила взаимо-

приведения к безразмерной силе использована сила

действия точечного заряда с наведенным им поверхност-

ным зарядом, определенная выражением (45)

взаимодействия точечного заряда с наведенным им

поверхностным зарядом, определяемая выражением

заряда от поверхности первой частицы она стано-

(

)_2n+1

∑

вится все меньше и меньше. Из рис. 7 также видно,

q²⁰

a₁

F_z1 =

(n + 1) β_1,n µ₀₁

(45)

что приближенная формула (40) является достаточ-

εr²⁰¹

r₀₁

n=1

но точной и ее точность растет по мере уменьшения

Как видно из выражения (45), эта сила при µ₀₁ = 1

радиуса второй частицы как при L = 10 мкм, так и

(как на рис. 7) положительна, поэтому знак приве-

при L = 1 мкм. Из вкладки на рис. 7b видно, что при

денной силы при изменении L₀₁ не меняется.

L = 1мкм для частиц одинакового размера форму-

Из рис.7 видно, что при малых расстояниях

ла (40) при L₀₁ > 0.1 мкм приводит к значитель-

между поверхностью первой частицы и точечной

ным ошибкам. Нужно отметить, что при выполне-

частицей сила взаимодействия точечного заряда с

нии условия a₂ ≪ R выражение (40) не теряет своей

наведенным им поверхностным зарядом оказывает-

точности и при меньших рассмотренных на рис.7

ся преобладающей, но по мере удаления точечного

значениях L.

331

М. М. Родин, А. В. Филиппов

ЖЭТФ, том 163, вып. 3, 2023

ной частицы и представляет собой обобщение (35)

на случай отсутствия аксиальной симметрии в рас-

положении частиц. Последний член дает вклад вто-

рого диэлектрического шара в соответствии с фор-

мулой (19) и первым уравнением (15). Полученная

формула обнаруживает хорошую скорость сходимо-

сти, в том числе при существенно более близких

к нулю расстояниях между сферической поверхно-

стью и точечным зарядом, чем рассматриваемые да-

лее.

(a)

Расчеты показывают, что при параметрах сфе-

рических частиц, как на рис. 4, степень поляриза-

ции поверхностного заряда на большей из них суще-

ственно выше, чем на меньшей: если в первом случае

значения плотности заряда на полюсах (ближайшем

ко второму шару и противоположном ему, соответ-

ственно) составляют -12.3 и +0.189, то во втором

лишь -0.150 и +0.00144 (здесь и далее плотность

выражена в элементарных зарядах на квадратный

микрон). Для исследования влияния точечной час-

тицы на картину распределения связанных зарядов

на сферах поместим ее в области, которым на рис. 4

(b)

соответствует смена знака проекций сил, действую-

щих на сферы, т. е. в области 2 на рис. 4a и 1 на

рис. 4b. Одну точку мы взяли на оси x на расстоя-

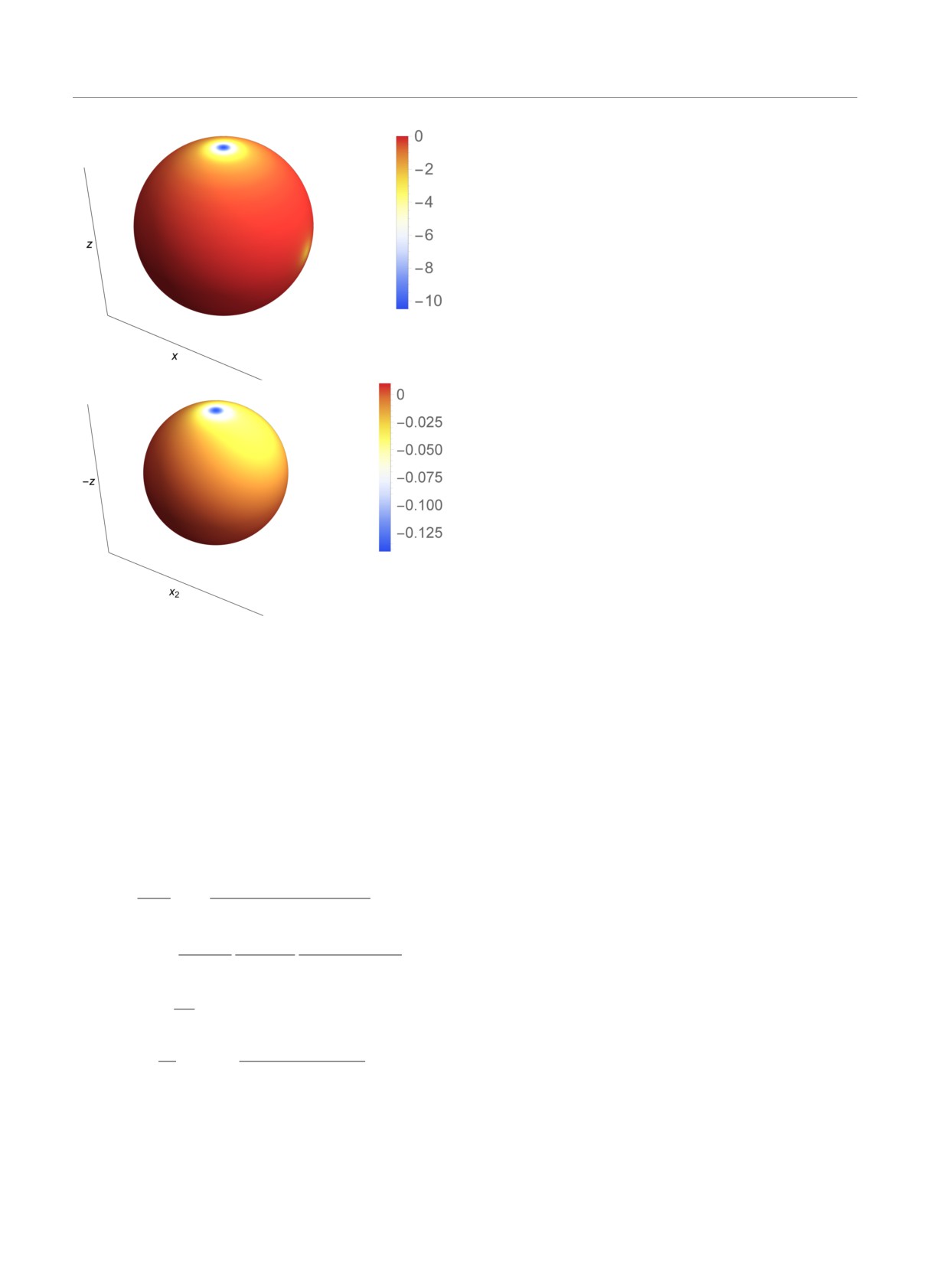
Рис. 8. Плотность связанных зарядов на поверхности пер-

нии 2 мкм от поверхности первого шара, вторую

вой (a) и второй (b) диэлектрических частиц с характери-

на оси x₂ на расстоянии 3 мкм от второго.

стиками, соответствующими рис. 4a; положение точечного

Рассмотрим первый случай (см. рис. 8). Как вид-

заряда: x = 15 мкм, z = 0, значения плотности приведены

но из рис. 8a, на фоне ¾шапки¿ отрицательного за-

в [e/мкм²], e элементарный заряд

ряда на полюсе первого шара возмущение плотно-

сти, вызванное близостью третьей частицы, не так

5.2. Плотность поверхностного заряда

велико. При этом оба участка отрицательной плот-

Перейдем к вычислению поверхностной плотно-

ности локализованы на довольно небольшой площа-

сти заряда на сферах и анализу влияния точечной

ди и разделены областью положительного заряда.

частицы на ее распределение. Как и в случае с про-

Иначе дело обстоит с плотностью заряда на мень-

екцией силы взаимодействия, приведем модифици-

шем из диэлектрических шаров (см. рис.8b). Ее рас-

рованную версию формулы (19):

пределение гораздо более равномерно, так что вли-

[

(

)

яние третьей частицы оказывается заметным даже

q^′0

r₀₁

r²⁰¹ - a²

σ_1,b =

при больших r₀₂. В рассматриваемом случае, когда

4πa²¹

(a²¹ + r²⁰¹ - 2a₁r₀₁ν)^3/2

другие две частицы расположены недалеко друг от

∑

друга, участки вызванного ими возмущения плотно-

(n - m)!

(2n + 1) ε

сти перекрываются, и область отрицательного заря-

+ (n + 1) ε

1 + δ_m0 (n + m)! nε₁

n=1 m=0

да занимает сравнительно большой телесный угол.

]

aⁿ¹

Если же точечная частица расположена ближе к

P^mn(µ₀) P^mn(µ)cosmϕ -

rⁿ

меньшему из шаров, то отрицательный пик плотно-

сти, индуцированный ей на его поверхности, оказы-

∑

n (2n + 1) (ε₁ - ε)

вается в разы заметнее расположенного на полюсе и

4π

nε₁

+ (n + 1) ε

n=1 m=0

вызванного первым диэлектрическим шаром; каче-

ственно картина распределения в этом случае напо-

× B^mn,1a^n-11Pmn (µ)cosmϕ.

(46)

минает рис. 8a, если поменять местами оси x и z. Что

Выражение в правой части, занимающее строки 1-

касается первой частицы, при данных параметрах

3 в приведенной формуле, отвечает вкладу точеч-

системы и на таком большом расстоянии точечный

332

ЖЭТФ, том 163, вып. 3, 2023

Взаимодействие двух заряженных диэлектрических шаров. . .

заряд не оказывает видимого влияния на распреде-

10.

A. V. Filippov, Contrib. Plasma Phys. 49, 433 (2009).

ление связанных зарядов на ее поверхности.

11.

E. Bichoutskaia, A. L. Boatwright, A. Khachatou-

rian, and A. J. Stace, J. Chem. Phys. 133, 024105

(2010).

6. ЗАКЛЮЧЕНИЕ

12.

V. Jadhao, Z. Yao, C. K. Thomas, and M. O. De La

В настоящей работе изучено взаимодействие

Cruz, Phys. Rev. E 91, 032305 (2015).

трех заряженных частиц, размером одной из ко-

13.

I. N. Derbenev, A. V. Filippov, A. J. Stace, and

торых можно пренебречь. Установлено, что при-

E. Besley, J. Chem. Phys. 152, 024121 (2020).

сутствие третьей частицы может существенно из-

менить характер взаимодействия двух одноимен-

14.

В. Р. Муниров, А. В. Филиппов, ЖЭТФ 142, 594

(2012).

но заряженных диэлектрических частиц, меняя от-

талкивание на притяжение и наоборот. Показано,

15.

A. Khachatourian, H.-K. Chan, A. J. Stace, and

что, несмотря на нарушение аксиальной симмет-

E. Bichoutskaia, J. Chem. Phys. 140, 074107 (2014).

рии при добавлении третьей частицы, при равно-

16.

В. Р. Муниров, А. В. Филиппов, ЖЭТФ 144, 931

мерной зарядке диэлектрической частицы сфериче-

(2013).

ской формы все компоненты вектора момента си-

лы, действующей на нее, принимают нулевое значе-

17.

B. A. Tinsley, Rep. Prog. Phys. 71, 066801 (2008).

ние. Продемонстрирована применимость метода вы-

18.

В. В. Батыгин, И. Н. Топтыгин, Сборник задач по

деления вкладов зарядов-изображений для значи-

электродинамике, Наука, Москва (1970).

тельного повышения точности расчета поверхност-

19.

В. Смайт, Электростатика и электродинамика,

ной плотности заряда и силы взаимодействия час-

Изд-во иностр. лит., Москва (1954) [W. R. Smythe,

тиц. Развитая в настоящей работе методика расчета

Static and Dynamic Electricity, McGraw-Hill, New

может быть использована для учета влияния сосед-

York - Toronto - London, 2-nd edition (1950)].

них зарядов на скорость коагуляции частиц в обла-

20.

J. D. Love, Q. J. Mech. Appl. Math. 28, 449 (1975).

ке заряженного аэрозоля, при этом влияние дальних

заряженных частиц может быть учтено в рамках ли-

21.

Y. Nakajima and T. Sato, J. Electrost.

45,

213

неаризованной теории Дебая - Хюккеля.

(1999).

Финансирование. Настоящая работа выполне-

22.

E. B. Lindgren, H.-K. Chan, A. J. Stace, and E. Bes-

на при финансовой поддержке Российского фон-

ley, Phys. Chem. Chem. Phys. 18, 5883 (2016).

да фундаментальных исследований (грант № 20-32-

23.

E. B. Lindgren, A. J. Stace, E. Polack, Y. Maday,

90054 Аспиранты).

B. Stamm, and E. Besley, J. Comp. Phys. 371, 712

(2018).

24.

M. Hassan and B. Stamm, ESAIM: Mathematical

ЛИТЕРАТУРА

Modelling and Numerical Analysis 55, S65 (2021).

1. A. A. Sickafoose, J. E. Colwell, M. Horanyi, and

25.

B. Bramas, M. Hassan, and B. Stamm, ESAIM:

S. Robertson, Phys. Rev.Let. 84, 6034 (2000).

Mathematical Modelling and Numerical Analysis 55,

S625 (2021).

2. J. D. Sartor, J. Geophys. Res. 65, 1953 (1960).

26.

E. В. Гобсон, Теория сферических и эллипсои-

3. H. T. Ochs and R. R. Czys, Nature 327, 606 (1987).

дальных функций, Изд-во иностр. лит., Москва

(1952) [E. W. Hobson, The Theory of Spherical and

4. E. B. Lindgren, B. Stamm, H.-K. Chan et al., Icarus

Ellipsoidal Harmonics, University Press, Cambridge

291, 245 (2017).

(1931)].

5. А. В. Филиппов, И. Н. Дербенев, ЖЭТФ 150, 1262

27.

Э. Т. Уиттекер, Д. Н. Ватсон, Курс современного

(2016).

анализа, ч. 2, Трансцендентные функции, Физмат-

гиз, Москва (1963).

6. J. Q. Feng, Phys. Rev. E 62, 2891 (2000).

28.

Л. Д. Ландау, Е. М. Лифшиц, Теоретическая фи-

7. M. H. Davis, Q. J. Mech. Appl. Math. 17, 499 (1964).

зика, т. VIII, Электродинамика сплошных сред,

Наука, Москва (1982) [L. D. Landau, E. M. Lifshitz,

8. J. Lekner, Proc. Roy. Soc. A 468, 2829 (2012).

and L. P. Pitaevskii, Electrodynamics of Continuous

9. А. В. Филиппов, ЖЭТФ 136, 601 (2009).

Media, Vol. 8, Pergamon Press, Oxford (1984)].

333