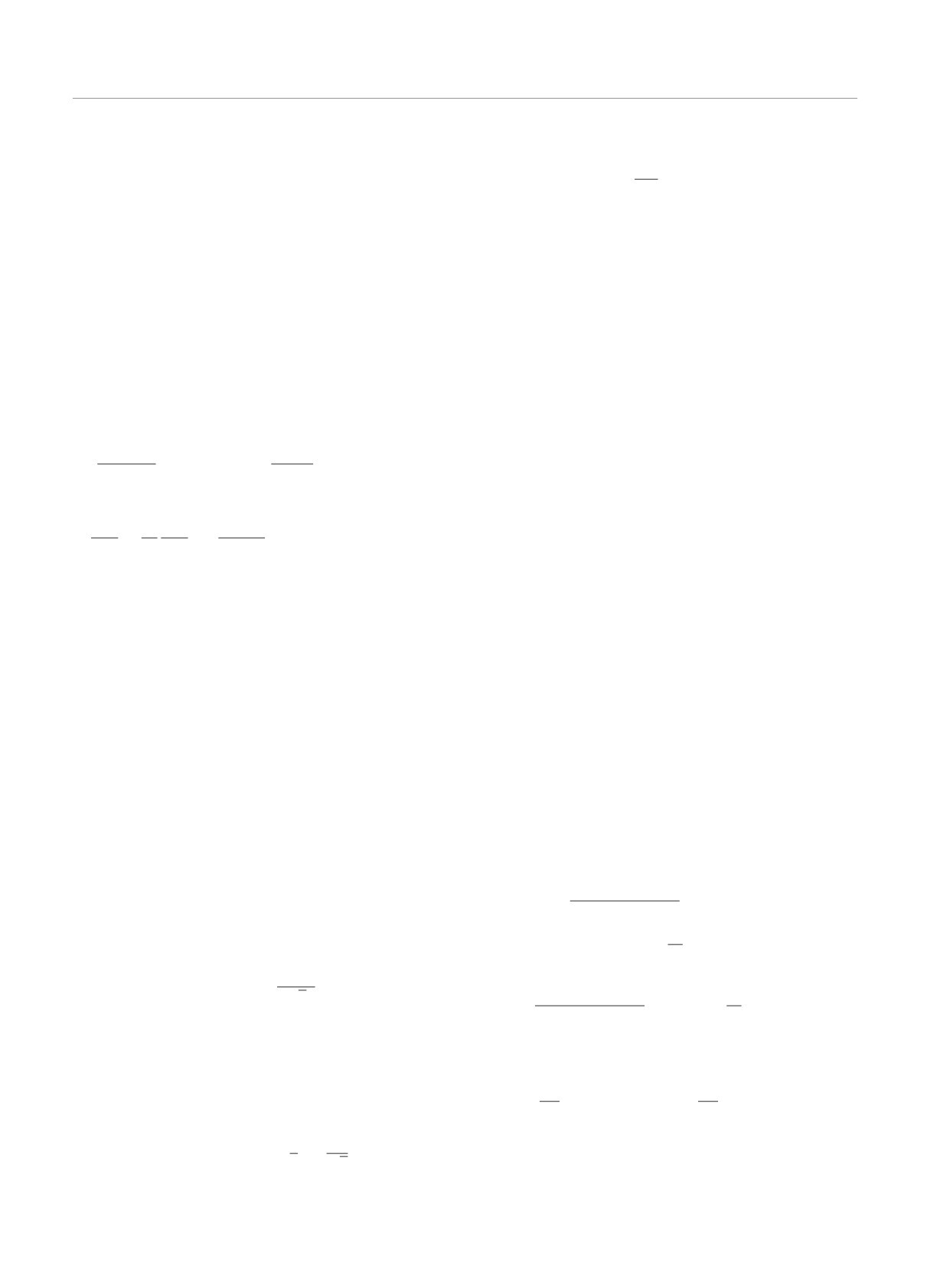ЖЭТФ, 2023, том 163, вып. 3, стр. 335-343
© 2023
ГЕНЕРАЦИЯ ПРОДОЛЬНОГО УЛЬТРАЗВУКА ИМПУЛЬСАМИ
СДВИГОВОЙ ДЕФОРМАЦИИ В РЕЖИМЕ СПИН-ФОНОННОГО
ЭХА
С. В. Сазонов*
Национальный исследовательский центр ¾Курчатовский институт¿
123182, Москва, Россия
Московский государственный университет им. М. В. Ломоносова
119991, Москва, Россия
Московский авиационный институт (национальный исследовательский университет)
125993, Москва, Россия
Поступила в редакцию 10 сентября 2022 г.,
после переработки 10 сентября 2022 г.
Принята к публикации 26 сентября 2022 г.
Предсказана возможность генерации импульсов продольного ультразвука гигагерцевых частот в режиме
спин-фононного эха с помощью воздействия на намагниченный изотропный парамагнетик резонансными
наносекундными импульсами сдвиговой деформации. Частота генерируемых эхо-сигналов продольного
ультразвука в два раза превышает частоту импульсов, подаваемых на среду. Для реализации эффекта
скорость продольного ультразвука не должна более чем в два раза превышать скорость волн деформации
сдвига. Данный резонансный механизм импульсного режима генерации второй гармоники, сопровожда-
ющегося нелинейным преобразованием поперечного ультразвука в продольный, не имеет оптического
аналога.
DOI: 10.31857/S0044451023030045
на парамагнитные кристаллы, а также регистри-
EDN: QDIKKL
ровались акустические и электромагнитные эхо-
сигналы.
Для наблюдения сигналов спин-фононного эха
1. ВВЕДЕНИЕ
важно, чтобы характерные частоты ω0 зееманов-
ского расщепления значительно превышали соот-
Открытие в 1950 г. Эрвином Ханом спинового
ветствующие неоднородные ширины δω образовав-
эха [1] стимулировало предсказание [2] и экспери-
шихся в результате данного расщепления пере-
ментальное наблюдение [3] аналогичного резонанс-
ходов. Обычно при температурах жидкого гелия
ного эффекта в видимом диапазоне электромагнит-
δω ∼ 107-108 с-1 [10]. Поэтому в экспериментах по
ных волн фотонного (светового) эха. Затем вышла
спин-фононному эху используются сильные магнит-
серия экспериментальных и теоретических работ по
ные поля, вызывающие зеемановские расщепления
спин-фононному (акустическому) эху в парамагнит-
с частотами ω0 ∼ 1011 с-1 [10, 11]. Тот же порядок
ных кристаллах [4-9], помещенных во внешнее маг-
имеют несущие частоты ω акустических импульсов,
нитное поле B. Квантовые переходы между зеема-
резонансно взаимодействующих с квантовыми пере-
новскими подуровнями парамагнитных ионов могут
ходами между зеемановскими подуровнями. Таким
быть инициированы как акустическими, так и элек-
образом, спектры возбуждающих акустических им-
тромагнитными полями. В свою очередь, данные пе-
пульсов и акустических эхо-сигналов лежат в гига-
реходы способны генерировать поля той и другой
герцевом диапазоне частот, принадлежащем даль-
природы. В работах [5-7] рассматривалось комби-
нему ультразвуку.
нированное (акусто-электромагнитное) воздействие
В твердом теле способны формироваться и рас-
* E-mail: sazonov.sergey@gmail.com
пространяться как продольные, так и поперечные
335
С. В. Сазонов
ЖЭТФ, том 163, вып. 3, 2023
акустические волны. Последние называют также
ственных функций оператора
Sz имеющие вид [12]
импульсами сдвиговой деформации. Данное обстоя-
тельство коренным образом отличает акустические
0
1
0
1
волны от электромагнитных. Комбинированное воз-
Sx =√
1
0
1
,
2
действие на кристаллы поперечными и продольны-
0
1
0
ми акустическими импульсами способно порождать
такие же комбинированные эхо-отклики. Важным
0
-i
0
1
представляется то, что скорости продольных и по-
Sy =√
i
0
-i
,
(2)
2
перечных упругих волн в твердом теле существенно
0
i
0
различаются между собой. Это может привносить
1
0
0
свои особенности в акустическое (спин-фононное)
эхо, отсутствующие в случаях спинового и фотон-
Sz = 0
0
0
.
ного эха.
0
0
-1
Настоящая работа посвящена теоретическо-
Спиновый гамильтониан свободного от спин-
му исследованию возможности формирования
фононного взаимодействия выделенного парамаг-
эхо-откликов продольного ультразвука при резо-
нитного иона имеет вид
нансном возбуждении парамагнитного кристалла
ультразвуковыми импульсами сдвиговой деформа-
Ĥs = ℏω′0
Sz,
(3)
ции.
где ℏ постоянная Планка, ω′0 частота зееманов-
ского расщепления спинового состояния.
2. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ
УРАВНЕНИЯ
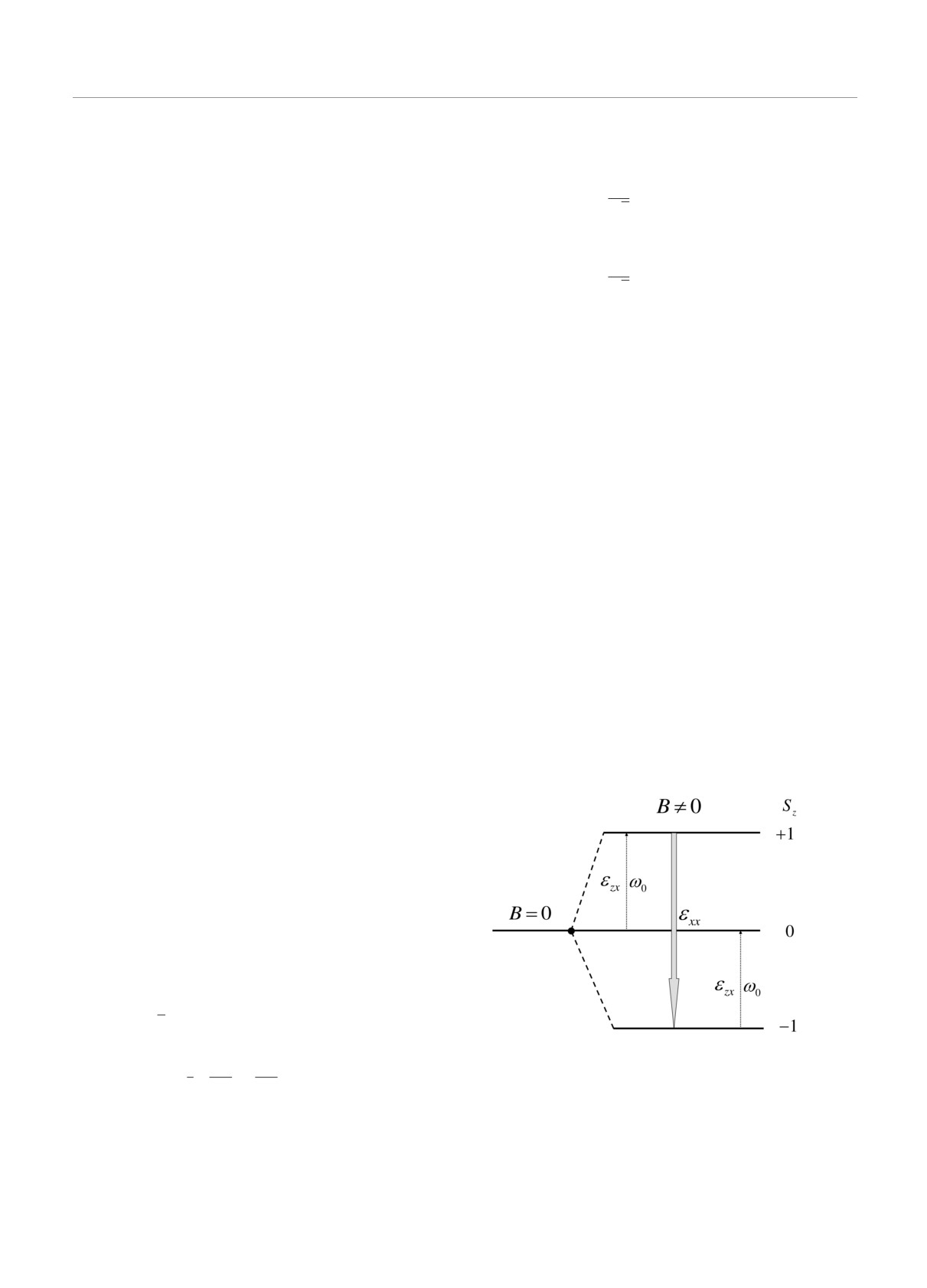
Основное, среднее и верхнее состояния эффек-
тивного спина обладают соответственно проекция-
Внедренные в твердое тело парамагнитные ио-
ми Sz = -1, 0, +1 на ось z (рис. 1).
ны характеризуются эффективным спином S [12],
Ниже будем считать, что подаваемые на сре-
значением которого определяется количество обра-
ду импульсы сдвиговой деформации поляризованы
зовавшихся зеемановских подуровней из наиболее
вдоль внешнего магнитного поля B, направленного
заселенного квантового состояния после помещения
параллельно оси z, и характеризуются компонентой
данных ионов в магнитное поле.
εzx = 0.5 ∂uz/∂x тензора упругой деформации. Дан-
Наиболее сильное спин-фононное взаимодей-
ную компоненту будем считать заданной, пренебре-
гая обратным воздействием на нее парамагнитных
ствие с динамическими локальными деформациями
твердого тела испытывают парамагнитные ионы,
обладающие эффективным спином S
= 1 [12].
Согласно механизму Ван Флека [11, 12], локальные
деформации приводят к появлению локальных
градиентов внутреннего электрического поля.
В свою очередь, данные градиенты вызывают
электрические квадрупольные переходы между
зеемановскими подуровнями парамагнитных ионов.
Гамильтониан спин-фононного взаимодействия в
таком случае имеет вид [10-12]
∑
(
)
1
Ĥint =
Gµνεµν
Sµ
Sν +
SνSµ
,
(1)
2
µ,ν=x,y,z
(
)
Рис. 1. Расщепление квантового уровня на три зееманов-
∂uµ
где Gµν , εµν =1
+ ∂uν
компоненты тензо-
2
∂xν
∂xµ
ских подуровня парамагнитного иона с эффективным спи-
ров спин-фононной связи и локальной деформации
ном S = 1 и разрешенные спин-фононные переходы для
соответственно, uµ проекция вектора u локальных
волн поперечного и продольного ультразвука, характери-
смещений на декартову координату xµ,
Sµ трех-
зуемых соответственно компонентами εzx и εxx тензора
рядные спиновые матрицы, в представлении соб-
относительной деформации
336
ЖЭТФ, том 163, вып. 3, 2023
Генерация продольного ультразвука импульсами сдвиговой деформации. . .
состояний парамагнитного иона (рис.1), матрицу
плотности представим в виде
ρ++ ρ+0 ρ+-
ρ=
ρ0+ ρ00 ρ0-
.
(6)
ρ-+ ρ-0 ρ--
Здесь нижние индексы +, 0 и - обозначают соот-
ветственно проекции эффективного спина +1, 0 и
-1. При этом выполняются условия эрмитовости
ρ+0 = ρ∗0+, ρ+- = ρ∗-+, ρ0- = ρ∗-0 и нормировки
ρ++ + ρ00 + ρ-- = 1.
Используя (2), (5) и (6), запишем уравнения для
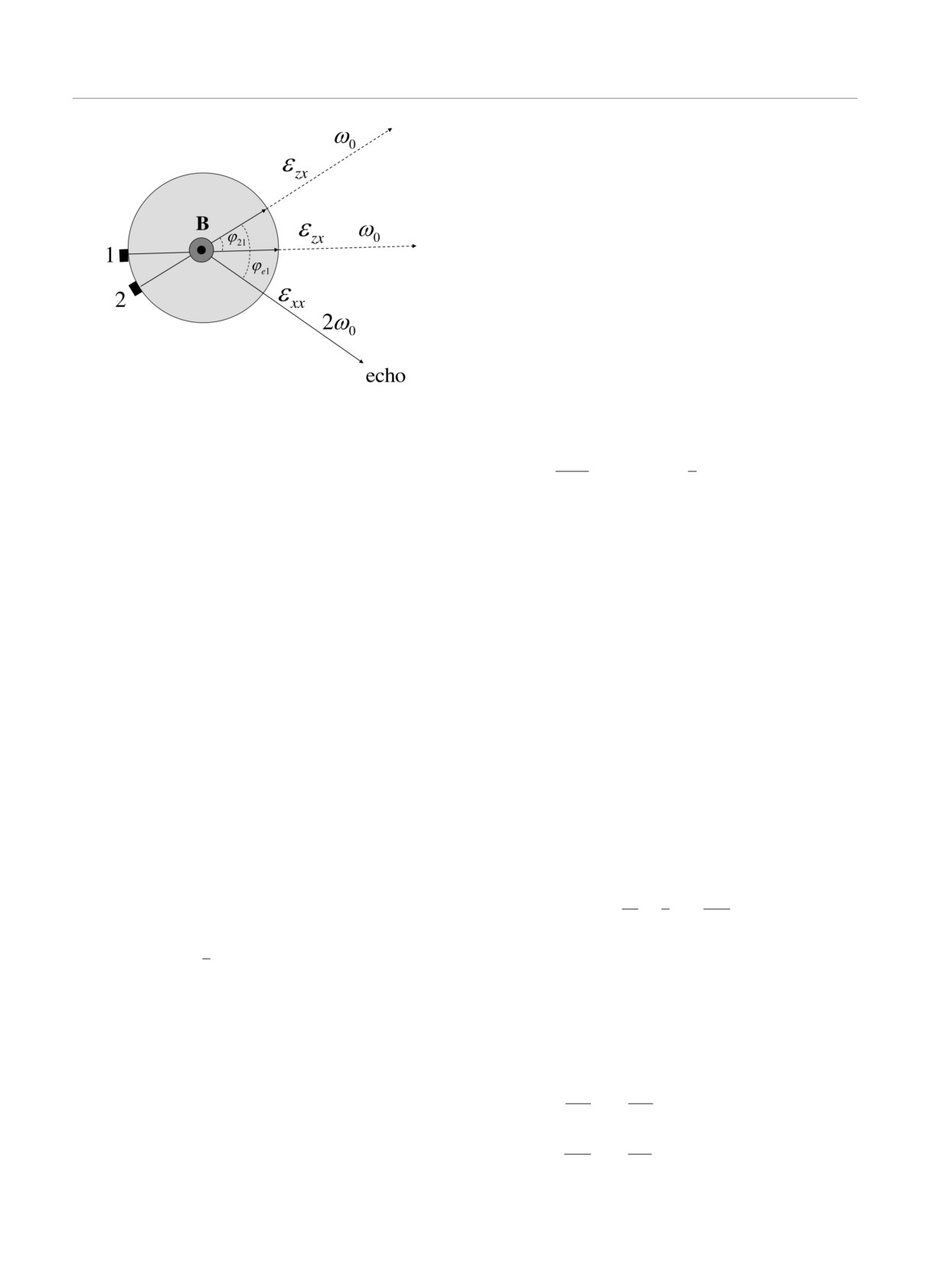
Рис. 2. Геометрическая cхема возбуждения парамагнит-
элементов ρµν (µ, ν = -, 0, +) матрицы плотности в
ного цилиндра импульсами сдвиговой деформации εzx с
виде
несущей частотой ω0 и ¾высвечивания¿ эхо-сигнала про-
∂ρµν
i
[
]
дольного ультразвука εxx с несущей частотой 2ω0. Черны-
= iω′νµρµν -
H⊥int , ρµν .
(7)
∂t
ℏ
ми прямоугольниками с номерами 1 и 2 обозначены соот-
ветственно генераторы первого и второго возбуждающих
Здесь
импульсов сдвиговой деформации. Магнитное поле B и
ось симметрии цилиндрического парамагнитного образца
ω′+0 = ω′0- = ω′0,
перпендикулярны к плоскости рисунка
ω′+- = 2ω′0,
ионов. Такой подход, типичный при исследовании
ω′++ = ω′00 = ω′-- = 0.
эффектов эха, оправдан при условии αl ≪ 1, где
α коэффициент поглощения поперечного ультра-
Здесь и ниже мы пренебрегаем энергетической
звука, l
характерный размер твердотельного об-
и фазовой необратимыми релаксациями, считая,
разца, на который данный ультразвук воздействует.
что характерное время Δt проведения эксперимен-
Кроме того, примем, что как воздействующие на об-
та значительно меньше характерных времен обоих
разец импульсы, так и эхо-сигнал распространяют-
видов релаксации.
ся перпендикулярно магнитному полю (рис. 2). При
этом поле продольного эхо-сигнала, распространя-
Применяя для расчета параметров эхо-сигнала
ющегося воль оси x, характеризуется компонентой
полуклассический подход, дополним (4) и (5) клас-
тензора деформаций. В соответствии со сказанным
сическим гамильтонианом поля продольной дефор-
∫
при учете аксиальной симметрии относительно вра-
мации Ha =
Ha d3r, где интегрирование ведется по
щений вокруг оси, параллельной B, представим (1)
всему объему образца среды, а плотность гамильто-
в виде суммы
ниана Ha определяется выражением
Ĥ⊥
Ĥint =
int
+ Ĥ∥int,
(4)
2
p
x
ρ
(∂ux)2
Ha =
+
a2
,
(8)
∥
где
2ρ
2
∂x
(
)
1
Ĥ⊥
=
G⊥εzx
Sx
Sz +
Sz
Sx
,
где ρ равновесная плотность среды, px декарто-
int
2
ва компонента плотности импульса продольных ло-
Ĥ∥
int
=G∥εx
S2x,
(5)
кальных смещений, a∥ скорость продольного зву-
ка в рассматриваемой среде.
G⊥ = Gzx, G∥ = Gxx.
Используем уравнения Гамильтона для механи-
Так как на парамагнитные ионы воздействуют
ки сплошных сред [13]:
только импульсы сдвиговой деформации, то в урав-
D
E)
нение для матрицы плотности ρ данных ионов вхо-
∂px
δ (
=-
Ha +
Ĥ∥
,
Ĥ⊥
int
дит часть гамильтониана, равная
Ĥs +
∂t
δux
int
(9)
В соответствии со значениями проекций эффек-
D
E)
∂ux
δ (
Ĥ∥
=
Ha +
тивного спина на ось z для различных квантовых
int
∂t
δpx
337
С. В. Сазонов
ЖЭТФ, том 163, вып. 3, 2023
D
E
(
)
Здесь
Ĥ∥
= Sp
ρĤ∥
квантовое среднее
формаций.
int
int
оператора Гамильтона, описывающего взаимодей-
Отсюда, а также из (2), (5), (6) и (8) приходим к
ствие эффективного спина с полем продольных де- волновому уравнению
∫
∂2εxx
∂2εxx
nG∥ ∂2
-a2
=
(ρ00 + ρ-+ + ρ∗-+) g(Δ) dΔ,
(10)
∂t2
∥ ∂x2
2ρ ∂x2
−∞
где n концентрация парамагнитных ионов, g(Δ)
ного уширения для переходов - ↔ 0 и 0 ↔ +, r
функция контура неоднородного уширения на кван-
радиус-вектор точки парамагнетика.
товом переходе - ↔ +, центрированная на частоте
Для периодов свободной эволюции (H⊥int = 0) за-
ω0, Δ = ω′0 - ω0 отстройка квантового перехода
пишем
- ↔ + выделенного парамагнитного иона от цен-
тральной частоты спектральной линии.
εxx = ψ∥ei(2ω0t-k∥·r) + c. c.,
(13)
Таким образом, в принятом приближении αl ≪ 1
ρ-+ = R-+ei(2ω0t-k∥·r),
возбуждение парамагнитных ионов происходит им-
пульсами сдвиговой деформации, что описывается
где ψ∥ и k∥ комплексная ММА и параллельный
последним слагаемым в (7). В свою очередь, про-
оси x волновой вектор продольного ультразвука со-
дольный ультразвук генерируется квантовым пере-
ответственно.
ходом - ↔ + в периоды свободной эволюции спи-
нов, когда в (7) можно положить H⊥int = 0. Этот
Матричные элементы ρ-0 и ρ0+ здесь по-
процесс описывается динамикой элемента ρ-+ мат-
прежнему представляются в виде (12).
рицы плотности. Что касается матричного элемента
Отметим, что величины волновых векторов для
ρ00, то его динамика в периоды свободной эволю-
волн сдвиговой деформации и продольного ультра-
ции описывается энергетической релаксацией, кото-
звука определяются соответственно выражениями
рой мы здесь, как было сказано выше, пренебрегаем.
k⊥ = ω0/a⊥, k∥ = 2ω0/a∥, где a⊥ скорость по-
Поэтому в правой части (10) можно с хорошей точ-
перечного ультразвука.
ностью считать ρ00 = const.
Будем считать ниже, что длительности τp
Используем далее стандартное приближение
воздействующих импульсов значительно меньше
медленно меняющихся амплитуд (ММА) [14]. В пе-
времен T∗0+, T∗-0 и T∗-+ обратимой релаксации,
риоды возбуждений для динамических переменных
обусловленной неоднородным уширением рассмат-
поля и среды имеем
риваемых квантовых переходов. Как результат,
ширины δωp
∼ 1/τp импульсных спектров зна-
εzx = ψ⊥ei(ω0t-k⊥·r) + c. c.,
чительно превышают неоднородные ширины
(11)
δω ∼ 1/T∗0+, 1/T∗-0, 1/T∗-+ данных переходов. По-
ρ-+ = R-+ei(2ω0t-k⊥·r),
этому при описании возбуждения парамагнитных
ионов пренебрежем в (7) частотными отстройками
ρ-0 = R-0ei(ω0t-k⊥·r),
ω′νµ - ωνµ от соответствующих резонансов.
(12)
Суммируя сказанное выше, из (2), (5)-(7), (10)-
ρ0+ = R0+ei(ω0t-k⊥·r),
(13) после пренебрежения в материальных уравне-
где ψ⊥ и Rµν
комплексные ММА импульсов
ниях быстро осциллирующими слагаемыми для пе-
сдвиговой деформации и недиагональных элементов
риодов возбуждения парамагнитных ионов получим
матрицы плотности соответственно (µ, ν = -, 0, +),
k⊥ волновой вектор импульсов сдвиговой дефор-
[
]
∂R
G⊥ψ⊥
мации, несущая частота ω0 данных импульсов сов-
=i
√
R,
Q
,
(14)
∂t
2
2ℏ
падает с центральной частотой контуров неоднород-
338
ЖЭТФ, том 163, вып. 3, 2023
Генерация продольного ультразвука импульсами сдвиговой деформации. . .
где
где
I
единичная матрица,
∫ t
G⊥
ρ++ R+0 R+-
θ=
ψ⊥ dt′.
(21)
2ℏ
R=R0+ ρ00 R0-
,
t0
R-+ R-0 ρ--
Для периодов свободной эволюции из (16) нахо-
(15)
дим
0
1
0
R-0,0+(t) = R-0,0+(t1)exp{iΔ(t - t1)} ,
Q=1
0
-1
.
(22)
R-+(t) = R-+(t1)exp{2iΔ(t - t1)} ,
0
-1
0
где t1
время начала этапа свободной эволюции.
В дальнейшем заданную амплитуду ψ⊥ будем
Пусть в момент времени t = 0 на среду воздей-
считать вещественной.
ствует импульс сдвиговой деформации длительно-
Для периодов свободной эволюции из (7), (10),
сти τ1. Затем, спустя промежуток времени τ, со-
(12) и (13) будем иметь ρ-- = ρ00 = ρ++ = const,
ответствующий первому этапу свободной эволюции,
среда подвергается воздействию второго импульса,
∂R-0,0+
∂R-+
= iΔR-0,0+,
= 2iΔR-+,
(16)
длительность которого равна τ2. После этого, при
∂t
∂t
t = τ + τ1 + τ2, начинается второй этап свобод-
ной эволюции, во время которого формируются эхо-
∫ +∞
сигналы (рис. 3).
∂ψ∥
1 ∂ψ∥
nG∥ω0
+
=i
R-+g(Δ)dΔ.
(17)
∂x
a∥ ∂t
2ρa3
Будем считать, что при t = 0 матрица
R опреде-
∥
-∞
ляется только начальными населенностями w+, w0 и
С помощью системы (14), (15) определяются
w- соответствующих спиновых состояний парамаг-
квантовые состояния парамагнитных ионов при воз-
нитных ионов и имеет вид
действии на них резонансных импульсов сдвиговой
w+
0
0
деформации. Уравнениями (16), (17) описывается
R(0) = 0 w0
0
.
генерация продольного ультразвука после данного
воздействия.
0
0
w-
Тогда, применяя в обозначенной последователь-
3. РЕЖИМ СПИН-ФОНОННОГО ЭХА
ности формулы (18), (20)-(22), найдем выраже-
ния для элементов матрицы
ˆ в моменты времени
Рассмотрим динамику квантовых состояний па-
t > τ + τ1 + τ2. Интересующая нас часть Recho-+ эле-
рамагнитных ионов в периоды возбуждений, полу-
мента R-+, вносящая вклад в эхо-отклик, имеет вид
чив решение операторного уравнения (14).
Recho-+ = R3τ/2-+ + R2τ-+,
(23)
Решение операторного уравнения (14) можно за-
где
писать в виде
R(t) =
Û (t, t0)R(t0)Û+(t, t0),
(18)
R3τ/2-+ = -w- -2w0 +w+
sin 2θ1×
4
θ2
где
× sinθ2 sin2
e2iΔ(t-3τ/2-τ1-τ2),
(24)
2
∫ t
Û(t,t0) = e-
S,
S =
Q √
ψ⊥ dt′,
(19)
w- - 2w0 + w+
θ2
2
2ℏt0
R2τ-+ =
sin2 θ1 sin4
e2iΔ(t-2τ-τ1-τ2).
4
2
t0
время начала воздействия импульса.
(25)
Разлагая в ряд Тейлора экспоненту от матрицы
Здесь
eiθ, после его суммирования с учетом (19) и второго
G∥
∫ τ1
G∥
∫ τ+τ1+τ2
выражения (15) будем иметь для оператора эволю-
θ1 =
ψ⊥ dt′, θ2 =
ψ⊥ dt′
2ℏ
2ℏ
ции
0
τ +τ1
Q
¾площади¿ соответственно первого и второго воз-
Û (t, t0) =
I-
Q2 sin2 θ
-i√
sin θ,
(20)
2
2
буждающих импульсов.
339
С. В. Сазонов
ЖЭТФ, том 163, вып. 3, 2023
В эхо-экспериментах с хорошей точностью вы-
родного уширения перехода - ↔ +
полняется неравенство τ ≫ τ1, τ2. Учитывая это, а
1
T∗-+
также больцмановский характер распределения на-
g(Δ) =
π 1 + (T∗-+Δ)2
чальных населенностей спиновых подуровней, после
интегрирования по лоренцевскому контуру неодно- будем иметь
∫
{
}
3τ /2
ch(ℏω0/kBT ) - 1
θ2
2
3τ
R-
g(Δ) dΔ = -0.5
sin 2θ1 sin θ2 sin2
exp
-
−
,
(26)
+
t
2 ch(ℏω0/kBT)+1
2
T∗-+
2
-∞
∫
{
}
ch(ℏω0/kBT ) - 1
θ2
2
R2τ-+ g(Δ)dΔ = -0.5
sin2 θ1 sin4
exp
-
|t - 2τ|
,
(27)
2 ch(ℏω0/kBT)+1
2
T∗
−+
-∞
где kB постоянная Больцмана, T абсолютная
температура среды.
Выражениями (26) и (27) описываются появле-
ния ультразвукового эхо-сигнала в моменты време-
ни 3τ/2 и 2τ соответственно (рис. 3).
Взяв за начало координаты x центр цилиндри-
ческого парамагнитного образца (рис. 2), запишем
решение уравнения (17) при x ≫ l. При этом будем
считать, что среда вне цилиндрического образца не
обладает парамагнитными свойствами. Тогда с уче-
том (26) и (27) для 3τ/2- и 2τ-эха найдем
ψ3τ/2∥ = -iµ sin2θ1 sinθ2 sin2 θ2×
Рис. 3. Временная последовательность воздействия на па-
2
рамагнетик двух импульсов сдвиговой деформации с оги-
{
}
2
бающей ψ⊥ и длительностями τ1 и τ2, разделенных проме-
× exp
-
t - 3τ/2 - x/a∥
,
T∗
жутком времени τ , а также появления двух эхо-сигналов
−+
продольного ультразвука с величиной огибающей
ψ∥
θ2
ψ2τ∥ = iµ sin2 θ1 sin4
×
(28)
2
жениями keτ/2 = 3k2/2 - k1/2 и k2τe = 2k2 - k1.
{
}
2
Заметим, что выражение для k2τe в точности сов-
× exp
-
t - 2τ - x/a∥
,
T∗
−+
падает с соответствующим выражением для фо-
тонного эха в двухуровневой системе [3,14]. Отсю-
где
да, учитывая, что keτ/2 = k2τe = k∥ = 2ω0/a∥ и
nG∥ω0l
ch(ℏω0/kBT ) - 1
µ=
(29)
k1 = k2 = k⊥ = ω0/a⊥, легко определить угол ϕ21
4ρa3
2 ch(ℏω0/kBT ) + 1
∥
между направлениями распространения первого и
Важным является вопрос о направлении рас-
второго возбуждающих импульсов, а также угол ϕe1
пространения эхо-сигналов. Так как характерные
между направлениями распространения первого им-
длины волн λ возбуждающих импульсов и сигна-
пульса и эхо-отклика (рис. 2). Для 3τ/2-эха и 2τ-эха
лов эха значительно меньше размеров среды, то
имеем соответственно
(
)
важную роль играют эффекты пространственной
1
a2⊥
интерференции, сопровождающиеся сильной диф-
cosϕ3τ/221 =
5-8
,
3
a2
ференциацией мод. Волновые векторы 3τ/2- и 2τ-
∥
(30)
сигналов эха, как следует из общих формул, най-
3τ /2
a∥
cosϕ
=
−2
a⊥ ,
e1
денных в [15], определяются соответственно выра-
a⊥
a∥
340
ЖЭТФ, том 163, вып. 3, 2023
Генерация продольного ультразвука импульсами сдвиговой деформации. . .
5
a2⊥
cosϕ2τ21 =
-
,
Следовательно, использованное здесь приближение
4
a2
∥
заданного поля для возбуждающих импульсов вы-
(31)
3a∥
полняется с хорошей точностью. Время обратимой
cosϕ2τe1 =
-
a⊥ .
фазовой релаксации для квантовых переходов меж-
4a⊥
a∥
ду зеемановскими подуровнями ионов Fe2+ в кри-
Простой анализ показывает, что для удовлетво-
сталле MgO, как и характерная длительность эхо-
рения данным соотношениям необходимо выполне-
сигналов (см. (28)), составляет T∗-+ ∼ 10-7 с [7, 9].
ние условия a∥/a⊥ ≤ 2. Поскольку в твердом теле
Для того чтобы удовлетворить использованному вы-
всегда a∥ > a⊥, приходим к ограничению вида
ше условию τp ≪ T∗-+, длительности возбуждающих
импульсов сдвиговой деформации должны быть по-
1 < a∥/a⊥ ≤ 2.
(32)
рядка τp ∼ 10-8 с. При этом временной промежу-
Таким образом, скорость продольного ультра-
ток τ между возбуждающими импульсами удовле-
звука не должна более чем в два раза превышать
творяет двойному неравенству T∗-+
≪ τ ≪ T2,
скорость поперечного ультразвука. Условие (32) яв-
где T2
характерное время фазовой релаксации
ляется необходимым для осуществления генерации
на разрешенных спин-фононных переходах. Взяв
продольного ультразвука импульсами сдвиговой де-
T2 ∼ 10-5 с-1 [10, 11], примем τ ∼ 10-6 с. Несу-
формации (поперечным ультразвуком) в резонанс-
щая частота импульсов сдвиговой деформации, рав-
ном режиме спин-фононного эха.
ная половине частоты генерируемого ультразвуко-
Из выражений (30) и (31) легко получаются
вого сигнала, составляет ω0 ∼ 1011 с-1.
неравенства ϕ3τ/221 > ϕ2τ21 и ϕ3τ/2e1 > ϕ2τe1 .
Скорость продольного ультразвука в рассмат-
Как известно, в случае первичного (двухим-
риваемом рабочем образце a∥ = 5.77 · 105 см/с [16].
пульсного) фотонного эха рассмотренные углы
Следовательно, характерный размер эхо-сигнала
должны быть настолько малы, чтобы удовлетворя-
в направлении распространения составляет
√
лось условие ϕe1 = 2ϕ21 <
λ/l [3, 14]. В реальных
∼ a∥T∗-+
∼
1 мм. Так как данная величина
экспериментах эти углы составляют всего единицы
сравнима с размером образца или превышает его,
градусов, что затрудняет пространственное раз-
то эффектами распространения эхо-сигнала внутри
решение возбуждающих сигналов и сигналов эха.
образца можно пренебречь. Это и было сделано при
Важно заметить, что здесь, в отличие от фотонного
получении выражений (28).
эха, отсутствует ограничение на величины рас-
Взяв для апертуры D возбуждающих импуль-
смотренных углов. Связано это с различием между
сов и сигналов эха D
≈ l ∼ 1мм, найдем для
скоростями распространения возбуждающих им-
характерной длины дифракционного расплывания
пульсов и эхо-сигналов, а также с различием их
lD ∼ ω0D2/a∥ ∼ 102-103 см. Это значительно пре-
несущих частот. Более того, выбрав только одно
восходит рассматриваемые нами пространственные
из условий синхронизма ((30) или (31)), можно
масштабы и поэтому хорошо согласуется с исполь-
наблюдать только эхо-сигнал, удовлетворяющий
зованным в (10), (17) и (28) одномерным приближе-
данному условию. Другой же эхо-сигнал при этом
нием. Таким образом, эхо-сигналы можно фиксиро-
будет подавлен.
вать, установив соответствующие датчики, на рас-
Приведем численные оценки для возможной ре-
стояниях нескольких сантиметров от рабочего об-
ализации рассмотренного варианта спин-фононного
разца.
эха в экспериментальных условиях. В качестве рабо-
Из (28) видно, что амплитуда 3τ/2-эха макси-
чего образца рассмотрим аморфный кристалл MgO
мальна, если ¾площади¿ двух возбуждающих им-
при температурах жидкого гелия с внедренными
пульсов равны соответственно θ1 = π/4, θ2 = 2π/3.
в него парамагнитными ионами Fe2+ [10]. Для та-
Аналогичные оптимальные ¾площади¿ для наблю-
кого кристалла имеем a∥/a⊥
= 1.89 [16]. Тогда
дения 2τ-эха имеют значения θ1 = π/2 и θ2 = π.
из (30) и (31) будем иметь ϕ3τ/221 = 23◦, ϕ3τ/2e1 = 34◦,
Тогда из (21) для амплитуды подаваемых на сре-
ϕ2τ21 = 14◦, ϕ2τe1 = 27◦. Таким образом, возбуждаю-
ду импульсов сдвиговой деформации имеем оценку
щие импульсы и импульсы эха обладают хорошей
ψ⊥ ∼ ℏ/G⊥τp ∼ 10-5. Взяв, в свою очередь, в случае
пространственной разрешимостью.
рассматриваемого образца T ∼ 1-4 К, n ∼ 1017 см-3,
Для рассматриваемого образца с характерным
G∥ ∼ 10-14 эрг [10,11], ρ = 3.6 г/см3, а также приве-
размером l ∼ 1 мм (рис. 2) в случае импульсов сдви-
денные выше оценки для ω0, a∥ и l, из (28) и (29) ам-
говой деформации имеем αl ∼ 0.01-0.1 ≪ 1 [10].
плитуд эхо-сигналов продольного ультразвука будем
341
С. В. Сазонов
ЖЭТФ, том 163, вып. 3, 2023
τ /2
иметь
ψ3
∼
ψ2τ∥ ∼ 10-5-10-6. Такие амплиту-
Представляет интерес исследовать ультразвуко-
∥
вое эхо при возбуждении среды последовательно-
ды относительной деформации вполне могут быть
стями из различных комбинаций поперечных и про-
зафиксированы в условиях реального эксперимен-
дольных импульсов.
та [12].
В настоящей работе рассмотрена ситуация, когда
длительности возбуждающих импульсов значитель-
но короче времен обратимой фазовой релаксации за-
4. ЗАКЛЮЧЕНИЕ
действованных квантовых переходов. В этом случае
Проведенное в настоящей работе исследование
временные профили эхо-сигналов представляют со-
демонстрирует принципиальную возможность гене-
бой фурье-образы соответствующих контуров неод-
рации импульсов продольного ультразвука гигагер-
нородного уширения [25] (см., например, (28) и вы-
цевого диапазона с помощью резонансных наносе-
ражение для g(Δ)). Как известно, в противополож-
кундных импульсов сдвиговой деформации посред-
ном случае (при импульсных длительностях, превы-
ством спин-фононного эха. Так как несущая частота
шающих времена обратимой фазовой релаксации)
импульсов продольного ультразвука здесь в два ра-
в оптике наблюдаются эффекты корреляции меж-
за превышает частоту подаваемых на образец попе-
ду профилями возбуждающих импульсов и сигна-
речных импульсов, то можно говорить о резонанс-
лов эха [26-32]. В этой связи возникает вопрос о том,
ном механизме генерации второй гармоники. Важ-
как аналогичные эффекты корреляции могут про-
но заметить, что данный механизм не имеет оптиче-
явиться в случае участия в формировании ультра-
ского аналога по трем основным причинам. Во-пер-
звукового эха поперечных и продольных импульсов.
вых, в трехуровневой системе не могут быть разре-
Такой вопрос является предметом отдельного рас-
шены все три оптических перехода. Это запрещено
смотрения.
правилами отбора по четности состояний. Во-вто-
рых, генерация второй гармоники здесь сопровож-
дается преобразованием поперечного ультразвука в
ЛИТЕРАТУРА
продольный. Данный процесс невозможен в оптике
1. E. L. Hahn, Phys. Rev. 80, 580 (1950).
по причине отсутствия продольных электромагнит-
ных волн. В-третьих, как уже отмечалось в преды-
2. У. Х. Копвиллем, В. Р. Нагибаров, Физ. металлов и
дущем разделе, углы ¾высвечивания¿ эхо-сигналов
металловед. 15, 313 (1963).
продольного ультразвука по отношению к направ-
3. N. A. Kurnit, I. D. Abella, and S. R. Hartmann, Phys.
лениям распространения возбуждающих импульсов,
Rev. Lett. 6, 567 (1964).
в отличие от случая первичного фотонного эха, не
4. В. Р. Нагибаров, У. Х. Копвиллем, ЖЭТФ
52,
являются малыми и никак не ограничены размера-
936 (1967) [V. R. Nagibarov and U. Kh. Kopvillem,
ми рабочего образца, в котором они формируются.
Sov. Phys. JETP 25, 618 (1967)].
Это обусловлено различием несущих частот, а также
скоростей продольного и поперечного ультразвуков.
5. N. S. Shiren and I. G. Kazyaka, Phys. Rev. Lett. 28,
Замечание об отсутствии оптического аналога
1304 (1972).
представляется важным. Дело в том, что многие
6. D. R. Taylor and I. G. Bartlet, Phys. Rev. Lett. 30, 96
нелинейно-акустические эффекты предсказывались
(1973).
и обнаруживались в результате проведения парал-
лелей с соответствующими оптическими явления-
7. У. Х. Копвиллем, В. Р. Ризаев, ЖЭТФ 65, 2297
(1973)
[U. Kh. Kopvillem and V. R. Rizaev, Sov.
ми [17-24].
Phys. JETP 38, 1147 (1974)].
Помимо рассмотренных здесь 3τ/2- и 2τ-сигна-
лов эха продольного ультразвука на частоте 2ω0 при
8. В. А. Голенищев-Кутузов, В. Ф. Тарасов, Н. К. Со-
описанной выше схеме возбуждений среды в момент
ловаров, Письма в ЖЭТФ
22,
266
(1975)
времени 2τ могут формироваться эхо-отклики сдви-
[V. A. Golenishchev-Kutuzov, N. K. Solovarov, and
говой деформации на частоте ω0. Однако условия
V. F. Tarasov, Sov.Phys. JETP Lett. 22, 123 (1975)].
синхронизма в этом случае значительно отличаются
9. В.А. Голенищев-Кутузов, А.И. Сиразиев, Н.К. Со-
от (30) и (31), имея явное сходство с аналогичными
ловаров, В. Ф. Тарасов, ЖЭТФ
71,
516
(1976)
условиями для наблюдения фотонного эха. Поэтому
[V. A. Golenishchev-Kutuzov, A. I. Siraziev, N. K. So-
при выполнении (30) и (31) данные сигналы будут
lovarov, and V. F. Tarasov, Sov. Phys. JETP 44, 562
сильно подавлены.
(1976)].
342
ЖЭТФ, том 163, вып. 3, 2023
Генерация продольного ультразвука импульсами сдвиговой деформации. . .
10.
N. S. Shiren, Phys. Rev.B 2, 2471 (1970).
21.
А. А. Заболотский, Письма в ЖЭТФ 77, 558 (2003)
[A. A. Zabolotskii, JETP Lett. 77, 464 (2003)].
11.
В.А. Голенищев-Кутузов, В.В. Самарцев, Н.К. Со-
ловаров, Б. М. Хабибуллин, Магнитная кванто-
22.
А. Н. Бугай, С. В. Сазонов, ЖЭТФ 139, 464 (2011)
вая акустика, Наука, Москва (1977).
[A. N. Bugay and S. V. Sazonov, JETP
112,
401
(2011)].
12.
Дж. Такер, В. Рэмптон, Гиперзвук в физике твер-
дого тела, Мир, Москва (1975) [J. W. Tucker and
23.
С. В. Сазонов, Н. В. Устинов, ЖЭТФ
141,
738
V. W. Rampton, Microwave Ultrasonics in Solid
(2012) [S. V. Sazonov and N. V. Ustinov, JETP 114,
State Physics, North-Holland, Amsterdam (1972)].
645 (2012)].
13.
S. V. Sazonov, J. Phys.: Condens. Matter
6,
6295
24.
С. В. Сазонов, ЖЭТФ 144, 1016 (2013) [S. V. Sazo-
nov, JETP 117, 885 (2013)].
(1994).
25.
Э. А. Маныкин, В. В. Самарцев, Оптическая эхо-
14.
Л. Аллен, Дж. Эберли, Оптический резонанс
спектроскопия, Наука, Москва (1984).
и двухуровневые атомы, Мир, Москва
(1978)
[L. Allen and J. H. Eberly, Optical Resonance and
26.
С. О. Елютин, С. М. Захаров, Э. А. Маныкин,
Two-Level Atoms, John Wiley and Sons, New York
ЖЭТФ 76, 835 (1979) [S. O. Elyutin, S. M. Zakha-
(1978)].
rov, and E. A. Manykin, Sov. Phys. JETP 49,
421
(1979)].
15.
А. Ю. Пархоменко, С. В. Сазонов, Письма в
ЖЭТФ 67, 887 (1998) [A. Yu. Parkhomenko and
27.
В. А. Зуйков, В. В. Самарцев, Р. Г. Усманов, Пись-
S. V. Sazonov, JETP Lett. 67, 934 (1998)].
ма в ЖЭТФ 32, 293 (1980) [V. A. Zuikov, V. V. Sa-
martsev, and R. G. Usmanov, Sov. Phys. JETP Lett.
16.
Г. Кайно, Акустические волны: устройства, визу-
32, 270 (1980)].
ализация и аналоговая обработка сигналов, Мир,
Москва (1990) [G. Kino, Acoustic Waves: Devices,
28.
T. W. Mossberg, Opt. Lett. 7, 77 (1982).
Imaging, and Analog Signal Processing, Prentice-Hall
Inc., New Jersey (1987)].
29.
N. W. Carlson, W. R. Babbit, Y. S. Bai, and
T. W. Mossberg, J. Opt. Soc. Amer. B 1, 506 (1984).
17.
Ф. В. Бункин, Ю. А. Кравцов, Г. А. Ляхов, УФН
149, 391 (1986) [F. V. Bunkin, Yu. A. Kravtsov, and
30.
N. W. Carlson, W. R. Babbit, Y. S. Bai, and
G. A. Lyakhov, Sov. Phys. Uspekhi 29, 607 (1986)].
T. W. Mossberg, Opt. Lett. 9, 232 (1984).
18.
Г. А. Денисенко, ЖЭТФ 60, 2270 (1971) [G. A. De-
31.
У. Х. Копвиллем, В. Р. Нагибаров, В. А. Пирож-
nisenko, JETP 33, 1220 (1971)].
ков, В. В. Самарцев, Р. Г. Усманов, Письма в
ЖЭТФ 20, 139 (1974) [U. Kh. Kopvillem, V. R. Na-
19.
В. В. Самарцев, Б. П. Смоляков, Р. З. Шарипов,
gibarov, V. A. Pirozhkov, V. V. Samartsev, and
Письма в ЖЭТФ 20, 644 (1974) [V. V. Samartsev,
R. G. Usmanov, Sov. Phys.JETP Lett.
20,
60
B. P. Smolyakov, and R. Z. Sharipov, JETP Lett. 20,
(1974)].
296 (1974)].
32.
Н. В. Знаменский, С. В. Сазонов, Письма в ЖЭТФ
20.
А. А. Заболотский, ЖЭТФ
123,
560
(2003)
85, 440 (2007) [N. V. Znamenskii and S. V. Sazonov,
[A. A. Zabolotskii, JETP 96, 496 (2003)].
JETP Lett. 85, 358 (2007)].
343
4
ЖЭТФ, вып. 3