ЖЭТФ, 2023, том 163, вып. 3, стр. 350-356
© 2023
ИССЛЕДОВАНИЕ СВЕРХТОНКИХ ВЗАИМОДЕЙСТВИЙ В
СИНТЕЗИРОВАННЫХ ПРИ ВЫСОКОМ ДАВЛЕНИИ
СОЕДИНЕНИЯХ Y(Fe1-xNix)2 (0 ≤ x ≤ 1) МЕТОДОМ
МЁССБАУЭРОВСКОЙ СПЕКТРОСКОПИИ
А. В. Боковa,b*, М. В. Магницкаяa,c, Д. А. Саламатинa, А. В. Цвященкоa
a Институт физики высоких давлений им. Л. Ф. Верещагина Российской академии наук
108840, Москва, Россия
b Научно-исследовательский институт ядерной физики им. Д. В. Скобельцына,
Московский государственный университет им. М. В. Ломоносова
119991, Москва, Россия
c Физический институт им. П. Н. Лебедева Российской академии наук
119991, Москва, Россия
Поступила в редакцию 17 июня 2022 г.,
после переработки 17 августа 2022 г.
Принята к публикации 28 августа 2022 г.
Выполнены измерения магнитных сверхтонких полей Hhf и изомерного сдвига δ в интерметаллических
соединениях Y(Fe1-xNix)2 (структурный тип MgCu2), синтезированных при высоком давлении. Значения
Hhf , возникающие на ядрах57Fe при концентрации никеля x ниже 20 ат.%, практически не изменяются
и примерно равны 22 Тл, а в интервале от x = 0.4 до x = 0.98 линейно уменьшаются с увеличением
концентрации Ni. Однако линейная экстрополяция сверхтонкого поля в зависимости от концентрации Ni
не приводит к его исчезновению в YNi2. Для YFe2 обнаружен поворот оси легкого намагничивания от
направления [101] к направлению [111] при повышении температуры. При увеличении концентрации Ni
до x = 0.3 при температуре 5 К наблюдается ось легкого намагничивания [101], а при x = 0.4 ось меняет
направление на [100]. Из вида концентрационной зависимости сверхтонкого поля сделано предположение,
что при кристаллизации Y(Fe1-xNix)2 в условиях высоких давлений на ионах Ni существует магнитный
момент. Выполнены ab initio-расчеты магнитных свойств и сверхтонких взаимодействий, согласующиеся
с экспериментом.
DOI: 10.31857/S0044451023030069
ных и щелочноземельных элементов с магнитными
EDN: QECNYL
3d-металлами. Только недавно соединение в систе-
ме K-Ni, полученное в работе [1] без расшифровки
структуры, было идентифицировано как K2Ni с по-
1. ВВЕДЕНИЕ
мощью теоретических ab initio-расчетов [4].
Примерно в то же время были впервые синте-
Хорошо известно, что высокое давление умень-
зированы и изучены соединения кальция с Fe, Co
шает средний объем элементарной ячейки кристал-
и Ni [2, 3]. В частности, были выполнены деталь-
лической структуры и может вызывать изменение
ные экспериментальные и теоретические исследова-
электронной конфигурации некоторых элементов. В
ния непрерывного ряда псевдобинарных соединений
некоторых случаях это может приводить к образо-
Ca(Fe1-xNix)2 (структурный тип MgCu2). В насто-
ванию соединений между элементами, которые при
нормальных условиях не образуются [1-4]. Напри-
ящей работе рассмотрен аналогичный этой систе-
ме ряд Y(Fe1-xNix)2 и изучены его свойства. Мето-
мер, в ранних работах [1-3] были синтезированы под
давлением не известные до этого соединения щелоч-
дом эффекта Мессбауэра на ядрах57Fe исследованы
сверхтонкие взаимодействия. Магнитные свойства и
* E-mail: bokov@hppi.troitsk.ru
сверхтонкие взаимодействия рассчитаны также ме-
350
ЖЭТФ, том 163, вып. 3, 2023
Исследование сверхтонких взаимодействий...
тодом ab initio.
Соединения Y(Fe1-xNix)2 для x от 0 до 1, син-
Топологически плотноупакованные фазы Лаве-
тезированные при высоких давлениях и температу-
са довольно распространены среди интерметалличе-
рах, по данным рентгеноструктурного анализа и на-
ских соединений. Материалы на их основе исполь-
магничивания кристаллизуются в кубическую фа-
зуются как контейнеры для хранения водорода, как
зу Лавеса со структурой С15. Магнитный момент
магнитомеханические датчики и приводы, а также в
ионов Ni составляет 0.36µB для всех значений x [13].
качестве износостойких и коррозионно-стойких по-
При x = 0.35 наблюдается аномалия зависимости
крытий в агрессивных средах и при высоких темпе-
постоянной решетки от состава x. Установлено так-
ратурах [5]. Исследования этих систем, содержащих
же [13], что в Y(Fe1-xNix)2 зависимость магнитного
металлы группы железа, представляют интерес так-
момента, приходящегося на один атом переходного
же для физики Земли и сходных с ней планет.
металла, от числа 3d-электронов Nd имеет харак-
В данной работе для соединений Y(Fe1-xNix)2,
тер кривой Слэтера-Полинга, аналогично системе
синтезированных при высоком давлении, мето-
Fe1-xNix.
дом мессбауэровской спектроскопии исследована
эволюция сверхтонких магнитных полей в узлах
3d-металлов при замещении железа (электронная
2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
конфигурация
[Ar]3d64s2) никелем (электронная
конфигурация [Ar]3d84s2). Мессбауэровские спек-
тры57Fe позволяют определить изомерные сдвиги,
Псевдобинарные интерметаллиды Y(Fe1-xNix)2
сверхтонкие поля и направление оси легкого
были получены путем воздействия высокой темпе-
намагничивания в поликристалле.
ратуры при постоянном давлении 7.7 ГПа в камере,
Кубическая фаза Лавеса (С15, тип MgCu2) со-
сконструированной Хвостанцевым и др. [14]. Дета-
единения YFe2 представляет собой ферримагнетик
ли процедуры, использованной в этих эксперимен-
с магнитными моментами на атомах Fe, равны-
тах, приведены в работе [15]. После синтеза под вы-
ми 1.77µB, и антипараллельными им моментами на
соким давлением кристаллическая структура образ-
4d-атомах Y, равными -0.67µB [6, 7]. Соединение
цов соединений была определена с помощью порош-
YNi2, которое образуется при нормальном давле-
ковой рентгеновской дифракции. Поликристалличе-
нии, кристаллизуется в сверхструктуру кубической
ские образцы были однофазнымии и кристаллизова-
фазы Лавеса C15 [8]. В этом соединении возника-
лись в структуре кубической фазы Лавеса (С15).
ют вакансии в узлах Y (до 5-7 ат.%), упорядочен-
Измерения эффекта Мессбауэра γ-перехода
ные при низких температурах. При комнатной тем-
14.4 кэВ 57Fe проводились для серии соединений
пературе эти вакансии обладают высокой подвиж-
Y(Fe1-xNix)2 с
ностью [9]. Показано, что при высоких темпера-
турах и/или при приложении внешнего давления
x = 0;0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;0.95;0.98
происходит обратимый структурный переход (ти-
па порядок-беспорядок) в кубическую фазу Лавеса
при T = 5 К. Образцы с 2, 5 и 10 ат.% Fe обогаща-
С15, связанный с разупорядочением вакансий [10].
лись изотопом57Fe до 100 %, а образцы с 20, 30 и
Соединение YNi2 в сверхструктуре кубической фа-
40 ат.% Fe обогащались57Fe до 20 %.
зы Лавеса является паулевским парамагнетиком,
Спектры получены с помощью спектрометра с
что связано с низкой плотностью электронных со-
стояний на уровне Ферми для этого соединения [11].
постоянным ускорением, описанного в работе [16]. В
В работе [12] было показано, что соединения
качестве источника γ-квантов использовали57Co в
медной матрице. Отметим, что все мессбауэровские
Y0.95(Fe1-xNix)2, где x ≤ 0.95, синтезированные при
нормальном давлении, кристаллизуются в кубиче-
спектры измерялись при атмосферном давлении.
ской фазе Лавеса С15. Из температурных измере-
Программа, использующая точное аналитиче-
ний электрического сопротивления было высказано
ское выражение для положений и интенсивностей
предположение, что в соединении с x = 0.95 суще-
мессбауэровских линий, была применена для
ствует локальный магнетизм, связанный с коротко-
определения параметров сверхтонкой структуры.
действующими спиновыми флуктуациями или обра-
Для каждого спектра, полученного от поглоти-
зованием основного состояния кластерного стекла.
теля Y(Fe1-xNix)2
(0
≤ x ≤ 1), была сделана
Для соединений с x = 0.85 и x = 0.75, вероятно,
компьютерная подгонка с использованием метода
имеет место дальнее магнитное упорядочение.
статистической регуляризации [17]. Среднее значе-
351
А. В. Боков, М. В. Магницкая, Д. А. Саламатин и др.
ЖЭТФ, том 163, вып. 3, 2023
ние сверхтонкого поля определялось из следующего
разце YFe2, приготовленном при нормальном дав-
соотношения:
лении [18] (см. рис. 1 и таблицу).
∕
∑
∑
Hhf = HiPi
Pi,
i=0
i=0
где Pi
вероятность существования локального
сверхтонкого поля Hi на диаграмме распределения
Pi(Hi).
3. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Для соединений RFe2 (R редкоземельный эле-
мент) мессбауэровские исследования57Fe показали,
что хотя эти соединения имеют одинаковую кри-
сталлографическую структуру типа С15, они пред-
ставляют несколько типов спектров [18]. В этих
соединениях ионы железа, лежащие в общей сет-
ке правильных тетраэдров с общими углами, име-
ют узловую симметрию 3m с тремя осями, па-
раллельными направлениям [111]. Позиции ионов
железа (16c) кристаллографически эквивалентны,
но в присутствии магнитного поля они магнитно-
неэквивалентны, поскольку электрические квадру-
польные взаимодействия зависят от угла θ между
осью аксиально-симметричного градиента электри-
ческого поля и магнитным полем, которое не бу-
дет одинаковым для всех ионов железа [19]. Ес-
ли вектор легкого намагничивания n совпадает с
кристаллографическим направлением [111], то су-
ществуют два магнитно-неэквивалентных узла же-
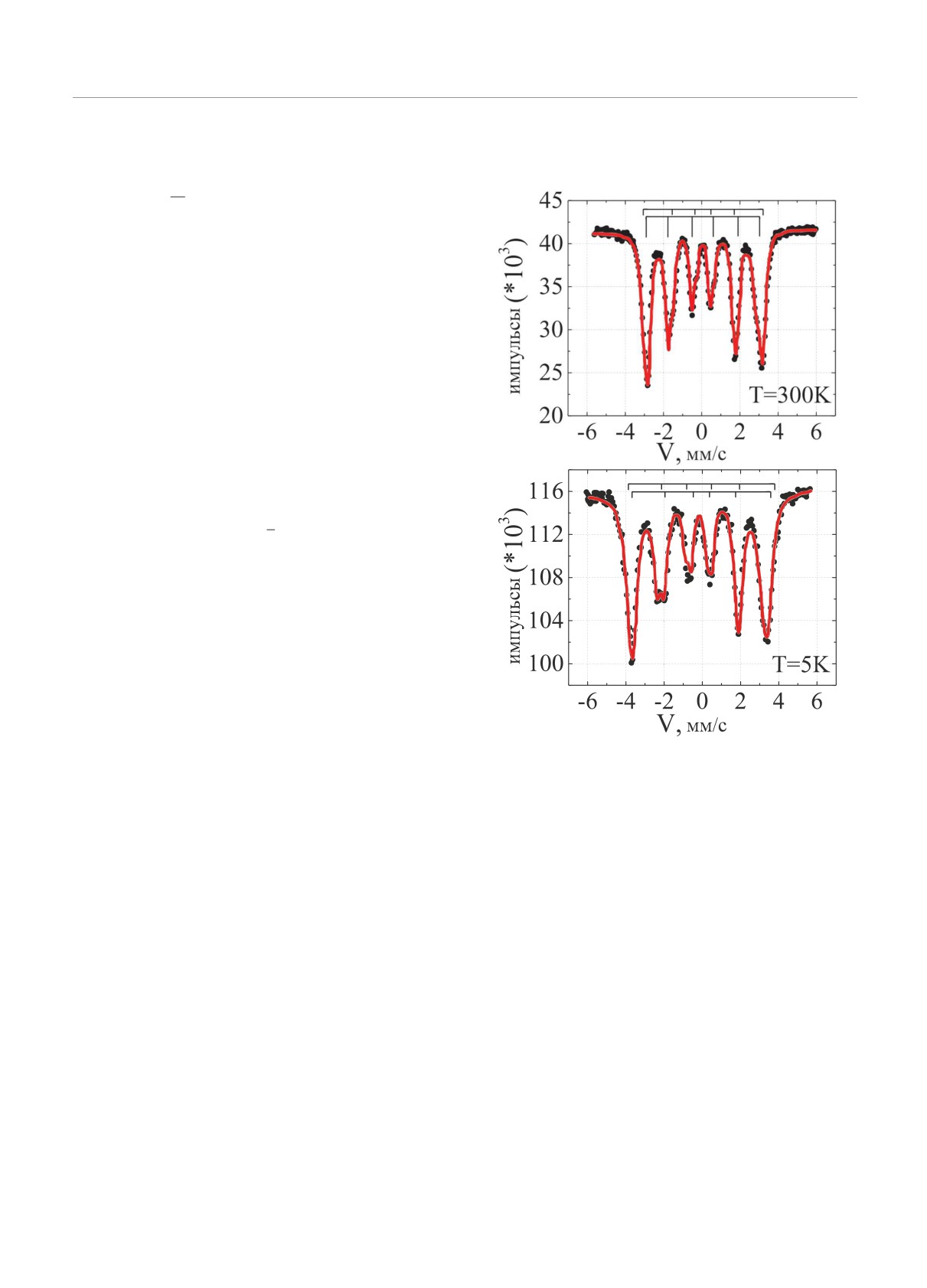
Рис. 1. Мессбауэровские спектры57Fe синтезированного
леза с относительной заселенностью 3 : 1, что при-
под высоким давлением YFe2 при различных температу-
водит к спектру, который представляет собой су-
рах. Точки экспериментальные данные, сплошные ли-
перпозицию двух шестилинейных структур, как это
нии
аппроксимации. Метки над спектрами означают
наблюдается для YFe2, синтезированного при нор-
вклады от сверхтонкого магнитного расщепления
мальном давлении в диапазоне температур от 1.7 К
до TC (545 К) [18]. При n, параллельном оси [101],
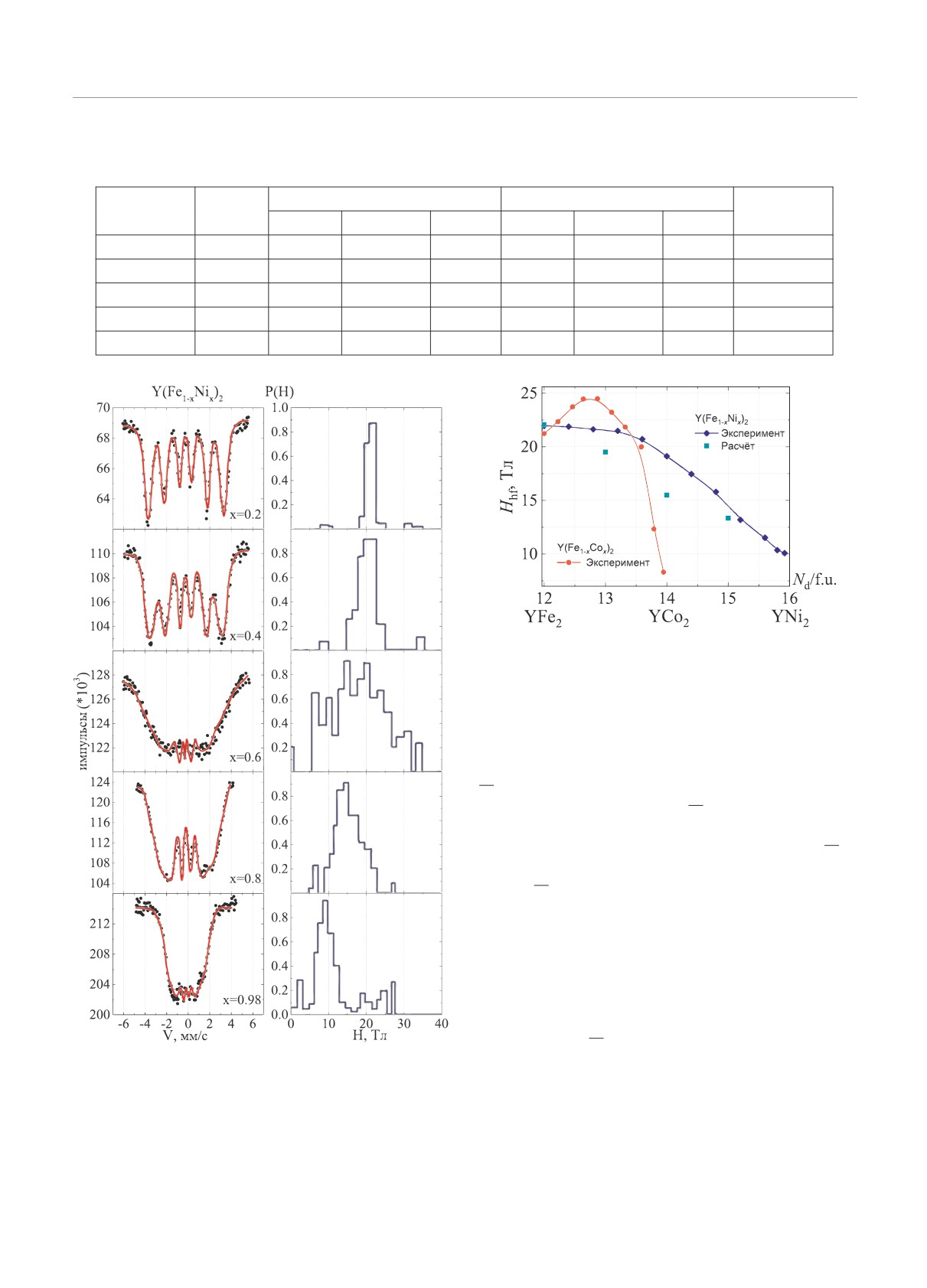
Для образцов Y(Fe1-xNix)2 с концентрацией Ni
присутствуют две магнитно-неэквивалентные пози-
в области 0 ≤ x ≤ 0.3 ось легкого намагничивания
ции железа с соотношением заселенностей 1 : 1, как
параллельна оси [101], а для x = 0.4 ось легкого на-
это наблюдается в LuFe2 и в SmFe2 [20]. При направ-
магничивания параллельна оси [100] при T = 5 К.
лении вектора легкого намагничивания n вдоль оси
Однако при 0.2 ≤ x ≤ 0.4 видно уширение линий
[100] все ионы железа эквивалентны и спектр опи-
на мессбауэровских спектрах, а при x = 0.4 шири-
сывается одной шестилинейной структурой.
на линий сильно увеличивается. Уширение может
Спектр синтезированного под высоким давлени-
быть связано с различными вариациями локально-
ем YFe2, измеренный при T = 5 К, состоит из двух
го окружения ядер57Fe. Поэтому для 0 ≤ x ≤ 0.98
сверхтонких ¾шестилинеек¿ с соотношением интен-
средние значения сверхтонкого поля определялись
сивностей 1 : 1 (рис. 1 и таблица). Это согласуется
из компьютерных подгонок с использованием ме-
с направлением оси легкого намагничивания вдоль
тода статистической регуляризации, который был
одного из направлений [101]. Однако установлено,
предложен для оценки неразрешенных мессбауэров-
что при T = 300 К ось легкого намагничивания на-
ских спектров многих перекрывающихся линий [17]
правлена вдоль [111], как это наблюдалось в об-
(рис. 2).
352
ЖЭТФ, том 163, вып. 3, 2023
Исследование сверхтонких взаимодействий...
Таблица. Параметры сверхтонкого взаимодействия57Fe в соединении YFe2, синтезированном при различных
давлениях (Psynth). Hhf
сверхтонкое магнитное поле (погрешность ±0.1 Тл), ΔE квадрупольное расщепление
(погрешность ±0.01 мм/с), δ изомерный сдвиг относительно α-Fe (погрешность ±0.01 мм/с)
Спектр I
Спектр II
Psynth ,ГПа
T,К
Легкая ось
Hhf ,Тл ΔE,мм/с δ,мм/с Hhf ,Тл ΔE,мм/с δ,мм/с
7.7
5
22.5
0.14
0.43
21.3
-0.17
0.34
101
7.7
300
18.7
0.19
0.13
18.2
-0.28
0.13
111
≈0
1.7 [18]
21.5
20.8
111
≈0
295 [21]
19.2
0.04
-0.18
18.5
-0.12
-0.03
111
≈0
300 [22]
18.0
18.9
111
Рис. 3. (В цвете онлайн) Среднее сверхтонкое поле на ядре
Fe для Y(Fe1-xNix)2 при 5 К (синяя линия наши изме-
рения) и для Y(Fe1-xCox)2 при 1.7 К (красная линия
работа [6]) как функция числа 3d-электронов Nd на фор-
мульную единицу. Результаты наших расчетов показаны
голубыми символами
На рис.3 средние значения сверхтонкого поля
Hhf при T = 5 К представлены в зависимости от
концентрации Ni. Значения Hhf при концентрации
Ni менее 20 ат.% почти не изменились. От x = 0.4
до x = 0.98 наблюдается линейное уменьшение Hhf .
Заметим, что в системе Y(Fe1-xCox)2 резкое умень-
шение Hhf было обнаружено уже при x
≥ 0.8
(см. рис. 3) и тесно связано с исчезновением магнит-
ного момента на атомах Со в этом ряду [18]. С дру-
гой стороны, установлено, что зависимость средней
величины сверхтонкого поля на ядре железа в ряду
R(Fe0.02Ni0.98)2 (где R = Gd, Dy, Ho, Tb, Er) опре-
деляется из выражения
Hhf = H0 + a(g - 1)J,
Рис. 2. (В цвете онлайн) Мессбауэровские спектры57Fe
где H0
постоянное сверхтонкое поле, связанное
некоторых соединений Y(Fe1-xNix)2, измеренные при
с железом, зависящее исключительно от взаимо-
T = 5К. Точки экспериментальные данные. Сплошные
действий Fe - Fe и Fe - Ni и равное 11(1) Тл [23].
красные линии и диаграмма распределений вероятностей
Из наших экспериментов также следует, что для
сверхтонких полей P (H) получены подгонкой
Y(Fe0.02Ni0.98)2 среднее значение сверхтонкого поля,
353
А. В. Боков, М. В. Магницкая, Д. А. Саламатин и др.
ЖЭТФ, том 163, вып. 3, 2023
измеренное при 5 К, равно 10.9 Тл. Это указывает
на то, что магнитное сверхтонкое поле определяет-
ся магнитным моментом Ni.
В отличие от усиленного парамагнетика Паули
YCo2, сплав YFeNi, в котором, вероятно, должно
быть такое же заполнение 3d-зоны, как и в YCo2,
является ферримагнетиком [13] и имеет значение
сверхтонкого поля, близкое к значению сверхтонко-
го поля в HoCo2, когда поляризующее влияние Но
приводит к возникновению момента на атомах Со,
равного 1.0µB [24, 25].
Таким образом, при воздействии, например,
внешнего или внутреннего магнитного поля или
давления (как в нашем случае) в 3d-электронной
зоне сплавов Y(Fe1-xNix)2, вероятно, 3d-электроны
Ni могут принимать участие в метамагнетизме
коллективизированных электронов так же, как
3d-электрон Co в сплавах Y(Fe1-xCox)2 [26-28].
Из изучения сверхтонкого поля на ядре Fe в
Рис. 4. (В цвете онлайн) Зависимости магнитного момен-
ряду сплавов Y(Fe1-xNix)2 можно сделать вывод,
та в Y(Fe1-xNix)2 от концентрации никеля x: в расчете
что индуцированный высоким давлением электрон-
на формульную единицу (a) и на атом переходного ме-
ный переход приводит к возникновению собствен-
талла (b). Результаты измерений [13] при 4.2 К и нашего
ного магнитного момента на ионах Ni, который от-
ab initio-моделирования показаны синим и красным цве-
ветственен за большие значения сверхтонкого поля
том соответственно
для всех значений x. При этом нужно понимать, что
непрерывный ряд соединений Y(Fe1-xNix)2 при ат-
Вообще говоря, замещение Fe на Ni понижает
мосферном давлении не образуется. А получение со-
симметрию решетки, и в результате структура трой-
единений при высоком давлении в метастабильной
ных соединений становится не кубической, а тетра-
форме связано с изменением электронных свойств
гональной. Это тетрагональное искажение доволь-
Ni [29].
но слабое, и структура с пониженной симметрией
очень близка к исходной решетке C15. Поэтому по-
рошковые рентгенограммы соответствующих спла-
4. РАСЧЕТЫ МЕТОДОМ AB INITIO
вов показывают лишь небольшое уширение рефлек-
Расчеты электронных и магнитных свойств
сов C15, вызванное легированием. Однако сверхтон-
Y(Fe1-xNix)2 проводились в рамках теории
кое взаимодействие является локальным свойством,
функционала электронной плотности методом
и его вычисленные значения очень чувствительны
присоединенных плоских волн (APW+lo), ре-
даже к небольшим изменениям симметрии и коор-
ализованным в пакете WIEN2k
[30], с полу-
динат атомов. В искаженной решетке координаты
локальным приближением PBE-GGA
[31] для
атомов становятся свободными, а не строго фикси-
обменно-корреляционного функционала. Использо-
рованными, как в кубической структуре C15. Поэто-
вался параметр RminKmax = 8.0 и сетки k-точек
му для составов c x = 0.25, 0.50, 0.75 была выполнена
Монкхорста - Пака, соотвествующие разрешению
релаксация положений атомов; при этом остаточные
в обратном пространстве около 0.15Å-1. Для Y и
атомные силы не превышали 5 мэВ/Å.
Fe/Ni были выбраны МТ-радиусы, равные 2.50 и
Спин-поляризованные расчеты проводились для
2.38 радиуса Бора соответственно.
коллинеарного расположения спинов. На рис. 4
Были выполнены расчеты для концентраций x,
представлена рассчитанная концентрационная
равных 0, 0.25, 0.50, 0.75, 1.00. Электронная структу-
зависимость магнитного момента в Y(Fe1-xNix)2,
ра псевдобинарных сплавов (x = 0.25, 0.50, 0.75) рас-
приходящегося на формульную единицу и на один
считывалась как структура гипотетических упоря-
атом переходного металла (ТМ). Вычисленный
доченных тройных соединений с той же стехиомет-
момент внутри сферы, окружающей атом Fe, слабо
рией. Для каждой концентрации x использовалась
зависит от концентрации x. Момент в сфере Ni
экспериментальная постоянная решетки a.
параллелен моменту Fe и для состава Y(Fe1.5Ni0.5)2
354
ЖЭТФ, том 163, вып. 3, 2023
Исследование сверхтонких взаимодействий...
Hhf (x) также удовлетворительно согласуется с экс-
периментом (см. рис. 3). Что касается квадруполь-
ного расщепления ΔE, то теоретическое значение
составляет около -1.0 мм/с для всех концентра-
ций, что значительно превышает эксперименталь-
ные значения.
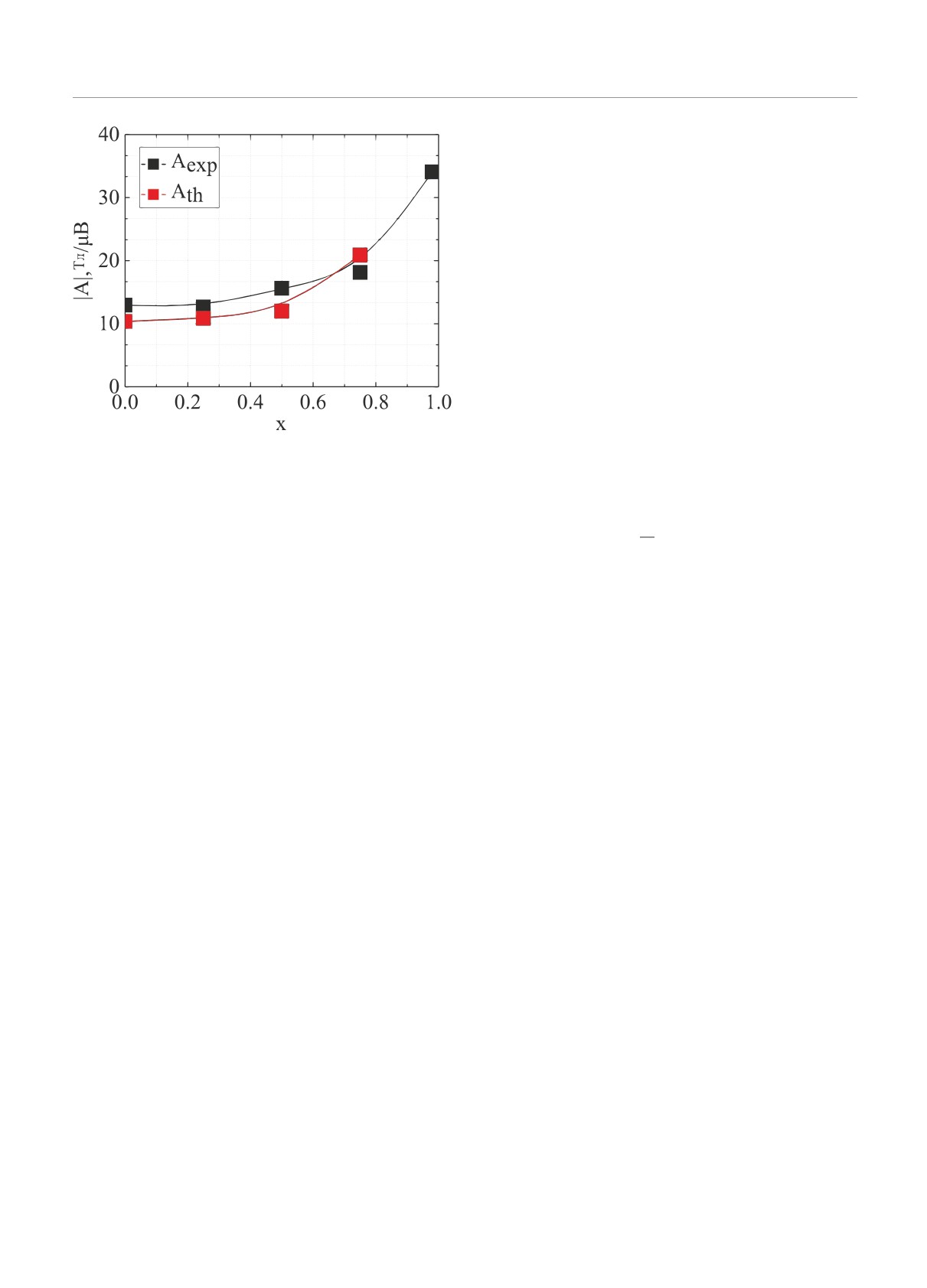
Константы спаривания между сверхтонкими по-
лями и магнитными моментами (A = Hhf /µTM ) так-
же рассчитаны в зависимости от концентрации x
для полученных экспериментальных результатов и
теоретических расчетов (рис.5). На рисунке показа-
но нелинейное увеличение значения A с увеличени-
ем концентрации Ni.
5. ВЫВОДЫ
Рис. 5. Константы спаривания: Aexp экспериментальные
Методом эффекта Мессбауэра на ядрах57Fe из-
результаты, Ath теоретические расчеты
мерены сверхтонкие взаимодействия в соединение
Y(Fe1-xNix)2 (0 ≤ x ≤ 0.98). Установлено, что экс-
равен 0.36µB, что совпадает с экспериментальным
трополяция концентрационной зависимости средне-
значением, найденным в работе [13]. Предпола-
го сверхтонкого поля Hhf не стремится к нулю при
галось
[13], что момент Ni, равный
0.36µB, не
x → 1. Это свидетельствует о наличии магнитного
меняется с увеличением x. Однако наш расчет
момента у ионов Ni в ряду соединений Y(Fe1-xNix)2,
показывает, что при увеличении x от 0.25 до 0.75
синтезированных при высоком давлении. Для YFe2,
момент на Ni монотонно уменьшается до 0.13µB.
синтезированного при высоком давлении, обнару-
Магнитный момент в сфере Y антипаралле-
жен поворот легкой оси намагничивания от на-
лен моментам Fe/Ni, что подтверждает предпо-
правления [101] к направлению [111] с повышением
ложение [13] о ферримагнитном упорядочении в
температуры. При увеличении концентрации Ni до
Y(Fe1-xNix)2. Вычисленный момент на Y изменя-
x = 0.3 (при температуре 5К) наблюдается ось лег-
ется монотонно примерно от -0.3µB для YFe2 до
кого намагничивания [101], а при x = 0.4 ось меня-
-0.1µB для Y(Fe0.5Ni1.5)2, что отличается от значе-
ет направление на [100]. Ab initio-расчеты сверхтон-
ния -0.67µB, принятого в работе [13] для всех кон-
ких взаимодействий находятся в разумном согла-
центраций x. Следует также отметить, что геомет-
сии с экспериментом. Таким образом, образование
рия метода APW предполагает наличие магнитного
непрерывного ряда соединений Y(Fe1-xNix)2 связа-
момента в междоузлии, который вносит существен-
но с возникновением при высоком давлении элек-
ный вклад (в данном случае отрицательный) в пол-
тронного перехода из конфигурации 3d94s1 в кон-
ный момент элементарной ячейки. Магнитное состо-
фигурацию 3d9-y4s1+y в ионах Ni, где y может из-
яние для YNi2 оказалось неустойчивым, т. е. момент
меняться с концентрацией Ni.
равен нулю, в отличие от результатов работы [13],
где был найден момент на Ni порядка 0.3µB.
Благодарности.
Авторы
признательны
В.И. Крылову за помощь в проведении экс-
На рис.3 показано сверхтонкое поле Hhf на ядре
перимента. Численные расчеты проводились с
Fe в зависимости от числа d-электронов Nd на фор-
мульную единицу, которое является линейной функ-
использованием оборудования центра коллектив-
ного пользования
¾Комплекс моделирования и
цией концентрации x. Это позволяет представить
Hhf для Y(Fe1-xNix)2 и Y(Fe1-xCox)2 на одном гра-
обработки данных исследовательских установок
мега-класса¿ НИЦ
¾Курчатовский институт¿
фике. Вычисленный изомерный сдвиг δ на ядре Fe
(относительно ОЦК α-Fe) практически не зависит
Межведомственного суперкомпьютерного центра
от концентрации и изменяется от 0.22 до 0.23 мм/с.
Российской академии наук (МСЦ РАН).
Для YFe2 рассчитанные значения сверхтонкого
поля Hhf и изомерного сдвига δ согласуются с экс-
Финансирование. Исследование выполне-
периментальными значениями для образцов, син-
но за счет гранта Российского научного фонда
тезированных при высоком давлении. Зависимость
355
А. В. Боков, М. В. Магницкая, Д. А. Саламатин и др.
ЖЭТФ, том 163, вып. 3, 2023
ЛИТЕРАТУРА
16.
С. И. Рейман, Н. И. Рохлов, В. С. Шпинель и др.,
ЖЭТФ 86, 330 (1984).
1.
L. J. Parker, T. Atou, and J. V. Badding, Science
273, 95 (1996).
17.
А. С. Меченов, Регуляризованный метод наимень-
ших квадратов, Изд-во Моск. ун-та, Москва
2.
А. В. Цвященко, Л. Н. Фомичева, М. В. Магницкая
(1988).
и др., Письма в ЖЭТФ 68, 864 (1998).
18.
M. G. Luijpen, P. C. M. Gubbens, A. M. van der
3.
A. V. Tsvyashchenko, L. N. Fomicheva, M. V. Mag-
Kraan et al., Physica B+C 86-88, 141 (1977).
nitskaya et al., The Physics of Metals and
19.
G. J. Bowden, D. St. P. Bunbury, A. P. Guimaraes et
Metallography 93, S59 (2002).
al., J. Phys. C 1, 1376 (1968).
4.
A. A. Adeleke and Y. Yao, J. Chem. Phys. 124, 4752
20.
K. H. J. Buschow, Rep. Progr. Phys. 40, 1179 (1977).
(2020).
21.
K. Itoh, K. Kanematsu, and K.-I. Kobayashi, J. Phys.
5.
F. Stein and A. Leineweber, J. Mater. Sci. 56, 5321
Soc. Jpn 58, 4650 (1989).
(2021).
22.
M. J. Besnus, P. Bauer, and J. M. Genin, J. Phys. F 8,
6.
C. Ritter, J. Phys.: Condens. Matter 1, 2765 (1989).
191 (1978).
7.
A. Posinger, M. Reissner, W. Steiner et al., J. Phys.:
23.
S. K. Arif, I. Sigalas,
and D. S. T. P. Bunbury,
Condens. Matter 5, 7277 (1993).
Phys. Stat. Sol. (a) 41, 585 (1977).
8.
V. Paul-Boncour, A. Lindbaum, M. Latroche et al.,
24.
A. M. van der Kraan and P. C. M. Gubbens,
Intermetallics 14, 483 (2006).
J. Phys. Colloques 35, C6-469 (1974).
9.
M. Forker, P. de la Presa, and A. F. Pasquevich,
25.
R. M. Moon, W. C. Koehler, and J. Farrell, J. Appl.
J. Phys.: Condens. Matter 18, 253 (2005).
Phys. 36, 978 (1965).
10.
E. Gratz and A. S. Markosyan, J. Phys.: Condens.
26.
O. Eriksson, B. Johansson, M. S. S. Brooks et al.,
Matter 13, R385 (2001).
Phys. Rev. B 40, 9519 (1989).
11.
F. Z. Mohammad, S. Yehia, and S. Aly, Int. J. Phys.
27.
K. Yoshimura, Y. Yoshimoto, M. Mekata et al.,
and Appl. 2, 135 (2010).
J. Magn. Magn. Mater. 70, 147 (1987).
12.
O. Myakush, V. Babizhetskyy, P. Myronenko et al.,
28.
T. Goto, K. Fukamichi, T. Sakakibara et al., Sol. St.
Chem. Met. Alloys 4, 152 (2011).
Comm. 72, 945 (1989).
13.
A. V. Tsvyashchenko, L. N. Fomicheva, and S. D. An-
29.
A. V. Tsvyashchenko, L. N. Fomicheva, E. N. Shirani
tipov, J. Magn. Magn. Mater. 98, 285 (1991).
et al., Phys. Rev. B 55, 6377 (1997).
14.
L. G. Khvostantsev, V. N. Slesarev, and V. V. Brazh-
30.
P. Blaha, K. Schwarz, F. Tran et al., J. Chem. Phys.
kin, High Press. Res. 24, 371 (2004).
152, 074101 (2020).
15.
A. V. Tsvyashchenko, J. Less Comm. Met.
99, L9
31.
J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev.
(1984).
Lett. 77, 3865 (1996).
356