ЖЭТФ, 2023, том 163, вып. 3, стр. 357-365

ДИНАМИЧЕСКАЯ ТРАНСФОРМАЦИЯ ДОМЕННЫХ СТЕНОК В

КИРАЛЬНЫХ ФЕРРИМАГНЕТИКАХ

Н. Е. Кулагин^*

Институт физической химии и электрохимии им. А. Н. Фрумкина Российской академии наук

119071, Москва, Россия

Национальный исследовательский университет ¾Высшая школа экономики¿

101000, Москва, Россия

Поступила в редакцию 16 июля 2022 г.,

после переработки 30 октября 2022 г.

Принята к публикации 31 октября 2022 г.

Теоретически исследована динамика доменных стенок в ферримагнетиках, в которых инвариантность

относительно пространственной инверсии нарушена из-за присутствия кирального взаимодействия Дзя-

лошинского - Мория, энергия которого линейна по градиентам спиновой плотности подрешеток. Анализ

проведен на основе численного интегрирования уравнений сигма-модели, обобщенной для случая фер-

римагнетика вблизи точки компенсации спинов подрешеток. Показано, что в киральных ферримагнети-

ках, в отличие от случаев обычных ферримагнетиков или киральных ферромагнетиков, при увеличении

скорости стенки возможны эффекты динамического преобразования структуры доменных стенок с обра-

зованием более сложных стенок с немонотонным поведением спиновой плотности в стенке. Эти эффекты

возможны в достаточно узкой окрестности точки компенсации, и ширина этой области растет при уве-

личении константы взаимодействия Дзялошинского - Мория.

DOI: 10.31857/S0044451023030070

торые имеют место для ДС в ФМ [18].

EDN: QEMESS

Недавно было показано экспериментально [19-

21] и обосновано теоретически [22-24]. что в образ-

1. ВВЕДЕНИЕ

цах ферримагнетиков (ФиМ), близких к точке ком-

пенсации спинов подрешеток, также можно полу-

Статические и особенно динамические свойства

чить высокую скорость ДС, которая достигает ки-

доменных стенок (ДС) в магнетиках являются пред-

лометров в секунду. Причина этого эффекта в том,

метом интенсивных экспериментальных [1-4] и тео-

что для ФиМ, находящихся в непосредственной бли-

ретических [5-8] исследований в связи с возможно-

зости от точки компенсации спинов, где совпадают

стью их применения в магнитных устройствах хра-

спиновые плотности подрешеток, возможны эффек-

нения и обработки информации [9]. Магнитные ДС

ты обменного усиления [25]. В частности, в самой

представляют собой простой, но важный пример

точке компенсации предельная скорость движения

топологических солитонов и представляют интерес

ДС становится, как и в АФМ, чисто обменной.

с точки зрения общей физики нелинейных явле-

ний [10-12]. Динамика ДС интересна не только для

Однако для нанообразцов различных магнети-

стандартных материалов ферромагнетиков (ФМ),

ков скорость движения ДС ограничена в большей

но и для антиферромагнетиков (АФМ), в которых

степени, чем для массивных образцов или микрон-

значение скорости ДС значительно выше и достига-

ных пленок. Насколько нам известно, для нанопле-

ет десятков километров в секунду [13-17]. Такие вы-

нок АФМ движение ДС с ¾обменными¿ скоростя-

сокие скорости определяются так называемым об-

ми не наблюдалось. Для ФиМ около точки компен-

менным усилением динамических параметров АФМ.

сации спина наблюдались скорости до 1 км/с, в то

Не менее важно, что для ДС в АФМ подавлены раз-

время как теоретические оценки дают значения до

личные эффекты нестабильности динамики ДС, ко-

5 км/с [22-24]. Причина уменьшения скорости ДС в

одноосных ФМ состоит в том, что стандартный ме-

^* E-mail: klgn@yandex.ru

ханизм формирования предельной скорости, связан-

357

Н. Е. Кулагин

ЖЭТФ, том 163, вып. 3, 2023

ный с магнитным дипольным взаимодействием, ста-

2. МОДЕЛЬ

новится неэффективным для нанопленок ФМ. Это

Рассмотрим магнетик с двумя подрешет-

же ограничение проявляется и для ФиМ с чисто од-

ками, плотности спина которых s₁ и s₂,

ноосной анизотропией. Оно заложено в модели, ис-

|s_1,2|

= s_1,2

= const. Для АФМ s₁

= s₂, а в

пользованной авторами работы [19] для численно-

интересующем нас случае ФиМ, близкого к точке

го моделирования результатов своего эксперимента.

компенсации спинов подрешеток, спиновые плотно-

Наличие достаточно сильной анизотропии в базис-

сти не равны, но имеют близкие значения s₁ ≈ s₂.

ной плоскости и (или) сильного магнитного поля,

Динамика векторов s₁ и s₂ определяется системой

перпендикулярного легкой оси магнетика, может ре-

двух уравнений Ландау - Лифшица, которые удоб-

шить эту проблему, но реализация этих механизмов

но переписать в терминах комбинации спиновых

для приборов магнитной наноэлектроники, исполь-

плотностей:

зующих динамику ДС, затруднительна.

s₁ - s₂

s₁ + s₂

(1)

Для нанопленок киральных ФМ, в которых

s₁ + s₂

за счет взаимодействия Дзялошинского - Мория

Наиболее простое и удобное описание динамики

(ВДМ) нарушена симметрия спиновой систе-

ФиМ вблизи точки компенсации базируется на ис-

мы относительно пространственной инверсии,

пользовании так называемой обобщенной сигма-мо-

предельная скорость ДС может существенно увели-

дели замкнутого уравнения для вектора l. Впер-

чиваться [26-28]. В текущем столетии обнаружено,

вые это уравнение было получено для анализа АФМ

что ВДМ может быть получено практически для

(см. историю вопроса и современное состояние про-

всех магнетиков, если приготовить их в виде

блемы в обзоре [29]), но оно допускает обобщение

сверхтонких (толщина менее

10 нм) пленок на

на случай почти скомпенсированных ФиМ [30, 31],

подложке из немагнитного металла с сильным

см. также недавний обзор [25]. В рамках этого под-

спин-орбитальным взаимодействием. В этом случае

хода основной динамической переменной при опи-

плотность энергии ВДМ определяется формулой

сании АФМ является нормированный вектор анти-

D [M_z(∇ · l) - (l · ∇)l_z], где D константа ВДМ, l

ферромагнетизма l, для которого получается урав-

параметр порядка ферримагнетика (см. формулу (

нение [25]

ref23040-eq1)), ось z выбрана перпендикулярно

[

]

[

]

∂l

∂²l

δW

поверхности пленки. Таким образом, нарушение

l×

(2)

∂t

ω_ex

∂t²

ℏ(s₁ + s₂)

δl

киральной симметрии является общим свойством

нанопленок магнетиков, и киральные магнетики

где W

= W[l]

статическая энергия ФиМ

могут рассматриваться как стандартные материалы

(4), записанная в виде функционала вектора l,

нанофизики магнетиков. Киральные ФиМ, допуска-

ℏω_ex = gµ_BH_ex , где H_ex так называемое обменное

ющие существование скирмионов (топологических

поле, и введено обозначение ν = (s₁ - s₂)/(s₁ + s₂).

солитонов малого радиуса) и ДС, интенсивно ис-

Специфика ФиМ проявляется только при весьма

следуются, для них получены значения скорости

малых значениях ν ≪ 1, в противном случае ФиМ

ДС до 1.3 км/с, что на настоящий момент является

ведет себя как ФМ и описывается уравнением Лан-

максимальным значением для всех магнетиков, за

дау - Лифшица с некоторой эффективной спиновой

исключением АФМ [21].

плотностью спина s_eff

= s₁ - s₂. В рамках сиг-

Исследована теоретически динамика ДС в тон-

ма-модели вектор m играет роль вспомогательной

ких пленках киральных ФиМ при всех значениях

переменной и выражается через l и ∂l/∂t простой

константы ВДМ D < D_c, где D_c известное крити-

формулой

]

[∂l

ческое значение; при D > D_c однородное состояние

m=νl+

×l

(3)

ω_ex

∂t

невыгодно термодинамически и энергия ДС отрица-

Таким образом, вместо двух уравнений для намаг-

тельна. Показано, что в киральных ФиМ, в отличие

ниченностей подрешеток можно использовать одно

от случаев обычных ФиМ (без киральных вкладов

уравнение для l. Энергию кирального магнетика вы-

в энергию) или киральных ФМ, динамические свой-

берем в простейшем виде, который допускает описа-

ства ДС в значительной мере определяются разру-

ние динамики ДС:

шением интегрируемости соответствующей динами-

∫

ческой задачи. Вблизи точки компенсации имеет ме-

(

)

W = dr

(∇ · l)² +K

l^2x + l^2y

сто динамическая конверсия стандартных ДС с об-

}

разованием более сложные стенок с немонотонным

− D[l_z(∇ · l) - (l · ∇)l_z)]

(4)

поведением намагниченности.

358

ЖЭТФ, том 163, вып. 3, 2023 Динамическая трансформация доменных стенок в киральных ферримагнетиках

где первое слагаемое определяет энергию неодно-

ϕ = ϕ(x - vt), v скорость ДС. Уравнения для θ и

родного обмена с константой A, второе энергию

ϕ принимают вид системы обыкновенных диффе-

одноосной анизотропии, легкая ось выбрана вдоль

ренциальных уравнений относительно переменной

оси z, K > 0. Последнее слагаемое под интегралом

x-vt. Для определенности будем считать что θ → 0

определяет киральное ВДМ, характерное для тон-

при x-vt → -∞ и θ → π при x-vt → +∞. Несмотря

кой пленки, поверхность которой перпендикулярна

на отсутствие точной лоренц-инвариантности, удоб-

оси z.

но выбрать в качестве независимой переменной ве-

Уравнение обобщенной сигма-модели (

личину

x-vt

ref23040-Eq2) было получено в предположении

ξ=

√

≪ 1. Для описания АФМ достаточно сделать

x₀

1 - v²/c²

√

простой предельный переход s₁ → s₂, т. е. положить

где x₀ =

A/K определяет ширину неподвижной

s₁

= s₂ или ν

= 0. При этом гироскопическое

стенки. Уравнения для θ и ϕ удобно записать в без-

слагаемое в выражении (

размерном виде:

ref23040-Eq2), линейное по ∂l/∂t, отсутствует, и

[

]

вторые производные вектора l входят в уравнения

θ^′′ -

1 + (ϕ^′)²

sin θ cos θ + ν√

ϕ^′ sinθ -

c² - v²

в комбинации

√

ϕ^′ sin² θ sinϕ = 0,

(7)

ℏ(s₁ + s₂) ∂²l

- πD_c

1 - v²/c²

- A(∇²l),

ω_ex

∂t²

(ϕ′ sin2 θ)′ - ν√

θ^′ sinθ +

что можно переписать как (∂²l/∂t²) - c²(∇²l), где

c² - v²

характерная скорость, которая совпадает с ми-

√

θ^′ sin² θ sinϕ = 0,

нимальной фазовой скоростью магнонов,

πD_c

1 - v²/c²

√

где штрихом обозначена производная по ξ, кри-

Aω_ex

(5)

тическое значение D_c

= 2E₀/π определяет гра-

ℏ(s₁ + s₂)

ницу термодинамической устойчивости однородно-

√

го состояния, величина E₀ =

AK и введено нор-

Наличие такой формальной лоренц-инвариант-

мированное значение параметра раскомпенсации ν,

ности значительно упрощает анализ различных ре-

√

ν = ν

ω_ex /ω_a, где ωa = K/ℏ(s1 + s2) харак-

жимов нелинейной спиновой динамики в АФМ,

терная частота, отвечающая энергии анизотропии.

включая эффекты квантового туннелирования [32],

Поскольку ω_ex ≫ ω_a, величина ν ≫ ν; для различ-

антиферромагнитную спинтронику

[33] и сверх-

ных нелинейных задач спиновой динамики значение

быструю спиновую динамику АФМ под действи-

ν ∼ 1 отвечает тому случаю, когда проявляются эф-

ем фемтосекундных лазерных импульсов [34, 35].

фекты, специфические для ФиМ [22-25, 31, 37, 38].

Однако для киральных магнетиков эта лоренц-

Важно отметить, что хотя при D > D_c выгодно спи-

инвариантность разрушена даже при ν = 0 [36].

ральное состояние, в этой области однородное состо-

Одновременное разрушение и точной интегрируемо-

яние является метастабильным, и на его фоне воз-

сти уравнений, и лоренц-инвариантности приводит

можно решение типа ДС, но энергия этой ДС отри-

к интересным особенностям динамики ДС, которые

цательна [39].

и являются предметом анализа настоящей работы.

Эта система уравнений формально эквивалент-

на механической задаче с двумя степенями свободы

3. СТРУКТУРА ДВИЖУЩЕЙСЯ СТЕНКИ

(переменная ξ играет роль времени) о движении ма-

Для анализа солитонных решений удобно ис-

териальной точки по поверхности сферы при нали-

пользовать угловые переменные для единичного

чии потенциала, равного -(K/2) sin² θ, и двух раз-

вектора l,

личных гироскопических слагаемых. Одно из них

является стандартным для ФМ или ФиМ, оно про-

l_z = cosθ, l_x = sinθ cosϕ, l_y = sinθ sinϕ.

(6)

порционально скорости ДС v и параметру раском-

пенсации s₁ - s₂, а второе обусловлено ВДМ. Для

Полярная ось z выбрана вдоль легкой оси магне-

этой системы можно построить один первый инте-

тика. По обе стороны от доменной стенки θ = 0 и

грал

θ=π.

Q = (θ^′)² + (ϕ^′)²sin²θ - sin²θ,

(8)

Движущиеся ДС описываются решениями ти-

па простых волн, для которых θ

= θ(x - vt) и

принимающий на решении типа ДС значение Q = 0.

359

ЖЭТФ, вып. 3

Н. Е. Кулагин

ЖЭТФ, том 163, вып. 3, 2023

Второй интеграл движения построить не удается, и

Во-вторых, для интегрируемой системы имеется

в общем случае система (

только одна пара ДС, которые могут двигаться со

ref23040-eq7) не является точно интегрируемой. Для

скоростью v ≤ v_c, где v_c критическая скорость.

одноосного магнетика с энергией, инвариантной от-

Эти две ДС соответствуют двум ветвям зависимо-

носительно произвольных поворотов вокруг оси z,

сти энергии ДС от ее скорости, E = E(v); эти ветви

сохраняется величина µ_z компонента вектора ¾ки-

существуют при v ≤ v_c и сливаются при критиче-

нетического момента¿ µ = l × l^′, что позволяет по-

ском значении v = v_c. Других решений типа ДС в

строить двухпараметрические солитоны со спино-

интегрируемом случае нет [41-43]. Если же интегри-

вой прецессией [11, 29, 40], но ВДМ нарушает эту

руемость разрушена, то возникают новые типы ДС.

симметрию.

Фактически, эти нетривиальные свойства опре-

Наличие ВДМ разрушает интегрируемость на-

делены различным характером поведения траекто-

шей задачи и не позволяет построить точные анали-

рий в интегрируемом и неинтегрируемом случаях.

тические решения, но приводит к интересным осо-

Гамильтоновость системы приводит к слоению фа-

бенностям решений типа ДС. Точно интегрируемые

зового пространства на уровни гамильтониана, а ин-

системы с двумя степенями свободы обладают неко-

тегрируемость (наличие дополнительного интегра-

торыми характерными чертами сепаратрисных ре-

ла) приводит к дополнительному слоению на уровни

шений, описывающих разные типы солитонов. В

второго интеграла. Хотя большинство таких уров-

принципе, проявление неинтегрируемости в случае

ней представляет собой инвариантные торы, инте-

ФиМ с любым значением ν такие же, как для ФМ,

ресующие нас уровни содержат особые точки и яв-

их анализ можно найти в работе [39]. Для случая

ляются более сложными двумерными поверхностя-

ФиМ оказываются важными две особенности, кото-

ми. При переходе к неинтегрируемой системе вто-

рые мы обсудим здесь.

рое слоение пропадает, и гомо- и гетероклинические

Во-первых, для интегрируемой системы тип осо-

траектории лежат в трехмерном уровне гамильто-

бой точки в значительной степени определяет свой-

ниана и ведут себя очень сложно. В частности, мо-

ства семейства солитонов. Гетероклинические тра-

жет возникать счетное множество гетероклиниче-

ектории (описывающие ДС) могут существовать

ских траекторий. Эти траектории описывают ДС

только для особых точек седлового типа [41-43]. Ха-

со сложной внутренней структурой. В частности,

рактер особой точки можно легко найти путем ана-

для них возможно немонотонное поведение компо-

литического продолжения спектра спиновых волн

нент вектора l, продольной l_z или поперечных l_x,y,

на комплексные волновые векторы и частоты [44,

вдали от стенки, что согласуется с возможностью

45]. Положения равновесия для уравнений типа (

движения со скоростью v > v_(-) (естественно, при

ref23040-eq7), (

v < v_c). Такое поведение наблюдалось для ДС в раз-

ref23040-eq8), описывающих простые волны намаг-

личных неинтегрируемых моделях [46-49]. В прин-

ниченности, соответствуют особой точке типа сед-

ципе, оно присутствует и для кирального ФМ, но

ло, если скорость волны меньше некоторой харак-

для них ДС с немонотонным поведением ранее не

терной скорости v_(-), |v| ≤ v_(-). Локализованные

рассматривались, во всяком случае в известных нам

решения возможны при |v| ≤ v₍₊₎, где v₍₊₎ совпада-

работах [26-28, 39] (см. также ссылки в них). Веро-

ет с минимальной фазовой скоростью магнонов [45].

ятно, это связано с тем, что немонотонные ДС в ФМ

Для известных нам моделей магнетиков значение

имеют более высокую энергию.

v(-) < v(+) [45]. В интервале v(-) < v < v(+) по-

При всех разумных значениях константы ВДМ

ложения равновесия являются особыми точками ти-

D ≤ D_c структура ДС хорошо описывается простым

па седло - фокус. В этом случае наличие гетерокли-

приближенным решением вида

нических траекторий является неким вырождением

ϕ = ϕ₀(v) = const, cosθ = th[(x - vt)/x₀],

системы, т. е. такие траектории могут существовать

только при некоторых изолированных значениях па-

при этом значение угла ϕ₀ определяется скоростью

раметров системы. Это позволяет легко найти пре-

ДС, sin ϕ₀(v) = v/v_c,FM , где v_c,FM

предельная

√

дельную скорость ДС для интегрируемых систем, но

скорость ДС в ФМ [39], v_c,FM = c(D/D_c)

ω_a/ω_ex .

не может быть использовано при нарушении инте-

Энергия ДС в ФМ определяется простой форму-

грируемости [46,47]. Это особенно важно для нашего

лой E_FM = 2E₀(1 - D cos ϕ₀/D_c), т. е. зависимость

случая, поскольку для киральных магнетиков с чи-

E_FM (v) описывается замкнутой выпуклой кривой,

сто одноосной анизотропией значение v_(-) = 0 [39],

она имеет две ветви с большей и меньшей энерги-

√

для ФиМ v₍₊₎ = c/

1 + ν²/4.

ями, которые сливаются в точке v = v_c,FM . Такая

360

ЖЭТФ, том 163, вып. 3, 2023 Динамическая трансформация доменных стенок в киральных ферримагнетиках

закономерность имеет место для ДС в рамках точ-

но интегрируемой модели Уокера [50].

4. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ДЛЯ ДС В

ФиМ

Приведенные выше простые формулы получены

в рамках приближения ϕ = ϕ₀(v) = const, но это

приближение с очень высокой точностью описывает

характеристики ДС в киральном ФМ, в частности,

зависимость энергии ДС от ее скорости. Рассмот-

рим, как эти соотношения трансформируются при

переходе к случаю ФиМ.

Уравнения Ландау - Лифшица получаются из

уравнений обобщенной сигма-модели в пределе

√

ν → 1 (при этом ν =

ω_ex /ω_a ≫ 1) и c → ∞.

Если предположить, что ϕ = ϕ₀(v) = const, то для

энергии ДС в ФиМ легко получается сходная связь

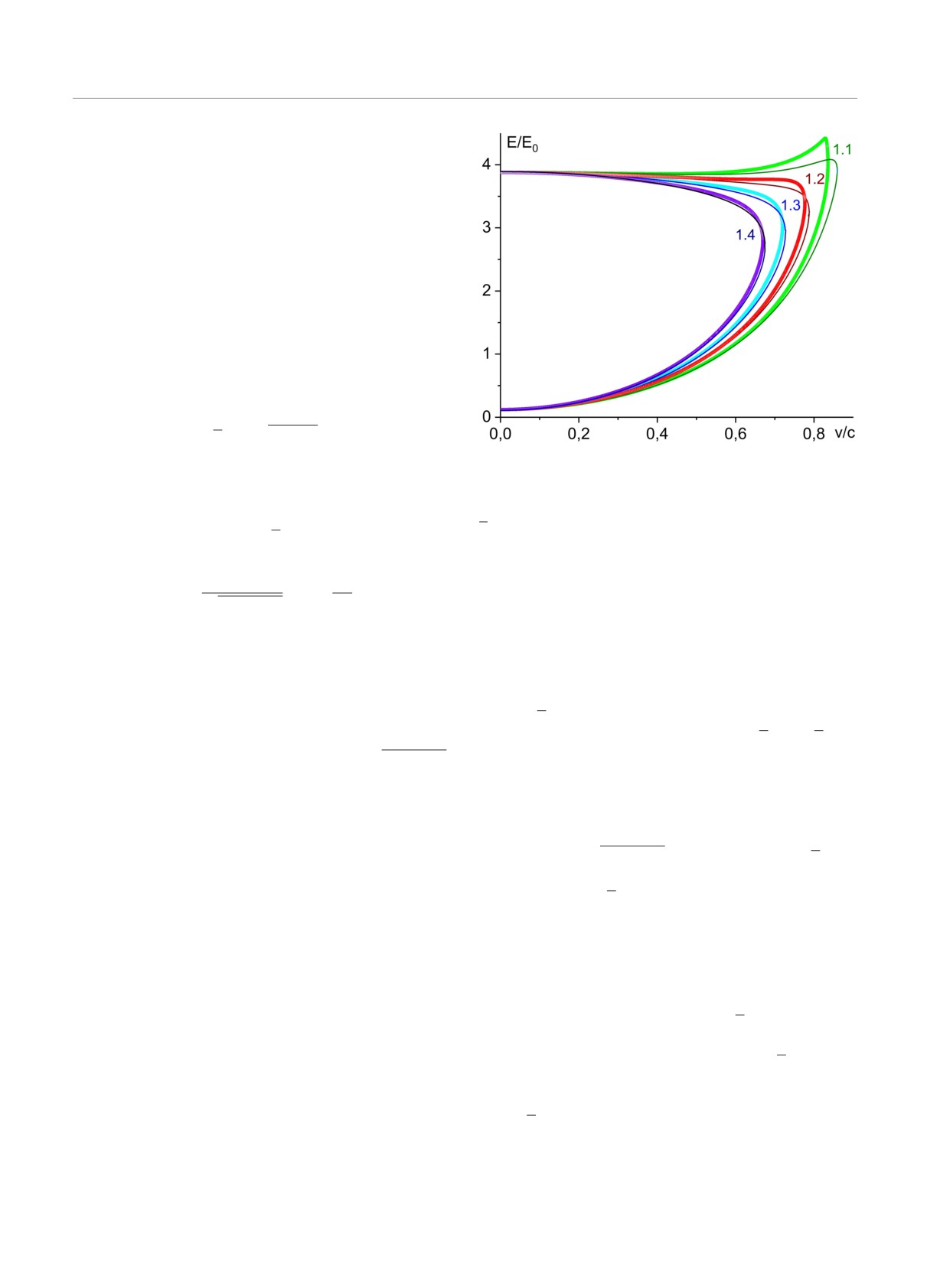
Рис. 1. Зависимость E(v) (здесь и далее энергия представ-

лена в единицах E0, а скорость в единицах c) для ФиМ с

sin ϕ₀(v)

= v/v_c,0, где v/v_c,0

предельная ско-

D/Dc = 0.945 при значениях параметра раскомпенсации

рость ДС, найденная в предположении ϕ = const,

ν = 1.1,1.2,1.3,1.4, которые обозначены цифрами около

v_c,0 = v_c,FM/ν = c(D/D_c)/ν. Формула для энергии

кривых. Тонкие линии аналитические результаты, полу-

ДС в этом же приближении имеет вид

ченные в приближении ϕ = const

2E₀

E(v, ϕ₀) =

√

- 2E₀

cosϕ₀.

(9)

когда роль эффектов разрушения интегрируемости

1 - v²/c²

D_c

минимальна. Фактически, анализ случая ФМ пока-

Первое слагаемое в формуле для энергии такое

зал именно такое поведение: приближение ϕ = const

описывает точные данные, полученные численно,

же, как в лоренц-инвариантной теории, а второе сла-

гаемое такое же, как в ФМ. Энергии ДС при нулевой

при всех допустимых значениях D ≤ D_c и при ско-

ростях v ≤ v_c,FM . Однако для ФиМ при малых зна-

скорости v = 0 остаются теми же, что для ФМ, они

чениях ν это приближение явно не адекватно; до-

равны E_(±) = 2E₀(1 ± D/D_c), но с ростом скоро-

сти энергии ДС в ФиМ E(v) выше, чем в ФМ, за

статочно заметить, что при D > D_c/ν (при ν < 1

√

это не противоречит условию D < D_c) значение v_c,0

счет ¾релятивистского¿ множителя 1/

1 - v²/c².

При уменьшении ν предельная скорость растет, и

становится больше c, что заведомо неверно. Дело в

том, что эффективное значение константы ВДМ в

этот ¾подъем¿ ветвей становится все более суще-

ственным. Ясно, что при определенном критиче-

уравнениях (

ref23040-eq7) усилено за счет

¾релятивистского¿

ском значении ν_nm выпуклость кривой, описываю-

√

щей зависимость E(v) нарушается. При ν < ν_nm

множителя 1/

1 - v²/c². При уменьшении ν пре-

дельная скорость ДС растет, следовательно, для

максимальное значение энергии E_max

= E(v_max)

отвечает некоторой конечной скорости vmax < vc,

ФиМ с малым ν растет эффективное значение

константы ВДМ и возрастают эффекты неинте-

E_max > E₍₊₎, и на верхней ветви имеет место ло-

грируемости. В частности, увеличиваются отклоне-

кальный минимум энергии. Таким образом, замкну-

тая кривая перестает быть выпуклой. Важно заме-

ния зависимости E(v), найденной в приближении

ϕ = const, от точной (рис.1).

тить, что в этом случае поведение импульса ДС и ха-

рактер закона дисперсии E = E(P ) меняется прин-

Надо заметить, что эти отклонения достаточ-

ципиально, и появляется точка окончания спектра

но малы при достаточно малых ν

∼ 1.3-1.4, но

ДС [22,23]. Поскольку данные закономерности такие

они очень резко увеличиваются при приближении

же, как для рассмотренной в работах [22, 23] ФиМ-

к некоторому критическому значению (ν = 1.1 на

версии точно интегрируемой модели Уокера, мы их

рис. 1). Такое же поведение имеет место для всех

не обсуждаем.

значений параметра D ≤ D_c, но критическое зна-

Условие ϕ = const характерно для ДС в ин-

чение ν уменьшается с уменьшением D. Именно в

тегрируемой модели Уокера [50], см. также [11], и

этой области значение предельной скорости ДС ве-

можно ожидать, что это приближение справедливо,

лико, и анализ этой ситуации особо важен с точки

361

Н. Е. Кулагин

ЖЭТФ, том 163, вып. 3, 2023

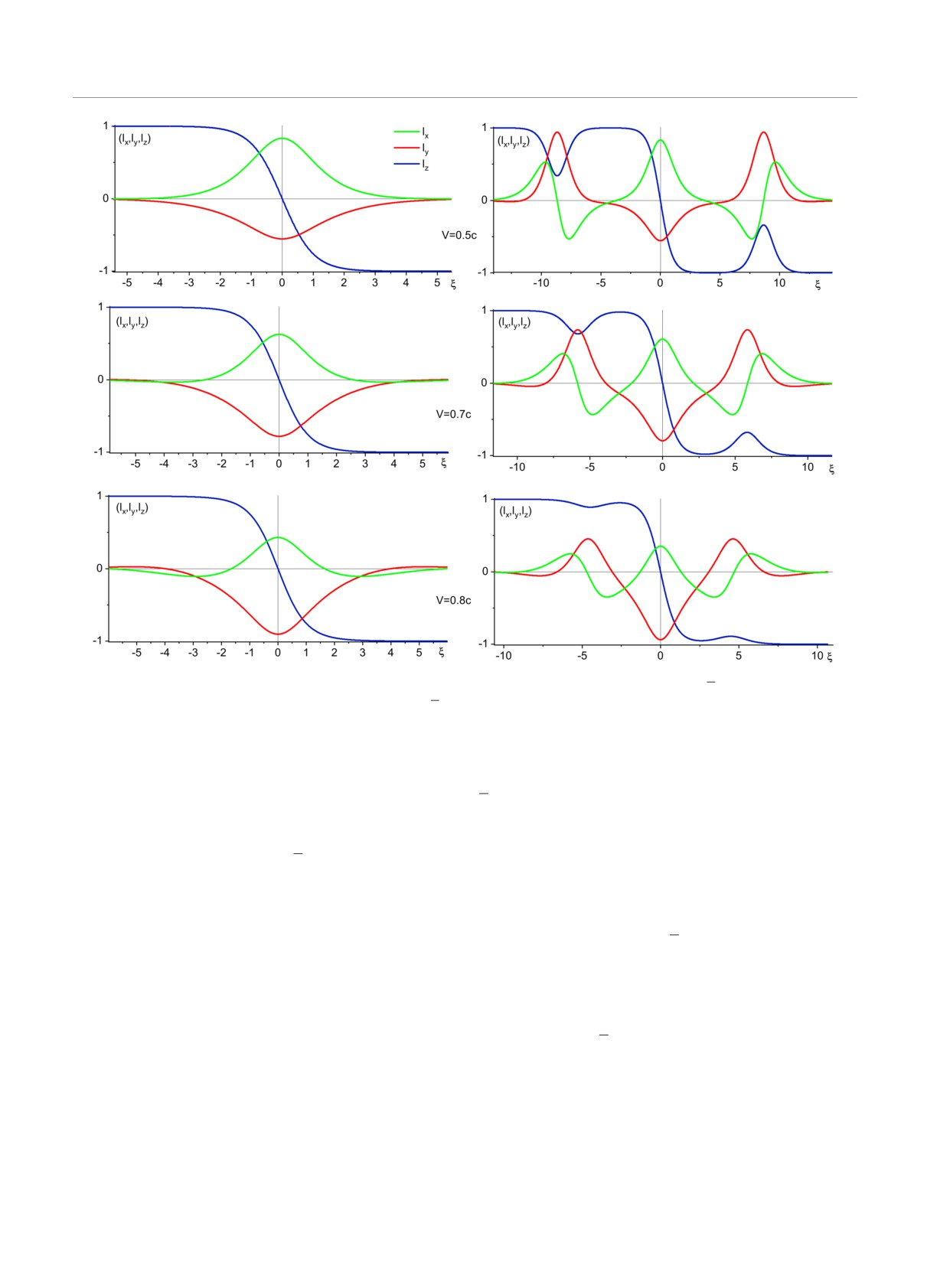
Рис. 2. Распределения компонент вектора l в ДС , найденное численно при значениях параметров ν = 1.1 и D/Dc = 0.95,

что несколько выше значения D_bif , которое при этом ν равно D_bif /Dc = 0.948. Представлены данные для ДС нижней

(слева) и верхней (справа) ветвей. Значения скоростей равны v = 0.5c, v = 0.7c и v = 0.8c соответственно для верхнего,

среднего и нижнего рядов

зрения применений ДС. Точное аналитическое ре-

ципе, все параметры, скорость стенки v, D/D_c или

шение для движущейся ДС построить не удается,

ν могут быть использованы в качестве этого варьи-

и был проведен интенсивный численный анализ ДС

руемого параметра.

во всей области их существования для различных

В качестве отправной точки можно использовать

значений параметров D/D_c и ν.

неподвижное решение с известной структурой, а в

качестве варьируемого параметра скорость стен-

ки. При этом можно построить все многообразие

5. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА

ДС с различными скоростями при заданных значе-

ДОМЕННЫХ СТЕНОК

ниях констант D/D_c или ν. Применение этого под-

Детальное описание используемого численного

хода привело к достаточно интересному результату.

метода можно найти в недавней работе [39]. Важ-

Получилось, что если в качестве начальной точки

ным моментом является использование надежного и

выбиралась неподвижная ДС с минимальной энер-

простого метода продолжения по параметру (метод

гией, то при определенных значениях D < Dbif,

продолжения Келлера [51]). В рамках этого метода,

где D_bif = D_bif (ν) некоторое характерное значе-

если известна одна фазовая траектория, может быть

ние, программа находит ДС с монотонным поведе-

построена другая траектория, близкая к исходной,

нием l_z(ξ) (далее для краткости будем называть их

с заранее заданным значением ¾расстояния¿ между

монотонными ДС), энергии которых описываются

ними. Для вновь построенной траектории значение

замкнутыми кривыми такого типа, как приведены

некоторого заданного параметра уравнения отлича-

выше на рис. 1. Если же D > D_bif , то при выхо-

ется от такового для исходной траектории. В прин-

де из той же начальной точки при изменении ско-

362

ЖЭТФ, том 163, вып. 3, 2023 Динамическая трансформация доменных стенок в киральных ферримагнетиках

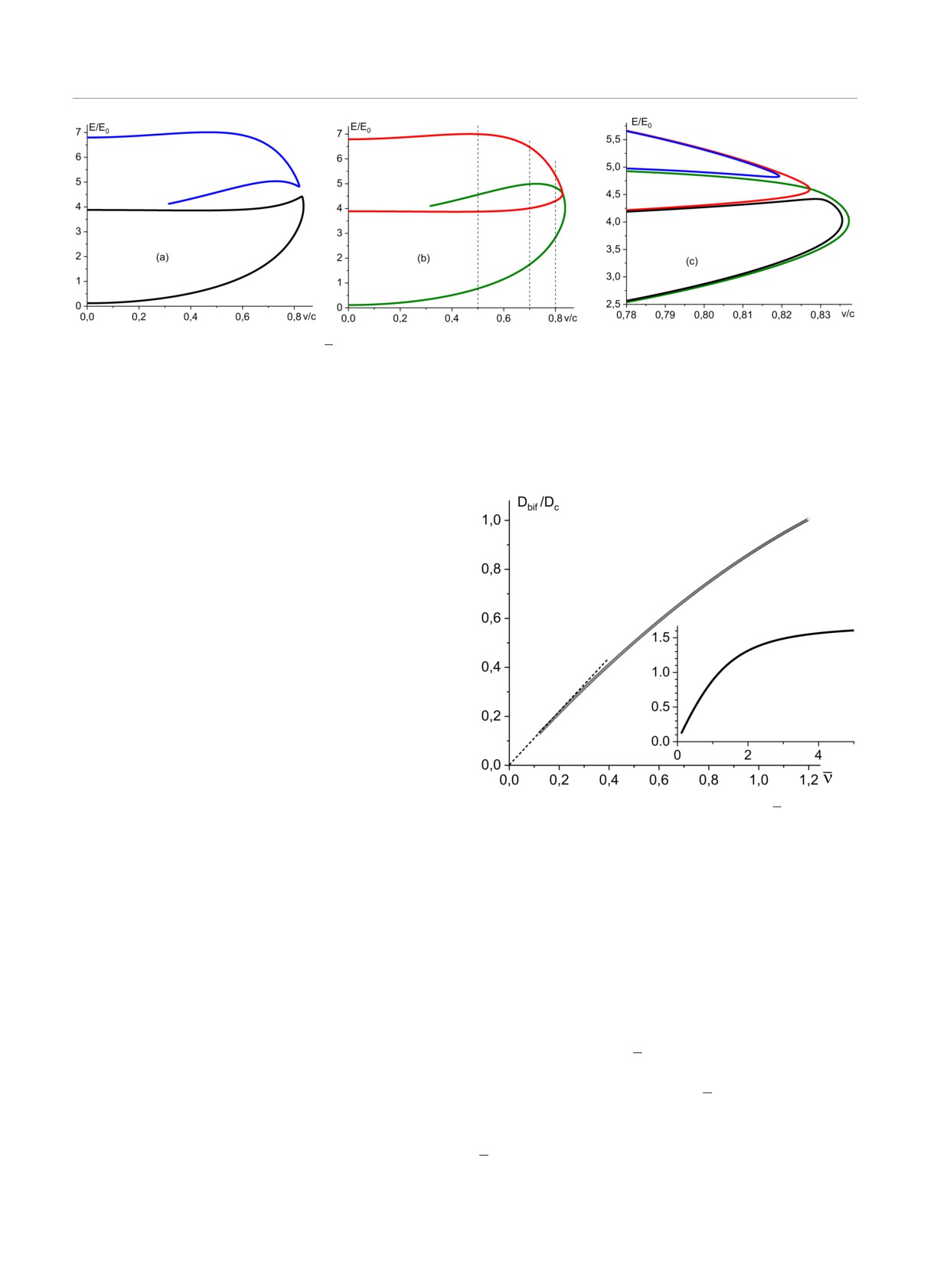
Рис. 3. Зависимости E(v) для ФиМ с ν = 1.1 при различных значениях константы ВДМ вблизи бифуркацонного значе-

ния D_bif = 0.94814Dc : a D = 0.945Dc < Dbif (нижняя и верхняя ветви соответствуют монотонным и немонотонным

ДС); b при D = 0.95Dc > Dbif происходит перезамыкание кривых; c обе кривые E(v) при указанных двух значениях

параметра D вблизи предельной скорости

рости непрерывно возникают ДС с немонотонным

для каждой из которых присутствуют как монотон-

поведением зависимости l_z(ξ) (немонотонные ДС).

ные, так и немонотонные ДС.

Структуры всех этих стенок представлены на рис. 2.

При этом зависимость E(v) описывается замкнутой

кривой, но в рамках одной такой кривой нижняя и

верхняя ветви соответствуют монотонным и немо-

нотонным ДС.

Отметим, что при немного меньшем значении

D/D_c = 0.945 поведение кривой E(v) и характер

стенок абсолютно иные. Вся нижняя кривая отвеча-

ет монотонным стенкам и, как видно из рис.1, ка-

чественно описывается ¾ферромагнитным¿ прибли-

жением ϕ = const. Таким образом, получается, что

при незначительном изменении скорости характер

кривых изменяется качественно, и в системе име-

ет место бифуркация решений. Характер этой би-

фуркации становится понятным, если включить в

рассмотрение и немонотонные ДС, энергия которых

при D < D_bif определяется отдельной замкнутой

Рис. 4. Связь между значениями D_bif /Dc и ν, найденная

кривой (рис. 3a). Вдали от бифуркации эти кривые

численно. На вставке приведена эта же зависимость для

находятся достаточно далеко друг от друга, энер-

более широкой области параметров

гия немонотонных стенок существенно выше, и их

Анализ показал, что наличие такого бифурка-

можно не рассматривать. Однако при увеличении

ционного поведения является общим свойством ки-

D в области D < D_bif нижняя кривая поднимается,

рального ФиМ, и оно присутствует при всех до-

а верхняя, отвечающая немонотонным ДС, опуска-

пустимых значениях приведенной константы ВДМ

ется; при этом кривые сближаются друг с другом,

D/D_c. Однако для наблюдения эффекта бифур-

образуя характерные выступы, направленные вверх

кации при малых значениях D/D_c ФиМ должен

и вниз, как на рис.3a.

быть достаточно близко к точке компенсации спина

При дальнейшем движении к точке бифуркации

(рис. 4). Фактически, при всех D ≤ D_c эффекты би-

происходит следующее: кривые E(v) движутся на-

фуркации проявляются только в узкой окрестности

встречу друг другу, при бифуркационном значении

точки компенсации, ν < 1.2. Однако при переходе

они касаются друг друга, а далее кривые расщепля-

в область метастабильности однородного состояния

ются, и их ветви перезамыкаются так, что верхняя и

D > D_c характерное значение ν быстро растет.

нижняя ветви для обеих функций меняются места-

Численный расчет проведен для значений

ми, см. рис. 3b и более детально рис. 3c. В результа-

D_bif /Dc > 0.118; при меньших Dbif /Dc значение

те появляются две новые непрерывные кривые E(v),

ν мало, предельная скорость v очень близка к c,

363

Н. Е. Кулагин

ЖЭТФ, том 163, вып. 3, 2023

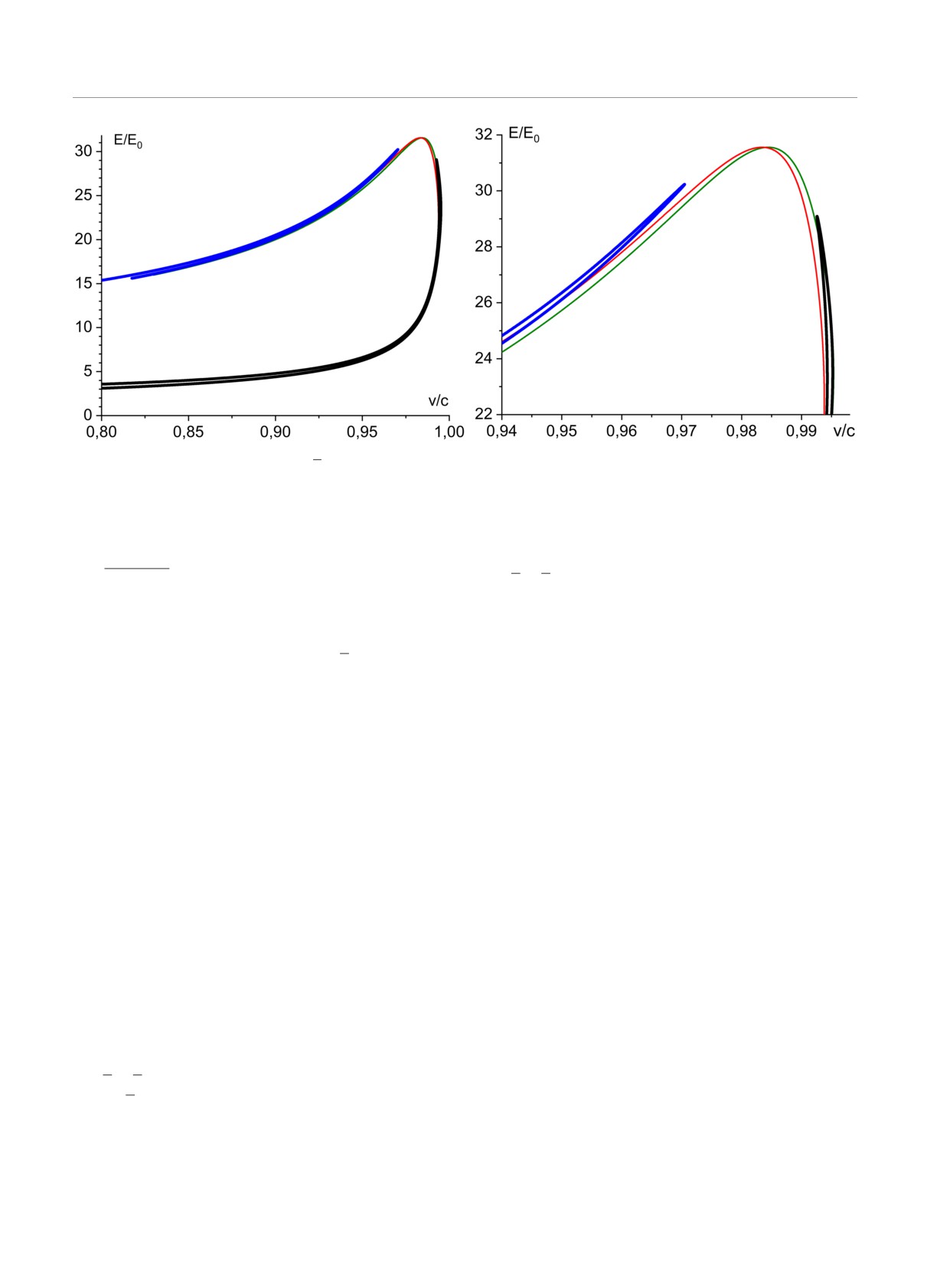
Рис. 5. Зависмости E(v) для ФиМ с ν = 0.17 при различных значениях константы ВДМ вблизи бифуркационного значе-

ния D_bif = 0.18302Dc ; слева зависимости при D = 0.18Dc < Dbif (жирные линии) и при D = 0.19Dc > Dbif (тонкие

линии); справа детали поведения кривых вблизи точки пересечения

гироскопические слагаемые в уравнениях (

няя кривая ДС с немонотонным поведением l_z(ξ).

ref23040-eq7) за счет ¾релятивистского¿ множителя

Выше кривой, т. е. при D > D_c или, эквивалентно,

√

1 - v²/c² сильно возрастают и программа ра-

при ν < ν_bif (D), каждой из этих двух кривых соот-

ботает нестабильно (штриховая линия на рис.4

ветствуют ДС и с монотонным, и с немонотонным

линейная интерполяция в эту область). На вставке к

поведением.

рис. 4 также приведены данные для более широкой

Благодарности. Автор благодарит Б. А. Ива-

области параметров, до значений ν

= 5, вклю-

нова и Л. М. Лермана за сотрудничество и плодо-

чающей область метастабильности

однородного

творные обсуждения.

состояния D_bif > D_c.

Финансирование. Работа поддержана Россий-

При малых значениях D/D_c характер бифурка-

ским научным фондом (грант 22-11-00027).

ции качественно такой же, как и для рассмотренного

выше случая D < D_c, но значения скорости в точке

бифуркации близки к c, а энергии стенок в районе

ЛИТЕРАТУРА

бифуркации высокие (рис. 5).

1. D. Atkinson, D. A. Allwood, G. Xiong et al., Nature

6. ЗАКЛЮЧЕНИЕ

Mater. 2, 85 (2003).

Анализ структуры и свойств ДС в киральных

ФиМ продемонстрировал более сложное поведение,

2. A. Yamaguchi, T. Ono, S. Nasu et al., Phys. Rev.

чем для рассмотренных ранее многими авторами

Lett. 92, 077205 (2004).

киральных ФМ [26-28, 39] или ФиМ без киральных

3. M. Hayashi, L. Thomas, R. Moriya et al., Science,

вкладов в энергию [22, 23]. Для ДС в киральных

320, 209 (2008).

ФиМ может иметь место ¾перемешивание¿ стан-

дартных ДС и ДС с немонотонным поведением

4. A. Hoffmann and S. D. Bader, Phys. Rev. Appl. 4,

l_z-проекции спиновой плотности в пределах одной

047001 (2015).

кривой зависимости E = E(v). Появление этого эф-

фекта имеет характер бифуркации и появляется при

5. G. Tatara and H. Kohno, Phys. Rev. Lett. 92, 086601

переходе через характерные значения D = D_bif (ν)

(2004).

или ν = ν_bif (D). При значениях параметров на плос-

6. A. Thiaville, Y. Nakatani, J. Miltat, and Y. Suzuki,

кости (ν, D) в области ниже бифуркационной кри-

Eur. Phys. Lett. 69, 990 (2005).

вой (см. рис.4) зависимость E = E(v) представлена

двумя замкнутыми кривыми, нижняя кривая соот-

7. O. A. Tretiakov, D. Clarke, G.-W. Chern et al., Phys.

ветствует ДС с монотонным поведением l_z(ξ), верх-

Rev. Lett. 100, 127204 (2008).

364

ЖЭТФ, том 163, вып. 3, 2023 Динамическая трансформация доменных стенок в киральных ферримагнетиках

A. V. Khvalkovskiy, V. Cros, D. Apalkov et al., Phys.

29.

E. G. Galkina and B. A. Ivanov, Low Temp. Phys. 44,

Rev. B 87, 020402 (2013).

618 (2018).

S. S. P. Parkin and S.-H. Yang, Nature Nanotechnol.

30.

A. B. Borisov, V. V. Kiseliev, and G. G. Talutz, Sol.

10, 195 (2015).

St. Comm. 44, 411 (1982).

10.

A. M. Kosevich, B. A. Ivanov, and A. S. Kovalev,

31.

Б. А. Иванов, А. Л. Сукстанский, ЖЭТФ 84, 370

Physica D 3, 363 (1981).

(1983).

32.

Е. Г. Галкина, Б. А. Иванов, Письма в ЖЭТФ 61,

11.

A. M. Kosevich, B. A. Ivanov, and A. S. Kovalev,

495 (1995).

Phys. Rep. 194, 117 (1990).

33.

V. Baltz, A. Manchon, M. Tsoi et al., Rev.Mod.

12.

А. Б. Борисов, В. В. Киселев, Нелинейные волны,

Phys. 90, 015005 (2018).

солитоны и локализованные структуры в маг-

нетиках, в двух томах, УроРАН, Екатеринбург

34.

A. Kirilyuk, A. V. Kimel, and Th. Rasing, Rev.Mod.

(2009).

Phys. 82, 2731 (2010).

13.

М. В. Четкин, Де Ла Кампа, Письма в ЖЭТФ 27,

35.

B. A. Ivanov, Low Temp. Phys. 40, 91 (2014).

168 (1978).

36.

S. Komineas and N. Papanicolaou, SciPost Phys. 8,

14.

А. Л. Звездин, Письма в ЖЭТФ 29, 605 (1979).

086 (2020).

15.

В. Г. Барьяхтар, Б. А. Иванов, А. Л. Сукстанский,

37.

C. E. Zaspel, E. G. Galkina, and B. A. Ivanov, Phys.

ЖЭТФ 75, 2183 (1978).

Rev. Appl. 12, 044019 (2019).

16.

В. Г. Барьяхтар, Б. А. Иванов, А. Л. Сукстанский,

38.

I. Lisenkov, R. Khymyn, J. Akerman et al., Phys.

ЖЭТФ 78, 1509 (1980).

Rev. B 100, 100409(R) (2019).

39.

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.,

17.

В. Г. Барьяхтар, Б. А. Иванов, М. В. Четкин, УФН

ЖЭТФ 159, 671 (2021).

146, 417 (1985).

40.

А. М. Косевич, Б. А. Иванов, А.С. Ковалев, Пись-

18.

A. P. Malozemoff and J. C. Slonczewski, Magnetic

ма в ЖЭТФ 25, 516 (1977).

Domain Walls in Bubble Materials, Acad. Press, New

York (1981).

41.

L. M. Lerman, Selecta Math. Sov. 12, 333 (1993).

19.

K.-J. Kim, S. K. Kim, Y. Hirata et al., Nature Mater.

42.

Л. М. Лерман, Письма в ЖЭТФ 51, 336 (1990).

16, 1187 (2017).

43.

Л. М. Лерман, Я. Л. Уманский, ПММ

47,

395

20.

M. V. Logunov, S. S. Safonov, A. S. Fedorov et al.,

(1983).

Phys. Rev. Appl. 15, 064024 (2021).

44.

E. Schlomann, Appl. Phys. Lett. 19, 274 (1971).

21.

L. Caretta, M. Mann, F. Buttner et al., Nature

45.

В. Г. Барьяхтар, Б. А. Иванов, А. Л. Сукстанский,

Nanotechnol. 13, 1154 (2018).

Письма в ЖЭТФ 27, 226 (1978).

22.

Е. Г. Галкина, К. Э. Заспел, Б. А. Иванов и др.,

46.

В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

Письма в ЖЭТФ 110, 474 (2019)

ЖЭТФ 75, 2210 (1978).

23.

B. A. Ivanov, E. G. Galkina, V. E. Kireev et al., Low

47.

В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

Temp. Phys. 46, 841 (2020).

ЖЭТФ 77, 409 (1979).

24.

A. K. Zvezdin, Z. V. Gareeva, K. A. Zvezdin, J. Magn.

48.

Б. А. Иванов, Н. Е. Кулагин, ЖЭТФ

112,

953

Magn. Mater. 509, 166876 (2020).

(1997).

25.

B. A. Ivanov, Low Temp. Phys. 45, 935 (2019).

49.

Н. Е. Кулагин, А. Ф. Попков, Письма в ЖЭТФ 43,

197 (1986).

26.

A. Thiaville, S. Rohart, E. Jue et al., Europhys. Lett.

100, 57002 (2012).

50.

L. R. Walker, in Magnetism, ed. by G. T. Rado and

H. Suhl, Pergamon, New York (1963), Vol. 3, p.451.

27.

V. V. Slastikov, C. B. Muratov, J. M. Robbins et al.,

Phys. Rev. B 99, 100403(R) (2019).

51.

T. F. C. Chan and H. B. Keller, SIAM J. Sci. Stat.

Comput. 3, 173 (1982).

28.

V. P. Kravchuk, J. Magn. Magn. Mater. 367, 9 (2014).

365