ЖЭТФ, 2023, том 163, вып. 3, стр. 366-374

СИНХРОНИЗАЦИЯ АВТОКОЛЕБАНИЙ МАГНИТНЫХ ВИХРЕЙ

В ОБМЕННО-СВЯЗАННЫХ ФЕРРОМАГНИТНЫХ ДИСКАХ

Д. А. Татарский^a,b*, В. Л. Миронов^a, А. А. Фраерман^a

^a Институт физики микроструктур Российской академии наук

607680, Нижний Новгород, Россия

^b Нижегородский государственный университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

Поступила в редакцию 24 сентября 2022 г.,

после переработки 24 сентября 2022 г.

Принята к публикации 13 октября 2022 г.

Методом численного моделирования исследованы низкочастотные (гиротропные) автоколебания маг-

нитных вихрей во взаимодействующих ферромагнитных дисках, вызванные протеканием спин-

поляризованного тока. Рассмотрены различные моды колебаний намагниченности в зависимости от

конфигурации магнитного состояния системы. Исследовано влияние неоднородности тока накачки на

разность фаз гирации вихрей в соседних дисках. Показано, что перекрытие дисков приводит к увели-

чению взаимодействия между вихрями и, как следствие, к уменьшению расфазировки колебаний коров

вихрей. Обсуждаются перспективы применения перекрывающихся дисков для обеспечения фазовой син-

хронизации массивов вихревых спин-трансферных генераторов.

DOI: 10.31857/S0044451023030082

решение проблемы синхронизации большого чис-

EDN: QEOJNZ

ла СТНО с целью увеличения суммарной генери-

руемой мощности. Существенный прогресс был до-

1. ВВЕДЕНИЕ

стигнут с переходом к СТНО на основе магнитных

Спин-трансферные наноосцилляторы (СТНО)

туннельных контактов (МТК) с туннельным барье-

на основе наноразмерных магнитных спиновых

ром MgO [7-9]. Данные СТНО обеспечивают гораз-

вентилей активно исследуются в последние десяти-

до большую мощность из-за высоких значений тун-

летия в связи с перспективой создания компактных

нельного магнитосопротивления. В работе [10] ав-

генераторов гигагерцевого диапазона частот [1, 2].

торы предложили СТНО на основе низкочастотных

В основе работы данных приборов лежит явление

колебаний магнитного вихря в металлических мно-

гослойных нанодисках. В этих структурах модуля-

возникновения автоколебаний намагниченности

ферромагнетика под действием поляризованного

ция электрического тока через туннельный контакт

осуществляется за счет вращающегося магнитного

по спину электрического тока [3, 4]. Из-за эффекта

магнитосопротивления колебания намагниченности

момента, индуцированного в магнитном вихре при

приводят к колебаниям напряжения на спиновом

круговом (гиротропном) движении кора вихря во-

вентиле. В первых СТНО индуцированные током

круг положения равновесия. Частота гиротропных

возбуждения представляли собой квазиоднородную

колебаний вихря лежит в мегагерцевом диапазоне

частот [11]. Использование вихревого наноосцилля-

прецессию магнитного момента в металлических

многослойных структурах с гигантским магни-

тора на основе МТК с барьером MgO позволяет реа-

лизовать достаточно большие микроволновые мощ-

тосопротивлением

[5, 6]. Однако такие СТНО

генерировали малую микроволновую мощность.

ности (на уровне 10^-7 - 10^-5 Вт) [11-13].

В настоящее время основные исследования в дан-

Отметим, что существенным фактором, влияю-

щим на работу наноосцилляторов на основе МТК,

ной области направлены как на увеличение гене-

рируемой мощности отдельного СТНО, так и на

является разброс их парциальных частот, обуслов-

ленный различием токов накачки. Это различие

^* E-mail: tatarsky@ipmras.ru

возникает как результат различия туннельных со-

366

ЖЭТФ, том 163, вып. 3, 2023

Синхронизация автоколебаний магнитных вихрей . . .

противлений контактов. Для синхронизации СТНО

размерный параметр, характеризующий процесс за-

используются магнитостатическое [14-16] и обмен-

тухания. Эффективное магнитное поле H_eff выра-

ное [17-20] взаимодействия между осцилляторами,

жается следующим образом:

обмен спиновыми волнами [21], а также внешние

H_eff = H_ex + H_ms + H_cur ,

(2)

электрические цепи и волноводы [22-27]. Хорошо из-

вестно [28, 29], что частотная синхронизация двух

где H_ex

обменное поле, H_ms

дипольное

осцилляторов возможна в том случае, если их взаи-

магнитостатическое поле, H_cur

поле спин-

модействие превышает некоторое критическое зна-

поляризованного тока. Слагаемое, описывающее

чение, зависящее от разности парциальных частот.

затухание прецессии, имеет вид

При этом разность фаз синхронизованных по час-

тоте колебаний тем больше, чем ближе взаимодей-

[m × [m × H_eff ]] .

(3)

TD = - |γ|

1+α²

ствие к критическому значению. Ситуация услож-

няется при попытке сфазировать большое количе-

Член, описывающий эффект переноса спина

ство автоосцилляторов. Как показано в работе [30],

(spintorque), записывается в форме [3, 34]

дисперсия разности фаз в системе из N осцилля-

αǫ

[m × [m_P × m]] + β

[m × m_P ] ,

торов возрастает примерно как N^4-D, где D раз-

TS = β

1+α²

мерность системы. Таким образом, в одномерной це-

(4)

почке наноосцилляторов (D = 1) дисперсия нарас-

где β

= j_zℏ/ehM_sat, j_z

плотность тока вдоль

тает по кубическому закону, что может приводить к

оси, перпендикулярной поверхности дисков, ℏ по-

уменьшению средней генерируемой мощности с уве-

стоянная Планка, M_sat магнитный момент насы-

личением числа генераторов [31].

щения, e

заряд электрона, h

толщина слоя-

Увеличения энергии взаимодействия вихревых

инжектора. Параметр ǫ определяется по формуле

спин-трансферных наноосцилляторов (ВСТНО)

PΛ²

можно добиться путем уменьшения расстояния

ǫ=

(5)

(Λ² + 1) + (Λ² - 1) (m · m_P )

между ферромагнитными дисками. Если диски не

перекрываются, то взаимодействие между вихрями

где P

степень поляризации носителей заряда, и

имеет исключительно магнитостатическую приро-

параметр Λ связан с кондактансом туннельного ба-

ду [29]. При перекрытии дисков между вихрями

рьера [34]. Для решения уравнения (1) использо-

включается обменное взаимодействие и их взаи-

вался симулятор MuMax3 [35]. В качестве базового

мовлияние значительно возрастает. В работе [32]

элемента для моделирования был выбран круглый

рассмотрена задача о динамике вихрей в эллип-

пермаллоевый диск радиусом r = 250 нм и толщи-

тической частице, находящейся в двухвихревом

ной t = 20 нм. В расчетах использовались следую-

состоянии. В работе

[33] исследована динамика

щие материальные параметры: магнитный момент

вихрей в системе перекрывающихся магнитных

насыщения M_sat = 800 кА/м, константа обменного

дисков. В нашей работе исследуются возможности

взаимодействия Jex = 1.3 · 10-11 Дж/м, параметр

фазовой синхронизации движения магнитных вих-

затухания α = 0.01, константа анизотропии K = 0,

рей в ферромагнитных дисках, которые ранее не

P = 0.2 и Λ = 1. При моделировании использовалась

рассматривались.

сетка 256 × 128 × 1 (для перекрывающихся дисков)

или 384 × 128 × 1 (для дисков без перекрытия) с раз-

2. МАГНИТНЫЕ СОСТОЯНИЯ В

мерами элементарной ячейки 4 × 4 × 20 нм³, размер

ПЕРЕКРЫВАЮЩИХСЯ

которой меньше обменной длины l_ex ≈ 5.7 нм [36].

ФЕРРОМАГНИТНЫХ ДИСКАХ

Высота ячейки равнялась толщине диска [37].

Моделирование равновесных распределений и

В ферромагнитном диске данных размеров реа-

колебаний намагниченности проводилось посред-

лизуется вихревое распределение намагниченности

ством численного интегрирования уравнения Лан-

(рис. 1a,b). В центральной части магнитного вихря

дау - Лифшица - Гилберта - Слончевского для маг-

(кор вихря) намагниченность направлена перпенди-

нитного момента с учетом переноса спина

кулярно плоскости диска (либо в положительном,

либо в отрицательном направлении по отношению к

∂m

|γ|

[m × H_eff ] + T_D + T_S ,

(1)

внешней нормали), а в периферической части (обо-

∂t

1+α²

лочка вихря) намагниченность лежит в плоскости

где m единичный вектор в направлении намагни-

диска и имеет разную завихренность (либо по часо-

ченности, γ гиромагнитное отношение, α без-

вой стрелке, либо против часовой стрелки).

367

Д. А. Татарский, В. Л. Миронов, А. А. Фраерман

ЖЭТФ, том 163, вып. 3, 2023

рекрытии могут реализовываться следующие двух-

вихревые состояния: двухвихревое состояние с про-

тивоположной завихренностью каждого из вихрей

VV (рис. 2а), двухвихревое состояние с одинаковой

завихренностью вихрей, разделенных антивихрем,

VAV (рис. 2b), сдвинутое из центров дисков двухвих-

ревое состояние, sVV (рис. 2с). При больших пере-

крытиях система переходит в одновихревое состоя-

ние, обозначенное как состояние V (рис. 2d).

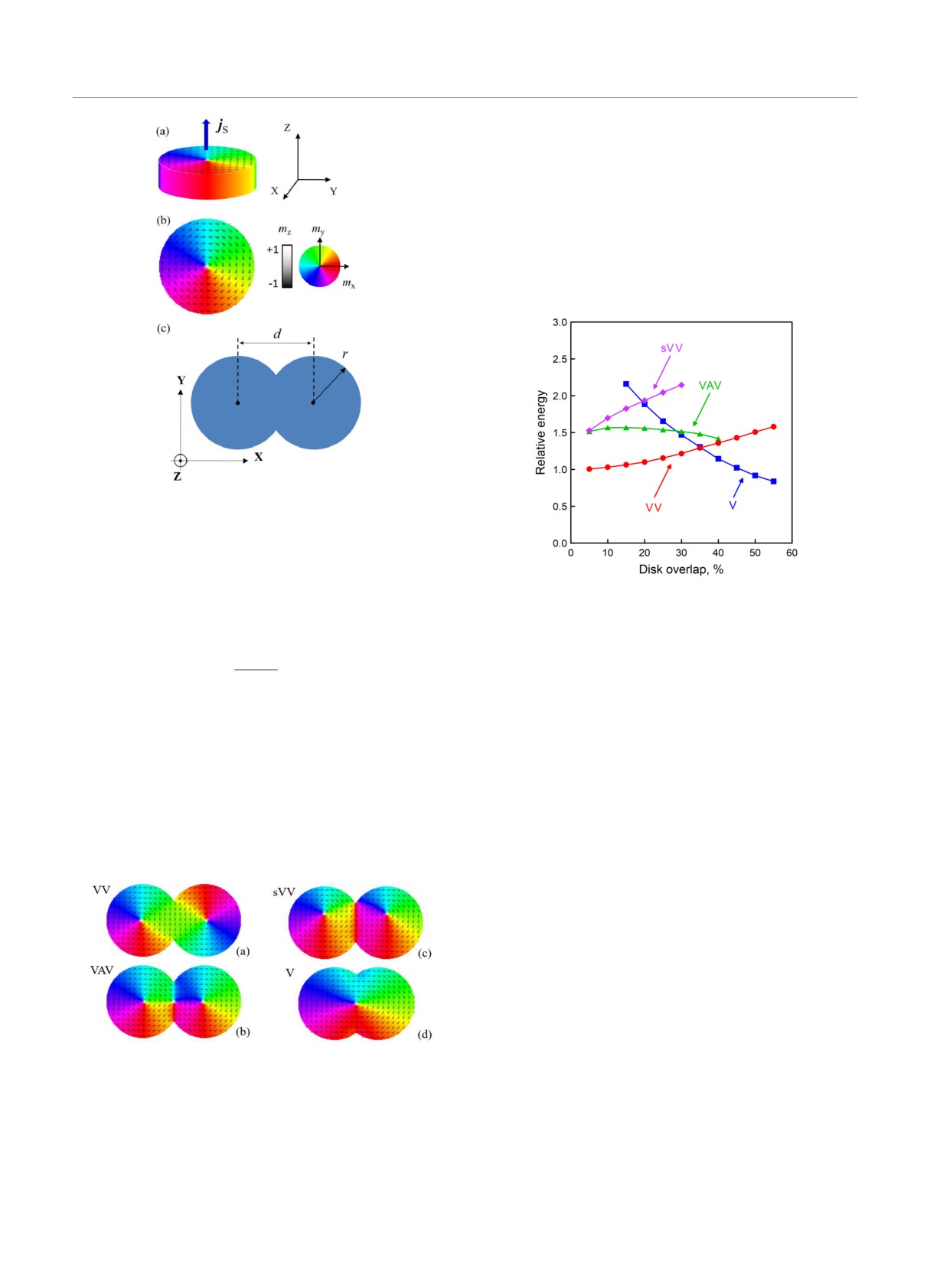
Рис. 1. a) Схематическое изображение ферромагнитного

диска с вихревым распределением намагниченности, jS

спин-поляризованный ток. b) Вид сверху на вихревое рас-

пределение в диске. c) Схематическое изображение двух

перекрывающихся дисков

В системе, состоящей из двух дисков, расстоя-

Рис. 3. Зависимости полной магнитной энергии для раз-

ние между дисками удобно характеризовать пара-

ных состояний от перекрытия дисков. Все энергии норми-

метром перекрытия

рованы на двойную энергию вихря в одиночном диске

2r - d

На рис.3 представлены зависимости энергии си-

ν =

100%,

(6)

стемы в различных магнитных конфигурациях от

где d расстояние между центрами дисков (рис. 1с).

степени перекрытия дисков. Энергия нормирована

При большом расстоянии (ν < 0) между магнитны-

на удвоенную энергию изолированного магнитного

ми вихрями существует только магнитостатическое

вихря. Как видно на рисунке, при малых перекры-

взаимодействие. Если диски перекрываются (ν > 0),

тиях в системе реализуются двухвихревые состоя-

существует вклад, связанный с прямым обменным

ния, а при перекрытии, превышающем 30%-35%, од-

взаимодействием.

новихревое состояние становится основным состоя-

В системе перекрывающихся дисков реализуют-

нием системы.

ся различные вихревые конфигурации в зависимо-

сти от степени перекрытия ν (рис.2). При малом пе-

3. АВТОКОЛЕБАНИЯ

ВЗАИМОДЕЙСТВУЮЩИХ ВИХРЕЙ ПОД

ДЕЙСТВИЕМ СПИН-ПОЛЯРИЗОВАННОГО

ТОКА

3.1. Гиротропные автоколебания одиночного

вихря

Прежде всего, мы исследовали автоколебания

вихревого распределения намагниченности в от-

дельном диске под действием спин-поляризованного

электрического тока, протекающего перпендикляр-

Рис. 2. Распределение намагниченности в перекрываю-

щихся дисках: a двухвихревое состояние с противопо-

но плоскости диска (рис. 1a). Низкочастотная мода

ложной завихренностью каждого из вихрей, VV; b двух-

колебаний представляет собой гиротропное движе-

вихревое состояние с одинаковой завихренностью вихрей,

ние кора вихря вокруг центра диска. Данное воз-

разделенных антивихрем, VAV; c сдвинутое двухвихре-

буждение реализуется только в том случае, если

вое состояние, sVV; d одновихревое состояние, V

направление тока и полярность кора вихря сов-

368

ЖЭТФ, том 163, вып. 3, 2023

Синхронизация автоколебаний магнитных вихрей . . .

падают (вне зависимости от направления завих-

взаимодействия вихрей также зависит от расстоя-

ренности оболочки вихря). Стационарные автоко-

ния между центрами дисков (она определялась как

лебания устанавливаются при достижении условия

разность между энергией колебаний в двух дисках

|T_S | = |T_D|. Амплитуда и частота гирации увели-

и удвоенной энергией колебаний намагниченности

чиваются с увеличением плотности тока накачки.

в изолированном диске [18]). При положительном

При некотором критическом токе происходит рез-

перекрытии дисков (ν > 0) между вихрями воз-

кое изменение направления поляризации кора вих-

никает дополнительное обменное взаимодействие и

ря и осцилляции затухают [38, 39]. По результа-

полная энергия взаимодействия резко увеличивает-

там моделирования установлено, что для выбран-

ся (рис. 4b).

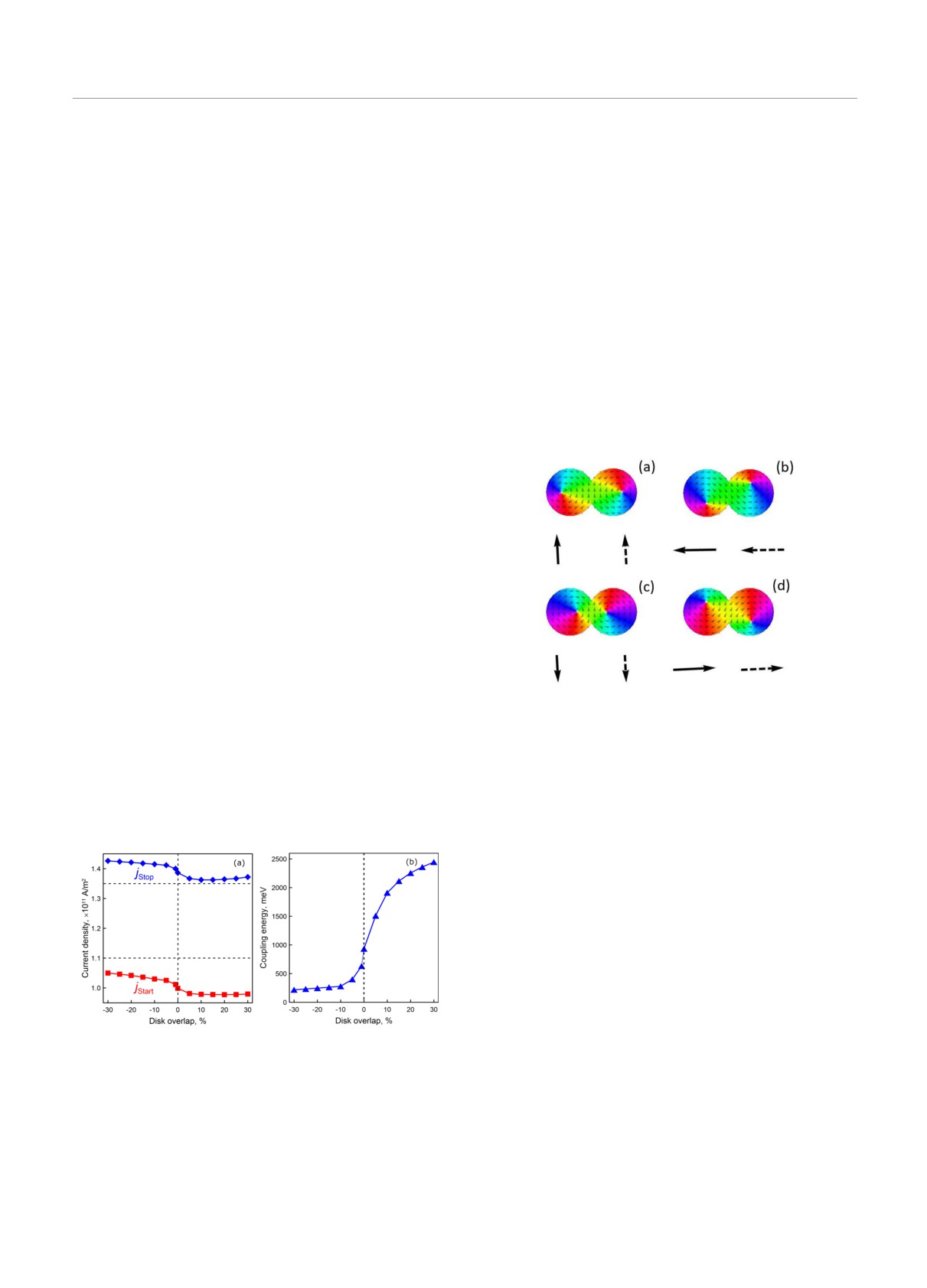
ных параметров диска пороговый ток начала ав-

В конфигурации VV с положительной полярно-

токолебаний составляет j_Start

= 1.067 · 10¹¹ А/м²,

стью коров гирация вихрей происходит вокруг со-

а критический ток прекращения гирации равен

стояний равновесия вблизи центров дисков против

jStop = 1.628 · 1011 А/м2. Магнитное поле тока на-

часовой стрелки. Фазы вращения коров сдвинуты

качки по-разному влияет на колебания магнитного

на 180 градусов, в то время как средние магнитные

вихря, увеличивая или уменьшая частоту гирации в

моменты, возникающие в плоскости дисков, враща-

зависимости от направления завихреннсти оболоч-

ются синфазно (рис. 5) [41].

ки. Обычно для оценки этого поля используется мо-

дель бесконечного проводника с током [40]. Одна-

ко для рассматриваемых нами дисков длина канала

тока составляет l ∼ 25 нм, что при плотности тока

10¹¹ А/м² и радиусе диска r ∼ 250 нм дает оценку

поля на краю диска 15 Э. Такое поле слабо влияет

на динамику магнитного вихря и в дальнейшем не

учитывалось.

3.2. Гиротропные автоколебания вихрей с

различной завихренностью

В системе двух дисков параметры j_Start и j_Stop

зависят от параметра ν вследствие взаимодействия

Рис. 5. Последовательные моментальные снимки состоя-

ний VV при возбуждении автоколебаний и соответствую-

между вихрями. Зависимости критических токов

щие наведённые магнитные моменты

j_Start и j_Stop от величины перекрытия для случая,

когда завихренности оболочек вихрей имеют проти-

Для анализа фазовых характеристик гирации

воположные направления, представлены на рис.4a.

вихрей мы исследовали установившиеся гиротроп-

Наблюдается убывание этих величин с уменьше-

ные колебания при изменении величины разности

нием расстояния между центрами дисков. Энергия

токов накачки и при различных расстояниях между

дисками. С этой целью к каждому из дисков прикла-

дывались небольшие (1 Э) ортогональные магнит-

ные поля, направленные вдоль осей x и y, которые

вызывали смещение вихрей и обеспечивали началь-

ную разность фаз гирации близкую 90 градусам. За-

тем включался ток накачки и поля выключались.

После установления стационарного режима опреде-

лялась стационарная разность фаз гирации вихрей.

Осциллирующий средний магнитный момент в каж-

дом диске описывался комплексной величиной

Рис. 4. a) Зависимости критических токов jStart (квад-

m_n = m_nx + im_ny,

(7)

раты) и jStop (ромбы) от величины перекрытия дисков

(VV-состояние). Горизонтальные линии обозначают гра-

где m_n индуцированный магнитный момент в пер-

ницы области токов, в которой далее исследовалась де-

вом и втором диске (n = 1, 2). Разность фаз осцил-

фазировка гирации вихрей. b) Зависимость энергии взаи-

ляций в дисках определялась по формуле

модействия для VV-состояния от перекрытия. Плотность

тока накачки j0

= 1.225 · 10¹¹ А/м²

Δϕ_1,2 = arg(m₁) - arg(m₂).

(8)

369

Д. А. Татарский, В. Л. Миронов, А. А. Фраерман

ЖЭТФ, том 163, вып. 3, 2023

Если токи накачки, протекающие в каждом из

дисков, равны (j₁ = j₂), то разность фаз равна нулю

и индуцированные магнитные моменты вращаются

синхронно. Если же j₁ = j₂, то появляется разность

фаз, зависящая как от разности токов в дисках, так

и от их взаимного расположения.

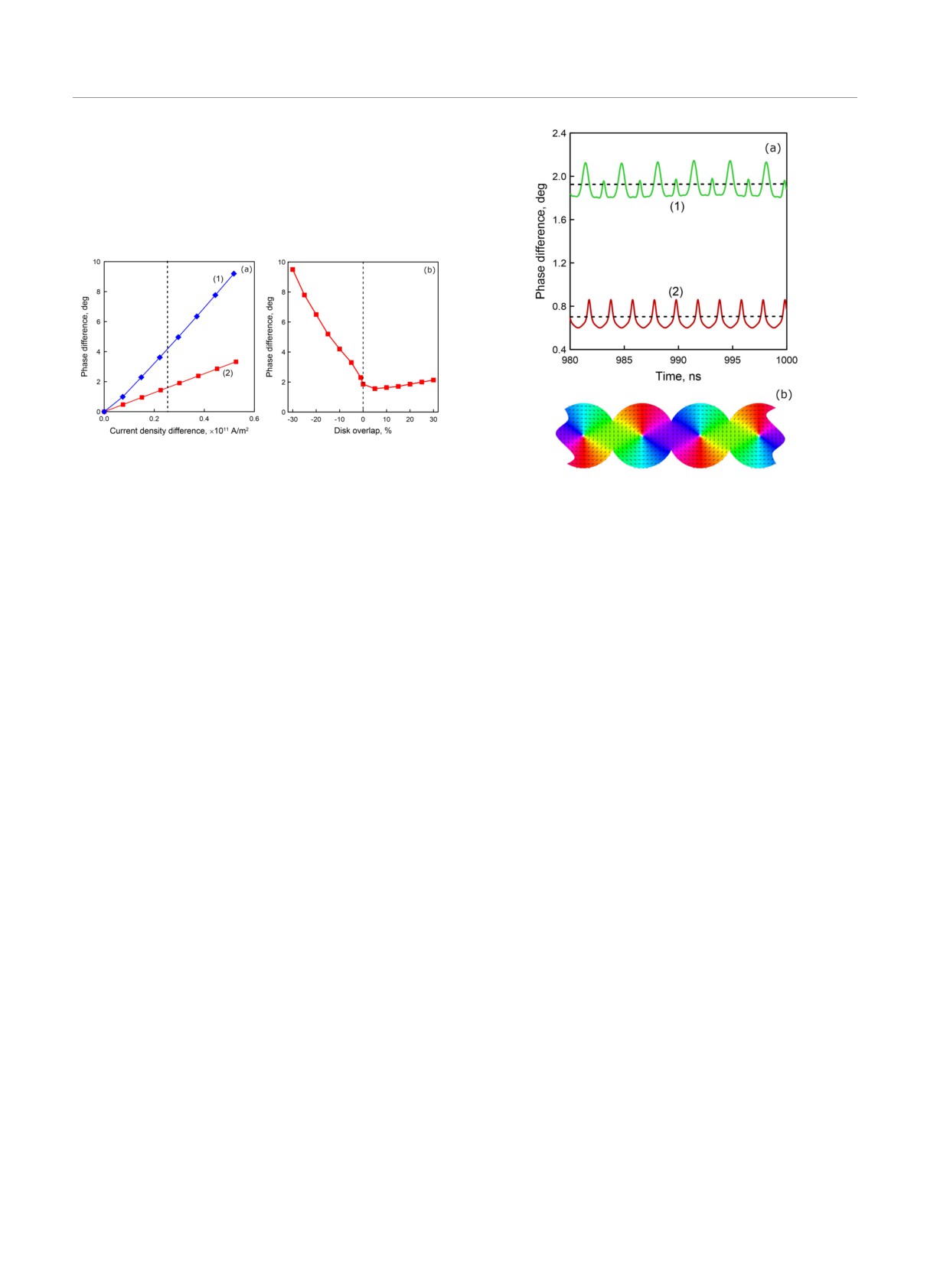
Рис. 6. a) Зависимости разности фаз от разности токов

накачки для состояния VV. Зависимость 1 для ν = -10%;

Рис. 7. a) Осциллограммы разности фаз гирации вихрей

2 для ν = +10%. Вертикальная пунктирная линия соот-

для состояния VV. Перекрытие ν = +10%, разность то-

ветствует разности токов, обозначенных пунктирными ли-

ков накачки Δj = 0.25 · 10¹¹ А/м². Осциллограмма 1 для

ниями на рис. 4a. b) Зависимость разности фаз от пере-

осцилляций разности фаз в двойном диске, осциллограм-

крытия дисков для состояния VV. Разность токов накач-

ма 2 для бесконечной цепочки дисков. b) Фрагмент цепоч-

ки Δj = 0.25 · 10¹¹ А/м²

ки вихрей с переменным направлением завихренности

При моделировании плотность тока в каждом из

дисков изменялась относительно среднего значения

Однако даже при сильной связи между дисками

наблюдаются достаточно большие пульсации разно-

j_1,2 = j₀ ± Δj,

(9)

сти фаз, обусловленные неизохронным вращением

коров вихрей, связанным с асимметричной формой

где j₀

средняя плотность тока, протекающего че-

двойного диска. На рис. 7а представлена осцилло-

рез диски (при моделировании она выбиралась рав-

грамма разности фаз (кривая 1) для перекрытия

ной j₀ = 1.225 · 10¹¹ А/м²). На рис. 6a представлены

ν = +10% и разности токов Δj = 0.25 · 1011 А/м².

зависимости разности фаз Δϕ от разности токов Δj

При данных параметрах среднее значении разности

при различных перекрытиях дисков. Как видно на

фаз составляет 1.9^◦. Амплитуда колебаний разности

рисунке, эти зависимости близки к линейным. Отме-

фаз составляет 0.3^◦. Влияние фактора асимметрии

тим, что даже при выходе значений токов накачки

системы можно снизить, объединяя диски в одно-

из области генерации j₁ < j_Start и j₂ > j_Stop ав-

мерную цепочку (рис. 7b). Осциллограмма колеба-

токолебания продолжаются. Как показало модели-

ний разности фаз для цепочки дисков приведена на

рование, для генерации автоколебаний достаточно

рис. 7а (кривая 2). Как видно, при тех же значениях

выполнения следующего условия для среднего зна-

Δj и ν в цепочке средняя разность фаз и амплитуда

чения плотности тока j_Start < j₀ < j_Stop . На рис. 6b

пульсаций уменьшаются и составляют соответствен-

показана зависимость разности фаз от расстояния

но 0.9^◦ и 0.2^◦.

между дисками при фиксированной разности токов

накачки Δj = 0.25 · 10¹¹ А/м². При этом токи в каж-

дом диске находились вблизи края области генера-

3.3. Гиротропные колебания вихрей с

ции j1 = 1.10 · 1011 А/м2 и j2 = 1.35 · 1011 А/м2

одинаковой завихренностью

(помечены горизонтальными пунктирными линия-

ми на рис. 4a). На рисунке видно, что разность фаз

Автоколебания вихрей с одинаковой завихренно-

монотонно убывает от значения Δϕ = 9.5^◦, при

стью при ν < 0 происходят синфазно, при этом ко-

относительно большом расстоянии между дисками

ры вращаются против часовой стрелки. Когда диски

(ν = -30%) до минимального значения 1.9^◦ для пе-

перекрываются (ν > 0), между вихрями формирует-

рекрывающихся дисков. Таким образом, увеличение

ся антивихрь и реализуется состояние VAV. В этом

энергии связи, как и ожидалось, приводит к улуч-

случае мода колебаний представляет собой сфази-

шению условий синхронизации гирации вихрей.

рованное движение коров вихрей против часовой и

370

ЖЭТФ, том 163, вып. 3, 2023

Синхронизация автоколебаний магнитных вихрей . . .

мость от перекрытия в области ν > 0, чем для вих-

рей с разной завихренностью. Кроме того, наблю-

дается очень сильная зависимость разности фаз ко-

лебаний вихрей от расстояния между дисками. На

рис. 9b приведена зависимость разноси фаз Δϕ от

перекрытия дисков ν при разности токов накачки

Δj = 0.25 · 10¹¹ А/м². Толщина линии на рисунке

показывает амплитуду пульсаций Δϕ. На рисунке

видно, что при перекрытии дисков разность фаз ме-

няет знак и продолжает нарастать.

Рис. 8. Последовательные моментальные снимки состоя-

ний VAV (a-d ) и sVV (e-h) при возбуждении автоколеба-

ний и соответствующие наведённые магнитные моменты

кора антивихря по часовой стрелке (рис. 8a-d). Ан-

Рис. 10. a) Осциллограммы разности фаз гирации вих-

тивихрь представляет собой метастабильное состоя-

рей для состояния sVV. Перекрытие ν = +10%, разность

токов накачки Δj = 0.25 · 10¹¹ А/м². Осциллограмма 1

ние, которое разрушается относительно малыми то-

для осцилляций разности фаз в двойном диске, осцил-

ками накачки. После “выхода” антивихря за преде-

лограмма 2 для бесконечной цепочки дисков. b) Зависи-

лы дисков формируется состояние sVV, в котором

мости разности фаз от разности токов накачки для вих-

вихри сдвинуты из центров дисков (рис. 8e-h).

рей с одинаковой завихренностью. Параметр перекрытия

ν = +10%. На кривых 1 сплошные линии (квадраты) по-

казывают зависимость максимума и минимума разности

фаз Δϕ, пунктиром показана зависимость среднего значе-

ния Δϕ. На кривых 2 сплошные линии (круги) показывают

зависимость максимума и минимума разности фаз Δϕ для

цепочки дисков, пунктиром показана зависимость средне-

го значения Δϕ. Вертикальная пунктирная линия соответ-

ствует разности токов Δj = 0.25 · 10¹¹ А/м². c) Фрагмент

цепочки вихрей с одинаковым направлением завихренно-

сти

На рис.10а представлена осциллограмма (кри-

Рис. 9. a) Зависимости критических токов jStart (квад-

вая 1) разности фаз колебаний вихрей в состоянии

раты) и jStop (ромбы) от перекрытия дисков для вихрей

sVV в двойном диске для перекрытия ν = +10%

с одинаковой завихренностью. Состояние sVV. b) Зависи-

и разности токов накачки Δj = 0.25 · 1011 А/м2.

мость разности фаз от перекрытия дисков. Разность токов

Среднее значение разности фаз составляет 17.5^◦.

накачки Δj = 0.25 · 10¹¹ А/м²

Амплитуда пульсации разности фаз составляет 13^◦.

На рис.9a показана зависимость критических то-

Отметим, что амплитуда пульсаций разности фаз

ков j_Start и j_Stop для системы двух вихрей с одинако-

практически не зависит от разности токов накач-

вой завихренностью от расстояния между дисками.

ки (рис. 10b, кривые 1) и равна 13^◦ даже при оди-

В этом случае наблюдается более сильная зависи-

наковых токах. Объединение дисков в одномерную

371

Д. А. Татарский, В. Л. Миронов, А. А. Фраерман

ЖЭТФ, том 163, вып. 3, 2023

цепочку (рис. 10с) также приводит к значительному

полнительной расфазировке гирации вихрей и пуль-

уменьшению среднего значения и амплитуды пуль-

сациям разности фаз. Как показало моделирова-

саций разности фаз. Осциллограмма колебаний раз-

ние, влияние этого нежелательного фактора может

ности фаз для цепочки дисков приведена на рис. 10а

быть значительно снижено посредством объедине-

(кривая 2). Как видно, при тех же значениях Δj и ν

ния дисков в одномерную цепочку. Такое объеди-

в цепочке средняя разность фаз и амплитуда пульса-

нение уменьшает как степень расфазировки, так и

ций уменьшаются и составляют соответственно 2.5^◦

амплитуду пульсаций разности фаз. Также важным

и 1^◦. Зависимость этих величин от разности токов

результатом является наблюдаемая сильная зависи-

накачки линейная (рис. 10b, кривые 2).

мость разности фаз гиротропного движения вихрей

от степени перекрытия дисков. Показано, что об-

менная связь значительно уменьшает разность фаз

гирации. Так, например, при разности токов накач-

4. ЗАКЛЮЧЕНИЕ

ки Δj = 0.25 · 10¹¹ А/м² эта разность для состоя-

Таким образом, методом микромагнитного мо-

ний VV составляет Δϕ₊₁₀ = 1.63^◦ для перекрытия

делирования исследованы гиротропные автоколеба-

ν = +10% и Δϕ_-10 = 4.20^◦ для ν = -10%. Это яв-

ния магнитных вихрей во взаимодействующих фер-

ляется важным фактором, поскольку при объедине-

ромагнитных дисках.

нии N дисков в одномерную цепочку даже неболь-

Показано, что пространственно-временная

шая разность фаз приводит к значительной потере

структура коллективной гиротропной моды авто-

генерируемой мощности вследствие кубической за-

колебаний в двойных дисках зависит от взаимной

висимости дисперсии фазы осцилляторов от их чис-

ориентации вихревых оболочек. Когда вихри име-

ла. Для сравнения приведем оценку выигрыша мощ-

ют разную завихренность (VV), вращение коров

ности при снижении разности фаз с Δϕ₊₁₀ до Δϕ_-10

с положительной полярностью происходит против

на основе модели Курамото [30]. Отношение генери-

часовой стрелки со сдвигом фаз на 180 градусов. В

руемой мощности для перекрытий ±10% составляет

случае же, когда завихренности одинаковы (sVV),

вращение коров также происходит против часовой

P_-10

{

(

)

}

≈ exp

Δϕ^2-10 - Δϕ²⁺¹⁰

N³

(10)

стрелки, но синфазно. Тем не менее, только в со-

P₊₁₀

стоянии VV индуцированные в вихревых оболочках

магнитные моменты вращаются синфазно, поэтому

Например, для N = 10 это отношение равно 100.

именно это состояние является перспективным для

Таким образом, можно ожидать, что перекрытие

использования в фазовой синхронизации ВСТНО.

дисков приведет к улучшению фазовой синхрониза-

Отметим, что направлением завихренности оболо-

ции цепочек ВСТНО и возрастанию генерируемой

чек вихрей можно управлять, изменяя форму фер-

мощности.

ромагнитного диска [42].

Благодарности.

Авторы

благодарят

Особое внимание уделено фазовым характери-

Е. А. Караштина, Е. В. Скороходова и Р. В. Горева

стикам гирации вихрей при различных значени-

за полезные обсуждения.

ях возбуждающего спин-поляризованного тока. Да-

же небольшая разница токов накачки в соседних

Финансирование. Работа выполнена при под-

дисках приводит к расфазировке вращения инду-

держке Российского научного фонда (проект № 21-

цированных магнитных моментов. Данный эффект

12-00271).

обусловлен разностью скоростей вращения коров

вследствие разности токов накачки. Условия для

фазовой синхронизации в системе VV значительно

ЛИТЕРАТУРА

лучше, чем в системе sVV, поскольку автоколебания

вихрей с одинаковой завихренностью демонстриру-

1. Z. Zeng, G. Finocchio, and H. Jiang, Nanoscale 5,

ют значительную разность фаз и амплитуду ее пуль-

2219 (2013).

саций даже при нулевой разности возбуждающих

2. T. Chen, R. Dumas, A. Eklund, P. Muduli, A. Hou-

токов.

shang, A. Awad, P. Durrenfeld, B. Malm, A. Rusu,

Важной особенностью гиротропных колебаний

and J. Akerman, Proc. IEEE 104, 7505988 (2016).

намагниченности двух перекрывающихся дисков яв-

ляется неизохронность вращения вихрей, связанная

3. J. Slonczewski, J. Magn. Magn. Mater.

159, L1

с асимметрией формы системы. Это приводит к до-

(1996).

372

ЖЭТФ, том 163, вып. 3, 2023

Синхронизация автоколебаний магнитных вихрей . . .

L. Berger, Phys. Rev. B 54, 9353 (1996).

20.

Q. Zhu, Q. Zheng, X. Liu, J. Wang, and Q. Liu,

J. Appl. Phys. 117, 173907 (2015).

S. Kiselev, J. Sankey, I. Krivorotov, N. Emley,

R. Schoelkopf, R. Buhrman, and D. Ralph, Nature

21.

T. Kendziorczyk, S. Demokritov and T. Kuhn, Phys.

425, 380 (2003).

Rev. B 90, 054414 (2014).

W. Rippard, M. Pufall, S. Kaka, S. Russek, and

22.

M. Kreissig, R. Lebrun, F. Protze, K. Merazzo-

T. Silva, Phys. Rev. Lett. 92, 272011 (2004).

Jaimes, J. Hem, L. Vila, R. Ferreira, M. Cyrille,

F. Ellinger, V. Cros, U. Ebels, and P. Bortolotti, AIP

A. Deac, A. Fukushima, H. Kubota, H. Maehara,

Adv. 7, 056653 (2017).

Y. Suzuki, S. Yuasa, Y. Nagamine, K. Tsunekawa,

D. Djayaprawira, and N. Watanabe, Nature Phys. 4,

23.

Y. Li, X. De Milly, Abreu F. Araujo, O. Klein,

803, (2008).

V. Cros, J. Grollier, and G. De Loubens, Phys. Rev.

Lett. 118, 247202 (2017).

A. Nazarov, H. Olson, H. Cho, K. Nikolaev, Z. Gao,

Stokes, S„ and B. Pant, Appl. Phys.Lett. 88, 162504

24.

S. Tsunegi, T. Taniguchi, R. Lebrun, K. Yakushiji,

(2006).

V. Cros, J. Grollier, A. Fukushima, S. Yuasa, and

H. Kubota, Sci. Rep. 8, 13475 (2018).

D. Houssameddine, S. Florez, J. Katine, J. Michel,

U. Ebels, D. Mauri, O. Ozatay, B. Delaet, B. Viala,

25.

M. Riou, J. Torrejon, B. Garitaine, F. Abreu Araujo,

P. Bortolotti, V. Cros, S. Tsunegi, K. Yakushiji,

L. Folks, B. Terris, and M. Cyrille, Appl. Phys. Lett.

93, 022505 (2008).

A. Fukushima, H. Kubota, S. Yuasa, D. Querlioz,

M. Stiles, and J. Grollier, Phys. Rev. Appl.

12,

10.

V. Pribiag, I. Krivorotov, G. Fuchs, P. Braganca,

024049 (2019).

O. Ozatay, J. Sankey, D. Ralph, and R. Buhrman,

26.

H. Singh, A. Bose, S. Bhuktare, A. Fukushima,

Nature Phys. 3, 498 (2007).

K. Yakushiji, S. Yuasa, H. Kubota, and A. Tulapur-

11.

R. Lehndorff, D. Burgler, S.Gliga, R.Hertel, P. Grun-

kar, Phys. Rev. Appl. 10, 024001 (2018).

berg, C. Schneider, and Z. Celinski, Phys. Rev. B 80,

27.

H. Singh, S. Bhuktare, A. Bose, A. Fukushima,

054412 (2009).

K. Yakushiji, S. Yuasa, H. Kubota, and A. Tulapur-

12.

A. Dussaux, B. Georges, J. Grollier, V.Cros, A. Khva-

kar, Phys. Rev. Appl. 11, 054028 (2019).

lkovskiy, A. Fukushima, M. Konoto, H. Kubota,

28.

A. Slavin and V. Tiberkevich, IEEE Trans. Magn. 45,

K. Yakushiji, S. Yuasa, K. Zvezdin, K. Ando, and

1875 (2009).

A. Fert, Nature Commun. 1, 8 (2010).

29.

A. Belanovsky, N. Locatelli, P. Skirdkov, F. Araujo,

13.

S. Tsunegi, K. Yakushiji, A. Fukushima, S. Yuasa,

J. Grollier, K. Zvezdin, V. Cros, and A. Zvezdin,

and H. Kubota, Appl. Phys. Lett. 109, 252402 (2016).

Phys. Rev. B 85, 100409 (2012).

14.

F. Mancoff, N. Rizzo, B. Engel, and S. Tehrani,

30.

H. Hong, H. Park, and M. Choi, Phys.Rev. E 72,

Nature 437, 393 (2005).

036217 (2005).

15.

Abreu F. Araujo, A. Belanovsky, P. Skirdkov,

31.

V. Flovik, F. Maclá, and E. Wahlstrom, Sci. Rep. 6

K. Zvezdin, A. Zvezdin, N. Locatelli, R. Lebrun,

32528 (2016).

J. Grollier, V. Cros, De G. Loubens, and O. Klein,

Phys. Rev. B 92, 045419 (2015).

32.

H. Hata, M. Goto, A. Yamaguchi, T. Sato, Y. Naka-

tani, and Y. Nozaki, Phys. Rev. B 90, 104418 (2014).

16.

N. Locatelli, A. Hamadeh, Abreu F. Araujo, A. Bela-

novsky, P. Skirdkov, R. Lebrun, V. Naletov, K. Zvez-

33.

S. Jain, H.Schultheiss, O. Heinonen, F. Fradin, J. Pe-

din, M. Munoz, J. Grollier, O. Klein, V. Cros, and

arson, S. Bader, and V. Novosad, Phys. Rev. B 86,

G. De Loubens, Sci. Rep. 5, 17039 (2015).

214418 (2012).

17.

S. Kaka, M. Pufall, W. Rippard, T. Silva, S. Russek,

34.

J. Xiao, A. Zangwill, and M. Stiles, Phys. Rev. B 70,

and J. Katine, Nature 437, 389 (2005).

172405 (2004).

18.

S. Erokhin and D. Berkov, Phys. Rev.B 89, 144421

35.

A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen,

(2014).

F. Garcia-Sanchez, and B. Van Waeyenberge, AIP

Adv. 4, 107133 (2014).

19.

A. Ruotolo, V.Cros, B. Georges, A. Dussaux, J. Grol-

lier, C. Deranlot, R. Guillemet, K. Bouzehouane,

36.

G. Abo, Y. Hong, J. Park, J. Lee, W. Lee, and

S. Fusil, and A. Fert, Nature Nanotech. 4, 528 (2009).

B. Choi, IEEE Trans. Magn. 49, 4937 (2013).

373