ЖЭТФ, 2023, том 163, вып. 3, стр. 392-400

МЕХАНИЗМ ПОПЕРЕЧНОГО ТРАНСПОРТА ЗАРЯДА В

ТОНКИХ ПЛЕНКАХ ГЕКСАГОНАЛЬНОГО НИТРИДА БОРА

Д. Р. Исламов^a,b*, Т. В. Перевалов^a, А. А. Гисматулин^a, И. А. Азаров^a,

Е. В. Спесивцев^a, В. А. Гриценко^a,c

^a Институт физики полупроводников им. А. В. Ржанова

Сибирского отделения Российской академии наук

630090, Новосибирск, Россия

^b Новосибирский государственный университет

630090, Новосибирск, Россия

^c Новосибирский государственный технический университет

630073, Новосибирск, Россия

Поступила в редакцию 1 июля 2022 г.,

после переработки 2 ноября 2022 г.

Принята к публикации 2 ноября 2022 г.

Изучен механизм поперечного транспорта заряда через многослойный гексагональный нитрид бора

(h-BN) в структурах металл- диэлектрик- полупроводник. Экспериментальные данные по транспорту

проанализированы в рамках различных моделей переноса заряда в диэлектриках. Показано, что транс-

порт заряда через h-BN описывается моделью фонон-облегченного туннелирования между нейтральными

ловушками. Определены значения термической и оптической энергий фонон-связанных ловушек в h-BN.

Из анализа транспортных измерений, рентгеновских фотоэлектронных спектров и электронной структу-

ры собственных дефектов в h-BN, рассчитанной методом ab initio, установлено, что наиболее вероятным

дефектом, ответственным за транспорт заряда в h-BN, является дивакансия бор - азот. При этом транс-

порт заряда осуществляется электронами.

DOI: 10.31857/S0044451023030112

тронных устройств. Решение этой задачи являет-

EDN: QEYBJE

ся актуальным для внедрения h-BN в производство

электронных элементов при дальнейшем масштаби-

ровании технологических процессов.

1. ВВЕДЕНИЕ

Транспорт заряда поперек механически рассло-

Гексагональный нитрид бора (h-BN) является

енных чешуек h-BN при толщине пленок 1-31 мо-

слоистым диэлектрическим материалом с широкой

нослоев изучался в работе [9] с использованием

запрещенной зоной 5.5-6 эВ [1], перспективным для

методики проводящей атомно-силовой микроскопии

использования в качестве диэлектрика в различных

(АСМ) [10]. Авторы отметили, что при толщинах

твердотельных и гибких микроэлектронных устрой-

слоев более 1 нм ток через h-BN описывается тун-

ствах [2-4]: в элементах резистивной памяти [5]; ге-

нелированием через треугольный барьер по Фау-

нераторах истинно случайных чисел [6,7]; электрон-

леру - Нордгейму, а в случае сверхтонких пленок

ных синапсах для нейроморфных систем [8]. Одна-

(моно-, двойные и тройные слои) эксперименталь-

ко перенос заряда через ультратонкие диэлектри-

ные данные при малых напряжениях описываются

ческие слои h-BN при приложении электрическо-

моделью прямого туннелирования (через трапеци-

го напряжения до сих пор изучен недостаточно. А

евидный барьер) с переходом в туннелирование по

это ключевое свойство диэлектрического матери-

Фаулеру - Нордгейму по мере повышения напряже-

ала, определяющее надежность и срок службы элек-

ния. Высота потенциального барьера для электро-

нов на границе Si/h-BN была оценена в 3.07 эВ [9],

^* E-mail: damir@isp.nsc.ru, d.islamov@g.nsu.ru

что сравнимо с 3.2 эВ для Si/SiO₂ [11]. Следует от-

392

ЖЭТФ, том 163, вып. 3, 2023

Механизм поперечного транспорта заряда ...

метить, что применение методики проводящей АСМ

(a)

(b)

может приводить к ложному обнаружению тунне-

лирования через трапециевидный либо треугольный

h-BN

барьер из-за ограниченности сканируемой площади

p-Si

(примерно 50 нм² [12]) механически расслоенных че-

шуек h-BN, которые имеют малое количество точеч-

ных дефектов.

1.5 cm × 1.5 cm

В настоящее время для синтеза слоев h-BN в

электронных приборах широко используется ме-

тод химического осаждение из парогазовой фазы

Рис. 1. МДП-структуры Ag/h-BN/Si: a

схематичное

(chemical vapour deposition, CVD) [13]. Данный ме-

изображение поперечного среза; b

фотография плен-

ки h-BN и контактных площадок. Числа в столбцах слева

тод широко применяется в полупроводниковой про-

от структур соотвествуют линейным размерам контактов

мышленности, он дешевле и приводит к меньше-

в микрометрах

му количеству точечных дефектов в h-BN по срав-

нению с образцом h-BN, полученным магнетрон-

Морфология структур Ag/h-BN/p-Si контроли-

ным распылением или молекулярно-лучевой эпи-

ровалась методами сканирующей АСМ (не приве-

таксией [13, 14]. Однако для h-BN, синтезированно-

дено) и сканирующей эллипсометрии. 2D-профили

го методом CVD, концентрация точечных дефектов

толщины (d) и показателя преломления (n) h-BN

(вакансий, примеси, оборванных связей и т. п.) су-

на Si-подложке исследовались с помощью сканиру-

щественно выше, чем в механически расслоенном

ющего монохроматического эллипсометра ¾Микро-

h-BN. В свою очередь, высокая концентрация де-

скан¿ (ИФП СО РАН, Новосибирск) [18]. Эллипсо-

фектов в h-BN приводит к большим токам утечки

метрические углы Ψ и Δ измерялись при длине вол-

и, как следствие, к снижению производительности

ны света λ = 632.8 нм; угол падения луча на обра-

приборов при использовании h-BN в качестве пас-

зец ϕ = 60^◦. Пространственное разрешение прибо-

сивного или активного диэлектрика [15, 16].

ра примерно 10 мкм (по осям x и y). Шаги скани-

Целью настоящей работы является выявление

рования по осям составляли 0.05 мм (x) и 0.02 мм

механизмов переноса заряда через h-BN (пер-

(y). Измеренные значения эллипсометрических уг-

пендикулярно слоям), синтезированного методом

лов в каждой точке использовались для решения

CVD, а также выяснение природы дефектов,

обратной задачи эллипсометрии. Для эллипсомет-

о‘тветственных за данную проводимость.

рических расчетов далее использовалась оптическая

модель: поглощающая подложка (Si) - прозрачная

пленка (h-BN) - среда.

2. МАТЕРИАЛЫ И МЕТОДЫ

Измерение рентгеновских фотоэлектронных

Исследуемые в работе образцы представляли

спектров (РФЭС) h-BN проводилось на спектромет-

собой структуры металл- диэлектрик- полупровод-

ре SPECS (Германия) с полусферическим анали-

ник (МДП) Ag/h-BN/Si. Многослойный h-BN тол-

затором PHOIBOS-150-MCD-9 и монохроматором

щиной 5-7 нм (17-19 слоев) был выращен на поли-

FOCUS-500 (излучение AlK_α, hν

= 1486.74 эВ,

кристаллической медной фольге методом CVD [17].

200 Вт). Положения фотоэлектронных линий

Далее h-BN был перенесен на подготовленные под-

калибровались по линии C1s

(284.8 эВ). Атом-

ложки p-Si (2-4 мОм · см) с использованием стан-

ные концентрации элементов

в зоне анализа

дартного метода переноса через жидкость

[17].

определялись по интегральным интенсивностям

Верхние Ag-электроды толщиной 50 нм были нане-

фотоэлектронных линий, скорректированных на

сены на образцы h-BN/p-Si с помощью электронно-

соответствующие коэффициенты атомной чувстви-

лучевого испарителя и теневой маски. Схематич-

тельности (0.486 для B1s, 1.0 для C1s, 1.8 для N1s

ное изображение полученных структур приведено

и 2.93 для O1s).

на рис. 1a. Фотография пленки h-BN на подложке

Вольт-амперные характеристики (ВАХ) синте-

и напыленных контактных площадок приведена на

зированных МДП-структур измерялись при темпе-

рис. 1b. Видно, что пленка h-BN на части подлож-

ратурах в диапазоне 300-450 К с помощью универ-

ки образца повреждена. Поэтому для транспортных

сального анализатора полупроводниковых приборов

измерений использовалась группа контактов с попе-

Keithley 4200-SCS и зондовой станции Cascade M150.

речными размерами 50 × 50 мкм².

Измерения проводились при отрицательной поляр-

393

Д. Р. Исламов, Т. В. Перевалов, А. А. Гисматулин и др.

ЖЭТФ, том 163, вып. 3, 2023

ности напряжения на металлическом электроде,

бор- азот (V_NB, пара ближайших V_N и V_B) со-

чтобы исключить влияние подложки на транспорт.

здавались удалением соответствующих атомов

Ниже при анализе экспериментальных данных при-

200-атомной суперъячейке h-BN, полученной

водятся абсолютные значения электрического поля

5 × 5 × 2-трансляцией элементарной ячейки, с

для упрощения изложения.

последующей релаксацией. Такой размер суперъ-

Моделирование ВАХ в рамках различных моде-

ячейки разделяет периодические изображения

лей осуществлялось минимизацией функции

дефектов на 12.5Å в плоскости BN и на 14Å по

слоям. В расчетах использовались сетка 2 × 2 × 2

√∑

k-точек в неприводимой части зоны Бриллюэна и

S(p) =

(ln (J_expt ) - ln (J_calc))² =

N_F,T

сетка 2 × 2 × 2 q-точек дискретизации оператора

Fi,Tj

Фока. Расположение атомов оптимизировано с

(

u∑

порогом сходимости полной силы 0.02 эВ/Å. Кор-

√

(J_expt))2,

(1)

N_F,T

J_calc

ректность сопоставления расчетных результатов

Fi,Tj

для 3D-кристалла с данными для тонких пленок

где N_F,T

общее количество экспериментально

h-BN обусловливается идентичностью их ближнего

измеренных значений плотности тока J_expt при

порядка [23].

различных электрических полях F_i и температурах

T_j (в наcтоящей работе N_F,T = 200), J_calc рассчи-

танная плотность тока для соответствующей пары

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

(F_i, T_j). Квадрат разности логарифмов токов в вы-

ражении (1) используется вместо (J_expt /J_calc - 1)²

3.1. Эллипсометрия

ввиду экспоненциальной зависимости тока от

электрического поля и температуры (обсужда-

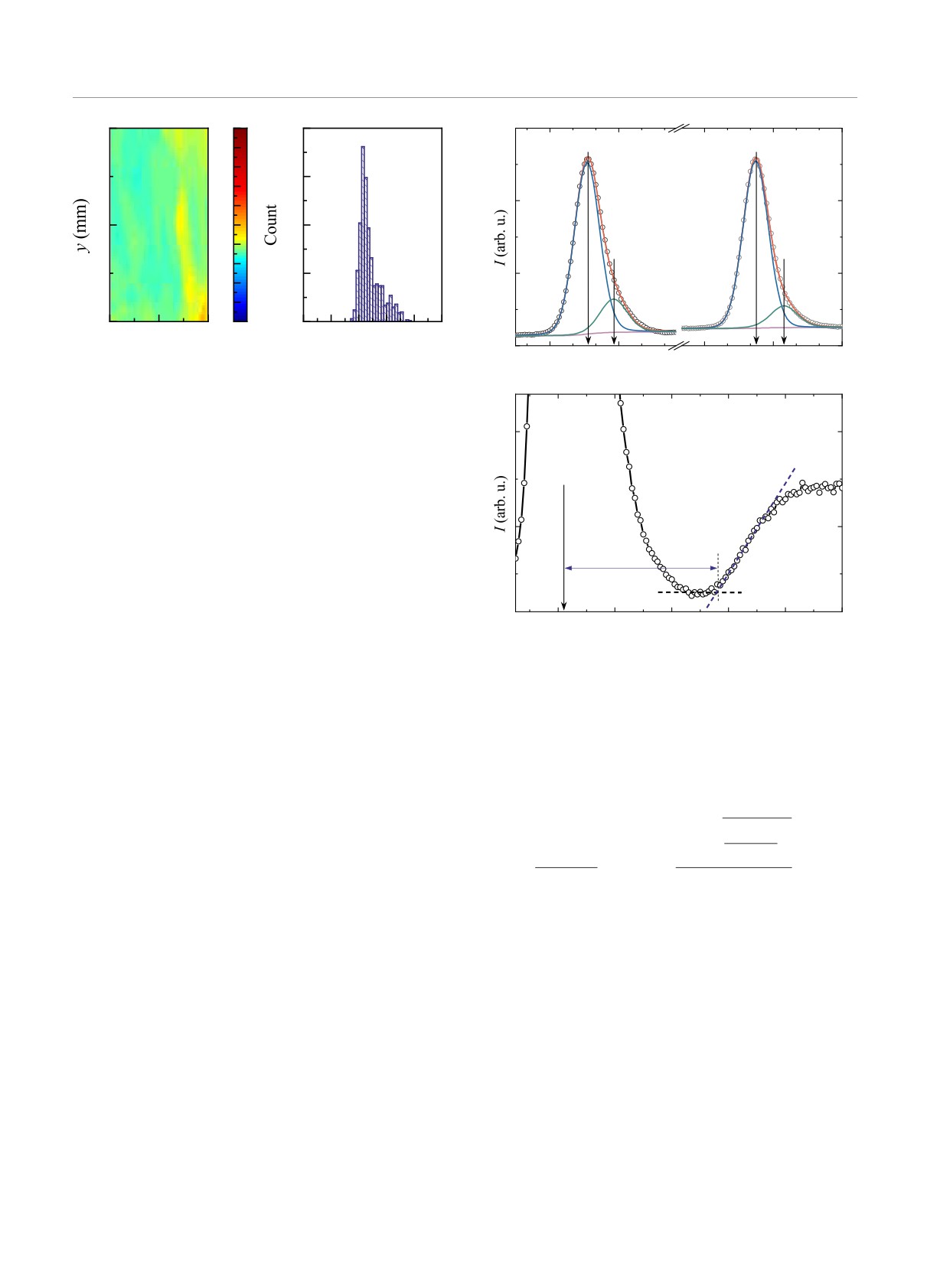
С помощью сканирующей эллипсометрии полу-

ется ниже в разд. 3.3). Стоит также отметить,

чены 2D-профили толщины d (рис. 2а) и показате-

что (J_expt /Jcalc - 1)2

является разложением в

ля преломления n для исследуемого образца h-BN.

ряд Тэйлора суммируемой функции в

(1) при

Значение n составило 1.51 ± 0.1. Распределение тол-

J_calc

→ J_expt. Вектор параметров приближения

щины по поверхности сканирования приведено на

p соответствовал модели транспорта заряда, в

рис. 2b. Видно, что максимум приходится на значе-

рамках которой проводилось моделирование ВАХ.

ние d ≈ 7 нм с небольшим хвостом до 8.5 нм.

Минимизация функции S проводилась методом

градиентного спуска с адаптивными шагами до

достижения отклонения между итерациями l значе-

3.2. РФЭС

ния |S_l - S_l-1| < 10^-12. При этом целевая функция

S достигала значения менее 10^-2.

РФЭС-спектр h-BN помимо пиков, обусловлен-

Моделирование электронной структуры соб-

ных B и N, иллюстрирует наличие C и O в зоне

ственных дефектов в h-BN проводилось в рам-

анализа пленки (глубина анализа около 3 нм). Спек-

ках спин-поляризованной теории функционала

тры B1s и N1s имеют типичную для h-BN фор-

плотности в модели периодической суперъ-

му несимметричных гауссовых функций с максиму-

ячейки с плосковолновым базисом с энергией

мами при энергиях 190.6 и 398.2 эВ соответствен-

отсечки

1100 эВ и сохраняющими норму псев-

но [24, 25] (рис. 3a). Наличие низкоинтенсивных пи-

допотенциалами Вандербильта

[19] в программе

ков B1s и N1s со стороны больших значений энер-

Quantum ESPRESSO [20]. Использовался ги-

гии связи (191.8 и 399.5 эВ соответственно) являет-

бридный обменно-корреляционный функционал

ся характерной особенностью CVD-пленок h-BN и

Хейда - Скузерии - Эрнцерхофа [21]. Такой подход

обусловливается присутствием в пленке кислорода

обеспечивает значение ширины запрещенной зоны

и углерода, формирующих связи O - B, O - B - N и

h-BN, равное

5.75 эВ. Равновесные параметры

C-N [24,25]. Расчет соотношений атомных концен-

решетки a = 2.506Å, c = 6.819Å хорошо согласу-

траций элементов показал, что доля C в зоне ана-

ются с экспериментальными значениями

2.504Å

лиза составляет 20% и доля O

9%. Столь высо-

6.661Å [22]. При моделировании заряженных

кое содержание C и O обусловлено особенностями

дефектов использовался метод нейтрализующе-

технологии переноса пленки на Si-подложку, а так-

го однородного фонового потенциала. Вакансия

же тем фактом, что пленки h-BN деградируют на

азота (V_N), вакансия бора (V_B) и дивакансия

воздухе. Отметим, что хранение и транспортировка

394

ЖЭТФ, том 163, вып. 3, 2023

Механизм поперечного транспорта заряда ...

1.0

200

(a)

(b)

(a)

190.6

398.2

B 1s

N 1s

150

0.5

100

191.8

399.5

0.0

0.5

1.0

x (mm)

(nm)

189

192

396

399

402

Binding energy (eV)

Рис. 2. Эллипсометрическое сканирование поверхности

пленки h-BN на Si: a

карта толщин; b распределе-

(b)

N 1s

ние толщин

образца осуществлялась в специальном вакуумиро-

398.2

ванном пакете.

Фотоэлектроны с уровня N1s, проходя через

слой h-BN, теряют часть кинетической энергии на

возбуждение межзонных переходов электронов, и

E =5.5

спектр этих потерь отражается в высокоэнергети-

ческой части спектра N1s. По краю этого спектра

потерь, путем его линейной интерполяции до уров-

398

400

402

404

406

408

ня фона, оценивается значение ширины запрещен-

Binding energy (eV)

ной зоны E_g h-BN (рис. 3b). Для исследуемого об-

разца данный метод дает значение E_g = 5.5 эВ, что

Рис. 3. a) Фрагменты РФЭС-спектра пленки h-BN: ли-

хорошо согласуется с данными других исследова-

нии B1s и N1s (символы экспериментальные данные,

ний [26, 27]. При этом полученное значение E_g для

кривые разложение на гауссовы функции. b) Фрагмент

исследуемой пленки меньше, чем определенное для

РФЭС-линии N1s, иллюстрирующий способ определения

h-BN ранее E_g

= 6.0 эВ [28, 29], вероятнее всего,

значения Eg пленки h-BN

ввиду относительно высокого содержания кислоро-

уменьшается из-за сил изображения:

да [30].



√



e³



Φ-



4πm^∗k²e



4πε_∞ε₀



J =

T² exp-

.

(2)





3.3. Транспорт

h³





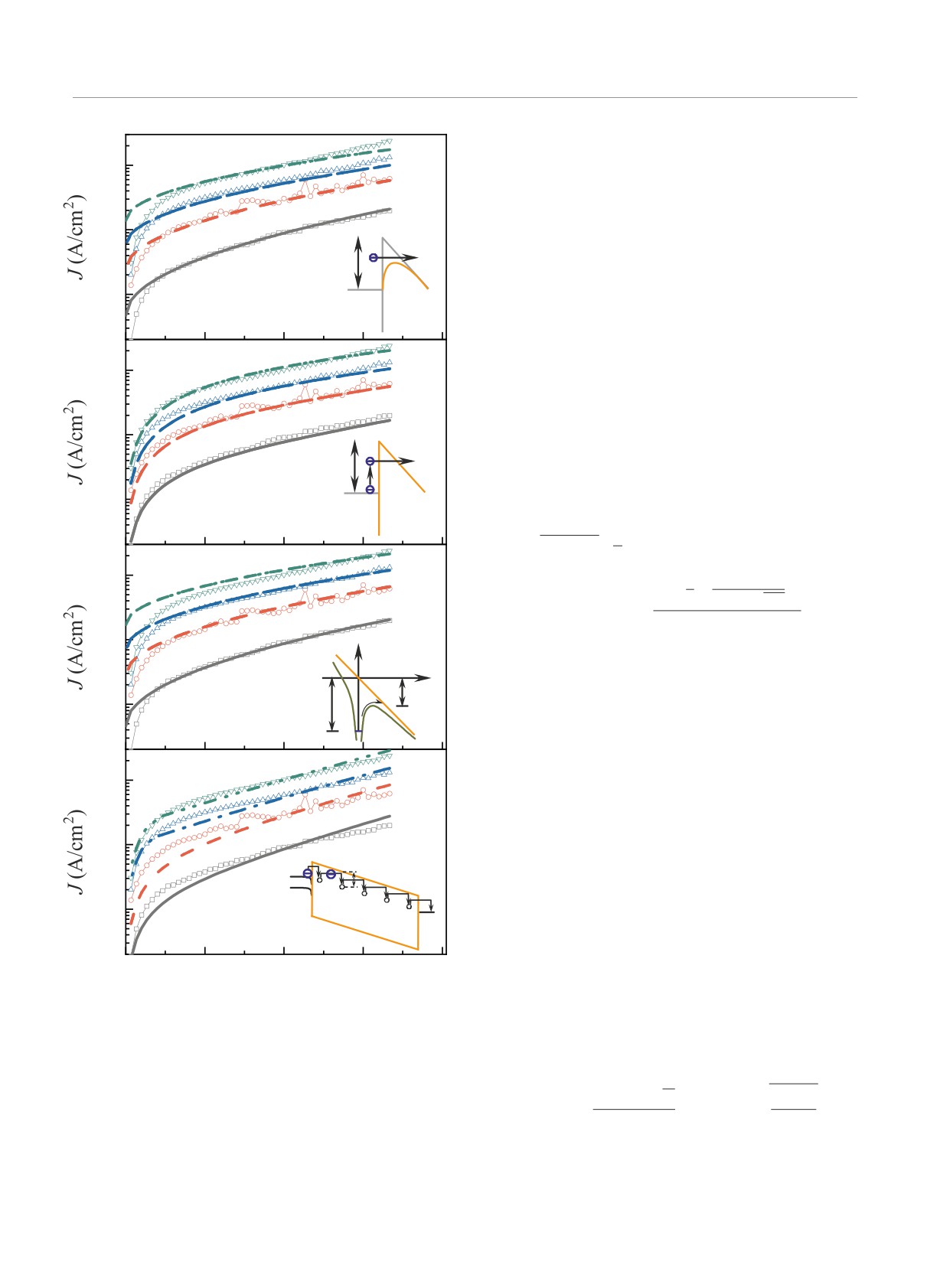
На рис.4 символами представлены эксперимен-

тальные ВАХ для структуры Ag/h-BN/p-Si при раз-

Здесь m^∗ эффективная масса носителя заряда в

личных температурах T в полулогарифмическом

диэлектрике, k

постоянная Больцмана, e за-

масштабе. Экспоненциальные зависимости тока от

ряд электрона (абсолютное значение), h постоян-

температуры и электрического поля показывают,

ная Планка, Φ потенциальный барьер на границе

что перенос заряда в структуре Ag/h-BN/p-Si не

Ag/h-BN, ε_∞ высокочастотная диэлектрическая

может быть описан ни туннельной инжекцией по

проницаемость диэлектрика, ε₀ электрическая по-

Фаулеру - Нордгейму, ни прямым туннелировани-

стоянная.

ем через трапециевидный барьер. Следовательно,

На рис.4a линиями представлены рассчитан-

контактно-ограниченный перенос заряда в структу-

ные зависимости J-F -T при следующих значени-

ре Ag/h-BN/p-Si может быть связан с эффектом

ях параметров: Φ = 0.2 ± 0.02 эВ, ε_∞ = 10 ± 0.1,

Шоттки [31], когда ток ограничен термоэлектрон-

m^∗ = (1 ± 0.1) · 10^-10m₀ (m₀ масса свободного

ной эмиссией электронов над барьером, который

электрона). Значения параметров модели не соот-

395

Д. Р. Исламов, Т. В. Перевалов, А. А. Гисматулин и др.

ЖЭТФ, том 163, вып. 3, 2023

ветствуют ожидаемым: Φ ≈ 0.2 эВ значительно ни-

450K

(a)

же значения 3 эВ, ε_∞ существенно превышает по-

-4

400K

перечную компоненту тензора высокочастотной ди-

360K

электрической проницаемости h-BN ε_⊥,∞

= 3.3-

300K

3.8 [32]. Эффективная масса электрона, при кото-

-5

рой модельные кривые совпадают с эксперименталь-

ными данными, имеет нефизично малое значение.

Можно сделать вывод, что перенос заряда через

-6

МДП-структуры на основе h-BN некорректно опи-

сывается моделью эффекта Шоттки.

Акт термически облегченного туннелирования

450K

(b)

из контакта можно условно разделить на два эта-

-4

400K

па. Вначале электрон возбуждается до некоторой

360K

энергии за счет поглощения фононов (вертикаль-

300K

ная стрелка на вставке рис. 4b). На втором шаге

-5

он туннелирует через треугольный барьер (горизон-

тальная стрелка на вставке рис. 4b). Выражение для

плотности тока для инжекции носителей из металла

-6

имеет следующий вид [33, 34]:

√

)₂

J =

2πm^∗kT

F ×

450K

(c)



(

)₂

-4

400K

ehF

Φ-

√

360K







4πkT

m^∗



× exp-



(3)

300K





-5

-eF

Сравнение экспериментальных данных с рассчитан-

1/2

ными в рамках модели термически облегченного

-6

туннелирования (3) приведено на рис.4b. Эта мо-

дель описывает экспериментальные данные при ра-

. Однако количе-

зумном значении m^∗ = (2.0±0.1)m₀

450K

(d)

-4

ственное согласие достигается при Φ = 0.2 ± 0.02 эВ

400K

и площади контакта 3 нм² при том, что реаль-

360K

ная площадь металлического электрода в структуре

300K

Ag/h-NB/p-Si составляет 2500 мкм². Можно сделать

-5

вывод, что термически облегченное туннелирование

также не объясняет транспорт в h-BN.

Экспоненциальная зависимость тока от напря-

-6

жения (электрического поля) указывает на то, что

модели омической проводимости и проводимости,

ограниченной пространственным зарядом, не при-

0.0

0.2

0.4

0.6

0.8

менимы в данном случае. Наиболее известной в ли-

F (MV/cm)

тературе моделью переноса носителей заряда через

ловушки, демонстрирующей такое поведение, явля-

Рис. 4. Экспериментальные (символы) и рассчитанные для

ется ионизация изолированной ловушки по Френке-

различных моделей (линии) ВАХ структуры Ag/h-BN/p-Si

лю [35]:

при различных температурах: a эффект Шоттки; b

(

)

√

модель термически облегченного туннелирования; c мо-

√

дель Френкеля; d

модель фонон-облегченного тунне-

W -β_F

e³

P = ν exp

β_F =

(4)

лирования между нейтральными ловушками. На вставках

πε_∞ε₀

схематично представлены соответствующие сценарии пе-

реноса заряда в диэлектриках

где P , ν и W скорость ионизации, частотный фак-

396

ЖЭТФ, том 163, вып. 3, 2023

Механизм поперечного транспорта заряда ...

тор и энергия ионизации ловушки соответственно.

(4) и (5) описывают экспериментальные данные при

Ток рассчитывается согласно выражению

концентрации ловушек N ∼ 10⁵ см^-3, соответствую-

щей неприемлемо большому расстоянию между ло-

J = eN^2/3P,

(5)

вушками a ≈ 200 мкм: на площадь 16-ти контак-

где N

концентрация ловушек. В приближе-

тов изучаемых структур приходится только одна ло-

нии равномерного распределения ловушек можно

вушка. Учитывая изложенные выше факты, можно

определить среднее расстояние между ними как

сделать вывод, что эффект Френкеля количественно

a = N^-1/3. Сравнение экспериментальных данных с

некорректно описывает перенос заряда через h-BN.

рассчитанными в рамках модели Френкеля (4), (5)

Ранее было показано, что транспорт во многих

приведено на рис. 4c. Модель Френкеля предсказы-

диэлектриках с высокой диэлектрической проница-

вает нефизично большое значение высокочастотной

емостью также не описывается моделью Френкеля,

диэлектрической проницаемости ε_∞ = 40. Значение

однако непротиворечивое объяснение эксперимен-

энергии ионизации ловушки может быть определено

тальным данным удалось получить с привлечением

из температурного разбега J-F -T -характеристик и

модели фонон-облегченного туннелирования между

составляет W = 0.28±0.02 эВ. В оригинальной рабо-

нейтральными ловушками, предложенной Насыро-

те [35] Френкель определил частотный фактор как

вым и Гриценко [36-42]. В настоящей работе мы

ν ≈ W/h, и для энергии ловушки W ≈ 0.3эВ он

проанализировали экспериментальные данные для

составляет ν ∼ 10¹⁴ с^-1. В этом случае выражения

структуры Ag/h-BN/p-Si в рамках этой модели [43]:

√

(

)

(

2πℏW_t

Wo - Wt

2a√2m∗Wt )

(eFa)

P =

√

exp

(6)

m^∗a²

(W_o - W_t )kT

2kT

ℏ

2kT

где W_t и W_o термическая и оптическая энергии

m^∗⊥ = 2.2m₀ для электронов и m^∗⊥ = 1.33m₀ для

ловушки. В выражении (6) предэкспоненциальный

дырок [44]. Среднее расстояние между ловушками

множитель представляет собой частотный фактор,

2.42 нм в 6-8 раз больше расстояния между слоя-

первая экспонента соответствует термической иони-

ми h-BN. Это означает, что ловушки изолированы

зации с энергией активации W_rlx /2 = (W_o - W_t )/2

друг от друга и не образуют непрерывного канала.

(здесь и далее W_rlx

энергия релаксации ловуш-

При этом расстояние между ловушками обеспечи-

ки), следующий множитель отражает туннельный

вает туннельную прозрачность энергетического ба-

фактор, последний член указывает на уменьшение

рьера между ними, что подтверждает применимость

энергии активации из-за внешнего электрического

модели (6) для описания транспорта в h-BN.

поля. Заметим, что согласно выражению (6) сред-

Ранее в рамках модели многофононной иони-

нее расстояние между ловушками можно опреде-

зации нейтральных ловушек для аморфного нит-

лить по наклону экспериментальных данных, отло-

рида бора были определены значения термической

женных в полулогарифмическом масштабе при фик-

Wt = 1.0 эВ и оптической Wo = 2.0 эВ энергий лову-

сированной температуре. Ток рассчитывается со-

шек [45]. Различие в энергиях ионизации ловушек

гласно выражению (5). Результаты моделирования

в гексагональном и аморфном BN обусловлено раз-

приведены на рис. 4d линиями с различной штри-

личным ближним порядком в структуре этих мате-

ховкой. Хорошее согласие рассчитанных зависимо-

риалов [23].

стей с экспериментальными достигается при следу-

ющих значениях параметров: W_t = 0.58 ± 0.01 эВ,

3.4. Моделирование методом ab-initio

0.9 ± 0.01 эВ, m^∗

(2.14 ± 0.001)m₀,

a = 2.42± 0.01нм (N = (7.2 ± 0.1)· 1019 см^-3). Этим

Открытым остается вопрос о природе ловушек,

значениям в изучаемом интервале температур со-

участвующих в транспорте заряда в h-BN. Наиболее

ответствует частотный фактор (1.2-1.5) · 10¹⁴ с^-1.

вероятными кандидатами являются вакансии азота

Следует отметить, что модель фонон-облегченного

и бора, а также дивакансия бор- азот (V_NB) [46].

туннелирования между нейтральными ловушками

Результаты моделирования электронной структуры

предсказывает эффективную массу носителей за-

VB и VN в h-BN описаны в ряде статей, в которых

ряда в h-BN m^∗ = 2.14m₀, что близко к теорети-

изучаются свойства, связанные с энергией образова-

чески рассчитанным методом ab initio значениям

ния, структурной релаксацией, мультиплетностью

397

Д. Р. Исламов, Т. В. Перевалов, А. А. Гисматулин и др.

ЖЭТФ, том 163, вып. 3, 2023

основного состояния и уровнями переходных состо-

Таблица. Рассчитанные значения электронной и

яний [47-49]. Недавно было показано, что V_NB яв-

дырочной термической Wt и оптической Wo энер-

ляется наиболее вероятным парамагнитным дефек-

гий ионизации, а также энергии формирования (в

том в h-BN [46]. Для выяснения природы дефектов,

эВ) вакансии бора (VB), вакансии азота (VN) и ди-

ответственных за транспорт заряда через исследу-

вакансии бор - азот (VNB) в h-BN

емые пленки h-BN, в настоящей работе методом ab

initio были рассчитаны значения термической W^e/ht

VB VN

VNB

и оптической

o энергий электронной и дырочной

W^et (V^-1)

4.9

1.7

0.4

ионизаций V_B, V_N и V_NB, а также значения энер-

W^eo (V^-1)

5.0

2.1

0.75

гии формирования E_form нейтральных дефектов по

формулам

W^ht (V⁺¹)

0.15

3.6

4.2

(

) (

)

W^ho (V⁺¹)

0.16

3.9

5.2

W^e/ht = E^-1/+1p - E⁰

- E^0p -E^-1/+1

(7)

E_form

8.4

10.9

12.6

W^e/ho = W^e/ht + W^e/hrlx =

(

)

(a) V_B + e^-

(b) V_B + h⁺

=W^e/ht + E^0d(q=-1/+1) -E⁰

d (q = 0)

(8)

E_form = E_d - E_p + µ.

(9)

Здесь E^p1/0/-1 и E^+1/0/-1d

энергии идеаль-

ной и дефектной суперъячеек с полным зарядом

(d) V_N + h⁺

q = +1/0/- 1 соответственно; E^0d(q=-1/+1) энер-

гия дефектной суперъячейки с зарядом q

= 0,

рассчитанная для геометрии, соответствующей

зарядовому состоянию q = +1/0/- 1; µ хими-

ческий потенциал удаляемого атома, который для

азота считался равным половине полной энергии

молекулы N₂, для бора энергии отдельного атома

(e) V_NB + e^-

(f) V_NB + h⁺

бора в стабильной кристаллической α-фазе.

Для всех моделируемых дефектов значения W_t

положительны (таблица), а поскольку рассчитыва-

емая величина также отражает выигрыш в энер-

гии при локализации заряда, можно сделать вы-

вод, что захват как электрона, так и дырки на V_B,

VN и VNB в h-BN энергетически выгоден. Следова-

Рис. 5. Разница в распределении плотности полного заря-

тельно, дефекты вакансионного типа в h-BN явля-

да электронов для отрицательно заряженной и нейтраль-

ются ловушками и для электронов, и для дырок.

ной суперъячеек h-BN для дефектов VB (a ), VN (c ) и

Однако с учетом ошибки метода расчета величи-

VNB (e ), а также для нейтральной и положительно заря-

ны W_t , составляющей ±0.15 эВ, полученные значе-

женной суперъячеек h-BN: VB (b ), VN (d ) и VNB (f ). Для

простоты приведен один монослой суперъячейки h-BN, в

ния W_t и W_o количественно согласуются с экспе-

котором находятся соответствующие дефекты

риментальными только для электронной ионизации

и только для дивакансий бор- азот: W_t = 0.4 эВ и

Wo = 0.75 эВ. Отметим, что энергия релаксации ло-

кансию V_NB. Следовательно, среди собственных де-

вушки W_rlx = W_o - W_t = 0.35 эВ совпадает с по-

фектов вакансионного типа в h-BN ключевым яв-

лученным из транспортных измерений значением

ляется V_NB. Таким образом, по данным анализа

Wrlx = (0.9 - 0.58) эВ = 0.32 эВ. Кроме того, соглас-

транспортных измерений и рассчитанной методом

но расчетам, E_form для V_NB значительно меньше,

ab initio электронной структуры собственных де-

чем сумма E_form для V_B и V_N (а также V_B + V_B

фектов в h-BN можно заключить, что проводимость

и V_N + V_N). Этот результат, в свою очередь, со-

h-BN в исследуемых структурах Ag/h-BN/p-Si явля-

гласуется с данными работы [46], согласно которым

ется электронной и осуществляется преимуществен-

VB может мигрировать, образуя стабильную дива-

но по дивакансиям бор - азот.

398

ЖЭТФ, том 163, вып. 3, 2023

Механизм поперечного транспорта заряда ...

Расчетное пространственное распределение

Финансирование. Работа была выполнена

электронной плотности добавленного в суперъячей-

в рамках государственного задания ИФП СО

ку заряда подтверждает локализацию и электрона,

РАН №0306-2019-0005 (код (шифр) научной темы

и дырки на V_N, V_B и V_NB в h-BN, как показано

FWGW-2022-0003), а также при поддержке Рос-

на рис. 5. Дефекты вакансионного типа в h-BN

сийского фонда фундаментальных исследований

способны локализовать как электроны, так и дыр-

(проект №18-57-80006 БРИКС_т).

ки. Для всех типов дефектов локализация заряда

наблюдается на ближайших к вакансии атомах. Для

VB отрицательный заряд распределен равномерно,

ЛИТЕРАТУРА

тогда как положительный заряд локализуется пре-

имущественно на одном из атомов N. В структуре

G. Cassabois, P. Valvin, and B. Gil,

Nature

с V_N заряд равномерно распределяется между бли-

Photonics 10, 262 (2016).

жайшими атомами B. Для V_B и V_N распределение

заряда имеет вид антисвязующих 2p^π-орбиталей, и

K. L. Pey, A. Ranjan, N. Raghavan et al., in 2019

в первом случае они перекрываются, а во втором

IEEE International Reliability Physics Symposium

(IRPS 2019), Monterey, California, USA (2019),

не перекрываются. Для V_NB добавленный заряд

p. 311.

распределяется равномерно между парой ближай-

ших атомов азота, причем распределение заряда

M.-Y. Li, S.-K. Su, H.-S. P. Wong, and L.-J. Li,

принимает вид связующих σ-орбиталей.

Nature 567, 169 (2019).

D. Akinwande, C. Huyghebaert, C.-H. Wang et al.,

Nature 573, 507 (2019).

4. ЗАКЛЮЧЕНИЕ

J. Ge, H. Huang, Z. Ma et al., Materials and Design

198, 109366 (2021).

Таким образом, в настоящей работе показано,

что поперечный транспорт заряда в тонких пленках

A. Ranjan, N. Raghavan, S.J. O’Shea et al., Sci. Rep.

гексагонального нитрида бора h-BN описывается

8, 2854 (2018).

фонон-облегченным туннелированием между ней-

L. Jiang, Y. Shi, F. Hui et al., ACS Appl. Mater. &

тральными ловушками. Установлено, что энергети-

Interfaces 9, 39758 (2017).

ческие параметры ловушек составляют W_t = 0.58 эВ

и W_o

= 0.9 эВ для термической и оптической

Y. Shi, X. Liang, B. Yuan et al., Nature Electronics

энергий соответственно. Ловушки не перекрывают-

1, 458 (2018).

ся, разделены друг от друга несколькими слоями

G.-H. Lee, Y.-J. Yu, C. Lee et al., Appl. Phys. Lett.

h-BN и не образуют непрерывного канала. Полу-

99, 243114 (2011).

ченные данные в купе с результатами ab initio-

моделирования указывают на то, что наиболее веро-

10.

F. Hui and M. Lanza, Nature Electronics 2, 221

ятным кандидатом на роль ловушки в h-BN явля-

(2019).

ется дивакансия бор- азот, а транспорт осуществля-

11.

L. A. Kasprzak, R. B. Laibowitz, and M. Ohring,

ется электронами. Однако, ввиду поликристалличе-

J. Appl. Phys. 48, 4281 (1977).

ской природы исследуемых пленок h-BN, ловушки

могут находиться как на границах зерен, так и вда-

12.

C. Pan, Y. Shi, F. Hui et al., in Conductive Atomic

ли от них. Определение точного положения ловушек

Force Microscopy, ed. by M. Lanza, ch. 1, Wiley-VCH

Germany (2017).

выходит за рамки настоящей работы.

13.

F. Hui, C. Pan, Y. Shi et al., Microelectr. Eng. 163,

Благодарности. Авторы выражают благодар-

119 (2016).

ность Марио Ланца (Mario Lanza) за предоставле-

ние образцов и помощь при проведении транспорт-

14.

K. S. Novoselov, V. I. Fal’ko, L. Colombo et al.,

ных измерений. За предоставление измерительно-

Nature 490, 192 (2012).

го оборудования авторы благодарят ЦКП ¾ВТАН¿

15.

C. R. Dean, A. F. Young, I. Meric et al., Nature

НГУ. Моделирование осуществлялось на кластере

Nanotechnology 5, 722 (2010).

НКС-30Т Центра коллективного пользования ¾Си-

бирский суперкомпьютерный центр СО РАН¿ (ЦКП

16.

H. Pandey, M. Shaygan, S. Sawallich et al., IEEE

ССКЦ СО РАН).

Trans. Electron Devices 65, 4129 (2018).

399

Д. Р. Исламов, Т. В. Перевалов, А. А. Гисматулин и др.

ЖЭТФ, том 163, вып. 3, 2023

17.

C. Pan, Y. Ji, N. Xiao et al., Adv. Funct. Mater. 27,

35.

Я. И. Френкель, ЖЭТФ 8, 1292 (1938).

1604811 (2017).

36.

A. V. Shaposhnikov, T. V. Perevalov, V. A. Gritsenko

18.

С. В. Рыхлицкий, Е. В. Спесивцев, В. А. Швец,

et al., Appl. Phys. Lett. 100, 243506 (2012).

В. Ю. Прокопьев, ПТЭ № 3, 155 (2009).

37.

D. R. Islamov, V.A. Gritsenko, C. H. Cheng, and

19.

D. R. Hamann, Phys. Rev.B 95, 239906 (2017).

A. Chin, Appl.Phys. Lett. 105, 222901 (2014).

20.

P. Giannozzi, O. Andreussi, T. Brumme et al.,

38.

D. R. Islamov, T. V. Perevalov, V.A. Gritsenko et al.,

J. Phys.: Condens. Matter 29, 465901 (2017).

Appl. Phys.Lett. 106, 102906 (2015).

21.

J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem.

39.

Д. Р. Исламов, А. Г. Черникова, М. Г. Козодаев

Phys. 118, 8207 (2003).

и др.,

Письма в ЖЭТФ

102,

610

(2015)

[D. R. Islamov, A. G. Chernikova, M. G. Kozodaev

22.

V. L. Solozhenko, G. Will, and F. Elf, Sol. St. Comm.

et al., JETP Lett. 102, 544 (2015)].

96, 1 (1995).

40.

Д. Р. Исламов, В. А. Гриценко, А. Чин, Автомет-

23.

R. Zallen, The Physics of Amorphous Solids, Wiley-

рия 53, 102 (2017) [D. R. Islamov, V. A. Gritsenko

VCH, Germany (1998).

and A. Chin, Optoelectr., Instrument. and Data Proc.

24.

Z. H. Cui, A. J. Oyer, A. J. Glover et al., Small 10,

53, 184 (2017)].

2352 (2014).

41.

V. A. Gritsenko, T. V. Perevalov, V. A. Voronkovskii

25.

H. Sediri, D. Pierucci, M. Hajlaoui et al., Sci. Rep. 5,

et al., ACS Appl. Mater. & Interfaces 10, 3769 (2018).

16465 (2015).

42.

D. R. Islamov, V. A. Gritsenko, T. V. Perevalov et al.,

26.

L. Song, L. J. Ci, H. Lu et al., Nano Lett. 10 3209

Materialia 15, 100980 (2021).

(2010).

43.

К. А. Насыров, В. А. Гриценко, ЖЭТФ 139, 1172

27.

H. Park, T. K. Kim, S.W. Cho et al., Sci. Rep. 7 40091

(2011)

[K. A. Nasyrov and V. A. Gritsenko, JETP

(2017).

112, 1026 (2011)].

28.

G. Cassabois, P. Valvin, and B. Gil, Nature Photonics

44.

Y.-N. Xu and W. Y. Ching, Phys. Rev. B 44, 7787

10, 262 (2016).

(1991).

29.

K. Watanabe, T. Taniguchi, and H. Kanda, Nature

45.

Ю. Н. Новиков, В. А. Гриценко, Письма в ЖЭТФ

Materials 3, 404 (2004).

114, 498 (2021) [Yu. N. Novikov and V. A. Gritsenko,

JETP Lett. 114, 433 (2021)].

30.

R. S. Singh, R.Y. Tay, W. L. Chow et al., Appl.Phys.

Lett. 104 163101 (2014).

46.

A. Zobelli, C. P. Ewels, A.Gloter, and G. Seifert,

Phys. Rev. B 75, 094104 (2007).

31.

W. Schottky, Phys. Z. 15, 872 (1914).

32.

A. Laturia, M. L. V. de Put, and W. G. Vandenberghe,

47.

T. T. Tran, K. Bray, M. J. Ford et al.,

Nature

npj 2D Mater. Appl. 2, 6 (2018).

Nanotechnology 11, 37 (2015).

33.

G. G. Roberts and J. I. Polanco, Phys. Stat. Sol. (a) 1,

48.

A. Sajid, J. R. Reimers, and M. J. Ford, Phys. Rev.B

409 (1970).

97, 064101 (2018).

34.

V. A. Gritsenko, E. E. Meerson, and Y. N. Morokov,

49.

L. Weston, D. Wickramaratne, M. Mackoit et al.,

Phys. Rev. B 57, R2081 (1998).

Phys. Rev. B 97, 214104 (2018).

400