ЖЭТФ, 2023, том 163, вып. 3, стр. 417-427

ЭФФЕКТ ХОЛЛА В ДОПИРОВАННОМ

МОТТ-ХАББАРДОВСКОМ ДИЭЛЕКТРИКЕ

Э. З. Кучинский^a*, Н. А. Кулеева^a**, М. В. Садовский^a***, Д. И. Хомский^b****

^a Институт электрофизики Уральского отделения Российской академии наук,

620016, Екатеринбург, Россия

^b II Physikalisches Institut, Universität zu Koeln,

50937, Koeln, Germany

Поступила в редакцию 8 ноября 2022 г.,

после переработки 8 ноября 2022 г.

Принята к публикации 15 ноября 2022 г.

Проведен теоретический анализ эффекта Холла в допированном моттовском диэлектрике, рассматрива-

емом в качестве прототипа купратного сверхпроводника. Рассматривается стандартная модель Хаббарда

в рамках DMFT-приближения. В качестве типичного рассматривается случай частичного заполнения

(дырочное допирование) нижней хаббардовской зоны. Рассчитана зависимость коэффициента Холла

и холловского числа от степени дырочного допирования и определено значение критической концен-

трации носителей, при которой происходит смена знака коэффициента Холла. Получена существенная

зависимость параметров эффекта Холла от температуры. Качественно анализируется роль рассеяния на

беспорядке. Проведено сравнение теоретических результатов с имеющимися экспериментами по концен-

трационной зависимости холловского числа в нормальном состоянии YBCO и Nd-LSCO, демонстрирую-

щее вполне удовлетворительное согласие теории и эксперимента. Полученная картина концентрационной

зависимости параметров эффекта Холла в рамках модели Хаббарда может быть альтернативой попу-

лярной модели квантовой критической точки.

DOI: 10.31857/S0044451023030136

ратов), которое реализуется в очень сильных внеш-

EDN: QFDCRI

них магнитных полях [2-4]. Наблюдающиеся при

этом аномалии эффекта Холла обычно связываются

с реконструкцией поверхности Ферми, связанной с

1. ВВЕДЕНИЕ

формированием (антиферромагнитной) псевдощели

и с близостью к соответствующей квантовой крити-

Изучение эффекта Холла в высокотемператур-

ческой точке [5].

ных сверхпроводниках ведется уже давно. Самые

С начала теоретического изучения купратов од-

ранние эксперименты показали существенные зави-

ной из основных является точка зрения о том, что

симости параметров эффекта Холла от температу-

эти системы являются сильно коррелированными и

ры и от степени допирования, качественно отличные

металлическое (в том числе сверхпроводящее) со-

от случая обычных металлов [1]. Полное теоретиче-

стояние в них реализуется в результате допирования

ское понимание эффекта Холла в купратах в насто-

исходной фазы моттовского диэлектрика, который

ящее время отсутствует.

в простейшем случае может быть описан в рамках

В последние годы большой интерес вызывают

модели Хаббарда. При этом имеется довольно мало

экспериментальные исследования эффекта Холла

работ, в которых в рамках этой модели проводилось

при низких температурах в нормальном состоя-

бы систематические исследования зависимости эф-

нии высокотемпературных сверхпроводников (куп-

фекта Холла от степени допирования и температу-

ры [6].

^* E-mail: kuchinsk@iep.uran.ru

Не до конца ясен даже ответ на классический во-

^** E-mail: strigina@iep.uran.ru

^*** E-mail: sadovski@iep.uran.ru

прос о том, при какой степени допирования (концен-

^**** E-mail: khomskii@ph2.uni-koeln.de

трации носителей) происходит смена знака эффекта

417

Э. З. Кучинский, Н. А. Кулеева, М. В. Садовский, Д. И. Хомский

ЖЭТФ, том 163, вып. 3, 2023

Холла? При малом дырочном допировании исходно-

а холловская (недиагональная) проводимость опре-

го диэлектрика, такого как La₂CuO₄ или YBCO он,

деляется как

очевидно, просто определяется концентрацией ды-

∫

∞

рок δ. Но при какой степени допирования происхо-

2π²e³aH

( df(ε))

σ^Hxy =

dε

дит смена знака коффициента Холла, когда проис-

3ℏ²

dε

ходит переход от дырочной поверхности Ферми к

−∞

электронной? Решение этого вопроса представляет-

∑(∂ε(p))2 ∂2ε(p)

A³(pε).

(3)

ся важным и для общей теории транспортных яв-

∂p_x

∂p²

pσ

лений в сильно коррелированных системах. Дан-

ная работа, в основном, посвящена изучению именно

Здесь a параметр решетки, ε(p) электронная

этого вопроса.

дисперсия, f(ε) функция распределения Ферми,

а H напряженность магнитного поля вдоль оси z.

Таким образом, коэффициент Холла

σ^Hxy

2. ХОЛЛОВСКАЯ ПРОВОДИМОСТЬ И

R_H =

(4)

Hσ²

КОЭФФИЦИЕНТ ХОЛЛА

также полностью определяется спектральной плот-

ностью A(pε), которую мы далее будем находить

Весьма общим подходом к исследованию модели

в рамках DMFT [6-8]. Эффективная однопримес-

Хаббарда является динамическая теория среднего

ная модель Андерсона DMFT в данной работе ре-

поля (DMFT) [6-8], которая дает точное описание

шалась с помощью метода численной ренормгруппы

системы в пределе бесконечномерного пространства

(NRG) [12].

(решетки с бесконечным числом ближайших сосе-

Далее мы рассматриваем две базовые модели за-

дей). Активно развиваются подходы, позволяющие

травочной электронной зоны. Модель с полуэллип-

выйти за рамки этого жесткого ограничения [9, 10],

тической плотностью состояний (DOS) (на элемен-

но они, как правило, сильно усложняют рассмотре-

тарную ячейку и один спин), что является неплохим

ние. В данной работе мы ограничимся рассмотрени-

приближением для трехмерного случая:

ем эффекта Холла в рамках стандартного прибли-

жения DMFT. Целью работы является системати-

√

N₀(ε) =

D² - ε²,

(5)

ческое исследование концентрационной и темпера-

πD²

турной зависимости эффекта Холла при различных

где D полуширина зоны проводимости. Мы пола-

степенях допирования нижней хаббардовской зоны,

гаем затравочный электронный спектр изотропным.

и сравнение полученных результатов с эксперимен-

Для нахождения в такой модели производных по

том на YBCO и Nd-LSCO [3,4]. Предварительные ре-

импульсу от электронного спектра, входящих в (2)

зультаты были опубликованы в краткой статье [11].

и (3), мы будем следовать подходу, предложенному

В стандартной DMFT [6-8] собственно энерге-

ранее в работе [13]. Технические детали соответству-

тическая часть одноэлектронной функции Грина

ющего анализа вынесены в Приложение.

G(pε) является локальной, т. е. есть не зависящей от

Для двумерных систем, имея в виду сравне-

импульса. В условиях такой локальности и обычная,

ние с экспериментальными данными для купратов,

и холловская проводимости полностью определяют-

мы ограничимся результатами для обычной модели

ся спектральной плотностью этой функции Грина:

электронного спектра в приближении сильной свя-

зи:

A(pε) = -

Im G^R(pε).

(1)

ε(p) = -2t(cos(p_xa) + cos(p_ya)) -

- 4t^′ cos(p_xa)cos(p_ya).

(6)

В частности, обычная (диагональная) статическая

проводимость имеет вид [6]

В такой двумерной модели мы далее рассмотрим

ряд случаев:

∫

∞

(

(1) спектр с перескоком лишь на ближайших соседей

)∑(∂ε(p))2

πe

df(ε)

σ_xx =

dε

A²(pε),

(t^′ = 0) и полной электрон-дырочной симметрией;

2ℏa

dε

∂p_x

pσ

(2) спектр с t^′/t = -0.25, качественно соответствую-

-∞

(2)

щий электронной дисперсии в системах типа LSCO.

418

ЖЭТФ, том 163, вып. 3, 2023

Эффект Холла в допированном мотт-хаббардовском диэлектрике

(3) спектр с t^′/t = -0.4, качественно соответствую-

нов с проекцией спина ¾вверх¿ имеет вид [14]

щий ситуации, наблюдаемой в YBCO.

1-n_↓

n_↓

Ниже приводятся подробные результаты расче-

G^R↑(εp) =

(7)

ε - ε_-(p) + iδ

ε - ε₊(p) + iδ

тов коэффициента Холла для всех этих моделей.

где ε_±(p) спектр квазичастиц в верхней и нижней

хаббардовских зонах. Видим, что в этом приближе-

3. КОЭФФИЦИЕНТ ХОЛЛА В ДВУМЕРНОЙ

нии число состояний с проекцией спина “вверх” в

МОДЕЛИ ЭЛЕКТРОННОГО СПЕКТРА В

нижней хаббардовской зоне (первое слагаемое в (7))

ПРИБЛИЖЕНИИ СИЛЬНОЙ СВЯЗИ

действительно есть 1 - n_↓. При допировании дыр-

ками моттовского диэлектрика практически весь

Проведем сначала простейший качественный

вклад в заполнение дает нижняя хаббардовская зо-

анализ. Нетрудно понять, что глубоко в состоянии

на, поэтому

моттовского диэлектрика с хорошо определен-

n=n_↑ ≈

ными верхней и нижней хаббардовскими зонами

∞

(

)

при допировании дырками коэффициент Холла

∫

∑

фактически определяется заполнением нижней хаб-

≈ (1 - n_↓)

dε f(ε)

≡

ε - ε_-(p) + iδ

бардовской зоны (верхняя находится существенно

-∞

выше по энергии и практически не заполнена).

≡ (1 - n)n₀.

(8)

В такой ситуации в модели с электрон-дырочной

Тогда при половинном заполнении нижней хаббар-

симметрией (в двумерном случае это соответствует

довской зоны n₀

= 1/2 происходит смена знака

спектру с t^′

= 0) оценка заполнения зоны, при

эффекта Холла (эффективной массы квазичастиц),

котором происходит смена знака коэффициента

так что снова получаем n = n_c = 1/3.

Холла, может быть получена из очень простых

В общем случае ситуация конечно сложнее.

соображений. Будем рассматривать парамагнитную

В сильно коррелированных системах коэффициент

фазу n_↑ = n_↓ = n, так что n далее обозначает

Холла (и другие электронные свойства) оказывает-

плотность электронов на одну проекцию спина, а их

ся существенно зависящими от температуры. При

полная плотность равна 2n. Качественно ситуация

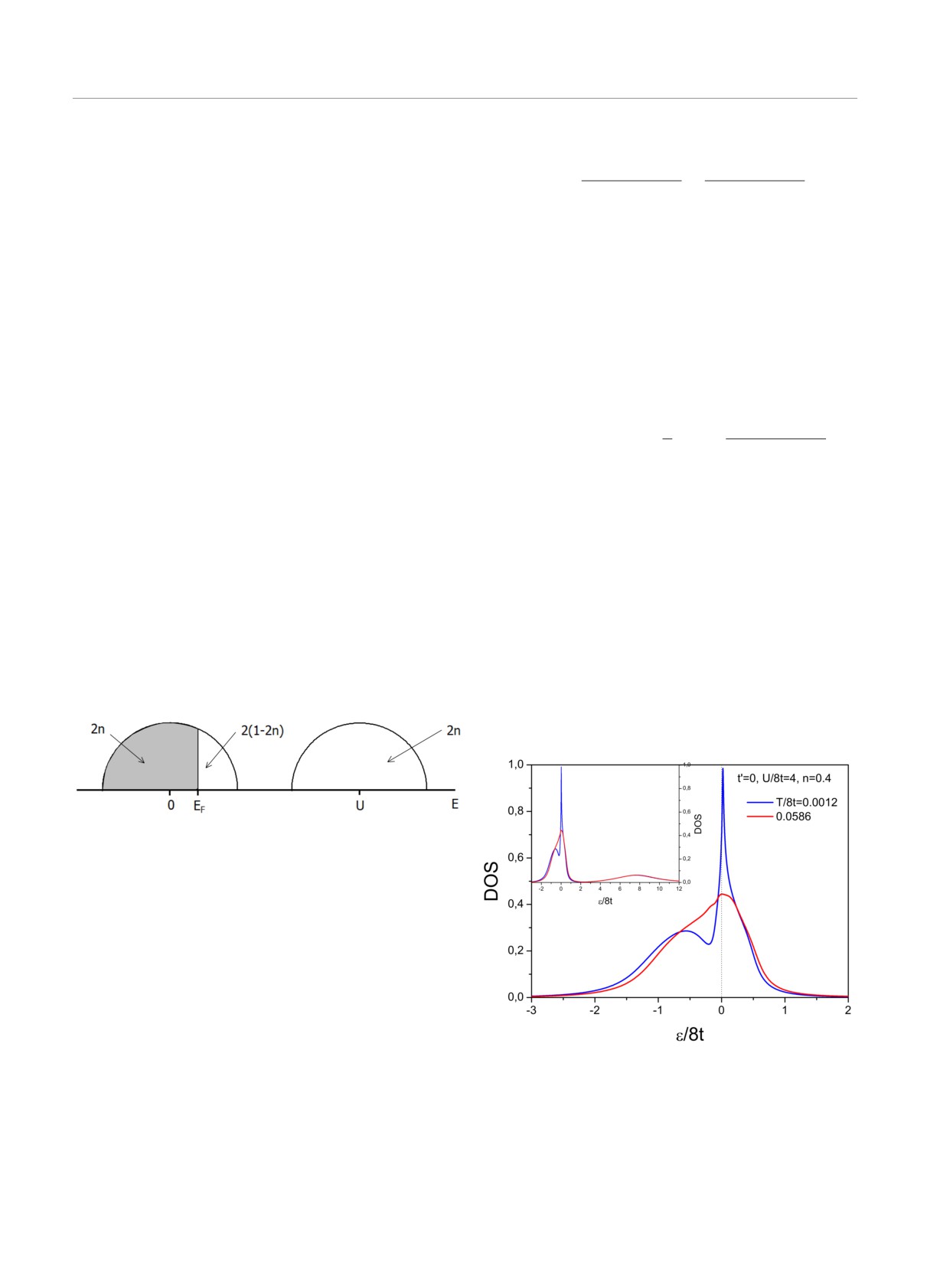
иллюстрируется рис. 1. В нижней хаббардовской

низкой температуре в таких системах в DMFT-

приближении наряду с нижней и верхней хаббардов-

скими зонами вблизи уровня Ферми формируется

узкая квазичастичная зона квазичастичный пик

Рис. 1. Схематическое изображение допирования хаббар-

довских зон в случае полной электрон-дырочной симмет-

рии

зоне (в окрестности энергии E = 0) 2n электронов

занимают состояния ниже энергии Ферми E_F . При

добавлении следующего электрона он может по-

пасть в верхнюю хаббардовскую зону в окрестности

E ∼ U, где также имеется 2n состояний. Он также

может попасть в нижнюю хаббардовскую зону, где

еще остается 2(1 - 2n) пустых состояний в области

E > E_F. В итоге имеем 2n + 2(1 - 2n) + 2n = 2,

как и должно быть. Знак коэффициента Холла

Рис. 2. Плотность состояний (DOS) в допированном мот-

изменится при половинном заполнении нижней

товском диэлектрике при различных температурах. Пара-

зоны, когда 2n

= 2(1 - 2n). Отсюда ясно, что

метры модели Хаббарда приведены на рисунке, 8t шири-

значение критической концентрации n_c = 1/3.

на исходной зоны. На вставке показана плотность состоя-

Этот же результат легко получается и в прибли-

ний в широком интервале энергий, включающем верхнюю

жении Хаббард I, где функция Грина для электро-

хаббардовскую зону

419

Э. З. Кучинский, Н. А. Кулеева, М. В. Садовский, Д. И. Хомский

ЖЭТФ, том 163, вып. 3, 2023

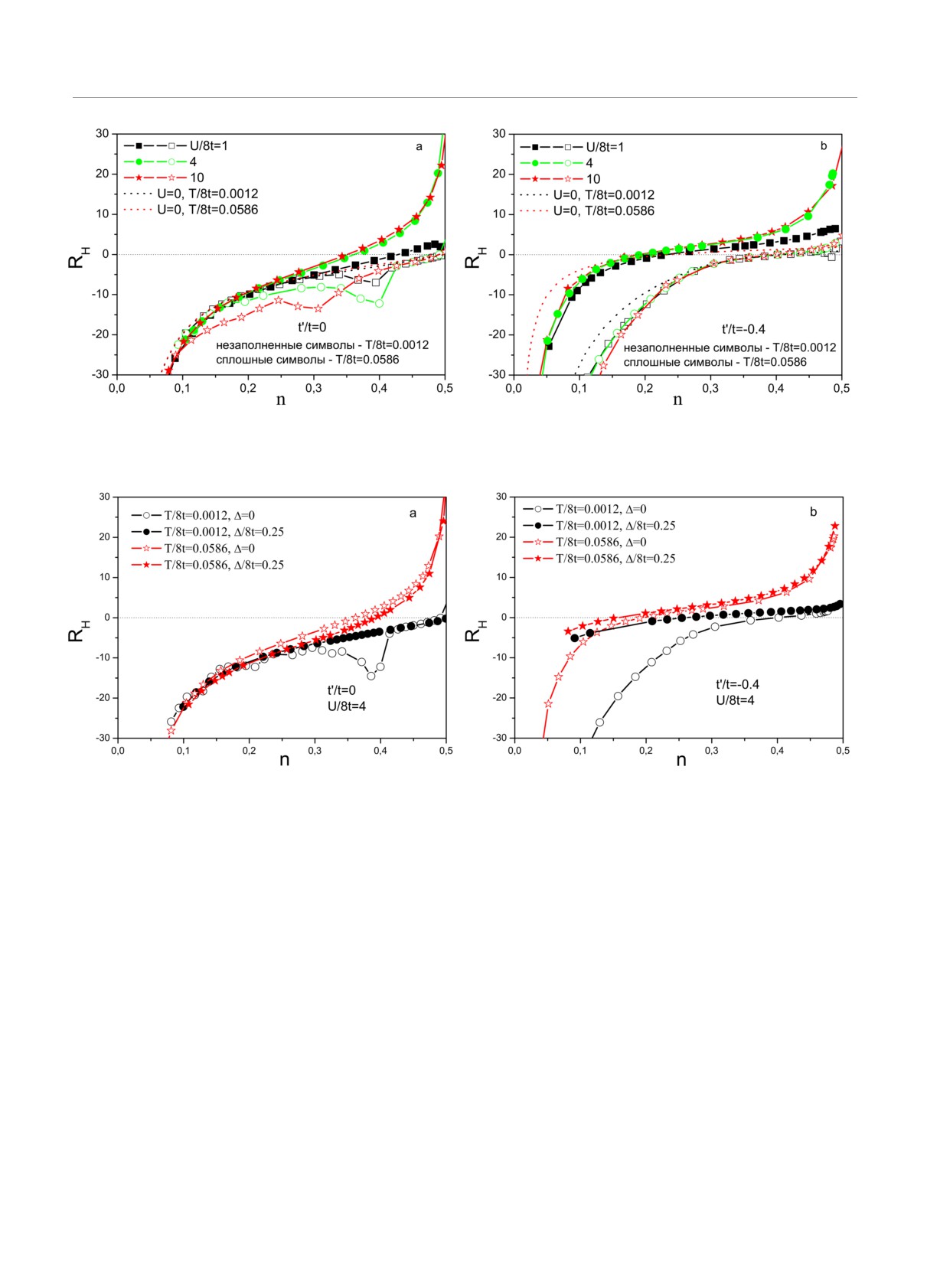
Рис. 3. Зависимость коэффициента Холла в случае t^′ = 0a и t^′/t = -0.4b от степени заполнения зоны для различных

значений силы электронных корреляций U в низкотемпературном режиме (незаполненные символы) и в высокотемпера-

турном режиме (заполненные символы)

Рис. 4. Зависимость коэффициента Холла от степени заполнения зоны в присутствии примесного рассеяния (Δ/8t = 0.25,

заполненные символы) и в его отсутствии (Δ = 0, незаполненные символы) для двух разных моделей двумерного элек-

тронного спектра: a полной электрон-дырочной симметрии (t^′ = 0); b t^′/t = -0.4

в плотности состояний [6-8]. В допированном дыр-

В низкотемпературном режиме и ширина, и ам-

ками моттовском диэлектрике (далее мы будем рас-

плитуда квазичастичного пика зависят как от за-

сматривать именно дырочное допирование) такой

полнения, так и от температуры. Рост температу-

пик лежит вблизи верхнего края нижней хаббардов-

ры приводит к уширению квазичастичного пика и

ской зоны (см. рис. 2). Поэтому при низкой темпе-

некоторому смещению уровня Ферми ниже макси-

ратуре коэффициент Холла во многом определяет-

мума этого пика (см. рис. 2). Это может приводить

ся заполнением этой квазичастичной зоны. При до-

к заметному уменьшению коэффициента Холла, од-

статочно высокой температуре (порядка или боль-

нако дальнейший рост температуры, размывая ква-

ше ширины квазичастичного пика) квазичастичный

зичастичный пик, приводит к росту этого коэффи-

пик размывается и тогда коэффициент Холла пол-

циента. Существенная зависимость квазичастично-

ностью определяется заполнением нижней хаббар-

го пика от заполнения зоны в низкотемпературном

довской зоны. Таким образом, в общем случае, необ-

режиме приводит к областям немонотонной зависи-

ходимо рассматривать два достаточно разных тем-

мости коэффициента Холла от степени заполнения

пературных режима для эффекта Холла.

(см. рис. 3a).

420

ЖЭТФ, том 163, вып. 3, 2023

Эффект Холла в допированном мотт-хаббардовском диэлектрике

На рис.3a видно, что высокотемпературное по-

купратных систем LSCO и YBCO соответственно.

ведение коэффициента Холла в допированном мот-

На зависимости R_H от степени заполнения зоны с

товском диэлектрике (U/2D = 4; 10) в модели с пол-

ростом температуры мы наблюдаем плавную эволю-

ной электрон-дырочной симметрией (t^′ = 0) полно-

цию от низкотемпературного режима к высокотем-

стью подтверждает приведенную выше качествен-

пературному с плавным ослаблением аномалий ко-

ную оценку. Но при заметном нарушении электрон-

эффициента Холла, связанных с квазичастичными

дырочной симметрии эта оценка перестает работать

пиками, которые наиболее ярко видны на рис. 3а и

(см. рис. 3b).

рис. 5а. Для всех рассмотренных случаев электрон-

Необходимо отметить, что к размытию и исчез-

ного спектра (t^′/t = 0; -0.25; -0.4) рост температу-

новению квазичастичного пика приводит не толь-

ры приводит к смещению величины заполнения зо-

ко рост температуры, но и разупорядочение [9,

ны, при которой R_H = 0, в область больших величин

13] (см. рис.4), а также, например, псевдощелевые

дырочных допирований. Также на рис. 5 b, d, f при-

флуктуации, которыми локальный подход DMFT

ведены температурные зависимости коэффициента

полностью пренебрегает [9, 15]. Таким образом, об-

Холла для различных степеней заполнений зоны.

ласть применимости приведенных выше простей-

Во всех случаях наблюдается существенная зависи-

ших оценок в реальности оказывается заметно ши-

мость R_H от температуры и при небольших значени-

ре.

ях дырочных допирований (n = 0.45-0.3) R_H растет

В общем случае расчет влияния рассеяния на

с ростом температуры и мы наблюдаем смену знака

беспорядке (тем более псевдощелевых флуктуаций)

R_H при существенных величинах дырочных допи-

на эффект Холла представляет собой очень слож-

рований (n = 0.3-0.2). В случае достаточно малых

ную задачу. Для простых оценок ниже приводятся

t′ (t′/t = 0; -0.25) может наблюдаться немонотонная

результаты расчетов по формулам (2), (3), (4), в ко-

зависимость коэффициента Холла от температуры,

торых просто использованы значения спектральной

когда при низких температурах R_H уменьшается с

плотности A(pε) для неупорядоченной модели Хаб-

ростом температуры, а при высоких T растет.

барда, полученные в рамках DMFT+Σ-подхода [9,

Смену знака коэффициента Холла обычно свя-

15]. Параметр беспорядка Δ обозначает эффектив-

зывают с изменением типа носителей заряда. Кро-

ную частоту рассеяния электронов случайным по-

ме того, стремление к нулю коэффициента Хол-

лем (в самосогласованном борновском приближе-

ла приводит к расходимости холловского числа

нии). Ясно, что такой подход, основанный только

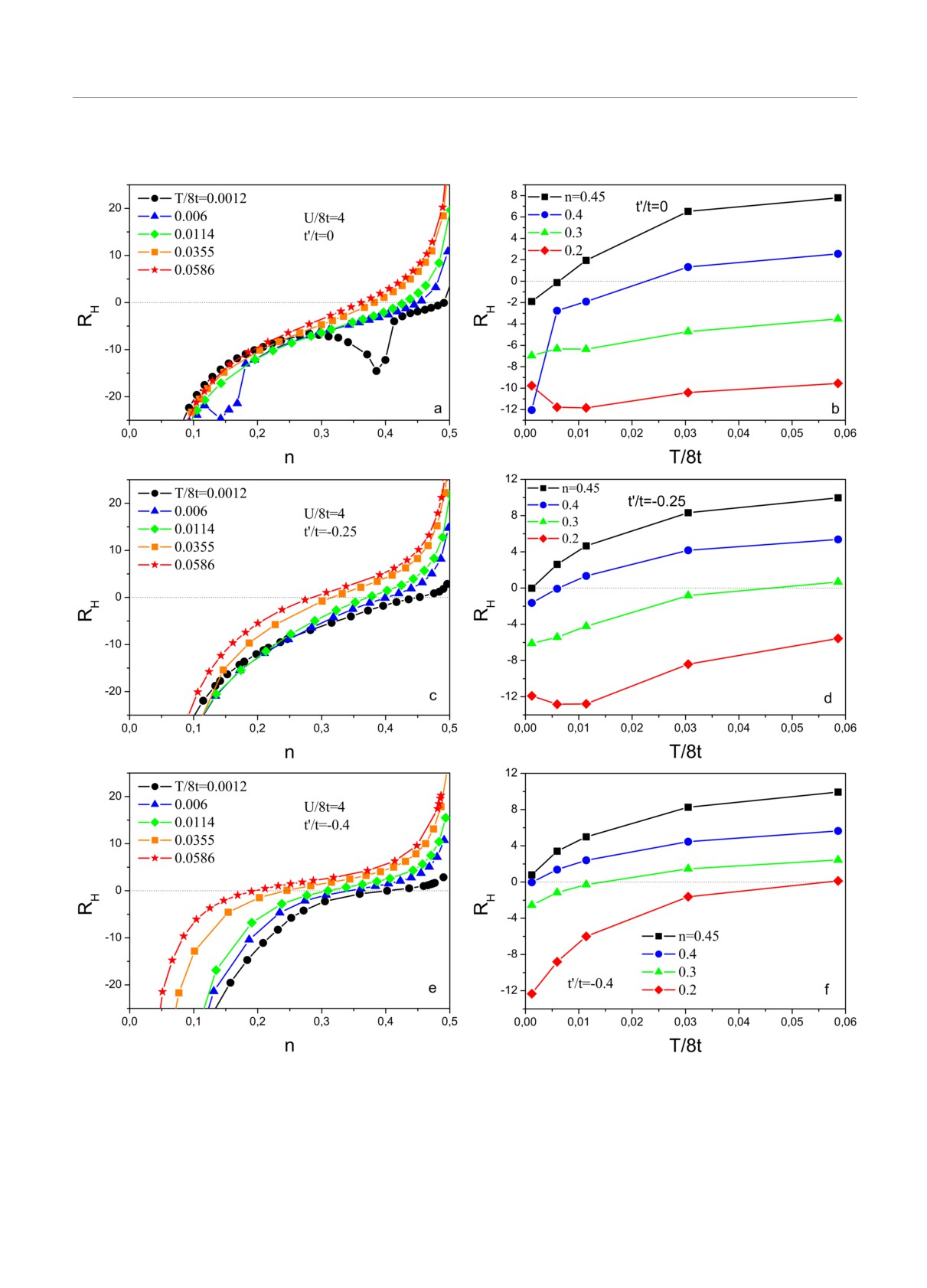
n_H ∼ 1/R_H. На рис.6 приведена зависимость степе-

на учете беспорядка в спектральной плотности, яв-

ни заполнения, при котором в моттовском диэлек-

ляется слишком упрощенным, но он представляется

трике происходит смена знака коэффициента Хол-

разумным для качественного анализа.

ла, от температуры для всех трех рассматривае-

На рис.4 приведено сравнение зависимостей ко-

мых нами значений t^′/t. Видим, что во всех моделях

эффициента Холла от степени заполнения зоны в

степень заполнения, при которой R_H меняет знак,

отсутствие беспорядка и для рассеяния на примесях

уменьшается с ростом температуры. В случае пол-

с Δ/8t = 0.25 для случая моттовского диэлектрика

ной электрон-дырочной симметрии t^′ = 0 мы видим,

с U/8t = 4. Видим, что для разных значений t^′ в вы-

что в высокотемпературном режиме величина ды-

сокотемпературном пределе беспорядок достаточно

рочного допирования δ = 1 - 2n, при котором R_H

слабо влияет на коэффициент Холла, лишь очень

меняет знак, действительно стремится к значению

незначительно смещая величину заполнения, при

1/3. Однако с ростом |t^′/t| наблюдается заметное

которой наблюдается смена знака R_H . В низкотем-

уменьшение величины дырочного допирования, при

пературном режиме примесное рассеяние, размывая

котором R_H меняет знак.

квазичастичный пик, приводит к исчезновению ано-

малий R_H , связанных с существованием такого пика

4. КОЭФФИЦИЕНТ ХОЛЛА В МОДЕЛИ

(см. рис. 4а), и ослабляя различие между низкотем-

ЭЛЕКТРОННОЙ ЗОНЫ С

пературным и высокотемпературным режимами.

ПОЛУЭЛЛИПТИЧЕСКОЙ ПЛОТНОСТЬЮ

На рис.5 приведены зависимости коэффициента

СОСТОЯНИЙ

Холла от степени заполнения зоны и температуры в

случае моттовского диэлектрика с U/8t = 4 для раз-

Кратко рассмотрим результаты, полученные

личных моделей электронного спектра, как в случае

в модели электронной зоны с полуэллиптической

полной электрон-дырочной симметрии t^′ = 0, так и

плотностью состояний, которая обладает полной

при t^′/t = -0.25 и t^′/t = -0.4, характерных для

электрон-дырочной симметрией. Основные ре-

421

ЖЭТФ, том 163, вып. 3, 2023

Эффект Холла в допированном мотт-хаббардовском диэлектрике

Рис. 6. Зависимость степени заполнения, при котором в

Рис. 7. Плотность состояний (DOS) в допированном мот-

моттовском диэлектрике происходит смена знака коэффи-

товском диэлектрике при различных температурах для мо-

циента Холла, от температуры для трех различных значе-

дели с полуэллиптической зоной (трехмерный случай)

ний t^′/t

зультаты оказываются качественно аналогичными

результатам для рассмотренной выше двумерной

модели электронного спектра с сильной связью с

t′ = 0, которая тоже обладает полной электрон-ды-

рочной симметрией. Аналогично двумерному

случаю коэффициент Холла в трехмерной модели

в сильно коррелированной системе существенно

зависит от температуры, и необходимо отдельно

рассматривать низкотемпературный и высоко-

температурный режимы для R_H, поскольку в

низкотемпературном режиме коэффициент Холла

во многом определяется заполнением квазичастич-

ной зоны (квазичастичного пика).

Рост температуры приводит к размытию квази-

частичного пика (см. рис. 7), и в высокотемператур-

ном режиме коэффициент Холла в основном опре-

деляется заполнением нижней (для рассматривае-

мого нами случая дырочного допирования) хаббар-

довской зоны.

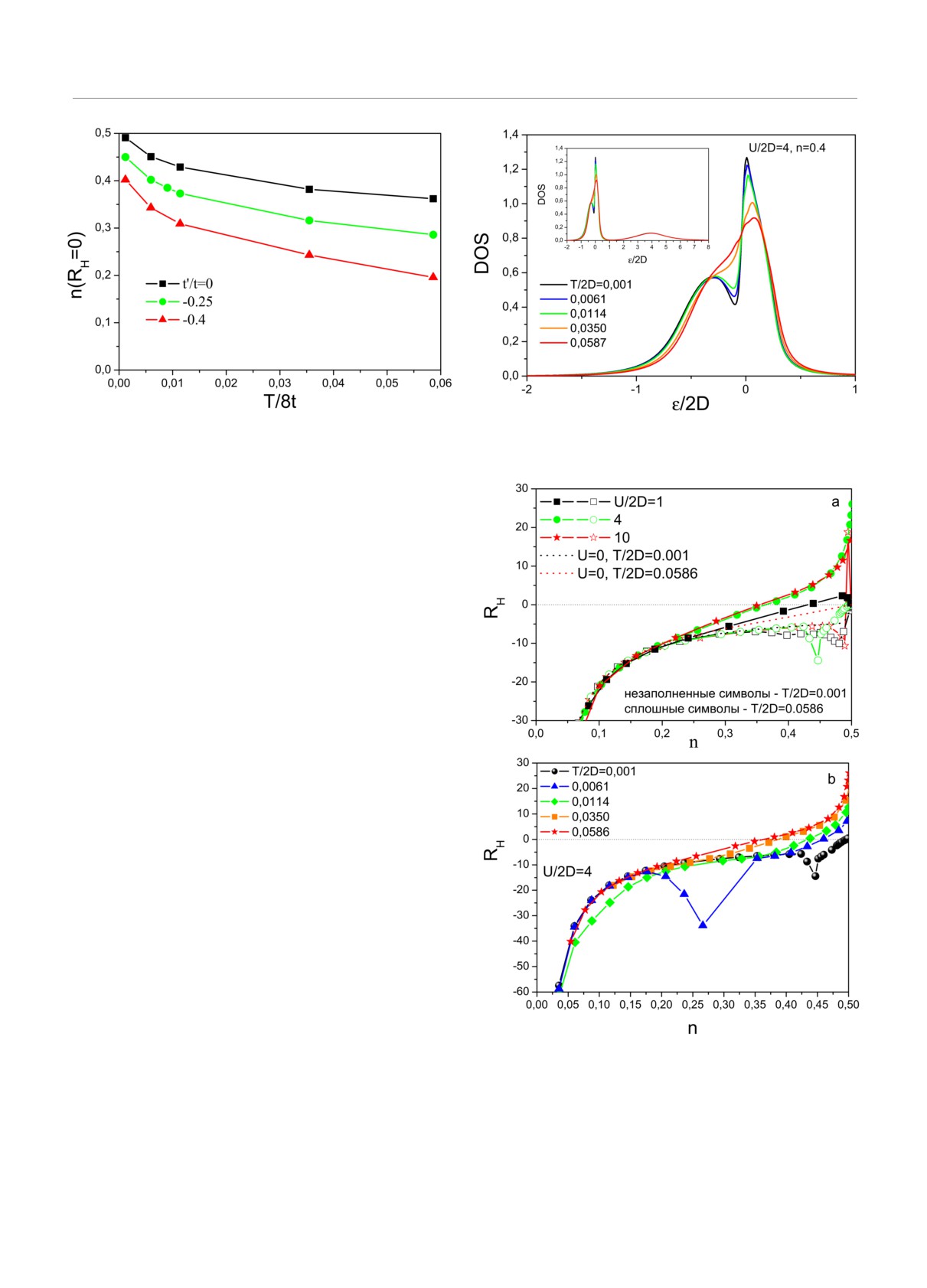
На рис.8a приведена зависимость коэффициен-

та Холла от заполнения электронной зоны в низ-

котемпературном (незаполненные символы) и в вы-

сокотемпературном (сплошные символы) режимах

как для случая сильно коррелированного металла

(U/2D = 1), так и допированного моттовского ди-

электрика (U/2D = 4; 10). Видим, что в низкотем-

пературном режиме, как и в двумерной модели с

Рис. 8. Зависимость коэффициента Холла от заполнения

t^′ = 0 (R_H практически при всех заполнениях зоны

в модели электронной зоны с полуэллиптической плотно-

отрицателен), при небольших величинах дырочного

стью состояний: a для различных значений U в низко-

допирования наблюдается существенная немонотон-

температурном (незаполненные символы) и в высокотем-

ность в зависимости R_H от уровня допирования.

пературном режиме (сплошные символы); b для различ-

В высокотемпературном режиме коэффициент

ных значений температуры при фиксированном значении

Холла при малой величине дырочного допирования

U/2D = 4

423

ЖЭТФ, вып. 3

Э. З. Кучинский, Н. А. Кулеева, М. В. Садовский, Д. И. Хомский

ЖЭТФ, том 163, вып. 3, 2023

Рис. 9. Зависимость коэффициента Холла от заполнения

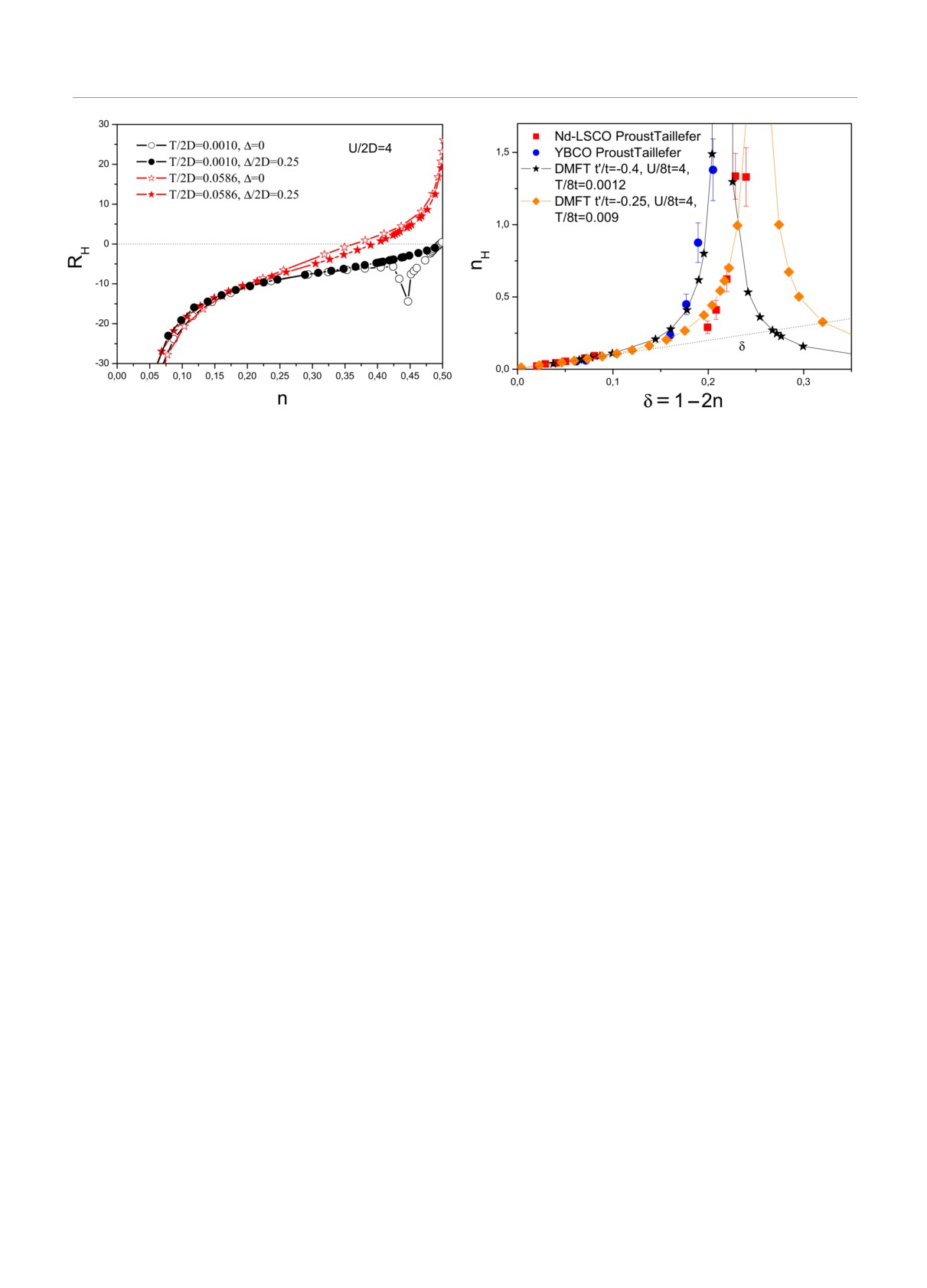
Рис. 10. Зависимость холловского числа nH от степени до-

зоны в низкотемпературном режиме (черные кривые) и

пирования сравнение с экспериментами [3,4] для YBCO

высокотемпературном режиме (красные кривые) в отсут-

и Nd-LSCO, δ = 1 - 2n концентрация дырок. Звездочки

ствии беспорядка Δ = 0 (незаполненные символы) и при

и ромбики результаты наших расчетов, синие кружочки

Δ/2D = 0.25 (сплошные символы)

и красные квадраты эксперимент

оказывается положительным (дырочным), умень-

ниям пропорциональным (1 + δ) в области доста-

шаясь с ростом уровня дырочного допирования и

точно больших концентраций порядка критической

при большом уровне допирования R_H становится

концентрации дырок, при которой происходит ис-

отрицательным, изменяя знак (в моттовском ди-

чезновение (закрытие) псевдощели. Эти данные, в

электрике) при δ = 1 - 2n ≈ 1/3, что снова под-

основном, интерпретируются в рамках картины ре-

тверждает приведенные выше качественные оцен-

конструкции поверхности Ферми вблизи предпола-

ки. Плавная эволюция зависимости коэффициента

гаемой квантовой критической точки в рамках до-

Холла от степени заполнения при росте температу-

статочно специфической модели купратов с неодно-

ры от низкотемпературного предела до высокотем-

родной локализацией носителей [5,16]. Нужно заме-

пературного в моттовском диэлектрике (U/2D = 4)

тить, что ни в одной из известных нам работ экс-

приведена на рис. 8b.

периментальные точки, надежно демонстрирующие

На рис.9 продемонстрировано влияние беспоряд-

зависимость, пропорциональную (1 + δ), отсутству-

ка на коэффициент Холла в моттовском диэлектри-

ют, а надежным экспериментальным фактом явля-

ке. В высокотемпературном пределе примесное рас-

ется только наблюдаемый рост холловского числа.

сеяние практически не влияет на R_H, а в низкотем-

Ниже предлагается альтернативная интерпрета-

пературном пределе беспорядок, размывая квазича-

ция роста холловского числа в этих экспериментах,

стичный пик, устраяет аномальную немонотонность

как связанного с приближением к критической кон-

в зависимости R_H от n.

центрации носителей, при которой меняется знак ве-

личины эффекта Холла (коэффициент Холла R_H

обращается в нуль) [11].

5. СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ

На рис.10 показано сравнение результатов на-

Как уже упоминалось выше, в последние годы

ших расчетов для холловского числа (холловской

были проведены уникальные экспериментальные ис-

концентрации) n_H = a²/|eR_H | для типичных значе-

следования эффекта Холла при низких температу-

ний параметров модели с экспериментальными дан-

рах в нормальном состоянии высокотемпературных

ными по YBCO и Nd-LSCO из работ [3, 4]. Видим,

сверхпроводников (купратов), которое было реали-

что даже при этом, достаточно произвольном, вы-

зовано в очень сильных внешних магнитных полях

боре параметров мы можем получить практически

[2-4]. При этом была получена зависимость холлов-

количественное согласие с экспериментом без вся-

ского числа n_H = a²/|eR_H | от степени допирования.

ких предположений о связи эффекта Холла с рекон-

Наблюдался постепенный переход от линейной за-

струкцией поверхности Ферми псевдощелью и бли-

висимости от концентрации дырок пропорциональ-

зостью к соответствующей квантовой критической

ной δ в области малой их концентрации к значе-

точке, которые использовались в работах [3-5, 16].

424

ЖЭТФ, том 163, вып. 3, 2023

Эффект Холла в допированном мотт-хаббардовском диэлектрике

Таким образом, оказывается, что интерпретация эф-

Вполне удовлетворительное согласие получен-

фекта Холла в купратах на основе картины допи-

ных концентрационных зависимостей холловского

рования нижней хаббардовской зоны моттовского

числа с экспериментами на YBCO и Nd-LSCO [3, 4]

диэлектрика может оказаться достаточно разумной

показывает, что рассмотренная нами модель мо-

альтернативой картине, основанной на близости к

жет быть достаточно разумной альтернативой кар-

квантовой критической точке.

тине эффекта Холла в окрестности квантовой кри-

тической точки, связанной с закрытием псевдоще-

С этой точки зрения, было бы крайне интерес-

но более детально изучить эффект Холла в окрест-

ли [5, 16].

ности критической концентрации, соответствующей

Финансирование. Работа Э.З.К., Н.А.К. и

смене знака коэффициента Холла (расходимости

М.В.С. выполнялась при частичной поддержке Рос-

холловского числа). Для этого требуется исследо-

сийского фонда фундаментальных исследований

вать системы (купраты), в которых такая смена зна-

(грант № 20-02-00011). Работа Д.И.Х. поддержана

ка реально достигается при изменении степени до-

грантом DFG по проекту № 277146847 CRC 1238.

пирования.

ПРИЛОЖЕНИЕ

¾Затравочная¿ электронная дисперсия и

6. ЗАКЛЮЧЕНИЕ

ее производные для зоны с полуэллиптиче-

ской плотностью состояний

Мы исследовали поведение коэффициента Холла

в металлической фазе, возникающей при допирова-

Будем считать электронный спектр, отве-

нии моттовского диэлектрика. Основное внимание

чающий плотности сотояний

(5) изотропным

мы уделили случаю дырочного допирования, харак-

ε(p) = ε(|p|) ≡ ε(p). Для нахождения проводимо-

терного для большей части купратов. Был рассмот-

стей (2) и (3) необходимо провести усреднение ¾по

рен ряд двумерных моделей сильной связи для элек-

углам¿ производных по компонентам импульса,

тронного спектра, подходящих для описания элек-

имеющихся в этих выражениях,

тронной структуры в купратах, а также и трехмер-

ная модель с полуэллиптической затравочной плот-

(∂ε(p))2

p^2x

= ε^′2(p)

ε^′2(p) =

ε^′2(p),

ностью состояний. Во всех моделях коэффициент

∂p_x

p²

Холла R_H в допированном моттовском диэлектрике

(9)

существенно зависит от температуры. В низкотем-

где

∫

пературном пределе R_H во многом определяется за-

dΩ

〈. . . 〉_Ω =

полнением квазичастичного пика, что может приво-

4π

дить к заметной немонотонности в зависимости ко-

усреднение по телесному углу в трехмерной

эффициента Холла от степени допирования. В вы-

(d = 3) системе, а

сокотемпературном пределе, когда квазичастичный

пик существенно подавлен, R_H в основном опреде-

dε(p)

ляется заполнением нижней (при дырочном допиро-

ε^′(p) =

вании) или верхней (при электронном допировании)

хаббардовской зоны. В этом пределе смена знака эф-

производная по модулю импульса

фекта Холла и соответствующая ей расходимость

холловского числа происходит в простейшем (сим-

(∂ε(p))2 ∂²ε(p)

метричном) случае вблизи величины заполнения зо-

∂p_x

∂p²

ны n = 1/3 в расчете на одну проекцию спина или

[

]

p^2xp^2y

ε^′(p) p^xp² - p^xp^y

2/3 для полной плотности электронов, что соответ-

= ε^′2(p) ε^′′(p)

(10)

p⁴

ствует дырочному допированию δ = 1-2n = 1/3, но

в общем случае это заполнение достаточно сильно

где ε^′′(p) = d²ε(p)/dp². Поэтому возникает задача

зависит от выбора параметров модели. Эта концен-

найти среднее по углам p^2xp^2y/p^4Ω. Введем обозна-

трация возникает из простых качественных оценок

чения:

и не связана с более сложными факторами, такими

p^4x

p^2xp^2y

как изменение топологии поверхности Ферми или с

≡a и

≡ b.

наличием квантовых критических точек.

p⁴

425

Э. З. Кучинский, Н. А. Кулеева, М. В. Садовский, Д. И. Хомский

ЖЭТФ, том 163, вып. 3, 2023

С одной стороны:

неявным образом определяет закон дисперсии ε(p)

на электронном участке спектра ε ∈ [-D, 0].

(p^2x + p^2y + p^2z)²

Можно определить характерный импульс p₀, со-

p⁴

ответствующий ε = 0:

(

)_1/3

(p^4x + p^4y + p^4z)² + 2p^2xp^2y + 2p^2xp^2z + 2p^2yp^2z

p₀ = p(ε = 0) =

3π²

(17)

p⁴

Нас интересуют первые две производные по импуль-

p^4x

p^2xp^2y

су от такого спектра. Из (15) получаем

+ d(d - 1)

= 3a + 6b = 1.

(11)

p⁴

dε

p²

ε^′(p) =

(18)

2π² N₀(ε)

С другой стороны:

где p определяется выражением (16).

(p^2x + p^2y)²

p^4x + p^4y + 2p^2xp^2y

p⁴

2pN₀(ε) - p2dN0(ε)dεdεdp

d dε

ε^′′(p) =

dp dp

2π²

N²⁰(ε)

= 2a + 2b =

(12)

[

]

dN₀(ε)

- ε^′2(p)

(19)

Поскольку

N₀(ε) π²

dε

где

∫

(p^2x + p^2y)²

dN₀(ε)

= 〈sin⁴

θ〉_Ω =

sin θ sin⁴ θ dθ =

√

p⁴

dε

πD²

D² - ε²

ε^′(p) определяется (18), а p определяется выражени-

∫

ем (16).

(1 - τ²)² dτ =

(13)

На дырочном участке спектра (ε ∈ [0, D]) для

−1

получения квадратичного закона дисперсии вблизи

где θ

угол между вектором p и осью z, из

верхнего края зоны (ε → D) вводим дырочный им-

пульс p = 2p₀ - p и приравниваем число состояний

системы

уравнений

(11),

(12) сразу находим

a = p^4x/p^4Ω = 1/5 и b = p^2xp^2y/p^4Ω = 1/15, так

в элементе фазового объема d³ p и в энергетической

полосе [ε, ε + dε]:

что получаем

[

]

4πp²dp

*(∂ε(p))2 ∂2ε(p)

ε^′2(p)

4ε^′(p)

= -N₀(ε)dε.

(20)

ε^′′(p) +

(14)

(2π)³

∂p_x

∂p²

Требуя p → 0 на верхнем крае зоны ε → 0, получаем

Для нахождения производных ε^′(p), ε^′′(p) для

[

(

)]_1/3

спектра, определяемого полуэллиптической плотно-

6π ϕ -

sin(2ϕ)

(21)

стью состояний (5), можно воспользоваться подхо-

дом, развитым в [13]. Приравнивая число состояний

Для скорости на дырочном участке спектра получа-

в элементе фазового объема d³p числу состояний в

ем

области энергий [ε, ε + dε], получаем дифференци-

dε

p²

альное уравнение для определения ε(p):

ε^′(p) = -

(22)

2π² N₀(ε)

4πp²dp

Выражения (18), (22) определяют зависимость ско-

= N₀(ε)dε.

(15)

(2π)³

рости ε^′(p) от энергии. Легко убедиться, что ско-

рость оказывается четной по энергии и обращает-

Предполагая квадратичность закона дисперсии ε(p)

ся в нуль на краях зоны. Вторая производная по

вблизи нижнего края зоны, получаем начальное

импульсу в таком подходе явно определена на элек-

условие к (15): p → 0 при ε → -D. В результате:

тронном участке спектра (ε ∈ [-D, 0]), на дырочном

[

(

)]_1/3

это сделать сложнее. Однако можно потребовать от

6π π - ϕ +

sin(2ϕ)

(16)

модели полной электрон-дырочной симметрии, ко-

торая сводится к требованию четности по ε(p) квад-

где ϕ = arccos(ε/D), а импульс дан в единицах

рата скорости, входящего в выражение (2) и нечет-

обратного параметра решетки. Данное выражение

ности (смена знака при изменении типа носителей

426

ЖЭТФ, том 163, вып. 3, 2023

Эффект Холла в допированном мотт-хаббардовском диэлектрике

заряда) величины (14), входящей в выражение (3)

and F. Mancini, AIP Conference Proceed.

для холловской проводимости. С учетом такой сим-

vol. 1297, AIP, Melville, New York (2010), p. 339;

метрии полученные в этом приложении выражения

ArXiV: 1004.5069.

позволяют перейти в (2), (3) от суммирования по

импульсам к интегрированию по энергии.

Э. З. Кучинский, И. А. Некрасов, М. В. Садов-

ский, УФН 182, 345 (2012) [Phys. Usp. 55, 325

(2010)].

ЛИТЕРАТУРА

10.

G. Rohringer, H. Hafermann, A. Toschi, A. A. Ka-

1. Y. Iye, J.Phys.Chem.Solids 53, 1561 (1992).

tanin, A. E. Antipov, M. I. Katsnelson, A. I. Lich-

tenstein, A. N. Rubtsov, and K. Held. Rev. Mod.

2. F.F. Balakirev, J.B. Betts, A. Migliori, I. Tsuka-

Phys. 90, 025003 (2018).

da, Y. Ando, and G. S. Boebinger, Phys. Rev. Lett.

101, 017004 (2009).

11.

Э. З. Кучинский, Н. А. Кулеева, Д. И. Хомский,

М. В. Садовский, Письма ЖЭТФ

115,

444

3. S. Badoux, W. Tabis, F. Laliberte, B. Vignolle,

(2022) [JETP Lett. 115, 402 (2022)].

D. Vignolles, J. Beard, D. A. Bonn, W. N. Hardy,

R. Liang, N. Doiron-Leyraud, L. Taillefer, and

12.

R. Bulla, T. A. Costi, and T. Pruschke, Rev. Mod.

C. Proust, Nature 531, 210 (2016).

Phys. 60, 395 (2008).

4. C. Collignon, S. Badoux, S.A.A. Afshar, B. Mi-

chon, F. Laliberte, O. Cyr-Choiniere, J.-S. Zhou,

13.

E. Z. Kuchinskii, I. A. Nekrasov, and M. V. Sadov-

S. Licciardello, S. Wiedmann, N. Doiron-Leyraud,

skii, ЖЭТФ 133, 670 (2008) [JETP 106, 581

and L. Taillefer, Phys. Rev. B95, 224517 (2017).

(2008)].

5. C. Proust and L. Taillefer, Annu.Rev.Condens.

14.

D. I. Khomskii, Basic Aspects of the Quantum

Matter Phys. 10 409 (2019).

Theory of Solids, Cambridge University Press, NY

(2010).

6. Th. Pruschke, M. Jarrell, and J.K. Freericks, Adv.

Phys. 44, 187 (1995).

15.

M. V. Sadovskii, I. A. Nekrasov, E. Z. Kuchinskii,

Th. Pruschke, and V. I. Anisimov, Phys. Rev. B72,

7. A. Georges, G. Kotliar, W. Krauth, and M.J. Ro-

155105 (2005).

zenberg, Rev.Mod.Phys. 68, 13 (1996).

8. D. Vollhardt in: Lectures on the Physics of

16.

D. Pelc, P. Popčević, M. Požek, M. Greven, and

Strongly Correlated Systems XIV, eds. A. Avella

N. Barišić, Sci. Adv. 5, eaau4538 (2019).

427