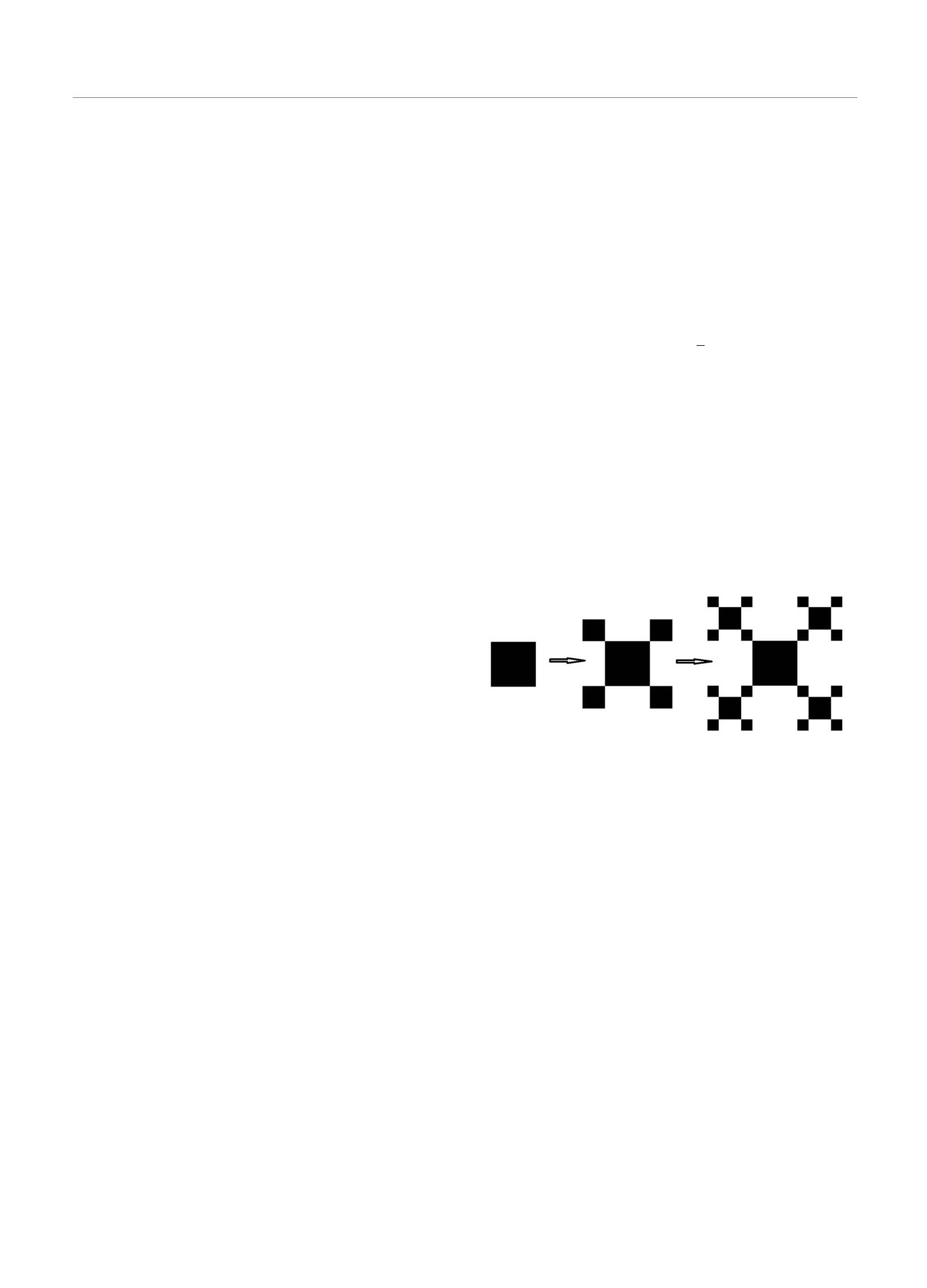ЖЭТФ, 2023, том 163, вып. 3, стр. 428-438

МОДЕЛЬ ФРАКТАЛЬНОЙ ОРГАНИЗАЦИИ ХРОМАТИНА В

ДВУМЕРНОМ ПРОСТРАНСТВЕ

С. В. Григорьев^a,b*, О. Д. Шнырков^a, К. А. Пшеничный^a, П. М. Пустовойт^a,

Е. Г. Яшина^a,b

^a Петербургский институт ядерной физики, НИЦ ¾Курчатовский институт¿

188300, Гатчина, Ленинградская обл., Россия

^b Санкт-Петербургский государственный университет

198504, Санкт-Петербург, Россия

Поступила в редакцию 25 марта 2022 г.,

после переработки 19 октября 2022 г.

Принята к публикации 29 октября 2022 г.

Хроматин, состоящий из метровой нити ДНК и сопутствующих белков, плотно, но без запутывания

упакован в ядре биологической клетки. При этом существует гипотеза, подтверждаемая эксперимента-

ми с использованием технологии захвата конформации хроматина [1], что кривые, плотно заполняю-

щие пространство (кривая Пеано или кривая Гильберта), являются хорошей теоретической моделью

для описания укладки хроматина в ядре. Однако эксперименты по малоугловому рассеянию нейтронов

демонстрируют бифрактальную организацию хроматина в интерфазном ядре, показывая наличие лога-

рифмического фрактала на больших масштабах и объемного фрактала на меньших [2]. В работе с

помощью метода численного фурье-анализа в двумерном пространстве смоделирован процесс рассеяния

нейтронов и представлена модель единого бифрактального объекта. Показано, что в численных экспе-

риментах по рассеянию излучения в двумерном пространстве массовые и логарифмические фракталы

существенно отличаются от кривых, заполняющих пространство, и от нефрактальных объектов. Так, для

логарифмического фрактала с размерностью Хаусдорфа 2 интенсивность рассеяния уменьшается с рос-

том координаты Фурье q по степенному закону q^-2. Для кривых, заполняющих двумерное пространство,

интенсивность убывает по степенному закону q^-3, как и для нефрактальных объектов с резкой грани-

цей на плоскости. Таким образом, во-первых, показана недостаточность модели кривых, заполняющих

пространство, для описания укладки хроматина в ядре биологической клетки, во-вторых, предложена

модель единого бифрактального объекта, соединяющего в себе логарифмический и массовый фракта-

лы на различных масштабах, и, в-третьих, предложена модель укладки хроматина, способная описать

данные экспериментов как по малоугловому рассеянию нейтронов, так и с использованием технологии

захвата конформации хроматина.

DOI: 10.31857/S0044451023030148

де работ с использованием малоуглового рассеяния

EDN: QFLNDR

нейтронов было показано, что структура хромати-

на в интерфазном ядре биологической клетки имеет

фрактальный характер [2, 7-12]. Более того, оказа-

1. ВВЕДЕНИЕ

лось, что в ядре существует два масштабных уров-

ня с двумя принципально разными фрактальными

Многие физические объекты и явления живой

организациями: на масштабе от единиц микромет-

природы обладают свойствами самоподобия или,

ра до сотни нанометров реализуется фрактальная

иначе, фрактальными свойствами [3-6]. Среди них

структура, называемая логарифмической, а на мас-

и такой важный для всего живого на Земле объ-

штабе от сотни нанометров до десятка нанометров

ект, как ядро биологической клетки. В целом ря-

структура объемного фрактала. Не вызывает сомне-

ний, что фрактальная модель укладки хроматина в

^* E-mail: grigoryev_sv@pnpi.nrcki.ru

ядре является одной из самых перспективных и при-

428

ЖЭТФ, том 163, вып. 3, 2023

Модель фрактальной организации хроматина в двумерном пространстве

влекательных, однако детального описания самой

динамическое моделирование равновесной глобулы

модели, описывающей его бифрактальную структу-

(гаусcова клубка) и складчатой глобулы [17-20] и по-

ру, так и не было представлено.

казывается, это экспериментальные данные [1] под-

Впервые гипотеза о фрактальной укладке хро-

тверждают выводы теории, а моделирование неза-

матина была сформулирована группой ученых, спе-

узленной складчатой глобулы приводит к образо-

циализировавшихся в области теоретической био-

ванию хромосомных территорий, подобных экспе-

физики и физики полимеров под руководством

риментально обнаруженным, и хорошо описывает

А. Ю. Гросберга [13, 14]. Ими была разработана мо-

не только расположение хроматина, но и процессы,

дель складчатой глобулы (crumpled globule), кото-

происходящие внутри ядра. Таким образом, была

рая предлагается в качестве трехмерной структу-

построена модель укладки хроматина в интерфаз-

ры ДНК [13]. Складчатая глобула модель одно-

ном ядре, которая основана на концепции незауз-

мерной полимерной цепи, плотно заполняющей про-

ленного полимера, плотно уложенного как кривые

странство без самопересечений, аналогом которой

заполняющие пространство (типа кривой Гильбер-

во фрактальной геометрии является кривая Пеано

та), которые, вследствие незаузленности, формиру-

или любая другая кривая, заполняющая трехмерное

ют отдельные хромосомные территории [17, 19].

пространство (Гильберта, Госпера и т. д.) В резуль-

Будучи несомненно успешной, модель складча-

тате складчатая глобула стала дополнительно назы-

той глобулы не различает структуры различных

ваться фрактальной.

компартментов A/B активного и пассивного (от-

Гипотеза складчатой глобулы получила подтвер-

крытого и закрытого, эу- и гетеро-) хроматина. В

ждение в экспериментах с использованием техно-

то же время метод захвата конформации хромати-

логии по захвату конформации хроматина (метод

на (метод Hi-C) демонстрирует возможности разли-

Hi-C) [1]. С помощью метода Hi-C были построены

чить эти два вида хроматина. Причем пассивный

карты пространственной близости генома человека.

хроматин B оказывается более плотным по сравне-

Эти карты подтвердили, во-первых, наличие хро-

нию с компартментами активного хроматина A, под-

мосомных территорий и, во-вторых, пространствен-

черкивая тот факт, что эти компартменты могут

ную близость небольших, богатых генами хромосом.

иметь разную пространственную структуру. Сле-

Таким образом был идентифицирован дополнитель-

дует особо отметить, что модель складчатой гло-

ный уровень организации генома, который характе-

булы как кривой, заполняющей пространство, не

ризуется пространственной сегрегацией открытого и

может описать экспериментальные данные малоуг-

закрытого хроматина (эухроматина и гетерохрома-

лового рассеяния нейтронов (МУРН), которые на

тина) с образованием двух полногеномных компарт-

больших масштабах (100-5000 нм) хорошо уклады-

ментов. Оказалось, что обнаруженная в экспери-

ваются в модель логарифмического фрактала [2].

менте конформация хроматина согласуется с фрак-

С точки зрения экспериментов МУРН складчатая

тальной глобулой, конформацией без узлов, кото-

глобула (типа кривой Пеано) неотличима от лю-

рая обеспечивает максимально плотную упаковку,

бого другого однородно заполненного объекта, вос-

сохраняя при этом способность легко сворачивать-

производящего ее форму. Следовательно, МУРН на

ся и разворачиваться в любом геномном локусе [1].

фрактальной глобуле должен представлять класси-

В настоящее время технология захвата конформа-

ческий случай рассеяния на нефрактальных трех-

ции хроматина широко используется в исследовани-

мерных неоднородностях [21]. В действительности

ях свойств хроматина в ядрах самых различных ти-

эксперименты МУРН на хроматине уверенно демон-

пов клеток [15, 16].

стрируют наличие фрактальной структуры на всех

С разработкой технологии по захвату конфор-

масштабах от нанометров до микрометров [7-12],

мации хроматина оказалось возможным как разви-

что не укладывается в модель складчатой глобу-

тие теории, так и моделирование укладки хромати-

лы и требует ее доработки. Можно предположить,

на на основе хорошо разработанного теоретического

что структура хроматина в компартментах А и В

базиса физики полимеров [17-20]. В этих работах ав-

различна, и если компартмент B описывается кри-

торы связывают концепцию складчатой (фракталь-

вой, заполняющей пространство (плотный, закры-

ной) глобулы с результатами работы [1] и утвер-

тый хроматин), то в компартменте А открытый, ак-

ждают, что именно топологические ограничения яв-

тивный хроматин представляет собой фрактальную

ляются основным фактором, управляющим фор-

структуру, на малых масштабах характеризующую-

мированием хромосомных территорий. Для дока-

ся объемным фракталом, а на больших масштабах

зательства этого тезиса используется молекулярно-

логарифмическим фракталом.

429

С. В. Григорьев, О. Д. Шнырков, К. А. Пшеничный и др.

ЖЭТФ, том 163, вып. 3, 2023

Концепция логарифмических фракталов остает-

фракталов в двумерном пространстве, а в разд. 5

ся малоизученной и практически неосмысленной на-

кривых, заполняющих двумерное пространство

учным сообществом. Концепция логарифмического

(кривые Пеано, Госпера, Гильберта). В разд. 6

фрактала для двумерного пространства была вве-

сконструирован бифрактальный объект, который

дена в работе [22] для описания роста и ветвления

может рассматриваться как иллюстрация модели

дерева по так называемому принципу Леонардо да

пространственной организации хроматина в ядре

Винчи. Этот принцип открытие Леонардо из-

биологической клетки, и в разд. 7 представлены

вестен также как правило сохранения площади, со-

выводы.

гласно которому площадь сечения ветки ниже точки

ветвления равна сумме площадей сечений дочерних

веток выше ее [23]. Основываясь на этом правиле,

2. КЛАССИФИКАЦИЯ ФРАКТАЛОВ

можно сделать вывод, что площадь сечения ствола

МЕТОДОМ МАЛОУГЛОВОГО РАССЕЯНИЯ

дерева равна сумме площадей сечений всех веток на

любом из уровней ветвления дерева. Отметим, что

Методы малоуглового рассеяния нейтронов и

в случае трехмерного пространства в логарифми-

малоуглового рентгеновского рассеяния (МУРР)

ческих фракталах неизменным оказывается объем,

уже давно стали классическим способом изучения

добавляющийся на каждом шаге ¾ветвления¿ объ-

фракталов нанометрового масштаба [24-27] и час-

екта, а сама концепция дополняет классификацию

то используются для измерения главного парамет-

фракталов, основанную на исследованиях методом

ра, характеризующего фрактальную структуру,

малоуглового рассеяния нейтронов и рентгеновских

размерности Хаусдорфа, которую также называют

лучей [21]. Пример такого трехмерного логарифми-

фрактальной размерностью.

ческого фрактала, состоящего из кубов различного

Этими методами измеряют степенную зависи-

размера, был дан в работе [12].

мость интенсивности рассеяния от переданного им-

В этой работе мы моделируем процесс рассея-

пульса q:

ния на различных типах фрактальных структур в

I(q) ∼ q^-Δ,

(1)

двумерном пространстве. Представлены результаты

численных экспериментов на классических фракта-

где Δ показатель степени, связанный с фракталь-

лах, логарифмических фракталах и на кривых, за-

ной размерностью изучаемого объекта.

полняющих пространство. Показано, что картина

Рассеяние на трехмерных однородных частицах

рассеяния на кривых, заполняющих пространство,

с гладкой границей хорошо описывается законом

существенно отличается от картины рассеяния на

Порода, который формулируется следующим обра-

фракталах. Кроме того, смоделирован бифракталь-

зом: интенсивность рассеянного излучения есть сте-

ный объект, который иллюстрирует возможность со-

пенная функция переданного импульса q (см. (1)) с

существования в одной структуре классического и

Δ = 4 для q ≫ 1/ξ, где ξ характерный размер рас-

логарифмического фракталов. Таким образом, мы

сеивающей частицы. Как было показано в [24-27],

показываем на примерах двумерного пространства,

показатель степени Δ напрямую связан с фракталь-

что эксперименты по рассеянию если не дают ключ

ной размерностью D, но для разных типов фракта-

к разгадке сложной организации хроматина, то ста-

лов эта связь разная. Для массовых фракталов в

вят фундаментальные вопросы о механизмах обра-

трехмерном пространстве Δ = D, для поверхност-

зования фрактальных структур в ядре на масшта-

ных фракталов Δ = 6 - D. Промежуточный слу-

бах от 10 нм до 10 мкм.

чай между массовыми и поверхностными фрактала-

Работа организована следующим образом. В

ми соответствует логарифмическим фракталам [21].

разд. 2 представлена классификация фрактальных

Этот тип фракталов может быть также идентифи-

объектов, проводимая с помощью метода малоугло-

цирован с помощью экспериментов по рассеянию,

вого рассеяния проникающих излучений для случая

в этом случае Δ = 3. Логарифмические фракта-

трехмерного пространства. Аналогичная класси-

лы отличаются особым типом самоподобия: в них

фикация фракталов для двумерного пространства

реализуется аддитивный закон масштабирования, а

разработана на основе численного анализа Фурье.

не мультипликативный, как в случае с массовы-

В разд. 3 описывается метод численного анализа

ми фракталами [8, 21]. Было показано, что куби-

Фурье, который моделирует эксперимент по мало-

ческая зависимость интенсивности рассеяния ней-

угловому рассеянию в двумерном пространстве. В

тронов связана преобразованием Фурье c корреля-

разд. 4

показано исследование логарифмических

ционной функцией объекта χ(r), пропорциональной

430

ЖЭТФ, том 163, вып. 3, 2023

Модель фрактальной организации хроматина в двумерном пространстве

ln(r/ξ), где r/ξ < 1, т.е. во фрактальной области [21].

Таблица 1. Классификация фрактальных и нефракталь-

Аналогично фракталам в трехмерном простран-

ных объектов в двумерном пространстве в экспериментах

стве, с помощью метода численного фурье-анализа

по рассеянию (^∗данные для логарифмического фрактала

и кривой Пеано получены в рамках данной работы). Здесь

проведена классификация и продемонстрированы

Δ показатель степени в зависимости интенсивности рас-

характерные особенности фрактальных объектов на

сеяния от переданного импульса, определяемой в реаль-

плоскости [28]. В двумерном пространстве также,

ном или численном эксперименте, D фрактальная раз-

помимо однородных объектов с гладкой границей,

мерность или размерность Хаусдорфа

можно выделить три типа фракталов: массовые,

граничные и логарифмические. Фрактальные объ-

Объект

Показатель Размерность

екты в двумерном пространстве также описываются

степени Хаусдорфа

с помощью меры Хаусдорфа. Мера нефрактального

Нефрактальный объект

Δ=3

D=Δ-1

объекта в двумерном пространстве равна r², где r

Кривая Пеано

Δ=3

D=2^(∗)

линейный размер объекта. Для фрактальных объек-

Граничный фрактал

2<Δ<3

D=4-Δ

тов мера Хаусдорфа содержит пробную степенную

функцию h(ε) = ε^D, а в случае логарифмических

Логарифмический фрактал Δ = 2

D=Δ^(∗)

фракталов пробная функция дополнительно содер-

Массовый фрактал

1<Δ<2

D=Δ

жит логарифм: h(ε) = ε^D(ln 1/ε)Δf , где ε линей-

ный размер пробного элемента, D топологическая

3. МЕТОД ЧИСЛЕННОГО ФУРЬЕ-АНАЛИЗА

размерность объекта, Δ_f логарифмическая под-

В ДВУМЕРНОМ ПРОСТРАНСТВЕ

размерность фрактала. В экспериментах по рассея-

нию пробные функции объектов на плоскости свя-

Следует отметить, что моделирование процес-

заны с показателем степени Δ в (1) соотношениями,

са рассеяния в двумерном пространстве с помощью

представленными в табл. 1.

фурье-анализа имитирует рассеяние света на дву-

Для однородно заполненных объектов с глад-

мерных объектах

¾масках¿, и давно вошло в учеб-

кой границей в двумерном пространстве (например,

ники [29,30]. Численное моделирование эксперимен-

для круга) интенсивность рассеяния убывает с рос-

тов по рассеянию света на двумерных регулярных

том q как q^-Δ с показателем степени Δ = 3. Этот

геометрических фракталах стало применяться срав-

показатель на единицу меньше, чем для шара в

нительно недавно [28,31]. В качестве модельной кар-

трехмерном пространстве. Для массовых фракталов

тины рассеяния определяют квадрат модуля фурье-

1 < Δ < 2 и Δ = D, для граничных 2 < Δ < 3

образа двумерного объекта. Эксперимент по малоуг-

и Δ = 4 - D. Промежуточный случай Δ = 2 со-

ловому рассеянию света моделируют, используя схе-

ответствует логарифмическому фракталу. Класси-

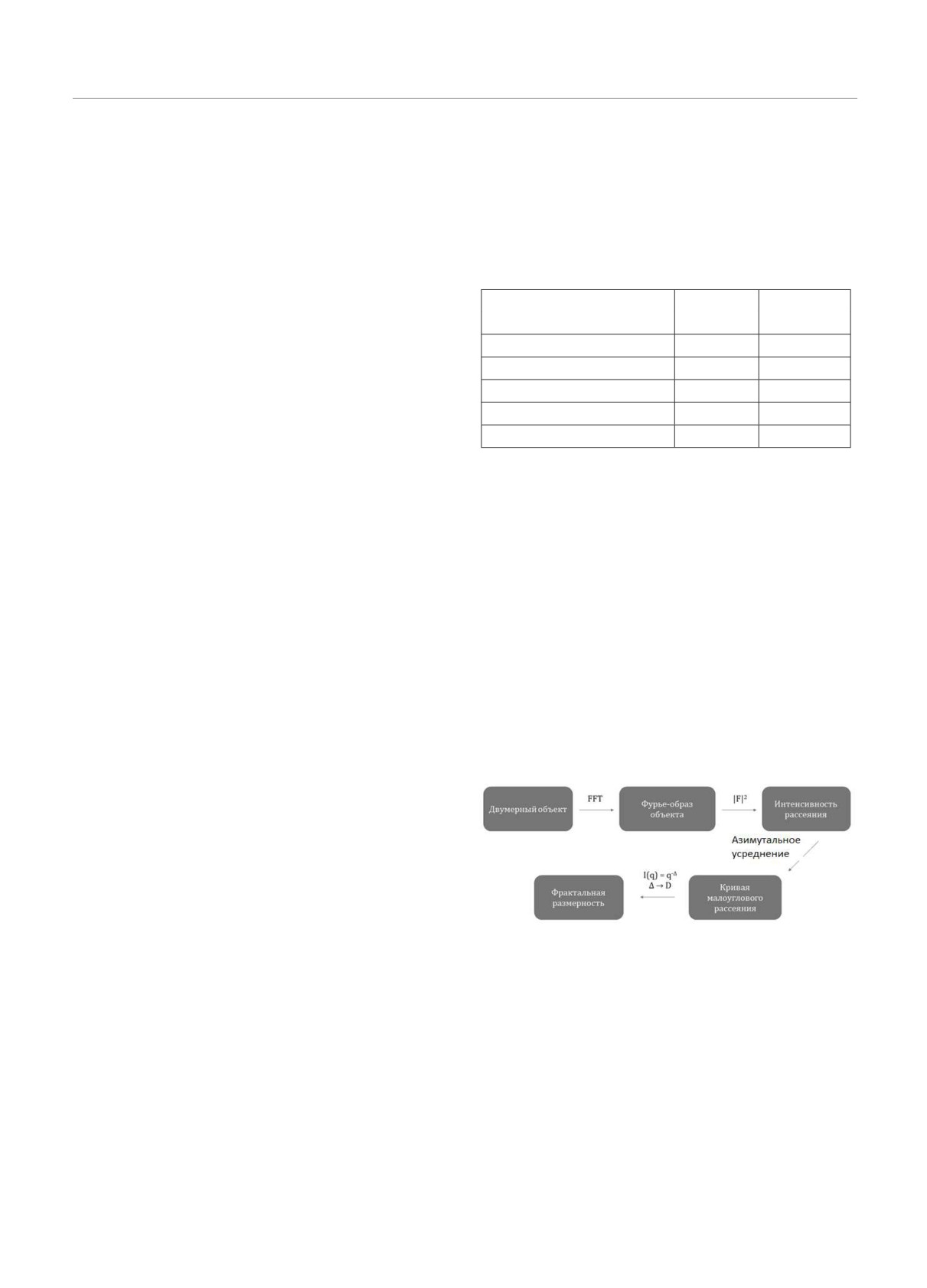
му, представленную на рис. 1.

фикация фрактальных и нефрактальных объектов

в двумерном пространстве, проведенная с помощью

численного фурье-анализа, представлена в табл. 1.

Таблица 1 содержит информацию о таких объек-

тах, как кривая Пеано и логарифмический фрактал,

исследования которых представлены в этой работе

(см. разд. 4 и 5).

Пользуясь классификацией, разработанной на

основе метода малоуглового рассеяния нейтронов

Рис. 1. Схема численного моделирования эксперимента по

и рентгеновского излучения, можно, сконструиро-

малоугловому рассеянию света на двумерных объектах

вав фрактальные и нефрактальные объекты в дву-

мерном пространстве, аттестовать их методом чис-

Схема такого численного эксперимента доста-

ленного фурье-анализа, моделирующего процессы

точно проста и состоит из четырех последова-

рассеяния. В данном случае численный экспери-

тельных шагов. Объект исследования представ-

мент по рассеянию используют как способ верифи-

ляет собой образ внутри квадрата с размерами

кации, удостоверяющий, что объект действитель-

1×1см², описывающегося бинарной двумерной мат-

но является фракталом, которому присваиваются

рицей. Первый шаг фурье-преобразование объ-

определенные свойства, характерные для массового,

екта. Полученный фурье-образ тоже двумерная

граничного, логарифмического фрактала или вовсе

матрица, каждый элемент которой

комплекс-

нефрактального объекта.

ное число

характеризуется амплитудой и фа-

431

С. В. Григорьев, О. Д. Шнырков, К. А. Пшеничный и др.

ЖЭТФ, том 163, вып. 3, 2023

зой. Второй шаг формирование двумерной кар-

тельно соответствует определению логарифмиче-

ты интенсивности, как квадрата модуля фурье-

ского фрактала, и определим нишу, в которую такой

образа объекта, моделирующей интенсивность рас-

объект попадает в рамках классификации по методу

сеяния. На этом шаге теряется информация о фазе

малоуглового рассеяния.

фурье-образа. Третий шаг алгоритма азимуталь-

По определению логарифмические фракталы

ное усреднение карты интенсивности вокруг центра

это фракталы с логарифмической мерой. Пробная

и получение кривой усредненной интенсивности, ко-

функция в такой мере является произведением сте-

торая имитирует кривую малоуглового рассеяния,

пенной функции с аргументом ε и степенной функ-

т.е. зависимость интенсивности рассеяния от пере-

ции от логарифма 1/ε [3, 22]:

данного импульса (I от q). Последним шагом явля-

(

)Δ_f

ется определение показателя степени Δ степенного

h(ε) = ε^D ln

(2)

закона I(q) как отношения логарифмов усредненной

интенсивности ln I и координаты Фурье ln q. Пока-

Здесь D фрактальная размерность, Δ_f фрак-

затель Δ напрямую связан с фрактальной размер-

тальная подразмерность, ε

линейный размер

ностью, но по-разному для разных типов фракталь-

пробных элементов, покрывающих фрактал.

ных объектов (см. табл. 1).

Известен двумерный логарифмический фрактал,

Для обработки фрактальных изображений мы

описывающий рост дерева и основанный на ¾прин-

создали программу на платформе Qt [32], кото-

ципе да Винчи¿ [22, 23]: сумма площадей попереч-

рая выполняет первые три шага этого алгоритма.

ных сечений ветвей на каждом уровне равна пло-

В этом методе двумерный объект представляет со-

щади поперечного сечения ствола дерева (фрактал

бой квадрат 1 × 1 см², состоящий из N × N единич-

¾Дерево да Винчи¿). На рис. 2 показан принцип по-

ных элементов (пикселей), где N должно быть рав-

строения этого фрактала.

но 2ⁿ, n = 1, 2, 3, . . . Мы используем быстрое пре-

образование Фурье, чтобы сократить время вычис-

лений. Карта интенсивности это распределение

интенсивности ¾рассеяния¿ по компонентам векто-

ра Фурье q_x, q_y, выраженным в единицах обратной

длины. Максимальное значение координаты q мож-

но вычислить как πN/X, где X общий размер

изображения в единицах длины, N размер изоб-

ражения в пикселях, X/N размер одного пикселя

в единицах длины. Оси q_x и q_y разделены на N рав-

Рис. 2. Построение логарифмического фрактала роста де-

ных интервалов, а размер пикселя в пространстве

рева по принципу ¾да Винчи¿ (базовый элемент квад-

Фурье равен π/X. Поскольку все реальные фракта-

рат, 1 и 2 поколения)

лы ограничены как по максимальному размеру, так

и по размеру минимального элемента, важно кон-

В каждом новом поколении к углам каждого

тролировать разрешающую способность метода Фу-

наименьшего на данный момент квадрата добавля-

рье. Во-первых, размер фрактального объекта дол-

ются четыре квадрата, каждый из которых по пло-

жен быть меньше размера всего изображения и, во-

щади в четыре раза меньше квадрата предыдущего

вторых, размер минимального элемента фрактала

поколения. Следует отметить, что в отличие от по-

должен быть в несколько раз (>3) больше размера

строения геометрических фракталов, таких как ко-

минимального элемента изображения (одного пик-

вер Серпинского, здесь добавление квадратов следу-

селя). При анализе кривых усредненных интенсив-

ющего поколения происходит не для всего фракта-

ностей необходимо отличать фрактальный диапазон

ла, а только для квадратов предыдущего поколения.

координаты Фурье от нефрактальных диапазонов,

Площадь фрактала с каждым новым поколе-

возникающих при очень малом и очень большом q.

нием увеличивается на площадь ¾ствола¿ (самого

большого квадрата). Таким образом, площадь все-

го фрактала n-го поколения будет в n раз больше

4. ЛОГАРИФМИЧЕСКИЙ ФРАКТАЛ В

площади ¾ствола¿.

ДВУМЕРНОМ ПРОСТРАНСТВЕ

Пусть линейный размер ¾ствола¿ равен 1. Тогда

Сконструируем пример логарифмического фрак-

площадь всего фрактала n-го поколения будет рав-

тала на плоскости, покажем, что объект действи-

на n, а линейный размер ε квадратов n-го поколения

432

ЖЭТФ, том 163, вып. 3, 2023

Модель фрактальной организации хроматина в двумерном пространстве

и число поколений n фрактала будут связаны сле-

дующими выражениями:

ε=

+ 1.

(3)

2^n-1

ln 2

Пусть N(ε) количество квадратов линейного раз-

мера ε, покрывающих весь фрактал. Тогда N(ε)

можно выразить как

(

)

N (ε) =

/ ln 2 + 1

(4)

ε²

Как известно [3,22], фрактальная мера µ(ε) это

величина, поведение которой определяется произ-

ведением пробной функции h(ε) и числа покрытий

N (ε). По определению, мера должна стремиться к

константе, когда значение ε стремится к нулю. Та-

ким образом, пробная функция этого объекта имеет

вид

(

)-1

h(ε) = ε² ln

N (ε)h(ε)

−-→

(5)

ε→0

ln 2

Сравнивая соотношения

(2) и

(5), получаем

D = 2, Δ_f = -1. Таким образом, фрактал, описы-

вающий рост дерева, построенный по принципу ¾да

Винчи¿, действительно является логарифмическим

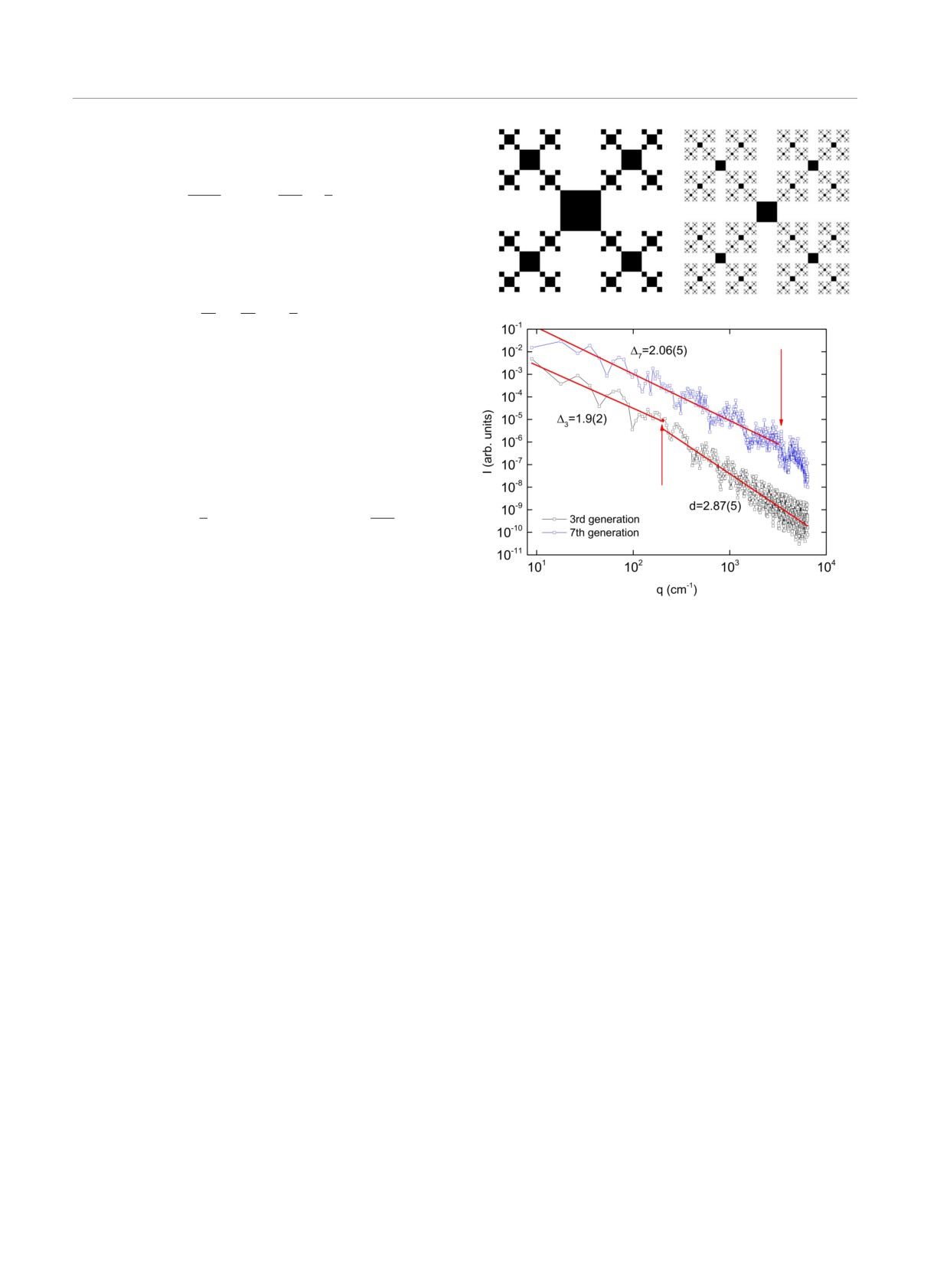
Рис. 3. Изображение логарифмического фрактала 3-го (a)

фракталом с фрактальной размерностью 2, что рав-

и 7-го (b) поколений. Усредненные зависимости интенсив-

ности от координаты Фурье q для 3-го и 7-го поколений ло-

но его топологической размерности [22].

гарифмического фрактала (c). Стрелками показана верх-

Мы исследовали изображения этого фрактала

няя (по переданному импульсу q) граница фрактального

разных поколений от 1-го до 7-го методом чис-

диапазона

ленного анализа Фурье. Для каждого изображе-

ния были получены усредненные зависимости ин-

поколения и 3217 см^-1 для фрактала 7-го поколе-

тенсивности от координаты Фурье q, моделирующие

ний. Мы оцениваем эти значения как π · 2048/32 и

кривые малоуглового рассеяния. Размер изображе-

π · 2048/2 для 3-го и 7-го поколений соответствен-

ний

1 × 1см² и 2048 × 2048 пикселей².

но, учитывая, что линейный размер минимального

На рис.3a, b показаны 3-е и 7-е поколения это-

элемента для фрактала 7-го поколения составляет 2

го фрактала. Усредненные значения интенсивности

пикселя, а для фрактала 3-го поколения

32 пик-

в зависимости от координаты Фурье q показаны на

селя.

рис. 3c.

Таким образом, кривые в диапазонах

Кривые, полученные в результате преобразова-

201 см^-1

и q

3217 см^-1 относятся к

ния Фурье на рис. 3c, демонстрируют осциллирую-

фрактальной области для

3-го и

7-го поколе-

щее поведение, затухающее при увеличении пере-

ний соответственно, а кривые для диапазонов

данного импульса q. Осцилляции имеют квазипери-

> 201 см^-1 и q

> 3217 см^-1 характеризуют

одический характер в логарифмическом масштабе в

минимальный элемент фрактала. Если усреднить

левой части кривых, при этом в правой части они

осцилляции и аппроксимировать зависимость ин-

становятся периодическими в линейном масштабе,

тенсивности от q степенным законом q^-Δ в разных

что указывает на переход к нефрактальному режи-

диапазонах, то показатель степени Δ будет равен

му. Кроме того, показатель степени (наклон кри-

1.9 ± 0.2 (q < q_c) и

2.87 ± 0.05 (q > q_c) для

3-го

вых в логарифмическом масштабе) изменяется при

поколения и 2.06 ± 0.05 (q < q_c) для 7-го поколения

смене режимов. Точка пересечения двух режимов

(рис. 3c). Таким образом, наклон кривой усред-

характеризует границу фрактала со стороны малых

ненной интенсивности Δ близок к -2 в пределах

размеров. Эти точки кроссовера различны для раз-

фрактального диапазона и близок к -3 вне фрак-

ных поколений и равны 201 см^-1 для фрактала 3-го

тального диапазона, что соответствует рассеянию

433

С. В. Григорьев, О. Д. Шнырков, К. А. Пшеничный и др.

ЖЭТФ, том 163, вып. 3, 2023

на объектах с резкой границей в двумерном про-

же выражения можно получить для других кривых

странстве (квадрат). Можно сделать вывод, что

типа Пеано: кривой Гильберта, кривой Госпера и

наклон Δ для фрактального диапазона иссле-

т. д. Принципы построения кривой Госпера и кри-

дуемого объекта равен размерности Хаусдорфа

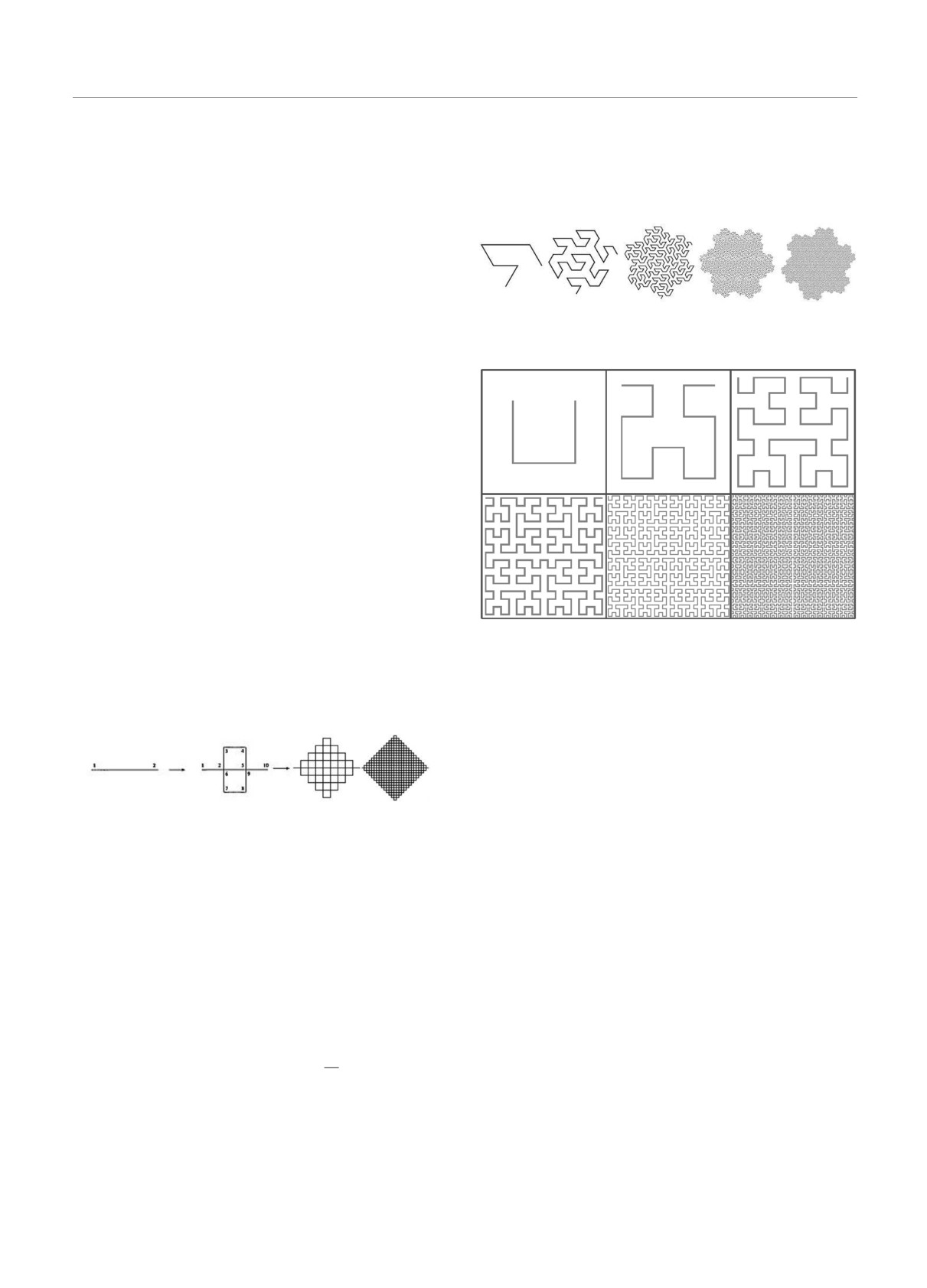
вой Гильберта показаны на рис.5 и рис.6.

строительного блока фрактального объекта Δ = D.

Как показано в работе [28], если объект не явля-

ется фрактальным, то наклон кривой рассеяния ра-

вен Δ = -3. Логарифмическая специфика фрактала

проявляется в том, что наклон кривой на 1 меньше

наклона кривой нефрактального объекта.

Рис. 5. Построение кривой Госпера от базового элемента

до четвертого поколения

5. КРИВЫЕ ПЕАНО В ДВУМЕРНОМ

ПРОСТРАНСТВЕ

Помимо логарифмических фракталов существу-

ет целый класс объектов, имеющих размерность Ха-

усдорфа равную двум кривые Пеано. По опреде-

лению кривые Пеано это кривые, заполняющие

пространство без самопересечений. Сконструируем

примеры кривой Пеано на плоскости, вычислим ее

меру и покажем, что объект, в соответсвии со своим

определением, попадает в нишу объектов, обладаю-

щих резкой границей и однородных внутри, в соот-

ветствии с классификацией по методу малоуглового

рассеяния.

Рассмотрим кривую, изобретенную самим Джу-

Рис. 6. Построение кривой Гильберта от базового элемен-

зеппе Пеано. Принцип ее построения показан на

та до пятого поколения

рис. 4. Числа на рис. 4 показывают порядок этапов

строительства.

С помощью метода численного анализа Фурье

мы получили кривую усредненной интенсивности,

моделирующую кривую малоуглового рассеяния,

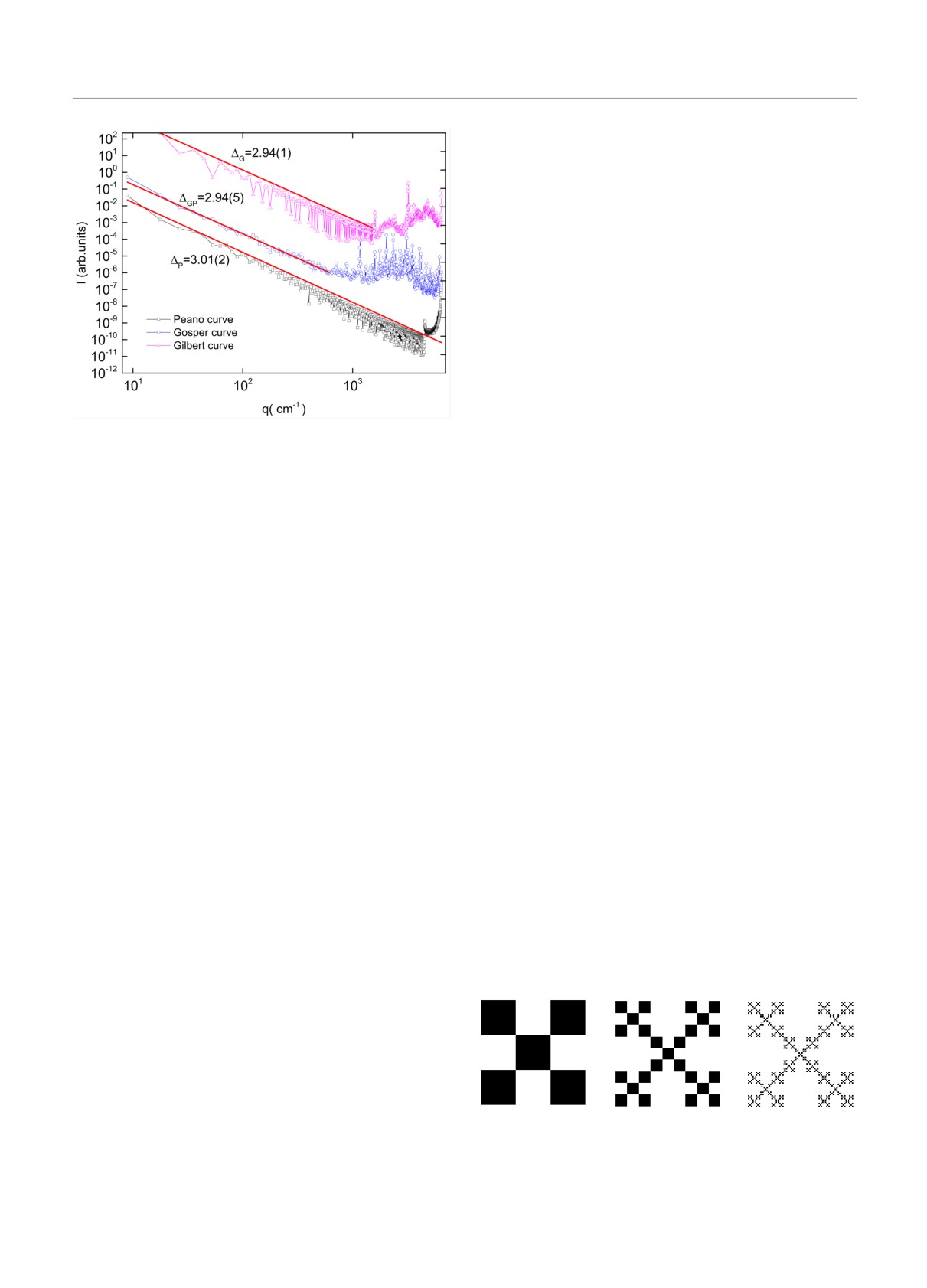
для кривых Пеано, Госпера и Гильберта. Они пред-

ставлены на рис. 7.

Все три кривые демонстрируют убывание ин-

тенсивности на левой стороне и систему пиков на

Рис. 4. Построение кривой Пеано от базового элемента до

правой стороне (рис. 7). Показатели наклона усред-

третьего поколения

ненных кривых интенсивности для кривых Пеано

и Гильберта рассчитывались как показатели накло-

Эта кривая не имеет самопересечения, хотя в

на огибающих. Для кривой Госпера мы использова-

некоторых точках происходит самокасание. Длина

ли линейную аппроксимацию данных. Было полу-

сегментов этой кривой уменьшается в три раза для

чено, что наклоны кривых Пеано, Госпера и Гиль-

каждого следующего поколения, а количество сег-

берта равны Δ = 3.01 ± 0.02, Δ = 2.94 ± 0.05 и

ментов линии увеличивается в 9 раз. Следовательно,

Δ = 2.94±0.02 соответственно. Таким образом, для

длина сегментов равна ε = 1/3ⁿ для n-го поколения

семейства кривых Пеано показатель Δ в (1) близок

кривой Пеано, а количество этих сегментов равно

к 3, как для объекта с резкой границей в двумер-

N (ε) = 9ⁿ. Тогда

ном пространстве. Другими словами, эксперимент

по рассеянию ¾видит¿ такие кривые как фигуры,

N (ε) = 3²ⁿ = 32log3(1/ε) =

=ε^-2.

(6)

ε²

которые имеют однородную ¾заливку¿. Как отмеча-

Это показывает, что пробная функция этого объ-

лось выше, в области больших значений координа-

екта равна h(ε) = ε², имеет размерность квадра-

ты Фурье q возникает некоторая система пиков, своя

та, при этом являясь линией. Никакой логарифми-

для каждой кривой. Анализируя кривые усреднен-

ческой подразмерности у этого объекта нет. Такие

ной интенсивности для разных поколений каждой

434

ЖЭТФ, том 163, вып. 3, 2023

Модель фрактальной организации хроматина в двумерном пространстве

благодаря системе пиков, которая присутствует на

кривых малоуглового рассеяния при больших зна-

чениях переданного импульса. Эта система пиков

характеризует фурье-образ минимального элемента,

по которому строится та или иная кривая Пеано. В

этом их главное отличие от простого нефрактально-

го объекта с резкой границей.

6. МОДЕЛЬ БИФРАКТАЛЬНОЙ

ОРГАНИЗАЦИИ ХРОМАТИНА В

ДВУМЕРНОМ ПРОСТРАНСТВЕ

Эта работа мотивирована необходимостью ин-

терпретации экспериментов по малоугловому рас-

Рис. 7. Кривые усредненной интенсивности для 6-го по-

сеянию нейтронов (МУРН) на хроматине внутри

коления кривой Пеано (квадраты), 6-го поколения кривой

ядра биологической клетки [7-12]. Эксперименты

Госпера (кружки) и 7-го поколения кривой Гилберта (тре-

МУРН демонстрируют бифрактальную организа-

угольники)

цию хроматина, которая не укладывается в кон-

цепцию складчатой глобулы по типу кривой Пеа-

кривой Пеано, мы пришли к выводу, что эта систе-

но, предложенной в работах [13,14]. Моделирование

ма пиков описывает формфактор базового элемен-

эксперимента по малоугловому рассеянию в двумер-

та кривой Пеано. Естественно, что базовый элемент

ном пространстве ясно демонстрирует, что модель

кривой, а также его преобразование Фурье для раз-

кривых заполнения пространства имитирует одно-

ных кривых различны.

родно заполненный объект с резкой границей и не

Таким образом, эксперимент по рассеянию ¾ви-

является ни фрактальным объектом с дробной раз-

дит¿ кривые Пеано как двумерные объекты с рез-

мерностью Хаусдорфа, ни логарифмическим фрак-

кими границами. Это легко понять: в случае, ко-

талом. Другими словами, в эксперименте по рассея-

гда кривая заполняет конечный плоский объект, он

нию излучения логарифмические фракталы и клас-

представляет собой двумерную фигуру (в данном

сические фракталы можно однозначно отличить от

случае квадрат), равномерно заполненную линиями

кривых Пеано и нефрактальных объектов.

и окруженную пустым пространством. Это равно-

Чтобы сконструировать модель бифрактальной

мерное заполнение плоского объекта дает нам пока-

организации хроматина в ядре клетки, мы созда-

затель степени Δ = 3, как и для любого двумерного

ли фрактал, который состоит из логарифмическо-

однородно заполненного объекта с гладкими грани-

го фрактала ¾Дерево да Винчи¿ и ¾вложенного в

цами.

него¿ фрактала Вишека (¾Снежинка Вишека¿).

Несмотря на то, что кривые Пеано удовлетворя-

Фрактал Вишека генерируется следующим обра-

ют нестрогому определению фрактала, которое дал

зом: берем квадрат, разбиваем его на девять одина-

в своей работе Мандельброт [3], поскольку их раз-

ковых квадратов и удаляем те квадраты, которые

мерность Хаусдорфа строго больше их топологиче-

находятся не в углах и не в центре. Затем повторяем

ской размерности равной 1, такие объекты нельзя

эту процедуру для каждого из оставшихся квадра-

считать фракталами. Они не фракталы не только

тов и т.д. (рис.8).

из-за их целочисленной размерности Хаусдорфа, но

и потому, что плотность кривых Пеано однородно

распределена в объекте, тогда как для фракталь-

ных объектов характерно неравномерное распреде-

ление плотности в занимаемой фракталом области

пространства.

Следует отметить, что, несмотря на то что раз-

мерности Хаусдорфа кривой Пеано и объекта с рез-

кой границей совпадают, их все же можно разли-

Рис. 8. Схема построения фрактала Вишека (2-е, 3-е, 4-е

чить в эксперименте по малоугловому рассеянию

поколения)

435

С. В. Григорьев, О. Д. Шнырков, К. А. Пшеничный и др.

ЖЭТФ, том 163, вып. 3, 2023

Именно такой фрактал мы использовали вме-

шека¿, теоретическая фрактальная размерность ко-

сто минимальных элементов фрактала ¾Дерева да

торого равна 1.465.

Винчи¿, которые обычно представляют собой одно-

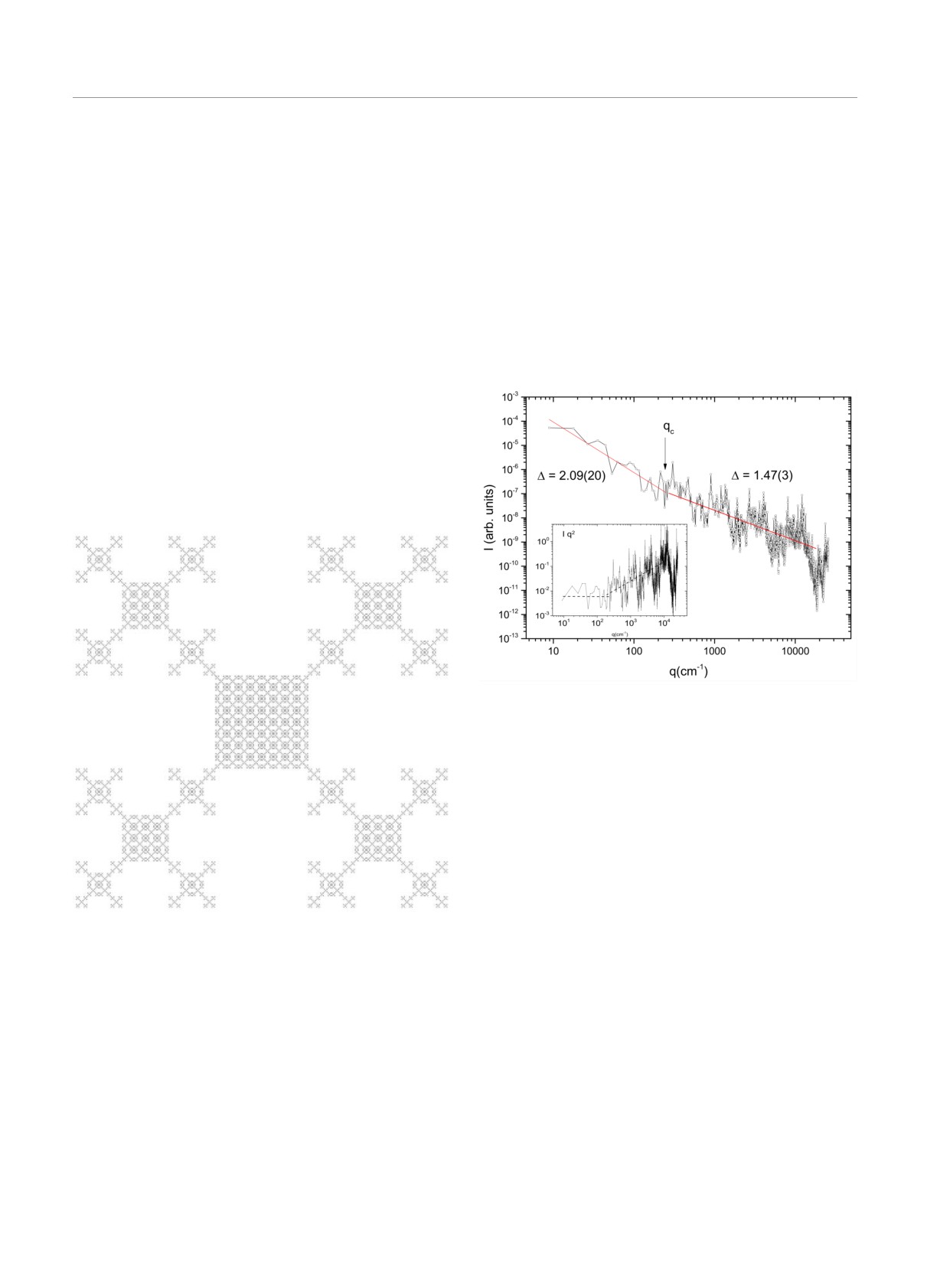
Чтобы четко различать два разных диапазона

родные квадраты (рис. 3). Полученный комбинаци-

по переданному импульсу q, мы приводим график

ей двух фракталов объект по существу и является

Кратки как произведение (I(q)q²) в зависимости от

бифракталом. Для того чтобы модель соответство-

q на вставке к рис.10. Такое представление экспе-

вала масштабам задачи, были выбраны 4-е поколе-

риментальных данных выделяет кривую рассеяния

ния каждого из фракталов. В этом случае мини-

q^-2, делая более очевидными другие особенности. В

мальный крест фрактала Вишека в 27 раз меньше

частности, произведение (I(q)q²) в q-диапазоне для

всей ¾Снежинки Вишека¿, которая является в этой

фрактала ¾Дерево да Винчи¿ теперь оказалось кон-

конструкции минимальным элементом ¾Дерева да

стантой. Наклон кривой в этой области оказался ра-

Винчи¿. При этом минимальный элемент ¾Дерева

вен нулю (Δ - 2 = 0.04 ± 0.20).

да Винчи¿ в 32 раза меньше всего ¾Дерева да Вин-

чи¿. Таким образом, минимальный крест фрактала

Вишека в 862 раза меньше всего бифрактала, т. е.

весь диапазон масштабов этого объекта пробегает

3 порядка по линейной шкале размеров, что соот-

ветствует, например, диапазону от 10 нм до 10 мкм.

Построенный бифрактал изображен на рис.9.

Рис. 10. Усредненная кривая интенсивности для бифрак-

тала, состоящего из 4-й генерации фрактала ¾Дерево да

Винчи¿ и 4-й генерации фрактала ¾Снежинка Вишека¿

Таким образом, сконструированный нами

бифрактальный объект точно воспроизводит

бифрактальный характер кривых малоуглового

рассеяния нейтронов, получаемых в эксперимен-

тах на ядрах различных типов биологических

клеток [7-12]. Построенная таким образом бифрак-

тальная конструкция, несмотря на то, что задача

решается в двумерном пространстве, может слу-

жить еще одним шагом на пути создания модели

Рис. 9. Бифрактал, состоящий из фрактала ¾Дерево да

организации хроматина в ядре биологической

Винчи¿ на крупном масштабе и фрактала ¾Снежинка Ви-

шека¿ на более мелком масштабе

клетки.

При переходе в трехмерное пространство вопрос

Результат численного эксперимента по модели-

о совместимости модели укладки хроматина, разра-

рованию процесса рассеяния на таком фрактале по-

ботанной в результате эксперимента методом захва-

казан на рис. 10. Как видно из рис. 10, кривая рассе-

та конформации хроматина (метод Hi-C) [1,17-20]

яния, построенная в двойном логаифмическом мас-

модель складчатой глобулы, и модели на основе

штабе, демонстрирует две фрактальные области: од-

данных МУРН модели бифрактальной структу-

на имеет наклон Δ = 2.09 ± 0.20 и соответствует

ры [7-12], остается открытым. Попытка комбина-

логарифмическому фракталу, вторая имеет наклон

ции данных этих двух экспериментов была сделана

1.47±0.03 и соответствует фракталу ¾Снежинка Ви-

в глубоком, всеобъемлющем обзоре [19].

436

ЖЭТФ, том 163, вып. 3, 2023

Модель фрактальной организации хроматина в двумерном пространстве

Как указывалось в [19], модель складчатой гло-

дит за рамки данной работы, но в ней представле-

булы основана на предположении об отсутствии

на целостная картина, непротиворечивым образом

сильных вариаций плотности на масштабах порядка

описывающая результаты экспериментов, как мето-

длины запутанности и выше. Классические цветные

да МУРН, так и метода Hi-C.

изображения хроматиновых территорий предпола-

гают однородную плотность по всему клеточному

7. ВЫВОДЫ

ядру. Это, однако, может ввести в заблуждение, по-

скольку длина волны видимого света слишком вели-

В этой работе cконструированы логарифмиче-

ка, чтобы можно было легко разрешить глазу боль-

ские фракталы и кривая Пеано в двумерном про-

шее изменение локальной плотности. Для того что-

странстве, а затем исследованы методом числен-

бы заглянуть внутрь ядра, необходимо прибегнуть

ного анализа Фурье, моделирующего эксперимен-

к экспериментам по рассеянию. Правда, единствен-

ты по малоугловому рассеянию нейтронов. Резуль-

ный известный на тот момент эксперимент на ядрах

таты сведены в классификационную таблицу фрак-

куриных эритроцитов не позволил провести адек-

тальных объектов в двумерном пространстве, кото-

ватную процедуру сравнения результатов МУРН и

рая дополнена новым классом логарифмическими

метода Hi-C, поскольку куриные эритроциты весь-

фракталами (табл. 1).

ма отличны от других эукариотических клеток. До-

Показано, что для логарифмических фракталов

полнительно авторами было выдвинуто предполо-

в экспериментах по рассеянию показатель степени

жение, на наш взгляд, ошибочное, что складчатая

Δ равен их размерности Хаусдорфа, а для кривых

глобула будет иметь закон рассеяния, пропорцио-

Пеано в экспериментах по рассеянию показатель Δ

нальный Q^-3.

равен 3, как для двумерного объекта с резкими гра-

В настоящей работе мы показываем, что ес-

ницами.

ли складчатая глобула описывается в большей или

Построена бифрактальная модель простран-

меньшей степени кривой Гильберта (или Пеано), то

ственной организации хроматина в ядре биоло-

закон рассеяния от нее должен иметь вид закона

гической клетки. Численные эксперименты по

Порода, как от частицы с гладкой поверхностью в

малоугловому рассеянию от единого бифрактально-

трехмерном пространстве, Q^-4. При этом закон Q^-3

го объекта, объединяющего в себе логарифмический

соответствует структуре логарифмического фракта-

фрактал и классический фрактал, подтверждают

ла, наблюдаемого в экспериментах по МУРН [7-12].

сходство предложенной модели и реального объ-

В то же время структура логарифмического фрак-

екта, поскольку модельная кривая повторяет

тала может быть сформирована некими структур-

характерные особенности реальных кривых ма-

ными единицами объемными фракталами, описы-

лоуглового рассеяния на ядрах биологической

ваемыми Q^-D, где D фрактальная размерность

клетки.

объекта. Опираясь на данные малоуглового рентге-

Финансирование. Работа поддержана Россий-

новского рассеяния, мы идентифицируем этот объ-

ским научным фондом (грант № 20-12-00188).

ект как единицу активного хроматина компарт-

мента А, наблюдаемого в методе Hi-C. Интересно

отметить, что характерный максимальный размер

ЛИТЕРАТУРА

этого объекта меняется в зависимости от степени

активности транскрипции в ядре клетки и состав-

1. E. Lieberman-Aiden, N. L. van Berkum, L. Williams,

ляет величину порядка 100 нм. Особенностью на-

M. Imakaev, T. Ragoczy, A. Telling, I. Amit, B. R. La-

шей модели является и тот факт, что вся структура

joie, P. J. Sabo, M. O. Dorschner, R. Sandstrom,

логарифмического фрактала, состоящего из малых

B. Bernstein, M. A. Bender, M. K. Groudine, A. Gnir-

единиц объемного фрактала активного хроматина,

ke, J. Stamatoyannopoulos, L. A. Mirny, E. S. Lan-

der, and J. Dekker, Science 326, 289 (2009).

окружена плотной укладкой неактиного, закрытого

гетерохроматина, который вполне может быть оха-

2. Е. Г. Яшина, С. В. Григорьев, ЖЭТФ

156,

540

рактеризован кривой типа Гильберта

компарт-

(2019).

мент B, наблюдаемый в методе Hi-C. Такой хрома-

3. B. Mandelbrot, The Fractal Geometry of Nature,

тин, по сути, является сплошной средой для ней-

Freeman, New York (1983).

тронного или рентгеновского излучения, которая, в

свою очередь, ограничена размерами ядра. Подроб-

4. H. О. Peitgen and P. H. Richter, The Beauty of

ное описание трехмерной модели хроматина выхо-

Fractals, Springer, Berlin (1986).

437

С. В. Григорьев, О. Д. Шнырков, К. А. Пшеничный и др.

ЖЭТФ, том 163, вып. 3, 2023

L. S. Liebovitch, Fractals and Chaos Simplified for the

17.

L. A. Mirny, Chromosome Res. 19, 37 (2011).

Life Sciences, Oxford University Press, New York

18.

J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Gros-

(1998).

berg, and K. Kremer, J. Chem. Phys. 134,

204904

I. C. Andronache,

H. Ahammer, H.F. Jelineck,

(2011).

D. Peptenatu, Ana-M. Ciobotaru, C. C. Draghici,

R. D. Pintilii, A.G. Simion, and C. Teodorescu,

19.

J. D. Halverson, J. Smrek, K. Kremer, and A. Y. Gros-

Chaos, Solitons and Fractals 91, 310 (2016).

berg, Rep. Prog. Phys. 77, 022601 (2014).

D. V. Lebedev, M. V. Filatov, A.I. Kuklin, A.K. Isla-

20.

M. V. Imakaev, K. M. Tchourine, S. K. Nechaev, and

mov, E. Kentzinger, R. A. Pantina, B. P. Toperverg,

L. A. Mirny, Soft Matter 11, 665 (2015).

and V. V. Isaev-Ivanov, FEBS Lett. 579, 1465 (2005).

21.

Е. Г. Яшина, С. В. Григорьев, Поверхность. Рентге-

E. G. Iashina,

E. V. Velichko,

M. V. Filatov,

новские, синхротронные и нейтронные исследова-

W. G. Bouwman, C. P. Duif, A. Brulet, and S. V. Gri-

ния 9, 5 (2017).

goriev, Phys. Rev. E 96, 012411 (2017).

22.

J. O. Indekeu and G. Fleerackers, Physica A 261, 294

E. G. Iashina,

M. V. Filatov,

R. A. Pantina,

(1998).

E. Yu. Varfolomeeva, W. G. Bouwman, Ch. P. Duif,

D. Honecker, V. Pipich, and S. V. Grigoriev, J. Appl.

23.

J. P. Richter and R. C. Bell, The Notebooks of

Cryst. 52, 844 (2019).

Leonardo da Vinci, Dover, New York (1970).

10.

S. V. Grigoriev, E. G. Iashina, V. Yu. Bairamukov,

24.

J. E. Martin and A. J. Hurd, J. App. Crystallogr. 20

V. Pipich, A. Radulescu, M. V. Filatov, R. A. Pan-

(2), 61 (1987).

tina, and E. Yu. Varfolomeeva, Phys. Rev. E

102,

25.

J. Teixeira, J. App. Crystallogr. 21, 781 (1988).

032415 (2020).

11.

S. V. Grigoriev, E. G. Iashina, B. Wu, V. Pipich,

26.

D. I. Svergun, M. H.J. Koch, P. A. Timmins, and

R. P. May, Small Angle X-ray and Neutron Scattering

Ch. Lang, A. Radulescu, V. Yu. Bairamukov, M. V. Fi-

latov, R. A. Pantina, and E. Yu. Varfolomeeva, Phys.

from Solutions of Biological Macromolecules, Oxford

University Press, Oxford (2013).

Rev. E 104, 044404 (2021).

12.

E. G. Iashina, E. Yu. Varfolomeeva, R. A. Pantina,

27.

T. Ficker, A. Len, and P. Nemec, J. Phys. D: Appl.

V. Yu. Bairamukov, R. A. Kovalev, N.D. Fedorova,

Phys. 40, 4055 (2007).

V. Pipich, A. Radulescu, and S. V. Grigoriev, Phys.

28.

П. М. Пустовойт, Е. Г. Яшина, К. А. Пшеничный,

Rev. E 104, 064409 (2021).

С. В. Григорьев, Поверхность. Рентгеновские, син-

13.

A. Yu. Grosberg, S.K. Nechaev, and E. I. Shakhno-

хротронные и нейтронные исследования

12,

vich, J. Phys. France 49, 2095 (1988).

(2020).

14.

A. Grosberg, Y. Rabin, S. Havlin, and A. Neer,

29.

Дж. Гудмен, Введение в фурье-оптику, Мир,

Europhys. Lett. 23, 373 (1993).

Москва (1970).

15.

Н. Р. Батуллин, В. С. Фишман, А. А. Хабарова,

30.

А. Н. Матвеев, Оптика, Высшая школа, Москва

М. Ю. Помазной, Т. А. Шнайдер, Д. А. Афонников,

(1985).

О. Л. Серов, Вавиловский журнал генетики и се-

лекции 18 (2), 338 (2014).

31.

А. А. Зинчик, Я. Б. Музыченко, А. В. Смирнов,

С. К. Стафеев,

Научно-технический вестник

16.

A. Zlotina, A. Maslova, N. Kosyakova, A.B.H. Al-

СПбГУ ИТМО 60 (2), 17 (2009).

Rikabi, T. Liehr, and A. Krasikova, Chromosome Res.

27, 253 (2019).

32.

https://github.com/tre3k/fractal

438