ЖЭТФ, 2023, том 163, вып. 3, стр. 439-453

КВАЗИИЗЭНТРОПИЧЕСКОЕ СЖАТИЕ НЕИДЕАЛЬНОЙ

ПЛАЗМЫ ГЕЛИЯ ПРИ ПОСТОЯННОЙ КОНЕЧНОЙ

ТЕМПЕРАТУРЕ 21000 К ПРИ ДАВЛЕНИЯХ ДО 600 ГПа

М. А. Мочалов^a,b, Р. И. Илькаев^a, В. Е. Фортов^c, С. В. Ерунов^a,b, В. А. Аринин^a,

А. О. Бликов^a,b*, В. А. Огородников^a,b, А. В. Рыжков^a, В. А. Комраков^a, А. Е. Ковалев^a,

М. Г. Новиков^a,b, И. П. Максимкин^a, С. А. Финюшин^a, Е. А. Чудаков^a,b, М. И. Лихутов^a,

В. К. Грязнов^d, И. Л. Иосилевский^c, П. Р. Левашов^c, Д. В. Минаков^c, М. А. Парамонов^c

^a Всероссийский научно-исследовательский институт экспериментальной физики

607188, Саров, Нижегородская обл., Россия

^b Нижегородский государственный технический университет им. Р. Е. Алексеева

603950, Нижний Новгород, Россия

^c Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

^d Институт проблем химической физики Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 15 августа 2022 г.,

после переработки 26 сентября 2022 г.

Принята к публикации 26 сентября 2022 г.

Представлены данные по квазиизэнтропической сжимаемости сильно неидеальной плазмы гелия в

области давлений 250-600 ГПа в устройствах цилиндрической геометрии. Измерена температура на

фронте цилиндрической ударной волны в гелии T ≈ 10000 К и скорость полета внутреннего каскада

W ≈ 3.5км/с, в полости которого и достигается максимальная плотность сжатой плазмы. Получены

данные о сжатии неидеальной плазмы гелия до плотности ρ ≈ 3 г/см³ при приблизительно постоян-

ной конечной температуре 21000 К. Траектории движения металлических оболочек, сжимающих плазму,

регистрировались с помощью мощных импульсных источников рентгеновского излучения с граничной

энергией электронов до 60 МэВ. Плотность плазмы гелия определялась по измеренному значению ради-

уса оболочек в момент их ¾остановки¿. Давление сжатой плазмы получено на основе газодинамических

расчетов. Проведены сравнительные теоретические расчеты параметров квазиизэнтропического сжатия

по двум теоретическим моделям: традиционной химической модели плазмы (код SAHA) и в рамках

подхода ab initio квантовой молекулярной динамики (QMD). Аномалия экспериментальных данных в

области давлений теоретически предполагаемого плазменного фазового перехода в гелии не зарегистри-

рована.

DOI: 10.31857/S004445102303015X

дов (ПФП). Следует подчеркнуть, что проблема су-

EDN: QFMCVP

ществования ПФП в неидеальной плазме гелия ин-

тересна не только сама по себе, но и в важном для

1. ВВЕДЕНИЕ

астрофизики аспекте свойств плотных и горячих

Интерес к исследованию свойств неидеальной

смесей гелия с водородом, где к собственно проблеме

плазмы гелия во многом связан с многочислен-

ПФП добавляется проблема специфических особен-

ными предсказаниями существования в плотном и

ностей таких переходов, т. е. возможности расслое-

горячем флюиде гелия аномалий типа необычных

ний на фазы c различающимся химическим соста-

¾плазменных¿ (ionization-driven) фазовых перехо-

вом [1]. Более простая задача расчета параметров

ПФП в плотной горячей смеси гелия с водородом во

^* E-mail: mcleodjr@mail.ru

439

ЖЭТФ, вып. 3

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

всем диапазоне пропорций Не/Н₂, но без учета этих

В последние годы во ВНИИЭФ удалось продви-

особенностей решалась еще в работе [2].

нуться в диапазон мегабарных давлений, используя

Теоретические предсказания свойств плазмен-

метод квазиизэнтропического сжатия газов в двух-

ных фазовых переходов в гелии достаточно мно-

каскадных устройствах цилиндрической и сфери-

гочисленны. До недавнего времени эти предсказа-

ческой геометрий. В экспериментах с гелием при

ния в основном использовали химическую модель

равном начальном давлении газа в обоих каска-

плазмы, называемую также иногда методом мини-

дах около 25 МПа свойства плазмы гелия, сжатой

мизации свободной энергии [3]. При этом предска-

до плотности примерно 8 г/см³ в области давле-

зания ПФП в плазме гелия делались как в варианте

ний до 4800 ГПа, исследовались в работах [15-18].

единого ПФП с одномоментной двукратной иони-

Согласно расчетам, проведенным в рамках хими-

зацией (He ↔ He⁺⁺ + 2e^-) [4], так и в варианте

ческой модели плазмы [3, 19], полученные состоя-

двух последовательных ПФП раздельно на первой

ния сильно неидеальной плазмы гелия при давлении

и второй стадиях ионизации гелия [2, 5-8]. В ра-

P ≈ 4800ГПа характеризуются высокими значения-

ботах [5, 8] показана возможность ионизационного

ми параметра кулоновской неидеальности Г_D ≈ 20 и

фазового перехода первого рода в гелиевой плазме

параметра вырождения электронов n_eλ^3e ≈ 20 (λ_e

при средней плотности ядер 10²²-10²³ см^-3 и тем-

тепловая длина волны де Бройля для электрона).

пературе T ≤ 50000 K. Несколько меньшая темпе-

В экспериментах [18,20] с использованием двух-

ратура фазового перехода c однократной иониза-

каскадной сферической камеры с разделенными по-

цией гелия была предсказана при T ≈ 28500 K в

лостями при соотношении начального давления га-

модели [6]. В работе [9] металлизация гелия пред-

за во внешней и внутренней полостях двухкаскад-

сказана при плотности ρ ≈ 5.3 г/см3. Различны-

ной сферической конструкции 9 : 1 исследованы

ми авторами на основе расчетов зонной структу-

свойства квазиизэнтропически сжатой плазмы ге-

ры были получены значения давления металлиза-

лия при высоких степенях сжатия до 900 раз. Вы-

ции гелия от 300 до 20000 ГПа [10-13]. Современные

бранные значения начальных давлений гелия позво-

расчеты, реализованные в рамках строгого подхода

лили обеспечить размер сжатой полости, доступный

ab initio (DFT/MD) [14], предсказывают металлиза-

для его регистрации на рентгенографическом обору-

цию в плотном жидком гелии в диапазоне давлений

довании ВНИИЭФ, и реализовать высокую степень

P = 10000-20000ГПа.

сжатия плазмы. В эксперименте [21] с использова-

Возвращаясь к обзору предсказаний ПФП в рам-

нием сферической двухкаскадной камеры и заряда

ках химической модели плазмы, отметим прежде

ВВ с массой M ≈ 85 кг в тротиловом эквивален-

всего работы [5, 7, 8], где с использованием в рас-

те неидеальная плазма гелия сжата до плотности

четах метода суммарного химического потенциала

ρ ≈ 9г/см³ давлением P ≈ 10000ГПа, а в экспери-

предсказан двухстадийный сценарий ПФП, состоя-

менте [22] до плотности ρ ≈ 13 г/см³ давлением

щий из двух фазовых переходов, начинающихся со-

P ≈ 16700ГПа.

ответственно из двух тройных точек с параметрами

Анализ опубликованных данных показывает, что

T₁ ≈ 1000 К и P₁ ≈ 200 ГПа (ПФП-1) и T₂ ≈ 4000 К

все результаты со сферическими устройствами из

и P₂ ≈ 3000ГПа (ПФП-2). Оба перехода заканчива-

работ [15-18,20-22] расположены на P -T -диаграмме

ются критическими точками C₁ и C₂ с параметрами

гелия в области однократно ионизованной плазмы

TC1 ≈ 35000 К, PC1 ≈ 660 ГПа и ρC1 ≈ 2.13 г/см³

выше критической точки ПФП-1 [7], а результаты

(ПФП-1) и TC2

≈ 120000 K, PC2

≈ 10000 ГПа и

опытов c цилиндрическими конструкциями с гели-

ρC2 ≈ 10 г/см³ (ПФП-2). Авторы работы [2] рассчи-

ем из [23] расположены ниже P(T)-границы ПФП-1.

тали в гелии параметры ПФП с однократной иониза-

Таким образом, до настоящего времени области со-

цией гелия и относительно высокими параметрами

стояний гелия, где предсказываются плазменные

участка P (T )-границы ПФП примерно между на-

фазовые переходы ПФП-1 и ПФП-2 [7], оставались

чальной точкой (T ≈ 4000 K, P ≈ 550 ГПа) и кри-

недоступными для исследователей.

тической точкой (T_C ≈ 20000 K, P_C ≈ 800 ГПа). Так

В настоящей работе представлены конструкции

же далеко находится гипотетическая граница еди-

новых двухкаскадных цилиндрических устройств,

ного ПФП с двукратной ионизацией, предсказанная

которые позволили при постоянной конечной тем-

в теоретической модели работы [4]. Согласно [4], эта

пературе T

≈ 21000 К исследовать свойства ква-

граница приближенно соответствует участку изохо-

зиизэнтропически сжатого гелия в диапазоне дав-

ры ρ ≈ 10 г/см³ c температурой от T ≈ 20000 K до

лений 200-600 ГПа, который включает в себя и

T ≈ 100000K.

область теоретически предполагаемого [7] ПФП-1

440

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

(P ≈ 400 ГПа при T ≈ 20500 К). Полученные данные

ции трех импульсов рентгеновского излучения дли-

позволили проверить гипотезу о возможных измене-

тельностью 150-180 нс. Это позволяет в эксперимен-

ниях в сжимаемости плазмы гелия в области гипо-

те зарегистрировать одновременно до девяти фаз

тетического плазменного перехода ПФП-1.

сжатия плазмы. В опытах использована оптико-

электронная система детектирования, которая акти-

вируется синхронно с импульсами бетатрона. В ка-

2. ПОСТАНОВКА ЭКСПЕРИМЕНТА

честве преобразователей рентгеновского излучения

Для исследования сжимаемости гелия в экспери-

в видимое использованы монокристаллы йодистого

ментах настоящей работы использованы конструк-

натрия и силикат лютеция. Для устранения влия-

ции цилиндрической геометрии [24, 25], в том числе

ния рассеянного излучения на высокочувствитель-

со стержнем из стали в центре, позволяющие реа-

ные детекторы размер поля регистрации в каждой

лизовать равномерный профиль давления по ради-

из проекций ограничен свинцовыми коллиматора-

усу в плазме сжатого вещества. Сжатие образую-

ми. Для защиты бетатронов и оптико-электронных

щейся плазмы в таких устройствах осуществляет-

регистраторов рентгеновского излучения примене-

ся системой ударных волн (УВ), циркулирующих в

ны алюминиевые конусы.

ее объеме, и стальных оболочек, сходящихся к цен-

При сохранении массы сжатого вещества его

тру под действием продуктов взрыва (ПВ) мощно-

плотность вычисляли из выражения

го конденсированного взрывчатого вещества (ВВ).

ρ = ρ0 (R₀/R_min)n ,

Этот процесс получил название квазиизэнтропиче-

где ρ₀

начальная плотность газа, R₀ и R_min

ского, так как после прохождения первой УВ даль-

внутренние радиусы оболочки в исходном состоянии

нейшее сжатие плазмы происходит при существенно

и в момент ее ¾остановки¿соответственно,n = 2 для

меньшем нагреве, чем в случае однократного сжа-

цилиндрической геометрии. Давление сжатой плаз-

тия, и при более длительном удержании вещества в

мы гелия получено на основе газодинамических рас-

сжатом состоянии. Целью такого эксперимента яв-

четов, учитывающих реальные характеристики экс-

ляется регистрация R(t)-траектории движения обо-

периментальных устройств.

лочек нагружающего устройства и определение раз-

Характеристики устройств и условия проведения

мера внутреннего каскада в момент его ¾останов-

опытов приведены в табл. 1. Геометрия эксперимен-

ки¿, когда достигается максимальное сжатие иссле-

тальных устройств показана на рис. 1.

дуемого вещества. Особенность конструкций [24,25]

Заполнение камеры гелием производилось от

состоит в возможности локализации металлогазовой

термокомпрессора. Величина давления в процес-

смеси, возникающей при выбросе частиц металличе-

се заполнения измерялась датчиком с классом

ской пыли [26,27], что не позволяет ей проникать во

точности

0.25. Температура контролировалась

внутреннюю полость, где измеряется сжимаемость

хромель-алюмелевой термопарой, расположенной

исследуемой плазмы. Для снижения возмущений от

внутри трубопровода, использованного для на-

системы инициирования в таких устройствах меж-

пуска газов. Давление газа Не1 и Не2 в полостях

ду ВВ и цилиндрическим устройством использовали

оболочек

было одинаковым. Окончатель-

прокладку из оргстекла с электроконтактными дат-

но плотность гелия вычислялась с учетом его

чиками на ее границах для контроля за движением

сжимаемости на основании известных табличных

УВ.

данных [29].

Схема экспериментов неоднократно приводилась

В данной работе геометрия экспериментальных

в наших работах, см, например, [24, 25]. Для ре-

устройств выбиралась таким образом, чтобы полу-

гистрации положения оболочек, сжимающих иссле-

чить равномерный профиль давления по радиусу,

дуемое вещество, использовано жесткое рентгенов-

P (R), при максимальном сжатии плазмы гелия. Для

ское излучение трех бетатронов БИМ234.3000 [28]

снижения кумуляции энергии в эксперименте №1 в

с граничной энергией электронов 60 МэВ, позво-

конструкции работы [25] вдоль оси установлен ме-

ляющих просвечивать объекты с массовой толщи-

таллический цилиндрический стержень. При нали-

ной до 230 г/см², что примерно эквивалентно тол-

чии стержня отраженная УВ формируется на грани-

щине 20 см свинца. Экспериментальное устройство

це R^∗, где R^∗ радиус стержня. Тем самым умень-

с гелием размещалось перед бетонным сооружени-

шается амплитуда отраженной УВ, снижается гео-

ем, в котором смонтированы бетатроны. Особен-

метрическая кумуляция энергии и выравнивается

ностью бетатронов ВНИИЭФ является их возмож-

распределение давления по радиусу полости со сжа-

ность работать в режиме последовательной генера-

той плазмой. Металлический стержень с начальным

441

10*

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

Таблица 1. Характеристики устройств и условия проведения опытов. Здесь M_expl масса ВВ, T0 температура газа,

давление, ρ0 плотность

№ опыта R_орг, мм M_expl, кг R^∗, см r₀₂, см R₀₂, см T₀, ^◦C P₀, атм ρ₀, г/см³

100

0.45

4.1

4.5

25.6

255.7

0.0363

122.5

3.0

3.4

19.6

245.5

0.0361

100

3.0

3.4

6.3

236.6

0.0359

100

3.4

3.78

22.25

243.6

0.0356

93.5

5.0

5.4

10.3

255

0.0378

Примечание. Здесь прочерк означает отсутствие стального стержня в конструкциях. Масса ВВ указана в

тротиловом эквиваленте. В опыте №4 внутренняя оболочка изготовлена из сплава ВНЖ-95 (95% вольфрама, 3.5%

никеля и 1.5% железа).

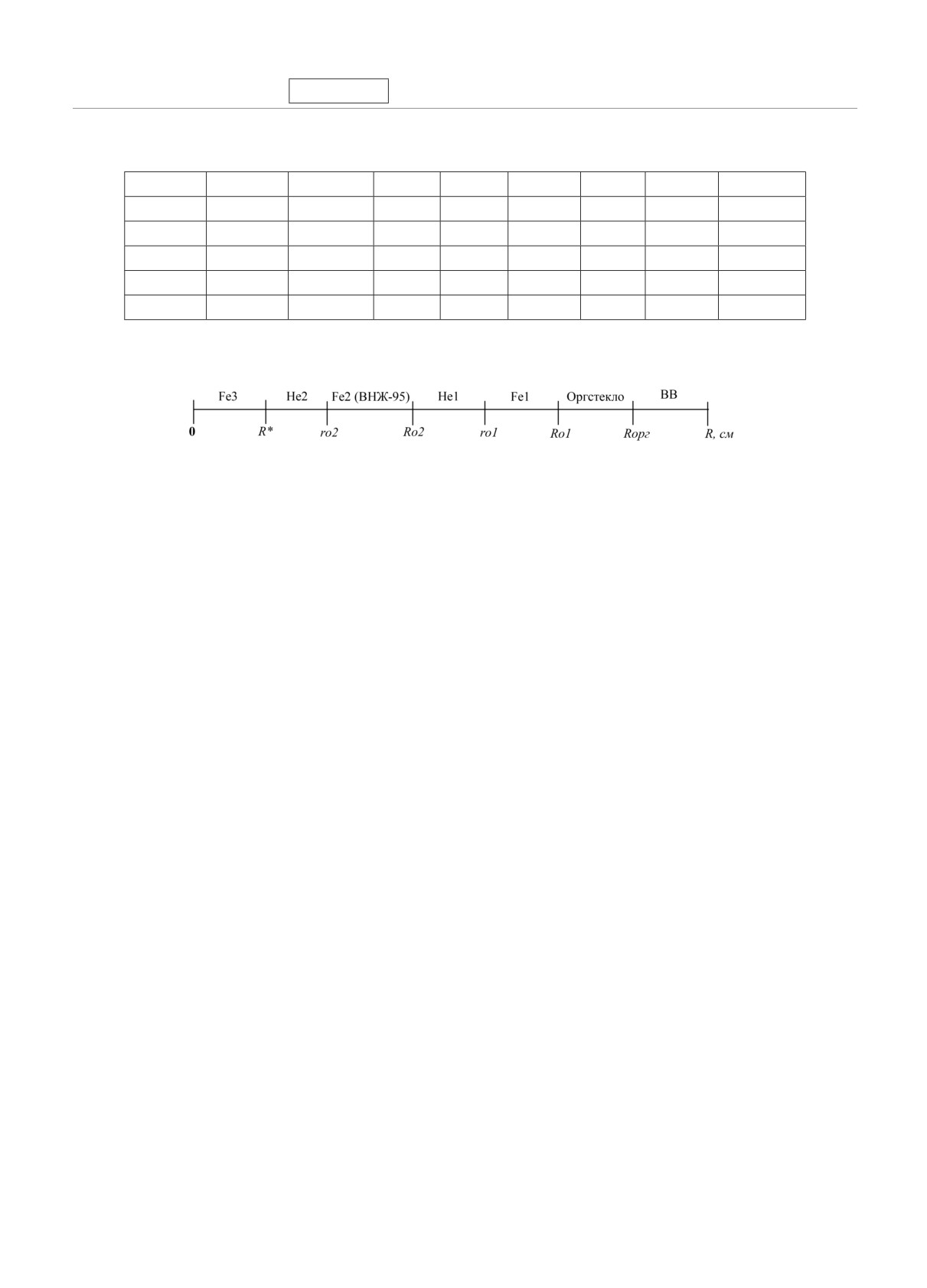
Рис. 1. Геометрия цилиндрического экспериментального устройства в экспериментах с гелием. Здесь R^∗ радиус сталь-

ного стержня, r01 = 7.1 см и R01 = 7.5 см внутренний и наружный радиусы оболочки первого каскада (Fe1) соответ-

ственно, r02 и R02 радиусы оболочки второго каскада (Fe2), Rорг внешний радиус оболочки из оргстекла, 1 и 2

состояния гелия в наружной и внутренней полостях устройства соответственно

радиусом R^∗ = 0.45 см изготовлен из стали. В после-

движений сплошной среды, тестированной по экс-

дующих экспериментах №2, №3, №4 и №5 стержень

периментальным данным, полученным в России и

отсутствовал, а задача создания равномерного про-

за рубежом. В расчетах устройств гелий описывали

филя давлений в сжатой плазме гелия решалась пу-

табличным уравнением состояния (УРС) Хрустале-

тем тщательного расчетного выбора геометрии экс-

ва из библиотеки обменного фонда ВНИИЭФ.

периментальных устройств.

Для всех областей железа использовали

Впервые в практике подобных исследований в

• УРС ОСА

[32] с откольной прочностью

эксперименте №5 использована конструкция из ра-

σ_x = -4 ГПа (хрупкий откол);

боты [25], внутри которой (рис.2) разместили опто-

волокно диаметром 400 мкм (1 ) для регистрации из-

• дислокационную модель [33] с параметрами

лучения с фронта цилиндрической УВ, PDV-датчик

C_t = 2.235, t₀ = 0.4, τ₀ = 1.9, a = 30000, H = 0.

(2 ) для измерения скорости движения границы

Однофазное УРС железа [32] хорошо описывает

внутренней оболочки цилиндрического устройства и

ударную адиабату, но сглаживает фазовый α - ε-пе-

минизеркала (3 ) диаметром 5 мм для передачи ин-

реход первого рода при P

≈ 13 ГПа. Расчеты с

формации в каждом канале регистрации.

учетом фазового перехода в железе по УРС из ра-

боты [34] не привели к существенному изменению

3. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

результатов. Область ВВ - ПВ описывали упрощен-

Опыт №1. В опыте зарегистрированы 9 фаз

ным уравнением состояния в форме Зубарева [35].

сжатия гелия. Типичные изображения сжатых по-

Сравнение экспериментальных данных, получен-

лостей в четыре момента времени приведены на

ных в опыте №1, и R(t)-траекторий, рассчитанных

рис. 3. Там же показаны результаты трассировки

с использованием для гелия УРС ВНИИЭФ, пока-

сжатой полости с гелием. Обработка эксперимен-

зано на рис.4a. Фрагмент R(t)-диаграмм вблизи мо-

тальных рентгенограмм выполнена функциональ-

мента максимального сжатия приведен на рис. 4b, на

ным методом из работы [30]. Здесь и далее времена

котором, как и ранее [36], показана также структу-

отсчитываются от подрыва детонаторов нагружаю-

ра двадцати УВ, циркулирующих в плазме гелия и

щего устройства.

стальном стержне.

Расчет характеристик экспериментальных

Подбор параметров расчетной схемы экспери-

устройств выполнен по одномерной газодина-

ментальной конструкции для этого и последующих

мической программе

[31], предназначенной для

экспериментов проводился по результатам тестиро-

численного моделирования неустановившихся

вания движения УВ с помощью электроконтакт-

442

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

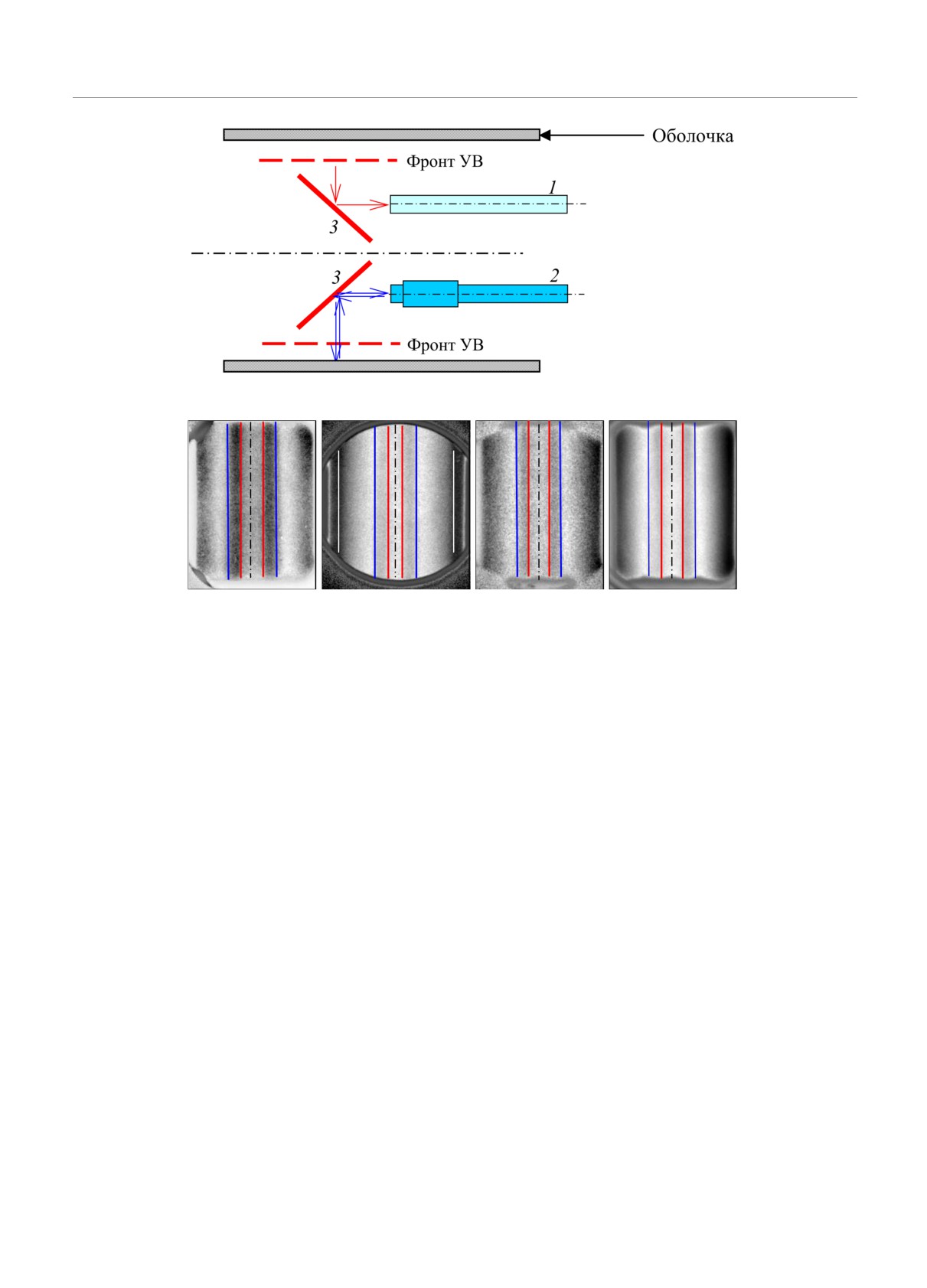
Рис. 2. Схема регистрации свечения фронта УВ и скорости движения границы оболочки:

оптоволокно; 2 PDV-датчик; 3 зеркала

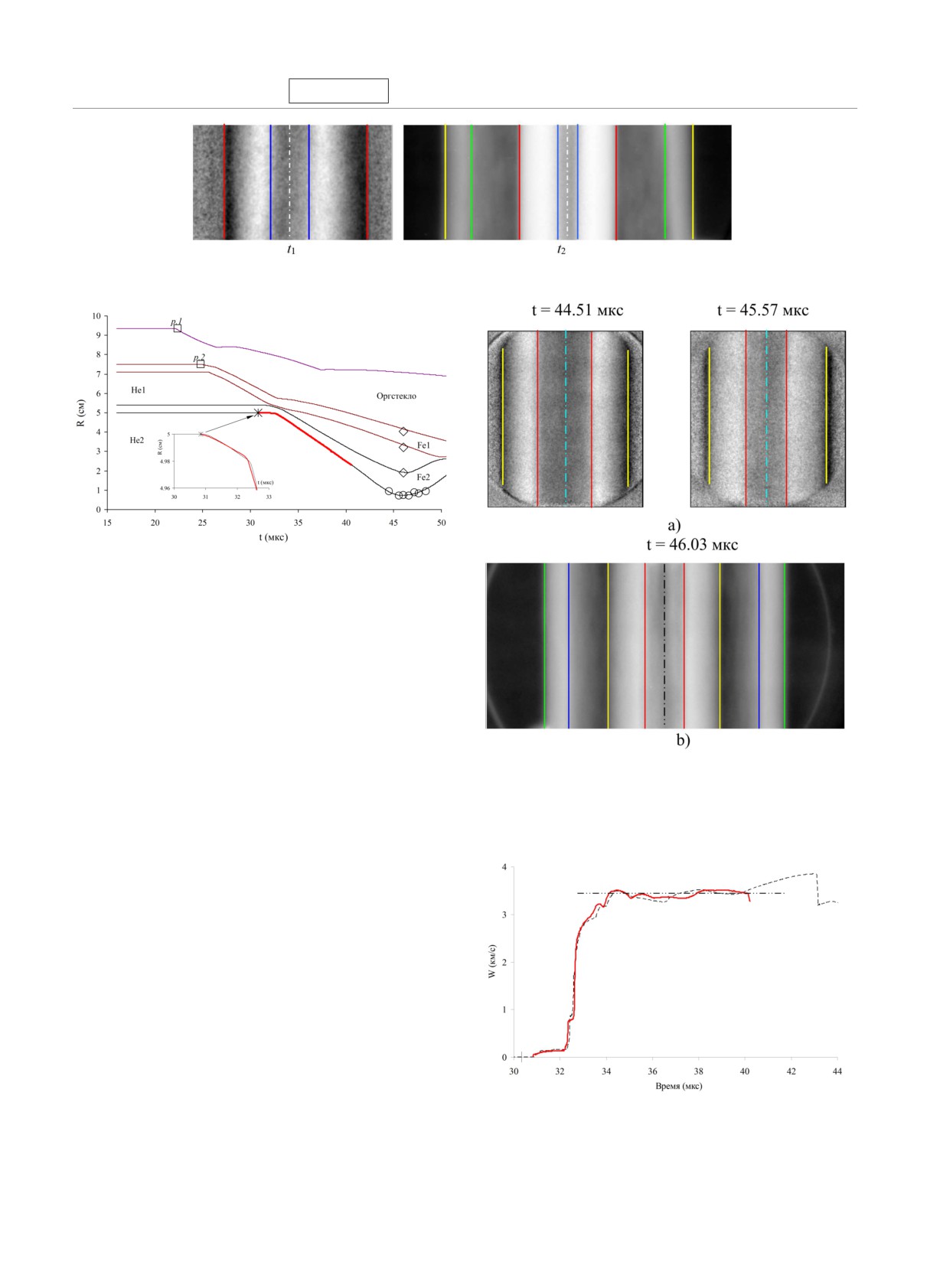
Рис. 3. (В цвете онлайн) Типичные рентгенограммы и результаты трассировки оболочек с плазмой гелия в экспери-

менте №1: красные линии границы стержня (сталь); синие внутренняя граница оболочки второго каскада (ВГО-2);

белые наружная граница оболочки второго каскада (НГО-2)

ных датчиков, расположенных на границах оболоч-

ные данные можно отнести к результатам измере-

ки из оргстекла (точки в виде светлых квадрати-

ния квазиизэнтропической сжимаемости.

ков). На рис. 4a видно, что расчет с использовани-

Для всех девяти фаз сжатия, зарегистрирован-

ем выбранной тактики счета хорошо описывает кон-

трольные точки (p. 1 и p. 2) движения УВ по оболоч-

ных в опыте, были выполнены расчеты термодина-

мических параметров P (R), ρ(R) и T (R) в плазме

ке из оргстекла и стальной оболочке первого каска-

гелия, которые приведены в табл.2.

да Fe1, а также измеренные рентгенографическим

методом значения радиусов границ внешней и внут-

Из анализа полученных данных следует, что при-

ренней оболочек второго каскада Fe2 эксперимен-

мерно с четвертой фазы сжатия распределение дав-

тального устройства. Данные расчета воспроизво-

ления в плазме гелия по радиусу становится прак-

дят также динамику границы оболочки стального

тически равномерным вплоть до последней (9) фа-

стержня Fe3. На рис.4b видно, что первая УВ в мо-

зы рентгенографирования. Рассчитанные профили

мент времени F достигает центра устройства и от-

давления P (R) для фаз рентгенографирования 4-9

ражается, а в момент K контакта отраженной УВ

приведены на рис. 5.

с внутренней границей оболочки Fe2 плазма оказы-

вается уже дважды (квазиизэнтропически) сжатой.

Опыт №2. В данном эксперименте использовано

С учетом дополнительного сжатия плазмы оболоч-

двухкаскадное цилиндрическое устройство без цен-

кой, кумуляции термодинамических параметров за

трального стержня. Сравнение экспериментальных

фронтом сходящейся УВ и ее поглощения последую-

и рассчитанных R(t)-данных для этого эксперимен-

щими волнами на этапе движения к центру устрой-

та показано на рис. 6, а профиль давления при мак-

ства, в некоторый момент времени между F и K

симальном сжатии плазмы гелия на рис. 7. В экс-

начинается квазиизэнтропическое сжатие плазмы.

перименте №2 плазма гелия была сжата до плот-

Поэтому, начиная с состояния K и во все последую-

ности ρ = 2.30 г/см³ давлением P = 376 ГПа при

щие моменты времени, получаемые эксперименталь-

температуре T = 19700 К.

443

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

Таблица 2. Параметры плазмы гелия в различных фазах сжатия в эксперименте №1

№ фазы t, мкс R_env , см R_bar , см P, ГПа ρ_exp, г/см³ ρ_calc, г/см³ T, K

47.34

1.077

0.437

23.08

0.62

0.66

7864

48.00

0.866

0.419

49.61

1.05

0.877

8078

48.43

0.743

0.379

127

1.48

1.390

15207

48.81

0.696

0.376

218

1.76

1.744

19220

49.20

0.673

0.361

256

1.87

1.880

20039

49.58

0.718

0.371

245

1.59

1.868

18746

49.94

0.729

0.375

216.5

1.54

1.778

17620

50.29

0.731

0.360

167

1.49

1.586

16102

50.59

0.81

0.388

138

1.19

1.466

14839

Примечание. Renv и Rbar внутренний радиус оболочки второго каскада и радиус стержня соответственно

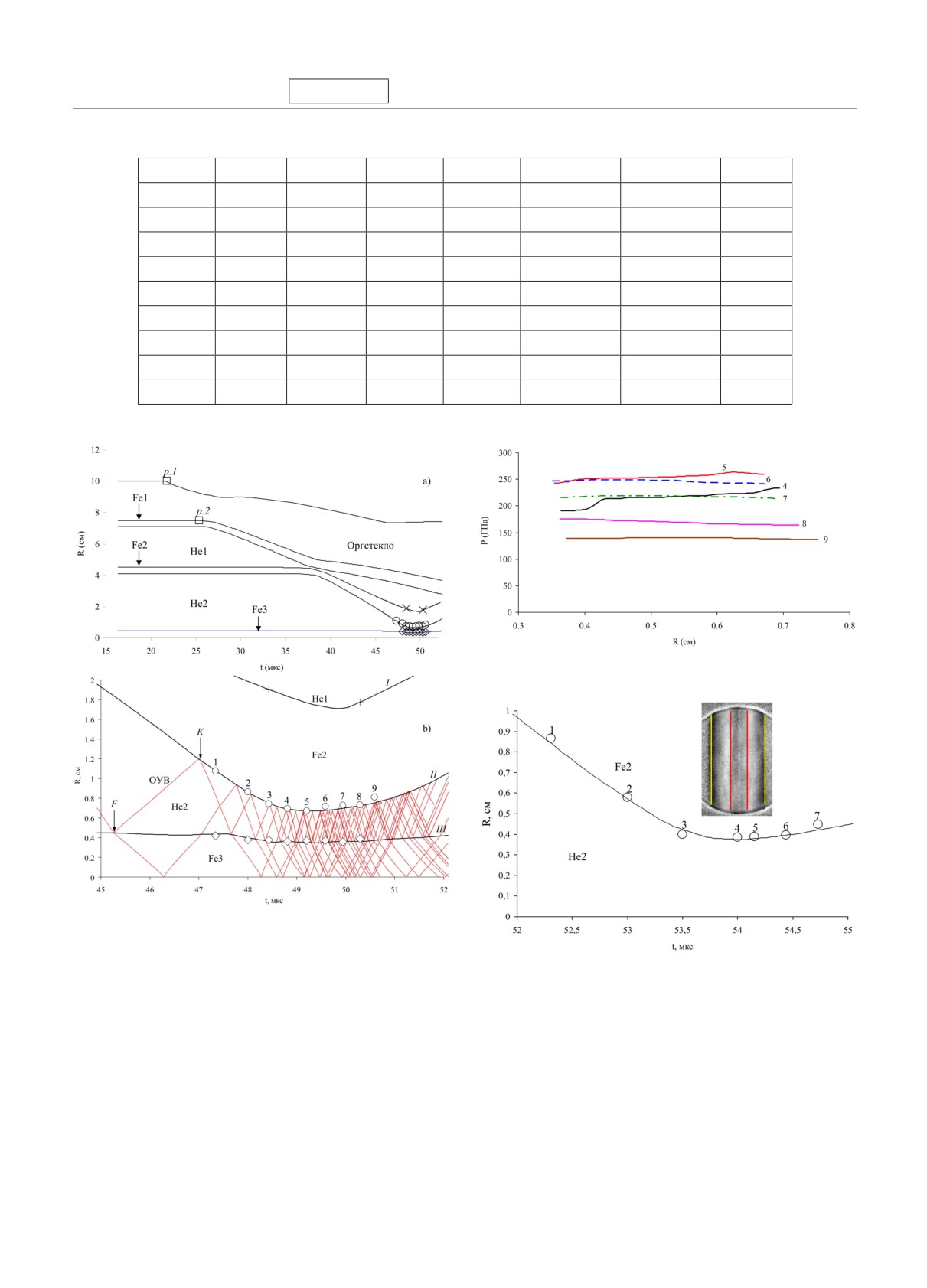
Рис. 5. Профили давления (расчет) в плазме гелия для

шести фаз 4-9 рентгенографирования в опыте №1

Рис. 4. a) Экспериментальные данные и рассчитанные

R(t)-диаграммы: □ электроконтактная методика; ⋄, ◦,

+, × данные рентгенографического эксперимента; b)

Рис. 6. (В цвете онлайн) Сравнение экспериментальных и

фрагмент R(t)-диаграмм вблизи момента максимального

рассчитанных R(t)-данных в опыте №2. Эксперимент: ○

сжатия: цифры 1-9 фазы сжатия, расчеты НГО-2 (I ),

движение ВГО-2. Сплошная линия

расчет. Показаны

ВГО-2 (II ) и наружней границы стального стержня Fe3

фрагмент рентгенограммы на момент времени t = 54 мкс

(III); F

фокусировка УВ; K момент прихода отра-

и результаты функциональной обработки: желтые линии

женной УВ (ОУВ) на ВГО-2

НГО-2; красные ВГО-2

Опыт №3. В данном эксперименте использова-

но то же двухкаскадное цилиндрическое устройство,

но на рис. 8a, а вблизи максимального сжатия на

как и в опыте №2, но с большей массой ВВ (см.

рис. 8b. В эксперименте №3 плазма гелия была сжата

табл. 1). Сравнение экспериментальных и рассчи-

до плотности ρ = 2.44 г/см³ давлением P = 476 ГПа

танных R(t)-данных для этого эксперимента показа-

при температуре T = 22300 К.

444

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

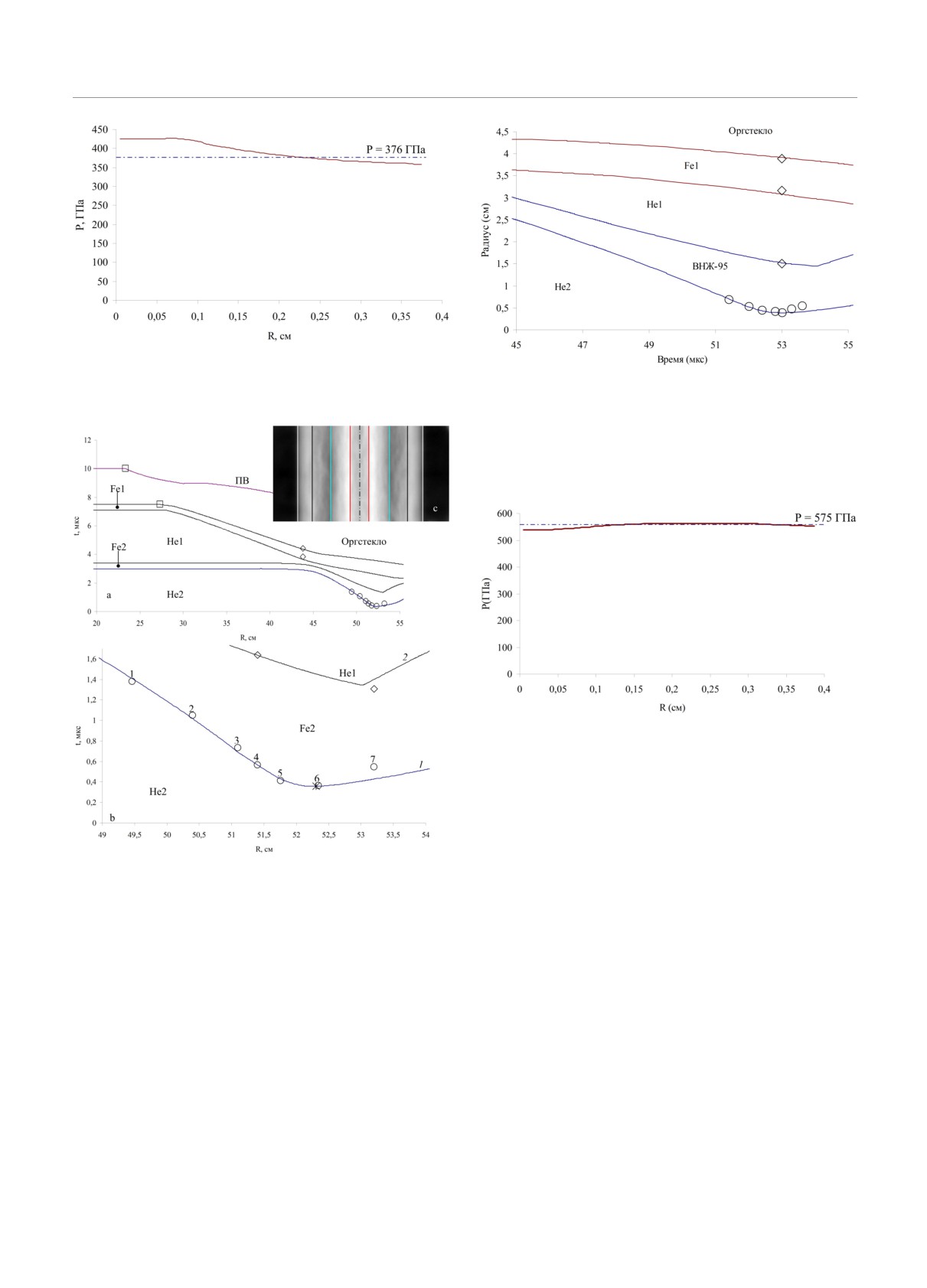
Рис. 7. Профиль давления в плазме гелия при макси-

мальном сжатии в опыте №2: сплошная линия расчет;

штрихпунктирная линия усредненное по массе значение

Рис. 9. Сравнение R(t)-данных, полученных в эксперимен-

давления при максимальном сжатии

те №4, с результатами расчета. Эксперимент: ◦ движе-

⋄ результаты для НГО-2 (ВНЖ-

ние ВГО-2 (ВНЖ-95);

95), а также для НГО-1 и ВГО-1 (Fe1). Сплошные линии

расчет

Рис. 10. Профиль давления при максимальном сжатии в

сжатой плазме гелия в эксперименте №4: сплошная ли-

ния расчет; штрихпунктирная линия усредненное по

массе значение давления при максимальном сжатии

устройства позволил получить практически равно-

мерный профиль давления в сжатой плазме гелия.

В эксперименте №4 плазма гелия была сжата до

Рис. 8. a) Экспериментальные данные в опыте №3 и рас-

плотности ρ = 2.87 г/см³ давлением P = 577 ГПа

считанные R(t)-диаграммы: □ электроконтактная ме-

при температуре T = 20842 К. На рис. 11 приведе-

тодика; ⋄, ◦ рентгенографическая методика; b) фраг-

ны фрагменты рентгенограмм опыта №4 в моменты

мент R(t)-диаграмм вблизи момента максимального сжа-

времени t₁ = 52.82 мкс и t₂ = 53.01 мкс с результата-

тия; c) фрагмент рентгенограммы на момент времени

ми трассировки по методике из работы [30]. Отме-

t = 51.4мкс. Сплошные линии расчет: 1 НГО-2; 2

тим, что на момент времени t₂ приведен фрагмент

ВГО-2; ∗ момент максимального сжатия

панорамной рентгенограммы, полученной с приме-

Опыт №4. Сравнение экспериментальных R(t)-

нением пакета из десяти сложенных вместе фото-

данных с результатами расчета показано на рис. 9.

хромных экранов, что позволило зарегистрировать

В расчете для ВНЖ-95 использовали УРС в фор-

положение всех границ экспериментального устрой-

ме Ми - Грюнайзена, построенное по данным рабо-

ства.

ты [37]. Распределение давления по радиусу в сжа-

Опыт

№5. В данном экспериментальном

той плазме гелия показано на рис.10. Видно, что

устройстве кроме сжимаемости регистрировали

тщательный выбор параметров экспериментального

скорость движения границы оболочки второго

445

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

Рис. 11. (В цвете онлайн) Фрагменты рентгенограмм в эксперименте №4 в моменты времени t1 и t2. Оболочка из сплава

ВНЖ-95: синие линии ВГО-2; красные НГО-2. Оболочка Fe1: зеленые ВГО-1; желтые НГО-1

Рис. 12. (В цвете онлайн) Сравнение R(t)-данных, полу-

ченных в эксперименте №5, с результатами расчета. Экс-

перимент: □ данные с электроконтактных датчиков; ре-

зультаты рентгенографирования: ◦ ВГО-2; ⋄ НГО-2,

НГО-1 и ВГО-1; данные PDV-датчика: красная линия

экспериментальная R(t)-траектория, ∗

время выхода

УВ на границу R = 5 см. Сплошные черные линии рас-

чет

каскада PDV-датчиком, а также яркостную темпе-

ратуру гелиевой плазмы на фронте первой УВ.

Рис. 13. (В цвете онлайн) Экспериментальные рентгено-

Сравнение экспериментальных R(t)-данных с ре-

граммы: a) начальная фаза движения; b) панорамное изоб-

зультатами расчета для этого устройства приведено

ражение полостей устройства при максимальном сжатии.

на рис. 12.

Цветными линиями обозначены границы полостей: крас-

На рис.12 видно, что расчет с использованием

ные линии ВГО-2; желтые НГО-2; синие ВГО-1;

выбранной тактики счета хорошо описывает кон-

зеленые НГО-1

трольные точки (p. 1 и p. 2) движения УВ по орг-

стеклу и стальной оболочке первого каскада Fe1,

а также измеренные рентгенографическим мето-

дом траектории НГО-2 и ВГО-2 экспериментально-

го устройства. Анализ данных показывает, что в экс-

перименте №5 плазма гелия была сжата до плот-

ности ρ_exp

= 1.65 г/см³ давлением P

= 240 ГПа

при температуре T

= 22388 К. Отличие экспери-

ментальной плотности от рассчитанного значения

(ρcalc = 1.75 г/см3) составляет 6.7%. Ряд экспери-

ментальных рентгенограмм, полученных в данном

опыте, показан на рис. 13.

Рис. 14. Cкорость движения внутренней границы оболочки

Экспериментальная диаграмма скорости W (t)

экспериментального устройства: сплошная линия экспе-

вместе с рассчитанной приведены на рис. 14, они

риментальная зависимость; штриховая расчет; штрих-

хорошо согласуются друг с другом. Средняя

пунктирная среднее значение W (t) = 3.45 км/с

446

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

скорость движения оболочки Fe2 в интервале

Экспериментальные значения текущих темпера-

времен dt

34-40 мкс оценивается значением

тур на фронте УВ в зависимости от времени дви-

W = 3.45км/с.

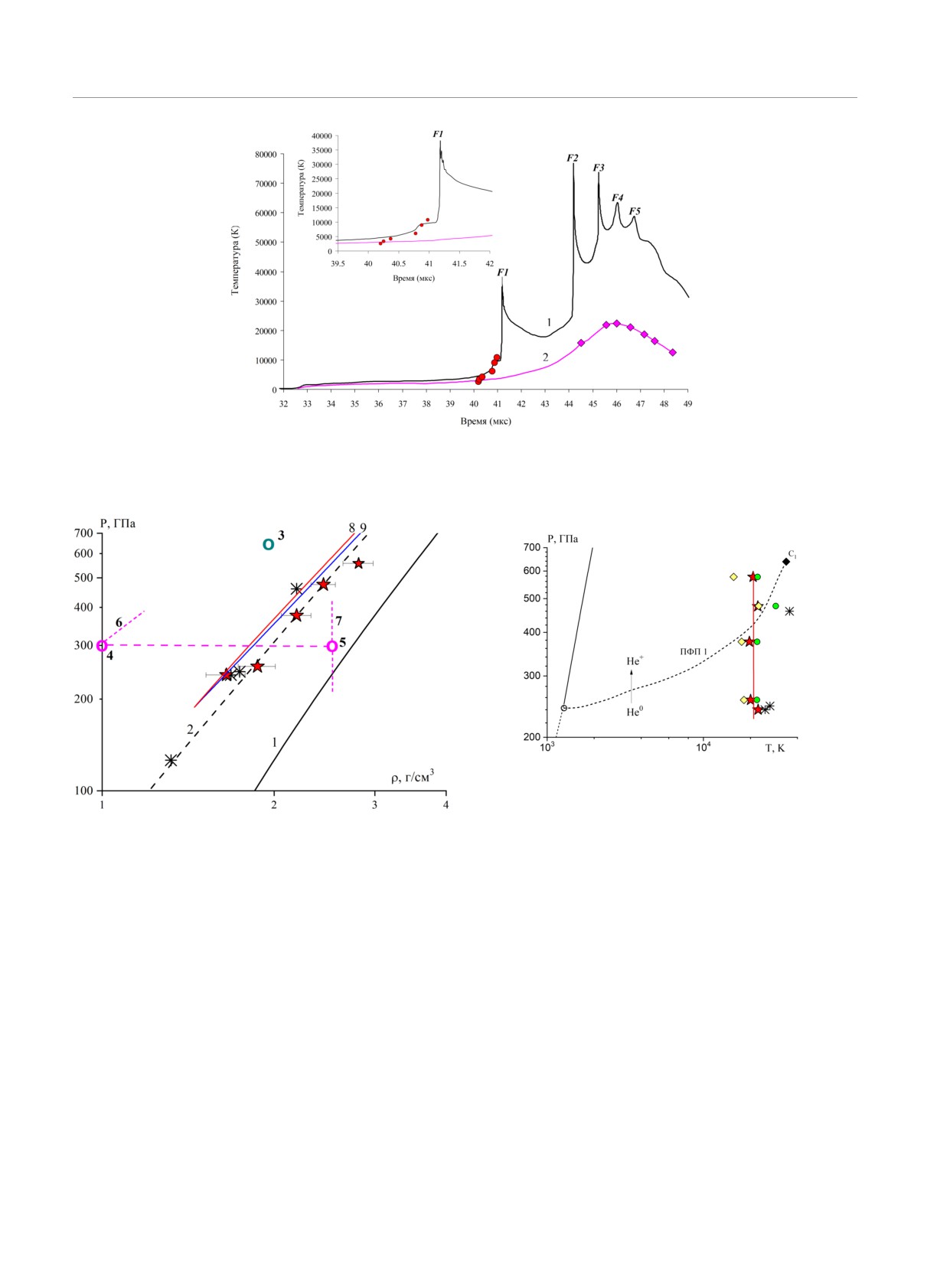
жения УВ SW⁺ показаны на рис. 17 в сравнении с

результатами расчета (кривая 1). Также на рис. 17

В эксперименте №5 в качестве регистратора из-

лучения с фронта цилиндрической УВ использован

приведена рассчитанная зависимость усредненных

по массе температур (кривая 2), на которую нанесе-

фотодиод ФД254 в комплексе с высокоскоростным

осциллографом. Излучение регистрировалось в по-

ны значения температур в плазме гелия в моменты

лосе пропускания фотодиода Δλ = 334-1140 нм при

рентгенографирования.

средней длине волны λ = 775 нм. Предварительно

измерительная линия была откалибрована с исполь-

Пиковые значения температур на фронте УВ в

зованием источника абсолютно черного тела с тем-

моменты F1 - F5 связаны с фокусировкой УВ на оси

пературой T = 1770 К. Типичная осциллограмма из-

экспериментального устройства, рассчитанная цир-

лучения фронта УВ, зарегистрированная в экспери-

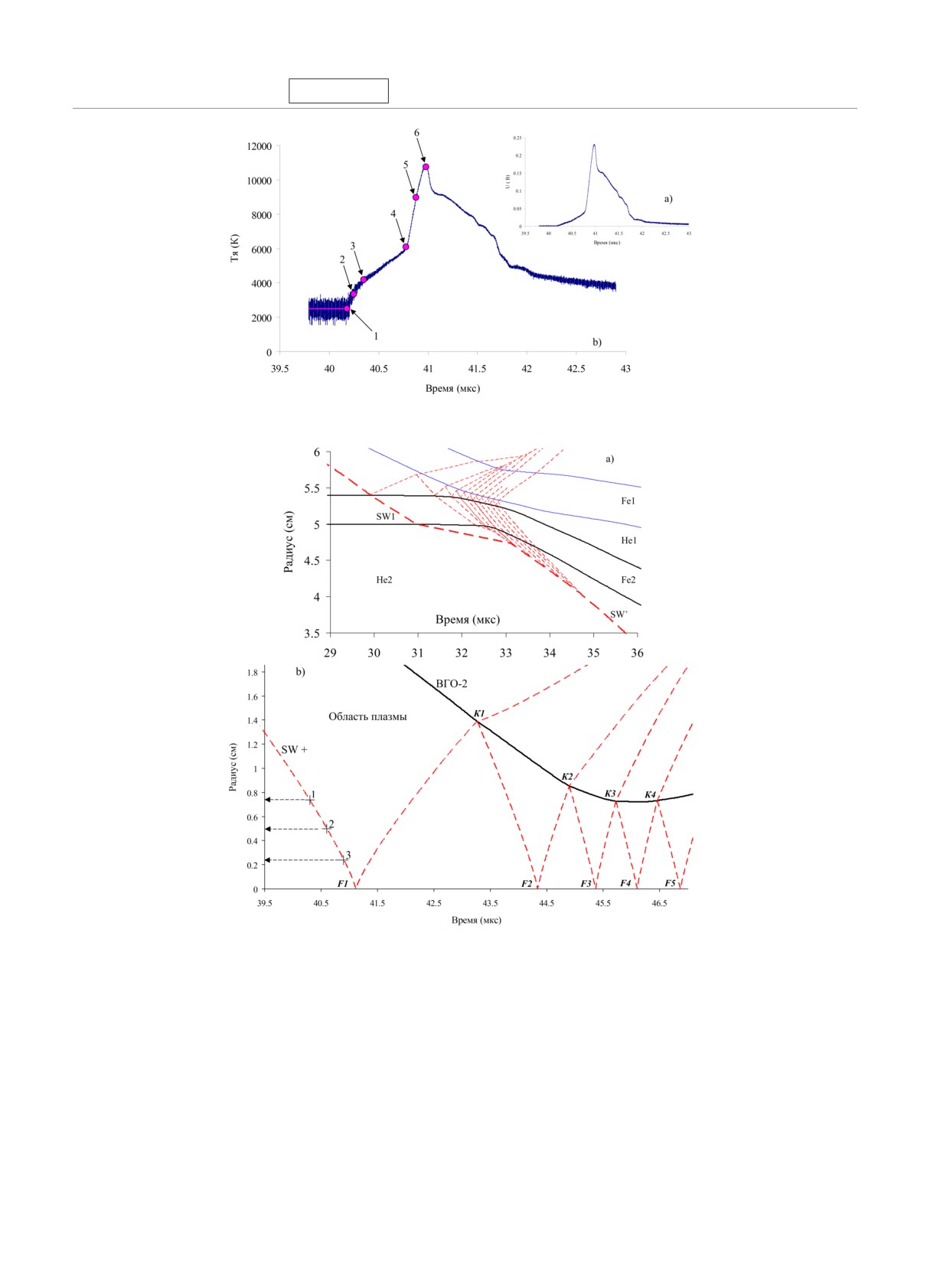
куляция которых показана на рис. 16b. Как видно на

менте, приведена на рис. 15a, по которой, с учетом

этом рисунке, в момент времени F1 суммарная УВ

калибровочных данных, рассчитана зависимость яр-

SW⁺ достигает центра устройства. В результате по-

костной температуры на фронте УВ от времени в

следующих отражений УВ SW⁺ от границы сходя-

плазме гелия (рис. 15b). Значения текущих темпера-

щейся к центру оболочки Fe2 в состояниях К1 - К4

тур на фронте УВ в плазме гелия в наиболее харак-

происходит кумуляция энергии в этом и последу-

терных точках, указанных стрелками, приведены в

ющих состояниях F2 - F5, сопровождающаяся рез-

подписях к рисунку.

ким изменением температуры плазмы гелия на оси

устройства T ≈ 44000, 78000, 73000, 63000, 58000 К.

После достижения максимального значения в состо-

4. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ ДАННЫХ

янии F2 рост пиковых значений температур замед-

ляется. В той фазе движения, пока УВ не достигнет

Как следует из рис.15b, при чувствительности

центра устройства, реализуется процесс УВ-сжатия

нашей методики T_min = 2500 К регистрация темпе-

и, как видно на рис. 17, температуры на фронте УВ

ратуры фронта УВ начинается в момент времени

и усредненные по массе практически совпадают до

t₀ ≈ 40.2 мкс (точка 1). За время dt ≈ 0.6 мкс темпе-

t ≈ 40мкс.

ратура возрастает до T ≈ 6000 К (т. 4), после чего в

течение короткого времени dt ≈ 0.2 мкс происходят

рост температуры до T ≈ 11000 К (т. 6) и последую-

Как было показано выше на рис.14, осцил-

щий спад. Проведенный анализ полученных данных

лограмма с PDV-датчика демонстрирует практи-

показал, что этот спад температуры связан со специ-

чески постоянную скорость движения внутренней

фикой конструкции канала регистрации излучения

границы оболочки второго каскада (ВГО-2) до

с фронта УВ.

t ≈ 40 мкс. Это позволяет сделать вывод, что до

≈ 4000 К не происходит образования плотного

Рассмотрим процесс формирования мощной пер-

слоя плазмы, способного экранировать зондирую-

вой УВ и ее циркуляции в области исследуемо-

щее лазерное излучение, используемое в гетеродин-

го вещества, показанные на рис.16. Как видно на

интерферометре [38].

рис. 16a, после ряда отражений первой УВ SW1 в

слое гелия Не1 в полости Не2 формируется сум-

марная УВ SW⁺, которая в момент начала свече-

Результаты по сжимаемости плазмы гелия, по-

ния фронта t₁ ≈ 40.2 мкс (т. 1) находится на радиусе

лученные в пяти экспериментах настоящей работы,

R ≈ 8мм (рис.16b). При дальнейшем движении УВ

приведены в P (ρ)-координатах на рис. 18 и демон-

SW⁺ к оси устройства амплитуда свечения фрон-

стрируют хорошее согласие в исследованной обла-

та УВ нарастает и к моменту времени t₂ ≈ 41 мкс

сти давлений с данными работы [23]. Там же при-

(т. 2) достигает своего максимального значения. К

ведены расчеты ¾холодной¿ (T = 0 К) адиабаты и

этому же времени УВ SW⁺ физически достигает от-

изэнтропы, описывающей экспериментальные дан-

ражающей грани минизеркала диаметром 2.5 мм, а

ные.

затем зоны расположения оптоволокна (т.3). Сни-

жение амплитуды излучения с этого момента может

На плоскости P(T) данные настоящей работы

быть связано с повреждением поверхности зеркала

показаны на рис. 19 вместе с результатами рабо-

и (или) световода ударной волной.

ты [23] и расчетами из работы [7].

447

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

Рис. 15. Зарегистрированная осциллограмма (a ) и яркостная температура на фронте УВ в плазме гелия (b ) в зависи-

мости от времени при T = 2500 (1 ), 3342 (2 ), 4190 (3 ), 6083 (4 ), 8954 (5 ), 10743 (6 ) К

Рис. 16. (В цвете онлайн) а) Траектории УВ в начальной фазе: SW1 первая УВ; SW⁺ суммарная УВ; Fe1 и Fe2

оболочки первого и второго каскадов. b) R(t)-диаграммы: сплошная линия траектория ВГО-2; красные штрихи

траектории УВ SW⁺; F1 - F5 моменты фокусировки УВ SW⁺; K1 - K4 моменты отражения УВ SW⁺ от ВГО-2

5. СРАВНЕНИЕ ПОЛУЧЕННЫХ

теоретических подходов помимо расчетов с УРС

ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ С

ВНИИЭФ в данной работе были проведены допол-

РЕЗУЛЬТАТАМИ РАСЧЕТА ПО МОДЕЛИ

нительные расчеты термодинамических параметров

SAHA И ПОДХОДА AB INITIO В РАМКАХ

ударно-сжатой плазмы гелия при параметрах

КВАНТОВОЙ МОЛЕКУЛЯРНОЙ

давления и плотности, достигнутых в настоящем

ДИНАМИКИ

эксперименте. Для этой цели, как и ранее [22, 36],

В рамках теоретического сопровождения экс-

использовались два подхода: традиционный метод

периментов ВНИИЭФ и сравнения различных

448

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

Рис. 17. Сравнение экспериментальных данных с рассчитанной зависимостью температуры на фронте цилиндрической

УВ (кривая 1) от времени. Эксперимент: кружки λ = 775 нм. Расчет: кривая 2 усредненная по массе температура в

плазме гелия в зависимости от времени; ромбы усредненные по массе значения температур в моменты рентгеногра-

фирования. На вкладке область диаграммы вблизи фокусировки первой УВ

Рис. 19. (В цвете онлайн) Термодинамические параметры

неидеальной плазмы гелия:

∗

[23]; красные звездоч-

Рис. 18. (В цвете онлайн) Сжимаемость неидеальной плаз-

ки настоящая работа; красная линия средняя изо-

мы гелия. Эксперимент: ∗

[23]; красные звездочки

терма 21045 К; штрихи граница плазменного фазового

настоящая работа. Расчет: 1

изотерма T = 0 K; 2

перехода из атомарного состояния гелия в состояние од-

изэнтропа S/R = 11.55 (УРС ВНИИЭФ); 3 критиче-

нократно ионизованной плазмы [7]; черный ромб кри-

ская точка (660 ГПа, 2 г/см³, 35000 K) [7]; 4, 5 границы

тическая точка плазменного фазового перехода [7]; ◦

участка изотермы-изобары T ≈ 8000 K ⇔ P ≈ 300 ГПа

гипотетическая тройная точка [7]; желтые ромбы рас-

в двухфазной зоне фазового перехода [7]; 6 и 7

ча-

чет температуры (см. табл. 3) в химической модели (код

сти границ ¾купола¿ двухфазной области [7] со сторо-

SAHA); зеленые кружки то же с использованием УРС

ны атомарной (6 ) и плазменной (7 ) областей; 8 и 9

QMD (код VASP с функционалом РВЕ [36])

изэнтропы плазмы гелия, выходящие из единой точки

{ρ = 1.45 г/см³, P = 188 ГПа}, рассчитанные согласно

УРС SAHA и УРС QMD соответственно

ab initio

квантовой молекулярной динамики

(QMD) [39]. Процедура расчетов QMD реализована

расчета состава и термодинамических функций

с использованием известного пакета VASP [40] с

неидеальной многократно ионизованной плазмы

обменно-корреляционным функционалом с исполь-

в рамках ¾Химической модели плазмы¿ (chemical

зованием обобщенно-градиентного приближения

picture), реализованной в коде SAHA

[3, 19], а

(GGA) с параметризацией PBE

[41]. Конкрет-

также расчет в рамках современного подхода

но, в нашей настоящей работе были проведены

449

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

следующие расчеты.

ставлен расчет с использованием УРС ВНИИЭФ

1) Для всех экспериментальных точек {P_i, ρ_i}_exp

изотермы T = 0 K и изэнтропы, наилучшим обра-

в рамках моделей SAHA и QMD были рассчита-

зом описывающей экспериментальные данные. Так-

ны соответствующие этим моделям значения темпе-

же на рис. 18 приведены результаты сравнительно-

ратур {T_i}. Пользуясь методическим достоинством

го расчета согласно УРС SAHA и УРС QMD для

модели SAHA, с помощью этого кода мы рассчи-

изэнтроп, выпущенных из единой точки с коорди-

тали также ряд дополнительных физически зна-

натами {ρ = 1.45 г/см³, P = 188 ГПа}, и показаны

чимых характеристик термодинамических состоя-

доступные параметры границы первой стадии гипо-

ний {P_i, ρ_i, T_i}, соответствующих в рамках мо-

тетического ПФП, предсказанного в [7]. Из приве-

дели SAHA экспериментально достигнутым пара-

денного на рис. 18 сравнения можно заключить, что

метрам {P_i, ρ_i}_exp, а именно, равновесные степени

все три рассчитанные изэнтропы имеют разный на-

ионизации гелия, фактор сжимаемости (P_iV_i/RT_i),

клон, т. е. предсказывают различную скорость зву-

характеризующий знак и величину степени неиде-

ка. Наиболее ¾жестким¿ является УРС ВНИИЭФ,

альности плазмы в целом, показательный (¾де-

более ¾мягким¿ оказывается УРС SAHA и наибо-

баевский¿) параметр кулоновской неидеальности

лее ¾мягким¿ УРС QMD. Следует еще раз под-

Γ_D = e²/kTr_D (r_D дебаевский радиус с учетом

черкнуть, что все три теоретические УРС, исполь-

многократной ионизации и частичного вырождения

зуемые в данной статье, не содержат в области па-

электронного газа) и, наконец, параметр квантового

раметров, представленных на рис. 18, никаких ано-

вырождения электронного газа n_eλ^3e.

малий типа фазовых переходов, как это предсказы-

2) Также в рамках обоих подходов были рас-

вает теория [7]. При этом все три изэнтропы боль-

считаны параметры показательной изэнтропы, ¾вы-

шей своей частью проходят глубоко в пределах гипо-

пущенной¿ из одной и той же начальной точки

тетической двухфазной области, предсказываемой

{ρ = 1.45 г/см³, P = 188 ГПа}, для сравнения с

теоретической моделью [7] (см. зону в границах 3,

приведенной на рис. 18 изэнтропой, рассчитанной с

4, 5, 6, 7), где по существующим представлениям

использованием УРС ВНИИЭФ.

равновесные изэнтропы должны иметь существенно

Для обоих указанных альтернативных расчетов

меньшую скорость звука, т. е. существенно меньшую

термодинамики гелия, SAHA и QMD, в настоящей

¾крутизну¿ в принятых на рис. 18 координатах [42].

работе использовались численные методики и реа-

Ввиду сказанного можно рассматривать большую

величину наклона серии экспериментальных точек

лизующие их расчетные коды, уже неоднократно ис-

пользовавшиеся в недавних работах [22, 36], где по-

как аргумент в пользу отсутствия фазового разры-

ва в представленной зоне фазовой диаграммы.

дробно описаны важнейшие особенности двух ука-

занных альтернативных методик. По этой причине

На рис.19 экспериментальные данные насто-

более подробное описание опущено в настоящей ра-

ящей работы показаны на плоскости P - T вме-

боте. Все указанные выше величины, рассчитанные

сте с результатами работы [23]. Помимо этого, на

как кодом SAHA, так и в рамках модели QMD (код

рис. 19 представлены температуры {Ti} в точках

VASP с функционалом РВЕ), вместе с эксперимен-

{P_i, ρ_i}_exp, рассчитанные по теоретическим моде-

тальными данными приведены в табл. 3, а также на

лям УРС SAHA и QMD.

рис. 18 и 19 в P (ρ)- и P (T )-плоскостях. Эти результа-

Сравнение представленных на рис. 19 результа-

ты демонстрируют хорошее согласие в исследован-

тов расчета температуры, полученных с помощью

ной области давлений как друг с другом, так и с

трех принципиально различных теоретических под-

экспериментальными данными работы [23].

ходов, позволяет сделать следующие выводы.

1. Все три варианта набора температур, соответ-

6. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

ствующих экспериментальным точкам {P_i, ρ_i}_exp,

СРАВНЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ

близки друг другу и в хорошем приближении со-

ДАННЫХ ВНИИЭФ И ТЕОРЕТИЧЕСКИХ

ответствуют изотермическому характеру всей со-

РАСЧЕТОВ

вокупности точек с несущественно различающей-

Результаты по сжимаемости плазмы гелия в

ся величиной средней температуры. Однако следует

P (ρ)-координатах, полученные в пяти эксперимен-

признать, что все три варианта УРС (ВНИИИЭФ,

тах настоящей работы, приведены на рис. 18 и де-

SAHA и QMD) исходно и не предполагают никаких

монстрируют хорошее согласие в исследованной об-

фазовых аномалий в зоне экспериментально иссле-

ласти давлений с данными работы [23]. Там же пред-

дованных параметров.

450

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

Таблица 3. Расчетные и экспериментальные параметры плазмы гелия в фазе максимального сжатия

УРС ВНИИЭФ

УРС SAHA

УРС QMD

Экспе-

римент ρexp,

P_calc,

T_calc,

ΓD

neλ^e

T_calc,

г/см³

ГПа

ρRT K

ni + na

ρRT K

ρRT

1.87

256

20039

3.27

18175

5.59 · 10^-4

1.758

2.67·10^-2

3.61

21997

2.97

2.30

376

19700

3.99

17564

5.66 · 10^-4

2.059

3.48·10^-2

4.48

22079

3.56

2.44

476

22300

4.20

22561

9.06 · 10^-3

5.828

4.06·10^-1

4.16

29081

3.22

2.87

577

20842

4.64

15606

3.05 · 10^-4

2.015

2.79·10^-2

6.20

22235

4.35

1.65

240

22388

2. Наиболее весомый аргумент в пользу отсут-

стоящему эксперименту, что для всех эксперимен-

ствия первого из предсказанных [7] обширных плаз-

тальных точек, приведенных в табл. 3, все состоя-

менных (ionization-driven) фазовых переходов сле-

ния обсуждаемых цепочек ударных сжатий и состо-

дует из анализа самого факта фиксации представ-

яния максимального сжатия оказываются (согласно

ленных на рис. 18 равновесных состояний плазмы

УРС ВНИИЭФ и расчетам работы [7]) попадающи-

гелия в переменных давление - плотность. Напом-

ми на фазовой диаграмме P - ρ внутрь двухфазной

ним, что плотность плазмы непосредственно изме-

области проверяемого фазового перехода [7] и да-

ряется в эксперименте, в то время как достовер-

же, по-видимому, внутрь ¾спинодальной¿ зоны это-

ность рассчитанных величин давления, строго гово-

го фазового перехода, т.е. зоны абсолютной термо-

ря, подкрепляется лишь хорошим совпадением из-

динамической неустойчивости вещества, для кото-

меренных и рассчитанных (с помощью не содер-

рой устойчивым равновесным состоянием является

жащего температуру калорического УРС ВНИИЭФ

состояние двухфазной смеси, обладающей бесконеч-

U (P, ρ)) основных измерявшихся кинематических

ной изотермической сжимаемостью, (∂ρ/∂P )_T = ∞.

параметров процесса квазиизэнтропического сжа-

Представляется достаточно убедительным, что ди-

тия, т. е. R(t)- и W (t)-траекторий сжатия, представ-

намика движения сжимающей оболочки в такой си-

ленных на рис. 5-10. Дело в том, что, как уже под-

туации, когда сжимаемое вещество вследствие фа-

черкивалось выше, каждая экспериментальная точ-

зового превращения теряет свою ¾упругость¿, будет

ка, приведенная на рис. 18 и 19 и в табл. 2 и 3,

существенно иной, нежели в случае ¾обычного¿ од-

в реальности является финалом цепочки равновес-

нофазного состояния вещества c конечной сжимае-

ных состояний, реализующихся в процессе ревер-

мостью. Поэтому можно полагать, что в принятой

берации последовательности ударных сжатий при

в настоящем эксперименте диагностике движение

квазиизэнтропическом достижении состояния мак-

сжимающей оболочки в случае фазового расслое-

симального сжатия. Примером такой цепочки явля-

ния в сжимаемом веществе будет по своему харак-

ется серия состояний сжатия 1-5 эксперимента №1

теру более походить на движение оболочки в специ-

в табл. 2. При этом в самой идеологии метода ква-

альных тестовых условиях сжатия ¾пустой¿ сбор-

зиизэнтропического сжатия [43-45] подразумевает-

ки, т. е. при отсутствии сжимаемого вещества в цен-

ся, что все обсуждаемые промежуточные состояния

тральной камере, когда упругость этого вещества не

на пути к состоянию максимального сжатия явля-

препятствует свободному ¾схлопыванию¿ оболочек.

ются равновесными и, следовательно, оправдываю-

Никаких признаков подобного поведения на R(t)-

щими применение двух фундаментальных инстру-

диаграммах в настоящих экспериментах не зафик-

ментов теоретического описания процесса квазииз-

сировано. Это может считаться прямым доказатель-

энтропического сжатия приближения локального

ством отсутствия предсказанного [7] ионизационно-

термодинамического равновесия и локального гид-

го фазового превращения в зоне изэнтропической

родинамического описания. Но в том-то и состо-

полосы, перекрываемой ¾цепочками¿ многократно-

ит обсуждаемая особенность гипотетического плаз-

го ударного сжатия настоящего эксперимента.

менного фазового перехода [7] по отношению к на-

451

М.А. Мочалов, Р.И. Илькаев, В.Е. Фортов и др.

ЖЭТФ, том 163, вып. 3, 2023

7. ЗАКЛЮЧЕНИЕ

(научная тема № FSWE-2021-0010 ¾Газодинамика

и физика взрыва¿) и Национального центра фи-

Полученные в настоящей работе эксперимен-

зики и математики (г. Саров Нижегородской обл.).

тальные данные в P (ρ)- и P (T )-координатах не за-

фиксировали наличия в гелии аномалий, которые

ЛИТЕРАТУРА

могли бы указывать на существование плазменного

фазового перехода, предсказанного ранее теорети-

I. Iosilevskiy, V. Gryaznov, E. Yakub et al., Contrib.

чески Эбелингом [5], а также в работах [1-14], но и

Plasma Phys. 43, 316 (2003).

не позволяют сделать окончательного вывода о его

M. Schlanges, M. Bonitz, and A. Tschttschjan,

отсутствии. Возможно, что область плазменного фа-

Contrib. Plasma Phys. 35, 109 (1995).

зового перехода для сжатой плазмы гелия находится

в диапазоне более высоких давлений, что обосновы-

В. К. Грязнов, И. Л. Иосилевский, В. Е. Фортов,

вает необходимость продолжения исследований.

Термодинамика ударно-сжатой плазмы в

квазихимическом представлении

/ Энцикло-

Полученные экспериментальные данные показы-

педия низкотемпературной плазмы под общей

вают, что расчет с использованием для гелия УРС

ред. В. Е. Фортова. Том приложений III-1

ВНИИЭФ адекватно описывает температуру сжа-

Ред. А. Н. Старостин и И. Л. Иосилевский, Физ-

той плазмы на фронте цилиндрической УВ. С долей

матлит, Москва (2004), cc. 111-139.

сдержанного оптимизма это позволяет утверждать,

что температура плазмы гелия в момент максималь-

C. Winisdoerffer and G. Chabrier, Phys. Rev. E 71,

026402 (2005).

ного сжатия, рассчитанная с использованием УРС

ВНИИЭФ, также вычисляется правильно.

W. Ebeling, Contrib. Plasma Phys. 30, 553 (1990).

В дальнейших исследованиях термодинамиче-

H. Hess, High Press. Res. 1, 203 (1989).

ских параметров сжатой плазмы гелия авторы пред-

полагают поднять диапазон исследований изотерми-

В. Эбелинг, А. Фёрстер, В. Фортов и др., Тепло-

чески сжатой плазмы гелия до давлений 2500 ГПа,

физические свойства горячей плотной плазмы,

продолжить исследования излучательных характе-

Москва - Ижевск: НИЦ ¾Регулярная и хаотиче-

ристик фронта УВ и экспериментально зарегистри-

ская динамика¿, Институт компьютерных иссле-

ровать температуру плазмы гелия при максималь-

дований (2007).

ном сжатии, по крайней мере, в экспериментах с ци-

A. Forster, T. Kalbaum, and W. Ebeling, High

линдрическими устройствами.

Press. Res. 7, 375 (1991).

Благодарности. Авторы выражают благодар-

В. Т. Швец, ЖЭТФ 143, 182 (2013).

ность сотрудникам, принимавшим участие в ор-

ганизации, проведении экспериментов и обработ-

10.

C. A. Seldam, Proc. Phys. Soc. A 70, 97 (1957).

ке полученных данных: С. Е. Елфимову, Е. В. Ку-

11.

В. П. Трубицын, Ф. Р. Улинич, ДАН СССР 142,

лакову, А. С. Пупкову, А. В. Романову, Д. П. Туру-

578 (1962).

тину, А. И. Гуркину, М. В. Логинову, Д. А. Линяеву,

Г. С. Яндубаеву, В. В. Ерастову, В. В. Ковалдову.

12.

D. A. Young, A.K. McMahan, and M. Ross, Phys.

Авторы также выражают благодарность А. В. Шу-

Rev. B 24, 5119 (1981).

тову за плодотворные обсуждения проблемы дина-

13.

J. Meyer-ter-Vehn and W. Zittel, Phys. Rev. B 37,

мического сжатия вещества при наличии в нем фа-

8674 (1988).

зовых превращений.

14.

M. Preising and R. Redmer, Contrib. Plasma Phys.

Финансирование. Настоящая работа выпол-

61, e202100105 (2021).

нена при финансовой поддержке Госкорпорации

¾Росатом¿ по Государственной программе развития

15.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

ЖЭТФ 142, 696 (2012).

техники, технологий и научных исследований в об-

ласти использования атомной энергии (РТТН) (про-

16.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

ект ¾Исследование теплофизических свойств ве-

Письма в ЖЭТФ 96, 172 (2012).

ществ при сжатии до рекордно высоких давлений и

17.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

магнитных полей¿), Российского фонда фундамен-

ЖЭТФ 146, 169 (2014).

тальных исследований (проект 20-02-00287), Мини-

стерства науки и высшего образования РФ в рамках

18.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

программы по созданию молодежных лабораторий

Письма в ЖЭТФ 101, 575 (2015).

452

ЖЭТФ, том 163, вып. 3, 2023

Квазиизэнтропическое сжатие неидеальной плазмы гелия...

19.

В. К. Грязнов, И. Л. Иосилевский, В. Е. Фортов, в

33.

И. Р. Трунин, С. В. Корицкая, В. Арнолд, Пре-

сб. Ударные волны и экстремальные состояния

принт

75-2000, Саров

(2000); S. V. Koritskaya,

вещества под ред. В. Е. Фортова и др., Наука,

I. R. Trunin, and W. Arnold, AIP Conf. Proc. 505,

Москва (2000), c. 299.

475 (2000).

20.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

34.

Б. А. Надыкто, А. И. Ломайкин, И. Н. Павлуша,

ЖЭТФ 151, 592 (2017).

М. О. Ширшова, ВАНТ. Сер.: Теоретическая и

прикладная физика, Вып. 2, 43 (2012).

21.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

Письма в ЖЭТФ 108, 692 (2018).

35.

А. А. Евстигнеев, М. В. Жерноклетов, В. Н. Зуба-

22.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

рев, ФГВ 12, 758 (1976).

ЖЭТФ 160, 735 (2021).

36.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.,

23.

М. В. Жерноклетов, В. К. Грязнов, В. А. Аринин и

ЖЭТФ 159, 1118 (2021).

др., Письма в ЖЭТФ 96, 479 (2012).

37.

Р. Ф. Трунин, Л. Ф. Гударенко, М. В. Жернокле-

24.

V. E. Fortov, R.I. Il’kaev, V.A. Arinin et al., Phys.

тов, Г. В. Симаков, Экспериментальные данные

Rev. Lett. 99, 185001 (2007).

по ударно-волновому сжатию и адиабатиче-

25.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др. ,

скому расширению конденсированных веществ,

ЖЭТФ 152, 1113 (2017).

под ред. Р. Ф. Трунина, РФЯЦ-ВНИИЭФ, Саров

(2001).

26.

В. А. Огородников, А. Г. Иванов, А. Л. Михайлов и

др., ФГВ 34, 103 (1998).

38.

O. T. Strand, D. R. Goosman, C. Martinez et al.,

Rev. Sci. Instrum. 77, 083108 (2006).

27.

В. А. Огородников, С. В. Ерунов, А. О. Бликов и

др., ЖЭТФ 160, 621 (2021).

39.

A. V. Chentsov and P. R. Levashov, Contrib. Plasma

28.

Yu. P. Kuropatkin, V. D. Mironenko, V. N. Suvorov

Phys. 52, 33 (2012).

et al., in 11^th IEEE Pulsed Power Conference/Digest

of technical papers, ed. by G. Cooperstein and

40.

G. Kresse and J. Hafner, Phys. Rev. B 47, 558 (1993).

I. Vitkovitsky (1997), p. 1669.

41.

J. P. Perdew, K. Burke, and M. Ernzerhof, Phys.

29.

В. В. Сычев, А. А. Вассерман, А. Д. Козлов и др.,

Rev. Lett. 77, 3865 (1996).

Термодинамические свойства гелия, ГСССД, Изд-

во стандартов, Москва (1984).

42.

В. Е. Фортов, Tepмодинамика динамических

воздействий нa вещество, Физматлит, Москва

30.

V. A. Arinin and B. I. Tkachenko, Pattern Recogn.

(2019).

and Image Anal. 19, 63 (2009).

43.

Ф. В. Григорьев, С. Б. Кормер, О. Л. Михайлова и

31.

Н. Ф. Гаврилов, Г. Г. Иванова, В. И.Селин, В. Н.Со-

фронов, ВАНТ. Сер.: Методики и программы

др., Письма в ЖЭТФ 16, 286 (1972).

численные решения задач математической

44.

Ф. В. Григорьев, С. Б. Кормер, О. Л. Михайлова и

физики, Вып. 3, 11 (1982).

др., ЖЭТФ 69, 743 (1975).

32.

Б. Л. Глушак, Л. Ф. Гударенко, Ю. М. Стяжкин,

ВАНТ. Сер.: Математическое моделирование фи-

45.

Ф. В. Григорьев, С. Б. Кормер, О. Л. Михайлова и

зических процессов, Вып. 2, 57 (1991).

др., ЖЭТФ 75, 1683 (1978).

453