ЖЭТФ, 2023, том 163, вып. 4, стр. 467-479

ЭНТРОПИЯ КОГЕРЕНТНЫХ СОСТОЯНИЙ ОПТИЧЕСКИХ

ПОЛЕЙ

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко^*

Институт физики им. Б. И. Степанова Национальной академии наук Беларуси

220072, Минск, Беларусь

Поступила в редакцию 14 октября 2022 г.,

после переработки 1 декабря 2022 г.

Принята к публикации 2 декабря 2022 г.

Рассмотрены статистические смеси двух и трех произвольных когерентных состояний, представляющих

собой состояния носителя информации в оптическом канале связи. В аналитическом виде найдены соб-

ственные значения и собственные векторы соответствующих операторов плотности. С этой целью введена

оригинальная параметризация треугольников на комплексной фазовой плоскости. Найдены аналитиче-

ские выражения для энтропии фон Неймана смесей двух и трех произвольных когерентных состояний и

численно рассчитано ее максимальное значение при заданном среднем числе фотонов. Установлено, что

использование трех когерентных состояний при заданном среднем числе фотонов обеспечивает более

высокую емкость оптического канала связи, чем использование двух.

DOI: 10.31857/S004445102304003X

применяться в качестве источников света, наиболь-

EDN: LFDZSY

шая емкость оптического канала связи достигается

при использовании лазерных источников поля и ко-

герентных оптических приемников. В современной

1. ВВЕДЕНИЕ

оптической линии связи состояния носителя инфор-

мации представляют собой несколько когерентных

Когерентные состояния оптического поля с хоро-

состояний одной моды оптического поля. Перекры-

шей точностью описывают излучение лазера, рабо-

тие двух когерентных состояний дается формулой

тающего высоко над порогом, и занимают централь-

ное место в формализме кантовой оптики. Когерент-

|〈α|β〉|² = e-|α-β|2 .

ное состояние одной моды оптического поля с без-

Таким образом, при достаточной близости амплитуд

размерной комплексной амплитудой α представля-

два когерентных состояния являются существенно

ется в виде [1]

неортогональными и их различение при измерении

∑

αⁿ

связано с возможной ошибкой, обусловленной кван-

|α〉 = e-|α|2/2

√ |n〉,

(1)

товым шумом. В подобном случае канал передачи

n=0

информации рассматривают как квантовый канал

где |n〉 — n-фотонное состояние Фока [2]. Когерент-

связи [3] и для определения уровня ошибок привле-

ные состояния представляют собой переполненный

кают квантовую теорию измерений [4].

базис в гильбертовом пространстве оптической мо-

В типичной современной системе волоконно-

оптической связи состояния носителя информации

ды и любое классическое состояние моды представ-

ляет собой взвешенную смесь таких состояний.

можно считать практически ортогональными. Дей-

ствительно, при использовании всего двух когерент-

Оптические поля в когерентных состояниях ши-

ных состояний с противоположными фазами, что

роко используются в современных системах переда-

чи информации, в которых сигнал передается как

соответствует популярной схеме фазового манипу-

лирования BSPK [5], величина перекрытия состо-

по оптическому волокну, так и по открытому про-

странству. Хотя в ряде случаев светодиоды могут

яний равна |〈α|β〉|² = exp(-4N), где N = |α|2 —

среднее число фотонов в одном окне модуляции.

^* E-mail: dhoroshko@yahoo.com

Следовательно, в данной схеме квантовое рассмот-

467

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

рение становится необходимым только при очень

ключевую роль [9]. Другим важным приложением,

низком уровне сигнала. По мере распространения

требующим квантового анализа оптического кана-

сигнала в оптическом волокне его мощность умень-

ла связи, является квантовая криптография, в кото-

шается из-за потерь, и когда она становится срав-

рой состояния поля намеренно создаются неортого-

нимой с пределом чувствительности фотодетекто-

нальными уже на входе в канал связи с целью сде-

ра, используемого в когерентном оптическом при-

лать незаметный перехват информации невозмож-

емнике, сигнал подвергается усилению на оптиче-

ным [10-12]. Таким образом, исследование емкости

ском повторителе. Типичные величины частоты мо-

оптического канала связи на основе перекрываю-

дуляции и чувствительности приемника в современ-

щихся когерентных состояний является весьма ак-

ных волоконно-оптических сетях составляют f = 10

туальной современной задачей с широкой областью

ГГц и P = 1 мкВт соответственно [6]. Таким об-

применения. Помимо этого, исследование ансамблей

разом, средняя энергия поля в окне модуляции мо-

когерентных состояний важно для таких приложе-

жет быть оценена как E = P/f

= 10^-16 Дж, в

ний, как квантовое кодирование [13, 14], оптическая

то же время энергия одного фотона на длине вол-

квантовая телепортация [15, 16], квантовые оптиче-

ны λ = 1.5 мкм составляет E_ph = 2πℏc/λ ∼ 10^-19

ские измерения при наличии обратной связи [17-19]

Дж. Это означает, что поле на приемнике содер-

и других.

жит в среднем N

= E/E_ph = 1000 фотонов на

В данной статье исследуется емкость оптическо-

один передаваемый бит информации. Перекрытие

го канала связи с использованием двух и трех произ-

двух когерентных состояний в данном случае ни-

вольных когерентных состояний. С этой целью вы-

чтожно мало и рассмотрение квантового шума не

числяется энтропия фон Неймана для статистиче-

требуется. Однако быстрый прогресс в области те-

ской смеси двух и трех равновероятных когерент-

лекоммуникаций приводит к использованию моду-

ных состояний. В литературе имеются вывод эн-

ляторов с частотой f = 25 ГГц и фотоприемников с

тропии смеси двух когерентных состояний [20] и

чувствительностью P = 0.1 мкВт, что снижает сред-

анализ монотонности энтропии смеси трех произ-

нее число фотонов до N = 40. Кроме того, необхо-

вольных состояний с равными перекрытиями [21].

димость повышения емкости каналов связи приво-

Случай двух когерентных состояний представлен в

дит к внедрению прогрессивных форматов фазового

разд. 2, где, помимо энтропии как функции пере-

и амплитудного манипулирования, в которых в од-

крытия, совпадающей с результатом работы [20],

ном окне модуляции может передаваться несколько

рассчитана максимальная энтропия при заданном

битов информации [5-7]. При этом перекрытие со-

среднем числе фотонов и найдены собственные век-

седних когерентных состояний уже определяется не

торы оператора плотности статистической смеси.

только уровнем сигнала, но и геометрией располо-

Случай трех когерентных состояний рассмотрен в

жения состояний на комплексной плоскости, обра-

разд. 3, где, в отличие от работы [21], рассматрива-

зующих так называемое «сигнальное созвездие» [8].

ются произвольные перекрытия сигнальных состоя-

Так, в перспективном формате M-PSK использует-

ний. Для этого случая также рассчитывается макси-

ся M значений фазы [5, 6], причем амплитуды ко-

мальная энтропия при заданном среднем числе фо-

√

герентных состояний имеют вид α_k =

Ne^i2πk/M,

тонов и проведено ее сравнение со случаем двух ко-

и перекрытие соседних состояний дается формулой

герентных состояний. В этом же разделе в аналити-

|〈α_k|α_k+1〉|²

= e-4Nsin2(π/M), что равно примерно

ческой форме выведены выражения для собствен-

2 · 10^-3 для N = 40, M = 16. Подобное перекры-

ных векторов оператора плотности смеси трех про-

тие приводит к ошибке в дискриминации состояний

извольных когерентных состояний. Обсуждение ре-

порядка 10^-3, что близко к максимально допустимо-

зультатов проводится в Заключении.

му уровню ошибок, исправляемых кодами коррек-

ции ошибок [6]. Таким образом, в ближайшем бу-

дущем квантовый шум может стать существенным

2. ЭНТРОПИЯ СМЕСИ ДВУХ

для массовых сетей телекоммуникаций. Кроме того,

ПРОИЗВОЛЬНЫХ КОГЕРЕНТНЫХ

квантовый шум имеет большое значение для оптиче-

СОСТОЯНИЙ

ской связи через открытое пространство, при кото-

рой усиление сигнала невозможно. В частности, для

Мы рассматриваем одну моду оптического поля с

спутниковой оптической связи требуется разработка

операторами рождения и уничтожения фотона a^† и

специальных приемников на основе детекторов оди-

a соответственно, удовлетворяющими каноническо-

ночных фотонов, в которых квантовый шум играет

му коммутационному соотношению: [a, a^†] = 1. Ко-

468

ЖЭТФ, том 163, вып. 4, 2023

Энтропия когерентных состояний . . .

герентное состояние моды с комплексной амплиту-

где L = |α - β| — расстояние между числами α и β

дой α имеет вид (1). Рассмотрим два когерентных

на комплексной плоскости, определяющее перекры-

состояния с произвольными комплексными ампли-

тие двух когерентных состояний:

тудами α и β. Эти состояния могут быть использо-

ваны для передачи информации в оптической линии

〈α|β〉 = e-|α-β|2/2+iIm(α∗β).

(9)

связи, представляя собой буквы двухбуквенного ал-

фавита [13]. В случае, когда частоты употребления

Помимо этого расстояния, пара комплексных чисел

обеих букв совпадают и равны 1/2, состояние слу-

может в общем случае характеризоваться еще тре-

чайно выбранной моды задается оператором плот-

мя действительными параметрами, которые можно

ности

назвать «абсолютными» — комплексной координа-

ρ=

(|α〉〈α| + |β〉〈β|) .

(2)

той центра отрезка, соединяющего эти два числа на

комплексной плоскости, κ = (α + β)/2, и углом на-

Оптимальное декодирование информации на прини-

клона этого отрезка к действительной оси arg(α-β).

мающей стороне реализуется посредством коллек-

Как следует из уравнения (8), собственные значения

тивного квантового измерения длинных блоков, со-

матрицы плотности, а значит и энтропия, не зави-

ставленных из оптических мод, несущих одно из

сят от этих трех параметров, что говорит об инвари-

указанных состояний. Максимальная доступная ин-

антности энтропии по отношению к сдвигам и вра-

формация при таких измерениях ограничена свер-

щениям на комплексной плоскости. Математически

ху информацией Холево [22], которая для чистых

вращение состояния на угол ψ описывается опера-

состояний-букв совпадает с энтропией фон Нейма-

тором вращения U(ψ) = exp(iψa^†a). Этот оператор

на

унитарен и не изменяет скалярные произведения,

S(ρ) = -Tr (ρ log₂ ρ) .

(3)

входящие в уравнение (6), а значит, и не влияет на

Для вычисления энтропии фон Неймана найдем

его решения. Сдвиг состояния на комплексную вели-

собственные значения λ_n и собственные векторы

чину δ описывается унитарным оператором сдвига

|λ_n〉 оператора плотности:

D(δ) = exp(δa^† - δ^∗a), действие которого на коге-

рентное состояние задается уравнением [23]

ρ|λ_n〉 = λ_n|λ_n〉.

(4)

D(δ)|α〉 = eiIm(δα∗)|α + δ〉.

(10)

Оба собственных вектора оператора плотности

лежат в линейной оболочке двух когерентных со-

Замена амплитуды α на амплитуду α + δ соответ-

стояний {|α〉, |β〉} и могут быть записаны как

˜(δ), такому

ствует несколько другому оператору

что

D(δ)|α〉 = |α + δ〉. Будем называть этот опе-

|λ_n〉 = C^αn|α〉 + C^βn |β〉,

(5)

ратор «оператором чистого сдвига». Этот оператор

где индекс n принимает значения 0 и 1, а C^αn и C^βn —

неунитарен и не сохраняет скалярные произведения:

комплексные коэффициенты. Подставляя (2) и (5) в

〈α|

D^†(δ)D(δ)|β〉 = 〈α+δ|β+δ〉 = 〈α|β〉, но сохраняет

(4) и используя линейную независимость когерент-

их модуль, так как отличается от унитарного опера-

ных состояний, получаем уравнение для комплекс-

тора D(δ) только фазовым множителем. Поскольку

ных коэффициентов:

уравнение (7) включает только модуль скалярного

произведения, а уравнение (6) — также и его фазу,

(

)(

)

1 - 2λ_n

〈α|β〉

C^αn

то собственные значения оператора плотности инва-

= 0.

(6)

риантны к чистому сдвигу, а коэффициенты разло-

〈β|α〉

1 - 2λ_n C^β

жения собственных векторов — нет. Таким образом,

Для того чтобы это уравнение имело ненулевое ре-

абсолютные параметры не влияют на собственные

шение, детерминант матрицы должен обращаться в

значения оператора плотности и, следовательно, на

нуль, что приводит к характеристическому уравне-

энтропию. В отличие от этих параметров, рассто-

нию

яние L характеризует относительное расположение

(1 - 2λ)² - |〈α|β〉|² = 0,

(7)

двух амплитуд и может быть названо «относитель-

ным» параметром, влияющим на энтропию.

два решения которого имеют вид

Подставляя диагональный вид оператора плот-

-L²/2

ности в уравнение (2) и используя формулу (8), по-

1 ± |〈α|β〉|

1±e

λ_1,2 =

(8)

лучаем энтропию смеси двух равновероятных коге-

469

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

рентных состояний в виде [20]

Состояния (14) являются суперпозициями двух ко-

(

)

герентных состояний. При оптимальном выборе

1-e-L2/2

β = -α они представляют собой четное и нечетное

S(ρ) = h₂

(11)

когерентные состояния [25], широко исследуемые в

связи с тем, что они являются оптическими реали-

где

зациями известного состояния «кота Шрёдингера»

h₂(s) = -s log₂ s - (1 - s)log₂(1 - s)

[26-29].

— энтропия Шеннона [24]. При L, возрастающем от

0 до ∞, аргумент функции в (11) монотонно возрас-

тает от 0 до 1/2. На этом участке энтропия h₂(s)

3. ЭНТРОПИЯ СМЕСИ ТРЕХ

монотонно возрастает, что можно показать, взяв ее

ПРОИЗВОЛЬНЫХ КОГЕРЕНТНЫХ

производную h^′2(s) = - log₂[s/(1 - s)] и убедившись

СОСТОЯНИЙ

в том, что она положительна при s ∈ (0, 1/2). Отсю-

Рассмотрим три когерентных состояния с про-

да следует, что энтропия смеси двух когерентных

извольными комплексными амплитудами α, β и γ.

состояний (11) является монотонно возрастающей

Эти состояния могут быть использованы для пере-

функцией L, стремящейся к своему асимптотическо-

дачи информации в оптической линии связи, пред-

му значению 1 при L → ∞.

ставляя собой буквы трехбуквенного алфавита. В

Среднее число фотонов в случайно выбранной

случае, когда частоты употребления всех трех букв

моде имеет вид

совпадают и равны 1/3, состояние случайно выбран-

(

)

(

)

ной моды задается оператором плотности

N = Tr

a^†aρ

|α|² + |β|²

= |κ|² +

(12)

ρ=

(|α〉〈α| + |β〉〈β| + |γ〉〈γ|) .

(15)

Следовательно, в отличие от энтропии, среднее чис-

ло фотонов зависит не только от длины L отрезка,

Как и в случае двух когерентных состояний, рас-

соединяющего амплитуды состояний на комплекс-

смотренном в предыдущем разделе, максимальная

ной плоскости, но и от абсолютного значения коор-

информация, которую можно передать с помощью

динаты центра этого отрезка |κ|. Если теперь рас-

таких состояний по оптической линии связи, дается

смотреть множество всех отрезков с фиксирован-

энтропией фон Неймана S(ρ), определяемой урав-

ным значением N и задаться вопросом, какова мак-

нением (3), вычисленной для оператора (15). Для

симальная энтропия S^max2 на этом множестве, то

нахождения этой величины, аналогично предыду-

ответ будет очевиден: максимум энтропии достига-

щему разделу, найдем собственные значения λ_n и

ется на отрезках с κ = 0. Действительно, рост |κ|

собственные векторы |λ_n〉 оператора плотности:

при фиксированном N означает уменьшение L и, в

силу установленной выше монотонности энтропии,

ρ|λ_n〉 = λ_n|λ_n〉.

(16)

уменьшение энтропии. Таким образом, максималь-

ная энтропия при заданном среднем числе фотонов

3.1. Собственные значения оператора

имеет вид

плотности

)

-2N

(1-e

Smax2

(N) = h₂

(13)

Все три собственных вектора оператора плотно-

сти лежат в линейной оболочке трех когерентных

и достигается при выборе β = -α. Такой выбор

состояний {|α〉, |β〉, |γ〉} и могут быть записаны как

букв двоичного алфавита обеспечивает максималь-

|λ_n〉 = C^αn|α〉 + C^βn |β〉 + C^γn |γ〉,

(17)

ную емкость оптического канала связи при заданной

средней энергии (числе фотонов) на фотоприемни-

где индекс n принимает значения 0, 1, 2, а C^αn, C^βn

ке.

и C^γn — комплексные коэффициенты. Подставляя

Подставляя (8) в (6), получаем собственные век-

(15) и (17) в (16) и используя линейную независи-

торы в виде

мость когерентных состояний, получаем уравнение

(

)

для комплексных коэффициентов:

|λ_1,2〉 = C^α1,2

|α〉 ± e-iImα∗β |β〉 ,

(14)

⎛

⎞⎛

⎞

1 - 3λ_n

〈α|β〉

〈α|γ〉

C^αn

где из условия нормировки находим

⎜

⎟⎜

⎟

(

)_-1/2

⎝ 〈α|β〉^∗

1 - 3λ_n

〈β|γ〉

⎠⎝Cβn⎠ = 0.

(18)

C^α1,2 =

2 ± 2e-L2/2

〈α|γ〉^∗

〈β|γ〉^∗

1 - 3λ_n C^γ

470

ЖЭТФ, том 163, вып. 4, 2023

Энтропия когерентных состояний . . .

Для того чтобы это уравнение имело ненулевое ре-

В нашем случае

шение, детерминант матрицы должен обращаться

x₁ = |〈α|β〉|² , x₂ = |〈β|γ〉|² , x₃ = |〈γ|α〉|² ,

в нуль, что приводит нас к характеристическому

уравнению

откуда искомое неравенство следует с учетом того,

что модуль косинуса не превышает единицу:

(1 - 3λ)³ - (1 - 3λ) 3T² + 2Q = 0.

(19)

Здесь T и Q — два действительных параметра, при-

|Q|^2/3 ≤³

√x₁x₂x₃ ≤ T².

нимающие значения от 0 до 1, причем первый из них

По определению угол 3θ принимает значения от

определяется как

-π/2 до π/2, а это значит, что угол θ лежит в ин-

√

тервале [-π/6, π/6].

|〈α|β〉|² + |〈α|γ〉|² + |〈β|γ〉|

T =

(20)

Одно решение уравнения (24) находится из фор-

мулы для куба синуса

и имеет смысл среднего перекрытия между

состояниями-буквами, а второй параметр опре-

sin³ θ = (3 sinθ - sin3θ)/4,

деляется геометрией взаимного расположения

откуда следует u₁ = sinθ. Два других корня имеют

состояний на комплексной плоскости и равен

вид

(

)

〈β|α〉〈α|γ〉〈γ|β〉 + 〈α|β〉〈γ|α〉〈β|γ〉

2π

u_2,3 = sin θ ±

= |〈β|α〉〈α|γ〉〈γ|β〉| cos (2S_αβγ ),

(21)

в чем можно убедиться, подставив их в уравнение

(12) и воспользовавшись той же формулой для куба

где

синуса с учетом 2π-периодичности синуса. Возвра-

Im (α^∗β + β^∗γ + γ^∗α)

S_αβγ =

(22)

щаясь к исходной переменной, получаем собствен-

ные значения оператора плотности в виде

— площадь ориентированного треугольника, обра-

[

(

)]

зованного точками α, β и γ на комплексной плоско-

2πn

λ_n =

1 - 2T sin θ +

n = 0,1,2.

(26)

сти, причем знак этой величины положителен при

обходе вершин против часовой стрелки и отрицате-

Величины Q, T и θ зависят только от расстояний

лен при обходе в обратном направлении. Для трех

между тремя когерентными состояниями-буквами

точек, лежащих на прямой, например, для действи-

на комплексной плоскости и от площади треуголь-

тельных α, β и γ, как следует из (22), S_αβγ = 0.

ника, образуемого ими. Это означает, что собствен-

С другой стороны, для треугольника с площадью

ные значения λ_n инвариантны по отношению к сдви-

S_αβγ = π/4 + mπ/2, где m — целое число, Q обра-

гам и вращению всех трех состояний-букв на ком-

щается в нуль.

плексной плоскости. Как и в случае двух состоя-

Для нахождения корней уравнения (19) прове-

ний, такая инвариантность определяется тем, что в

дем замену переменной

уравнение (18) входят только скалярные произведе-

1 - 3λ

ν =

(23)

ния векторов, которые не изменяются унитарными

операторами сдвига D(δ) и вращения U(ψ). Как и

и перепишем его в виде

в предыдущем разделе, введем три «абсолютных»

параметра для набора состояний-букв: координату

4ν³ - 3ν + sin3θ = 0,

(24)

центроида треугольника (точки пересечения медиан

где введен новый параметр θ, определяемый из со-

[31]) ξ = (α + β + γ)/3 и угол наклона медианы, опу-

отношения

щенной из точки α, к действительной оси arg(α- ξ).

sin3θ =

(25)

Таким образом, хотя три комплексных амплиту-

T³

ды задаются шестью действительными параметра-

Подобная параметризация возможна всегда в силу

ми, собственные значения оператора плотности бу-

ограничения |Q| ≤ T³, которое следует из известно-

дут зависеть только от трех «относительных» па-

го неравенства арифметического и геометрического

раметров, в силу инвариантности по отношению к

средних [30]: для любых трех положительных чи-

трехпараметрической группе сдвигов и вращений.

сел x₁, x₂, x₃ их геометрическое среднее ограничено

Как показывает уравнение (26), число параметров

сверху их арифметическим средним,

может быть даже уменьшено до двух, T и θ, од-

√x

1x2x3 ≤ (x1 + x2 + x3)/3.

нако эти параметры не являются независимыми в

471

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

том смысле, что пределы изменения одного из них

зависят от значения другого. Это следует из следу-

ющего требования: оператор плотности в квантовой

механике всегда положительно определен, а значит

его собственные значения λ_n всегда неотрицатель-

ны. Полагая θ = -π/6, имеем sin(θ + 2π/3) = 1 и

из уравнения (26) получаем, что λ₁ неотрицательно

только при T ≤ 1/2. В общем случае верхняя гра-

ница T будет сложной функцией θ, что затрудняет

анализ энтропии.

3.2. Представление треугольника точкой в

трехмерном пространстве

Для удобства вычислений собственных значений

и энтропии необходимо правильно ввести три «от-

носительных» параметра, характеризующих взаим-

ное расположение амплитуд α, β, γ на комплексной

плоскости. В качестве первого шага переходим в си-

стему координат с центром, расположенным в цен-

троиде ξ = (α + β + γ)/3. В этой системе координат

амплитуды α, β, γ преобразуются в амплитуды

α₁ = α - ξ, β₁ = β - ξ, γ₁ = γ - ξ,

(27)

представленные на рис. 1a. При этом остается неис-

ключенным еще один «абсолютный» параметр —

угол arg(α₁) поворота треугольника α₁β₁γ₁ на ком-

плексной плоскости амплитуд. Чтобы его исклю-

чить, перейдем в трехмерное пространство, коорди-

натами точек которого являются стороны треуголь-

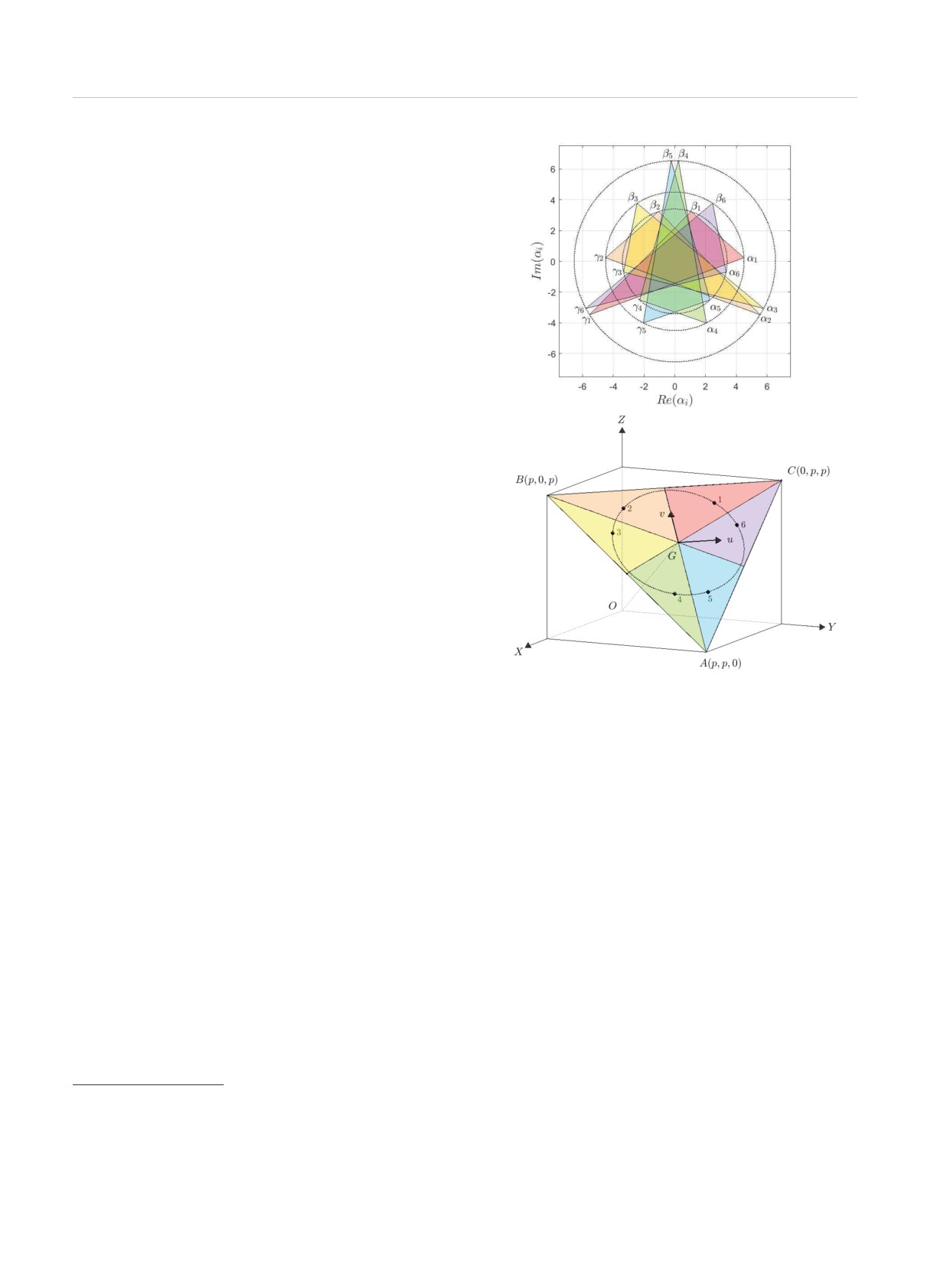
Рис. 1. a) Треугольник α1β1γ1, образуемый амплитудами

(27), и треугольники αiβiγi (i = 2, . . . , 6), получаемые

ника

при перестановке его сторон (28), вместе образующие эле-

менты группы S3. b) Отображение треугольников αiβiγi

x = |α - β|, y = |γ - β|, z = |γ - α|.

(28)

из комплексной плоскости амплитуд в точки трехмерно-

го пространства i, координаты которых задают стороны

Очевидно, что построенная таким образом точка в

треугольников (αiβiγi → i). Цвет сектора на рис. b соот-

пространстве (x, y, z), например, точка 1 на рис. 1b,

ветствует цвету отображаемого треугольника на рис. a

соответствующая треугольнику α₁β₁γ₁ на плоско-

сти рис. 1a, не зависит от угла arg(α₁). Однако при

4 = (z,y,x), 5 = (y,z,x), 6 = (x,z,y),

таком отображении геометрически эквивалентные

треугольники отображаются в разные точки трех-

и генерирующие одинаковые собственные значения,

мерного пространства. Так, геометрически эквива-

представлены шестью разными точками в трехмер-

лентные треугольники α_iβ_iγ_i (i = 1, 2, . . ., 6) на

ном представлении на рис. 1b.

рис. 1a, являющиеся шестью элементами симметри-

Введем параметризацию, позволяющую избе-

ческой группы перестановок S₃₁₎ сторон треуголь-

жать этой многозначности. 3D-область, в которую

ника:

отображаются треугольники, ограничивается

неравенствами

1 = (x,y,z), 2 = (y,x,z), 3 = (z,x,y),

x + y ≥ z, x + z ≥ y, y + z ≥ x,

¹⁾ Изоморфной диэдральной группе D₃ преобразований

треугольника α₁β₁γ₁: например, тождественного преобразо-

образующими треугольный конус с вершиной в на-

вания, четырех поворотов относительно изоцентра на 120^◦

чале координат. Точки, изображающие треугольни-

(1 → 3, 3 → 5, 2 → 4, 4 → 6) и отражения относительно мни-

мой оси 1 → 2.

ки с заданным полупериметром p, расположенные

472

ЖЭТФ, том 163, вып. 4, 2023

Энтропия когерентных состояний . . .

на плоскости x + y + z = 2p, ограничены ее сече-

достаточно ограничить одним из этих секторов, на-

нием с данным конусом рис. 1b. Вершинами этой

пример, ϕ ∈ [π/6, π/2], где z ≥ y ≥ x. В этом секто-

[

(√

)]

равносторонней треугольной области являются точ-

ре, для заданного угла ϕ, r ∈

0, p/

6sinϕ

(см.

ки A = (p, p, 0), B = (p, 0, p) и C = (0, p, p). Ее центр

также рис. 2a, где этот сектор обозначен штрихов-

— точка

кой).

(

)

Таким образом, любой треугольник полностью

описывается тремя параметрами (p, r, ϕ), где полу-

есть 3D-отображение равностороннего треугольни-

периметр p задает его размер, параметр r характе-

ка из комплексной плоскости. Введем в плоскости

ризует его деформацию — степень удаленности от

ABC декартову систему координат (u, v) с центром

равностороннего, а ϕ задает форму треугольника

в точке G, с осью v, лежащей в одной плоскости с

при заданном размере и деформации.

осью z, и с осью u, перпендикулярной ей (рис. 1b).

Для известных (x, y, z) параметры (p, r, ϕ) можно

Обозначим единичные векторы вдоль направлений

получить, обращая уравнения (31)-(33). Для полу-

u и v через e_u и e_v соответственно. Эти векторы

периметра p получаем просто его определение, для

можно выразить следующим образом:

деформации —

√

e_u = (-e_x + e_y)/

(29)

√

r = (x - 2p/3)² + (y - 2p/3)² + (z - 2p/3)²,

(34)

e_v = (-e_x - e_y + 2e_z)/

(30)

и, наконец, для угла —

где e_x, e_y и e_z — единичные векторы вдоль направ-

(√

)

лений x, y и z соответственно.

3 z - 2p/3

ϕ = arcsin

(35)

В плоскости треугольника ABC будем пользо-

ваться полярными координатами (r, ϕ), которые

вводятся стандартным образом: u

= rcosϕ,

В последнем уравнении мы полагаем z ≥ y ≥ x,

v = rsinϕ. Вектор

в результате чего ϕ попадает в интересующий нас

сектор ϕ ∈ [π/6, π/2].

r_(x,y,z) = xe_x + ye_y + ze_z,

3.3. Энтропия фон Неймана

расположенный в плоскости ABC и представляю-

щий треугольник (x, y, z), можно записать как

Энтропия фон Неймана для оператора плотно-

сти дается энтропией Шеннона его собственных зна-

2p(e_x + e_y + e_z)/3 + r cosϕe_u + r sinϕe_v.

чений:

∑

Приравнивая эти два выражения, с использовани-

S = - λn log2 λ_n.

(36)

ем уравнений (29) и (30) получаем после некоторых

n=0

преобразований

Эта величина стремится к своему максимально-

√

му значению log₂

3 = 1.585 при достаточном вза-

x = [2p +

6r sin (ϕ + 4π/3)]/3,

(31)

имном удалении всех трех точек на комплекс-

√

y = [2p +

6r sin (ϕ + 2π/3)]/3,

(32)

ной плоскости. Для произвольного треугольника

√

z = [2p +

6r sin (ϕ)]/3.

(33)

с относительными параметрами (p, r, ϕ) величины

(x, y, z) рассчитываются по формулам

(31)-(33).

При r = 0 получаем равносторонний треуголь-

Площадь треугольника дается формулой Герона

√

ник, а при ϕ = (2k + 1)π/6, где k пробегает значения

S_αβγ

p(p - x)(p - y)(p - z), которая вместе с

от 0 до 5 — равнобедренные треугольники, причем

формулой (9) позволяет выразить T и Q через

в треугольниках с k = 0, 2, 4 основание меньше, чем

(x, y, z), а затем найти собственные значения опера-

боковые стороны, а в треугольниках с k = 1, 3, 5 —

тора плотности по формуле (26). На рис. 2 показаны

больше. Так, для r = 0, при изменении ϕ от π/6

результаты такого расчета для различных значений

до π/2 треугольник плавно изменяет свою форму

полупериметра p.

от равнобедренного с x < y = z до другого равно-

При малых значениях полупериметра p (малых

бедренного с x = y < z. В остальных пяти секто-

отличий амплитуд когерентных состояний) макси-

рах, однозначно задаваемых параметром ϕ, имеем

мальной энтропией обладают вырожденные конфи-

геометрически эквивалентные треугольники с пере-

гурации A, B и C, когда одна из букв двухбуквен-

ставленными сторонами, т.е. исследование энтропии

ного алфавита когерентных состояний повторяется

473

ЖЭТФ, вып. 4

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

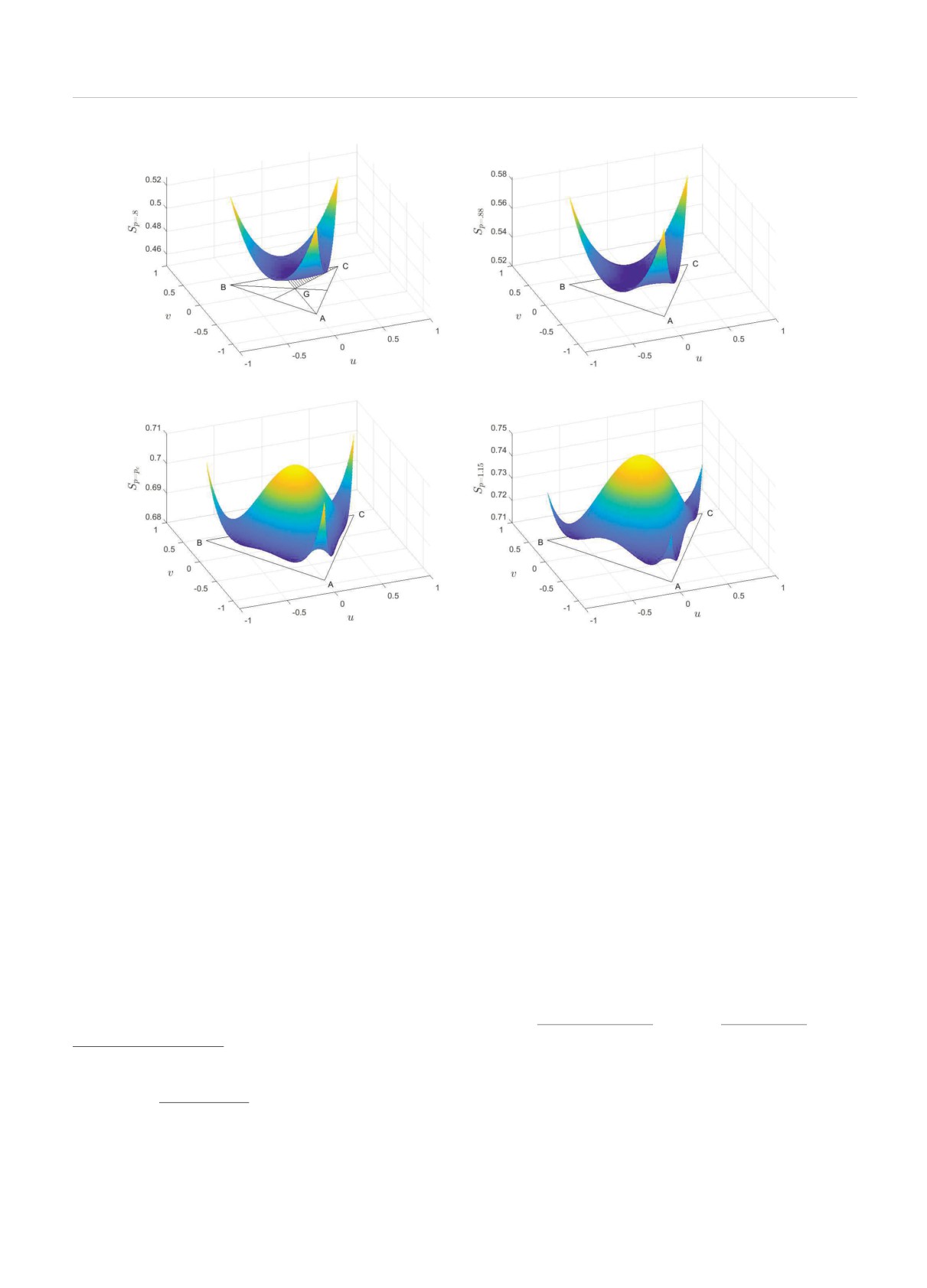
Рис.

2. Энтропия Sp равновероятной смеси трех когерентных состояний, образующих треугольник с полупери-

метром p, для всевозможных конфигураций треугольников, каждый из которых представлен точкой на плоскости

{u = r cos ϕ, v = r sin ϕ} из области ABC. Точка G на рис.a соответствует равностороннему треугольнику когерентных

состояний. Точки A, B и C обозначают вырожденные равнобедренные треугольники {x = y, z = 0}, {x = z, y = 0} и

{y = z, x = 0} соответственно. Заштрихованная область на рис.a выделяет сектор ϕ ∈ [π/6 , π/2 ] , где z ≥ y ≥ x. Точки

из пяти других секторов соответствуют перестановкам сторон x, y, z треугольника когерентных состояний из данного

сектора. p = 0.8 (a) , 0.88 (b) ; pc = 1.097 (c) , 1.15 (d)

в два раза чаще другой²⁾. На рис. 2a эта ситуа-

симумам для вырожденных конфигураций A, B, C

ция представлена тремя максимумами в точках A,

(рис. 2с). При p > p_c энтропия в точке G становится

B, C и минимумом в точке G (равносторонний тре-

глобальным максимумом для всевозможных конфи-

угольник когерентных состояний). При увеличении

гураций трех когерентных состояний (рис. 2d).

p в области значений p = 1 происходит изменение

Задачей, важной для практических приложений,

структуры зависимости энтропии S_p от конфигу-

является нахождение максимальной энтропии для

рации треугольника когерентных состояний. Вна-

заданного среднего числа фотонов

чале (рис. 2b) появляется локальный максимум в

(

)

точке G, величина которого быстро растет и при

N = Tr

a^†aρ

p = p_c = 1.097 его значение становится равным мак-

|α|² + |β|² + |γ|²

x² + y² + z²

= |ξ|² +

(37)

²⁾ В этом случае, например для конфигурации A,

где последнее равенство получено путем перехода

матрица плотности

(15) трансформируется в матрицу

к координатам амплитуд относительно цент-

ρ = (2|α〉〈α| + |β〉〈β|)/3, имеющую два собственных значения √ ][

роида α₁, β₁, γ₁

(27) и использования свойства

λ_± =

3±

1 + 8exp(-p²) /6, которые, как можно пока-

α₁ + β₁ + γ₁ = 0. Как и в случае двух когерентных

зать, совпадают с собственными значениями, вычисляемыми

состояний, рассмотренном в разд. 2, среднее число

по формуле (26): λ₊ = λ₀, λ_- = λ₂. Третье собственное зна-

чение λ₁ = 0.

фотонов зависит не только от относительных пара-

474

ЖЭТФ, том 163, вып. 4, 2023

Энтропия когерентных состояний . . .

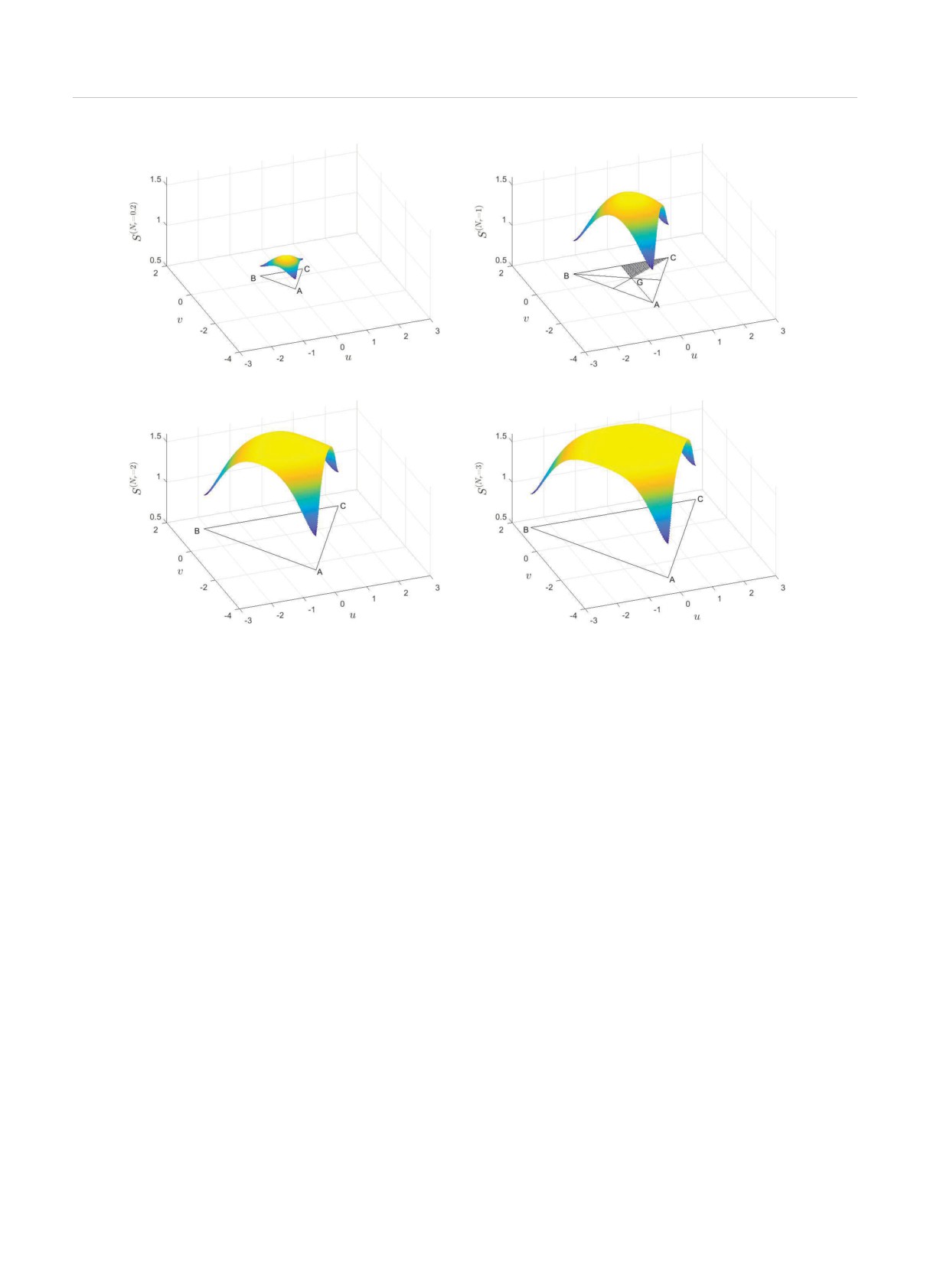
Рис. 3. Энтропия S(Nr) смеси трех когерентных состояний (15) с заданной относительной энергией ℏωNr для всевоз-

можных конфигураций треугольников, каждый из которых представлен точкой на плоскости {u = r cos ϕ, v = r sin ϕ} из

области ABC (см. обозначения на рис. 2). Nr = 0.2 (a), 1 (b), 2 (c) , 3 (d)

метров, но и от абсолютного — модуля координаты

r = 0, т.е. равностороннему треугольнику, центри-

центроида |ξ|. Энтропия как мера различимости

рованному в начале координат. Найденная величи-

состояний (букв), используемых для кодирования

на сравнивается с зависимостью S^max2(N), опреде-

сообщений, зависит только от относительной части

ляемой уравнением (13). Как для двух, так и для

энергии этих состояний, т.е. от величины

трех когерентных состояний максимальная энтро-

пия стремится к своему максимальному значению

N_r = (x² + y² + z²)/9.

с ростом среднего числа фотонов N. Важно, что не

только предельное значение для трех состояний вы-

В отличие от энтропии для множества треуголь-

ше предельного значения для двух, но и что кривая

ников с заданным полупериметром (рис. 2), энтро-

S^max3(N) всегда лежит выше кривой S^max2(N), да-

пия множества треугольников с заданной относи-

же при малых N, что видно на вставке на рис. 4.

тельной энергией ℏωN_r является выпуклой функ-

Это означает, что при сколь угодно высоком уровне

цией переменных {u = r cos ϕ, v = r sin ϕ}, как пока-

потерь в оптической линии связи кодирование на ос-

зывают примеры, приведенные на рис. 3. При этом

нове трех состояний превосходит по емкости коди-

ее максимум достигается для равностороннего тре-

рование на основе двух.

угольника и этот максимум растет с ростом N_r.

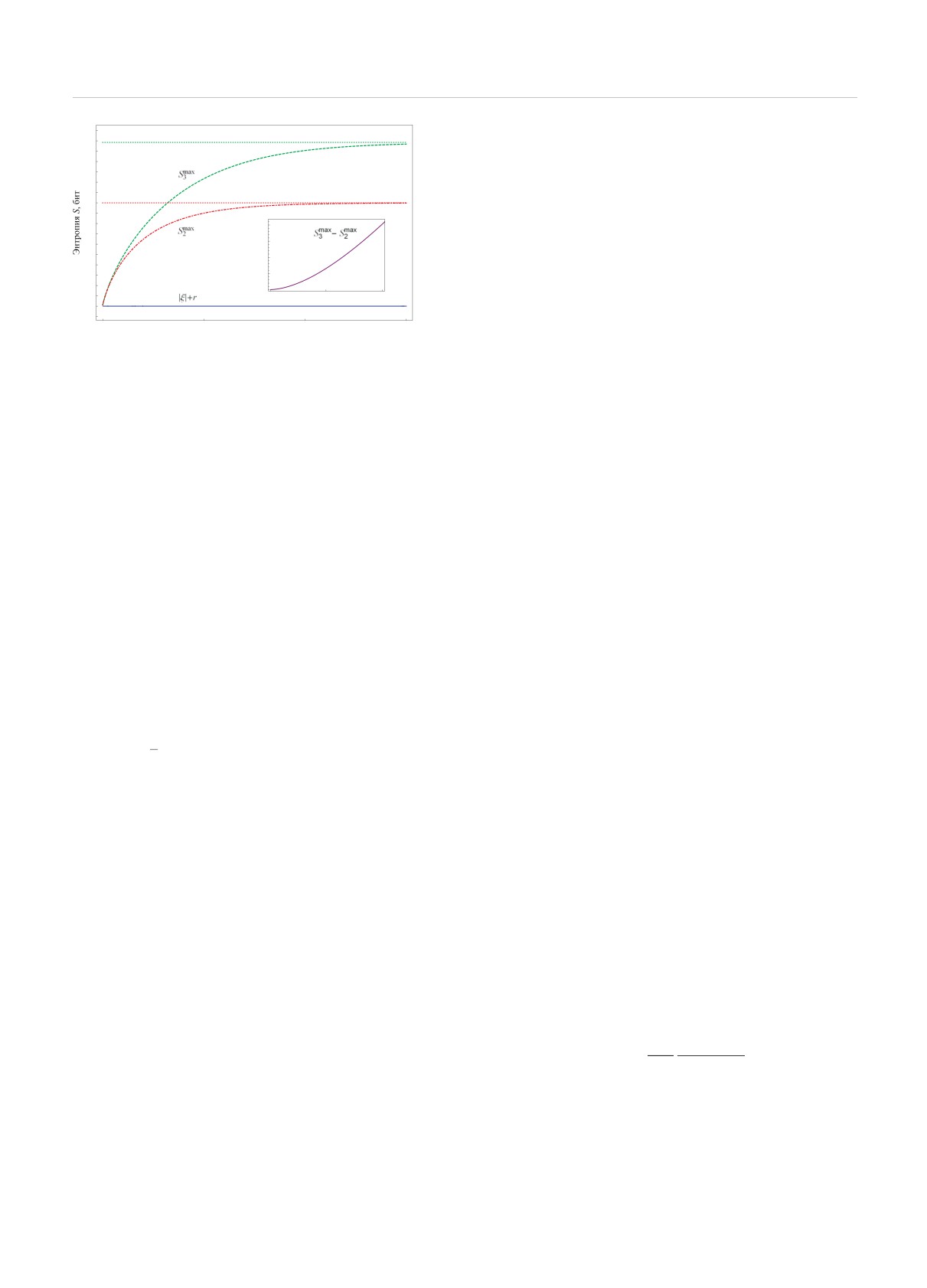
На рис. 4 показан результат численного поис-

ка максимальной энтропии S^max3(N) при заданном

3.4. Собственные векторы оператора

среднем числе фотонов N, где оптимизация прово-

плотности

дится по всем шести параметрам, как относитель-

ным, так и абсолютным. Максимальное значение

Для нахождения собственных векторов опера-

энтропии при каждом N соответствует |ξ| = 0 и тора плотности введем три новых вектора, являю-

475

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

чьи коэффициенты разложения можно получить,

действуя оператором D(-ξ) на обе части уравнения

(17) и воспользовавшись соотношением (38):

C^μn = C^μne-iIm(ξμ∗).

Учитывая, что модули скалярных произведений

пар когерентных состояний |〈μ|δ〉| в уравнениях (18)

определяются одним параметром — расстоянием

между ними (28), равным в рассматриваемом случае

стороне треугольника, противоположной третьему

когерентному состоянию, не входящему в пару {μ, δ}

из множества трех амплитуд A = {α, β, γ}:

Рис. 4. Максимальная энтропия при заданном среднем

числе фотонов при использовании трех (штриховая зеле-

(A\ {α, β} = {γ} , A\ {β, γ} = {α} , A\ {α, γ} = {β}) ,

ная линия) и двух (штрих-пунктирная красная линия) ко-

введем функцию

герентных состояний. Значение |ξ| + r, при котором до-

стигается максимум S^max3 (сплошная синяя линия), равно

s(γ) = x, s(α) = y, s(β) = z,

(41)

нулю. Вставка показывает, что разность энтропий для трех

и двух состояний всегда положительна

которая, с учетом полученных собственных значе-

ний (26), позволяет представить уравнения (18) для

щихся результатом действия унитарного оператора

векторов с центроидом в начале координат (40)

сдвига (10) на состояния-буквы:

в виде

⎛

⎞

ν_n

q_s(γ)eiψαβ q_s(β)eiψαγ

⎞

C^αn

|ψ_μ〉 = D(-ξ)|μ〉 = e-iIm(ξμ∗)|μ₁〉,

(38)

⎜

⎟⎜

⎟

⎝q_s(γ)eiψβα

ν_n

q_s(α)eiψβγ

⎠

C^βn⎠ = 0.

где μ принимает значения α, β и γ. Если новые со-

q_s(β)eiψγα q_s(α)eiψγβ

ν_n

C^γ

стояния моды поля служат буквами алфавита для

(42)

кодирования сообщений в квантовом канале связи

Здесь

и имеют равные статистические веса, то оператор

ν_n = sin(θ + 2πn/3),

плотности случайно выбранной моды имеет вид

q_s(μ) = e-(s(μ))2/2/(2T)

ρ=

(|ψ_α〉〈ψ_α| + |ψ_β 〉〈ψ_β | + |ψ_γ 〉〈ψ_γ |) =

— набор нормированных скалярных произведений

(

)

= D(-ξ)ρD^†(-ξ).

(39)

q^2s(α) + q^2s(β) + q^2s(γ) = 3/4 ,

Поскольку оператор ρ получен из оператора ρ по-

а ψ_μδ = Im(μ^∗δ) — фазы соответствующих произве-

средством унитарного преобразования, его собствен-

дений 〈μ₁|δ₁〉:

ные значения равны λ_n, а собственные векторы име-

ют вид

ψ_αβ = ψ_βγ = ψ_γα =

|λn〉 = D(-ξ)|λ_n〉.

= -ψ_αγ = -ψ_βα = -ψ_γβ = ψ = 2S_αβγ/3 > 0.

Таким образом, найдя собственные векторы ρ, что

Решение уравнений (42) дает три ортонормиро-

проще, чем находить собственные векторы ρ, мы по-

ванных, 〈λn|λm〉 = δ_nm, собственных вектора (40),



₂

лучим последние в виде



распределение девяти амплитуд вероятностей

C^μn

в которых определяется соотношением

|λ_n〉 = D(ξ)|λn〉.



ν²ⁿ - q^2s(μ)



C^μn2 =

(43)

Три собственных вектора оператора плотности ρ

9λ_n ν²ⁿ - 1/4

лежат в линейной оболочке трех когерентных состо-

а их фазы задаются с точностью до произвольного

яний {|α₁〉, |β₁〉, |γ₁〉} и могут быть записаны в виде

слагаемого, например, фаз амплитуд

C^γn для различ-

суперпозиции

ных n,



|λn〉 =

C^αn|α₁〉 +

C^βn|β₁〉 +

C^γn|γ₁〉,

(40)

C^μn =

C^μneiΨn

^γ,

μ = α,β,

(44)

476

ЖЭТФ, том 163, вып. 4, 2023

Энтропия когерентных состояний . . .

посредством выражения

выполненных для равностороннего треугольника,

собственные векторы (46) можно также предста-

-2iψμγ

-ν_nq_s(A/{μ,γ})eiψμγ + q_s(μ)q_s(γ)e

вить, используя три проекционных оператора

eiΨnγ =

√

(ν²ⁿ - q^2s(μ))(ν²ⁿ - q^2s(γ))

(

)

2π

P^(g)3

â^†â

(1+2 cos

(â^†â+g)), g = 0, ±1, (48)

(45)

Наиболее простой вид собственные векторы при-

которые удовлетворяют соотношениям

нимают в случае равностороннего треугольника с

P⁽ⁱ⁾³P^(j)3 = δ_ij P⁽ⁱ⁾³

центром в начале координат (ξ = 0), для которого,

как было установлено выше, энтропия максималь-

и образуют полный набор

на при заданном среднем числе фотонов. Для него

∑

√

q_s(μ) = 1/2, θ = ψ + π/6, ψ =

3|γ|²/2, что, соглас-

P^(g)3 =

но уравнениям (43)-(45), приводит к следующим яв-

g=0,±1

ным выражениям для собственных векторов:

а именно,



(

)



(

)

λ

√ P(gn)3

â^†â

|γ〉 ,

(49)

|λn〉 =

√ eⁱ

(n+1)|α〉 + e^-i

(n+1)|β〉 + |γ〉 ,

λ_n

n = 0, 1, 2,

(46)

где индексы g_n однозначно связаны с индексами n:³⁾

g_n = (2 + n)mod3 - 1,

(50)

и собственных значений (26) (рис. 5):

[

(

)]

т.е. g₀ = 1, g₁ = -1, g₂ = 0, при этом

π (1 + 4n)

λ_n =

1-2e^-

|γ|² sin ψ +

(47)

(

)

λ_n = 〈γ| P(gn)3

â^†â

|γ〉 .

Оператор P⁽⁰⁾³ осуществляет проецирование на под-

пространство фоковских состояний | n〉, индекс ко-

торых n кратен 3:

(

)

P⁽⁰⁾³

â^†â

| n〉 = δ_n,3k | n〉, k = 0, 1, 2, . . .

(51)

Если рассматривать целые неотрицательные числа,

кратные трем, как неотрицательную часть P (H₃)

подгруппы H₃ аддитивной группы целых чисел, то

операторы P^(±1)3 осуществляют проецирование на

подпространства фоковских состояний, индексы ко-

торых соответствуют неотрицательной части сме-

щенных классов по подгруппе H₃,

P (H₃) = 0, 3, 6, 9, . . .,

P (H₃ + 1) = 1, 4, 7, 10, . . .,

P (H₃ + 2) = 2, 5, 8, 11, . . .,

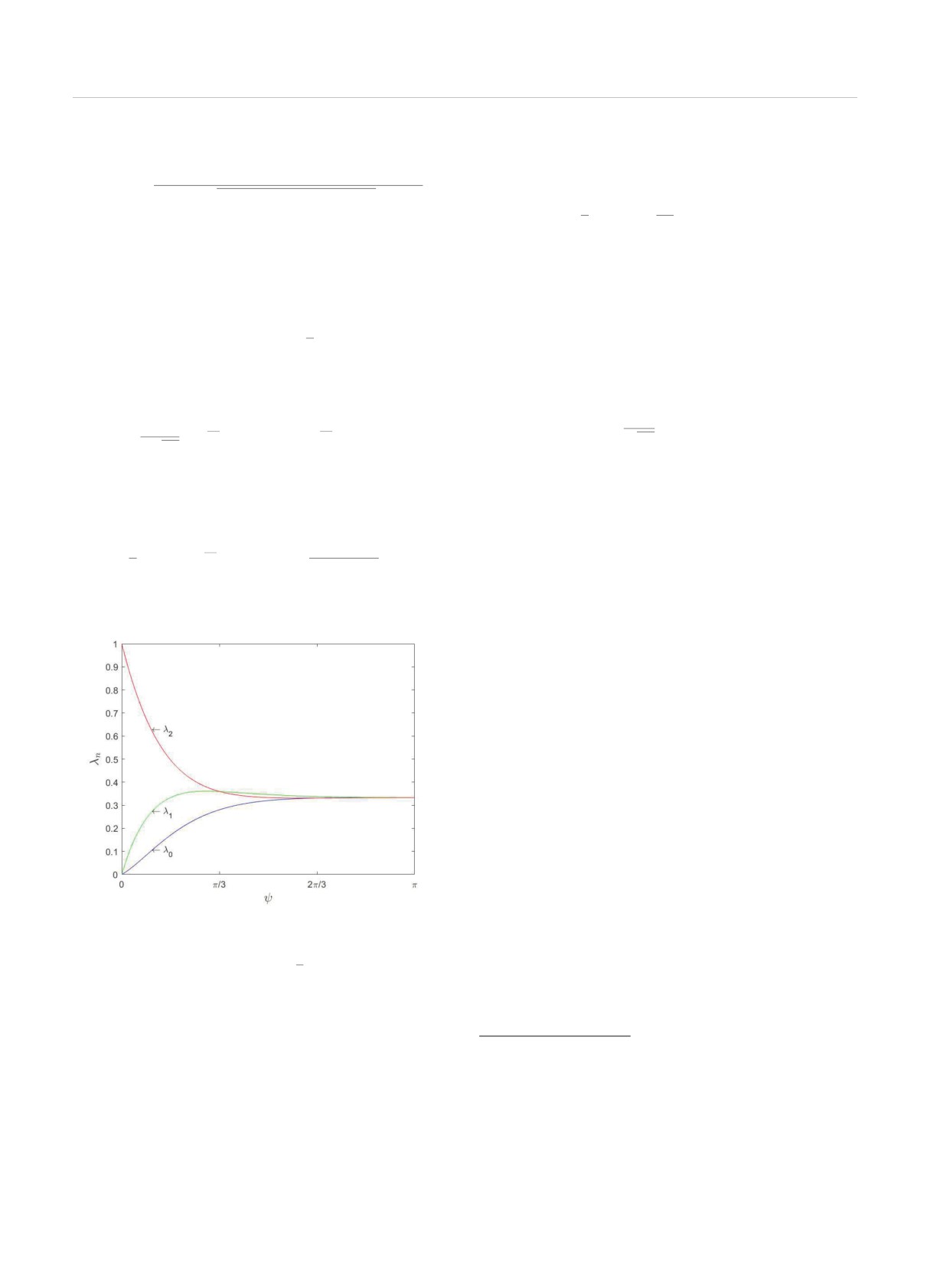
Рис. 5. Собственные значения λn (47) для случая рав-

так как имеют место соотношения

ностороннего треугольника как функции его площади

√

(

)

ψ = 2S_αβγ/3 =

3|α|²/2

P^(-1)3

â^†â

| n〉 = δ_n,3k+1 | n〉,

(

)

k = 0,1,2,...

(52)

(+1)

P₃

â^†â

| n〉 = δ_n,3k+2 | n〉,

Состояния (46) представляют собой суперпози-

ции когерентных состояний, лежащих на окружно-

³⁾ Для доказательства данного равенства удобно

сти в фазовой плоскости, и широко изучаются в свя-

представить выражения для проекционных операторов

зи с тем, что являются оптическими реализациями

P(gn)3

(â† â) в нормально-упорядоченном виде. Стар-

многокомпонентного кота Шрёдингера [26, 32].

туя с соотношения eiuâ†â

:e(eiu-1)â†â :, получим

В силу соотношений

cos

(u(â†â + g))

:e(cosu-1)â†â cos(sin(u)â^†â + g) :,

что приводит к равенству λn

= γ|P(gn)3

(â† â) |γ с λn,

α=e^i2π/3γ, β = e^-i2π/3γ,

определенным выше в (47).

477

М. М. Эскандери, С. Я. Килин, Д. Б. Хорошко

ЖЭТФ, том 163, вып. 4, 2023

Следовательно, ортогональность состояний |λn〉

деляется конструкцией ресивера, используемого на

проявляется как непересечение подпространств,

принимающей станции. Однако энтропийные соот-

в которых расположены векторы

|λ2〉, |λ1〉, |λ0〉.

ношения, исследованные в данной статье, определя-

Уравнения (51) и (52) также демонстрируют причи-

ют фундаментальный предел, достижимый с совер-

ну соотношения собственных значений λ₂ > λ₁ > λ₀

шенствованием оптических ресиверов.

при ψ < π/3 (см. рис. 5), связанную с тем, что

при малых амплитудах когерентных состояний бу-

дут преобладать состояния из подгруппы, содержа-

ЛИТЕРАТУРА

щей вакуумные состояния, т.е. состояния |λ2〉, созда-

С. Я. Килин, Квантовая оптика. Поля и их де-

ваемые проектором P⁽⁰⁾³ (49). При увеличении ам-

тектирование, Едиториал УРСС, Москва (2003).

плитуд когерентных состояний веса состояний |λ1〉

и |λ0〉 поочередно становятся равными λ₂. Сначала,

В. А. Фок, Начала квантовой механики, Наука,

Москва (1976).

при ψ = π/3, достигается равенство λ₂ = λ₁, демон-

стрируя увеличение веса однофотонных состояний

С. Я. Килин, УФН 169, 507 (1999).

из |λ1〉 . Затем, при ψ = 2π/3, становятся значимы-

К. Хелстром, Квантовая теория проверки гипо-

ми двухфотонные состояния из |λ0〉 и достигается

тез и оценивания, Мир, Москва (1979).

равенство λ₂ = λ₀ (рис. 5). Веса состояний |λ1〉 и

|λ0〉 выравниваются при ψ = π. При дальнейшем

Дж. Прокис, Цифровая связь, Радио и связь,

увеличении амплитуд данное чередование собствен-

Москва (2000).

ных значений продолжается с периодом π и с од-

T. Muciaccia, F. Gargano, and V. M. N. Passaro,

новременным их стремлением к значению 1/3. От-

Photonics 1, 323 (2014).

меченное различие собственных значений в опреде-

ленном диапазоне амплитуд когерентных состояний

I. A. Burenkov, O. V. Tikhonova, S. V. Polyakov,

является основанием для использования процедуры

Optica 5, 227 (2018).

компрессии квантовых данных [14] при кодировании

B. Djordjevic,

Advanced Coding for

передаваемых сообщений с помощью когерентных

Optical Communications, in Optical Fiber

состояний.

Telecommunications (Sixth Edition), ed. by I.

P. Kaminow, T. Li, and A. E. Willner, Academic

Press, Boston (2013).

4. ЗАКЛЮЧЕНИЕ

I. Khan, D. Elser, T. Dirmeier et al., Phil. Trans. Roy.

Soc. A 375, 20160235 (2017).

В данной статье исследована емкость оптическо-

го канала связи с использованием сигнальных со-

10.

Квантовая криптография: идеи и практика, под

ред. С. Я. Килина, Д. Б. Хорошко, А. П. Низовце-

звездий в виде двух и трех произвольных когерент-

ва, Белорусская наука, Минск (2007).

ных состояний. С этой целью была вычислена энтро-

пия фон Неймана для статистической смеси двух и

11.

D. Sych and G. Leuchs, New J. Phys. 12, 053019

трех равновероятных когерентных состояний. Для

(2010).

случая трех состояний была введена оригиналь-

12.

Д. Б. Хорошко, Д. И. Пустоход, С. Я. Килин, Опт.

ная параметризация треугольника, представляюще-

и спектр. 112, 373 (2012).

го три когерентных состояния на комплексной плос-

кости, и на ее основе установлены собственные зна-

13.

B. Schumacher, Phys. Rev. A 51, 2738 (1995).

чения и собственные векторы оператора плотности

14.

S. Ya. Kilin, Progr. Opt. 42, 3 (2001).

смеси трех произвольных когерентных состояний.

Для практических применений наибольшее зна-

15.

A. Furusawa, J. L. Sørensen, S. L. Braunstein et al.,

Science 282, 706 (1998).

чение имеет следующий основной результат: при за-

данном среднем числе фотонов энтропия оптималь-

16.

D. B. Horoshko and S. Ya. Kilin, Phys. Rev. A 61,

ной смеси трех состояний всегда превосходит энтро-

032304 (2000).

пию оптимальной смеси двух состояний и оптималь-

17.

J. H. Shapiro, G. Saplacoglu, S.-T. Ho et al., J. Opt.

ной конфигурацией является равносторонний тре-

Soc. Amer. B 4, 1604 (1987).

угольник с центром в начале координат. Следует от-

метить, что энтропия определяет верхний предел пе-

18.

A. V. Masalov, A. A. Putilin, and M. V. Vasilyev, J.

редаваемой информации, а ее реальный объем опре-

Mod. Opt. 41, 1941 (1994).

478