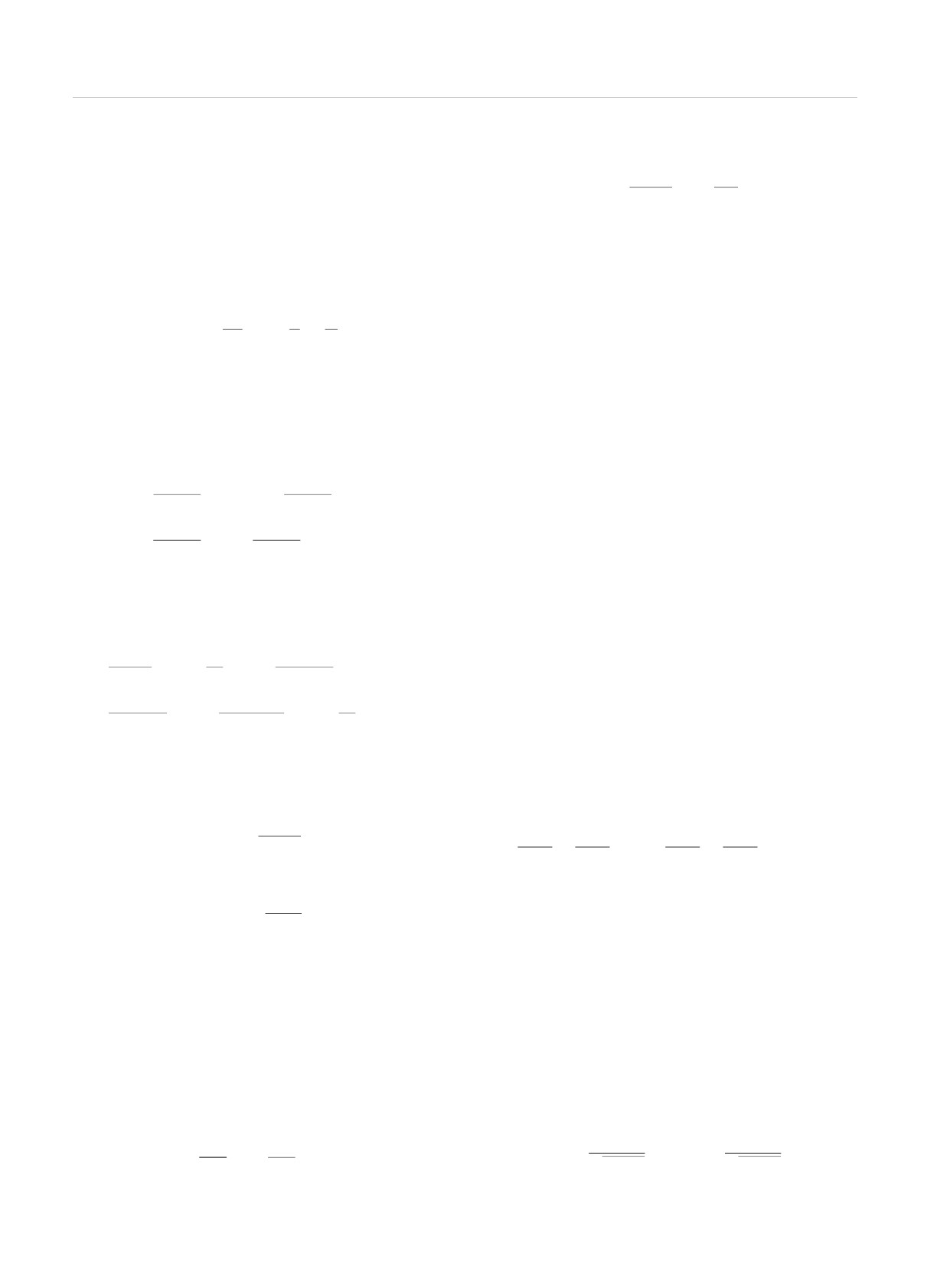ЖЭТФ, 2023, том 163, вып. 5, стр. 734-743

ЭВОЛЮЦИЯ НЕЛИНЕЙНЫХ ВОЛНОВЫХ ИМПУЛЬСОВ В

ТЕОРИИ УРАВНЕНИЯ СИНУС-ГОРДОН

А. М. Камчатнов^a*

^a Институт спектроскопии Российской академии наук

108840 Москва, Троицк, Россия

Поступила в редакцию 27 декабря 2022 г.,

после переработки 27 декабря 2022 г.

Принята к публикации 26 января 2023 г.

Дано решение модуляционных уравнений Уизема, описывающих эволюцию огибающих однофазных пе-

риодических волн, подчиняющихся уравнению синус-Гордон. Методом годографа задача сведена к ли-

нейному уравнению в частных производных и описан класс решений этого уравнения с разделяющимися

переменными. Теория иллюстрируется примером, в котором получено полное аналитическое решение

задачи о самосжатии нелинейного волнового пакета, которое сопровождается уходом волн из области

нелинейных колебаний.

DOI: 10.31857/S0044451023050127

шение для пучка с параболическим начальным про-

EDN: BFLYCL

филем интенсивности [9], а С. А. Ахманов, А. П. Су-

хоруков, Р. В. Хохлов [10] — для пучков с началь-

ным профилем интенсивности вида ch^-2(x). В рабо-

1. ВВЕДЕНИЕ

тах [11,12] аналогичный подход был сформулирован

независимо от теории НУШ, но также в приближе-

Явление модуляционной неустойчивости нели-

нии умеренной амплитуды волны, и в результате мо-

нейных волн было открыто независимо в нескольких

дуляционная гидродинамическая система была све-

различных физических контекстах: как самофоку-

дена методом годографа к линейному уравнению эл-

сировка интенсивных пучков света, распространяю-

липтического типа. Примеры решений этого уравне-

щихся в нелинейной среде [1-3], как разбиение га-

ния, описывающих самофокусировку пучков света и

за ленгмюровских плазмонов на отдельные сгустки

самокомпрессию импульсов, были даны в [13] и дру-

[4, 5], как самосжатие волновых пакетов для волн в

гие многочисленные примеры можно найти в книге

оптике [6] и на глубокой воде [7, 8]. Если началь-

[14].

ное распределение физических параметров волны

Естественно, эти решения, предполагающие

промодулировано достаточно плавными функция-

плавную модуляцию волны, справедливы лишь до

ми, то в главном приближении динамика модуля-

ций описывается уравнениями гидродинамического

момента фокусировки. Кроме того, они неустойчи-

вы относительно малых возмущений, нарушающих

типа, для решения которых могут быть использо-

ваны методы газовой динамики. Первые примеры

плавность профиля волны. Еще в работах [15, 16]

было замечено, что в теории фокусирующего НУШ

такого подхода были даны в теории самофокуси-

локализованное начальное возмущение однородной

ровки, когда эволюция пучка света описывается фо-

плоской волны ведет к образованию расширяю-

кусирующим нелинейным уравнением Шредингера,

щейся со временем промодулированной волновой

так что модуляционными параметрами служат ин-

структуры. Применение модуляционной теории

тенсивность света и поперечное волновое число све-

Уизема [17-20] к описанию эволюции этой струк-

товой волны, которые подчиняются уравнениям гео-

метрической оптики, эквивалентным гидродинами-

туры показало [21-23], что фронт неустойчивости

движется с минимальной групповой скоростью

ческим уравнениям для волн на «опрокинутой мел-

действительной ветви закона дисперсии, и этот

кой воде». Для этого случая В. И. Таланов нашел ре-

результат был подтвержден в [24] в рамках метода

^* E-mail: kamch@isan.troitsk.ru

обратной задачи рассеяния для НУШ. Обобщение

734

ЖЭТФ, том 163, вып. 5, 2023

Эволюция волновых импульсов

[25] этой теории на неоднородные эволюционирую-

Целью настоящей работы является развитие ме-

щие волны позволило найти закон движения границ

тода решения модуляционных уравнений Уизема

области нелинейных осцилляций для произволь-

для однофазных периодических волн, эволюция ко-

ных плавных начальных профилей неустойчивого

торых подчиняется уравнению синус-Гордон. Ра-

импульса.

нее уравнения релятивистской гидродинамики изу-

Описанные выше результаты основаны на том,

чались в теории множественного рождения час-

что в главном приближении волна является линей-

тиц при ультрарелятивистских столкновениях ядер

ной, так что нелинейность вносит лишь небольшую,

и нуклонов [30-33]. Мы покажем, что развитые в

зависящую от амплитуды, поправку в закон диспер-

этих работах методы, использующие крайне про-

сии. В геометро-оптическом приближении это экви-

стое уравнение состояния ультрарелятивистской ма-

терии p = e/3 (p — давление, e — плотность энер-

валентно зависимости показателя преломления сре-

ды от интенсивности света, и тогда уравнения гео-

гии), могут быть модифицированы применительно

к существенно более сложному случаю уравнения

метрической оптики для пучков света, распростра-

няющихся в фокусирующей среде, превращаются

синус-Гордон. В результате будет выведено линей-

в гидродинамические уравнения для «опрокинутой

ное уравнение в частных производных, определя-

мелкой воды», простота которых позволяет исполь-

ющее решение уравнений релятивистской гидроди-

зовать хорошо разработанные методы газовой дина-

намики в методе годографа, и описан класс реше-

мики. Ситуация меняется, однако, в случае извест-

ний этого уравнения с разделяющимися переменны-

ного нелинейного уравнения Клейна-Гордона

ми. Теория будет проиллюстрирована примером са-

мосжатия нелинейного волнового пакета, когда его

эволюция демонстрирует уход волн из области нели-

ϕ_tt - ϕ_xx + U^′(ϕ) = 0, U^′ =

U^′(0) = 0,

(1)

нейных осцилляций через малоамплитудный край

dϕ

этой области.

имеющего многочисленные приложения к физиче-

ским задачам, особенно в частном случае так на-

2. УРАВНЕНИЯ УИЗЕМА

зываемого уравнения синус-Гордон с U^′(ϕ) = sin ϕ

(см., например, [26, 27] и имеющиеся там ссылки).

Приведем здесь основные соотношения модуля-

Это уравнение имеет решения в виде нелинейных

ционной теории Уизема [17, 18] для нелинейного

периодических волн ϕ = ϕ(A, kx - ωt), для кото-

уравнения Клейна-Гордона (1). Легко видеть, что

рых зависимость частоты ω от амплитуды волны A

это уравнение имеет решения в виде бегущей волны

уже не может считаться малой поправкой. В про-

ϕ = ϕ(ξ), ξ = x - V t, где ϕ(ξ) определяется неявно

модулированной волне ее амплитуда A и фазовая

уравнением

скорость V

= ω/k становятся медленными функ-

√

∫

циями координаты x и времени t, мало изменяю-

V² - 1

dϕ

ξ-ξ₀ =

√

(2)

щимися на одной длине волны и за один период.

A - U(ϕ)

ϕ0

Соответствующие модуляционные уравнения, опре-

деляющие динамику A и V , были получены Уизе-

так что V и постоянная интегрирования A являются

мом [17,18]. В работе [28] на основе метода усредне-

постоянными параметрами, ϕ(ξ₀) = ϕ₀, и перемен-

ния Боголюбова-Митропольского было указано, что

ная ϕ осциллирует между двумя корнями уравнения

уравнения квазиклассической асимптотики для (1),

A - U(ϕ) = 0 в интервале положительности под-

совпадающие с уравнениями Уизема, эквивалент-

коренного выражения. Следуя Уизему [17, 18], мы

ны уравнениям релятивистской гидродинамики (см.

определяем функцию

также обзор [29]). Существенно, что в наиболее ин-

√

∮ √

тересном случае уравнения синус-Гордон эта дина-

W (V, A) =

2(V² - 1)

A - U(ϕ)dϕ ≡

(3)

мика снова оказывается модуляционно неустойчи-

√

≡

V² - 1G(A),

вой, однако как ввиду сложности уравнения состоя-

ния, отвечающего закону дисперсии ω = ω(k, A) для

где интеграл берется по контуру вокруг указанного

волн в «эффективной релятивистской материи», так

интервала положительности подкоренного выраже-

и сложности уравнений релятивистской гидродина-

ния. Тогда длина волны найденного периодического

мики, задача об эволюции нелинейных волновых па-

решения выражается формулой

кетов в теории уравнения синус-Гордон пока деталь-

√

∂W

но не исследовалась.

V² - 1G^′(A).

(4)

∂A

735

А. М. Камчатнов

ЖЭТФ, том 163, вып. 5, 2023

Мы определяем волновое число k как величи-

введением римановых инвариантов

ну, обратную длине волны, k

= 1/L, так что

∫

∫A

k²(V²-1) = (G^′)^-2, и получаем для частоты ω = kV

cG^′

r_± =

dA,

(12)

закон дисперсии

1-v²

что существенно упрощает решение задач в случае

ω² = k² + (G^′(A))^-2,

(5)

вещественности скорости звука c (положительности

выражения в правой части (10)). Нас, однако, бу-

существенным образом зависящий от амплитуды A.

дет интересовать противоположный случай мнимой

Групповая скорость определяется выражением

«скорости звука» c, для чего необходимо обсудить

)

(∂ω

более детально свойства релятивистской гидродина-

(6)

∂k_A

мики для модели синус-Гордон.

В промодулированной волне параметры V и A

становятся медленными функциями координаты x

3. РЕЛЯТИВИСТСКАЯ ГИДРОДИНАМИКА

и времени t, и их эволюция подчиняется модуляци-

ДЛЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ

онным уравнениям Уизема [17, 18], которые могут

КЛЕЙНА-ГОРДОНА

быть записаны в наших обозначениях в виде

Еще Уизем в своей основополагающей работе [17]

(

)

(

)

kV W

заметил, что процедура усреднения законов сохра-

= 0,

V² - 1

V²

-1

нения волнового движения по быстрым осцилляци-

(

)

(

)

(7)

kV W

kV²W

ям аналогична переходу от микроскопического опи-

-A

= 0.

сания движения среды в статистической механике

V² - 1

к ее усредненному гидродинамическому описанию,

Для перехода к релятивистской интерпретации этих

справедливому при условии малости градиентов фи-

уравнений удобно исключить из них W и V с помо-

зических параметров, характеризующих среду. В

щью формул (3) и (6), и тогда мы получаем

нашем случае такими параметрами служат A и V ,

)

уравнение (1) релятивистски инвариантно, так что

( G/G^′

( (G/G^′)v)

+A-

= 0,

естественно ожидать, что после усреднения законов

1-v²

G^′t

1-v²

сохранения мы должны прийти к уравнениям реля-

)

(8)

( (G/G^′)v)

( (G/G^′)v²

тивистской гидродинамики. В рамках асимптотиче-

-A+

= 0.

1-v²

G^′

ского метода ВКБ это было показано в работе [28].

Однако для записи уравнений Уизема (8) в форме

Линеаризация этих уравнений относительно малых

уравнений релятивистской гидродинамики удобнее

отклонений от постоянных значений A и v дает ха-

исходить из закона сохранения энергии-импульса в

рактеристические скорости

релятивистском течении (см. [34]):

v±c

v_± =

(9)

∂T⁰⁰

∂T¹⁰

∂T¹¹

1±vc

= 0,

(13)

∂t

∂x

∂t

∂x

где c определяется выражением

где

′′

T^ij = wuⁱu^j - pg^ij, i, j = 1, 2,

(14)

c² = -

(10)

(G^′)²

— тензор энергии импульса в двумерном простран-

стве Минковского с метрикой

В случае положительности этого выражения фор-

(

)

мулы (9) имеют простой физический смысл: они да-

g^ij =

(15)

ют скорости распространения звукового сигнала со

-1

звуковой скоростью c по или против течения «сре-

ды», движущейся со скоростью v, так что в лабора-

w = e + p — тепловая функция на единицу объе-

торной системе отсчета скорость сигнала равна ре-

ма, e — плотность энергии, p — давление, uⁱ — дву-

лятивистской сумме скоростей.

мерный вектор «4-скорости». Для отождествления

Уравнения (8) могут быть преобразованы к диа-

уравнений Уизема (8) с уравнениями (13) мы вво-

гональной форме

дим стандартным образом 4-вектор uⁱ:

∂r_±

u⁰ =

√

u¹ =

√

(16)

+v_±

(11)

∂t

∂x

1-v²

736

ЖЭТФ, том 163, вып. 5, 2023

Эволюция волновых импульсов

и тогда легко видеть, что уравнения (8) и (13) сов-

согласующееся со стандартным термодинамическим

падают, если

определением энтропии.

В переменных T, σ, uⁱ гидродинамические урав-

G/(2G^′)

T⁰⁰ =

-p=

нения можно записать в особенно простом виде. За-

1-v²

2G^′

мечаем, что формулы для волнового числа k = 1/L

(G/(2G^′))v

T¹⁰ = T⁰¹ =

(17)

и частоты ω = kV = k/v переходят в

1-v²

G/(2G^′)

( dG)-1

T¹¹ =

+p=

k = 2u¹

u¹T,

1-v²

2G^′

(22)

u⁰

где мы поделили для дальнейшего удобства уравне-

ω=k

u⁰T.

ния (8) на 2. Отсюда следует связь амплитуды вол-

u¹

ны A с термодинамическими функциями эффектив-

Следовательно, следующий из уравнений (7) закон

ной материи, подчиняющейся гидродинамическим

сохранения числа волн (см. [17, 18])

уравнениям (13):

k_t + ω_x = 0

(23)

w=e+p=

(18)

переходит в

2G^′

Существенно, что давление p зависит только от

(u¹T )_t + (u⁰T )_x = 0.

(24)

плотности энергии e. Это означает, что масса час-

Отметим, что это соотношение было получено

тиц эффективной материи пренебрежимо мала, хо-

И. М. Халатниковым [31] из уравнений (13) для

тя уравнение состояния p = p(e) определяется суще-

любого одномерного течения, что доказывает его

ственно более сложной формулой, чем обычно пред-

потенциальность. В теории Уизема уравнение (23)

полагаемое уравнение состояния p = e/3 для ультра-

следует из того, что волновое число и частота

релятивистской материи (см. [30-33]). Легко видеть,

определены как производные фазы: k = θ_x, ω = -θ_t.

что выражение (10) для скорости звука можно за-

Как мы видим, обе картины — модуляционная

писать в стандартном виде

уиземовская и релятивистская гидродинамическая

— математически согласованы друг с другом, отли-

c² =

(19)

чаясь лишь обозначениями и физическим смыслом

переменных.

Температуру T и плотность энтропии σ эффектив-

Еще одно уравнение легко получаем из формулы

ной материи можно определить следующим обра-

зом. В случае безмассовых частиц химический по-

∂(wuⁱ)

∂p

-uⁱ

= 0,

(25)

тенциал равен нулю, так что тепловая функция вы-

∂xⁱ

ражается формулой w

= Tσ, а из соотношения

являющейся следствием уравнений (13), (14) (см.

dw = T dσ + dp = d(T σ) следует dp = σdT (см. [35]).

формулу (134.5) и задачу 2 в §134 книги [34]). Под-

Следовательно, квадрат скорости звука можно за-

становка в нее w = T σ, dp = σdT мгновенно дает

писать двумя способами: из (10) и (18) находим

уравнение

∂(σu⁰)

∂(σu¹)

d²G/de

= 0,

(26)

c² = -w

∂t

∂x

dG/de

выражающее сохранение энтропии, то есть адиаба-

а из формулы (19) с учетом dp = σdT = (w/T )dT

тичность течения.

имеем

Конкретизируем эти соотношения для уравне-

w dT

ния синус-Гордон, когда в (1)

c² =

T de

U^′(ϕ) = sin ϕ,

U (ϕ) = 1 - cos ϕ.

(27)

Сравнение этих двух выражений дает формулы

)_-1

В этом случае интеграл в (2) сводится к эллиптиче-

( dG

T =γ

σ=

G(e),

(20)

скому интегралу первого рода и его обращение дает

периодическое решение в явном виде

)]

где постоянный множитель γ имеет в обеих форму-

ξ-ξ₀

лах одно и то же значение. Отсюда следует соотно-

ϕ = 2arcsin

[√e sn(√

V² - 1

шение

)]

(28)

1 dG

v(x - x₀) - t

dσ =

de =

(21)

= 2arcsin

[√e sn(

√

γ de

1-v²

737

А. М. Камчатнов

ЖЭТФ, том 163, вып. 5, 2023

При e → 1 это решение переходит в известное реше-

4. ПРЕОБРАЗОВАНИЕ ГОДОГРАФА

ние уравнения синус-Гордон в виде «кинка»,

Для проведения преобразования годографа вво-

)]

[√

(v(x - x₀) - t

дим вместо скорости v «быстроту» y согласно урав-

ϕ = 2arcsin e th

√

(29)

1-v²

нениям

то есть волны, переходящей от значения ϕ = -π

u⁰ = chy,

u¹ = shy,

v = thy,

(36)

при x → -∞ к значению ϕ = π при x → +∞. Вы-

а также переходим к переменным светового конуса

числение интеграла в (3) с помощью подстановки

sin(ϕ/2) =

√e sin ψ дает

x- = t - x,

x+ = t + x.

(37)

∫

√

Тогда уравнение (24) приобретает вид

G(e) = 2

2e - 1 + cosϕdϕ =

(

)

(

)

(30)

∂

e^-y

∂

e^y

-ϕ0

= 0,

(38)

∂x_- K(e)

∂x₊ K(e)

= 16{E(e) - (1 - e)K(e)},

и оно удовлетворяется, если

где K(e), E(e) — полные эллиптические интегралы

e^-y

∂φ

e^y

∂φ

первого и второго рода, соответственно, определен-

(39)

K(e)

∂x_-

K(e)

∂x₊

ные здесь согласно справочнику [36] (±ϕ₀ являют-

ся нулями подынтегрального выражения). Выбирая

для некого потенциала φ = φ(x_-, x₊). Теперь, сле-

для постоянной γ в (20) значение γ = 8 и исполь-

дуя Халатникову [31], мы делаем преобразование

зуя известные формулы для производных эллипти-

Лежандра, переходя к потенциалу W = W(e, y),

ческих интегралов по параметру e,

W =φ-K^-1e^yx_- -K^-1e^-yx₊

(40)

E - (1 - e)K

E-K

(31)

2e(1 - e)

так что

мы находим выражения для термодинамических

dK^-1

dW = -

(e^yx_- + e^-yx₊)de-

функций

(41)

e^-yx₊)dy,

T =

σ = 4e(1 - e)

= 2[E - (1 - e)K]. (32)

− K(eyx^- -

откуда

Уравнение состояния p = p(e) имеет вид

(

)

e^-y

∂W

(

)

x- = -

E(e)

dK^-1/de ∂e

∂y

p=2

-1

+ e.

(33)

(

)

(42)

K(e)

e^y

∂W

x₊ = -

-K

dK^-1/de ∂e

∂y

Квадрат скорости звука

Эти формулы осуществляют преобразование годо-

)₂

( 1 dK

графа: если функция W = W(e, y) известна, то они

c² = -4e(1 - e)

(34)

K de

дают в неявном виде зависимость e и y от перемен-

ных (37) и тем самым от x и t.

отрицателен в области 0 ≤ e < 1 существования

Уравнение (26) после замен (36), (37) переходит

периодических решений, то есть модуляционная си-

стема Уизема отвечает модуляционной неустойчиво-

сти периодической волны. Соответственно римано-

∂(σe^-y)

∂(σe^y )

вы инварианты (12) являются комплексными:

∂x_-

∂x₊

(43)

∂(σe^-y, x₊)

∂(x_-, σe^y)

1+v

= 0.

r± =

± iarcsin

√e.

(35)

∂(x_-, x₊)

1-v

Умножая его на якобиан ∂(x_-, x₊)/∂(e, y), получа-

Тем не менее, подобно теории НУШ, эволюция

ем после простых преобразований с учетом формул

плавных распределений модуляционных парамет-

(32) и dσ/de = 1/T = K(e) уравнение для W:

ров подчиняется гидродинамическим уравнениям

[

]

(24), (26), решение которых может быть получено

∂

∂W

K² ∂²W

e(1 - e)K²

(44)

преобразованием годографа.

∂e

∂y²

738

ЖЭТФ, том 163, вып. 5, 2023

Эволюция волновых импульсов

или

f₁, f₂

∂²W

(E(e)

) ∂W

1∂²W

e(1 - e)

-e

= 0. (45)

∂e²

K(e)

∂e

4 ∂y²

f₂(e)

Это уравнение является эллиптическим и оно за-

меняет уравнение Эйлера-Пуассона, возникающее в

приложении метода годографа к уравнениям газо-

вой динамики (см., например, [34]). В модуляци-

f₁(e)

онно неустойчивой бездисперсионной динамике тео-

рии НУШ, описываемой уравнениями опрокинутой

мелкой воды, аналогом уравнения (45) оказывается

0.2

0.4

0.6

0.8

1.0

двумерное уравнение Лапласа, записанное в поляр-

ных координатах (см., например, [11-13]). Уравне-

-1

ние (44) переходит в это уравнение Лапласа в пре-

деле малых e.

Рис. 1. Графики функций f1(e) и f2(e), определенных фор-

Важный класс решений уравнения (45) получа-

мулами (54)

ется после разделения переменных

W (e) = Z(e)Y (y),

(46)

5. ПРИМЕР: САМОСЖАТИЕ

НЕЛИНЕЙНОГО ВОЛНОВОГО ПАКЕТА

так что

Возьмем в качестве примера, иллюстрирующего

d²Y

поведение нелинейных модулированных волн в мо-

=λ²Y,

Y (y) = e^±λy ,

(47)

dy²

дели синус-Гордон, решение с F = P₁(z) = 1 - 2e, то

есть с n = 1 и, значит, λ = 3:

и Z = Z(e) удовлетворяет уравнению

1 - 2e

d²Z

(E(e)

) dZ

W (e, y) =

e^3y.

(52)

e(1 - e)

-e

Z = 0.

(48)

K(e)

de²

K(e)

Его подстановка в формулы (42) дает соотношения

С помощью формул (31) можно проверить, что при

λ² = 1 его решением является функция Z = 1/K(e).

x- = t - x = -2f1(e)e^2y,

Поэтому делаем в (48) подстановку

(53)

x+ = t + x = -f2(e)e^4y

F (e)

Z =

(49)

где

K(e)

(1 - 2e)E(e) - (1 - e)(1 - 3e)K(e)

и получаем для F (e) гипергеометрическое уравне-

f₁(e) =

E(e) - (1 - e)K(e)

ние

(54)

(1 - 2e)E(e) - (1 - e)K(e)

f₂(e) = -

d²F

λ² - 1

E(e) - (1 - e)K(e)

e(1 - e)

+ (1 - 2e)

F = 0,

(50)

de²

Графики этих функций показаны на рис. 1. Их зна-

решением которого является гипергеометрическая

чения при e = 0 и e = 1 равны

функция F = F((1 + λ)/2, (1 - λ)/2, 1; e) (см., на-

пример, [36, 37]). Подстановкой e = (1 - z)/2 оно

f₁(0) = f₂(0) = 3,

преобразуется к уравнению Лежандра

(55)

f₁(1) = -1, f₂(1) = 1,

d²F

λ-1

(1 - z²)

- 2z

+ n(n + 1)F = 0, n =

а разложения вблизи e = 0 имеют вид (0 < e ≪ 1)

dz²

(51)

которое при n = 0, 1, 2, . . . имеет решения в виде

f₁(e) = 3 -

e² + . . . ,

многочленов Лежандра P_n(z) = P_n(1 - 2e) и функ-

(56)

ций Лежандра 2-го рода Q_n(z) = Q_n(1 - 2e). Ясно,

f₂(e) = 3 -

e² +

что любая линейная комбинация решений (46) так-

же является решением уравнения (45).

Формулы (53) задают в неявном виде зависи-

Проиллюстрируем развитую теорию примером.

мость переменных e и y от x и t. Удобно выразить

739

А. М. Камчатнов

ЖЭТФ, том 163, вып. 5, 2023

эволюционирует с уменьшением |t|. Положив в (59)

e = 0, находим с помощью (55) закон движения ма-

-140

-120

-100

-80

-60

-40

-20

лоамплитудного края пакета:

(√

)

-20

x_R(t) = t + 6

1 - 2t/3- 1

(61)

x_L

-40

Скорость этого края равна

dx_R

-60

=1-

√

(62)

1 - 2t/3

x_R

-80

и она как раз совпадает с групповой скоростью (60)

-100

при e = 0: dx_R/dt = v(e = 0).

Закон движения противоположного левого края

пакета с e = 1 находим из (59), положив в этой фор-

Рис. 2. Траектории левого xL и правого xR краев нелиней-

муле соответствующие значения (55):

ного волнового пакета на плоскости (x, t) согласно форму-

√

лам (63) и (61), соответственно.

x_L(t) = t - 2

1 - 2t - 2,

(63)

так что его скорость равна

все функции при фиксированном значении времени

t параметрически, где в качестве параметра высту-

dx_L

=1+

√

(64)

пает переменная e. В самом деле, из (53) находим

1 - 2t

2t = -2f₁e^2y - f₂e^4y,

2x = 2f₁e^2y - f₂e^4y,

(57)

Для групповой скорости (60) находим на этом крае

значение

√1 - 2t

так что первое уравнение дает

v(1) =

√

(65)

1 - 2t + 2

√(

)₂

1+v

f₁

то есть ввиду соотношения (6) скорость этого края

e^2y ≡

f₁ ,

(58)

1-v

f₂

(64) равна фазовой скорости волны в этой точке:

dx_L/dt = V = 1/v(1). Это соответствует тому, что

где мы выбрали положительный корень ввиду поло-

на крае с e → 1 имеется последовательность кин-

жительности функции e^2y. Подстановка e^2y во вто-

ков (29), в которые вырождается в этом пределе пе-

рую формулу (57) дает

риодическая волна (28): скорость кинка, очевидно,

⎛

⎞

равна V = 1/v. Траектории краев нелинейного вол-

)

√(f₁

f₁

нового пакета показаны на рис. 2, из которого видно,

x = x(e) = t + 2f1 ⎝

−

⎠.

(59)

f₂

что пакет сжимается с течением времени.

Подстановка формул для x = x(e) и v = v(e)

Эта формула определяет зависимость e от x в фик-

из (59), (60) в периодическое решение (28) дает нам

вместе с (59) в параметрической форме профиль

сированный момент времени t. Зависимость скоро-

сти v от e находим из (58):

промодулированной волны в момент времени t (где

мы пренебрегли, естественно, дополнительным мед-

√

f²¹ - 2f₂t - f₁ - f₂

ленным сдвигом фазы вдоль волновой структуры;

v = v(e) =

√

(60)

f²¹ - 2f₂t - f₁ + f₂

см., например, [38]), и огибающие этого профиля, не

зависящие от сдвига фазы, определяются, очевидно,

Эта формула вместе с (59) определяет распределе-

формулой

√

ние v по x в параметрическом виде. Полученные

a = ±2arcsin

e(x).

(66)

формулы дают частное решение уравнений Уизема

Типичный такой профиль изображен на рис.

об эволюции нелинейного волнового пакета. Обсу-

сплошной линией, а его огибающие (66) — штрихо-

дим его основные свойства.

выми линиями.

Прежде всего из положительности f₂ и ограни-

Длина волны (4) для случая уравнения синус-

ченности функций f₁, f₂, очевидной из рис. 1, мы за-

Гордон выражается формулой

ключаем, что должно быть t < 0, то есть пакет был

√

сформирован при достаточно больших по абсолют-

1 - v²(e)

L=4

K(e).

(67)

ной величине отрицательных значениях t и затем он

v(e)

740

ЖЭТФ, том 163, вып. 5, 2023

Эволюция волновых импульсов

уменьшении числа осцилляций в волновой струк-

туре согласуется с тем, что в силу v < 1 фазо-

вая скорость V

= 1/v(0) на правом крае всегда

больше групповой скорости v(0) правого края, так

что с течением времени волны покидают уиземов-

скую область нелинейных колебаний через ее мало-

амплитудный край. Стоит отметить, что ситуация

-120

100

-8

-60

здесь противоположна теории дисперсионных удар-

ных волн в модуляционно устойчивых системах [39],

в которых волны входят в уиземовскую нелинейную

область через малоамплитудный край [40], что дает

возможность вычислить число солитонов, образую-

-π

щихся из начальной интенсивной простой волны при

асимптотически больших временах [41] (см. также

Рис. 3. Профиль волны в промодулированном нелинейном

[42-46]).

импульсе ϕ(x, t) при t = -100

Отметим, что согласно формулам (42) измене-

ние знака функции W эквивалентно одновремен-

ному изменению знаков x и t. Следовательно, при

изменении знака W мы получим решение, описы-

вающее расширение нелинейного волнового пакета

с ростом t > 0, аналогичное формированию вол-

новой структуры при распаде ступеньки в теории

НУШ (см., например, [21-23,47]), однако в этом слу-

чае эволюция не является автомодельной и опреде-

ление движения малоамплитудного края волновой

структуры остается за пределами теории Уизема-

Гуревича-Питаевского.

Эволюция нелинейных волновых пакетов, для

описания которых в формуле (49) используются

-200

-150

-100

-50

функции Лежандра второго рода, имеет качествен-

но такой же характер, как и в случае многочленов

Лежандра, и поэтому мы здесь не будем останавли-

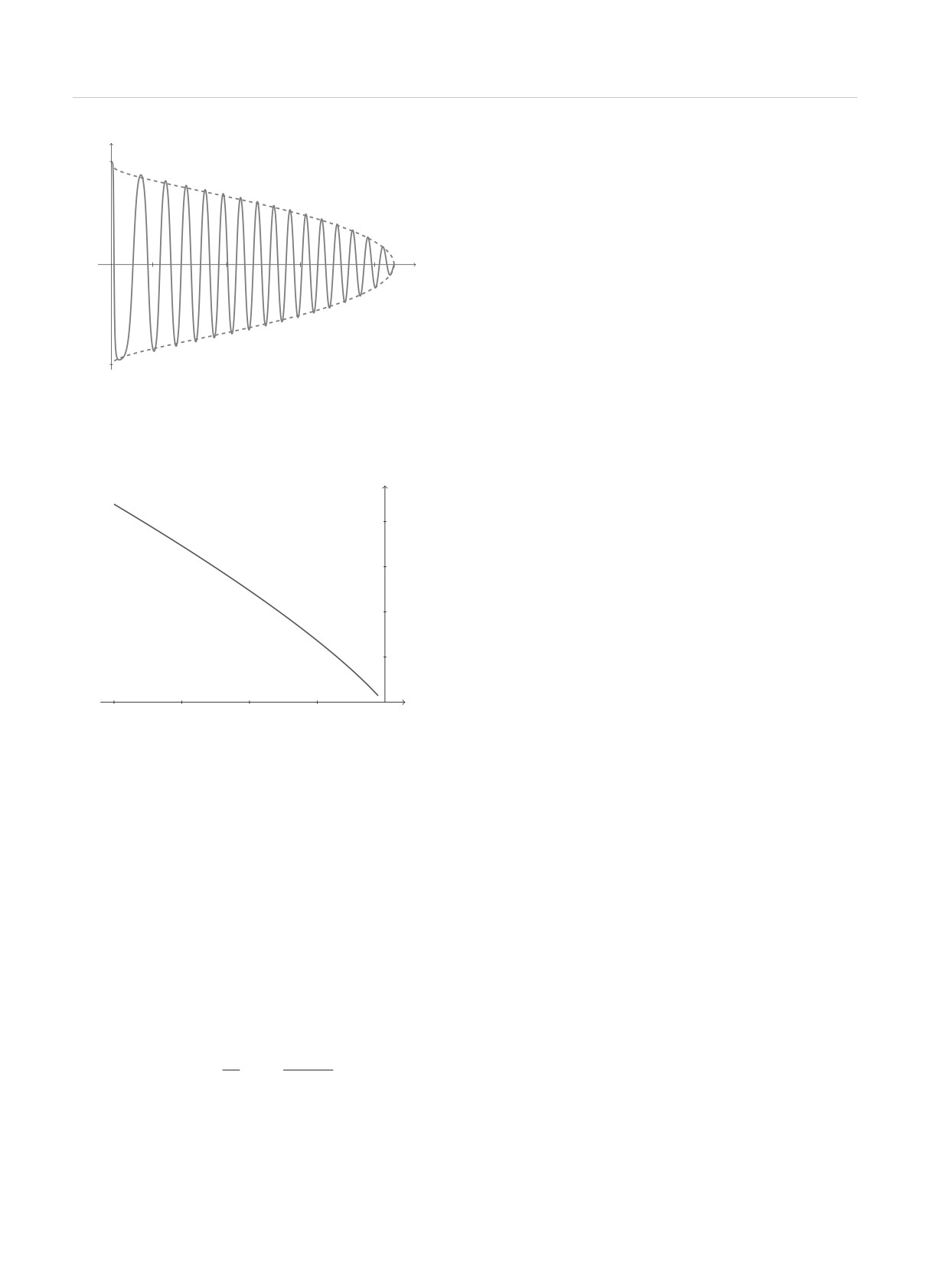
Рис. 4. Число колебаний в нелинейном волновом пакете в

ваться на конкретных деталях.

зависимости от времени

Естественно, для применимости модуляционной тео-

6. ЗАКЛЮЧЕНИЕ

рии Уизема необходимо, чтобы длина волны L была

много меньше, чем длина всей волновой структу-

Как известно, методы газовой динамики могут

ры. С практической точки зрения можно заметить,

быть с успехом применены для описания эволюции

что L стремится к бесконечности при v → 0, а ско-

не только устойчивых, но также и неустойчивых си-

рость правого края dx_R/dt = v(0) (62) обращается

стем (см., например, [14]). Создание модуляционной

в нуль при t = -9/2. Следовательно, наше частное

теории Уизема [17, 18], открытие метода обратной

решение уравнений Уизема применимо только при

задачи рассеяния [48] и развитие общей теории си-

t < 0, |t| ≫ 5.

стем гидродинамического типа [49] позволило рас-

Число нелинейных колебаний в структуре при-

пространить эти методы на обширную область тео-

ближенно равно

рии дисперсионных ударных волн (см., например,

∫xR

∫1

обзоры [41,50]). Хотя эти методы применимы и к мо-

|dx/de|

дуляционно неустойчивым системам (см., например,

N =

de,

(68)

L(e)

работы [51-54] по теории уравнения синус-Гордон),

тем не менее практические приложения модуляци-

и, как видно из рис. 4, оно убывает со временем,

онной теории к однофазным волнам в неустойчи-

становясь порядка единицы при t = -5 на грани-

вых системах пока ограничивались лишь частными

це области применимости теории Уизема. Вывод об

741

А. М. Камчатнов

ЖЭТФ, том 163, вып. 5, 2023

случаями типа «эволюции ступеньки» [21-23] (см.

В. И. Таланов, Письма в ЖЭТФ 2, 218 (1965).

также [47] и приведенные там ссылки). Развитие об-

10.

С. А. Ахманов, А. П. Сухоруков, Р. В. Хохлов,

ласти неустойчивости в неоднородных системах об-

ЖЭТФ 50, 1537 (1966).

суждалось в работе [25] также только для малоам-

плитудного края и не затрагивало вопроса об эво-

11.

M. J. Lighthill, J. Inst. Math. Appl. 1, 269 (1965).

люции параметров во всей области нелинейных ос-

12.

W. D. Hayes, Proc. Roy. Soc. Lond. A 332, 199

цилляций. В настоящей работе дано точное решение

(1973).

модуляционных уравнений Уизема для модуляцион-

но неустойчивой нелинейной волны в модели синус-

13.

А. В. Гуревич, А. С. Шварцбург, ЖЭТФ 58,

Гордон. Развитая теория показывает весьма нетри-

2012 (1970).

виальную эволюцию нелинейного волнового пакета,

14.

С. К. Жданов, Б. А. Трубников, Квазигазовые

которая заключается в его сжатии, сопровождаемом

уходом волн из области нелинейных осцилляций,

неустойчивые среды, Наука, Москва (1991).

так что за конечное время в этой области остается

15.

В. И. Карпман, Письма ЖЭТФ 6, 829 (1967).

лишь малое число порядка единицы нелинейных ко-

лебаний. На этой стадии теория Уизема теряет свою

16.

В. И. Карпман, Е. М. Крушкаль, ЖЭТФ 55,

применимость и вопрос о дальнейшей эволюции вол-

530 (1968).

нового импульса должен рассматриваться другими

17.

G. B. Whitham, Proc. Roy. Soc. Lond. A, 283, 238

методами.

(1965).

Можно предполагать, что предложенный здесь

подход окажется эффективным и при обсуждении

18.

Дж. Уизем, Линейные и нелинейные волны,

модуляционно неустойчивых для других вариан-

Мир, Москва (1974).

тов нелинейного уравнения Клейна-Гордона, в част-

19.

M. G. Forest and J. E. Lee, in: Oscillation Theory,

ности для уравнения, описывающего возбуждение

Computation, and Methods of Compensated

волн ветром (см. [55]) или уравнений, описывающих

Compactness, ed. by C. Dafermos et al., IMA

распространение электромагнитных волн в нелиней-

Volumes on Mathematics and its Applications,

ных средах (см., например, [56-58]).

Vol. 2,(Springer, New York (1986).

Благодарности. Автор выражает благодар-

ность С. Ю. Доброхотову, Е. А. Кузнецову и

20.

М. В. Павлов, ТМФ 71, 351 (1987).

С. В. Сазонову за полезные обсуждения.

21.

A. M. Kamchatnov, Phys. Lett. A 162, 389 (1992).

Финансирование. Работа выполнена при под-

держке Российского научного фонда (грант N 19-72-

22.

G. A. El, A. V. Gurevich, V. V. Khodorovskii, and

30028).

A. L. Krylov, Phys. Lett. A 177, 357 (1993).

23.

Р. Ф. Бикбаев, В. Р. Кудашев, Письма в ЖЭТФ

ЛИТЕРАТУРА

59, 741 (1994).

24.

G. Biondini and D. Mantzavinos, Phys. Rev. Lett.

1. Г. А. Аскарьян, ЖЭТФ 42, 1568 (1962).

116, 043902 (2016).

2. Г. А. Аскарьян, УФН 111, 249 (1973).

25.

A. M. Kamchatnov and D. V. Shaykin, EPL 136,

3. R. Y. Chiao, E. Garmire, and C. H. Townes, Phys.

40001 (2021).

Rev. Lett. 13, 479 (1964).

26.

Э. Скотт, Нелинейная наука. Рождение и

4. А. А. Веденов, Л. И. Рудаков, ДАН СССР 159,

развитие когерентных структур, Физматлит,

767 (1964).

Москва (2007).

5. В. Е. Захаров, ЖЭТФ, 62, 1745 (1972).

27.

In: The sine-Gordon Model and its Applications,

ed. by J. Cuevas-Maraver, P. G. Kevrekidis,

6. Л. А. Островский, ЖЭТФ 51, 1189 (1966).

F. Williams, Cham, Springer (2014).

7. T. B. Benjamin and J. E. Feir, J. Fluid Mech. 27,

28.

В. П. Маслов, ТМФ 1, 378 (1969).

41 (1967).

29.

С. Ю. Доброхотов, В. П. Маслов, Итоги науки

8. В. Е. Захаров, ЖПМТФ, 9, 86 (1968).

и техн. Сер. Соврем. пробл. мат. 15, 3 (1980).

742

ЖЭТФ, том 163, вып. 5, 2023

Эволюция волновых импульсов

30.

Л. Д. Ландау, Изв. АН СССР, серия физ. 17, 51

44.

A. M. Kamchatnov, Chaos 30, 123148 (2020).

(1953).

45.

А. М. Камчатнов, ЖЭТФ 151, 76 (2021).

31.

И. М. Халатников, ЖЭТФ 27, 529 (1954).

46.

L. F. Calazans de Brito, A. M. Kamchatnov, Phys.

32.

В. Г. Носов, А. М. Камчатнов, ЖЭТФ 70, 768

Rev. E 104, 054203 (2021)

(1976).

47.

A. M. Kamchatnov, Phys. Rep. 286, 199, (1997).

33.

А. М. Камчатнов, ЖЭТФ 156, 689 (2019).

48.

В. Е. Захаров, С. В. Манаков, С. П. Новиков,

34.

Л. Д. Ландау, Е. М. Лифшиц, Гидродинамика,

Л. П. Питаевский, Теория солитонов. Метод

Физматлит, Москва (2001).

обратной задачи, Физматлит, Москва (1980).

35.

Л. Д. Ландау, Е. М. Лифшиц, Статистическая

49.

Б. А. Дубровин, С. П. Новиков, УМН 44, 29

физика, часть 1, Физматлит, Москва (2001).

(1989).

36.

М. Абрамовиц, И. Стиган, Справочник по спе-

50.

G. A. El, M. A. Hoefer, Physica D 333, 11 (2016).

циальным функциям, Наука, Москва (1979).

51.

M. J. Ablowitz, D. J. Kaup, A. S. Newell, and

37.

Э. Т. Уиттекер, Дж. Н. Ватсон, Курс современ-

H. Segur, Phys. Rev. Lett. 30, 1262 (1973).

ного анализа, т. II, Физматлит, Москва (1963).

52.

Л. А. Тахтаджян, ЖЭТФ66, 476 (1974).

38.

С. Ю. Доброхотов, Д. С. Миненков, ТМФ 166,

350 (2011).

53.

В. А. Козел, В. П. Котляров, ДАН УССР, сер.

А 10, 878 (1976).

39.

А. В. Гуревич, Л. П. Питаевский, ЖЭТФ 65,

590 (1973).

54.

P. G. Grinevich and S. P. Novikov, Comm. Pure

Appl. Math. 56, 956 (2003).

40.

А. В. Гуревич, Л. П. Питаевский, ЖЭТФ 93,

871 (1987).

55.

Е. А. Кузнецов, П. М. Лушников, ЖЭТФ 108,

614 (1995).

41.

А. М. Камчатнов, УФН 191, 52 (2021).

56.

С. В. Сазонов, Н. В. Устинов, Письма ЖЭТФ

42.

G. A. El, A. Gammal, E. G. Khamis,

83, 873 (2006).

R. A. Kraenkel, and A. M. Kamchatnov, Phys.

Rev. A 76, 053813 (2007).

57.

С. В. Сазонов, ЖЭТФ 146, 483 (2014).

43.

G. A. El, R. H. J. Grimshaw, and N. F. Smyth,

58.

S. V. Sazonov and N. V. Ustinov, Phys. Rev. A

Physica D 237, 2423 (2008).

98, 063803 (2018).

743