МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 10, стр. 7-21
СРАВНЕНИЕ МЕТОДОВ АППРОКСИМАЦИИ ГРАДИЕНТОВ
В СХЕМАХ, ОРИЕНТИРОВАННЫХ
НА ВИХРЕРАЗРЕШАЮЩИЕ РАСЧЕТЫ
2019 г. С. Бахнэ1, С.М. Босняков1,2, С.В. Михайлов1,2, А.И. Трошин1,2
1Московский физико-технический институт
2Центральный аэрогидродинамический институт
bakhne@phystech.edu
Работа выполнена при поддержке гранта РФФИ № 18-08-01436 А.
DOI: 10.1134/S0234087919100010
Рассмотрены различные способы аппроксимации градиентов повышенной точнос-
ти, входящих в диффузионные потоки. Исследовались линейные комбинации раз-
ностных схем второго порядка для неравномерной сетки, переходящие в схемы
четвёртого порядка в равномерном случае. Также рассматривались схемы третьего
и четвёртого порядка аппроксимации градиентов на неравномерной сетке в нор-
мальном и касательном направлении к грани ячейки соответственно, построенные
на основе полиномов Лагранжа. Первоначальное тестирование схем было прове-
дено на одномерных функциях: гладкой функции Гаусса и кусочно-линейной функ-
ции-зубце. Далее схемы были применены в прямом численном моделировании вих-
ря Тейлора-Грина.
Ключевые слова: порядок аппроксимации, диффузионные потоки, градиенты.
COMPARISON OF GRADIENT APPROXIMATION METHODS
IN SCHEMES DESIGNED FOR SCALE-RESOLVING SIMULATIONS
S. Bakhne1, S.M. Bosniakov1,2, S.V. Mikhailov1,2, A.I. Troshin1,2
1Moscow Institute of Physics and Technology
2Central Aerohydrodynamic Institute
Various methods for improved accuracy approximation of the gradients entering the dif-
fusion fluxes are considered. Linear combinations of 2nd order difference schemes for a
non-uniform grid that transform into 4th order schemes in the uniform case were investi-
gated. We also considered 3rd and 4th order schemes for approximating gradients on a
non-uniform grid in the normal and tangent directions to the cell face, respectively, based
on Lagrange polynomials. The initial testing was carried out on one-dimensional func-
8
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
tions: a smooth Gauss function and a piecewise linear function. Next, the schemes were
applied in direct numerical simulation of the Taylor-Green vortex.
Key words: approximation order, diffusion fluxes, gradients.
1. Введение
В настоящее время для решения актуальных задач вычислительной аэ-
родинамики начинают применяться гибридные вихреразрешающие методы,
которые в пристенной части пограничного слоя используют RANS-модели
[1,2]. За счет этого сокращается количество ячеек расчётной сетки по срав-
нению с подходом «LES вплоть до стенки». Известно, что стандартные
TVD-схемы малопригодны для вихреразрешающих расчетов из-за их высо-
кой численной вязкости [3]. Один из путей уменьшения численной вязкости
- аппроксимация конвективного оператора схемами повышенного порядка
точности [4-6]. В указанных работах используется расширенный шаблон
(обычно 7-11 ячеек), состоящий из нескольких более простых. При этом
для расчёта диффузионных и источниковых членов чаще всего применяют-
ся центральные разности второго порядка точности.
В [7] рассмотрены расчёты вихря Тейлора-Грина при числах Рейнольд-
са выше 103, т.е. в ситуации, когда шаг сетки существенно превышает мас-
штаб Колмогорова. Показано, что недооценка скорости диссипации тем
меньше, чем выше порядок центральных разностей, применяемых для рас-
чёта, в том числе и диффузионных членов. Поэтому уточнение центрально-
разностных схем целесообразно для гибридных RANS-LES-расчётов. В [8]
предлагается использовать скошенные формулы 4-го порядка для аппрок-
симации производных так, чтобы конечный шаблон состоял из 5 точек. Та-
кой подход обладает хорошими спектральными свойствами. Также популя-
рен метод наименьших квадратов [9].
Данная работа продолжает анализ способов снижения ошибки при вы-
числении диффузионных членов в конечно-объемных методах. В качестве
отправной точки взят подход, описанный в [10]. Суть заключается в разде-
лении исходной задачи на аппроксимацию трех типов градиентов: в центре
ячейки, на грани ячейки в нормальном к ней направлении и в касательном.
Основой для получения аппроксимаций градиентов 3-го и 4-го порядков в
данной работе служит теория полиномов Лагранжа [11].
Структура данной статьи следующая. В разделе 2 представлены ап-
проксимации различных типов градиентов. В разделе 3 проводится их тес-
тирование на модельных задачах о дифференцировании заданных функций.
Раздел 4 посвящен тестированию аппроксимаций в задаче о вихре Тейлора-
Грина при Re 1600, в разделе 5 делаются выводы из работы.
Сравнение методов аппроксимации градиентов ...
9
2. Аппроксимации различных типов градиентов
2.1. Вычисление градиентов в центре ячейки. Рассмотрим фрагмент
четырехугольной расчетной сетки (рис.1). Пренебрегая искривлением се-
точных линий на масштабах шаблона схемы, рассмотрим методы нахожде-
ния производной функции u, заданной в центрах ячеек, в направлении ка-
кой-либо сеточной линии.
Пустьuj ,hj ,xj - значение функции в j-й ячейке расчетной сетки, раз-
мер ячейки и координата центра соответственно. Обозначим искомую про-
изводную функции в центре ячейкиuj , а расстояние между центрами со-
седних ячеек -LL ,L ,R ,RR (рис.1).
Рис.1. Фрагмент расчётной области.
В общем случае на неравномерной сетке, используя трёхточечный шаб-
лон, можно получить второй порядок аппроксимации производной:
2
2
(u
u
)
(u
u
)
j
j1
R
j1
j
L
2
u
O(h
)
(1)
j
2
2
L R
R L
Можно предложить следующую идею повышения точности метода. Рас-
смотрим формулу 4-го порядка аппроксимации на пятиточечном шаблоне в
случае равномерной сетки [12]:
u
8u
8u
u
j2
j1
j1
j2
4
u
O(h
)
j
12h
Её можно переписать как комбинацию двух центральных разностей - на уз-
ком и широком шаблонах:
u
u
u
u
4u
1
u
2
4
j1
j1
j2
j2
u
O(h
), где
u
,
u
(2)
j
1
2
3
2h
4h
Формально заменим эти центральные разности трехточечными аппрок-
симациями (1) на шаблонах { j 1, j, j 1} и { j 2, j, j 2}. Полученная схе-
ма будет иметь 4-го порядок точности на равномерной сетке. На неравно-
10
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
мерной сетке порядок такого подхода будет снижаться до 2-го, но все равно
можно ожидать уточнения по сравнению с исходным методом (1).
С другой стороны, используя 5-точечный шаблон, можно построить и
более точную аппроксимацию производной. Следуя [11], запишем интерпо-
ляционную формулу Лагранжа для производной в общем виде
N/2
N/2
u
u
x
x
ji
j
j
jk
u
(3)
j
x
x
x
x
iN /2
ji
j
kN/2
ji
jk
i0
k0,i
Легко убедиться, что при N = 2 формула (3) совпадает с (1). При N = 4
получим аппроксимацию производной, использующую значение функции в
5 точках и сохраняющую 4-й порядок на неравномерной сетке.
2.2. Вычисление касательных градиентов на грани ячейки. Вторая
задача состоит в интерполяции ранее вычисленных производных
u
u
,
j
1,
j
u
u
из центров ячеек на грань. Интерполированное значение далее
j
1,
j
2,
(рис.2).
Рис.2. Интерполяция производных из центров ячеек на грань.
В качестве базового подхода возьмем линейную интерполяцию по 2
ближайшим ячейкам. Она имеет второй порядок аппроксимации:
u
u
j
R j1
L
2
u
O(h
),
(4)
j1/2
L
R
где
x
x
0.5h
,
x
x
0.5h
L
j1/2
j
j
R
j1
j1/2
j1
Идея повышения точности аналогична предыдущей задаче. Возьмем
формулу 4-точечной интерполяции
u
9u
9u
u
j1
j
j1
j2
4
u
O(h
),
j1/2
16
имеющую 4-й порядок точности на равномерном шаблоне [12], и представим
ее как комбинацию полусумм производных на узком и широком шаблонах:
Сравнение методов аппроксимации градиентов ...
11
9u
u
1/2
3/2
4
u
O(h
),
j1/2
8
u
u
u
u
j1
j
j2
j1
где
u
,
u
(5)
1/2
3/2
2
2
Формально заменим полусуммы на линейные интерполяции (4) и снова по-
лучим метод, обладающий 4-м порядком точности на равномерной сетке и 2
- на неравномерной.
Дальнейшее уточнение можно сделать, выписав интерполяционную фор-
мулу Лагранжа, которая будет обладать 4-м порядком точности на нерав-
номерном шаблоне при N = 4:
N/2
N/2
x
x
j1/2
jk
u
u
(6)
j1/2
ji
x
x
iN
/21
kN
/21
ji
jk
k i
2.3. Вычисление нормальных градиентов на грани ячейки. Третья
задача: имея значения функции и ее производных в центрах ячеек, необхо-
димо восстановить значение производной
(
u
)
на грани в направлении
j1/2
нормали к ней (рис.3).
Рис.3. Аппроксимация производной на грани в нормальном направлении.
Интерполяция, используемая для касательных градиентов, имеет низ-
кое качество, так как приводит к потере взаимодействия между четными и
нечетными слоями ячеек [10]. Вместо этого в [10] предлагается вычислять
производную на грани по двум ближайшим точкам, а затем в случае нерав-
номерной сетки корректировать ее с помощью производных из этих же двух
точек:
u
u
(
)(u
u
)
j1
j
R
L
j1
j
2
u
O(h
).
(7)
j1/2
L
R
L
R
Этот подход обеспечивает второй порядок точности на неравномерных сет-
ках. Будем считать данную аппроксимацию базовой.
Точность аппроксимации можно повысить, взяв производные (7) на уз-
ком и широком шаблонах
12
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
u
u
(
)(u
u
)
j1
j
R
L
j1
j
2
u
O(h
),
1/2
L
R
L
R
u
u
(
)(u
u
)
j2
j1
RR
R
L
LL
j2
j1
2
u
O(h
)
3/2
L
R
LL
RR
и подставив их в выражение
9u
u
1/2
3/2
4
u
O(h
).
(8)
j1/2
8
Полученный метод снова будет обладать 4-м порядком точности на равно-
мерной сетке и 2-м - на неравномерной.
Продифференцировав интерполяционную формулу Лагранжа, можно
выразить производную на грани через значения функции в центрах ячеек:
N/2
N/2
(x
x
)
j1/2
jq
kN/21
qN/2
1
N/2
k i
qi,k
u
u
(9)
j1/2
ji
N/2
iN /21
(x
x
)
ji
jk
kN
/21
k i
Приняв N = 4, получим формулу 4-го порядка точности на равномер-
ной сетке и 3-го - на неравномерной.
3. Тестирование аппроксимаций на модельных задачах
3.1. Описание тестовых задач. Рассмотрим функцию одной перемен-
ной u(x) . Возьмем один из рассмотренных конечно-разностных шаблонов и
будем перемещаться вдоль графика функции, вычисляя с его помощью при-
ближенные значения производной. Рассмотрим два распределения точек в
шаблоне: равномерное с шагом h = 0.2 и неравномерное с изменением шага
по геометрической прогрессии со знаменателем q = 2. Второй случай вос-
производит «агрессивный» вариант роспуска сетки в пограничном слое.
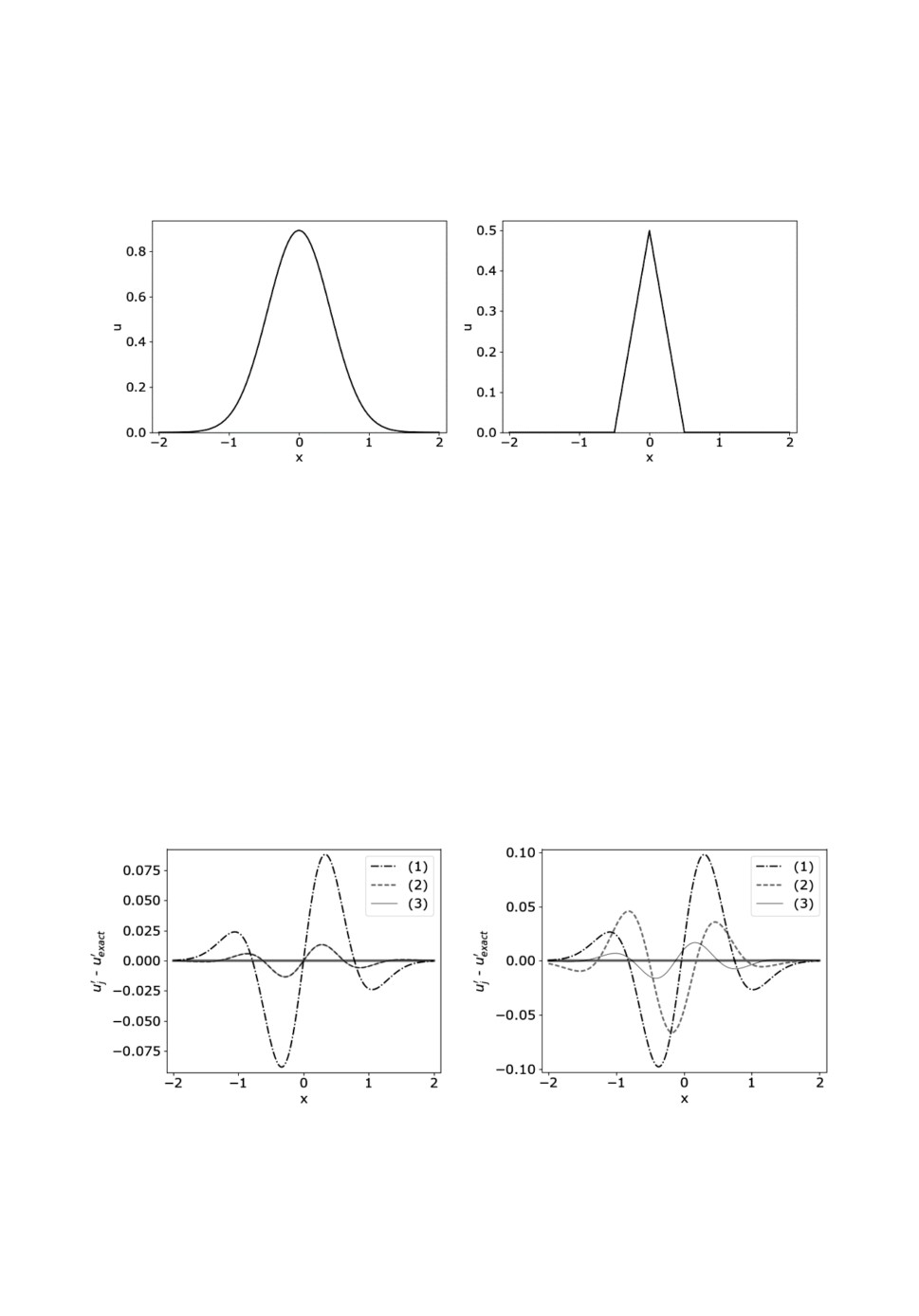
В качестве u(x) возьмём гладкую функцию Гаусса (рис.4, слева):
2
1
x
u x)
exp
0.4
0.4
и кусочно-линейную функцию-зубец (рис.4, справа):
Сравнение методов аппроксимации градиентов ...
13
x
0.5,
x 0.5, 0],
u x)
0.5
x,
x[0, 0.5],
0,
xR
\[0.5, 0.5].
Рис.4. Функция Гаусса (слева) и кусочно-линейная функция-зубец (справа).
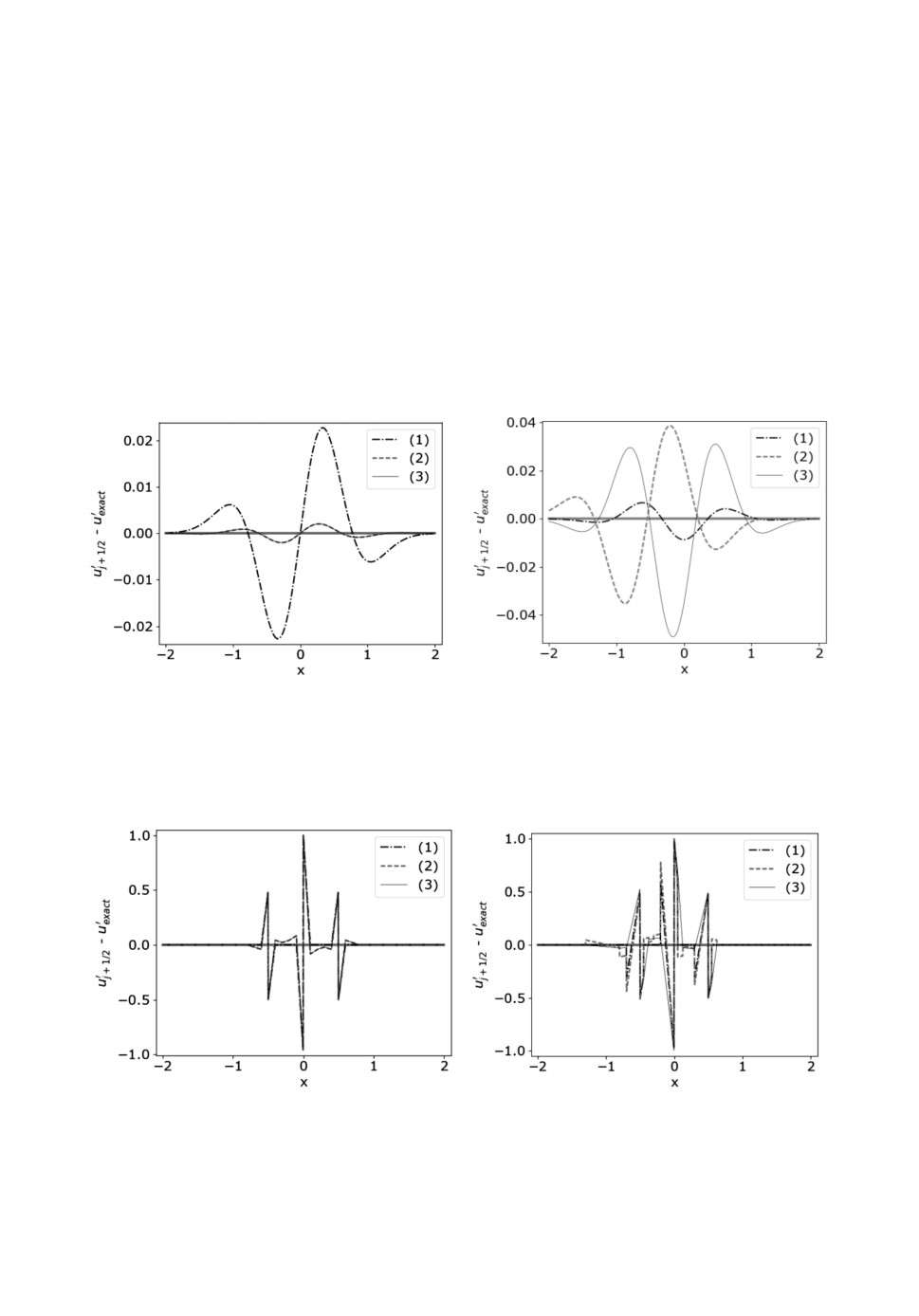
3.2. Анализ точности вычисления градиентов в центре ячейки. По-
скольку в случае функции Гаусса графики приближенных значений произ-
воднойuj качественно похожи для всех трёх методов, будем рассматривать
du(x) / dx (рис.5).
Для выбранных параметров теста оказалось, что на равномерном шаб-
лоне методы повышенной точности (2) и (3) дают ошибку примерно на по-
рядок меньшую, чем базовый метод (1), совпадая между собой, а на нерав-
номерном шаблоне повышенную точность сохраняет только схема (3), по-
строенная по интерполяционной формуле Лагранжа. «Комбинированная»
схема (2) снижает точность до уровня базового метода (табл.1).
Рис.5. Точность аппроксимаций производной в центре ячейки в случае равномерной
(слева) и неравномерной (справа) сетки для функции Гаусса. Аппроксимации:
1 - базовая (1), 2 - уточненная (2), 3 - высокого порядка точности (3)
14
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
Таблица 1. Ошибки аппроксимаций производной в центре ячейки.
Функция Гаусса
Кусочно-линейная функция
Равномер.
Геом.
Равномер.
Геом.
Схема
сетка
прогрессия
сетка
прогрессия
Норма ошибки
L∞
L2
L∞
L2
L∞
L2
L∞
L2
Базовая (1)
0.088
0.078
0.098
0.087
1.00
0.447
1.333
0.452
Уточненная (2)
0.013
0.011
0.066
0.052
1.00
0.425
1.215
0.430
Лагранжа (3)
0.013
0.011
0.017
0.014
1.00
0.425
1.594
0.437
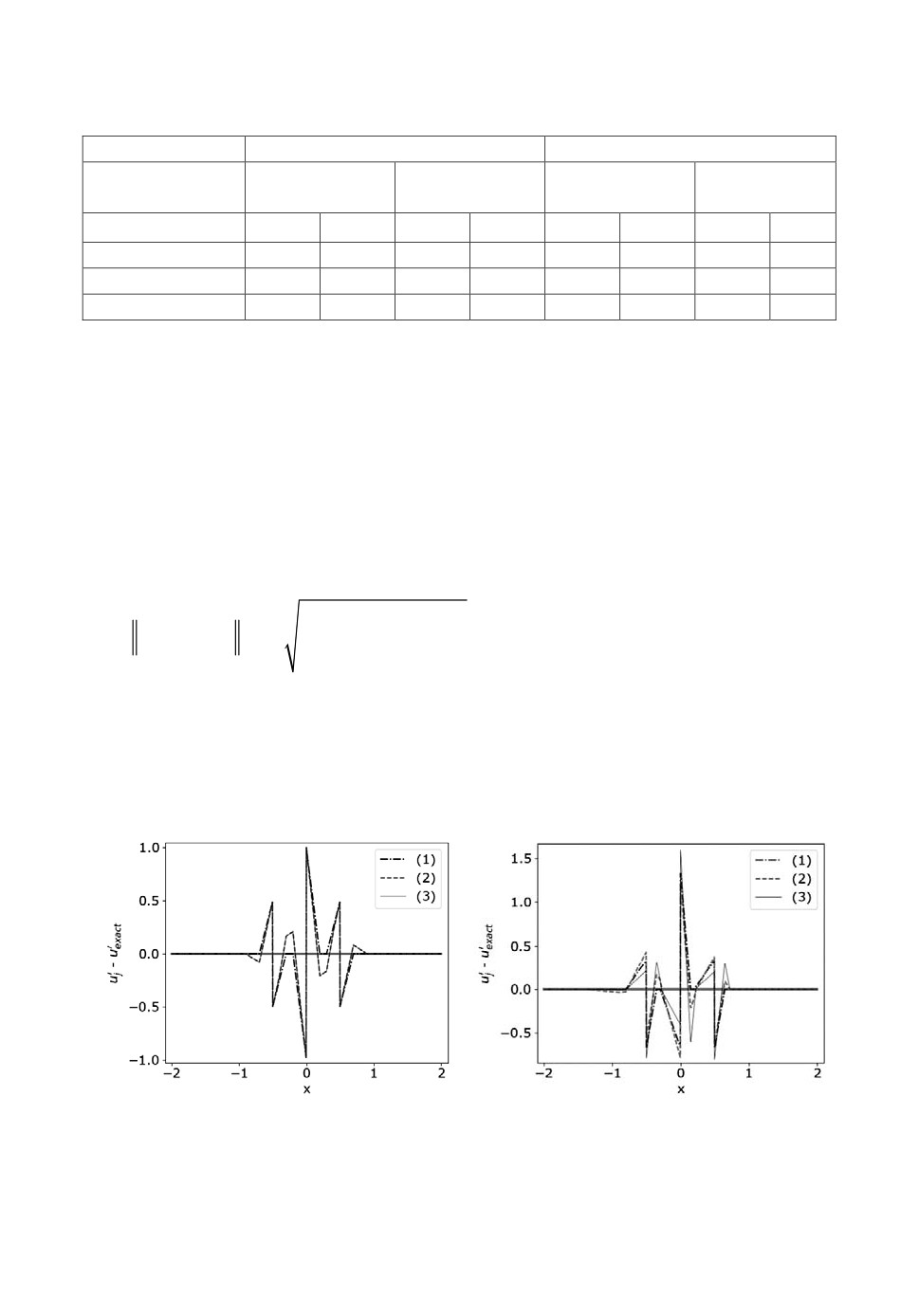
Аналогичные данные для кусочно-линейной функции представлены на
рис.6 и в табл.1. В этот раз все методы дали примерно одинаковый уровень
ошибки (разброс между ними порядка 10%) как на равномерной сетке, так и
на неравномерной. При этом уточенные методы, в отличие от базовой схе-
мы 2-го порядка, порождают забросы производной.
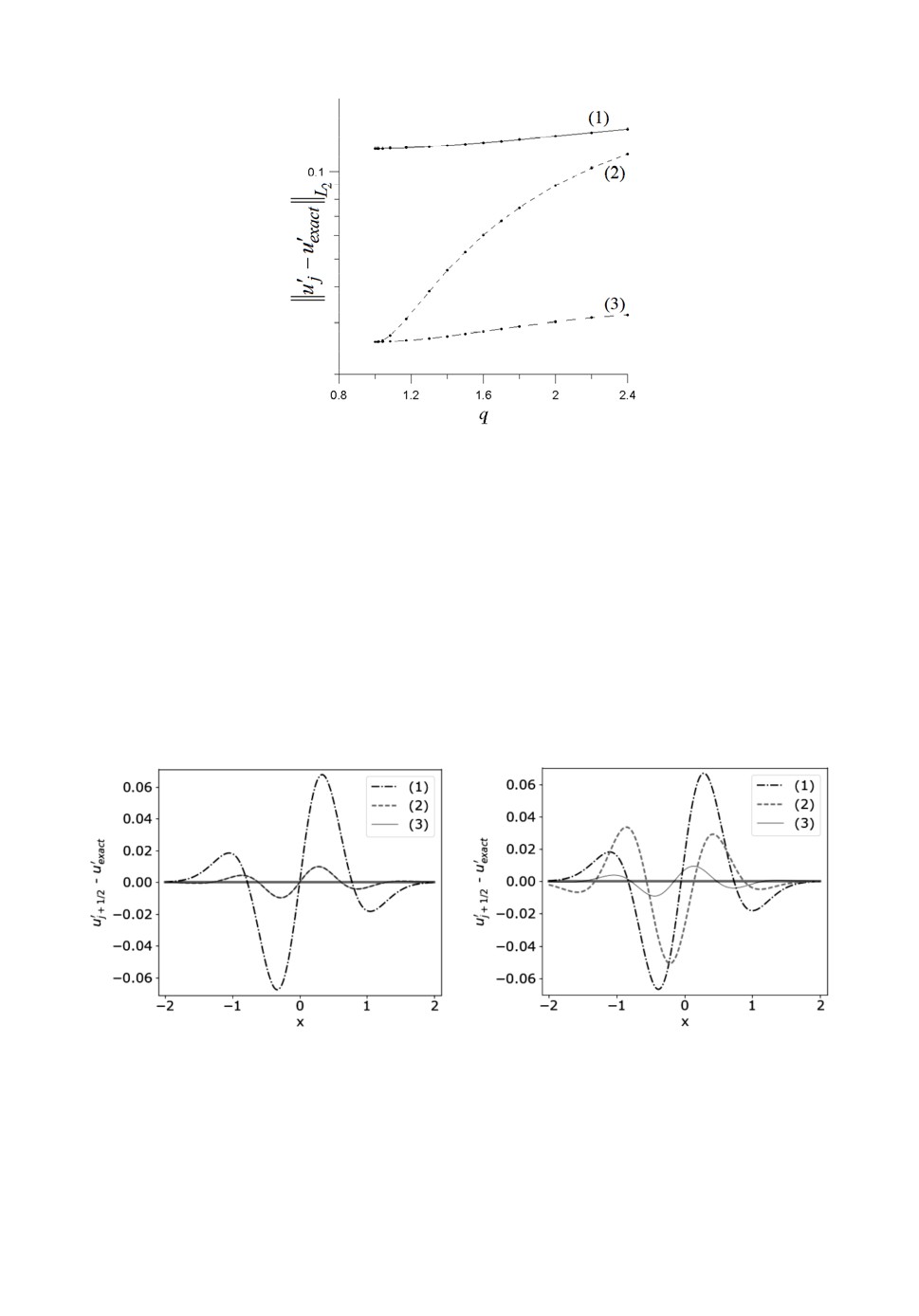
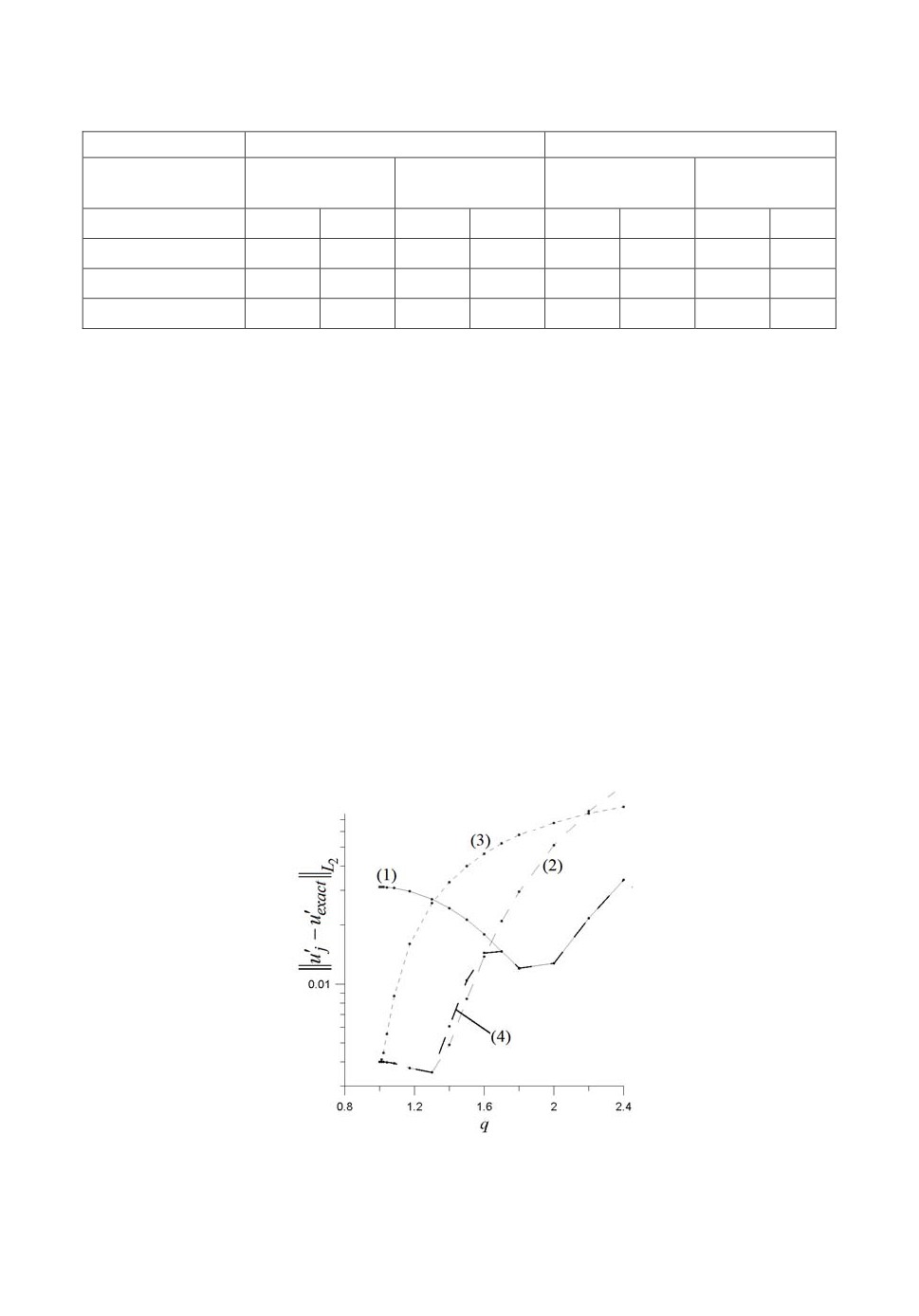
Также для функции Гаусса была проведена серия тестов на неравно-
мерном шаблоне, в котором от 1 до 2.4 варьировалось значение q. Зависи-
мость ошибки по норме L2 от q изображена на рис.7, где
2
2
uu
(uu
)
dx
j
exact
j
exact
L
2
2
Видно, что при использовании метода 4-го порядка величина ошибки
меньше, чем при использовании базового метода, а у комбинированного под-
хода точность совпадает с методом 4-го порядка на равномерной сетке и
уменьшается по мере роста q, приближаясь к ошибке базового метода.
Рис.6. Точность аппроксимаций производной в центре ячейки в случае равномерной
(слева) и неравномерной (справа) сетки для кусочно-линейной функции.
Аппроксимации: 1 - базовая (1), 2 - уточненная (2), 3 - высокого порядка
точности (3).
Сравнение методов аппроксимации градиентов ...
15
Рис.7. Точность аппроксимаций производной в центре ячейки в зависимости
от знаменателя геометрической прогрессии. Аппроксимации: 1 - базовая
(1), 2 - уточненная (2), 3 - высокого порядка точности (3).
3.3. Анализ точности вычисления касательных градиентов на гра-
ни ячейки. Для аппроксимаций (4)-(6) была проведена такая же серия тес-
тов, как и в случае градиентов в центрах ячеек. Для функции Гаусса на рав-
номерном шаблоне методы повышенной точности снова дают улучшение
по сравнению с базовой линейной интерполяцией примерно на порядок
(рис.8, слева), а при переходе к неравномерному шаблону с геометрической
прогрессией повышенную точность сохраняет только метод, использующий
формулу Лагранжа (рис. 8, справа). Числовые данные собраны в табл. 2.
Рис.8. Точность аппроксимаций касательных градиентов на грани ячейки в случае
равномерной (слева) и неравномерной (справа) сетки для функции Гаусса.
Аппроксимации: 1 - базовая (4), 2 - уточненная (5), 3 - высокого порядка
точности (6).
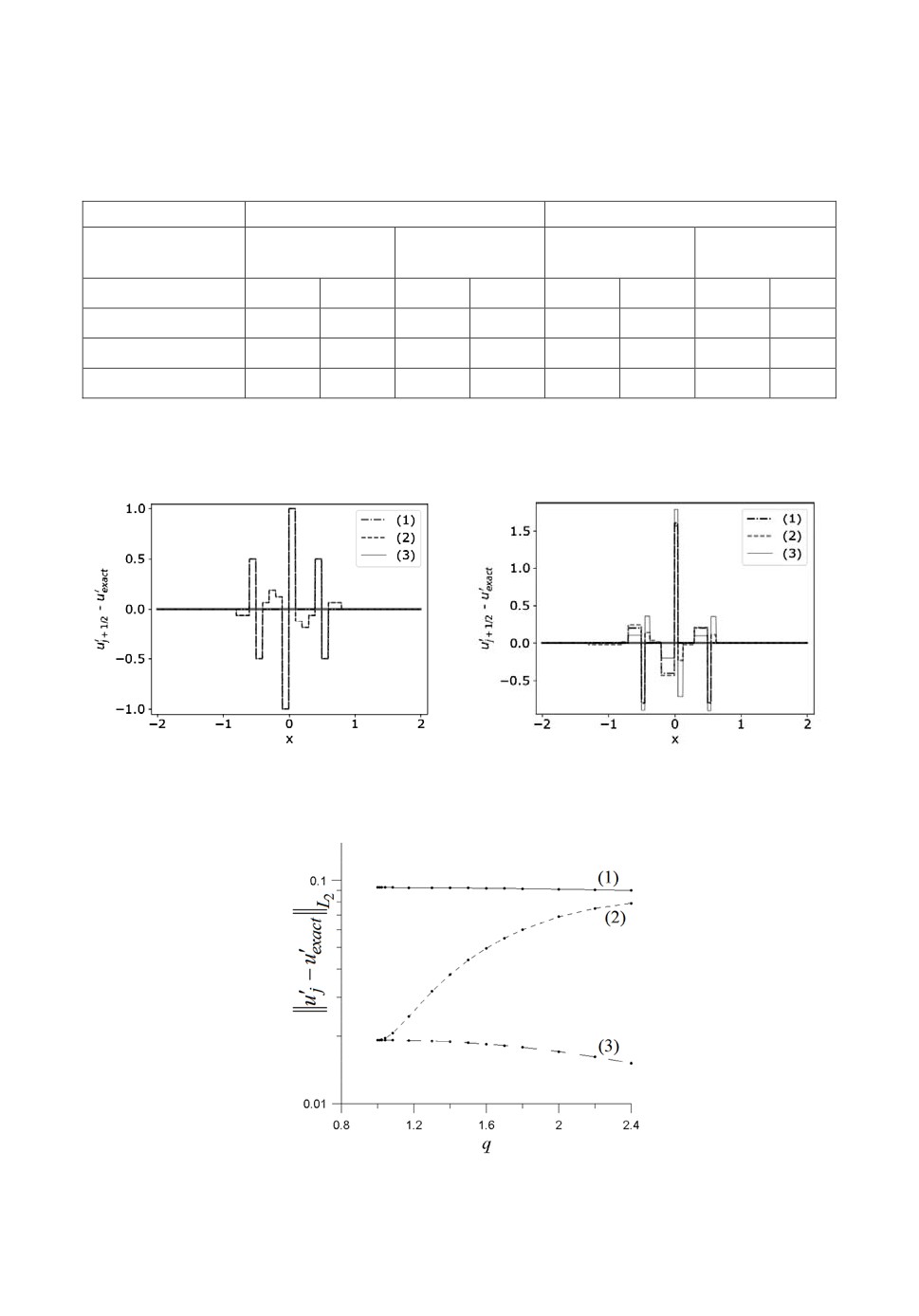
При аппроксимации производной кусочно-линейной функции (рис.9),
как и в прошлый раз, методы повышенной точности теряют свои преиму-
16
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
щества и порождают забросы. Интересно, что самый точный на гладких ре-
шениях метод дает в этом тесте наихудший результат (табл.2).
Таблица 2. Ошибки аппроксимаций касательных градиентов на грани ячейки.
Функция Гаусса
Кусочно-линейная функция
Равномер.
Геом.
Равномер.
Геом.
Схема
сетка
прогрессия
сетка
прогрессия
Норма ошибки
L∞
L2
L∞
L2
L∞
L2
L∞
L2
Базовая (4)
0.0677
0.06
0.0669
0.059
1.00
0.548
1.6
0.498
Уточненная (5)
0.0098
0.008
0.0508
0.04
1.00
0.559
1.567
0.505
Лагранжа (6)
0.0098
0.008
0.0094
0.008
1.00
0.559
1.798
0.568
Результаты тестов с разными значениями q представлены на рис.10.
Наблюдается такое же поведение величины ошибки, как и в тесте с гради-
ентами в центре ячейки.
Рис.9. Точность аппроксимаций касательных градиентов на грани ячейки в случае
равномерной (слева) и неравномерной (справа) сетки для кусочно-линейной
функции. Аппроксимации: 1 - базовая (4), 2 - уточненная (5), 3 - высокого
порядка точности (6).
Рис.10. Точность аппроксимаций касательных градиентов на грани ячейки в зави-
симости от знаменателя геометрической прогрессии. Аппроксимации:
1 - базовая (4), 2 - уточненная (5), 3 - высокого порядка точности (6).
Сравнение методов аппроксимации градиентов ...
17
3.4. Анализ точности вычисления нормальных градиентов на гра-
ни ячейки. С функцией Гаусса на равномерном шаблоне методы повышен-
ной точности, как и раньше, продемонстрировали улучшение по сравнению
с базовой формулой (рис.11, слева). В противоположность этому, на нерав-
номерной сетке наилучший результат получился при использовании базо-
вого метода (рис.11, справа), причём ошибка оказалась меньше, чем на рав-
номерной сетке (табл.3).
В случае кусочно-линейной функции базовая аппроксимация снова де-
монстрирует самый точный результат (рис.12, табл.3), однако по порядку
величины все схемы дают почти одинаковый уровень ошибки.
Рис.11. Точность аппроксимаций нормальных градиентов на грани ячейки в случае
равномерной (слева) и неравномерной (справа) сетки для функции Гаусса.
Аппроксимации: 1 - базовая (7), 2 - уточненная (8), 3 - высокого порядка
точности (9).
Рис.12. Точность аппроксимаций нормальных градиентов на грани ячейки в случае
равномерной (слева) и неравномерной (справа) сетки для кусочно-линейной
функции. Аппроксимации: 1 - базовая (7), 2 - уточненная (8), 3 - высокого
порядка точности (9).
18
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
Таблица 3. Ошибки аппроксимаций нормальных градиентов на грани ячейки.
Функция Гаусса
Кусочно-линейная функция
Равномер.
Геом.
Равномер.
Геом.
Схема
сетка
прогрессия
сетка
прогрессия
Норма ошибки
L∞
L2
L∞
L2
L∞
L2
L∞
L2
Базовая (7)
0.023
0.02
0.0087
0.007
1.00
0.316
1.00
0.355
Уточненная (8)
0.002
0.002
0.0386
0.033
1.00
0.306
1.005
0.369
Лагранжа (9)
0.002
0.002
0.0490
0.038
1.00
0.306
0.9965
0.413
В тесте с зависимостью ошибок от величины q (рис.13) оказалось, что
метод, использующий формулу Лагранжа, при q (1,2) имеет бóльшие ошиб-
ки, чем комбинированный метод (8). С другой стороны, метод (8) уступает
базовой аппроксимации при q 1.7 . В связи с этим предлагается гибридная
f
(q), позволяющая переключать-
ся между комбинированной и базовой аппроксимацией:
1,
q
1.3,
f
q)
0.5(1+sin((2.5q
2.75))),
q
(1.3;1.7),
mesh (
0,
q
1.7.
:
(8)
(7)
u
f
(q) u
(1
f
(q)) u
(10)
j1/2
mesh
j1/2
mesh
j1/2
Точность этой аппроксимации также изображена на рис.13.
Рис.13. Точность аппроксимаций нормальных градиентов на грани ячейки в зави-
симости от знаменателя геометрической прогрессии. Аппроксимации:
1 - базовая (7), 2 - уточненная (8), 3 - высокого порядка точности (9),
4 - гибридная (10).
Сравнение методов аппроксимации градиентов ...
19
4. Тестирование аппроксимаций в задаче о вихре Тейлора-Грина
Описание задачи представлено в [13]. В кубической расчетной области
с периодическими границами задано начальное поле в виде нескольких круп-
ных вихрей. В процессе расчета вихри разрушаются, порождая квазиизо-
тропную турбулентность. Число Рейнольдса 1600 позволяет проводить пря-
мое численное моделирование этого течения. Описанные выше методы бы-
ли включены в расчётный модуль ZEUS [14] пакета EWT-ЦАГИ [15] и ис-
пользовались в этом тесте. Расчеты проводились конечно-объёмным мето-
дом по явной схеме с WENO-реконструкцией [16] на 9-точечном шаблоне в
каждом сеточном направлении. Исследовалась зависимость энстрофии (сред-
него квадрата завихренности)
ερ
ω
ω
d / (2ρ
)
от времени, где Ω -
0
объём расчётной области, ω - вектор завихренности,
ρ
- средняя плот-
0
ность газа.
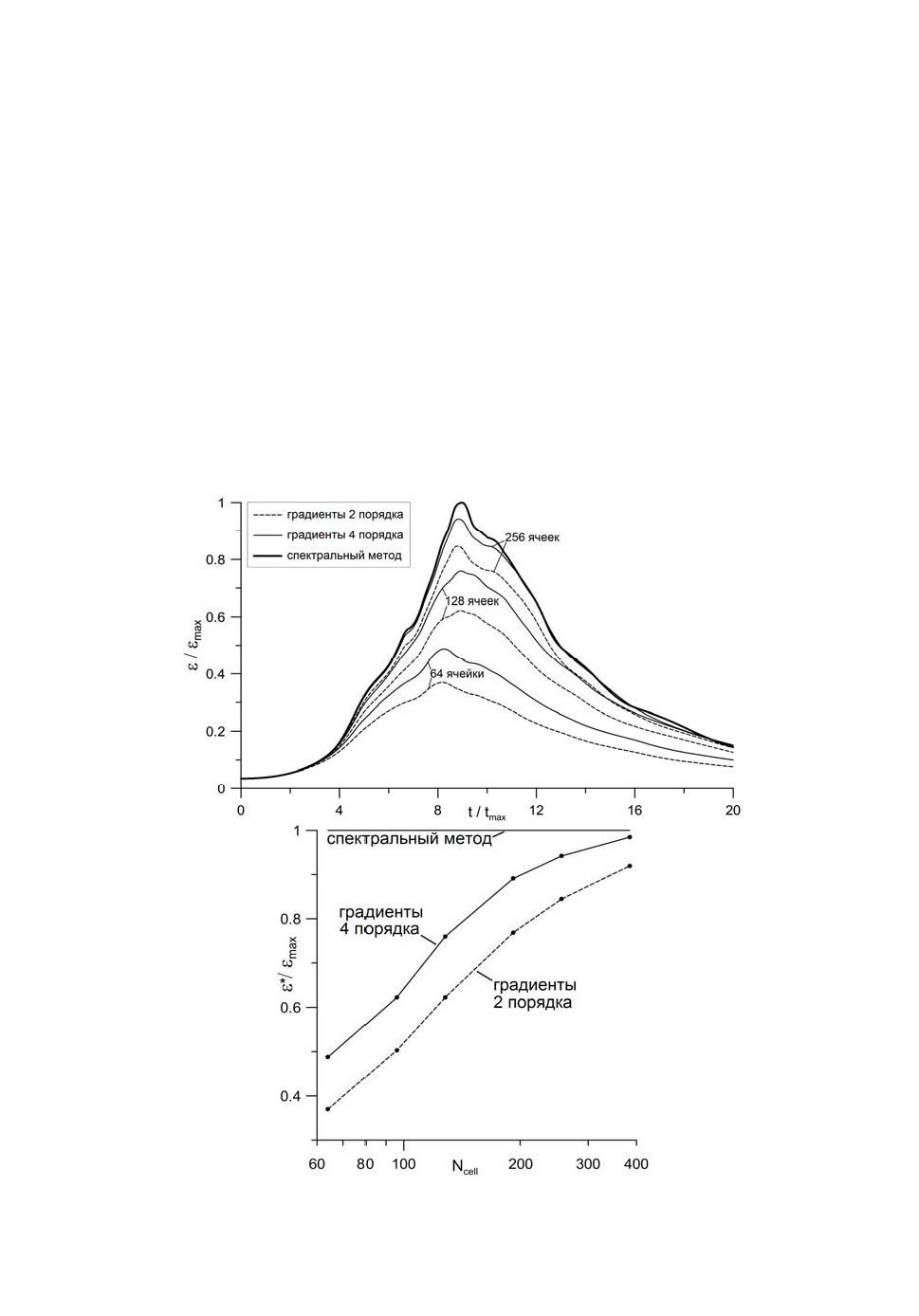
Рис.14. Сходимость расчетов вихря Тейлора-Грина. Сверху - зависимость ε(t) на сетках
различной густоты, снизу - зависимость пикового значения ε от густоты сетки.
20
С. Бахнэ, С.М. Босняков, С.В. Михайлов, А.И. Трошин
На рис.14 сверху представлены решения, полученные на сетках сNcell
64 384 ячейками в каждом направлении, и эталонные данные спектраль-
ного метода на сетке сNcell 512 [13]. С измельчением сетки решения при-
ближаются к эталонным данным, причем переход от базовой аппроксима-
ции градиентов к уточненной приблизительно соответствует 1.5-кратному
измельчению сетки в каждом направлении. На рис.14 снизу изображена за-
висимость пикового значения энстрофии ε от густоты сетки, где виден
этот же эффект. Полученное уточнение можно оценить как экономию в
4
1.5
5 раз по времени счета. Все значения энстрофии обезразмерены на
ε
- ее пиковое значение в эталонном расчете.
max
Выводы
Исследована точность различных способов аппроксимации градиентов
функций. Полученные результаты позволяют сделать следующие выводы.
Методы повышенного порядка точности позволяют уточнить аппрок-
симацию производных гладких функций в центрах ячеек и в касательном
направлении на гранях. Градиенты в нормальном к грани направлении наи-
более точно аппроксимируются «комбинированной» формулой, если нерав-
номерность сетки не слишком велика ( q 1.7 ), и базовой формулой второго
порядка точности, если качество сетки неприемлемо низкое ( q 1.7 ). В свя-
зи с этим предложена гибридная схема, которая переключается между эти-
ми двумя аппроксимациями в зависимости от параметра q .
Аппроксимация производных негладких функций не может быть уточ-
нена с помощью схем повышенного порядка. Более того, эти схемы приво-
дят к появлению забросов значений производной, чего не наблюдается с ба-
зовыми аппроксимациями 2-го порядка точности.
В прямом численном моделировании вихря Тейлора-Грина схемы по-
вышенного порядка позволили снизить уровень ошибки по сравнению с ба-
зовыми методами. Уточнение приблизительно соответствует измельчению
сетки в 1.5 раза в каждом направлении. Это приводит к экономии времени
4
расчета в
1.5
5 раз.
СПИСОК ЛИТЕРАТУРЫ
1. P.R. Spalart, S.Deck, M.L. Shur, K.D. Squires, M.K. Strelets, A.Travin. A new version of
detached-eddy simulation, resistant to ambiguous grid densities // Theor. Comput. Fluid
Dyn., 2006, v.20, p.181-195.
2. M.S. Gritskevich, A.V. Garbaruk, J. Schütze, F.R. Menter. Development of DDES and
IDDES formulations for the k-ω shear stress transport model // Flow Turb. Combust.,
2012, v.88, №3, p.431-449.
3. A. Travin, M. Shur, M. Strelets, P.R. Spalart. Physical and numerical upgrades in the deta-
ched-eddy simulation of complex turbulent flows // Fluid Mech. Appl., 2004, v.65, p.239-254.
Сравнение методов аппроксимации градиентов ...
21
4. L. Fu, X.Y. Hu, N.A. Adams. A family of high-order targeted ENO scheme for compres-
sible-fluid simulations // J. Comput. Phys., 2015, v.305, p.333-359.
5. L. Fu. A low-dissipation finite-volume method based on a new TENO shock-capturing
scheme // Comp. Phys. Comm., 2019, v.235, p.25-39.
6. H. Yee, B. Sjögreen. Recent developments in accuracy and stability improvement of non-
linear filter methods for DNS and LES of compressible flows // Comput. Fluids, 2018,
v.169, p.331-348.
7. F.S. Schranner, J.A. Domaradzki, S. Hickel, N.A. Adam. Assessing the numerical dissipa-
tion rate and viscosity in numerical simulations of fluid flows // Comput. Fluids, 2015,
v.114, p.84-97.
8. А.Н. Кудрявцев, Т.В. Поплавская, Д.В. Хотяновский. Применение схем высокого по-
рядка точности при моделировании нестационарных сверхзвуковых течений // Мат.
моделирование, 2007, т.19, №7, c.39-55;
A.N. Kudriavtsev, T.V. Poplavskaia, D.V. Khotianovskii. Primenenie skhem vysokogo po-
riadka tocnnosti pri modelirovanii nestatsionarnykh sverkhzvukovyh techenii // Mat. mo-
delirovanie, 2007, t.19, №7, s.39-55.
9. Н.Б. Петровская. Выбор весовых коэффициентов в задаче аппроксимации градиента
методом наименьших квадратов // Мат. моделирование, 2004, т.16, №5, c.83-93;
N.B. Petrovskaia. Vybor vesovykh koeffitsientov v zadache approksimatsii gradienta
metodom naimenshikh kvadratov // Mat. modelirovanie, 2004, t.16, №5, s.83-93.
10. S. Bosnyakov, I. Kursakov, A. Lysenkov, S. Matyash, S. Mikhailov, V. Vlasenko, J. Quest.
Computational tools for supporting the testing of civil aircraft configurations in wind
tunnels // Progress in Aerospace Sciences, 2008, v.44, №2, p.67-120.
11. М.Е. Ильин. Аппроксимация и интерполяция. Методы и приложения: учеб. пособие.
- Рязань: Изд-во РГРТА, 2003, 56 с.
M.E. Ilin. Approksimatsiia i interpoliatsiia. Metody i prilozheniia: ucheb. posobie. - Ri-
azan: Izd-vo RGRTA, 2003, 56 s.
12. B. Fornberg. Generation of finite difference formulas on arbitrarily spaced grids // Math.
Computation, 1988, v.51, №184, p.699-706.
13. W.M. Rees, A. Leonard, D.I. Pullin, P. Koumoutsakos. A comparison of vortex and pseudo-
spectral methods for the simulation of periodic vortical flows at high Reynolds number // J.
Comput. Physics, 2011, v.230, p.2794-2805.
14. С.В. Михайлов, В.В. Власенко. Программа ZEUS для расчёта нестационарных тече-
ний в рамках подходов RANS и LES // Материалы XX школы-семинара "Аэродина-
мика летательных аппаратов", пос. Володарского, 2009.
S.V. Mikhaylov, V.V. Vlasenko. Programma ZEUS dlia rascheta nestatsionarnykh techenii v
ramkah podhodov RANS i LES // Materialy XX shkoly-seminara “Aerodinamika letatel-
nykh apparatov”, pos. Volodarskogo, 2009.
15. С.М. Босняков. Концепция программного продукта EWT-ЦАГИ и основные этапы её
развития // Труды ЦАГИ, 2007, №2671, с.3-19;
S.M. Bosniakov. Kontseptsiia programmnogo produkta EWT-TsAGI i osnovnye etapy ee
razvitiia // Trudy TsAGI, 2007, №2671, s.3-19.
16. R. Zhang, M. Zhang, C.W. Shu. On the order of accuracy and numerical performance of
two classes of finite volume WENO schemes // Comm. Comput. Physics, 2011, v.9, №3,
p.807-827.
Поступила в редакцию 04.03.2019
После доработки 08.04.2019
Принята к публикации 20.05.2019