МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 10, стр. 98-116
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ АКУСТИЧЕСКИХ ПОЛЕЙ,
ИНДУЦИРОВАННЫХ КОЛЕБАНИЕМ ТЕЛ В ПОТОКЕ
©
2019 г.
И.В. Абалакин1, В.А. Вершков2, Н.С. Жданова1,
Т.К. Козубская1
1Институт прикладной математики им. М.В. Келдыша РАН
2Центральный аэрогидродинамический институт им. Н.Е. Жуковского
ilya.abalakin@gmail.com; nat.zhdanova@gmail.com
Проведенные исследования выполнены при поддержке Российского науч-
ного фонда (Проект РНФ 16-11-10350).
DOI: 10.1134/S0234087919100083
Представлены две вычислительные методики, не требующие изменения топологии
сетки, для моделирования течения около колеблющихся тел. Первая методика ис-
пользует метод погруженных границ, вторая - метод деформируемых сеток. Воз-
можности этих двух подходов демонстрируются на примере решения модельных
задач в двумерной постановке по расчету акустических полей, генерируемых в
дозвуковом потоке осциллирующим цилиндром - как одиночным, так и в присут-
ствии неподвижного тела цилиндрической формы.
Ключевые слова: течение вязкого газа, сжимаемый газ, акустическое поле, колеба-
ние цилиндра, математическое моделирование, метод погруженных границ, де-
формируемая сетка, вычислительная аэроакустика.
NUMERICAL SIMULATION
OF ACOUSTIC FIELDS INDUCED BY FLOW PAST OSCILLATING SOLID
I.V. Abalakin1, V.A. Vershkov2, N.S. Zhdanova1, T.K. Kozubskaya1
1Keldysh Institute of Applied Mathematics of RAS
2Central Aerohydrodynamic Institute
The paper presents two computational techniques that do not require a change in the to-
pology of the mesh, to simulate the flow around oscillating bodies. The first technique
uses the immersed boundary method, the second - the method of deformed meshes. The
capabilities of these two approaches are demonstrated by solving model problems in a
two-dimensional formulation for simulating acoustic fields generated by an oscillating
cylinder, both single and in the presence of a fixed cylindrical body, in subsonic flow.
Key words: compressible viscous flow, acoustic field, cylinder oscillation, mathematical
modeling, immersed boundary condition, moving mesh, computational aeroacoustics.
Численное моделирование акустических полей, индуцированных колебанием ...
99
Введение
Исследование генерации и распространения акустического излучения
представляет собой в наши дни актуальную задачу, напрямую связанную с
улучшением экологической обстановки в населенных пунктах и на терри-
ториях промышленных предприятий.
При решении задач по снижению шума, производимого авиационной
техникой, автомобилями и другими устройствами, может быть использован
метод математического моделирования как одно из эффективных средств в
дополнение к физическому эксперименту и теоретическим оценкам.
В авиации одним из акустических источников шума являются выпус-
каемые шасси самолёта, выдвигающиеся или задвигающиеся предкрылки и
закрылки. То есть генерация звука обусловлена обтеканием конструкции с
подвижными элементами.
При моделировании течения вокруг тел, движущихся с переменной
скоростью, в методику численного моделирования необходимо включать
специальные подходы для воспроизведения движения или, как минимум,
его учёт. В последнем случае можно использовать математическое описа-
ние в неинерциальной системе отсчёта, связанной с движущимся препятст-
вием и позволяющей работать на неизменной расчётной сетке. Однако этот
подход неприемлем в общем случае, когда рассматривается система из двух
и более тел, движущихся с разными скоростями, или одно из которых не-
подвижно относительно других. В настоящей работе разрабатываются два
других подхода, основанных на методе погруженных границ и методе де-
формируемой сетки.
Метод погруженных границ основан на идее, предложенной в [1]. Она
заключается в имитации алгебраического условия на границе твердого тела
путём модификации системы уравнений газодинамики (или разностного
шаблона ее аппроксимации) в точках сетки, находящихся в окрестности
границы. При этом модифицированная математическая модель работает в
односвязной области, включающей зону локализации препятствия. Соответ-
ственно и расчёт проводится во всей области, включая препятствие. Отказ
от отслеживания границы раздела сред граничными узлами сетки даёт сво-
боду для моделирования перемещений тела и его возможной деформации.
В настоящей работе применяется вариант метода погруженных границ,
основанный на методе Бринкмана штрафных функций [2]. Метод Бринкмана
штрафных функций успешно применяется для численного моделирования
вязких как несжимаемых (например, [35]), так и сжимаемых течений (напри-
мер, [6, 7]). Немногочисленные методики численного моделирования невязких
100
И.В. Абалакин и др.
течений на основе этого метода представлены в [8] и работе авторов данной
статьи [9]. Свойства течения в невязком случае определяются системой ли-
неаризованных уравнений Эйлера, а граничное условие непротекания (ра-
венство нулю нормальной составляющей скорости на твердой поверхности)
моделируется методом Бринкмана штрафных функций. Результаты числен-
ного моделирования акустических полей течения представлены в [10], где
использован модифицированный метод Бринкмана, а именно объёмный ме-
тод штрафных функций (Volume Penalization Method).
Другим подходом к моделированию движения твердых тел, имеющих
все шесть степеней свободы, является деформирование расчётной сетки.
Существуют три основные разновидности алгоритмов этого подхода: метод
деформации сеточных элементов без изменения топологии (см., например,
[11]), метод вложенных сеток [12] и метод перестроения расчетной сетки на
каждом шаге [13].
Первый метод заключается в том, что на каждом шаге по времени узлы
расчетной сетки изменяют свои координаты по заранее заданным законам
так, чтобы не изменилась общая топология расчетной сетки. В общем слу-
чае алгоритмы данного класса могут описывать движения лишь с относи-
тельно небольшой амплитудой.
В настоящей работе в качестве альтернативы методу погруженных
границ представлен метод, относящийся к первому подходу. В нем узлы
расчетной сетки меняют свои координаты так, чтобы не испортить качество
сеточных элементов. Главной особенностью построенного алгоритма явля-
ется возможность работать с гибридными сетками, а также возможность
напрямую управлять движением каждого узла расчетной сетки.
Два рассматриваемых в статье подхода имеют принципиальные разли-
чия. При первом подходе, основанном на использовании метода Бринкмана
штрафных функций, модифицируется сама математическая модель за счет
добавления источникового члена. Начальная задача при этом численно ре-
шается, вообще говоря, на неизменной сетке в односвязной области. Изме-
нения сетки могут касаться лишь динамической сеточной адаптации, кото-
рая помогает снизить вычислительные затраты. Второй подход, наоборот,
оставляет неизменной математическую модель и оперирует с сеточными
технологиями для описания движущегося препятствия. В этом случае реша-
ется начально-краевая задача в многосвязной области. Из множества мето-
дов сеточной деформации мы выбираем метод движущейся сетки с сохране-
нием её топологии, который представляется наиболее эффективным для рас-
смотрения задач с небольшими колебаниями тел.
В настоящей работе оба подхода используются для моделирования акус-
Численное моделирование акустических полей, индуцированных колебанием ...
101
тических полей, генерируемых при дозвуковом обтекании вязким сжимае-
мым газом двумерного круглого цилиндра, колеблющегося под действием
вынужденных сил в направлении, перпендикулярном набегающему потоку,
а также тандема цилиндров, один из которых колеблется аналогичным об-
разом.
1. Математическая модель
В качестве базовой математической модели в работе используется сис-
тема уравнений Навье-Стокса для идеального сжимаемого газа. Запишем ее
в виде законов сохранения относительно вектора искомых консервативных
переменных
Q
u,
E
)T
в векторном виде как
Q
Q
Q,Q
S
Q
,
(1)
t
где
u(u
,u
,u
) - вектор скорости,
- плотность, p- давление, E
1
2
3
2
u
/2 - полная энергия, - внутренняя энергия.
В системе (1) введены составные векторы и
, каждая компонента
x (i=1, 2, 3) представляет
собой вектор потока конвективного переноса и вектор потока диффузии,
соответственно. Оператор () есть оператор взятия дивергенции по каж-
дой компоненте составного вектора.
Система уравнений Навье-Стокса (1) замыкается уравнением состоя-
ния совершенного газа p ( 1), где 1.4 есть показатель адиабаты.
Векторы потоков конвективного переноса задаются как функции физи-
ческих переменных , u, p следующим образом:
T
F
Q
u
, u
u pI
,
Ep
u
,
(2)
i
i
i
i
где I - единичная матрица. Векторы потоков диффузии определяются как
функции физических переменных и их градиентов по формуле:
T
F
Q,
Q
0,
,
,
,
u q
,
(3)
i
i1
i
2
i3
ij j
i
и вектора теплового пото-
каqi имеют вид
u
u
j
2
u
γ
i
i
,
q
,
(4)
ij
ij
i
x
x
3
x
Pr
x
j
i
i
102
И.В. Абалакин и др.
- символ Кронекера, - коэффициент молекулярной вязкости,
Pr 0.72 - число Прандтля. Вектор S(Q) представляет собой источнико-
вый член, описывающий влияние внешних сил, не связанных с процессами
переноса искомых переменных Q.
Для дальнейшей численной реализации систему уравнений (1) удобнее
рассматривать в интегральной формулировке, записанной относительно
произвольного движущегося объема V (t). Для этого проинтегрируем сис-
тему (1) по движущемуся объёму V (t) с границей V (t) в некоторый мо-
мент времени. После применения теоремы Остроградского - Гаусса и тео-
ремы о производной по времени от интеграла по жидкому объему [14] по-
лучаем смешанную эйлерово-лагранжеву (СЭЛ) формулировку системы
уравнений Навье - Стокса
d
QdV
Q
ndS
· Q
Q
dV S
Q
dV
,
(5)
dt
V
V
V
V
где n - единичная внешняя нормаль к границе V (t), движущейся со скоро-
стью v , а компоненты составного вектора конвективного потока имеют вид
T
F
Q
u
v
,
u
uv
pI,
E
u
v
pu
(6)
i
i
i
i
i
i
i
Система вида (5), (6) уже рассматривалась авторами в [15,16] при расчёте
шума от винта вертолета, где под скоростью v понималась линейная ско-
рость вращения лопасти винта (в системе координат, связанной с лопа-
стью), и в [17, 18] при проведении расчётов на подвижной сетке (в частно-
сти, динамически адаптивной сетке), где скорость v полагалась равной
скорости движения сетки v(r,t) , r - радиус вектор точки в расчётной об-
ласти. В настоящей работе для моделирования движущихся объектов ис-
пользуются два подхода также на основе системы уравнений (1)-(6). Разли-
чие между ними состоит в разном определении источникового члена S(Q)
и разном выборе скорости v .
При проведении расчетов уравнения Навье-Стокса записывались в без-
размерном виде относительно переменных:
,
tU
D
,
/
,
0/
0
2
2
,
/
,
p
/
U
/U
, где
,
U
,
- характерные па-
0
0
0
0
0
0
0
0
раметры течения (в задачах обтекания - параметры набегающего невозму-
щённого потока), D - геометрический характерный размер задачи. В без-
размерных переменных вид системы уравнений не меняется за исключени-
ем замены коэффициента вязкости
на выражение
, где Re
U
D
/
- число Рейнольдса.
0
0
0
Численное моделирование акустических полей, индуцированных колебанием ...
103
2. Метод Бринкмана штрафных функций
При использовании метода Бринкмана штрафных функций [6] как од-
ного из вариантов метода погруженных границ в системе уравнений Навье-
Стокса (5), (6) скорость v 0 , т.е. используется абсолютная система коор-
динат. В качестве источникового члена S(Q) выбирается вектор-функция
(
)
S
Q
, которая работает только внутри области твёрдого тела и имеет сле-
дующий вид:
1
T
S
0,(uu
), 0
,
(7)
B
гдеuB - скорость движения тела, 1 - штрафной параметр, (t) - ха-
рактеристическая функция, определяющая геометрическое положение об-
текаемого тела,
1,
x
(t),
B
t
0,
x
(t).
F
ЗдесьB - замкнутая область, занимаемая телом, включая его поверх-
ность,F - область течения.
С физической точки зрения метод Бринкмана штрафных функций
можно интерпретировать как взаимодействие жидкой среды с твердым те-
лом, рассматриваемым в приближении пористой среды с низкой проницае-
мостью . С математической точки зрения наличие в системе (1) источни-
ковых членов типа (7) определяет быструю релаксацию скорости (порядка
expt , 1) к нулевым условиям Дирихле в тех точках сетки, где ха-
рактеристическая функция отлична от нуля, в том числе и на границе
твёрдого тела. В [3, 4] дается теоретическое обоснование сходимости реше-
ния
Q
системы уравнений Навье-Стокса (1) с источником (7) к решению
Q системы уравнений (1) с источником S(Q) 0 при стремлении параметра
к нулю.
3. Метод деформации расчетной сетки
При использовании метода деформации расчётной сетки в системе
уравнений Навье-Стокса (5), (6) скорость v полагается равной скорости
движения узлов сетки, а источниковый член полагается равным нулю
(S(Q) 0). Заметим, что подвижные сетки без изменения топологии могут
быть востребованы и в случае применения метода погруженных границ.
Дело в том, что эффективность этого подхода для описания движущегося
104
И.В. Абалакин и др.
препятствия существенно повышается при использовании динамической
сеточной адаптации к поверхности неявно заданного твёрдого тела. Наибо-
лее подходящим типом адаптации при этом являются методы класса дви-
жущихся сеток, которые не меняют топологии исходной сетки.
3.1. Алгоритм выделения зоны деформации и задания весовой
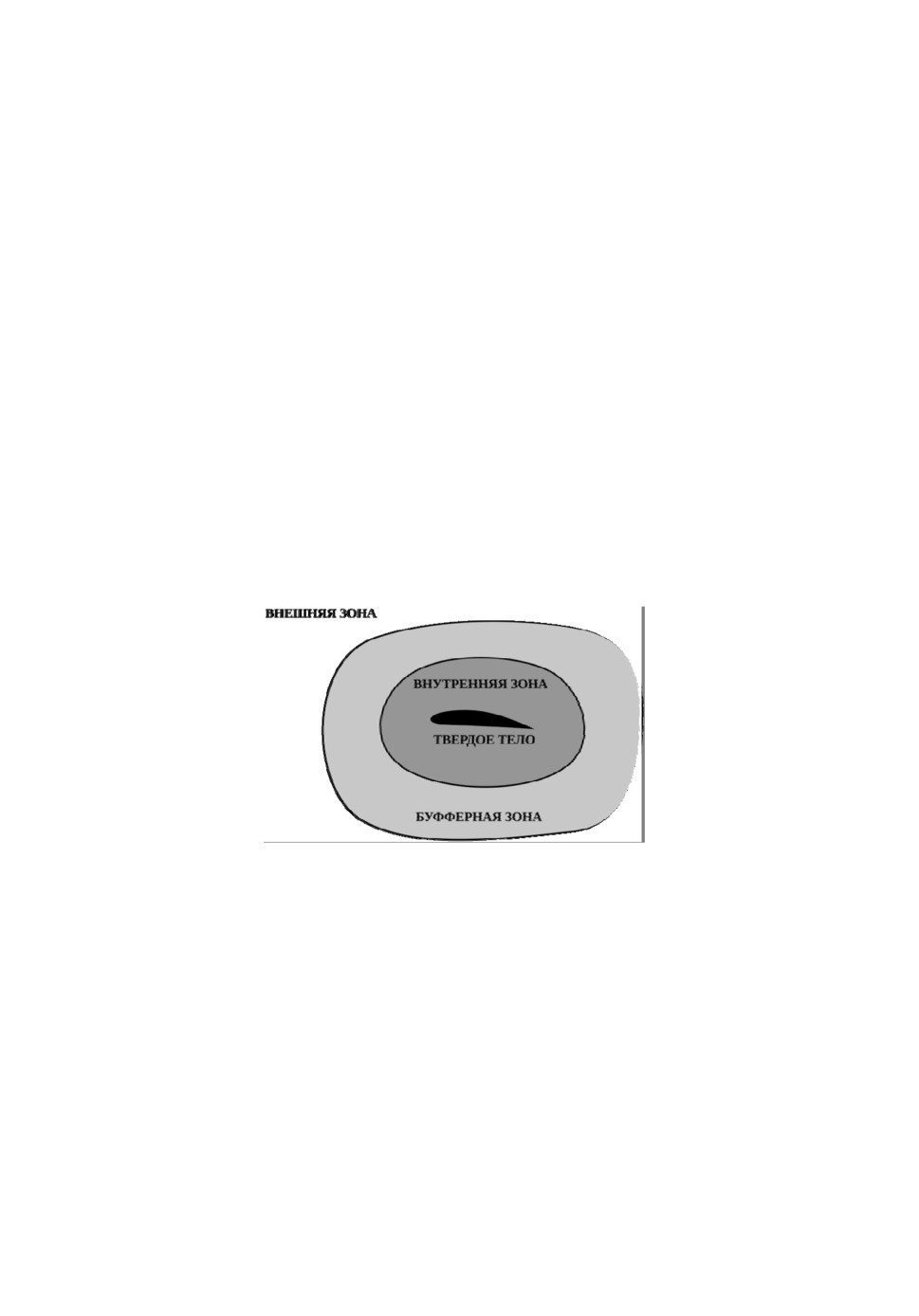
функции. В общем случае вся расчетная область разбивается на три подоб-
ласти: внутреннюю, буферную и внешнюю (рис.1). Внутренняя область
примыкает к поверхности подвижного твёрдого тела. Предполагается, что
все узлы расчётной сетки «заморожены» относительно окружаемого ими
твердотельного препятствия и смещаются с ним вместе как единое целое,
без движения друг относительно друга. В качестве внутренней области мо-
жет рассматриваться, например, пограничный слой течения, покрываемый
обычно в расчётах слоистой сеткой с регулярной структурой по нормали.
Во внешней зоне все узлы расчетной сетки в процессе расчёта покоятся. В
буферной же области узлы меняют свои координаты друг относительно
друга по определенному закону, обеспечивая гладкий переход от внешней к
внутренней зоне.
Рис.1. Подобласти деформации сетки.
Каждому узлу расчетной сетки присваивается значение весовой функ-
ции
F(r
)
r - радиус-вектор сеточного узла i в абсолютной системе
i
координат, которая отвечает за амплитуду деформации сеточного элемента
и входит в уравнение сеточной деформации в виде коэффициента. Внутри
движущейся как единое целое внутренней области значение весовой функ-
ции постоянно и равно единице
(
)
1
F
r
. Во внешней зоне сетка неподвиж-
i
на и весовая функция равна
(
)
0
F
r
. В буферной же зоне весовая функция
i
(
)
F
r
имеет линейное распределение от 1 до 0 вдоль некоторого отрезка
i
прямой между точкойRinti внешней границы внутренней зоны и точкой
ext
R
внутренней границы внешней зоны. В качестве такой прямой можно
i
Численное моделирование акустических полей, индуцированных колебанием ...
105
выбирать, например, линию, соединяющую сеточный узел i с заданным
центром тела, или нормаль к поверхности тела, проходящую через узел i .
Линейное распределение весовой функции между внутренней и внешней
областями обеспечивает монотонность смещения узлов и исключает воз-
можность «перехлеста» узлов в буферной зоне. При линейном распределе-
нии значения весовой функции определяются согласно формуле
ext
R
r
i
i
F(r
) max0,min1,
(8)
i
ext
int
R
R
i
i
Следует отметить, что, вообще говоря, можно использовать не только ли-
нейный, но и более сложные законы распределения.
В общем случае конфигурация и размеры внутренней и внешней об-
ластей задаются вручную, принимая во внимание особенности конкретной
задачи и, в частности, амплитуду возможного движения тела. В качестве
внешней границы буферной зоны удобно выбирать достаточно простую по-
верхность, задаваемую аналитически, - например, в форме цилиндра или
сферы. В программном комплексе NOISEtte [19], который используется для
проведения всех численных экспериментов, представленных в данной ста-
тье, реализована процедура проверки ограничений на каждом шаге по вре-
мени на допустимые границы буферной области. Эта процедура при необ-
ходимости меняет размеры зоны деформации на оптимальные.
3.2. Алгоритм движения узлов в зоне деформации сетки. После при-
своения значения весовой функции
(
)
F
r
каждому узлу сетки в расчётной
i
области выполняется поиск новой координаты узла на каждом шаге по вре-
мени. Результатом работы данного алгоритма является новая координата
точки с учётом всех определяемых законом движения отклонений относи-
тельно её первоначального положения. В общем случае координата узла
n1
r
в момент времени t t определяется положением узлаrni на момент
i
времени t и зависящей от вектора параметров смещенияpn функцией G ,
n
умноженной на весовую функцию
(
)
F
r
типа (8),
i
n1
n
n
n
r
G(r
,p
)F(r
)
i
i
i
Функция смещения G определяется на основе заданного извне закона
движения, описывающего перемещение. Более точно, эта функция опреде-
ляется переносом и поворотом центра тяжести твёрдого тела и его враще-
нием
106
И.В. Абалакин и др.
n
n
n
n
n
n
n
n
n
n
n
n
n n
G(r
,p
)A
(
,
,
)(r
s)A
(
,
,
)
A
(
,
,
)(r
r
),
o
R
R
o
R
гдеrn - радиус-вектор узла (индекс i опускаем) в абсолютной системе ко-
ординат (x, y, z) с центром в точке O . Вектор параметров смещения p оп-
ределяется как
n
n
n
n
n
n
n
n
p
r s
,
,
,
,
,
R
ЗдесьrnR - радиус-вектор центра вращения, лежащий внутри тела, s - век-
A
- матрица поворота вокруг оси, проходящей через центр
абсолютной системы координат,AR матрица поворота вокруг оси, прохо-
дящей через центр R системы координат (x,y,z), связанной с телом. Центр
n
новой системы координат Rзадается радиус-вектором
(
)
A
r
s
. Матрицы
o R
поворотов зависят от углов Эйлера , , в соответствующей системе ко-
ординат, определяющих последовательные повороты вокруг осей x , y , z .
Несомненным преимуществом данного алгоритма является скорость
его работы. За счет того, что буферная область ограничена, в процесс се-
точной деформации вовлекается относительно небольшое по сравнению с
общим числом ячеек количество узлов сетки.
Отметим, что изложенный алгоритм был впервые предложен в [20] для
расчета движущихся лопастей вертолета. В настоящей работе данный алго-
ритм сформулирован для произвольного движения недеформируемого твер-
дого тела.
4. Численный метод
Аппроксимацию системы уравнений Навье-Стокса будем проводить на
основе наиболее общей интегральной формы записи этой системы в СЭЛ
форме (5), (6).
Запишем систему (5), (6) в дискретном виде для контрольного объёма
K
, построенного вокруг сеточного узла i в рамках вершинно-центрирован-
i
ной формулировки,
d
QdV
(Q)
vQ
n
dS
· Q
Q
dV
S(Q)dV
,
dt
K
i
K
i
K
i
K
i
K
- граница контрольного объёма (или ячейки)Ki , а v - вектор ско-
рости движения грани, который отвечает за изменение во времени конт-
рольного объёма [18]. Численная схема метода конечных объёмов при этом
строится как
Численное моделирование акустических полей, индуцированных колебанием ...
107
dK
i
Q
i
с
h
K
S
Q
,
h
h
h
,
ij
i
i
ij
ij
ij
dt
jN
1(
i
)
где
K
K ,
N
(i) - множество сеточных узлов, соседних по
i
1
отношению к узлу i ,hij - численный поток, аппроксимирующий физиче-
ский поток на границе между узлами i и j , состоящий из аппроксимации
конвективных и вязких потоковhсij иhj соответственно. Аппроксимация
конвективного потока строится с использованием того или иного прибли-
жённого метода решения задачи о распаде разрыва. В настоящей работе ис-
пользуется метод Роу, при котором численный конвективный поток можно
представить в виде суммы двух членов, соответствующих центрально-раз-
ностной и противопотоковой аппроксимациям, отвечающим за перенос и
диссипацию соответственно:
Q
Q
Q
Q
c
i
j
i
j
δ
1
h
t
n
v
S
Λ
v
I
S
Q
Q
,
ij
ij
ij
ij
j
i
2
2
2
перенос
диссипация
(9)
1
d
1
v (t)
v·
n
dS,
A
Q
S
Λ
S
ij
ij
ij
ij
ij
ij
n
dQ
ij
K t)K t)
i
j
ЗдесьAij есть матрица якобиана, зависящая от значения вектора консерва-
тивных переменныхQij , определенного на интерфейсе (или середине реб-
ра) ij ,Λij - диагональная матрица собственных значений ЯкобианаAij ,nij
- ориентированная площадь грани ij , δ - параметр, контролирующий чис-
ленную диссипацию.
Для повышения пространственного порядка аппроксимации конвек-
тивного потока схемы (9) используется реберно-ориентированная реконст-
рукция на расширенном шаблоне [21, 22]. При таком подходе переменные
Q
иQj в (9) заменяются реконструированными слева и справа от грани
i
ячейки значениямиQj иQj , а матрицы S и не изменяются. Способ опре-
деленияQj иQj определяет конкретную рёберно-ориентированную схе-
му. В случае схемы EBR5, которая была использована при проведении рас-
четов, представленных в настоящей статье, реконструкция приведена в [22].
Аппроксимация вязких потоковhj в уравнении Навье-Стокса прово-
дится методом Галёркина на основе полиномов 1-го порядка как в случае
покоящейся, так и в случае движущейся сетки.
108
И.В. Абалакин и др.
При решении рассматриваемых в статье задач интегрирование по вре-
мени проводилось по неявной схеме Эйлера первого порядка для метода
деформируемых сеток и по неявной трёхслойной схеме второго порядка -
для метода Бринкмана штрафных функций.
5. Результаты численных экспериментов
Постановки всех рассмотренных в работе задач предложены в [10], где
их численное решение получено с применением структурированных расчет-
ных сеток. Для моделирования движения цилиндра в [10] применяется одна
из разновидностей метода погруженных границ, предложенного в [7]. Чис-
ленное решение задач получено двумя методами - методом погруженных
границ (IBC - Immersed Boundary Condition) и методом деформируемых се-
ток (MM - MovingMesh).
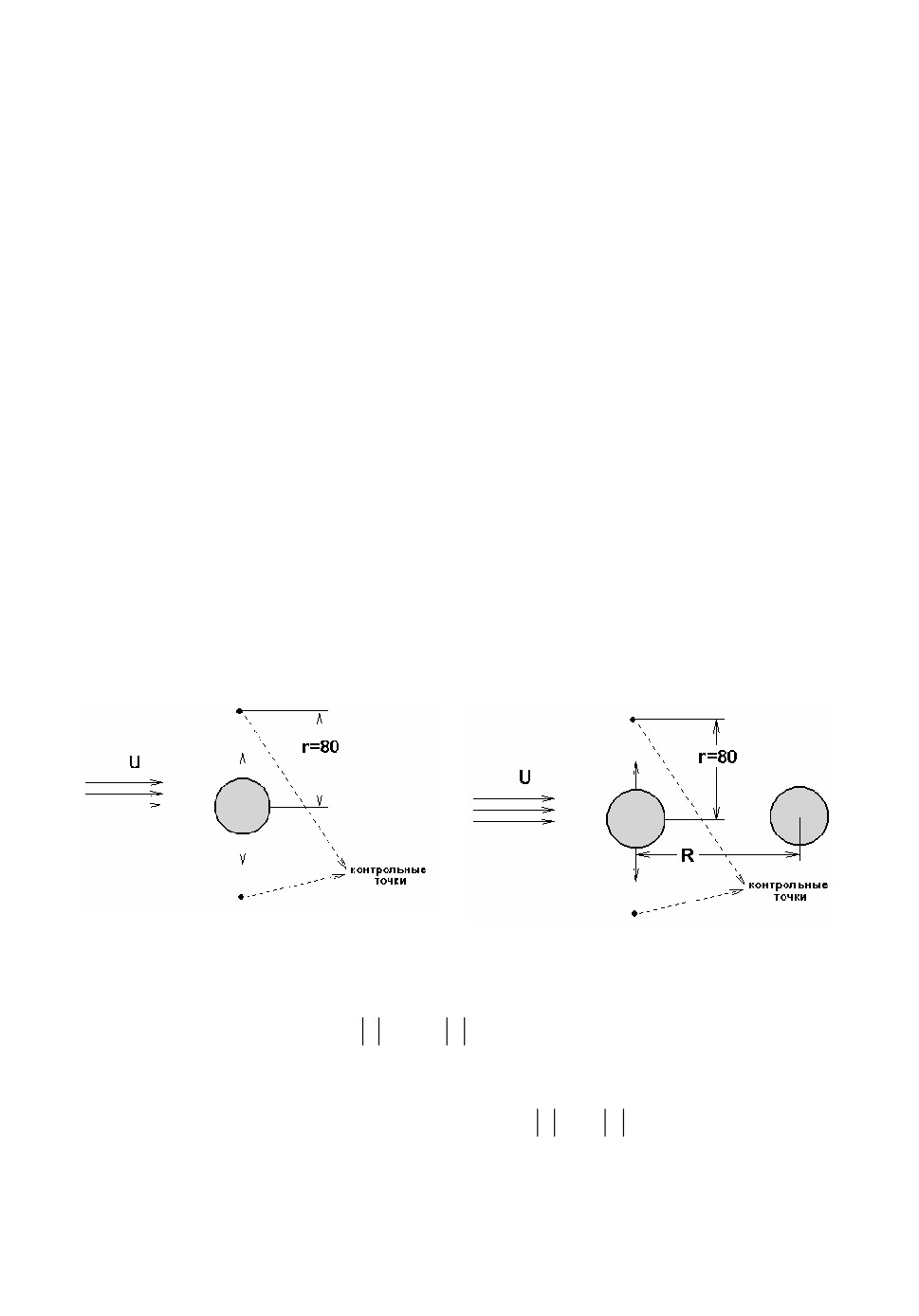
5.1. Задача о колебании цилиндра в потоке. В первой задаче рас-
сматривается генерация звука колеблющимся двумерным цилиндром (см.
рис.2 (слева)). Цилиндр с диаметром D=1, расположенный в начале коорди-
нат, совершает гармонические колебания. Положение центра масс (x
,
y
)
c c
цилиндра задается соотношениями:
x
0,
y
Asin(2f
t) , где амплитуда
c
c
c
колебаний A0.2 , а их линейная частота
f
0.15. Перпендикулярно на-
c
правлению колебаний, слева на цилиндр набегает поток, характеризуемый
числом Маха M 0.2 и числом Рейнольдса Re 150.
Рис.2. Постановка задач об обтекании одного осциллирующего цилиндра
(слева) и тандема цилиндров, один из которых осциллирует (справа).
Для проведения численного моделирования выбиралась расчетная об-
ласть следующего размера:
x
<500,
y
<500. Внутри нее строилась неструк-
турированная треугольная сетка со сгущением в окрестности цилиндра и
числом узлов, приблизительно равным 550000. Линейный размер сеточного
элемента в области максимального сгущения
x
1,
y
1.5 не превосходил
величины 0.01. При численном моделировании методом погруженных гра-
ниц расчетная сетка покрывает внутреннюю часть цилиндра, при использо-
вании подвижных сеток узлы расчетной сетки определяют его поверхность.
Численное моделирование акустических полей, индуцированных колебанием ...
109
В методе деформируемых сеток для данной задачи задана весовая
функция F, которая в общем случае задается соотношением (8). Внутренняя
и буферная зоны определены в виде концентрических окружностей радиу-
сов
R
иR
соответственно.
1
2
Результаты расчетов в обоих случаях показали, что при достижении
времени t 50 вокруг цилиндра устанавливается периодическое течение,
характеризуемое образованием звуковых волн.
Для оценки точности моделирования распространения и генерации
звука проанализированы пульсации давления в контрольных точках, распо-
ложенных на окружности (r, ) с центром в начале координат, где радиус
r 80 и угол отсчитывается против часовой стрелки. В качестве рефе-
ренсных данных использованы результаты работы [10]. Их достоверность
подтверждается хорошим согласованием с данными, полученными с при-
менением согласованных с границей сеток.
Дополнительно был проведен расчет методом IBC неподвижного ци-
линдра (частота
0
f
) с теми же параметрами набегающего потока, как и у
c
колеблющегося цилиндра. Для верификации этого расчёта использовались
данные из [23], в которой расчёты проводились с использованием согласо-
ванной с телом сетки1.
Здесь и далее числом Струхаля St называется безразмерная частота схода
вихрей с поверхности цилиндра, определяемая как основная частота в спек-
тральном представлении распределения коэффициента подъёмной силыCL .
Сила, действующая на тело со стороны жидкости, определяется по сле-
дующей формуле:
F
(pn
Sn
)dS
B
B
B
(10)
u
1
B
dV
(u
u
)dV
(u
u
)dV,
B
B
B
t
B
B
B
полученной с помощью разложения переменных по малому параметру ,
аналогично асимптотическому анализу системы уравнений (1), (7), прове-
дённому в [3, 6]. Формула (10) является обобщением для переменной скоро-
сти формулы, полученной в [6] для постоянной скорости.
В табл.1 суммированы характеристики, полученные при моделирова-
1 Подробное сравнение результатов расчёта методом IBC и классическим методом с ис-
пользованием согласованной с телом сетки приведено в [24], где рассматривалась задача
о моделировании нестационарного турбулентного течения около трёхмерного цилиндра.
110
И.В. Абалакин и др.
нии одиночного цилиндра - колеблющегося и стационарного. Можно заме-
тить, что число Струхаля неподвижного цилиндра есть величина 0.184, сов-
падающая со значением, полученным в расчёте [23] (см. табл.1), а частота
схода вихрей для подвижного цилиндра есть величина 0.150, совпадающая
с частотой его вынужденных колебаний. Это связано с тем, что при колеба-
нии цилиндра срыв вихрей происходит в его крайнем верхнем и нижнем
положении (для данных значений частоты и амплитуды). В данных, приве-
денных в табл.1, наблюдается значительное расхождение (более чем в два
раза) среднеквадратичных значений коэффициента подъемной силыC r.m.sL
колеблющегося и неподвижного цилиндров, но средний коэффициент силы
сопротивленияCD отличается незначительно.
Таблица 1. Число Струхаля St, безразмерная частота пульсаций давления
U
f D в
0
точке (r,
)
(80, 90 )
, среднее значение коэффициента сопротивления
C
и среднеквадратичное значение коэффициента подъемной силы
D
r.m.s
C
при различных режимах обтекания цилиндра.
L
Подвижный
Неподвижный
Неподвижный
цилиндр
цилиндр
цилиндр [22]
St
0.150
0.184
0.184
U
0
f D
0.150
0.184
—
C
D
1.29
1.33
1.311.33
r.m.s
C
L
0.16
0.37
0.350.36
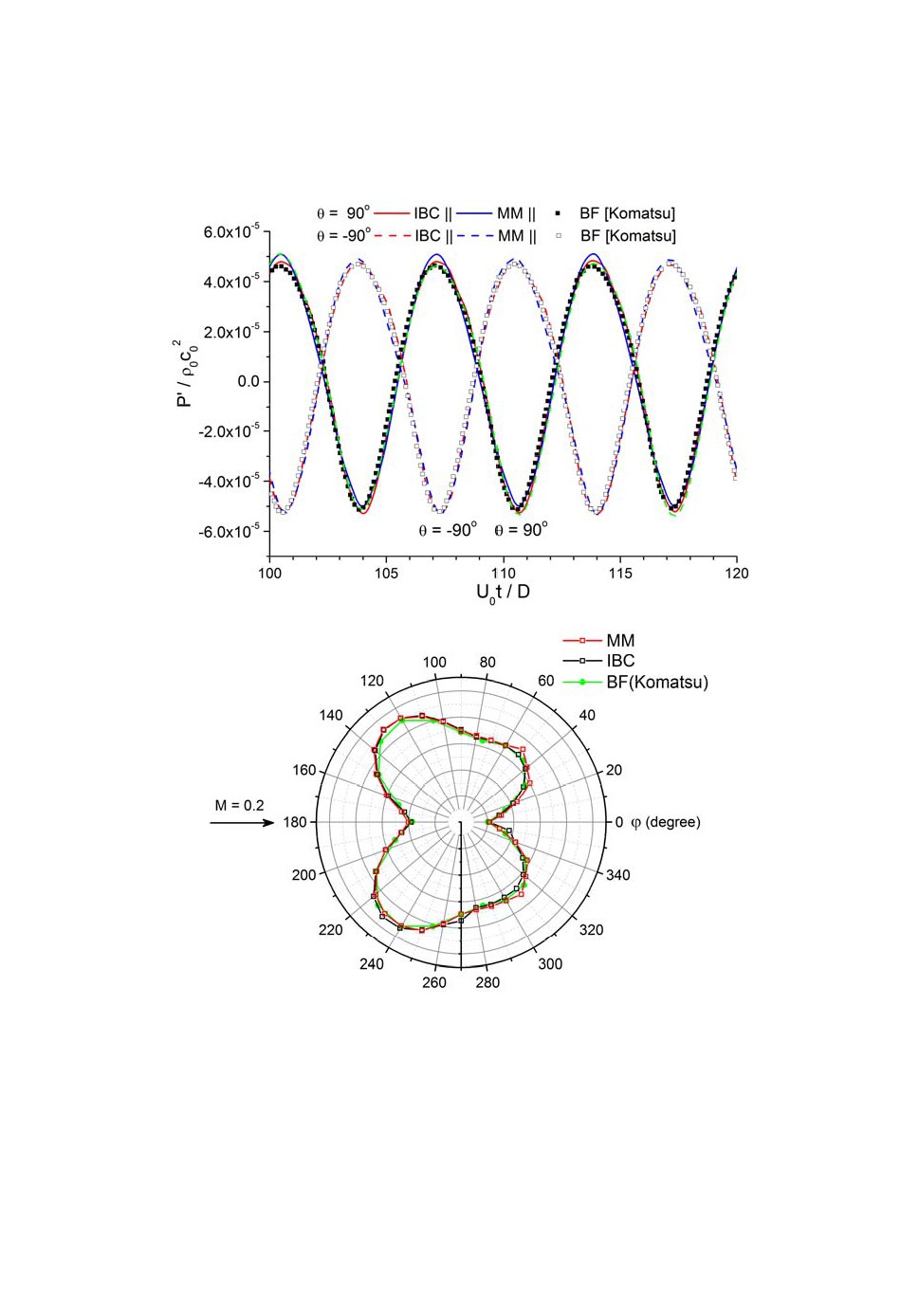
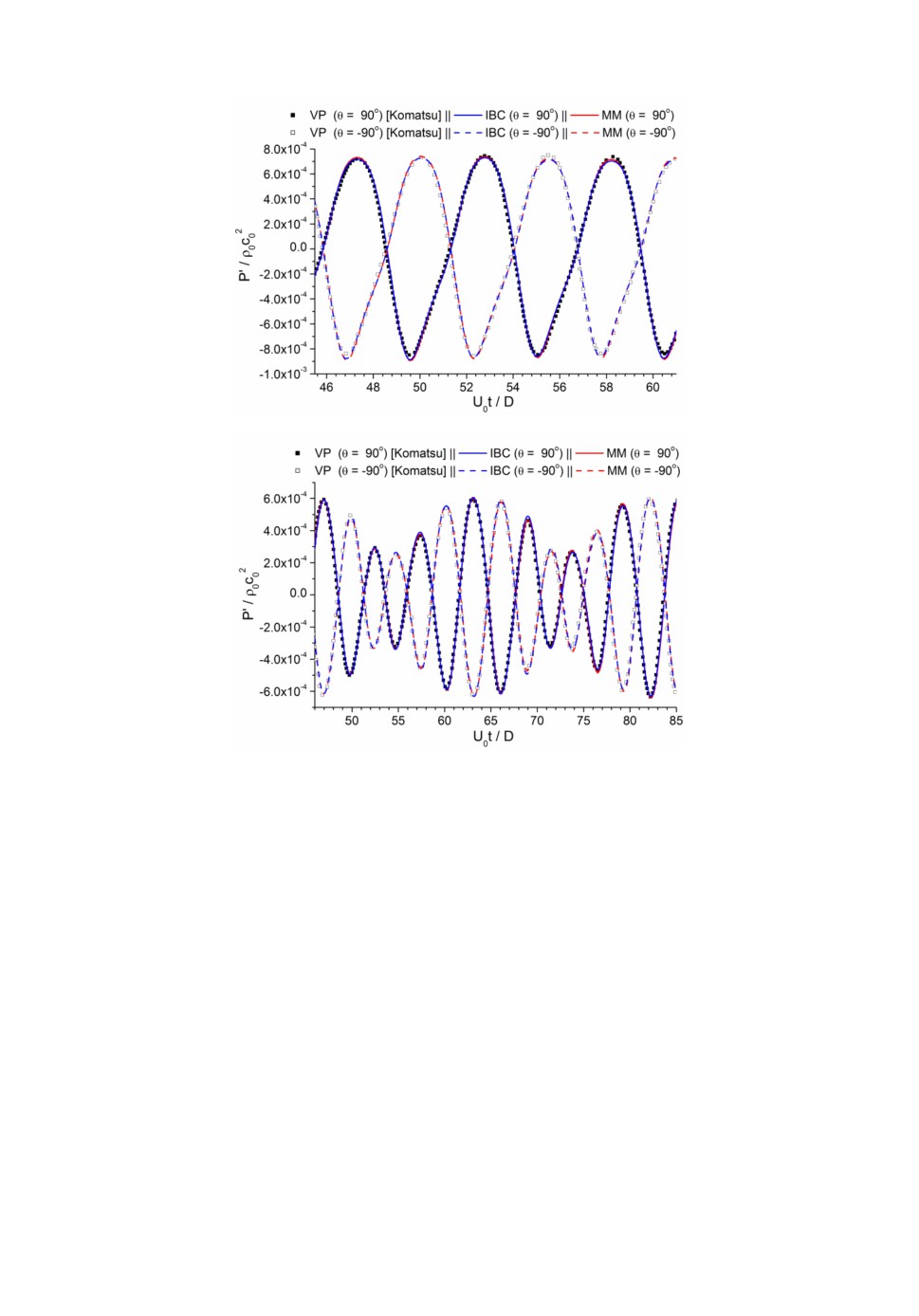
На рис.3 (сверху) приведено распределение пульсаций давления в точ-
ке (r,)
(80, 90
)
. Можно видеть строго периодическое поведение распре-
делений с периодами, соответствующими безразмерным частотам, равным
числам Струхаля. На рис.3 (снизу) представлена диаграмма направленности
при r 80 . Как видно из графиков, все характеристики хорошо согласуются
с референсными данными.
5.2. Задача о колебании цилиндра в потоке в присутствии непод-
вижного тела цилиндрической конфигурации. Во второй задаче рассмат-
ривается генерация звука осциллирующим двумерным цилиндром в присут-
ствии неподвижного цилиндра того же размера. Центры двух цилиндров рас-
полагаются на расстоянии R друг от друга. Цилиндр, расположенный слева,
Численное моделирование акустических полей, индуцированных колебанием ...
111
совершает колебательные движения в направлении, перпендикулярном пото-
ку, набегающему слева (см. рис.2 (справа). Закон колебания задается анало-
гично предыдущей задаче. Число Маха M 0.2 и число Рейнольдса Re 150.
Рис.3. Характеристики звукового давления при моделировании обтекания
осциллирующего цилиндра: пульсации давления (сверху) и диаграм-
ма направленности (снизу).
Численное решение задачи получено для двух вариантов взаимного
расположения цилиндров: R 1.5D и R 3D , при этом амплитуды колеба-
ний цилиндра равны 0.5D и 0.2D соответственно, а их частота
0.184
f
c
Параметры сгущения и размер расчетной сетки соответствуют сетке,
использованной для предыдущей задачи.
112
И.В. Абалакин и др.
Граничные условия на поверхности неподвижного цилиндра в обоих
случаях задаются традиционным подходом с применением согласованной с
границей сетки. Это означает, что граница цилиндра справа описывается
сеточными узлами, а требуемое граничное условие прилипания для скоро-
сти и адиабатическое граничное условие для температуры задается алгеб-
раическими соотношениями в этих узлах
Рис.4. Распределение пульсаций давления при R 1.5D (слева) и при R 3D (справа)
Численный расчет проводился до времени t 100. На рис.4 в виде чис-
ленной шлирен-визуализации и изолиний пульсаций давления представле-
ны мгновенные поля течения, полученные в расчетах с помощью метода
погруженных границ для двух различных взаимных положений цилиндров
на момент времени, соответствующий максимальному положительному от-
клонению движущегося цилиндра. Можно заметить, что пространственное
распределение акустической волны, генерируемой колеблющимся цилин-
дром, на фиксированный момент времени в случаях R 1.5D и R 3D
имеют схожую структуру.
Но пульсации давления существенно различаются. Это видно на рис.5,
где приведены распределения пульсаций давления по времени в фиксиро-
ванной точке (r,)
(80,
90)
. Так в случае R 3D распределение пульса-
ций имеет многочастотную структуру.
Численное моделирование акустических полей, индуцированных колебанием ...
113
Рис.5. Распределение пульсаций давления для задачи с R 1.5D (сверху) и
задачи с R 3D (снизу).
Так же из вида распределений, приведённых на рис. 5, следует хорошее
согласование результатов расчета, полученных разными методами, с рефе-
ренсными данными.
Заключение
Расчёты осциллирующего цилиндра, проведенные по двум моделям,
описывающим движение твердого тела, показали хорошее согласование ре-
зультатов по акустическим пульсациям в дальнем поле. Из этого можно
сделать вывод о пригодности этих двух подходов для моделирования дви-
жущихся тел. В заключение укажем на их преимущества и недостатки.
Первый подход заключается в модификации математической модели,
описывающей течение вязкого сжимаемого газа, с целью имитации присут-
ствия твердотельного препятствия. С математической точки зрения происхо-
дит замена начально-краевой задачи на задачу Коши в односвязной области.
114
И.В. Абалакин и др.
Преимущество такого подхода заключается в возможности проведения рас-
чёта при достаточно произвольном характере движения обтекаемого объекта.
Сложности при этом могут быть численного характера. Они связаны с уже-
сточением требований для обеспечения устойчивости численного метода
решения модифицированной системы, вызванных жёсткостью дискретных
уравнений при малом коэффициенте проницаемости. Решением данной про-
блемы является уменьшение шага интегрирования по времени, что, в свою
очередь, ведет к увеличению вычислительной стоимости расчета.
Второй подход не требует модификации системы уравнений Навье-
Стокса. Получаемая при этом начально-краевая задача решается на дефор-
мируемой во времени сетке, обеспечивающей возможность движения ис-
следуемого объекта. При этом не возникает проблем, связанных с неустой-
чивостью алгоритма и необходимостью уменьшать шаг по времени. Однако
естественным ограничением данного подхода является воспроизведение
лишь относительно малых движений, которые могут описываться деформи-
рованием сетки без изменения топологии.
Отметим, что оба подхода позволяют работать на одноблочной сетке и
пригодны для расчета аэродинамических и акустических характеристик
движущихся тел. Важным свойством обоих подходов является возможность
эффективного распараллеливания. Выбор того или иного метода зависит от
особенностей конкретной задачи, в частности, от ожидаемой траектории
движения.
СПИСОК ЛИТЕРАТУРЫ
1. Peskin C.S. Flow patterns around heart valves: a numerical method // J. Comp. Phys.,
1972, v.10, No. 2, p.252-271.
2. Mittal R., Iaccarino G. Immersed boundary Methods // Annu. Rev. Fluid Mech., 2005,
v.37, p.239-261.
3. Angot Ph., Bruneau C.-H., Fabrie P. A penalization method to take into account obstacles
in incompressible viscous flows // Numer. Math., 1991, v.81, No. 4, p.497-520.
4. Feireisl E., Neustupa J., Stebel J. Convergence of a Brinkman-type penalization for com-
pressible fluid flows // J. Diff. Equ., 2011, v.250, No. 1, p.596-606.
5. Vasilyev O.V., Kevlahanv N.K.-R. Hybrid wavelet collocation-Brinkman penalization
method for complex geometry flows // Int. J. Numer. Meth. Fluids, 2002, v.40, No. 3-4,
p.531-538.
6. Boiron O., Chiavassa G., Donat R. A high-resolution penalization method for large Mach
number flows in the presence of obstacles // Comp. Fluids, 2009, v.38, No. 3, p.703-714.
7. Liu Q., Vasilyev O.V. A Brinkman penalization method for compressible flows in complex
geometries // J. Comp. Phys., 2007, v.227, No. 2, p.946-966.
8. Bae Y., Moon Y.J. On the use of Brinkman penalization method for computation of acous-
Численное моделирование акустических полей, индуцированных колебанием ...
115
tic scattering from complex boundaries // Comp. Fluids, 2012, v.55, p.48-56.
9. Абалакин И.В., Жданова Н.С., Козубская Т.К. Метод погруженных границ для чис-
ленного моделирования невязких сжимаемых течений // ЖВМиМФ, 2018, т.58, № 9.
Abalakin I.V., Zhdanova N.S., Kozubskaia T.K. Immersed Boundary Method for Numerical
Simulation of Inviscid Compressible Flows // Comp. Math. Math. Phys., 2018, v.58, No. 9,
p. 1411-1419.
10. Komatsu R., Iwakami W., Hattori Y. Direct numerical simulation of aeroacoustic sound by
volume penalization method // Comput. Fluids, 2016, v.130, p.24-36.
11. Mavriplis D.J. Mesh generation and adaptivity for complex geometries and flows // Hand-
book of Computational Fluid Mechanics (Ed. Peyret R.) - Elsevier, 1996, p.417-459.
12. Renzoni P., et al. EROS a common European Euler code for the analysis of the helicopter
rotor flowfield // Progress in Aerospace Sciences, 2000, v.36, No. 5-6, p.437-485.
13. Steijl R., Barakos G. Sliding mesh algorithm for CFD analysis of helicopter rotor-fuselage
aerodynamics// Int. J. Numer. Meth. Fluids, 2008, v.58, No. 5, p.527-549.
14. Победря Б.Е., Георгиевский Д.В. Основы механики сплошной среды. Курс лекций. —
М.: Физматлит, 2006, 272 с.
Pobedria B.E., Georgievskii D.V. Osnovy mekhaniki sploshnoi sredy. Kurs lektsii. — M.:
Fizmatlit, 2006, 272 s.
15. Абалакин И.В., Аникин В.А., Бахвалов П.А., Бобков В.Г., Козубская Т.К. Численное
исследование аэродинамических и акустических свойств винта в кольце // Известия
РАН. Механика жидкости и газа, 2016, № 3, с. 130-145.
Abalakin I.V., Anikin V.A., Bakhvalov P.A., Bobkov V.G., Kozubskaya T.K. Numerical In-
vestigation of the Aerodynamic and Acoustical Properties of a Shrouded Rotor // Fluid
Dynamics, 2016, v.51, No. 3, p.419-433.
16. Абалакин И.В., Бахвалов П.А., Бобков В.Г., Козубская Т.К., Аникин В.А. Численное
моделирование аэродинамических и акустических характеристик винта в кольце //
Матем. моделирование, 2015, т.27, № 10, с.125-144.
Abalakin I.V., Bakhvalov P.A., Bobkov V.G., Kozubskaya T.K., Anikin V.A. Numerical
Simulation of Aerodynamic and Acoustic Characteristics of a Ducted Rotor // Math. Mod-
els & Comp. Simul., 2016, v.8, No. 3, p.309-324.
17. Абалакин И.В., Бахвалов П.А., Доронина О.А., Жданова Н.С., Козубскаvя Т.К. Моде-
лирование аэродинамики движущегося тела, заданного погруженными границами на
динамически адаптивной неструктурированной сетке // Матем. моделирование, 2018,
т.30, № 5, с.57-75.
Abalakin I.V., Bakhvalov P.A., Doronina O.A., Zhdanova N.S., Kozubskaia T.K. Simulat-
ing Aerodynanics of a Moving Body Specified by Immersed Boundaries on Dynamically
Adaptive Unstructured Meshes // MM & Comp.Simul., 2019, t.11, № 1, s.35-45.
18. Бахвалов П.А, Вершков В.А. Рёберно-ориентированные схемы на подвижных гиб-
ридных сетках в коде NOISEtte // Препринты ИПМ им. М.В. Келдыша, 2018, №127.
Bakhvalov P.A, Vershkov V.A. Reberno-orientirovannye skhemy na podvizhnykh gibrid-
nykh setkakh v kode NOISEtte. Preprinty IPM im. M. V. Keldysha, 2018, №127.
19. Абалакин И.В., Бахвалов П.А., Горобец А.В., Дубень А.П., Козубская Т.К. Параллель-
ный программный комплекс NOISETTE для крупномасштабных расчетов задач аэ-
родинамики и аэроакустики // Выч. методы и программ., 2012, т.13, с.110-125.
Abalakin I.V., Bakhvalov P.A., Gorobets A.V., Duben A.P., Kozubskaia T.K. Parallelnyi
116
И.В. Абалакин и др.
programmnyi kompleks NOISETTE dlia krupnomasshtabnykh raschetov zadach aerodi-
namiki i aeroakustiki // Vychislitelnye metody i programmirovanie, 2012, t.13, s.110-125.
20. Вершков В.А. Алгоритм деформации сетки для учета циклического управления и ма-
ховых движений лопастей в задаче обтекания несущего винта вертолета // Научный
вестник МГТУ ГА, 2019, т.22, № 2, с.62-74.
Vershkov V.A. Algoritm deformatsii setki dlia ucheta tsiklicheskogo upravleniia i mak-
hovykh dvizheniĭ lopasteĭ v zadache obtekaniia nesushchego vinta vertoleta // Nauchnyi
vestnik MGTU GA, 2019, t.22, № 2, s.62-74.
21. Бахвалов П.А., Козубская Т.К. О построении реберно-ориентированных схем, обес-
печивающих точность на линейной функции, для решения уравнений Эйлера на гиб-
ридных неструктурированных сетках// ЖВМ и МФ., 2017, т.57, № 4, с. 682-701.
Bakhvalov P.A., Kozubskaya T.K. Construction of edge-based 1-exact schemes for solving
the Euler equations on hybrid unstructured meshes // Comp. Math.&Math. Phys., 2017,
v.57, No. 4, p.680-697.
22. Abalakin I., Bakhvalov P., Kozubskaya T. Edge-based reconstruction schemes for unstruc-
tured tetrahedral meshes // Int. J. Numer. Meth. Fluids, 2002, v.81, No. 6, p.331-356.
23. Qu L., Norberg C., Davidson L., Peng S.-H., Wang F. Quantitative numerical analysis of
flow past a circular cylinder at Reynolds number between 50 and 200 // J. Fluid Struct.,
2013, v.39, p.347-370.
24. Абалакин И.В., Дубень А.П., Жданова Н.С., Козубская Т.К. Моделирование неста-
ционарного турбулентного течения вокруг цилиндра методом погруженных границ //
Матем. моделирование, 2018, т. 30, № 5, с. 117-133
Abalakin I.V., Duben A.P., Zhdanova N.S., Kozubskaia T.K. Simulating an Unsteady
Turbulent Flow around a Cylinder by the Immersed Boundary Method // Mathematical
Models and Computer Simulations, 2019, t.11, № 1, s.74-85.
Поступила в редакцию 04.03.2019
После доработки 23.05.2019
Принята к публикации 01.07.2019