МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

2019 год, том 31, номер 11, стр. 61-78



МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФУНКЦИОНИРОВАНИЯ

КАБЕЛЬ-ТРОСА ПРИВЯЗНОЙ БЕСПИЛОТНОЙ ПЛАТФОРМЫ

ПРИ ВОЗДЕЙСТВИИ ВЕТРОВЫХ НАГРУЗОК

2019 г.

В.М. Вишневский, Е.А. Михайлов*, Д.А. Тумченок,

А.М. Ширванян

Институт проблем управления им. В.А. Трапезникова РАН, Москва

vishn@inbox.ru, dtumchenok@gmail.com, artshirvanyan@mail.ru

*МГУ имени М.В. Ломоносова, физический факультет

ea.mikhajlov@physics.msu.ru

DOI: 10.1134/S0234087919110054

Работа посвящена описанию математической модели привязной высотной беспи-

лотной платформы, в которой электропитание двигательных установок и полезной

нагрузки осуществляется от наземного источника энергии по кабель-тросу. Для

выведенной системы дифференциальных уравнений определены величины и на-

правления сил воздействия на беспилотный аппарат, что позволит произвести рас-

чет необходимой мощности энергии, передаваемой с земли на борт, в зависимости

от высоты подъема и ветровой нагрузки при проектировании привязной беспилот-

ной платформы.

Ключевые слова: привязная телекоммуникационная платформа, система передачи

энергии большой мощности, система дифференциальных уравнений, беспилотный

летательный аппарат.

MATHEMATICAL MODEL OF THE OPERATION

OF A TETHERED UNMANNED PLATFORM

IN THE CASE OF WIND INFLUENCE

V.M. Vishnevsky, E.A. Mikhailov*, D.A. Tumchenok, A.M. Shirvanyan

Trapeznikov Institute of Control Sciences of RAS

*Lomonosov Moscow State University

The article is devoted to the description of a mathematical model of a tethered high-

altitude unmanned platform in which the power supply of propulsion systems and pay-

load is carried out from a ground-based energy source via a cable. The magnitudes and

directions of the forces acting on the unmanned vehicle by the cable are determined from

the concluded system of differential equations, which will allow to calculate the required

power of energy transmitted from the ground to the side, depending on the lift height and

the wind load.

Key words: tethered telecommunications platform, high power transmission system, dif-

ferential equation system, unmanned aerial vehicle.

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

1. Введение

В настоящее время широкое развитие получили высотные платформы,

реализуемые на автономных беспилотных летательных аппаратах, и под-

водные роботы. Основным недостатком автономных беспилотных летатель-

ных аппаратов (БПЛА) является ограниченное время функционирования,

связанное с малым ресурсом аккумуляторов БПЛА, оснащенных электриче-

скими двигателями или ограниченным запасом топлива для двигателей

внутреннего сгорания [1]. В связи с этим такие БПЛА не могут быть эффек-

тивно использованы в системах, где требуется длительное время функцио-

нирования, например, в системах управления безопасностью и охраны от

террористических угроз критически важных объектов (атомных станций,

аэродромов, протяженных мостов, участков границы). Длительное функци-

онирование могут обеспечивать привязные высотные беспилотные плат-

формы, в которых электропитание двигателей и аппаратуры полезной на-

грузки осуществляется от наземных источников энергии [2-5]. Возможность

передачи энергии большой мощности (10-15кВт) по кабелю с земли на борт

БПЛА позволяет осуществлять подъем и удержание на высотах 200-300 м

полезной телекоммуникационной нагрузки в течение длительного времени,

ограниченного лишь надежностными характеристиками БПЛА [3-6]. При-

вязные высотные платформы занимают промежуточное положение между

спутниковыми системами и наземными системами, оборудование которых

(базовые станции сотовой связи, радиорелейное и радиолокационное обо-

рудование и т.д.) располагается на высотных сооружениях. По сравнению с

дорогостоящими спутниковыми системами, привязные высотные платфор-

мы обладают высокой экономичностью, а наземные телекоммуникацион-

ные системы превосходят по обширности зон телекоммуникационного и

видео покрытия. Ввиду перспективности практического применения при-

вязных беспилотных высотных платформ как в гражданских, так и в обо-

ронных отраслях, в исследовательских центрах передовых стран мира ве-

дутся интенсивные работы по проектированию и реализации таких плат-

форм [7-9].

Дифференциальные уравнения равновесия привязи и расчет действу-

ющих сил были рассмотрены ранее для различных привязных объектов. В

известных книгах [10,11] рассмотрены задачи расчета сил привязных аэро-

статов. Привязным беспилотным подводным роботам также уделяется не-

малое внимание [12,13]. В зарубежных статьях рассматриваются различные

вариации задачи с привязными БПЛА: контроль натяжения кабеля, следо-

вание за движущимся транспортным средством и др. [1,14,15]. Однако в пе-

Математическая модель функционирования кабель-троса …

речисленных работах не рассматривались вопросы воздействия кабель-тро-

са на беспилотный аппарат при ветровых нагрузках, что оказывает сущест-

венное влияние на функционирование привязной беспилотной платформы.

В настоящей работе рассмотрена слабо исследованная в мировой лите-

ратуре модель функционирования привязной беспилотной платформы, учи-

тывающая воздействие кабель-троса на БПЛА при наличии ветровой на-

грузки. Исследование динамики изменения положения кабеля при ветровых

нагрузках и определение соответствующих сил, действующих на беспилот-

ный аппарат, является важным этапом проектирования привязной высотной

платформы.

2. Математическая модель функционирования кабель-троса при воз-

действии ветра

При расчете сил, действующих на БПЛА при наличии ветра, необхо-

димо учитывать силу тяжести, определяемую весом кабель-троса, взлетным

весом БПЛА, и силу ветровой нагрузки. В отличие от известного в литера-

туре вывода систем дифференциальных уравнений равновесия нити [10] в

статье учитывается постоянное натяжение, создаваемое лебедкой, а также

отклонение платформы по горизонтали и вертикали от целевой точки зави-

сания. Также существенным отличием от частных решений, приведенных в

книге, является неизвестность угла наклона кабеля, как в верхней точке, так

и в нижней.

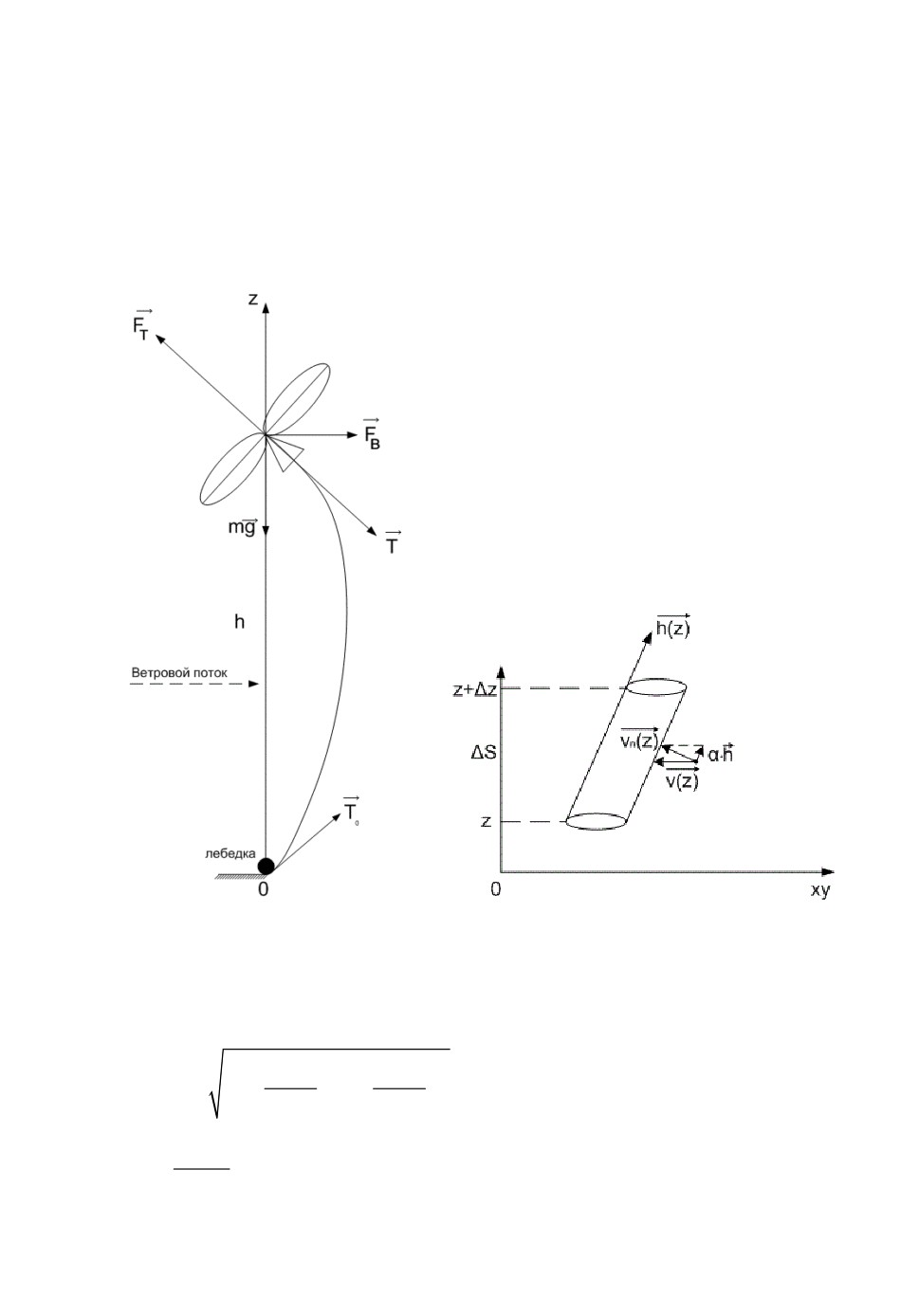
Рассмотрим беспилотный летательный аппарат, который снабжается

электроэнергией, передаваемой по кабелю от наземного пункта питания.

Предполагается, что нижний конец кабеля крепится с помощью лебедки,

обеспечивающей постоянное натяжение нижнего конца кабеля

(рис.1), а

верхний конец шарнирно крепится к платформе. Платформа обеспечивает

натяжение кабеля по всей его длине вплоть до лебедки.

Положение кабеля в пространстве будем задавать в прямоугольной

системе координат (x, y, z) . Равновесное положение кабеля в системе коор-

динат OXYZ задается двумя уравнениями:

x

x z);



(1)

y z),



где z[0;H], H - высота подъема платформы.

Для расчета ветровой нагрузки на кабель предположим, что скорость

ветра задается двумя детерминированными проекциями

(z)

x x

(

)

на оси OX и OY соответственно. Проекция скорости ветра на вер-

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

тикальную ось OZ тождественно равна нулю. Скорость ветра не изменяется

во времени. При расчете нагрузки будем учитывать только нормальную по

отношению к оси кабеля ветровую нагрузку. Тангенциальную нагрузку бу-

дем считать равной нулю.

Рассмотрим элемент кабеля длиной S (рис.2), имеющий координаты

по оси OZ от z до z  z .

Рис.1. Схематичное изображение при-

Рис.2. Элемент кабеля.

вязной высотной платформы и

сил, действующих на нее.

Его длина удовлетворяет равенству



dx z)



dy z)

S

z

1



o(z

) ,

(2)

















o(

где

lim

z

z

Математическая модель функционирования кабель-троса …

Вектор

dx z)

dy z)

h z)=

i

jk,

(3)

где i , j, k - единичные векторы осей OX , OY и OZ соответственно, зада-

ет направление касательной к кабелю (рис.2). Скорость ветра выражается в

виде

v z)=

v z)iv z)j0k .

(4)

Нормальная составляющая скорости ветра к оси кабеля определяется

из соотношения:

v z)=

v z)h(z),

(5)

где  - некоторый коэффициент, характеризующий скорость ветра в на-

правлении касательной.

Отсюда

v z)h z)

=

(6)

(z)

Учитывая, что



dx z)



dy z)

h z)=1



(7)

















получим

dx z)

dy z)

v z)



v z)



(8)



dx z)



dy z)



















Подставляя (3), (4), (8) в (5) и учитывая, что

v z)



v z)v

)

(9)

получим значение скорости ветра, воздействующего на элемент кабеля, в

виде



dy z)

dx z)

v





v











v z)

(10)



dx z)



dy z)

1



















В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

Давление ветра на кабель вычисляется по формуле:

Av

(11)

где A - коэффициент аэродинамического сопротивления, кг/м² [16];v - ско-

рость ветра, м/с.

Нормальная ветровая нагрузка на элемент кабеля длины S равна

F z)=A

v z)

v z)

S

(12)

Подставляя (2), (10) в (12), получим



dy z)

dx z)

Az v

v





v











(z)=





dx z)



dy z)

1





























dx z





dy z)



dy z)

v

1

v



i 



















(13)























dx z)



dx z)

dy z)

 v

1

v



j

o z).



























dx z)

dy(z)



v



v



k

















Проекция силы тяжести элемента кабеля длины S отлична от нуля

только на ось OZ и равна



dx z)



dy z)

F z)=

 

gS

 

gz

1



o(z),

(14)

















где  - линейная плотность провода (кг/м).

Запишем проекцию силы T (z) на ось OX :

T z)=

T

(

z)cos

 .

(15)

Учитывая (2), получим

dx z)/dz

T z)=

T

(

z)

(16)



dx z)



dy z)



















Математическая модель функционирования кабель-троса …

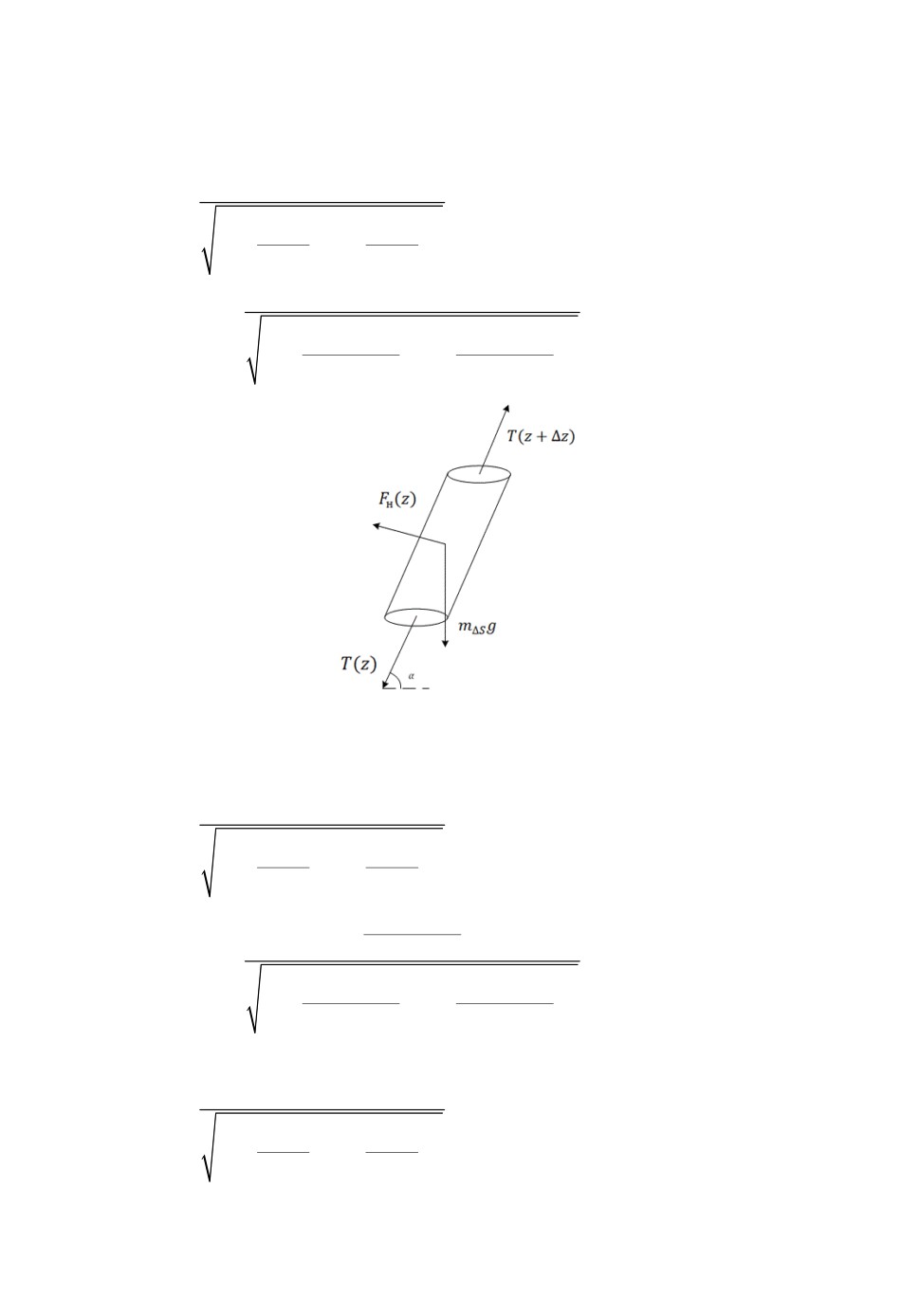
Спроецируем остальные силы (рис.3) на ось OX и запишем уравнение

равновесия сил, действующих на элемент кабеля длины S :

dx z)/dz

T(z)





dx z)



dy z)

1



















(17)

dx(z

z)/dz

T(z

z)



F z)=o(z).



dx(z

z

) 



dy(z

z)

1



















Рис.3. Силы, действующие на элемент кабеля.

Проекция на ось OY имеет вид

dy z)/dz

T(z

)





dx z)



dy z)

1



















z)

(18)

T(z

z)



F z)=o(z).



dx(z

z

) 



dy(z

z)

1



















Проекция на ось OZ имеет вид

T(z

)





dx z)



dy z)

1



















В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

T(z

z)





dx(z

z)



dy(z

z)

1



















(19)



dx z)



dy z)

F z)gz



1



=o(z).

















Подставим в уравнения (17)(19) величину нормальной ветровой на-

грузки на элемент кабеля (12). Затем разделим на z и перейдем к пределу

z

. Тогда получим следующие проекции.

Проекция на ось OX :

dx dx d

x dy d















x dT dx

dz  dz















dz dz



dx z)



dy z)

1























A v z)v z)

v z)



v z













(20)



dx z)





dy(z)



1

























dy z)

dx dy





v z)1



v z





= 0.













dz dz





Проекция на ось OY :

dy dx d

x dy d















y dT dy

dz  dz















dz dz



dx z)



dy z)























A v z)

v z)

v z)



v z)













(21)



dx z)





dy z)



























dx z)



dx dy



v z1











= 0.













dz dz





Математическая модель функционирования кабель-троса …

Проекция на ось OZ :



dx d

x dy d

















A v z)v z)

v z)

v z)

























dx z)



dy z)



dx z)



dy(z)

1











1











(22)



























dx z



dy z

 v z



v z

g1





= 0.































Здесь и далее аргумент z у производных и некоторых функций опущен

для краткости написания. Тогда система уравнений (20)(22) эквивалентна

следующей системе дифференциальных уравнений:





g

= 0;









dx z)



dy z)

T



g

1









































A v





v z)

v z)

v z)

















dx z)





dy z)

v z

1



= 0;

(23)



























dx z)



dy z)









1









































A v z)

v z)

v z)

v z)

















dx z)



dy z)

v z)



=0.





















Положение равновесия кабеля описывается системой дифференциаль-

ных уравнений (23), из которых одно является линейным дифференциаль-

ным уравнением первого порядка, а два других - нелинейными дифферен-

циальными уравнениями второго порядка. Первое уравнение системы стро-

го выводится из полученных ранее уравнений (20)(22), что совпадает с

уравнением положения нити, выведенным в [10].

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

Длина кабеля L описывается следующим дифференциальным уравне-

нием первого порядка:



dx z)



dy z)

1



(24)

















с начальным условием L0 = 0 .

Таким образом, положение равновесия кабеля при горизонтальной ско-

рости ветра и длина кабеля описываются системой нелинейных дифферен-

циальных уравнений (23), (24).

Сложность рассматриваемой задачи заключается в том, что необходи-

мо решать не задачу Коши, а краевую задачу, когда условия задаются при

различных значениях аргумента z .

Полученная математическая модель будет использоваться в расчетах

определения сил, действующих на платформу со стороны кабеля.

3. Решение системы дифференциальных уравнений

Совместим нижний конец кабеля с началом системы координат OXYZ .

Предположим, что лебедка обеспечивает постоянное натяжение нижнего

конца кабеля

. Платформа с помощью системы управления удерживается

в окрестности точки, расположенной по вертикали на заданной высоте. Не-

обходимо оценить величину и направление силы, действующей от кабеля

на беспилотный летательный аппарат при различной скорости ветра.

Для упрощения расчетов будем предполагать, что направление ветра

совпадает с направлением оси OX , что позволяет рассматривать положение

кабеля в плоскости OXZ . Систему уравнений (23), (24) запишем в виде

dx

=g

;



;





(25)

 

gx

(1

) 

Av



1



;



x₁



dx

1



Здесь z - текущая высота (м) элемента кабеля

над поверхностью Земли;

x1 - сила натяжения кабеля (Н); =0.005- линейная плотность провода

(кг/м); g=9.8 - ускорение свободного падения (м/с²); x₂ - отклонение кабеля

от вертикали (м); x₃ - тангенс угла наклона кабеля от вертикали; A=0.003 -

Математическая модель функционирования кабель-троса …

коэффициент аэродинамического сопротивления (кг/м²) [16]; v - скорость

ветра (м/с);

- длина кабеля от лебедки до текущей высоты (м).

Для системы дифференциальных уравнений (25) заданы следующие ус-

ловия: при z = 0

= 150 Н,

=0,

= 0; при

z hvert

x xzadan

. По-

скольку при z = 0 значение

не определено, то, учитывая структуру сис-

темы (25), удобно решить первое и третье уравнения системы с дополни-

тельным условием:

z_max

z)dz  x

(26)



zadan

После этого можно найти длину кабеля по формуле:

vert

L

1



(z)

²

(27)



Используемый метод решения является, по сути, одной из вариаций

метода стрельбы [17].

Решение для функции

(z) может быть найдено аналитически так:

(z)  x

(0)  gz .

(28)

Чтобы найти

(z) , разобьем интервал 0zh

на N интервалов длины

vert

zh

z iz , i0,1,, N .

vert

В качестве начального значения функции

, соответствующее



бралось значение

)

 B, которое варьировалось. Для решения будем ис-

3 0

пользовать метод Рунге - Кутта четвертого порядка [17, 18]. На каждом i-м

шаге (i  1,2,, N ) вычислим следующие коэффициенты:

g(x

)

((x

)

)2) 

(1((x

)

)2)

3 (i1)



;

(29)

1 (



g[(

)

k

z

/ 2](1

((x

)

k

z

/ 2)

)

3 (i1)





)

 

3 (

i1)

(30)

(1

((

)

k



/ 2)

3 (i1)



;

)

 

3 (i

1)

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

g[(x

)

k

z

/ 2](1((x

)

k

z

/ 2)

)

3 (i1)





)

 

3 (

i1)

(31)

(1((x

)

k



/ 2)

3 (i1)



;

)

 

3 (i1)

g[(x

)

k

z

](1((x

)

k

z)

)

3 (i1)





)

 

3 (i

(32)

(1((x

)

k



3 (i1)



 

3 (



Тогда значение

(

)_i

имеет вид

)



)



2

2k

k

)

(33)

i1

Вычисление интеграла в правой части (27) целесообразно проводить с

помощью метода Симпсона, который, с одной стороны, достаточно прост в

реализации (являясь модификацией метода трапеций), с другой - позволяет

добиться высокой точности результата [19, 20]:







)

4(x

)



2(x

)

4(x

)

(x

)



(34)

3 2

3 3

N1

Что касается выбора коэффициента B , то определить его наилучшее

значение можно с помощью дихотомии следующим образом. Определим из

физических соображений значения коэффициентов

такие, что при

(0) P

можно гарантировать, что

) x

, а при

(0)  Q

vert

zadan

)

x

vert

zadan

Будем последовательно решать численно по описанной выше схеме

уравнения для

с начальным условием

B(P

Q

)/2, где j 0,1, 2,.

Если

Ix

, то на следующем шаге необходимо взять

P



zadan

j1

Если

Ix

, то



Q

. Последовательность продолжается

zadan

j1

до тех пор, пока не будет достигнуто условие

)_N

x

 , где  - тре-

zadan

буемая точность решения. В нашем случае выбиралось значение



10^

м,

что более чем достаточно в условиях ограничений, наложенных на модель

кабеля.

Математическая модель функционирования кабель-троса …

После этого вычислялась длина кабеля, интеграл (27) для которой так-

же можно найти по методу Симпсона:

z





(1((x

) )

4 1((x

) )

2 1((x

) )



3 2

3 3



(35)



4 1((x

)



1((x

)

3 (N1)



Задача решалась на сетке, состоящей из N  6000 точек. В частности, в

 300 м, z  0.05 м. Как метод Рунге-Кутты четвертого

порядка, так и метод Симпсона обеспечивают четвертый порядок погреш-

ности [19], дающий ошибку, которую можно оценить как

O(z

). Таким

образом, можно быть уверенным, что численное решение отличается от

точного решения исходной задачи не более, чем на величину порядка

10^

Для решения системы уравнений была составлена программа на языке

C++, которая позволяет получить значения при различных наборах входных

данных. Пользователь имеет возможность ввести в программу линейную

, а также

его смещение в верхней точкеx_last .

Для различных значений скорости ветра и высоты зависания БПЛА вы-

полнено решение системы (25). Результаты вычислений приведены в табл.1-3.

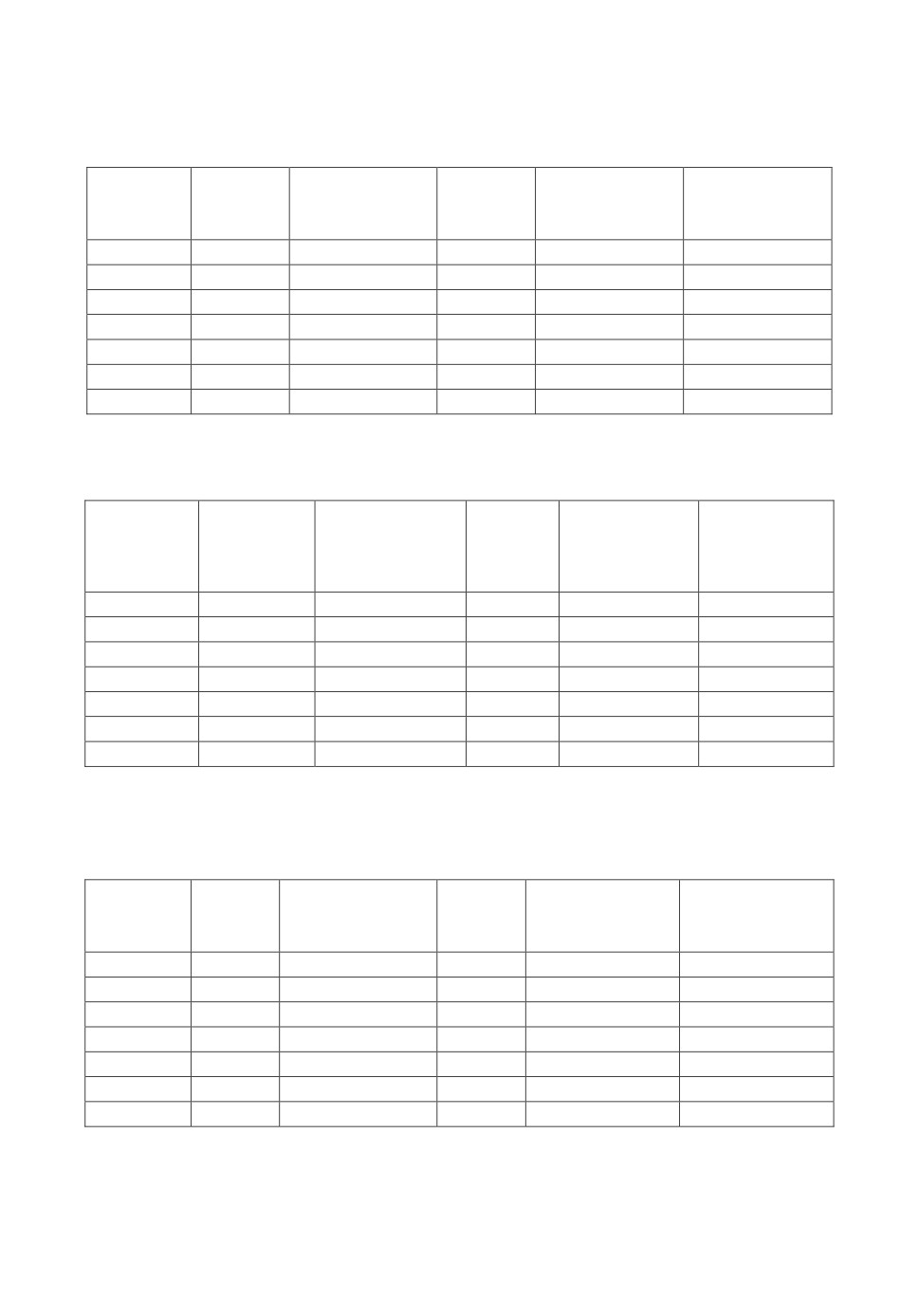
Таблица 1. Высота подъема ПБВП ( z ) - 100 м, отклонение от вертикали (x

) - 0 м.

Тогда из формулы (25) сила натяжения кабеля (T ) вверху

 199 H.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная

ветра

в верхней

кабеля в верхней

кабеля, м

составляющая си-

составляющая

(v), м/c

точке

точке, градусы

лы натяжения, Н

силы натяжения, Н

0.258322

14.5

101.319

49.7683

192.676

0.178452

10.1

100.635

34.9688

195.904

0.113879

6.5

100.26

22.5205

197.722

0.063969

3.7

100.082

12.71

198.594

0.028416

1.6

100.016

5.64932

198.92

0.007103

0.4

100.001

1.41286

198.995

100

199

Данные из табл.1-3 указывают, что на высоте 100 м и 200 м при скорости

ветра 18 м/с длина кабеля увеличивается незначительно (менее 5%). На высо-

те 300 м увеличение скорости ветра значительнее увеличивает длину кабеля.

Кроме того, с ростом высоты при одинаковой скорости ветра возрастает угол

наклона кабеля к вертикали в верхней точке. С увеличением высоты и скоро-

сти ветра также значительно увеличивается горизонтальная составляющая

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

силы, действующей от кабеля на БПЛА. Так, на высоте 300м при скорости

ветра 18м/с угол достигает почти 30градусов (arctg(0.570625)29.7 ). Гори-

зонтальная составляющая равна 147.192Н, а вертикальная - 257.96 Н. Это

означает, что платформа должна будет сильнее поворачиваться в сторону на-

правления ветра, тем самым увеличивая площадь, на которую оказывает дав-

ление ветер. Значительная часть мощности будет тратиться на сопротивление

ветру. Соответственно, чтобы поддерживать платформу на заданной высоте,

потребуется передача большего количества энергии.

x ) - 0 м.

Тогда из формулы (25) сила натяжения кабеля вверху

 248 Н.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная со-

ветра (v),

кабеля в верхней

кабеля, м

составляющая си-

ставляющая силы

в верхней

м/c

точке, градусы

лы натяжения, Н

натяжения, Н

точке

0.436177

23.6

208.495

99.155

227.315

0.298762

16.6

204.063

71.0006

237.619

0.189746

10.7

201.657

46.2213

243.655

0.106341

6.1

200.523

26.2147

246.611

0.047198

2.7

200.103

11.6926

247.724

0.011796

0.7

200.006

2.9262

247.983

200

248

Таблица 3. Высота подъема ПБВП ( z ) - 300 м, отклонение от вертикали (

) - 0 м.

Тогда из формулы (25) сила натяжения кабеля вверху

 297 H.

Скорость

dz в

Угол отклонения

L - длина

Горизонтальная

Вертикальная со-

ветра (v), м/c

верхней

кабеля в верхней

кабеля, м

составляющая си-

ставляющая си-

точке

точке, градусы

лы натяжения, Н

0.570625

29.7

324.178

147.192

257.96

0.387592

21.2

311.437

107.336

276.926

0.244978

13.8

304.637

70.6748

288.468

0.136975

7.8

301.46

40.3124

294.251

0.060741

3.5

300.288

17.9948

296.454

0.015177

0.9

300.018

4.51388

296.966

300

297

На основании анализа табл.4 и 5 можно сделать вывод о том, что не-

значительное отклонение БПЛА от точки зависания не оказывает сущест-

венного влияния на длину кабеля и силу натяжения кабеля в верхней точке.

Учитывая, что система управления будет стремиться вернуть платформу в

точку зависания, при расчетах сил, действующих на кабель, данным влия-

нием можно пренебречь.

Математическая модель функционирования кабель-троса …

Таблица 4. Высота подъема ПБВП ( z ) - 200 м, отклонение от вертикали (x

) - 1 м.

Тогда из формулы (25) сила натяжения кабеля вверху

 248 Н.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная со-

ветра (v),

в верхней

кабеля в верхней

кабеля, м

составляющая си-

ставляющая силы

м/c

точке

точке, градусы

лы натяжения, Н

натяжения, Н

0.43223

23.4

208.544

98.394

227.646

0.29482

16.4

204.096

70.13

237.878

0.18581

10.5

201.678

45.304

243.827

0.10241

5.8

200.536

25.265

246.71

0.04327

2.5

200.11

10.721

247.768

0.00786

0.5

200.01

1.95

247.992

0.003928

0.2

200.003

248

Таблица 5. Высота подъема ПБВП ( z ) - 200 м, отклонение от вертикали (x

) - 2 м.

Тогда из формулы (25) сила натяжения кабеля вверху

 248 Н.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная

ветра (v), м/c

в верхней

кабеля в верхней

кабеля, м

составляющая

точке

точке, градусы

силы натяже-

ния, Н

0.42827

23.2

208.598

97.635

227.973

0.29087

16.2

204.134

69.266

238.131

0.18188

10.3

201.705

44.378

243.997

0.09848

5.6

200.554

24.306

246.806

0.03934

2.3

200.123

9.749

247.808

0.00394

0.2

200.019

0.976

247.998

0.007856

0.5

200.01

248

Таблица 6. Высота подъема ПБВП ( z ) - 200 м, отклонение от вертикали (

) - 0 м.

Сила натяжения лебедкой 100 Н. Тогда из формулы (25) сила натяжения

кабеля вверху

x1=198 Н.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная со-

ветра (v),

в верхней

кабеля в верхней

кабеля, м

составляющая си-

ставляющая силы

м/c

точке

точке, градусы

лы натяжения, Н

натяжения, Н

0.57062

29.7

216.119

98.131

171.972

0.3876

21.2

207.625

71.557

184.618

0.24498

13.8

203.091

47.113

192.313

0.13698

7.8

200.973

26.871

196.168

0.06074

3.5

200.192

12.005

197.636

0.01518

0.9

200.012

3.004

197.977

0.000002

200

198

На основании анализа табл.6 и 7 можно сделать вывод о том, что изме-

нение силы натяжения лебедки существенно меняет профиль кабеля и его

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

длину. При этом стоит отметить, что горизонтальная составляющая силы

меняется не столь существенно.

Таблица 7. Высота подъема ПБВП ( z ) - 200 м, отклонение от вертикали (

) - 0 м.

Сила натяжения лебедкой 200 Н. Тогда из формулы (25) сила натяжения

кабеля вверху

=-298 Н.

Скорость

Угол отклонения

L - длина

Горизонтальная

Вертикальная

ветра (v), м/c

в верхней

кабеля в верхней

кабеля, м

составляющая

точке

точке, градусы

силы

натяжения, Н

0.35423

19.5

205.291

99.502

280.898

0.24368

13.7

202.539

70.552

289.528

0.15514

8.8

201.037

45.685

294.477

0.08705

5

200.328

25.844

296.877

0.03865

2.2

200.065

11.509

297.778

0.00966

0.6

200.004

2.878

297.986

0.000003

200

298

Таким образом, решение системы уравнений позволяет моделировать

различные ситуации и проводить численные расчеты. Вычисленные значе-

ния углов отклонения кабеля в верхней точке, натяжения и длины кабеля в

зависимости от различных скоростей ветра позволяют оценить горизон-

тальную и вертикальную составляющие силы, действующей от кабеля на

платформу. Полученные данные важны для оценки величины полезной на-

грузки и необходимой передаваемой с земли на борт мощности для полетов

в ветровых условиях, а также при проектировании системы управления по-

зиционированием БПЛА.

4. Заключение

В статье сформулирована задача определения воздействий кабеля на

платформу при наличии ветровой нагрузки. Для поставленной задачи раз-

работана математическая модель поведения системы платформа-кабель,

учитывающая ветровое воздействие, а также необходимое для успешной

работы системы натяжение кабеля лебедкой. Положение равновесия кабеля

описывается системой дифференциальных уравнений, из которых одно яв-

ляется линейным дифференциальным уравнением первого порядка, а два

других - нелинейными дифференциальными уравнениями второго порядка.

На основе решения системы вычислены зависимости горизонтальной и вер-

тикальной составляющих воздействия кабеля на платформу как функции

высоты положения платформы, ее бокового отклонения от заданной точки

зависания, направления и скорости ветра.

Математическая модель функционирования кабель-троса …

СПИСОК ЛИТЕРАТУРЫ

S. Kiribayashi, J. Ashizawa, K. Nagatani. Modeling and design of tether powered multi-

copter // In 2015 IEEE International Symposium on Safety, Security, and Rescue Robotics,

2015.

В.М. Вишневский, Б.Н. Терещенко. Способ удаленного проводного электропитания

объектов // Патент на изобретение № 2572822 РФ; Зарег. 16.12.2015;

V.M. Vishnevskii, B.N. Tereshchenko. Sposob udalennogo provodnogo elektropitaniia

obieektov // Patent № 2572822 RF; Reg. date 16.12.2015.

V. Raj, N. Raj, J. Kumar. An Approach for Power Optimization of Tethered UAV. IOSR //

Journal of Electrical and Electronics Engineering, 2016, v.11, Issue 5, ver. I, p.23-25.

G.W. Wasantha and S. Wang. Heavy Payload Tethered Hexaroters for Agricultural Appli-

cations: Power Supply Design, 2015.

G. Wang, W. Samarathunga, S. Wang. Uninterruptible Power Supply Design for Heavy

Payload Tethered Hexaroters // International Journal of Emerging Engineering Research

and Technology, 2016, v.4, Issue 2, p.16-21.

V.M. Vishnevsky, B.N. Tereschenko, D.A. Tumchenok, A.M. Shirvanyan. Optimal Method

for Uplink Transfer of Power and the Design of High-Voltage Cable for Tethered High-

Altitude Unmanned Telecommunication Platforms. Distributed Computer and Communi-

cation Networks, series Communications in Computer and Information Science, 2017,

v.700, p.240-247.

В.М. Вишневский, Б.Н. Терещенко. Разработка и исследование нового поколения вы-

сотных привязных телекоммуникационных платформ. T-Comm, 2013, № 7, с.20-24;

V.M. Vishnevskii, B.N. Tereshchenko. Razrabotka i issledovanie novogo pokoleniia vysot-

nyh priviaznyh telekommunikatsionnyh platform. T-Comm, 2013, № 7, s.20-24.

ECA Group, French DGA. Доступно: http://www.ecagroup.com/en/corporate/navy-recog-

nition-reports-eca-group-and-french-dga-working-tethered-uav-project-similar (Дата обра-

щения: 27.12.2018).

Aerial Dragnet. Доступно: https://www.fbo.gov/index?s=opportunity&mode=form&id= 84-

ea6bae9dc2a6e6437abeb570c3a77a&tab=core&_cview=0 (Дата обращения: 27.12.2018).

10. Д.Р. Меркин. Введение в механику гибкой нити.  М.: Наука, Главная редакция фи-

зико-математической литературы, 1980, 240 с.;

D.R. Merkin. Vvedenie v mekhaniku gibkoi niti.  M.: Nauka. Glavnaia redaktsiia fiziko-

matematicheskoi literatury, 1980, 240 s.

11. Н.Е. Кочин. Об изгибе троса змейкового аэростата под действием ветра. Собр. соч.,

т.II.  МЛ.: изд. АН СССР, 1949, с.536548;

N.E. Kochin. Ob izgibe trosa zmeikovogo aerostata pod deistviem vetra. Sobr. soch., t.II. 

ML.: izd. AN SSSR, 1949, s.536548.

12. В.В. Костенко, О.Ю. Львов. Комбинированная система связи и навигации автоном-

ного подводного робота с поплавковым модулем // Подводные исследования и робо-

тотехника, 2017, №1 (23), с.3143;

V.V. Kostenko, O.Iu. Lvov. Kombinirovannaia sistema sviazi i navigatsii avtonomnogo

podvodnogo robota s poplavkovym modulem // Podvodnye issledovaniia i robototekhnika,

2017, №1 (23), s.31-43.

В.М. Вишневский, Е.А. Михайлов, Д.А. Тумченок, А.М. Ширванян

13. В.Т. Грумондз, Р.В. Пильгунов, М.В. Виноградов. Динамика продольного движения

подводного буксируемого аппарата в задаче мониторинга заданной области конти-

нентального шельфа // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение,

2017, №7, с.19-34;

V.T. Grumondz, R.V. Pilgunov, M.V. Vinogradov. Dinamika prodolnogo dvizheniia pod-

vodnogo buksiruemogo apparata v zadache monitoringa zadannoi oblasti kontinentalnogo

shelfa // Vestnik MGTU im. N.E. Baumana. Ser. Mashinostroenie, 2017, №7, s.19-34.

14. M. Tognon, A. Franchi. Position tracking control for an aerial robot passively tethered to

an independently moving platform. IFACPapersOnLine, 2017, v.50, №1, p.1069-1074.

15. S. Kiribayashi, K. Yakushigawa, K. Nagatani. Design and Development of Tether-Powered

Multirotor Micro Unmanned Aerial Vehicle System for Remote-Controlled Construction

Machine // Springer, Field and Service Robotics, 2018, p.637-648.

16. Г. Эберт. Краткий справочник по физике: справочное издание / пер. со 2-го нем. изд.

[Н.М. Шикуниной]; под ред. К.П. Яковлева.  М.: Физматгиз, 1963, 552 с.;

H. Ebert, (ed.). Physikalisches Taschenbuch // Vieweg, Braunschweig, Germany, 1976.

17. Н.Н. Калиткин. Численные методы. - М.: Наука, 1978, 508 с.;

N.N. Kalitkin. Chislennye metody. - M.: Nauka, 1978, 508 p.

18. E. Süli, D. Mayers. An Introduction to Numerical Analysis.  Cambridge: Cambridge Uni-

versity Press, 2003. ISBN 0-521-00794-1.

19. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. 2 изд.  М.: Гос. изд-

во физ.-мат. лит., 1963, 659 с.;

B.P. Demidovich, I.A. Maron. Osnovy vychislitelnoi matematiki. 2 izd.  M.: Gos. izd-vo.

Fiz.-Mat. Lit., 1963, 659 s.

20. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. 4 изд. - М.: БИНОМ,

2006, 636 с.;

N.S. Bakhvalov, N.P. Zhidkov, G.M. Kobelkov. Chislennye metody. 4 izd. - M.: BINOM,

2006, 636s.

Поступила в редакцию 05.03.2019

После доработки 23.05.2019

Принята к публикации 01.07.2019