МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

2019 год, том 31, номер 11, стр. 102-116



РАДИАЛЬНЫЙ ДВУХСЕКТОРНЫЙ ГАЗОВЫЙ ПОДШИПНИК

С МАКСИМАЛЬНОЙ НЕСУЩЕЙ СПОСОБНОСТЬЮ

2019 г.

Ю.Я. Болдырев

Санкт-Петербургский политехнический университет Петра Великого,

Институт прикладной математики и механики

boldyrev@phmf.spbstu.ru

DOI: 10.1134/S023408791911008X

Рассматривается вариационная задача для радиального газового подшипника

скольжения, имеющего два сектора. Поле давления в газовом слое описывается не-

линейным уравнением Рейнольдса для произвольных чисел сжимаемости. В каче-

стве функционала вариационной задачи выступает величина главного вектора сил

давления. Проводится качественный анализ системы необходимых условий экс-

тремума, на основе которого построена вычислительная процедура. На основе ана-

лиза полной системы необходимых условий показано, что на каждом из секторов

профиль является кусочно линейным и одноступенчатым, при этом один сектор

обеспечивает только разряжение, тогда как другой  только сжатие газа.

Ключевые слова: газовая смазка, вариационное исчисление, максимум подъемной

силы, произвольные числа сжимаемости.

TWO SECTORS RADIAL GAS BEARING

WITH MAXIMUM LOAD CAPACITY

Y.Y. Boldyrev

Peter the Great Saint-Petersburg Polytechnic University,

Institute of Applied Mathematics and Mechanics

boldyrev@phmf.spbstu.ru

The variational problem for a radial gas sliding bearing with two sectors is considered.

The pressure distribution in the gas layer is described by a nonlinear Reynolds equation

for arbitrary compressibility numbers. Magnitude of the principal pressure force vector is

used as the variational problem functional. A qualitative analysis of the extremum neces-

sary conditions is carried out, and a computational procedure is constructed. It is shown

on the basis of complete system of necessary conditions analysis that the profile of each

sector is piecewise linear and single-stage, herewith one sector provides only a gas de-

pression, while the another one - only the gas compression.

Keywords: gas lubrication, calculus of variations, load capacity maximum, arbitrary

compressibility numbers.

Радиальный двухсекторный газовый подшипник с максимальной несущей ...

103

Введение. Узлы на газовой смазке относятся к высокотехнологичным

изделиям и используются в широком круге отраслей: от прецизионного

приборостроения и машиностроения до мощных турбокомпрессорных ма-

шин. Обладая массой достоинств (малое трение, способность работать в

широком диапазоне температур, работа на очень высоких оборотах и др.),

они имеют серьезный недостаток  относительно низкую несущую способ-

ность. Работа посвящена проблеме повышения несущей способности узлов

на газовой смазке на основе подходов оптимального проектирования. Отме-

тим, что принципиально сами технологии оптимального проектирования

любых изделий возможны только на основе подходов математического мо-

делирования. Оно, являясь универсальным инструментарием, пожалуй, наи-

более сильно проявляется именно в задачах оптимизации, поскольку этот

класс задач, опять-таки принципиально, не разрешим на основе физическо-

го эксперимента.

Впервые задача об оптимальной форме профиля в задачах теории смаз-

ки была рассмотрена Рэлеем в 1918 г. [1]. Отметим, что Рэлей сильно опе-

редил свое время,  первая работа, продолжившая его исследования, была

опубликована почти через 50 лет [2]. В дальнейшем это направление разви-

валось преимущественно в работах отечественных и американских иссле-

дователей [2-13].

В настоящей работе, в качестве характерного примера подходов мате-

матического моделирования к решению задач оптимизации, рассматривает-

ся вариационная задача для одномерного радиального подшипника с газо-

вой смазкой, имеющего два сектора. Приведены результаты качественного

анализа системы необходимых условий экстремума, на основе которых по-

строена численная процедура. Установлено позитивное влияние области

разряжения в газовом слое на величину подъемной силы.

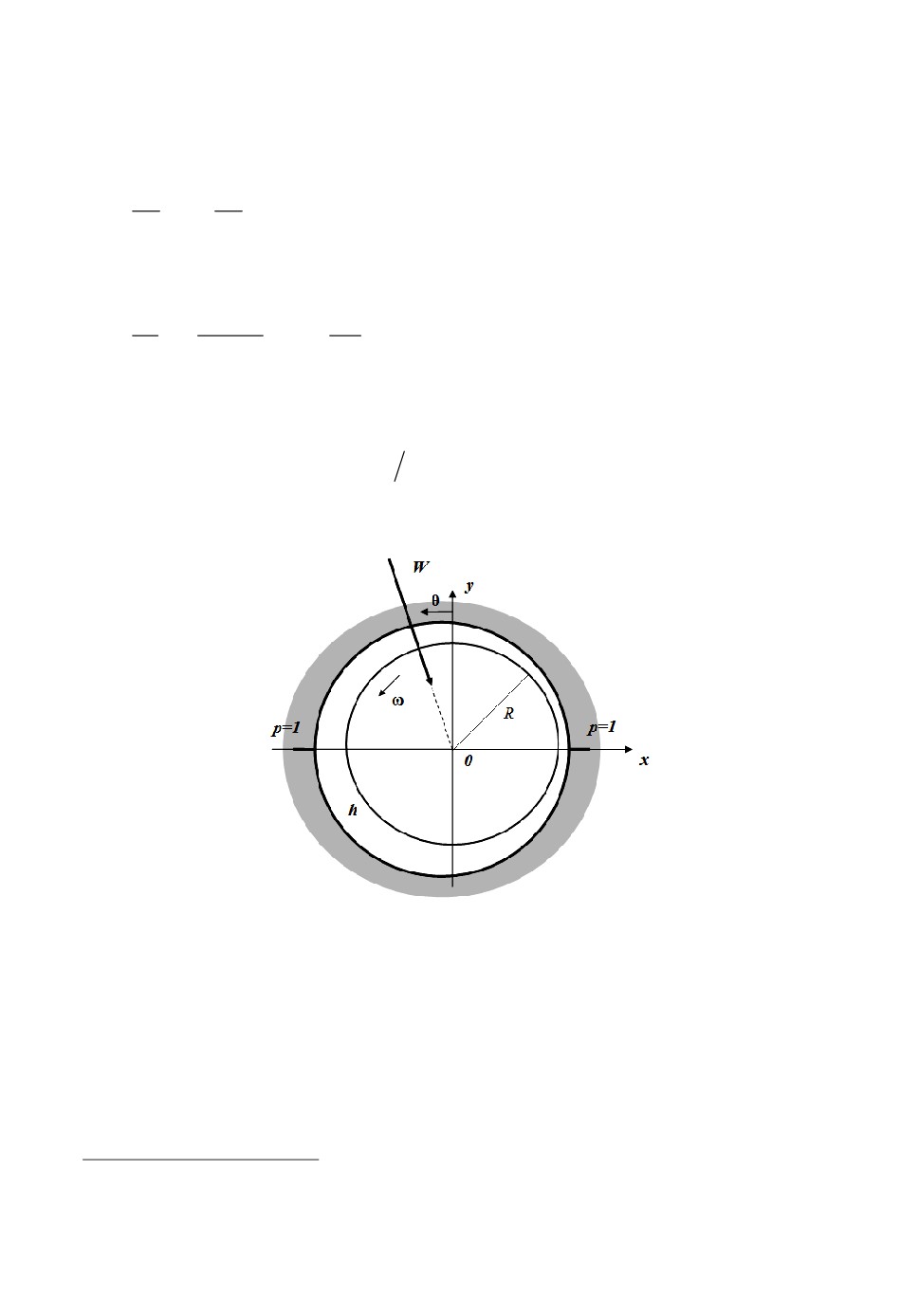
1. Постановка задачи. Рассмотрим одномерный радиальный газовый

подшипник, имеющий два сектора с одинаковыми углами охвата: [π/2, π/2]

и [π/2, 3π/2] соответственно (рис.1). Сектора сообщаются с внешней средой

на границах, которые расположены на оси x декартовых координат (x,y)¹,

в центре которых находится ось ротора подшипника радиуса R. Централь-

ный угол  отсчитывается от оси y (направленной вверх) в направлении

вращения ротора против часовой стрелки. Угловая скорость ω постоянна.

Предполагаем, что линия действия вектора нагрузки W имеет угол ψ с

¹ Штрихом всюду далее, где это необходимо, отмечены размерные величины.

104

Ю.Я. Болдырев

осью y. Стационарное поле давления в газовом слое описывается уравнени-

ем Рейнольдса газовой смазки² [12],





ph







d

d



которое запишем в следующем безразмерном виде:

Q+ ph

=

=0,

(1)

dθ

где p и h  безразмерные избыточное давление и толщина смазочного слоя,

отнесенные к давлению внешней среды p_a и к заданному минимальному

значению зазора h_min;

Λ=6μωR h

 число сжимаемости,   вязкость

min

газа и   угловая скорость. Безразмерная величина Q=const в уравнениях

(1), отнесенная к h_minωR, пропорциональна расходу газа.

Рис.1. К постановке задачи.

Запишем краевые условия к уравнениям (1), заключающиеся в равен-

стве давления атмосферному на границах секторов:

p(  π/2)=p(π/2)=1.

(2)

В качестве функционала задачи выберем взятую со знаком минус ве-

личину модуля главного вектора сил давления F, направленную по линии

² Отметим, что уравнение Рейнольдса может быть получено из уравнения Навье-Стокса

в предположении, что величина отношения h_min/R имеет порядок малости 103 - 104.

Радиальный двухсекторный газовый подшипник с максимальной несущей ...

105

действия нагрузки W и нормированную к R p_a

J |F

| F

F

(3)

где F_x и F_y  соответствующие компоненты вектора F, у которых знак ми-

нус обусловлен направлением внешней нормали к поверхности ротора:

2π

=

(p1)sinθdθ,

=

(p1)cosθdθ

(4)



Будем разыскивать минимум функционала (3) при условии, что тол-

щина газового слоя должна удовлетворять неравенству

1h(x),

(5)

определяемому способом нормировки функции h (для заданного значения

h_min).

Сформулируем задачу Лагранжа вариационного исчисления, которая

сводится к разысканию кусочно-непрерывной функции h(x), непрерывной

функции p(x) и постоянной Q, удовлетворяющих ограничениям (1),(2), (5) и

реализующих экстремум функционала (3), составляющие которого опреде-

ляются соотношениями (4). Отметим, что первая вариационная задача для

радиальных подшипников, являющаяся обобщением задачи Рэлея [1], была

решена Мэдеем в 1970 г. [4], где было показано, что в случае несжимаемого

газа оптимальным является кусочно-ступенчатый профиль. В [6] было ус-

тановлено, что для радиальных секторных подшипников в случае несжи-

маемого газа оптимальными также являются кусочно-постоянные профили.

И, наконец, в [7] было установлено, что оптимальный радиальный подшип-

ник с газовой смазкой является замкнутым и имеет кусочно-линейный про-

филь во всем диапазоне чисел сжимаемости. Результаты [7] можно рас-

сматривать как случай «односекторного» подшипника. Наличие двух секто-

ров в настоящем случае порождает совокупность двух отдельных задач (для

каждого из секторов), которые «аэродинамически независимы» и связаны

только посредством функционала (3).

2. Система необходимых условий экстремума [14,15]. Начнем с того,

что заменим ограничение  неравенство (5) ограничением  равенством

h1ν

0,

где (x)  вспомогательная функция, и составим расширенный функционал

106

Ю.Я. Болдырев

2π



dp dQ



f  p,

h, ν,

dθ

(6)







d dθ



Запишем первую вариацию функции f в согласии с системой ограничений

задачи (1),(2),(5)



Q+ ph



δf=

(F cosθ+F sinθ)δp



Λ

+λ

δψ,

(7)

+λ





|F|

dθ





где ₀, ₁ и ₂  функциональные множители Лагранжа, а символ δ обозна-

чает варьирование стоящих за ним величин.

Уравнения Эйлера - Лагранжа [14,15] функционала (6)

dλ

ΛQ d



= 0,

(F cosθ+F sinθ)+λ



=0,

(8)

dθ

|F|

dθ



Λ(3Q+2ph)λ

= 0,

ν=0

(9)

Условия трансверсальности [14,15] в концевых точках каждого из сек-

торов, которые обозначим θi и θ^isf (i=1,2), имеют вид в согласии с (6) и (7)



dQ dp



dQ dp

θ



θ



λ

λ









d





d

d





(

)Q(

) 

(

)

Q(



)



1,2,



где учтены краевые условия (2). Далее, с учетом неподвижности границ

секторов для вариаций координат в граничных точках, имеем: θ

θ



(i=1,2), откуда получаем краевые условия для множителей Лагранжа ₀ для

каждого из секторов

(θi )=0,

i

1,2

(10)

λ if )=0, λ0

Из условий Эрдманна-Вейерштрасса [14,15]









dQ dp











Q(



)

p(

)



















d













Радиальный двухсекторный газовый подшипник с максимальной несущей ...

107

в точках θ_r возможного разрыва функции h на каждом из секторов, где на-

ряду с независимостью вариаций учтена непрерывность давления, а симво-

лом []^ обозначена разность величин, вычисленных непосредственно сле-

ва и справа от точки разрыва θ_r функции h; имеем систему соотношений





dp



λ



[λ

]



[λ

]



(11)









d



показывающих непрерывность величин в квадратных скобках при переходе

через точки разрыва функции h.

Неравенство Вейерштрасса сильного минимума функционала [14,15]

имеет вид

E

(dp / d  dp / d)  0,

(12)

где чертой обозначены допустимые значения производной, откуда следует,

что на оптимальном профиле величина



d имеет максимальное зна-

чение по отношению к допустимым решениям.

Форма профиля определяется уравнениями (9), второе из которых дает

такие возможные варианты на каждом из секторов

₂=0, ν=0, h=1;

₂≠0, ν=0, h=1;

₂=0, ν≠0, h>1,

(13)

но тогда для последнего случая (13) из первого уравнения (9) получаем

h  (3Q /2p).

(14)

Уравнение (14) показывает, что величина Q<0, при этом в согласии с

(1) на участках с h>1 на каждом из секторов имеем





(15)

dθ

т.е. там где h>1, dp/dθ >0. Для случая h=1 аналогично получим





1Q



(16)

d

откуда находим, что в областях, где h=1, давление может только понижать-

ся, причем здесь величина Q/p отрицательна и |Q/p|≥1. Обращаясь к услови-

ям Эрдмана-Вейерштрасса (11), по непрерывности функции ₁ в точках θ_r

108

Ю.Я. Болдырев

разрыва функции профиля h получаем, что на каждом из секторов

₁(θ_r)=0.

(17)

Знак функции ₁ определяется неравенством Вейерштрасса (12). Дей-

ствительно, при h>1 c учетом (15) для любого допустимого H имеем



HH





2

1











h  h



откуда ₁≥0 при h>1. Аналогично при h=1 для любого допустимого H

















1



1

1



























откуда ₁≤0 .

Далее условимся при необходимости отмечать индексами «1» и «2»

параметры первого, «верхнего», и второго, «нижнего», секторов соответст-

венно.

Итак, на каждом секторе знак градиента dp/dθ совпадает со знаком

функции ₁, при этом число ступеней-переходов от h=1 к h>1 определяется

числом нулей у ₁ в согласии с (17). Прежде чем переходить к определению

числа ступеней на секторах, необходимо уточнить класс непрерывных до-

пустимых функций p(θ), дающих минимум функционалу (3). Будем предпо-

лагать, что главный вектор сил давления F имеет направление, близкое к

направлению оси y. В таком случае характер работы секторов кардинально

различен,  первый, «верхний», должен обеспечить максимальное пониже-

ние давления, т.е. там всюду p≤1, тогда как второй, «нижний», должен

обеспечить максимальное повышение давления, т.е. там всюду p≥1. Эти ус-

ловия выделяют в классе непрерывных функций подмножества допустимых

функций для каждого из секторов. В силу сказанного можем утверждать,

что в начальной точке

=π/2

«нижнего» сектора dp/dθ>0, тогда как в ко-

нечной точке

=3π/2

должно быть dp/dθ<0. Отсюда по неравенству Вей-

ерштрасса в этих точках получим:

(θ

)



0, λ

(θ

)



0. Тогда в согласии с

(10) и (12), множитель Лагранжа λ₀(θ) в окрестности левой границы

s рас-

тет от нуля, тогда как на правой границе

f убывает до нуля. В то же время

в точках разрыва профиля h, в согласии с (11), функция λ₁ обязана обра-

Радиальный двухсекторный газовый подшипник с максимальной несущей ...

109

щаться в ноль, откуда из (7) и (17) находим для таких точек

d



θ= θ_r.

d

Отсюда следует, что точки разрыва h являются точками экстремума

функции λ₀(θ), при этом число таких точек определяет число ступеней на

секторе. Сразу же укажем, что число ступеней на «нижнем» секторе не бо-

лее одной, поскольку как двухступенчатый профиль, с размещением облас-

ти с h=1 между областями с h>1, так и многоступенчатый профили приво-

дят к менее эффективным допустимым функциям давления p(θ).

Итак, «нижний» сектор одноступенчатый, причем в передней части,

где h>1 давление растет, тогда как в области с h=1 оно падает. Кардинально

иная ситуация имеет место на первом, «верхнем», секторе. Действительно,

здесь в начальной точке

=π/2

необходимо dp/dθ<0, и p≤1 всюду при

θ[θ

,θ

]

 как того требует указанный выше выбор допустимых функций,

s f

тогда как в конечной точке

=π/2

для выполнения краевых условий (2)

необходимо dp/dθ>0. При этом качественное поведение функции λ₀(θ) с

точностью до знака аналогично её поведению на нижнем секторе. Т.о.,

«верхний» сектор в передней части по направлению скольжения имеет об-

ласть с h=1, где давление падает до некоторого минимального значения в

точке

 точке разрыва профиля, а затем при h>1 давление растет до его

значения на границе

f .

Интегрируя уравнения для давлений (1) в областях с h>1, получим для

«нижнего» сектора







(2)

p(θ)

1

1

(θθ

)

(18)













откуда из (14) имеем такое выражение, показывающее, что профиль h здесь

линейный







(2)





h(θ)



1

(θθ

)









где Q₂ отвечает величине расхода на «нижнем» секторе. Интегрируя (16),

получим выражение для давления в области с h=1

110

Ю.Я. Болдырев

(2)





(θ

θ)

p1

p(θ)



(1Q

)exp

Q

(19)









Аналогичные выражения можно записать и для «верхнего» сектора.

Отметим, что как на «нижнем», так и на «верхнем» профиле h имеет место

традиционный «смазочный клин». При этом если на «нижнем» секторе:

(2)

h(θ

)

h(θ

) , что обеспечивает повышение давления газа в направлении

(1)

вращения, то на верхнем:

h(θ

)

h(θ

), что также приводит к росту дав-

(1)

ления в направлении вращения от его минимального значения в точке

r .

Таким образом, на «верхнем» профиле на участке с h=1 происходит пони-

(1)

жение давления газа до его минимального значения в точке

с после-

дующим восстановлением его величины до значения во внешней среде на

участке с h>1.

Итак, вариационная задача свелась к параметрической  при заданном

(1)

значении числа Λ требуется найти четыре параметра: Q₁ и

r для первого

(2)

сектора, и Q₂ и

 для второго. Однако определением этих параметров

решение задачи не исчерпывается, поскольку характер функционала (3) тре-

бует определенности в выборе направления действия нагрузки W, которая

должна действовать по линии направления главного вектора сил давления

F. Последнее приводит к требованию поиска угла положения ψ, который

определяется на основе рассмотрения отношения величин компонент F_y и

F_x главного вектора сил давления (4).

Задача решалась численно, на основе определения параметров Q₁,

(1)

(2)

=θ₁ и Q₂,

=θ₂, путем сшивания давления на основе выбора расходов

Q₁ и Q₂ в точках θ₁ и θ₂ с использованием соотношений (18) и (19). Отметим

плохую обусловленность уравнения (19), усугубляющуюся для его аналога

на «верхнем» секторе, где с ростом числа Λ величина Q₁→1.0 и, например,

для Λ=50 имеем Q₁=1.0000000003218853448, и для больших значений Λ

при вычислениях уже недостаточно 32-значной мантиссы.

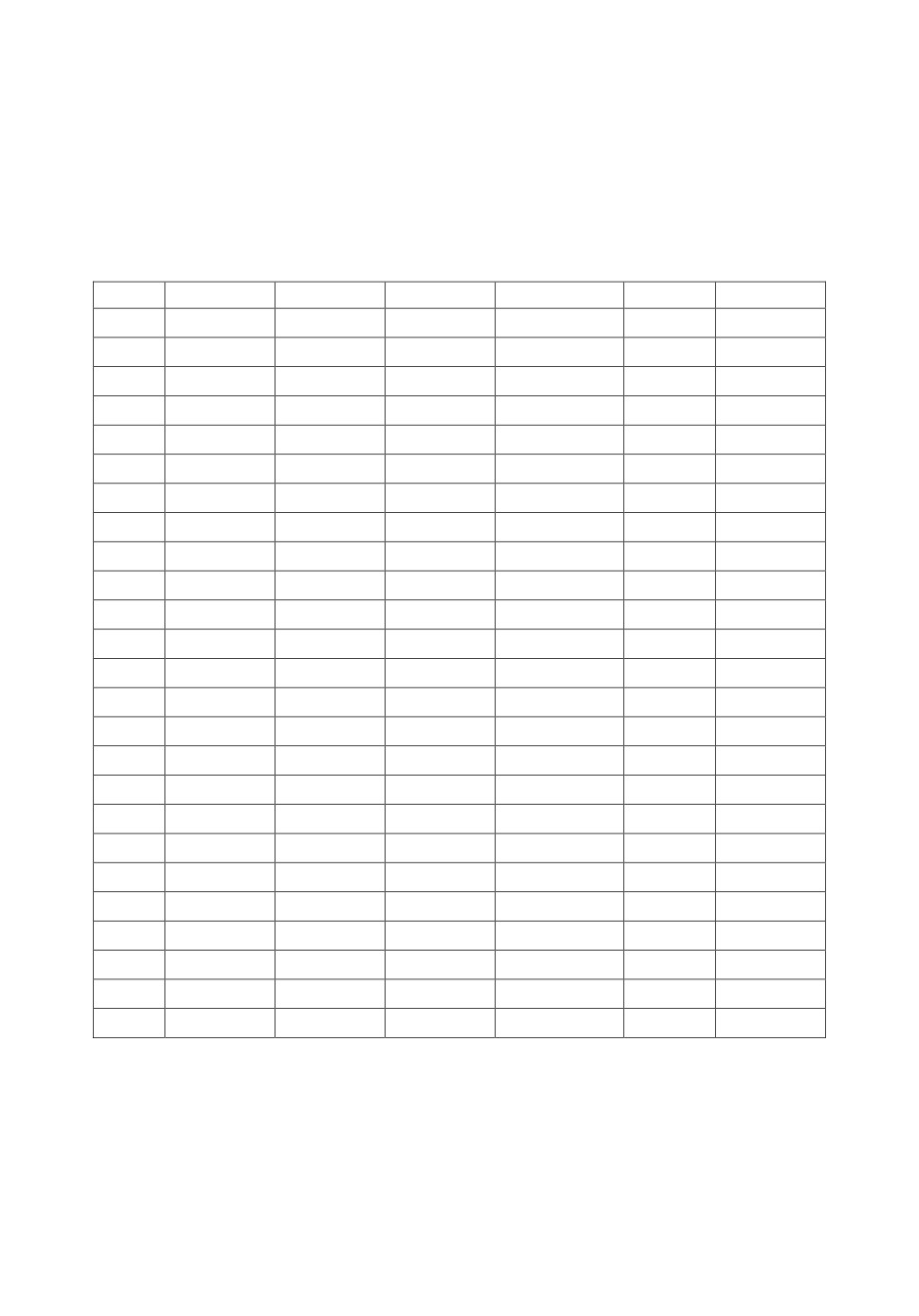
В табл.1 и 2 приведены характеристики оптимальных профилей при

различных числах сжимаемости. Отметим немонотонный характер измене-

ния положения точки разрыва θ₁ на «верхнем» секторе. Как видно из табл.2,

точка разрыва θ₁ с ростом числа сжимаемости Λ сдвигается к началу про-

(1)

филя, т.е. к точке

=π/2

до значения θ₁=1.24911≈71.6º при Λ≈17, а

затем удаляется от него вплоть до некоторого предельного положения, от-

вечающего Λ=∞. Такой характер профиля обусловлен тем, что при неболь-

Радиальный двухсекторный газовый подшипник с максимальной несущей ...

111

ших числах Λ малая длина участка с h=1 обеспечивает наибольшее падение

давления при относительно малых величинах |dp/dθ|, тогда как с ростом

числа Λ длина участка с h=1 растет вместе с Λ, что и дает значительные ве-

личины |dp/dθ|, приводя к большему падению давления.

Таблица 1.





p_min

Q₁

p_max

Q₂

0

0.530846

0.000000

0.214347

1.208154

0.214346

1.208154

0.01

0.005308

0.000440

0.997856

1.207205

1.002143

1.209131

0.1

0.053071

0.004348

0.978541

1.198724

1.021393

1.217921

0.5

0.263787

0.021374

0.893165

1.164540

1.105346

1.259783

1.0

0.518426

0.040991

0.791608

1.130082

1.204117

1.316662

2.0

0.978220

0.073071

0.622320

1.084524

1.375943

1.435302

3.0

1.365381

0.098142

0.500847

1.058606

1.518218

1.550319

4.0

1.691174

0.119131

0.414913

1.042769

1.639746

1.657699

5.0

1.970011

0.137437

0.352543

1.032320

1.746899

1.757251

7.5

2.529194

0.175282

0.254547

1.017443

1.974699

1.977605

10.0

2.965812

0.205503

0.198686

1.009833

2.166861

2.167776

12.5

3.328971

0.230839

0.163004

1.005451

2.336657

2.336973

15.0

3.643568

0.252969

0.138433

1.002836

2.490569

2.490891

16.0

3.759186

0.261175

0.130655

1.002120

2.548965

2.549045

16.5

3.815148

0.265164

0.127108

1.001821

2.577417

2.577483

16.75

3.842698

0.267132

0.125411

1.001685

2.591491

2.591551

17.0

3.869971

0.269083

0.123763

1.001557

2.605467

2.605523

17.5

3.923716

0.272934

0.120605

1.001323

2.633133

2.633179

18.0

3.976441

0.276721

0.117619

1.001119

2.660431

2.660469

19.0

4.079035

0.284100

0.112109

1.000787

2.713979

2.714006

20.0

4.178126

0.291224

0.107139

1.000542

2.769602

2.766235

25.0

4.630781

0.322741

0.088058

1.000068

3.010417

3.010422

30.0

5.029394

0.347546

0.074963

1.000006

3.231425

3.231426

50.0

6.311245

0.407571

0.047211

1.000000

3.967492

3.967492

100.0

8.557549

0.469500

0.024670

1.000000

5.311328

5.311328

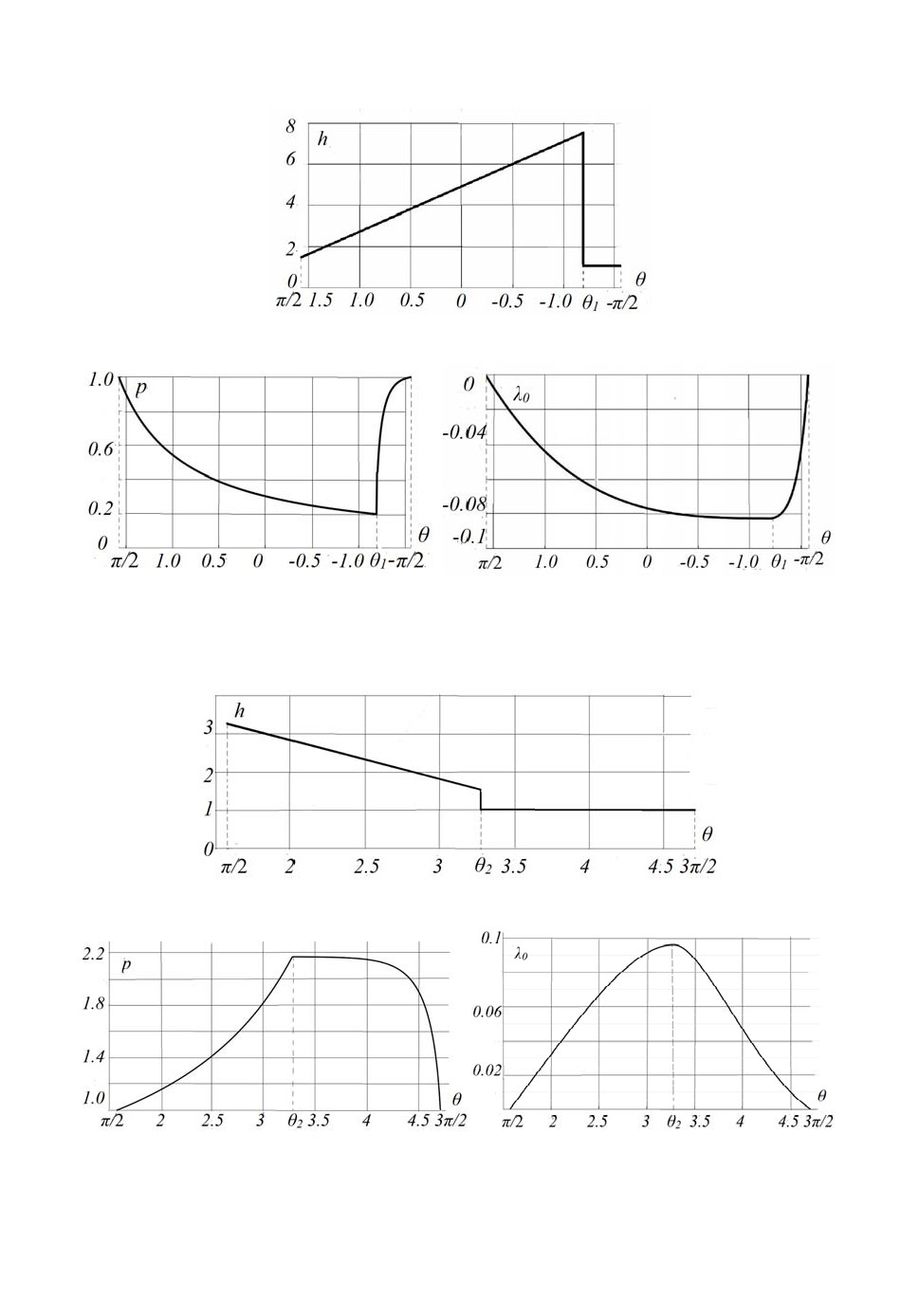
На рис.2 и 3 приведены графики, демонстрирующие характерный вид

функций h(θ), p(θ) и λ₀(θ) для каждого из секторов.

Представляет интерес рассмотрение асимптотического поведения па-

раметров оптимальных профилей при Λ→0 и Λ→∞.

112

Ю.Я. Болдырев

Таблица 2.



θ₁

h(π/2)

h(θ₁)

θ₂

h(π/2)

h(θ₂)

0

0.530846

0.541050

1.812231

3.682640

1.812231

0.01

0.005308

0.542592

1.810808

1.814698

3.681216

1.813696

1.809817

0.1

0.053071

0.556200

1.798085

1.837516

3.667882

1.826882

1.788618

0.5

0.263787

0.619112

1.746810

1.955753

3.612750

1.889674

1.709577

1.0

0.518426

0.698513

1.695124

2.141366

3.554440

1.974993

1.640200

2.0

0.978220

0.838350

1.626786

2.614068

3.470483

2.152953

1.564711

3.0

1.365381

0.942137

1.587910

3.170452

3.416674

2.325479

1.531716

4.0

1.691174

1.016719

1.564153

3.769832

3.379994

2.486548

1.516423

5.0

1.970011

1.071379

1.548479

4.392318

3.353156

2.635876

1.508889

7.5

2.529194

1.157647

1.526165

5.995609

3.308161

2.966407

1.502207

10.0

2.965812

1.205321

1.514750

7.623826

3.278926

3.251665

1.500634

12.5

3.328971

1.232309

1.508176

9.252371

3.257839

3.505459

1.500204

15.0

3.643568

1.245764

1.504249

10.86626

3.241885

3.736337

1.500070

16.0

3.759186

1.248167

1.503180

11.50496

3.236571

3.823567

1.500047

16.5

3.815148

1.248812

1.502732

11.82250

3.234106

3.866225

1.500039

16.75

3.842698

1.249003

1.502527

11.98080

3.232919

3.887327

1.500035

17.0

3.869971

1.249113

1.502335

12.13877

3.231761

3.908284

1.500032

17.5

3.923716

1.249088

1.501985

12.45371

3.229525

3.949769

1.500026

18.0

3.976441

1.248758

1.501678

12.76729

3.227392

3.990704

1.500022

19.0

4.079035

1.247285

1.501181

13.39039

3.223408

4.071009

1.500015

20.0

4.178126

1.244880

1.500813

14.00815

3.219755

4.149353

1.500010

25.0

4.630781

1.225740

1.500099

17.03539

3.204893

4.515632

1.500002

30.0

5.029394

1.205742

1.500010

20.01015

3.193201

4.847139

1.500000

50.0

6.311245

1.153683

1.500000

31.77199

3.160219

5.951238

1.500000

100.0

8.557549

1.097883

1.500000

60.80399

3.116471

7.966993

1.500000

В первом случае (при Λ→0) уравнения (1) линеаризуются и при анали-

зе соответствующей вариационной задачи приводят к кусочно-постоянным

профилям на каждом из секторов с такими параметрами: Q₁=Q₂=1.208154,

θ₁=31.000º, θ₂=211.000º, причем p(θ₁)=0.214346 и p(θ₂)=0.214346. При

этом значение функционала есть: J=0.5308449Λ. Замечательным является

тот факт, что это решение совпадает с двумя другими решениями, связан-

ными с совершенно иными постановками краевых задач для радиальных га-

зовых подшипников. Это задача Рэлея для случая радиального подшипника

[4]  задача с краевыми условиями первого рода для давления на границах,

и периодическая задача, т.е. задача с условием периодичности для давления

на границах и условием газообмена на бесконечно удаленных торцах [10].

114

Ю.Я. Болдырев

В случае, отвечающем Λ→∞, различие в характере поля давления на

каждом из секторов проявляется наиболее сильно. На «нижнем» секторе, в

согласии с исходным уравнением Рейнольдса, при Λ→∞ имеем: ph=Q₂, и

профиль безразмерного давления будет вырождаться в ступенчатый про-

филь вида





π/2

θ ,

p(θ)



(20)

Q





3π/2.



При этом, используя «сшивку» давления по непрерывности в точке

разрыва профиля θ₂ на основании (18), можно установить связь между Q₂ и

положением точки θ₂ при Λ→∞ (с учетом условия p=Q₂ при h=1, исходя

из предельного соотношения (20)) в виде

1





1+ 1+ Λ(θ

π/2)

(21)



 .





Аналогично на «верхнем» секторе, исходя из требований минимизации

расхода Q₁, при Λ→∞ получаем: Q₁=1, и безразмерный профиль давления

принимает следующий предельный вид:

1, θ



θπ/2,

p(θ)





(22)

0, π/2





где равенство p(θ)=0 на промежутке (θ₁,π/2) необходимо понимать в смысле

раскрытия неопределенности (p→0, h→∞³ при Λ→∞). Т.е. здесь величина

давления всюду на промежутке (θ₁,π/2) равна нулю, что также указывает на

предельный экстремальный характер оптимального решения.

Подставляя соотношения (20) и (22) в выражения для F_x и F_y (4), полу-

чим следующее предельное выражение для функционала J (3) при Λ→∞:

J  (cosθ

+(1+Q

)cosθ

)

((1sinθ

)(1+Q

)(1+sinθ

))

Используя далее выражение для Q₂(θ₂) (21), получаем явную зависи-

мость функционала J от положения точек разрыва θ₁и θ₂, который (при

Λ→∞) принимает экстремальное значение при θ₁≈0.91781 (52.5864º) и

θ₂≈2.87734 (164.8594º).

Речь идет о предельном значении h(θ) в левой окрестности точки θ₁ при Λ→∞.

Радиальный двухсекторный газовый подшипник с максимальной несущей ...

115

Заключение. На основании математической модели Рейнольдса рас-

смотрена вариационная задача теории газовой смазки для двухсекторного

радиального подшипника при произвольных числах сжимаемости Λ. Уста-

новлено, что профиль микрогеометрии является кусочно-линейным на каж-

дом из секторов, при этом «верхний» профиль работает в режиме разряже-

ния, а «нижний»  в режиме сжатия газа. Исследована зависимость харак-

тера решения для предельных значений числа сжимаемости Λ, т.е. при

Λ→0 и Λ→∞.

СПИСОК ЛИТЕРАТУРЫ

Lord Rayleigh. Notes on the theory of lubrication// Phil. Mag., 1918, v.35, №1, p.1-12.

Maday C.J. A. The One  Dimensional Optimum Hydrodynamic Gas Slider Bearing //

Trans. ASME. Ser. F. J. Lubr. Technol., 1968, v.90, №1. (J. Tribol. 90(1), 281-284 (Jan

01, 1968) (4 pages) (Рус. перевод. Проблемы трения и смазки.  М.: Мир. 1968).

Maday C.J. A bounded variable approach to the optimum slider bearing // Trans. ASME.

Ser. F. J. Lubr. Technol., 1968, v.90, №1, p.240-242. (Рус. перевод. Проблемы трения и

смазки.  М.: Мир, 1968, №4, с.252-255).

Maday C.J. The Maximum Principle Approach to the Optimum One-Dimensional Journal

Bearing, Transactions of the American Society of Mechanical Engineers, Series F. 1970,

v.92, p.482-489.

Болдырев Ю.Я., Троицкий В.А. Одна пространственная вариационная задача теории

газовой смазки // Известия АH СССР МЖГ, 1975, N5, с.34-39.

Boldyrev Iu.Ia., Troitskii V.A. Odna prostranstvennaia variatsionnaia zadacha teorii gazo-

voi smazki // Izvestiia AH SSSR MZhG, 1975, N5, s.34-39.

Болдырев Ю.Я. Вариационная задача для радиального секторного подшипника, ра-

ботающего в режиме малых чисел «сжимаемости» // Прикладная математика. Труды

ТПИ, 1977, с.30-35.

Boldyrev Iu.Ia. Variatsionnaia zadacha dlia radialnogo sektornogo podshipnika, rabo-

taiushchego v rezhime malykh chisel «szhimaemosti» // Prikladnaia matematika. Trudy

TPI, 1977, s.30-35.

Болдырев Ю.Я., Слесарев М.Е. Одномерный радиальный газовый подшипник с мак-

симальной несущей способностью // Машиноведение, 1987, №4, с.97-103.

Boldyrev Iu.Ia., Slesarev M.E. Odnomernyi radialnyi gazovyi podshipnik s maksimalnoi

nesushchei sposobnostiu // Mashinovedenie, 1987, №4, s.97-103.

Грабовский В.И. Оптимальный радиальный газовый подшипник с минимумом мо-

мента сопротивления // Изв. РАН, МЖГ, 1999, № 6, с.63-75.

Grabovskii V.I. Optimalnyi radialnyi gazovyi podshipnik s minimumom momenta so-

protivleniia // Izv. RAN, MZhG, 1999, № 6, s.63-75.

Грабовский В.И. Оптимальный зазор упорного газового подшипника с максимальной

несущей способностью // Изв. РАН, МЖГ, 2000, № 4, с.68-78.

Grabovskii V.I. Optimalnyi zazor upornogo gazovogo podshipnika s maksimalnoi nesu-

shchei sposobnostiu // Izv. RAN, MZhG, 2000, № 4, s.68-78.

116

Ю.Я. Болдырев

10. Болдырев Ю.Я. Замечание о периодической вариационной задаче для радиального

газового подшипника.  СПб.: Научно-технические ведомости СПбГПУ, 2007, № 1,

с.258-262.

Boldyrev Iu.Ia. Zamechanie o periodicheskoi variatsionnoi zadache dlia radialnogo gazovo-

go podshipnika.  SPb.: Nauchno-tekhnicheskie vedomosti SPbGPU, 2007, № 1, s.258-262.

11. Болдырев Ю.Я., Петухов Е.П. Вариационная задача для радиального газового под-

шипника // Известия РАH МЖГ, 2015, т.50, № 2, с.16-26.

Boldyrev Iu.Ia., Petukhov E.P. Variatsionnaia zadacha dlia radialnogo gazovogo podship-

nika // Izvestiia RAH MZhG, 2015, t.50, № 2, s.16-26.

12. Сипенков И.Е., Филиппов А.Ю., Болдырев Ю.Я., Григорьев Б.С. и др. Прецизионные

газовые подшипники.  СПБ: Изд. ЦНИИ «Электроприбор», 2007, 504 с.

Sipenkov I.E., Filippov A.Iu., Boldyrev Iu.Ia., Grigorev B.S. i dr. Pretsizionnye gazovye

podshipniki.  SPB: Izd. TsNII «Elektropribor», 2007, 504 s.

13. Болдырев Ю.Я., Петухов Е.П. Вариационная задача для радиального газового под-

шипника // Известия РАH МЖГ, 2015, т.50, № 2, с.16-26.

Boldyrev Iu.Ia., Petukhov E.P. Variatsionnaia zadacha dlia radialnogo gazovogo podship-

nika // Izvestiia RAH MZhG, 2015, t.50, № 2, s.16-26.

14. Теория оптимальных аэродинамических форм. (Редактор А. Миеле).  М.: Мир,

1971, 507 с.

Teoriia optimalnykh aerodinamicheskikh form. (Redaktor A. Miele).  M.: Mir, 1971, 507s.

15. Болдырев Ю.Я. Вариационное исчисление и методы оптимизации. Учебное пособие.

 Санкт-Петербург: Издательство Политехнического университета, 2016, 240 с.

Boldyrev Iu.Ia. Variatsionnoe ischislenie i metody optimizatsii. Uchebnoe posobie. 

Sankt-Peterburg: Izdatelstvo Politekhnicheskogo universiteta, 2016, 240 s.

Поступила в редакцию 27.11.2017

После доработки 13.12.2018

Принята к публикации 01.07.2019