МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 12, стр. 21-32
ЗАКОНЫ СОХРАНЕНИЯ
И КОМПАКТНАЯ КВАЗИГАЗОДИНАМИЧЕСКАЯ СИСТЕМА
©
2019 г.
Б.Н. Четверушкин1, А.Е. Луцкий1, В.П. Осипов1, 2
1 Федеральный исследовательский центр «Институт прикладной математики
им. М.В. Келдыша РАН»
2 Федеральное государственное бюджетное образовательное учреждение выс-
шего образования "Российский экономический университет им. Г.В. Плеханова"
office@keldysh.ru, allutsky@yandex.ru, osipov@keldysh.ru
DOI: 10.1134/S0234087919120025
На основе применения законов сохранения осуществляется вывод компактной ква-
зигазодинамической системы, которая ранее была получена с помощью использова-
ния кинетической модели. Обсуждается возможность применения для решения этой
системы алгоритмов, ранее применяемых для решения уравнений Навье-Стокса.
Ключевые слова: квазигазодинамическая система уравнений, законы сохранения,
время между столкновениями молекул, пограничный слой на пластине.
CONSERVATION LAWS AND A COMPACT QUASI-GASDYNAMIC SYSTEM
B.N. Chetverushkin1, A.E. Luzkiy1, V.P. Osipov1,2
1Keldysh Institute of Applied Mathematics (Russian Academy of Sciences)
2Plekhanov Russian University of Economics
Based on the application of conservation laws, a compact quasi-gasdynamic system is
derived, which was previously obtained using a kinetic model. The possibility of using
algorithms previously used to solve the Navier-Stokes equations to solve this system is
discussed.
Key words: quasi-gasdynamic system of equations, conservation laws, time between mo-
lecules collisions, boundary layer on a plate.
1. Введение
Квазигазодинамическая система уравнений (КГУ) получена из кинети-
ческой модели с помощью процедуры, аналогичной той, на основе которой
уравнения газовой динамики получаются из уравнения Больцмана [1-5].
При этом сама КГУ система для моделирования течения вязкого теплопро-
водного газа отличалась от аналогичной системы уравнений Навье-Стокса
22
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
на члены по порядку величины второго порядка малости по числу Кнудсена
2
O(Kn
). Этот важный факт подтверждался как результатами численных
расчетов по сравнению данных, полученных на основе использования КГУ
и уравнений Навье-Стокса, так и результатами теоретического анализа вхо-
дящих в КГУ уравнений [1,2, 6-9].
Вывод КГУ системы из кинетической модели в явном виде опирался на
тот факт, что вблизи равновесия (близости к локально-максвелловскому
распределению) одночастичная функция распределения слабо меняется на
расстоянии длины свободного пробега l или за время порядка характерного
времени между столкновениями молекул . Это обеспечивает корректность
КГУ системы по крайней мере с физической точки зрения и с самого начала
ее появления в середине 80-х годов XX века давало возможность успешного
моделирования сложных газодинамических течений вязкого теплопровод-
ного газа [1,2].
В последнее время еще одним востребованным свойством КГУ систе-
мы явилась возможность адаптации алгоритмов, построенных на ее основе,
к архитектуре вычислительных систем высокой и сверхвысокой производи-
тельности. Эта возможность, актуальная при использовании в расчетах экс-
трамассивного параллелизма, связана с наличием в рамках КГУ системы
членов со вторыми производными по времени от газодинамических пара-
метров [10]. Заметим также, что гиперболический характер КГУ, связанный
с наличием вторых производных по времени, дает возможность на алгорит-
мическом уровне способствовать решению проблемы отказоустойчивости,
актуальной при одновременном использовании больших количеств незави-
симых вычислителей [11].
Недостатком КГУ системы является ее более громоздкий вид по срав-
нению с уравнениями Навье-Стокса. Особенно наглядно этот недостаток
проявляется для варианта КГУ системы для моделирования задач магнит-
ной газовой динамики, в которых помимо молекулярной вязкости и тепло-
проводности учитывается также магнитная вязкость. Кроме того, нестан-
дартный вид членов, входящих в КГУ систему, вызывал определенные
трудности при использовании алгоритмов, ранее разработанных для реше-
ния уравнений Навье-Стокса.
В [12,13] был предложен компактный вариант КГУ системы, который
выглядит следующим образом:
W
(u
u
p),
(1)
i
i k
ik
2
x
k
Законы сохранения и компактная квазигазодинамическая система
23
2
div
(u w)
0
,
(2)
2
t
2
t
2
u
u
div
(u w)
u
p
divP
,
(3)
NS
2
t
2
t
2
E
E
div
(
E p)(u w)
div
q
div(P
u)
(4)
NS
2
t
2
t
Здесь t
x
пространственная координата k 1,2,3, плот-
ность, u скорость, p давление, E полная энергия, q вектор тепло-
вого потока
T
q
,
(5)
k
x
k
P
тензор вязких напряжений в
уравнениях Навье-Стокса.
Эта система (1)-(4) была получена из исходной квазигазодинамической
системы путем оценки по порядку величины входящих в нее членов. В дан-
ной работе система (1)-(4) будет получена непосредственно из законов со-
хранения при условии ограничения снизу времени между столкновения-
ми молекул на интервал изменения по времени t .
2. Уравнение неразрывности КГУ системы
Одним из главных отличий КГУ системы от уравнений газовой дина-
мики является наличие вторых производных по времени от газодинамиче-
ских параметров и появление диссипативного члена в уравнении неразрыв-
ности. Их появление связано с тем, что в дискретной кинетической модели
минимальным масштабом времени является время между столкновениями
. Еще раз опишем эту модель [1,2].
j
Предположим, что на момент времени
tt
одночастичная функция
распределения молекул имеет локально-максвелловский вид:
2
(t,
x
)
u
(t,x)
j
i
i
f
(t x,)
f
l
(6)
0
3/2
2
RT
2
RT t,x)
Здесь дополнительно использовались обозначения: R газовая постоянная,
вектор скорости молекул.
24
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
j
1
j
В течение времени
t
t
предположим, что молекулы газа совер-
j
1
шают бесстолкновительный разлет. Затем в момент времени
t
t
проис-
ходит мгновенный процесс столкновения молекул и функция распределе-
ния вновь становится локально-максвелловской. После этого процесс по-
вторяется. Вновь обратим внимание на то, что в наших рассуждениях мас-
штабы времени меньше не рассматриваются.
Связь между значением функции распределения до максвеллизации на
j1
момент времени
t
и значением локально-максвелловской функции на
момент времениtj выражается соотношением1
j1
j
f
(t
,x,)
f
t
, x
)
(7)
0(
Разложим правую часть (7) в ряд Тейлора с точностью до членов третьего
порядка малости по величине
f
f
j1
j
0
0
f
(t
,x,)
f
(t x,)
(8)
0
i
i k
x
x
2
x
i
k
i
Умножим левую и правую часть (8) на сумматорный инвариант m массу
молекулы и проинтегрируем аналогично получению уравнения неразрывно-
сти из уравнения Больцмана по скоростям молекул. Учитывая, что
f ()d f
()d,
(9)
0
2
где (x) сумматорные инварианты
(x) m,m,(m
/2), получим
j1
j
divu
(u
u
p
)
(10)
i k
ik
x
2
x
k
i
Разлагая левую часть (10) в ряд Тейлора, окончательно придем к урав-
нению:
2
divu
(u
u
p)
(11)
2
i k
ik
t
2
t
x
2
x
k
i
Это уравнение отличается от классического уравнения неразрывности
/ t div u 0
(12)
1 Здесь для простоты предположим, что поле внешних сил, влияющих на изменение ,
отсутствует.
Законы сохранения и компактная квазигазодинамическая система
25
2
на совокупность членов
(u
u
p),
(13)
2
i k
ik
2
t
x
2
x
k
i
2
которые в сумме составляют величину порядка
O(Kn
) [1,2,9].
Таким образом, рассматриваемая дискретная кинетическая модель, в
которой минимальным масштабом времени является , привела к уравне-
нию неразрывности (11), отличающемуся от классического уравнения (12)
2
на сумму членов по порядку величины
O(Kn
). Такой же порядок различия
между КГУ и уравнениями Навье-Стокса наблюдается для уравнений, опи-
сывающих изменение импульса и полной энергии E и энтропии [8, 9]. На-
помним, что сами уравнения Навье-Стокса получены из кинетического
уравнения Больцмана с помощью процедуры Чепмена-Энскога с той же
2
точностью
O(Kn
) [3-5].
Рассмотрим теперь способ получения уравнения (2.6), оставаясь в рам-
ках традиционных методов, используемых в механике сплошной среды.
При этом из кинетических моделей используем только ограничение снизу
временем интервала t , на котором происходит изменение газодинамиче-
ских параметров.2
3. Традиционный способ получения уравнения неразрывности КГУ
1
j
Рассмотрим изменения массы в конечном объеме Ω за время
Δttj
t
j1
t
j1
j
j1
j
M
M
dx
dx
∮
uds,
(14)
Ω
Ω
t
j S
где S поверхность, ограничивающая объем Ω, M масса объема Ω.
В отличие от общепринятого способа получения уравнения неразрыв-
ности рассмотрим конечный временной интервал, на котором происходит
1
j
изменение массы объема Ω
Δttj
t
.
j
j
Представим импульс u на отрезке
t[t
,t
] в виде
j
u
j
2
u t)
u
O(t
)
(15)
t
Подставим (15) в правую часть (14), проинтегрируем по времени на отрезке
2 Выбор в качестве минимального масштаба t не случаен, так как установление газо-
динамических параметров происходит за время, не меньшее характерного времени меж-
ду столкновениями молекул .
26
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
j
j1
[t
,t
]
и воспользуемся теоремой Гаусса-Остроградского. В итоге полу-
чим
j
u
j1
j
j
2
divu
O(t
)
(16)
2
t
Левую часть выражения (16) представим в виде
j
2
2
j
j1
j
2
O(
),
(17)
2
t
2
t
а для нахождения (u / t) воспользуемся выражением
u
u
u
p
i
i k
ik
,
(18)
t
x
k
которое выполняется точно для уравнения, описывающего изменение им-
пульса в идеальном газе. В неидеальном газе это выражение выполняется с
точностью до членов, описывающих вязкое напряжение, то есть O() .
Комбинируя (16)-(18), окончательно получим
2
div(u)
(u
u
p),
(19)
i k
ik
2
t
2
t
x
i
2
x
k
которое в точности совпадает с уравнением (11), полученным на основе
дискретной кинетической модели.
Таким образом, введение ограничения снизу на допустимый интервал
по времени приводит как в рамках дискретной кинетической модели, так и
макроскопического описания, к появлению дополнительных членов в урав-
нении неразрывности. В сумме эти дополнительные члены составляют ве-
2
личину порядка
O(Kn
), то есть значительно меньше диссипативных вяз-
ких и теплопроводных членов системы Навье-Стокса, порядок величины
которых O(Kn) . Процедура сглаживания по времени ранее проводилась в
работе [14], без связи времени с характерным временем между столкно-
вениями молекул. Кроме того, в полученном в [14] аналоге уравнения (19)
2
2
отсутствует член со второй производной по времени
(/2)(
/t
).
Представим уравнение (19) в виде
2
div
(u w)
0,
(20)
2
t
2
t
где
w
(u
u
p)
(21)
i k
ik
2
x
k
Законы сохранения и компактная квазигазодинамическая система
27
дополнительный импульс, возникающий при учете ограничения снизу на
минимальный масштаб изменения t .
Наличие этого импульса, а также вторых производных по времени,
связанных с ограничением снизу на t , является главным отличием КГУ от
системы уравнений Навье-Стокса.
Характерной особенностью этого импульса является то, что он может
рассматриваться как составная часть общего импульса u w, который
влияет на изменение плотности (20).
Учтем наличие скорости w, связанной с этим дополнительным им-
пульсом при построении других уравнений газовой динамики. Так при вы-
воде баланса сохранения импульса будем учитывать газокинетическое дав-
ление, тензор вязких напряженийPNS и обобщенный импульс u w.
Изменение импульса в течение времени так же, как и для плотности,
выпишем в виде:
j
2
j
j1
j
u
u
2
j1
j
(u)
(u)
O(
)t
t
.
2
t
2
t
В итоге уравнение для переноса импульса запишется в следующем виде:
2
u
u
div
(u w)u
p
divP
(22)
NS
2
t
2
t
Аналогично при выводе баланса для полной энергии E примем во
внимание перенос энергии за счет скорости u w , вектора теплового пото-
ка q (5), работы вязких силPNSu :
E
E
div
(E p)(u w)
divq
div(P
u)
(23)
2
NS
t
2
t
Объединяя уравнения (19), (22) и (23), придем к компактной КГУ системе
(1)-( 4).
Аналогичное рассмотрение для задач магнитной газовой динамики
приведет к соответствующим компактным квазигазодинамическим уравне-
ниям магнитной газовой динамики:
2
1
B
W
p
u
u B
B
,
(24)
k
ik
i k
i k
x
8
i
28
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
2
div
u w
0,
(25)
2
t
2
t
2
2
u
u
B
div
(u w) B
B
p
divP
,
(26)
i k
NS
2
t
2
t
8
2
2
E
E
B
div
E p
(u w)
div
q
divP
u
,
(27)
NS
2
t
2
t
8
2
B
B
m
rot
(
u w
) B
rot
B
,
(28)
m
2
t
2
t
div B 0 .
(29)
Здесь дополнительно использовались обозначения: B вектор напряжен-
ности магнитного поля,m магнитная вязкость.
Уравнения (24)-(27) могут быть получены с помощью процедуры, ана-
логичной получению уравнений компактной КГУ системы (1)-(4). Уравне-
ния (28)-(29) получены на основе использования комплекснозначной функ-
ции [7, 15]
f
exp
u
i(B/
4
)
/ 2RT
(30)
OM
k
k
2
3/2
(2RT)
(здесь k 1,2,3; i мнимая единица) и последующего использования дис-
кретной кинетической модели, приведшей к балансному уравнению, анало-
гичному (8) [15]
2
f
f
f
OM m OM
OM
div(f
)
(31)
2
m
OM
m i k
t
2
t
x
x
k
i
Время m характерное время установления равновесия в совокупном ан-
самбле, состоящем из нейтральных и заряженных частиц, а также магнит-
ного поля B , можно определить с помощью магнитной вязкостиm
2
m
(32)
2
m p
(B
/(8))
определяется аналогично через соотношение вязкости и пол-
ного газокинетического и магнитного давления.
Законы сохранения и компактная квазигазодинамическая система
29
4. Вычислительные алгоритмы для компактной КГУ системы
За десятилетия существования и развития вычислительной гидро- и га-
зовой динамики разработано большое количество алгоритмов, обладающих
теми или иными свойствами. Посмотрим, насколько эти алгоритмы могут
быть адаптированы для решения компактной КГУ системы (1)-(4).
Рассмотрим вначале аппроксимацию пространственных производных,
входящих в систему (1)-(4). ВеличинаWk (1) с точностью до множителя
/(2) совпадает с пространственными производными, входящими в урав-
нение, описывающее изменение импульса в системе уравнений Эйлера. По-
сле нахождения W определяем скорость u w v . В дальнейшем для ап-
проксимации пространственных производных, входящих в систему (2)-( 4),
можно использовать алгоритмы, применяемые при решении уравнений На-
вье-Стокса.
Таким образом, для аппроксимации по пространственным переменным
в компактной квазигазодинамической системе можно использовать весь ар-
сенал методов, ранее накопленных для моделирования уравнений Навье-
Стокса.
Уравнения (2)-(4) могут быть записаны в виде
2
Q
Q
divS
(33)
2
Q
t
2
t
Здесь Q вектор газодинамических переменных, Q ,u, E ;SQ поток,
зависящий от Q .
Наиболее простой аппроксимацией является трехслойная явная схема:
j1
j1
*
j1
j
j1
Q
Q
Q
2Q
Q
j
divS
(34)
2
Q
2t
2
t
Для получения вычислительного эффекта от использования второй
*
производной по времени вместо выберем большую величину
. Наибо-
*
лее оптимальным является
, по порядку величины совпадающее с отно-
шением характерного шага сетки h к характерной скорости :
*
~h/.
(35)
*
При таком значении
выполняется необходимое условие
*
2
Q
Q
,
(36)
2
2
t
t
30
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
а устойчивость трехслойной схемы обеспечивается при следующем ограни-
чении на шаг по времени t [17]:
3/2
t h
(37)3
Целью данной работы являлся анализ и выявление возможностей ком-
пактной КГУ системы, а не моделирование конкретных газодинамических
течений. Поэтому для иллюстрации возможностей системы (1)-(4) восполь-
зуемся результатами расчетов обтекания плоской пластины однородным
5
потоком вязкого газа при числе Маха M 0.2 и числе Рейнольдса
Re 10
,
взятым из [13].
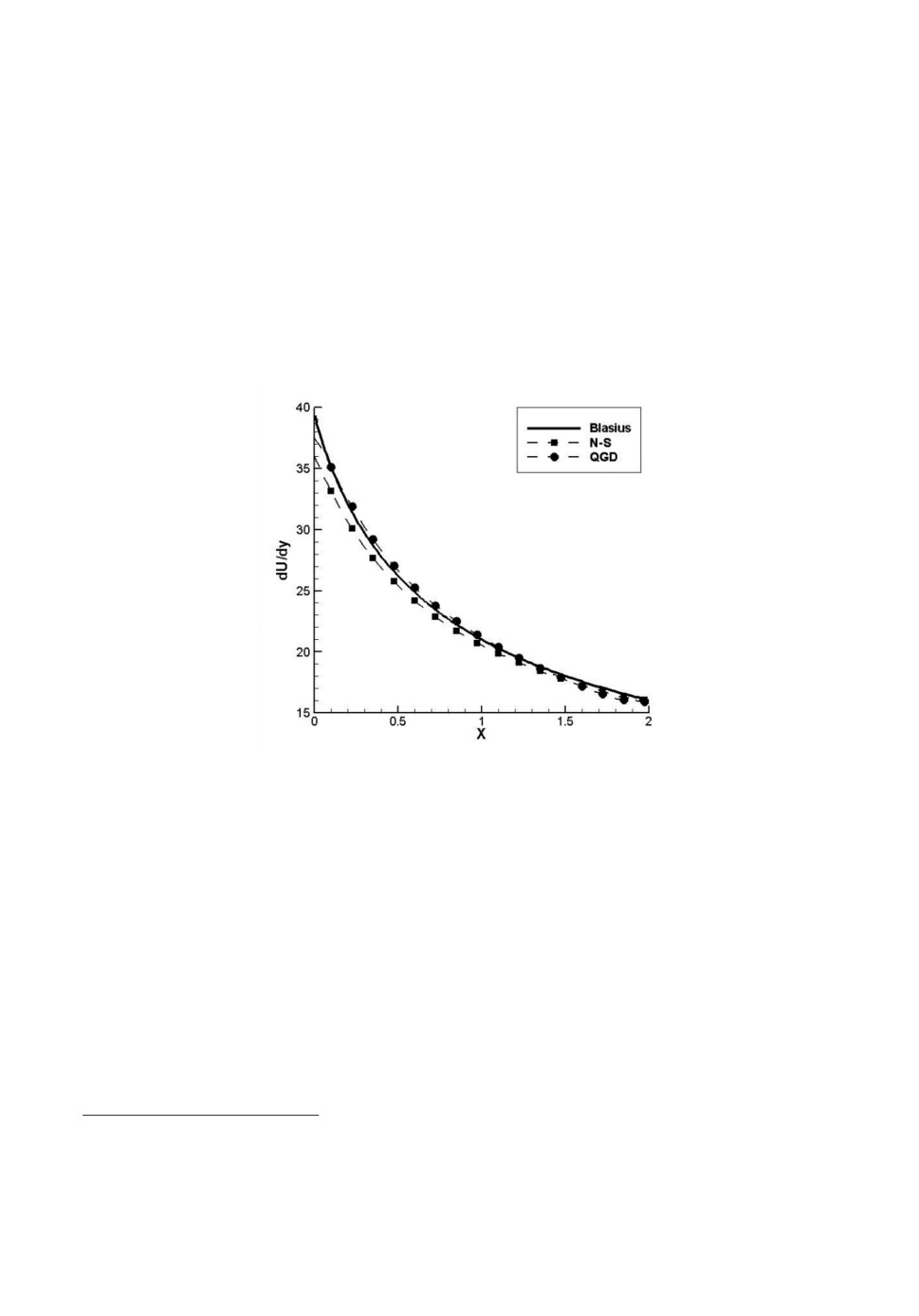
Рис.1.
На рис.1 изображено напряжение трения u/y вдоль плоской пласти-
ны. Сравнивались результаты, полученные с помощью решения Блазиуса
[17], решения, полученного на основе использования уравнений Навье-
Стокса, и компактной КГУ системы.
Видно, что все три решения при удалении от кромки пластины близки
друг к другу. Тем не менее вблизи кромки решение на основе уравнений
Навье-Стокса сильнее отличается от решения Блазиуса, чем решение на ос-
нове КГУ. Это связано с тем, что вблизи кромки эффективное число Кнуд-
сена увеличивается. В отличие от уравнений Навье-Стокса КГУ система
дает возможность правильного описания газодинамических параметров при
значительно больших числах Кнудсена [1, 18].
3 Преимущества условия (37) по сравнению с условием устойчивости явных схем для
2
параболических уравнений
(t h
) особенно наглядно проявляются при подробных
пространственных аппроксимациях (малые h), которые реализуются на высокопроизво-
дительных вычислительных системах.
Законы сохранения и компактная квазигазодинамическая система
31
Заключение
На основе законов сохранения при учете наличия минимального мас-
штаба по времени описан способ получения компактной квазигазодинами-
ческой системы. Таким образом, реализуется связь между кинетическим и
макроскопическим способом вывода как квазигазодинамической системы,
так и ее компактного варианта. Очевидным достоинством рассматриваемо-
го компактного варианта КГУ является возможность адаптации алгоритмов,
используемых для ее решения, на архитектуру вычислительных систем
сверхвысокой производительности. Кроме того, возможен простой перенос
ранее разработанных алгоритмов для моделирования течений вязкого газа к
решению компактной КГУ системы.
СПИСОК ЛИТЕРАТУРЫ
1.
Четверушкин Б.Н. Кинетически-согласованные схемы в газовой динамике. М.:
изд. МГУ, 1999, 226 с.;
Chetverushkin B.N. Kineticheski-soglasovannye skhemy v gazovoi dinamike. M.: izd.
MGU, 1999, 226 s.
2.
Chetverushkin B.N. Kinetic Schemes and Quasi-Gas Dynamic System of Equations /
CIMNE. Barcelona: 2008, 298 p.
3.
Chapman S. and Cawling T.G. The Mathematical Theory of Non-uniform gases. Cam-
bridge: Univ. Press. Cambridge, 1990, 423 p.
4.
Liboff R.L. Introduction to the Theory of Kinetic Equations. Wiley, New York: 1969, 397 p.
5.
Веденяпин В.В. Кинетические уравнения Больцмана и Власова. М.: Физматлит,
2001, 112 с.
Vedeniapin V.V. Kineticheskie uravneniia Boltsmana i Vlasova. M.: Fizmatlit, 2001, 112 s.
6.
Злотник А.А., Четверушкин Б.Н. О параболичности квазигазодинамической системы
уравнений, ее гиперболической модификации и устойчивости малых возмущений
для них // ЖВМ и МФ, 2008, т.8, №3, с.445-472;
англ. пер.: Zlotnik A.A., Chetverushkin B.N. Parabolicity of the quasi-gasdynamic system
of equations, its hyperbolic second-order modification, and the stability of small perturba-
tions for them // Comput. Math. Math. Phys., 2008, v.48, №3, p.420-446.
7.
Четверушкин Б.Н. Гиперболическая квазигазодинамическая система // Матем. моде-
лирование, 2018, т.30, № 2, с.81-98;
англ. пер.: Chetverushkin B.N. Hyperbolic Quasi-Gasdynamic System // Mathematical
Models and Computer Simulations, 2018, v.10, №5, p.588-600.
8.
Злотник А.А., Четверушкин Б.Н. О балансе энтропии для одномерной квазигазоди-
намической системы уравнений // Докл. Акад. наук, 2017, т.474, №1, с.22-27.
англ. пер.: B. Chetverushkin B.N., Zlotnik A.A. Entropy balance for the one-dimensional hy-
perbolic quasi-gasdynamic system of equations // Dokl. Math., 2017, v.95, №3, p.276-281.
9.
Zlotnik A.A., Chetverushkin B.N. On a hyperbolic perturbation of a parabolic initial-
boundary valey problem // Applied Mathem. Letters, 2018, v.83, p.116-122.
32
Б.Н. Четверушкин, А.Е. Луцкий, В.П. Осипов
10. Четверушкин Б.Н., Ачензо Н., Савельев В.И. Об одном алгоритме решения парабо-
лических и эллиптических уравнений // ЖВМ и МФ, 2015, т.55, № 8, с.1320-1328.
англ. пер.: Chetverushkin B.N., D’Ascenzo N., Saveliev V. On an algorithm for solving
parabolic and elliptic equations // Comput. Math. Math. Phys., 2015, 55(8), p.1290-1297.
11. Четверушкин Б.Н., Якобовский М.В. Вычислительные алгоритмы и отказоустойчи-
вость гиперэкзафлопсных вычислительных систем // ДАН, 2017, т.472, № 1, с.13-17.
англ. пер.: B.N. Chetverushkin and M.V. Yakobovskiy. Numerical Algorithms and Fault
Tolerance of Hyperexascale Computer Systems // Doklady Math., 2017, v.95, №1, p.7-11.
12. Четверушкин Б.Н., Савельев А.В., Савельев В.И. Квазигазодинамическая модель для
описания магнитогазодинамических явлений // ЖВМиМФ, 2018, т.58, №8, с.1384-1394;
англ. пер.: Chetverushkin B.N., Savel’ev A.V., Savel’ev V.I. A quasi-gasdynamic model for
the description of magnetogasdynamic phenomena // Comput. Math. Math. Phys., 2018,
58(8), p.1384-1394.
13. Луцкий А.Е., Четверушкин Б.Н. Компактная квазигазодинамическая система для мо-
делирования вязкого, сжимаемого газа // Дифф. уравнения, 2019, т.55, № 4, с.588-592;
англ. пер.: Lutskii A.E., Chetverushkin B.N. Compact Version of the Quasi-Gasdynamic Sys-
tem for Modeling a Viscous Compressible Gas // Diff. Equations, 2019, 55(4), p.575-580.
14. Елизарова Т.Г. Осреднение по времени как приближенный способ построения квази-
газодинамических и квазигидродинамических уравнений // ЖВМ и МФ, 2011, т.51,
№ 11, с.2096-2105;
англ. пер.: Elizarova T.G. Time averaging as an approximate technique for constructing
quasi-gasdynamic and quasi-hydrodynamic equations // Comp. Math. and Math. Physics,
2011, v.51, №11, p.1973-1982.
15. Четверушкин Б.Н., Асчензо Н., Савельев В.И. Кинетически согласованные уравнения
магнитной газовой динамики и их использование в высокопроизводительных вычис-
лениях // ДАН, 2014, т.457, № 5, с.526-529;
англ. пер.: Chetverushkin B.N., D’Ascenzo N., Saveliev V. Kinetically consistent mag-
netogasdynamics equations and their use in supercomputer computations // Doklady
Mathematics, 2014, 90(1), p.495-498.
16. Четверушкин Б.Н., Гулин А.В. Явные схемы и моделирование на вычислительных
системах сверхвысокой производительности // ДАН, 2012, т.446, № 5, с.501-503;
англ. пер.: A.V. Gulin, B.N. Chetverushkin. Explicit schemes and numerical simulation us-
ing ultrahigh-performance computer systems // Dokl. Math., 2012, v.86, №2, p.681-683.
17. Шлихтинг Г. Теория пограничного слоя. М.: 1974, 712 с.
Schlichting H. Boundary-Layer Theory. 7th Edition. - McGraw-Hill, Inc., New York,
USA, 1979, 419 p. - ISBN: 0070553343
18. Лукшин А.В., Ярчук Л.В. О методе декомпозиции областей для уравнения Больцмана.
// Дифф. уравнения, 1998, т.34, № 7, с.958-964,
Lukshin A.V., Iarchuk L.V. O metode dekompozitsii dlia uravneniia Boltsmana // Diff.
uravneniia, 1998, t.34, № 7, s.958-964.
Поступила в редакцию 20.05.2019
После доработки 20.05.2019
Принята к публикации 01.07.2019