МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 3, стр. 83-96
РАЗНОСТНАЯ СХЕМА КАБАРЕ
С УЛУЧШЕННЫМИ ДИСПЕРСИОННЫМИ СВОЙСТВАМИ
©
2019 г.
А.И. Сухинов, А.Е. Чистяков
Донской государственный технический университет, г. Ростов-на-Дону
sukhinov@gmail.com, cheese_05@mail.ru
Работа выполнена при поддержке РНФ (проект № 17-11-01286).
DOI: 10.1134/S0234087919030067
Предложена разностная схема для задачи переноса, построенная как линейная ком-
бинация схемы «кабаре» и схемы с центральными разностями. Проведено исследо-
вание устойчивости и дисперсионных свойств схемы. Показано, что построенная
схема обладает лучшими дисперсионными свойствами для высокочастотных гар-
моник при малых числах Куранта по сравнению с известной схемой «кабаре» для
уравнения переноса. Проведено сравнение погрешностей данной схемы и двухпа-
раметрической разностной схемы третьего порядка точности на основе численных
экспериментов на использовавшихся ранее наборах тестовых задач. Показано, что
в норме сеточного пространства L1 разработанная схема имеет меньшие погрешно-
сти, а также использует более компактный шаблон (при расчете i-го узла исполь-
зуются значения узлов i1, i, i+1), и переход на следующий временной слой осу-
ществляется за меньшее число арифметических операций.
Ключевые слова: задача переноса, схема «кабаре», дисперсные свойства схем, точ-
ность решения.
CABARET DIFFERENCE SCHEME WITH IMPROVED DISPERSION PROPERTIES
A.I. Sukhinov, A.E. Chistyakov
Don State Technical University, Rostov-on-Don
Difference scheme for the advection transport equation has been constructed as the linear
combination of "cabaret" scheme and the scheme with the central differences. The re-
search of stability and dispersion properties of the scheme is conducted. It is shown that
the constructed scheme has the best dispersion properties for high harmonicas in case of
small numbers of Courant in comparison with the known scheme of "cabaret" for advec-
tion transport equation. Comparison of errors of this scheme and two-parameter difference
scheme of the third order of accuracy on the basis of numerical experiments on sets of test
tasks used earlier is carried out. It has been showed, that developed scheme has smaller er-
rors in grid space L1 in comparison of mentioned above scheme. Additionally the devel-
oped scheme uses more compact set of nodes (when calculating i-go of knot values of the
hubs i1, i, i+1 are used), and requires smaller number of arithmetic operations.
Key words: advection transport problem, “cabaret” scheme, dispersion of schemes, accuracy.
84
А.И. Сухинов, А.Е. Чистяков
1. Введение
Рассматривается численное решение задачи переноса на основе усо-
вершенствованной схемы «кабаре» [1], разностный оператор которой пред-
ставляет собой линейную комбинацию разностных операторов схемы с цен-
тральными разностями и схемы «кабаре», рассмотренной В.А. Гущиным.
Несмотря на неустойчивость схемы с центральными разностями, использо-
вание линейной комбинации двух разностных схем позволяет получить ус-
тойчивую схему, обладающую лучшей точностью по сравнению со схемой
«кабаре». Другой подход для построения схем для уравнения переноса свя-
зан с использованием двухпараметрического семейства разностных схем [2,
3]. Данный класс схем характеризуется высоким порядком аппроксимации
(лучшей точностью), минимальной схемной диссипацией, дисперсией и мо-
нотонностью. Несмотря на различие в используемых подходах при по-
строении разностных схем, в частности, сеточных шаблонов и свойств двух
описанных выше схем, результаты расчетов качественно совпадают в об-
ластях с большими градиентами исследуемых функций. Целью данной ра-
боты является количественно сопоставить схему, полученную как линей-
ную комбинацию схемы «кабаре» и схемы с центральными разностями, с
двухпараметрической разностной схемой третьего порядка точности.
2. Построение разностной схемы
Рассмотрим уравнение переноса
q
q
u
0,
(1)
t
x
0
где t[0,T], x[0,L],
q(0,x) q
(x), q(t,0) q(t,L) 0, u const.
Введем равномерную сетку
,
h
где
{x
x
ih,
i0,1,...,N,
Nh L},
{t
j 0,1,...},
t
t
const
h
i
i
j
n1
n
Для численного решения поставленной задачи можно использовать
следующие конечно-разностные схемы:
- схема, ориентированная «против потока» или, в случае u 0 «ле-
вый уголок» [4]:
n1
n
n
n
q
q
q
q
i
i
i
i1
u
0,
u0;
(2)
h
n1
n
n
n
q
q
q
q
i
i
i1
i
u
0,
u0;
h
- центральная разностная схема:
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
85
n1
n
n
n
q
q
q
q
i
i
i1
i1
u
0;
(3)
2h
- схема «кабаре» [5]:
n1
n
n
n1
n
n
q
q
q
q
q
q
i
i
i1
i1
i
i1
u
0,
u0;
(4)
2
2
h
n1
n
n
n1
n
n
q
q
q
q
q
q
i
i
i1
i1
i1
i
u
0,
u0.
2
2
h
Для решения задачи конвекции можно использовать схему, получен-
ную в результате линейной комбинации центральной разностной схемы (3)
и схемы «кабаре» (4)
n1
n
n
n1
n
n
n
q
q
q
q
q
4q
5q
i
i
i1
i1
i1
i
i1
u
0,
u0;
(5)
2
4h
n1
n
n
n1
n
n
n
q
q
q
q
5q
4q
q
i
i
i1
i1
i1
i
i1
u
0,
u0.
2
4h
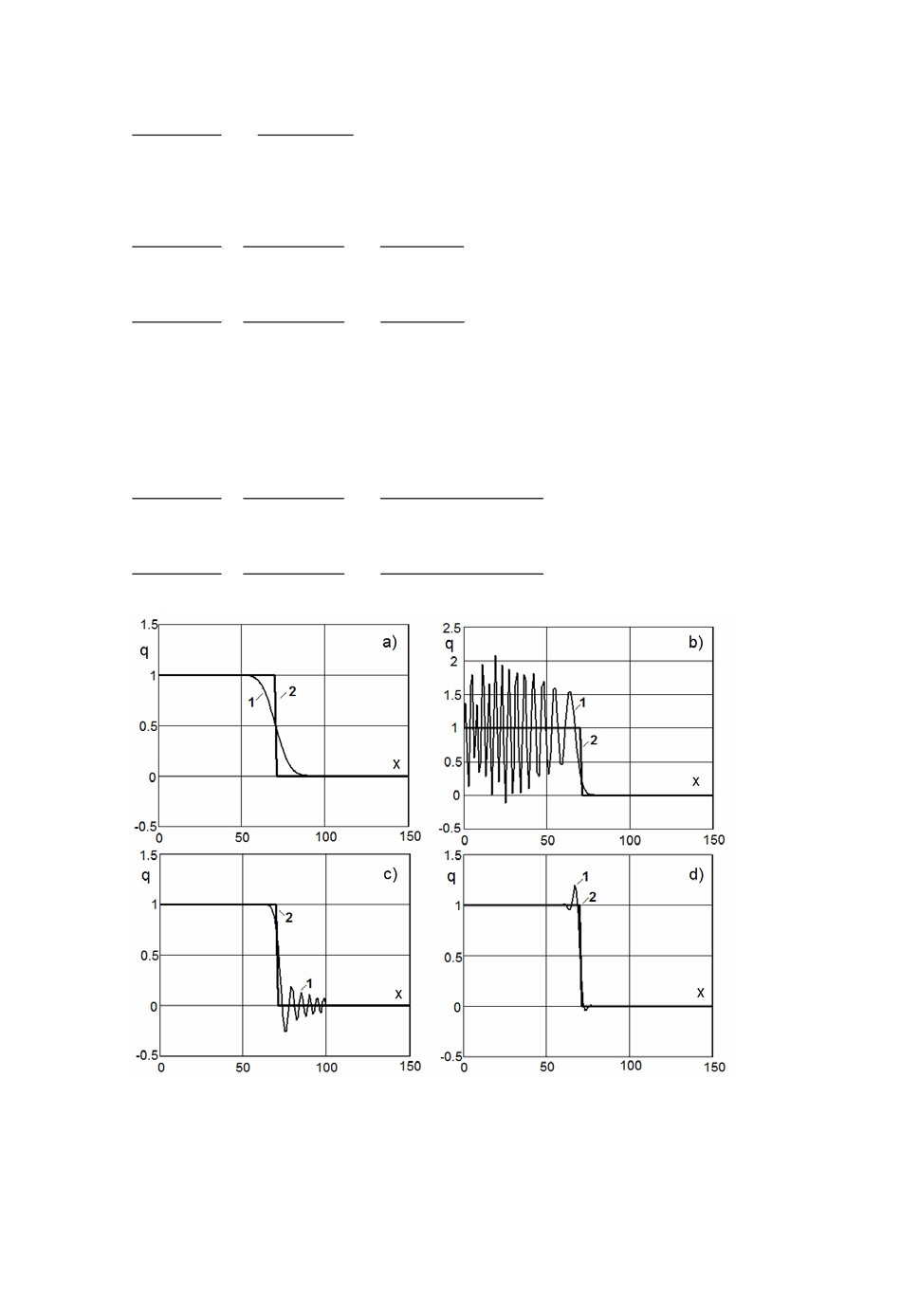
Рис.1. Решения модельной задачи на основе схем (2)(5): a) левая разностная схема;
b) центральная разностная схема; c) схема «кабаре»; d) предложенная разностная
схема.
Найдем численные решения на основе схем (2)(5) модельной задачи с
0
начальными условиями
q
(x)h(20 x), где h(x) - функция Хэвисайда. На
86
А.И. Сухинов, А.Е. Чистяков
рис.1 приведены решения модельной задачи (1 - численное решение, 2 -
точное).
Из рис.1 видно, что разностная схема типа «левый уголок» аппрокси-
мирует скачок недостаточно точно, центральная разностная схема неустой-
чива, решение, полученное на основе схемы «кабаре», имеет осцилляции
(энтропийные возмущения) [6]. Предложенная разностная схема дает наи-
более точное решение модельной задачи. Левая разностная схема имеет по-
рядок аппроксимации O( h) , центральная разностная схема аппроксими-
2
рует непрерывную модель с порядком
O( h
) [7,8], схема «кабаре» ап-
2
2
проксимирует уравнение переноса с погрешностью
O(
h
) .
3. Устойчивость и дисперсионные свойства схемы
Для исследования устойчивости схемы (5) применен метод гармоник.
, где j
1 , тогда уравнение (5) примет вид (случай u 0 ):
1
exp(
jk)exp(
jk)/
exp(
jk)
45exp(
jk)
u
0
2
4h
или
2
1
u
1
sink
3u
exp(
jk)
1cos
k
j
1
sink
0
2
h
2
2
h
2
Решение данного квадратного уравнения относительно запишется в виде
1
u
1
sink
3u
1cosk
j
1
1,2
4
h
4
4
h
2
1
u
1
sink
3u
exp(
jk)
1cosk
j
1
4
h
4
4
h
2
Обозначим c u / h - число Куранта, тогда
1/4c
(1 cosk) 1/ 4 j(sin k / 4)(3c 1)
1,2
1/4c
(1 cosk) 1/ 4 j(sin k / 4)(3c 1)
2
exp( jk) / 2 .
Будем считать, что при расчете
берется значение корня комплекс-
1
ного числа с неотрицательной вещественной частью (аргумент
принад-
1
лежит полуинтервалу [/2,/2) ). Рассмотрим случай c 0 . Данный слу-
n
n1
чай соответствует значению 0 или
q
q
; при этом значение функ-
i
i
ции равно 1.
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
87
2
(2
exp(
jk
)) / 4
(2
exp(
jk
)) / 4
exp(
jk
)/2
1,2
(2
exp(
jk
)) / 4
(2
exp(
jk
)) / 4.
Отсюда получаем:
1
,
exp( jk)/2, следовательно,
не яв-
1
2
2
ляется решением. Исследование поведения функции
(c,k) производилось
1
численно. Исследовались значения функции
(c,k)
[0,1] при k [0,] и
1
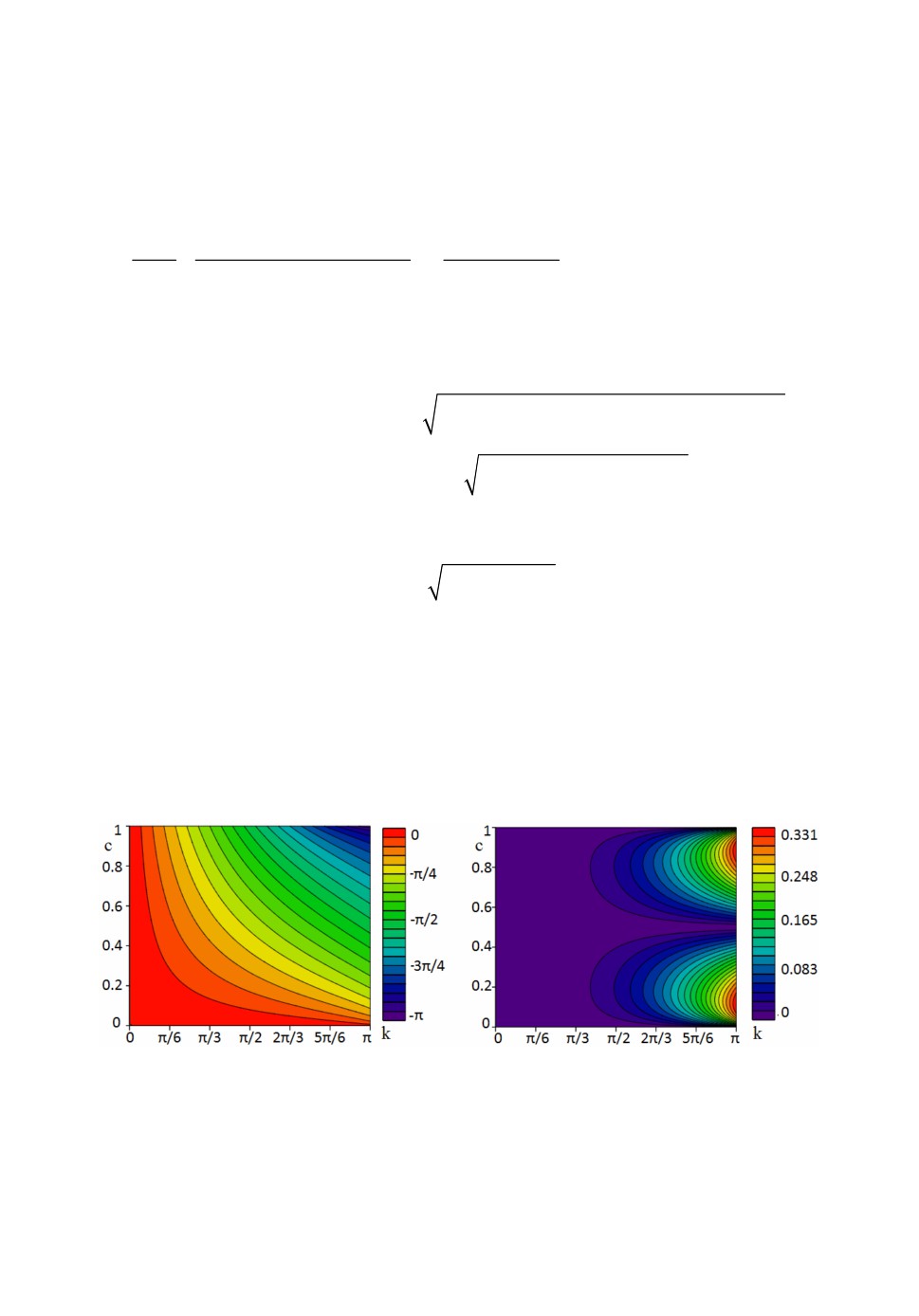
c[0,1]. На рис.2 приведены значения модуля и аргумента функции
(c,k)
1
в зависимости от значений параметров k и c.
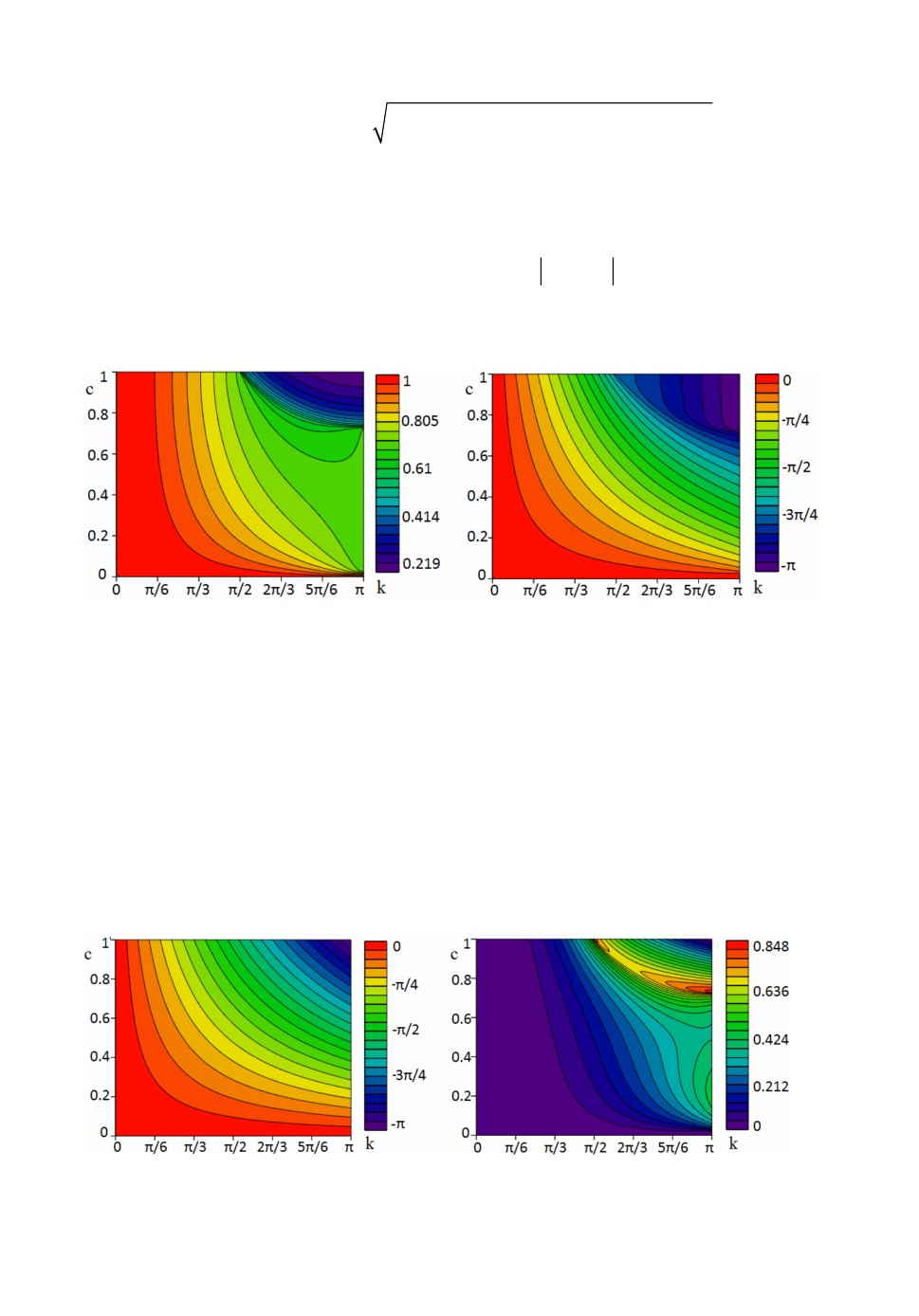
Рис.2. Значения модуля (слева) и аргумента (справа) функции
(c,k) .
1
Решение уравнения переноса с начальными условиями:
q x)exp(
j
x)
n
равно
q t,x)exp
j
(
x ut
). Здесь
n k
/ h угловая частота, n
n
n
номер гармоники, 2/L 2/(hN ) . Таким образом, при решении задачи
переноса с начальными условиями, заданными гармонической функцией,
переход между временными слоями соответствует умножению на функцию
c,k)exp(
u exp(
)
j
jkc
при k [0,]. Аргумент функции (c,k)
n
запишется в виде: Arg (c,k) kc .
Сопоставление аргументов функций
(c,k) и
(c,k) приведено на
1
рис.3.
Рис.3. Значения модуля аргумента функции (c,k) (слева) и
модуля разности аргументов
1
(c,k) и (c,k) (справа).
88
А.И. Сухинов, А.Е. Чистяков
На основе рис.2, 3 можно проанализировать ошибки в «фазовых скоро-
стях» [5] для предложенной схемы (5). Из приведенных на рисунках «изо-
бражений» фазовых поверхностей видно, что погрешность численных рас-
четов на основе схемы (5) возникает преимущественно на высоких частотах.
Исследуем зависимость погрешности расчетов при различных гармо-
никах в случай малых чисел Куранта (c 0). Параметр k с номером гар-
моники связан соотношением: k 2n / N . Рассмотрим разность функций
(c,k) и (c,k)
1
(c,k) (c,k) (2 exp( jk)) / 4 c
1cosk j3sink 4
exp( jk)
1
(2 exp( jk)) / 4 c
1cosk j3sink 4
2
exp( jk) / 2
(2 exp( jk)) / 4 c1cosk j3sink
4
2exp(
jk)
3sink
(2exp(
jk)) / 4
18
c
1
cosk j
exp(
jk)
2
(2
exp(
jk))
4
4c
3sin
k
4exp(
jk) 4
jsin k
jck
1
cosk j
jck
c
2exp(
jk)
4
2exp(
jk)
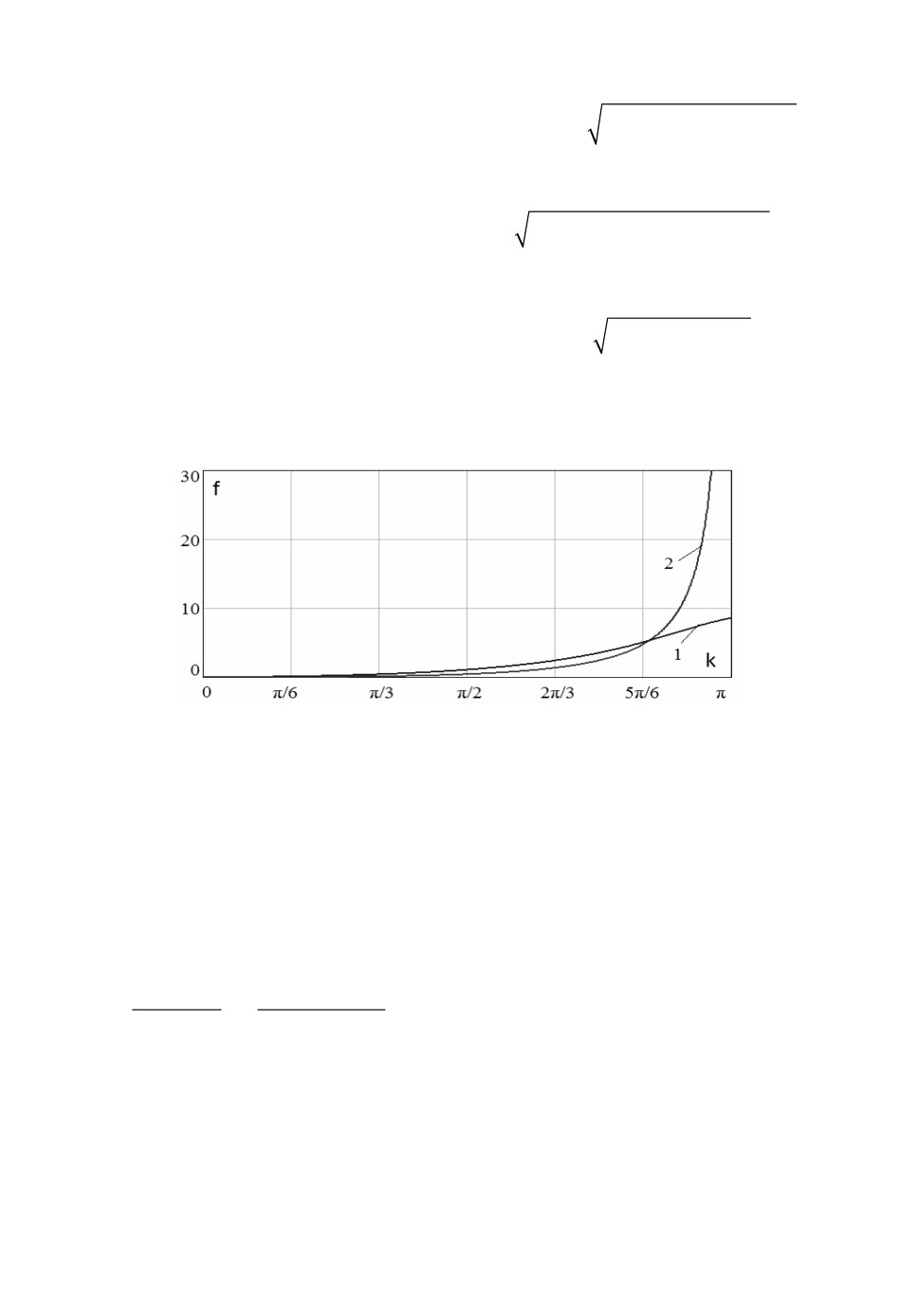
Измельчение сетки приводит к линейному росту количества слоев по
времени. Из полученного выражения следует, что при малых числах Куран-
та уменьшение шага по времени не приводит к повышению точности. По-
грешность решения модельной задачи для уравнения переноса на основе
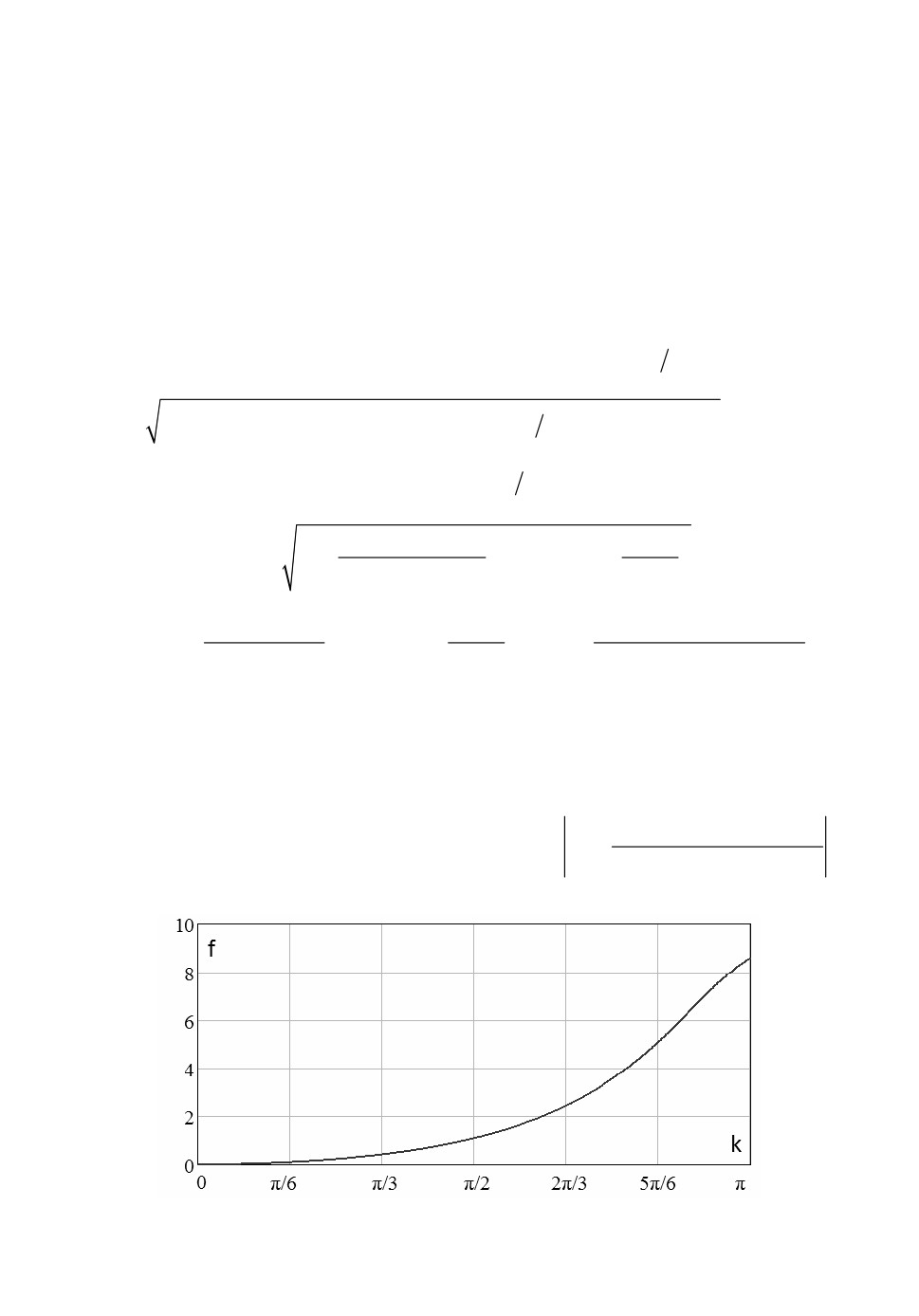
4 exp(
jk)
4
jsin k
схемы (5) пропорциональна функции:
f k)
jk
,
2exp(
jk
)
график которой приведен на рис.4.
Рис.4. График функции f (k) .
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
89
4. Дисперсионные свойства схемы «кабаре»
Для исследования устойчивости схемы «кабаре» на основе метода гар-
n
n
моник воспользуемся подстановкой
q
exp(
jki), тогда уравнение (4)
i
примет вид (случай u 0)
1
exp(
jk)exp(
jk)/
1exp(
jk)
u
0
2
2
h
2
или
(12c)(1exp( jk))exp( jk) 0, c u/h. Решение данного
квадратного уравнения относительно запишется в виде
(1/ 2 c)(1 exp( jk))
(1/ 2 c)(1 exp( jk))
2
exp( jk)
1,2
exp( jk / 2) j
12c
sin(k / 2)
1
(12c)sin(k / 2)
2
Рассмотрим случай c 0 .
exp(
jk
/ 2)jsin(k/ 2)
1sin2(k/2)
1,2
exp(
jk
/ 2)( jsin(k/2) cos(k/2)).
В результате получим:
1
,
exp( jk), следовательно,
не яв-
1
2
2
ляется решением. На рис.5 приведено «изображение» дисперсионной по-
верхность первого корня характеристического уравнения для схемы «каба-
ре», а также ее отклонение от точных значений (точное значение дисперси-
онной поверхности равно Arg((c,k)) kc ).
Рис.5. Дисперсионная поверхность характеристического уравнения схемы «кабаре»
(слева), отклонение дисперсионной поверхности корня характеристического
уравнения схемы «кабаре» от точных значений (справа).
Исследуем зависимость погрешности расчетов для различных гармо-
ник в случае малых чисел Куранта (c 0). Рассмотрим разность функций
(c,k) и (c,k)
1
90
А.И. Сухинов, А.Е. Чистяков
2
c k)(c,k)exp(
jk
/ 2)
j
(12c)sin(k/2)
1
(12c)sin(k/2)
1(
exp(
jck
)
2
2
exp(
jk
/ 2)
j
sin(k/2)
2
jc
sin(k/2)
1
(1
4c
4c
)sin
(k/2)
exp(
jck
)
2
exp(
jk
/ 2)
j
sin(k/2)
2
jc
sin(k/2) cos(k/2)
1
4c
tg
(k/2)
exp(
jck
)
1exp( jck) 2exp( jk / 2)csin(k/2)tg(k/2) j jc(k 2tg(k/2)).
Рис.6. Погрешности решения задачи переноса в случае малых чисел Куранта:
1 - на основе схемы (5); 2 - схема «кабаре».
Погрешность расчетов задачи переноса на основе схемы (4) пропорцио-
нальна функции: f (k) 2 tg(k/2) k . Графики оценки погрешностей реше-
ния задачи переноса в случае малых чисел Куранта на основе схемы (5) и
схемы «кабаре» приведены на рис.6.
5. Схема третьего порядка точности для уравнения переноса
Рассмотрим двухпараметрическое семейство разностных схем
n1
n
n
n
q
q
i
i
i
1/2
i
1/2
u
0,
(6)
h
где
n
n
n
q
q
q
u
0,
n
i1
i
i1
1
,
(7)
i
1/2
n
n
n
u
0.
q
q
q
i2
i
1
i
n
1
Воспользуемся разложением функций
q
иqnik в ряд Тейлора в ок-
i
рестности точки (i, n):
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
91
2
3
4
n1
n
n
n
n
n
5
q
q
(q
)
(q
)
(q
)
(q
)
O(
),
(8)
i
i
t i
tt i
ttt i
tttt i
2
3!
4!
2
3
4
n
n
n
(kh)
n
(kh)
n
(kh)
n
5
q
q
kh(q
)
(q
)
(q
)
(q
)
O(h
)
(9)
ik
i
x i
xx i
xxx i
xxxx i
2
3!
4!
2
3
4
С учетом уравнения (1) имеем
q
uq
, q u
q
, q
u
q
,
q
u
q
t
x tt
xx ttt
xxx tttt
xxxx
Подставляя (7) в (6), с учетом (8), (9) получаем
2
u
2
2
2
q
uq
u
h(1/2)
u
/2
q
u
h
(16)
f
t
x
xx
xxx
6
3
4
3
u
h
u
h
4
4
(1/ 2
7)
f
O(
h
)
xxxx
12
24
2
3
ch
ch
2
или
q
uq
2()1
c
q
sign(u)(c
16)
f
t
x
xx
xxx
2
6
3
ch
3
4
4
(1142c
)
f
O(
h
)
xxxx
24
3
3
Для получения схемы третьего порядка точности
O(
h
) необходимо,
чтобы
2
2
1c 0, c
16 0.
Данные равенства выполняются при
2
(c
1)/6, (1 c)/2
2
или
(c
1)/6, (c 1)(c 2)/6 .
(10)
6. Сопоставление результатов расчета на основе предложенной схемы и
схемы повышенного порядка точности
Рассмотрим численные решения, полученные на основе предложенной
схемы (5) и схемы третьего порядка точности (6), на примере задачи пере-
0
носа с начальными условиями:
q
(x) h(20 x) , где h(x) - функция Хэви-
сайда. Входные параметры: скорость u=0.5 м/с, шаг по времени τ=0.02с,
шаг по пространству h=1 м, длина интервала по времени T равна 300 с. На
рис.7 приведены результаты расчета для модельной задачи (1 - схема «ле-
вый уголок», 2 - схема повышенного порядка точности, 3 - предложенная
разностная схема, 4 - точное решение).
92
А.И. Сухинов, А.Е. Чистяков
n
n
n
n
n
Значение погрешностей в норме L1 (
h,
q
q(x
,t
)
,
nT
)
i
i
i
i
i
для схемы левый уголок, третьего порядка точности и предложенной разно-
стной схемы составляет 9.673, 2.262, 1.723 соответственно.
Рис.7. Решения модельной задачи на основе предложенной схемы (5) и схемы третьего
порядка точности а) графики полученных значений функций; b) графики по-
грешностей.
Данный пример демонстрирует поведение решения при скачках функ-
ций. Далее рассмотрим поведение численного решения для функции, пред-
ставляющей собой «тонкий сигнал» и заданной начальными условиями:
0
q
(x)h(20 x)h(10 x). При решении подобного класса задач на точность
решения влияет сеточная вязкость [9], при наличии которой происходит
существенное падение амплитуды функции и информация об объектах с ма-
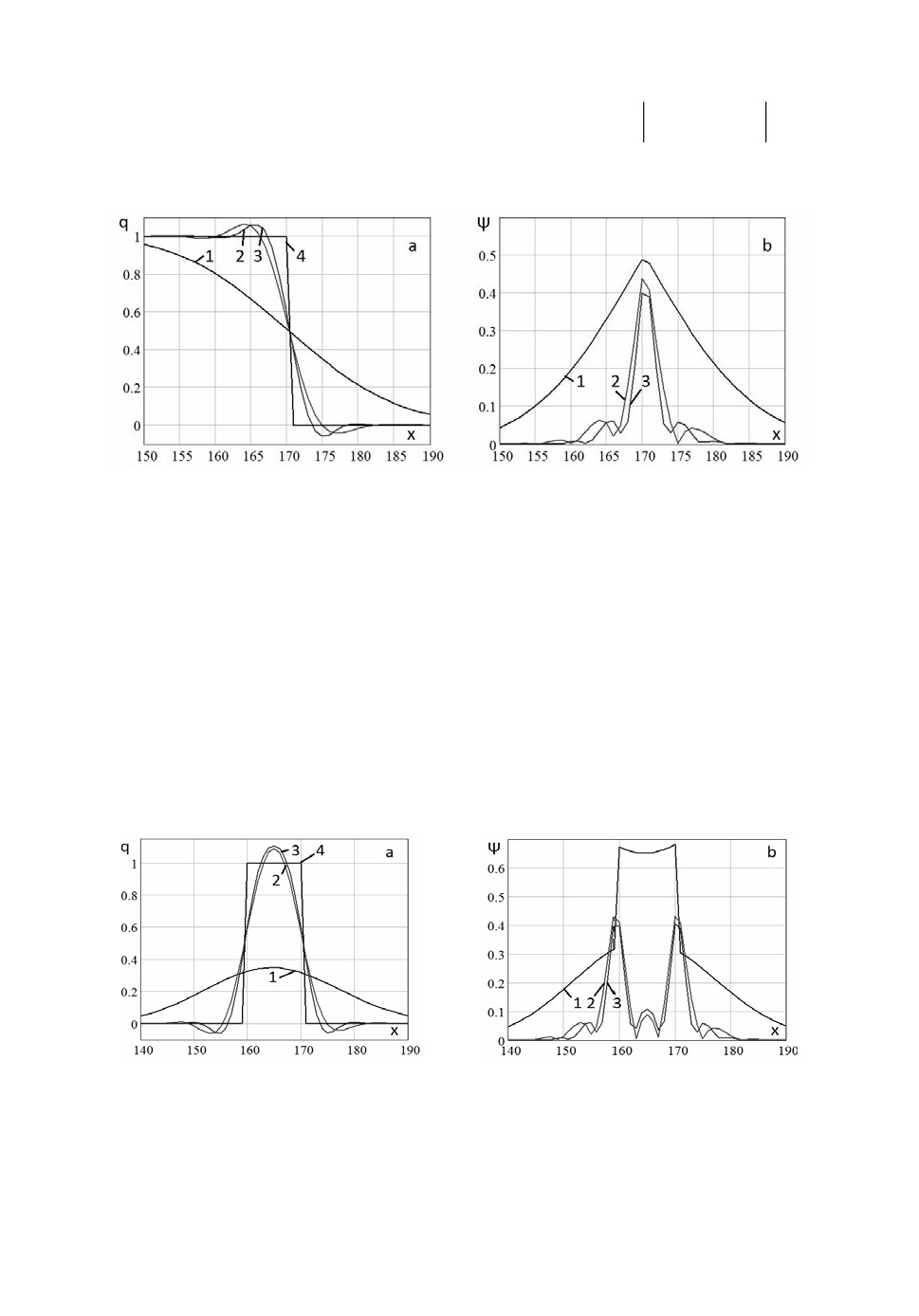
лыми размерами практически теряется [10]. На рис.8 приведены результаты
расчета для модельной задачи (1 - схема «левый уголок», 2 - схема третьего
порядка точности, 3 - предложенная разностная схема, 4 - точное решение).
Рис.8. Решения модельной задачи на основе предложенной схемы (5) и
схемы третьего порядка точности: а) графики полученных значе-
ний функций; b) графики погрешностей.
Значение погрешностей в норме L1 для схемы «левый уголок», третьего
порядка точности и предложенной разностной схемы составляет 14.531,
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
93
4.059, 3.434 соответственно. Из рис.8 видно, что решения, полученные на ос-
нове схемы (5) и третьего порядка точности, находятся близко друг к другу.
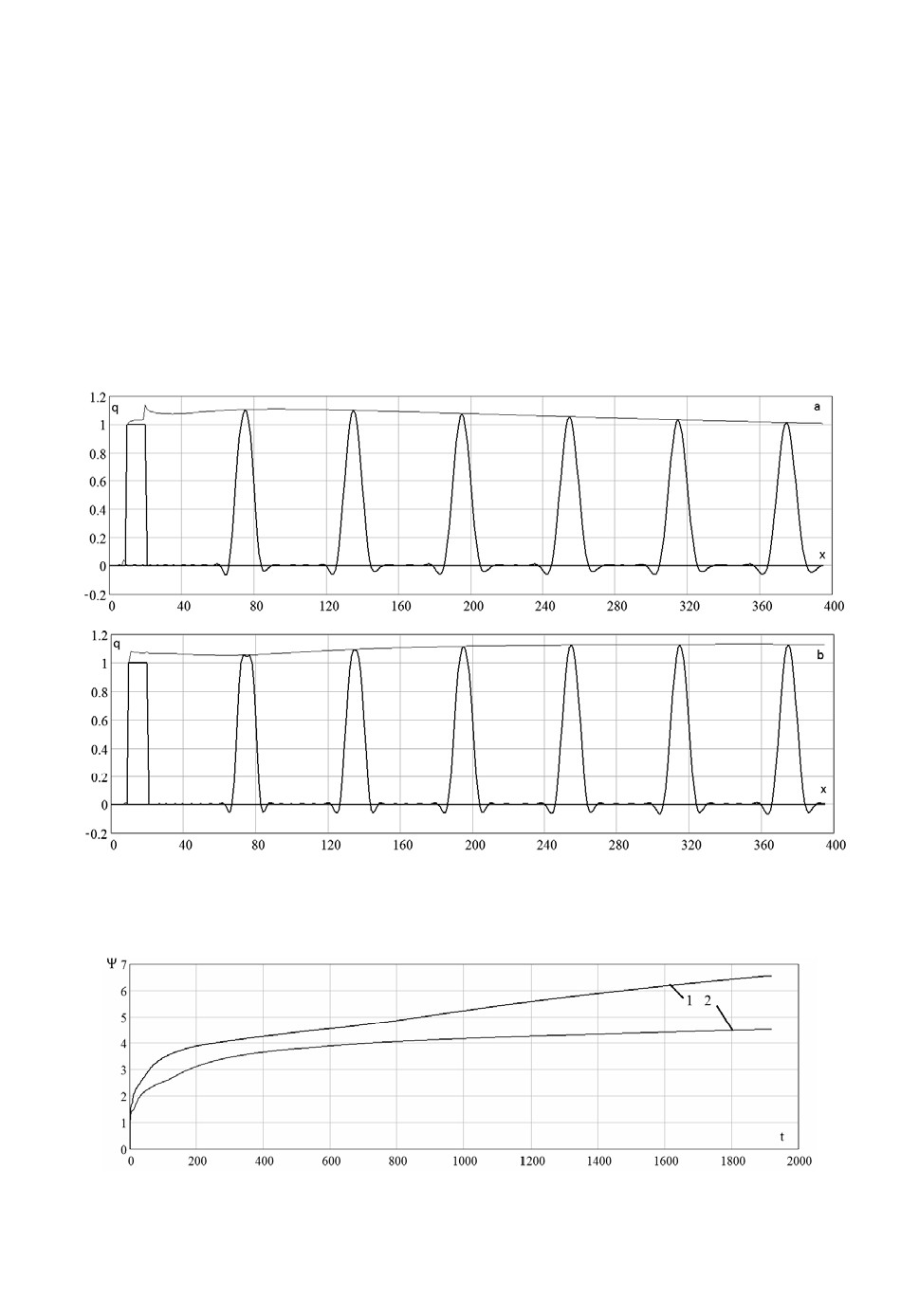
На рис.9 показано поведение решений для данных разностных схем при счете
на более длительные временные интервалы. Расчетный интервал составлял
800 с. Приведены решения в моменты времени 120, 240, 360, 480, 600 и 720с.
Из рис.9 видно, что при расчете на длительные времена амплитуда
функции решения, полученного на основе схемы третьего порядка со вре-
менем начинает убывать, а график функции решения, полученного на осно-
ве предложенной разностной схемы, начиная с некоторого момента, прак-
тически не изменяется со временем.
Рис.9. Решения модельной задачи на длительные временные интервалы (a - для
схемы третьего порядка точности, b - предложенной разностной схемы).
На рис.10 приведены графики функции погрешности в норме L1, зави-
сящей от длины расчетного интервала.
Рис.10. Функции погрешности в норме L1, зависящей от длины расчетного интервала (1 -
для схемы третьего порядка точности, 2 - для предложенной разностной схемы).
94
А.И. Сухинов, А.Е. Чистяков
7. Аппроксимация задачи конвекции-диффузии
Рассмотрим нестационарное уравнение конвекции-диффузии [11]
2
q
q
q
u
,
(11)
2
t
x
x
0
где t[0,T], x[0,L],
q(0,x) q
(x), q(t,0) q(t,L) 0, u const.
Для аппроксимации оператора конвекции будем использовать схему,
полученную в результате линейной комбинации центральной разностной
схемы (3) и схемы «кабаре» (4)
n1
n
n
n
n
n
n
1
q
q
q
q
q
2q
q
i
i
i1
i1
i1
i
i1
u
2
2
2h
h
n1
n
n
n1
n
n
n
n
n
q
q
q
q
q
q
q
2q
q
i
i
i1
i1
i
i1
i1
i
i1
u
0
2
2
2
h
h
или
n1
n
n
n1
n
n
n
n
n
n
q
q
q
q
q
4q
5q
q
2q
q
i
i
i1
i1
i1
i
i1
i1
i
i1
u
3
0
(12)
2
2
4h
2h
На рис.11 приведены решения модельной задачи с начальными усло-
0
виями
q
(x) h(20 x) , где h(x) - функция Хэвисайда.
Рис.11. Решения модельной задачи. 1 - точное решение задачи переноса, 2 - численное
решение на основе предложенной разностной схемы при различных значениях
чисел Пекле, 3 - численной решение задачи переноса на основе «против» потока.
Разностная схема «кабаре» с улучшенными дисперсионными свойствами
95
8. Заключение
Для решения задачи конвекции предложена разностная схема, полу-
ченная на основе линейной комбинации центральной разностной схемы и
схемы «кабаре». Данная схема при близости получаемых решениях и зна-
чений погрешностей имеет следующие преимущества по сравнению со
схемой третьего порядка точности: использует более компактный шаблон
(при расчете i-го узла используются значения узлов i1, i, i+1), переход на
следующий временной слой осуществляется за меньшее число арифметиче-
ских операций и обладает меньшей погрешностью в норме L1.
СПИСОК ЛИТЕРАТУРЫ
1.
А.И. Сухинов, Ю.В. Белова, А.Е. Чистяков. Решение задачи переноса веществ при
больших числах Пекле // Выч. методы и программир., 2017, т.18, № 4, с.371-380;
A.I. Sukhinov, Iu.V. Belova, A.E. Chistiakov. Reshenie zadachi perenosa veshchestv pri
bolshikh chislakh Pekle // Vych. metody i programmirovanie, 2017, t.18, №4, s.371-380.
2.
В.А. Гущин. Об одном семействе квазимонотонных разностных схем второго порядка
аппроксимации // Математ. моделирование, 2016, т.28, № 2, с.6-18;
V.A. Gushchin. Family of quasi-monotonic finite-difference schemes of the second-order
of approximation // Math. Models and Comp. Simulations, 2016, v.8, № 5, p.487-496.
3.
О.М. Белоцерковский, В.А. Гущин, В.Н. Коньшин. Метод расщепления для исследо-
вания течений стратифицированной жидкости со свободной поверхностью // Ж. вы-
числ. матем. и матем. физ. 1987, т.27, № 4, с.594-609;
O.M. Belotserkovskii, V.A. Gushchin, V.N. Kon'shin. The splitting method for investigating
flows of a stratified liquid with a free surface // USSR Computational Mathematics and
Mathematical Physics, 1987, v.27, № 2, p.181-191.
4.
А.А. Самарский, П.Н. Вабищевич. Численные методы решения задач конвекции-диф-
фузии. - М.: Эдиториал УРСС, 1999;
A.A. Samarskiy, P.N. Vabishchevich. Numerical methods for solving convection-diffusion
problems. M.: Editorial URSS, 1999.
5.
В.М. Головизнин, А.А. Самарский. Разностная аппроксимация конвективного перено-
са с пространственным расщеплением временной производной // Математ. модели-
рование, 1998, т.10, №1, с.86-100;
V.M. Goloviznin, A.A. Samarskii. Raznostnaia approksimatsiia konvektivnogo perenosa s
prostranstvennym rasshchepleniem vremennoi proizvodnoi // Matemat. modelirovanie,
1998, t.10, №1, s.86-100.
6.
М.Е. Ладонкина, О.А. Неклюдова, В.Ф. Тишкин. Использование разрывного метода
Галеркина при решении задач газовой динамики // Математ. моделирование, 2014,
т.26, №1, с.17-32;
M.E. Ladonkina, O.A. Neklyudova, V.F. Tishkin. Application of the RKDG method for gas
dynamics problems // Math. Models and Comp. Simulations, 2014, v.6, № 4, p.397-407.
7.
А.А. Самарский. О регуляризации разностных схем // ЖВМиМФ, 1967, т.7, № 1, с.62-93;
A.A. Samarskii. On the regularization of difference schemes // U.S.S.R. Comput. Math.
Math. Phys., 1967, v.7, № 1, p.62-93.
96
А.И. Сухинов, А.Е. Чистяков
8. А.А. Самарский. Классы устойчивых схем // ЖВМиМФ, 1967, т.7, № 5, с.1096-1133;
A.A. Samarskii. Classes of stable schemes // U.S.S.R. Comp. Math. Math. Phys., 1967, v.7,
№ 5, p.171-223.
9. Р.П. Федоренко. Применение разностных схем высокой точности для численного
решения гиперболических уравнений // ЖВМиМФ, 1962, т.2, №6, с.1122-1128;
R.P. Fedorenko. The application of difference schemes of high accuracy to the numerical solution
of hyperbolic equations // U.S.S.R. Comp. Math. Math. Phys., 1963, v.2, № 6, p.1355-1365.
10. А.И. Сухинов, А.Е. Чистяков, М.В. Якобовский. Точность численного решения урав-
нения диффузии-конвекции на основе разностных схем второго и четвертого поряд-
ков погрешности аппроксимации // Вестн. ЮУрГУ. Сер. Выч. матем. информ., 2016,
т.5, № 1, с.47-62.
A.I. Sukhinov, A.E. Chistakov, M.V. Iakobovskii. Accuracy of the Numerical Solution of the
Equations of Diffusion-Convection Using the Difference Schemes of Second and Fourth Order
Approximation Error // Vestn. YuUrGU. Ser. Vych. Matem. Inform., 2016, v.5, № 1, p.47-62.
11. A.I. Sukhinov, A.E. Chistyakov, A.V. Shishenya, E.F. Timofeeva. Mathematical model for cal-
culating coastal wave processes // Math. Mod. & Comp. Simul., 2013, v.5, №5, p.122-129.
Поступила в редакцию 09.04.2018
После доработки 09.04.18
Принята к публикации 10.09.18