МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

2019 год, том 31, номер 3, стр. 124-140



НЕКОТОРЫЕ ТОЧНЫЕ РЕШЕНИЯ ЗАДАЧИ

О ТЕЧЕНИИ ЖИДКОСТИ

В СОКРАЩАЮЩЕМСЯ ЭЛАСТИЧНОМ СОСУДЕ

2019 г.

А.С. Мозохина, С.И. Мухин

Московский государственный университет имени М.В. Ломоносова

asm@cs.msu.ru, vmmus@cs.msu.ru

DOI: 10.1134/S0234087919030092

Рассматриваются некоторые точные решения уравнений гемодинамики в сокра-

щающемся сосуде в квазиодномерном приближении применительно к задачам,

возникающим при описании течения лимфы. Приведены решения для линеаризо-

ванной задачи в случае принудительных малых сокращений просвета сосуда. По-

лучено и исследовано аналитическое решение нелинейной системы при зависимо-

сти сечения сосуда только от времени. Точные решения воспроизведены в числен-

ном расчёте.

Ключевые слова: уравнения гемодинамики, квазиодномерный подход, сокращения,

аналитические решения.

SOME EXACT SOLUTIONS OF THE PROBLEM OF LIQUID FLOW

IN THE CONTRACTING OR EXPANDING VESSEL

A.S. Mozokhina, S.I. Mukhin

Lomonosov Moscow State University

Some exact analytical solutions of the quasi-onedimensional hemodynamic equations in

the contracting or expanding vessel are considered in the article. Such equations appear

in the modeling of lymph flow in the lymphatic system. Solutions of the linearised prob-

lem in the case of periodical changing of the vessel lumen with small amplitude are pre-

sented. Also the solution of the not linear problem is obtained in the case when cross-

section area depends only on time. Analytical solutions are reproduced numerically.

Key words: hemodynamic equations, quasi-onedimensional approach, contractions, ana-

lytical solutions.

1. Введение

Задачи, которые рассматриваются в данной работе, возникают при ма-

тематическом моделировании течения лимфы. Описание течения лимфы в

лимфатических сосудах - сложная задача не только с математической, но и

с физиологической точки зрения, и ее удовлетворительное решение на дан-

Некоторые точные решения задачи о течении жидкости ...

125

ный момент не получено. Общее описание лимфотока включает в себя два

принципиальных элемента: построение топологической схемы лимфатиче-

ской системы и собственно расчёт течения лимфы по этой системе. Для

описания гидродинамики течения в первом приближении достаточным

представляется квазиодномерный подход, хорошо зарекомендовавший себя

при моделировании течения крови в сердечно-сосудистой системе.

Движение лимфы в лимфатической системе с гидродинамической точ-

ки зрения представляет собой течение несжимаемой жидкости в сложной

разветвленной незамкнутой сети разнородных эластичных сосудов с раз-

личными специфическими свойствами. Принято считать [1, 2], что лимфа в

системе движется за счёт градиента давления и за счёт активных или пас-

сивных сокращений сосудов, имеющих клапаны. В общей модели течения

лимфы оба этих процесса должны быть учтены. В квазиодномерном подхо-

де перепад давления может задаваться как входное условие задачи, что по-

зволяет исследовать его влияние на лимфоток, в том числе с учётом грави-

тационного воздействия. Создание же моделей сокращения сосудов с кла-

панами в рамках квазиодномерного описания требует проработки как в ма-

тематическом, так и в алгоритмическом плане.

Учет активных и пассивных сокращений естественно осуществлять

введением принудительного изменения параметров сечения как функции

некоторых величин в уравнение состояния. Такой подход широко использу-

ется в моделях течения лимфы по сокращающемуся сосуду как в нульмер-

ных [3-5], так и в одномерных [6] и многомерных [7] постановках. В [6,7]

сокращения моделируются синусоидальной функцией, включаемой в урав-

нение, связывающее давление и площадь поперечного сечения, а результа-

ты сравниваются либо с физиологическим экспериментом, либо с результа-

тами расчётов по другим моделям, в частности, с расчётами Reddy [3], чья

модель уже стала классической в области моделирования течения лимфы.

Интерес представляет ряд работ, в которых безотносительно к лимфо-

току рассматривается течение жидкости в цилиндрической трубке с сокра-

щающимися стенками, исследуемое, в том числе, и аналитическими метода-

ми. Например, после перехода к новым неизвестным - функции Стокса и

завихрённости - система уравнений Навье-Стокса сводится к обыкновенно-

му дифференциальному уравнению, которое затем либо решается численно

[8,9], либо анализируется асимптотически, и результаты анализа сравнива-

ются с численным решением [10,11]. Указанные работы получают в качест-

ве результата зависимость решения от числа Рейнольдса и от амплитуды

сокращений, которая подробно исследуется, в частности, в [9]. Качествен-

126

А.С. Мозохина, С.И. Мухин

ный анализ полученной в результате преобразований уравнений Навье-

Стокса системы проведён в [12].

В квазиодномерном приближении течения в пульсирующем сосуде ис-

следованы Регирером в [13], где приведено асимптотическое решение. От-

дельно следует отметить работу [14], где в квазиодномерном приближении

получена система уравнений для описания распространения перистальтиче-

ской волны по сосуду с учётом синоптической передачи импульса сокра-

щений и её асимптотическое исследование.

Лимфатическая система (и, соответственно, ее модель) состоит из со-

тен сосудов, эти сосуды образуют сеть сложной топологии. Течение в такой

системе очень чувствительно к параметрам сети, и даже малые локальные

изменения свойств сосудов могут привести к достаточно радикальной пере-

стройке общей картины лимфотока. В связи с этим, прежде чем исследовать

влияние сокращений лимфатических сосудов на течение лимфы во всей

системе, полезно выяснить, какие локальные течения возникают в отдель-

ных сокращающихся сосудах.

Для численного исследования течения лимфы авторы применяют хо-

рошо зарекомендовавшую себя разностную схему, используемую для опи-

сания течения крови в кровеносной системе в квазиодномерном приближе-

нии [15]. Свойства этой разностной схемы подробно исследованы, напри-

мер, в [16,17]. Реализации этой разностной схемы для расчета на одном со-

суде и на произвольной сети описаны в [15]. В [18] проведено сравнение

ряда аналитических решений уравнений гемодинамики, в том числе и ли-

неаризованных, с решением данной схемы. Однако для течений под дейст-

вием активных сокращений сосуда такого анализа не проводилось. В связи

с этим в настоящей работе приводятся решения линеаризованной системы

гемодинамики, порожденные активными сокращениями сосуда, и прово-

дится их сравнение с численным решением по аналогии с [18].

Наиболее интересным, разумеется, представляется течение, возникаю-

щее в результате активных сокращений в полной нелинейной задаче. Для

этой задачи получено аналитическое решение в случае, когда площадь попе-

речного сечения при сокращениях зависит только от времени. Это решение

представляет самостоятельный интерес и также используется как тестовое.

2. Постановка задачи

Пусть жидкость является несжимаемой, продольная составляющая её

скорости много больше поперечной, течение осуществляется по симмет-

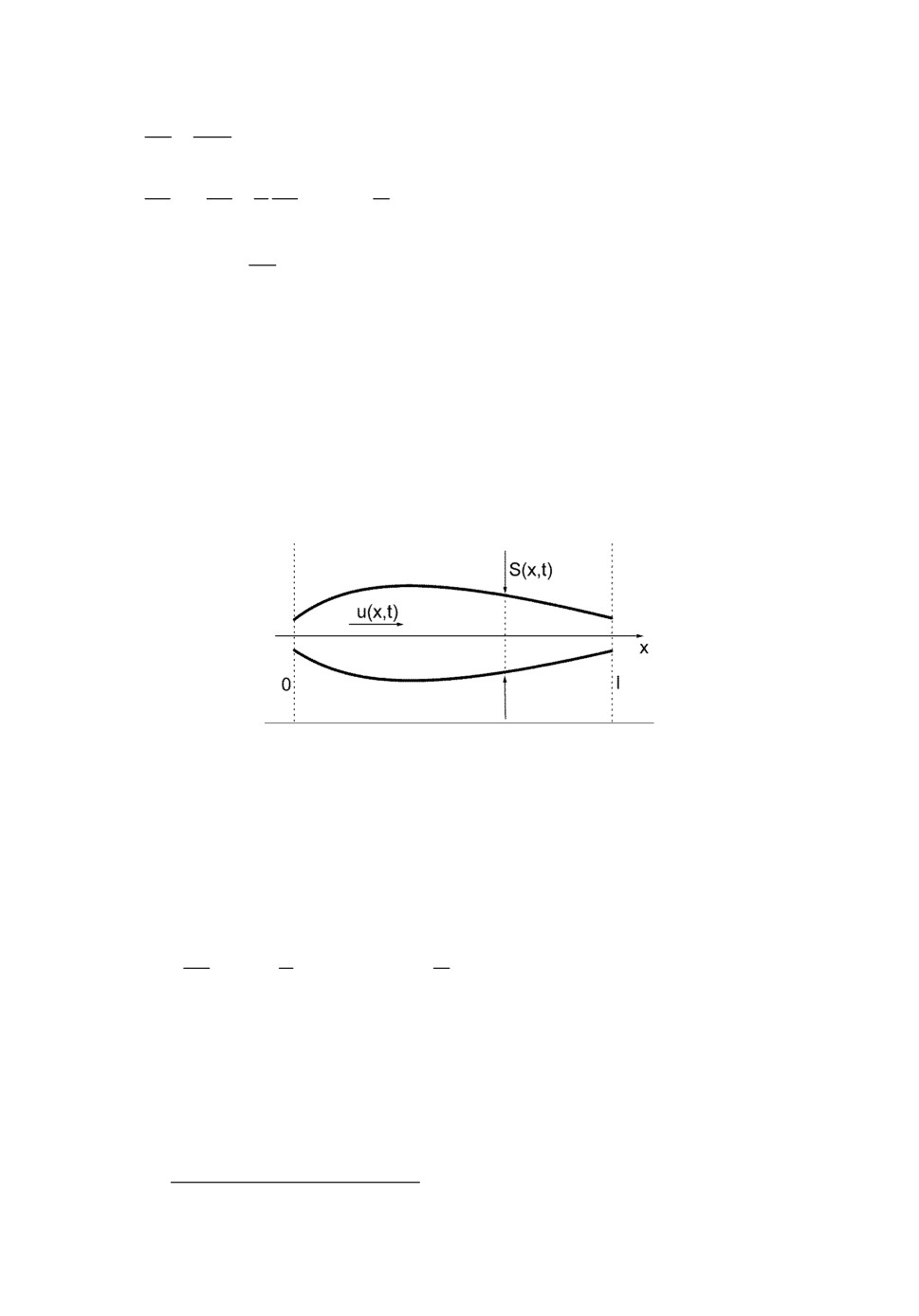
ричному цилиндрическому сосуду и является осесимметричным (рис.1). В

этом случае течение может быть описано квазиодномерными уравнениями

гемодинамики [19]:

Некоторые точные решения задачи о течении жидкости ...

127

S uS





t

x



u

u

p

u



8

0

x l,



(1)

t

x

x



S S p),





где x - пространственная координата, t - время, u(x,t) - скорость жидкости,

p(x,t) - давление, S(x,t) - площадь поперечного сечения сосуда, ρ = const -

плотность, ν = const - коэффициент кинематической вязкости лимфы, l -

длина сосуда. Третье уравнение системы выражает зависимость площади

поперечного сечения сосуда от давления (уравнение состояния). Добавле-

ние в это уравнение дополнительных зависимостей позволяет учитывать

активные и пассивные сокращения лимфатических сосудов.

Рис.1. Течение в сосуде в квазиодномерном приближении. Координатная прямая на-

правлена вдоль оси сосуда, сосуд симметричен относительно продольной оси.

Для численного решения системы (1) будем использовать конечно-раз-

ностную схему [15]. В безындексной форме [20] она имеет вид

(

)

(Su)





(

)

(

)

 u



(

)











8

(2)























S  S p).

Здесь

(



)

yy(x

)

yy

(



(1

)y

j n

j n1

y(x

)

)

j1

n1

j1

n1





128

А.С. Мозохина, С.И. Мухин

 jh,t

 h , h, τ - шаги по про-

σ_i[0,1], i=1,2,3,4 - весовые множители,

странству и времени соответственно.

Для первой тестовой задачи рассмотрим однородную систему:

S uS





t

x



u

u

p

u





0

x l,



(3)

t

x

x



S S p).





Как показано в [18], решение нелинейной системы (3) хорошо приближает-

ся решением линеаризованной системы при введении определённых огра-

ничений на параметры задачи. В случае описания течения лимфы такие ог-

раничения на малых временах являются оправданными.

3. Линеаризованные задачи

3.1. Рассмотрим задачу о течении жидкости на положительной полуоси

с сокращениями по некоторому закону в граничной точке. Такая постановка

часто встречается при исследовании влияния сокращений на течение, на-

пример, в [8, 21].

Пусть система (3) рассматривается на множестве x>0, t>0. В начальный

момент времени жидкость покоится, а давление равно некоторой постоян-

ной величине:

u(x,0)  0, p(x,0)  p,

0 x  .

(4)

На левой границе скорость равна нулю:

u(0,t)  0, t  0,

(5)

там же задан закон вынужденных сокращений:

S(0,t)  (t), t  0,

(6)

и потребуем, чтобы (0)  S(p) .

Будем искать приближённое решение задачи (3)-(6) в виде малых от-

клонений функций p(x,t), u(x,t) от постоянных значений [22, 20]:

p(x,t)  p 



(7)

причём

 x,t)



 x,t)



S S p)

(8)



S p)

Некоторые точные решения задачи о течении жидкости ...

129

Подставляя выражения (7) в уравнения (3), в начальные условия (4) и в гра-

ничные условия (5), (6) и отбросив все члены второго порядка малости, по-

лучим однородную линейную задачу относительно



с одно-

родными начальными условиями:



c









0

 ,

















(9)

(x,0)



 t)





0

 ,





(x,0)



 t)

(t)



где

S/[S'(p)]. Решение этой задачи находится методом продолжений

[22, 23].

Если площадь поперечного сечения S линейно зависит от давления p,

S(p)S

 ( p  p

dS / dp 

,



const

(10)

а функция μ(t) имеет вид



2



(t)  S

Asin

at,



(11)









где A - амплитуда сокращений на границе, λ - длина волны, a - параметр

сокращений, то решение задачи (9) имеет вид



ct  x





 x,t)





2





Asin

at



ct  x



















ct  x





 x,t)





2





(12)

sin

at



ct  x









c









Сравним полученное решение с численным решением задачи (3)-(6), (10),

(11) для случая малых по амплитуде возмущений.

Расчет будем проводить на отрезке длины l, достаточно протяжённом по

пространству. На левой границе x=0 задано S(0,t)=μ(t) (11), А=0.1мм рт.ст.,

λ = 0.1 см, а = 1 см/с. Сравнение решений корректно при

tt

, где

cryt

l

c , т.е. пока возмущение не дойдёт до правой границы расчётного

cryt

отрезка. Остальные параметры расчета приведены в табл.1, для данных зна-

чений скорость звука c  203см/с, а



0.49

с.

cryt

130

А.С. Мозохина, С.И. Мухин

Таблица 1.

Длина сосуда l

100 см

Минимальная площадь поперечного сечения сосуда S₀

0.0081 см²

Параметр θ

0.0003 см²/мм рт.ст.

Давление p

4 мм рт.ст.

Скорость u(x,0)

0 см/с

Шаг сетки по пространству h

0.1 см

Шаг сетки по времени τ

0.001 с

а)

б)

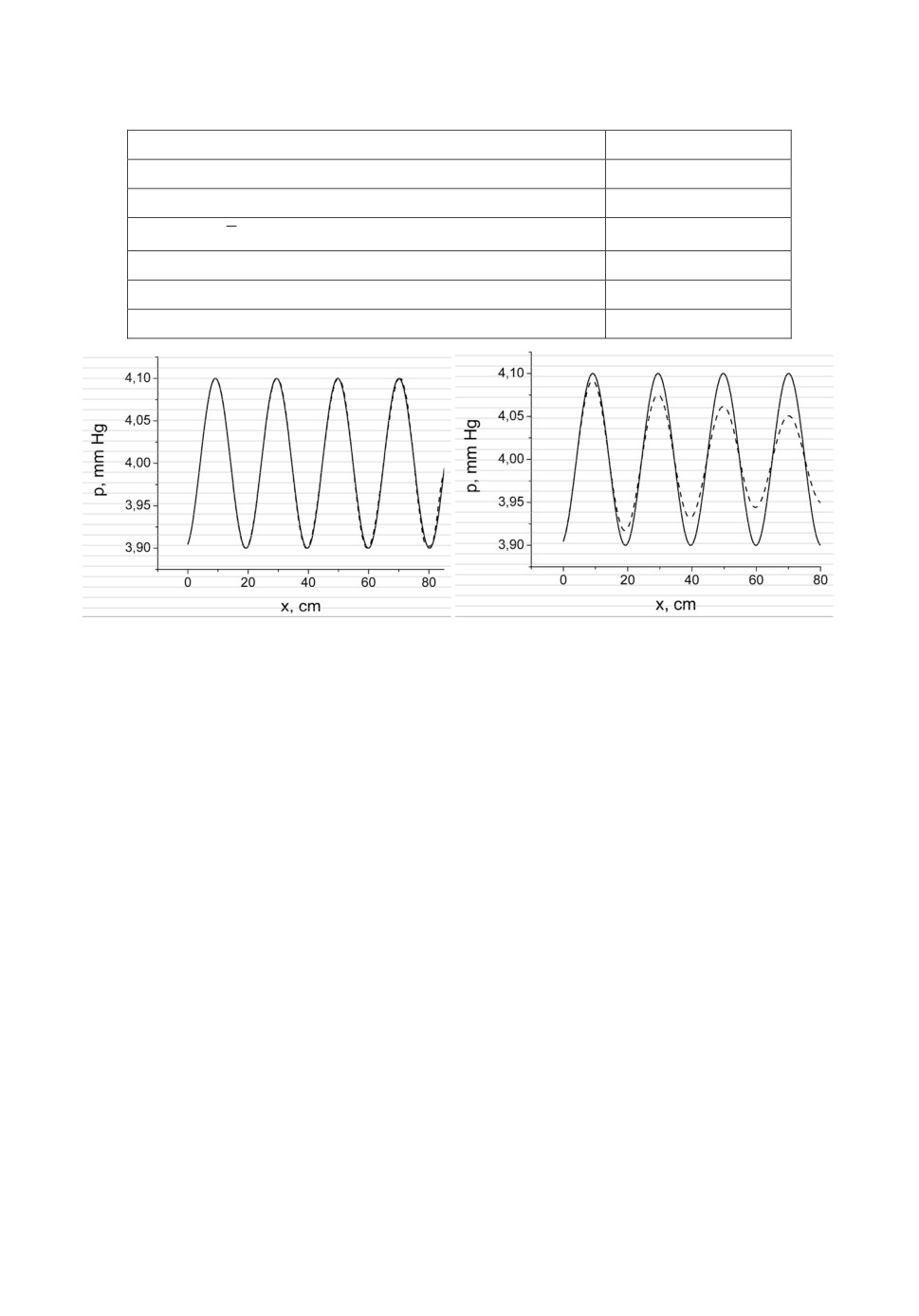
Рис.2. Сплошная линия - аналитическое решение линеаризованной задачи, пунктир-

ная линия - численное решение нелинейной задачи на момент времени 0.42 с.

а) численное решение с весами σ_i = 0.5, i = 1,2,3,4; б) численное решение с ве-

сами σ_i = 1, i = 1,2,3,4.

Hа рис.2 приведены результаты расчёта на момент времени 0.42 с,

рис.2а соответствует весовым множителям σ_i=0.5, рис.2б - σ_i= 1, i = 1,2,3,4.

Видно, что в обоих случаях численное решение (сплошная линия) соответ-

ствует аналитическому (пунктирная линия) по частоте и длине волны, что

свидетельствует о правильном воспроизведении колебательного режима.

При σ_i=0.5, i = 1,2,3,4 (рис.2а) схема имеет второй порядок аппроксимации,

в первом приближении бездиссипативна [16], и численное решение с высо-

кой точностью воспроизводит аналитическое. При σ_i=1, i=1,2,3,4 (рис.2б)

амплитуда численного решения убывает со временем по сравнению с ам-

плитудой аналитического решения линеаризованной задачи. Уменьшение

амплитуды связано с воздействием схемной диссипации, которая приводит

к затуханию гармоник, и соответствует известным теоретическим и расчет-

ным результатам для гиперболических систем [20, 15, 17, 18].

Приведенные расчеты показывают, что разностная схема (2) с рассмат-

риваемыми граничными условиями правильно передает точное решение, а

ее свойства по-прежнему описываются дифференциальным приближением

[16, 17].

Некоторые точные решения задачи о течении жидкости ...

131

3.2. Рассмотрим задачу о течении в сосуде, сокращающемся в каждой

точке. Причём рассмотрим данную задачу на всей действительной оси, что-

бы избежать влияния граничных условий на решение.

Пусть уравнение состояния в системе (3) имеет вид

SS(p,x,t)S

 ( p  p

)(x,t).

(13)

Здесь первые два слагаемых выражают зависимость площади поперечного

сечения от давления, а третье слагаемое описывает вынужденные сокраще-

ния стенок сосуда.

Рассмотрим систему (3), (13) на множестве   x   , t > 0 со сле-

дующими начальными условиями:

u(x,0)  0, p(x,0)  p,

  x  .

(14)

Действуя по аналогии с предыдущей задачей, при выполнении соотноше-

ний (7), условий (8) и условия на амплитуду вынужденных сокращений

|(x,t)|

x,t :

 

 , t



(15)

получим неоднородную линейную задачу с однородными начальными ус-

ловиями:



c



 





(x,0)















(x,0)



(16)







,



 









Решение этой задачи имеет вид [22]

 x,t)









xc(t),







xc(t),



d,



 x,t)









xc

),









xc(t

),



d,

(17)



2c

и для вынужденных сокращений с амплитудой A, длиной волны λ и скоро-

стью распространения волны a







2



2



(x,t)



Acos

(

xat),



(x,t)

Aa

sin

(xat)

(18)



















решение (17) принимает вид

132

А.С. Мозохина, С.И. Мухин

cos



(2/)(xat)



cos



(2/)(xct)



 x,t)







a



(19)

cos



(2/

)(xat)



cos



(2/

)(xct)









a



cos



(2/)(

xat

)



cos



/)(

xct

)



 x,t)







2c

a



(20)

cos



(2/



)(xat

)



cos



(2/

)(xct)







a



где



S S

(pp

)

(21)



Снова сравним численное решение исходной задачи (3), (13), (14), (18), по-

лученное с помощью конечно-разностной схемы (2), σ_i = 1, i = 1,2,3,4, для

случая малых по амплитуде возмущений с точным решением линеаризо-

ванной задачи. Функция η(x,t) задана в соответствии с (21), А = 0.1мм рт.ст.,

λ = 25 см, а = 10 см/с. На концах отрезка задано давление 4мм рт.ст. Ос-

тальные параметры те же, что и в предыдущем расчете (табл.1). Поскольку

численное решение ищется на конечном отрезке по пространству, сравне-

ние численного решения с аналитическим возможно на ограниченном от-

резке времени

tt

. При выбранных значениях параметров



0,25

с.

cryt

а)

б)

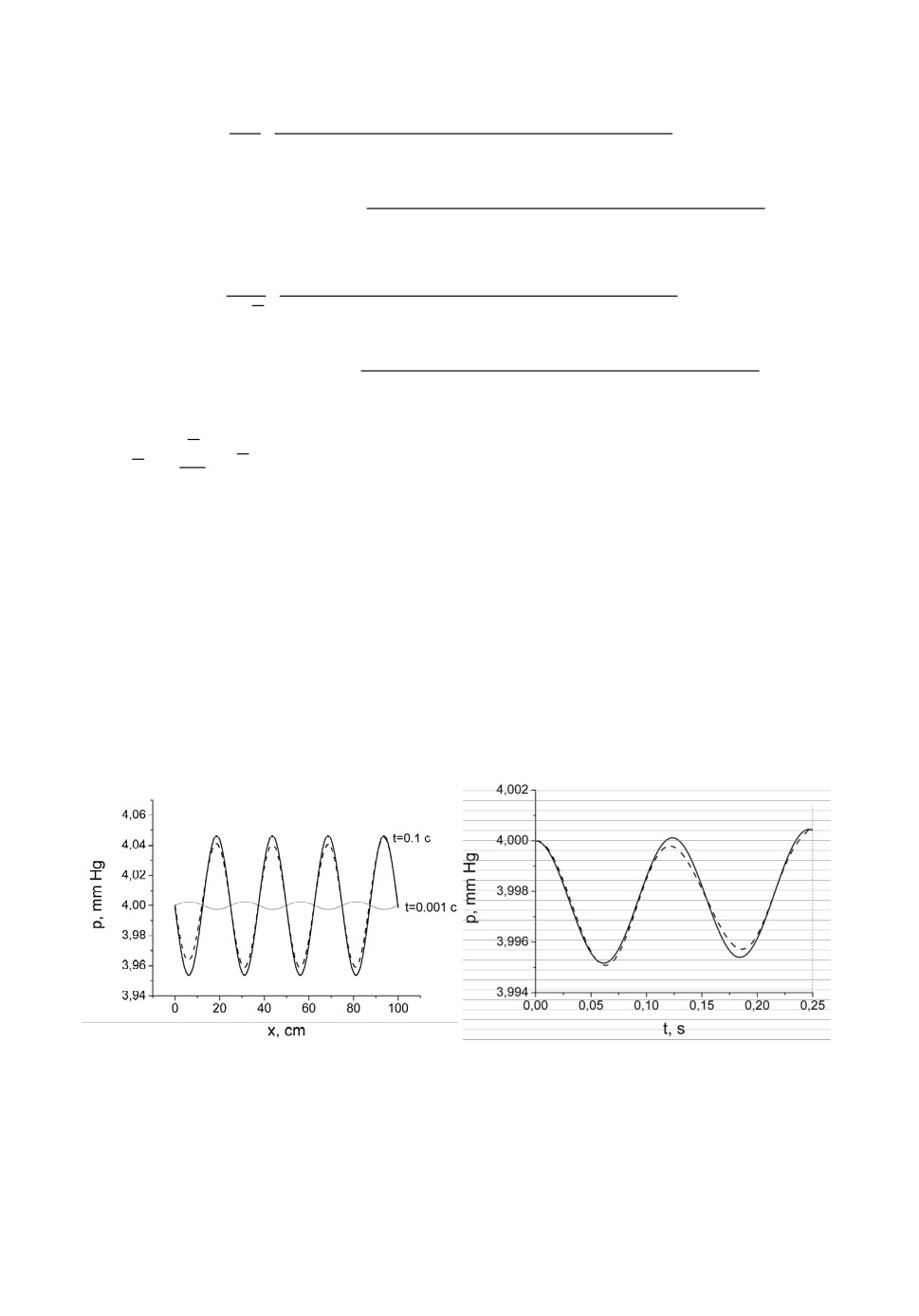
Рис.3. Результаты численного решения нелинейной задачи с малыми сокращениями в

каждой точке и аналитическое решение линеаризованной задачи (сплошная

линия): a) развёртка по пространству для времён 0.001 c и 0.1 с; б) развёртка по

времени при t < 0.25 с.

На рис.3а приведены графики давления для численного и аналитиче-

ского решений рассматриваемой задачи в моменты времени t = 0.001 с и

Некоторые точные решения задачи о течении жидкости ...

133

t = 0.1 с, рис.3б содержит график зависимости давления от времени для

численного и аналитического решений при t < 0.25 c. Результаты расчёта

показывают, что численное решение хорошо согласуется с аналитическим

решением.

Таким образом, схема (2) правильно передает в численном решении

качественные и количественные характеристики и в случае пространствен-

но распределенных сокращений.

4. Нелинейный случай

4.1. Рассмотрим теперь неоднородную нелинейную задачу (1) с посто-

янным коэффициентом кинематической вязкости ν на конечном отрезке

0 ≤ x ≤ l. Будем полагать, что уравнение состояния задано и имеет вид

SS(t),

(22)

т.е. в каждый момент времени сосуд имеет постоянное по x сечение. Обо-

значим

u(0,t)  u

(t), p(0,t)  p

(t) .

(23)

Уравнение сохранения массы преобразуется к виду

u





(24)

x

Интегрируя это уравнение, получим выражение для скорости u(x,t) в зави-

симости от функции S(t):

S t)

u x,t)



xu

(t)

(25)

(t)

Уравнение движения запишем в виде

p

u

u

u

 

u

8 .

(26)





x



t

x

S

Подставим в правую часть (26) найденную функцию u(x,t), проинтег-

рируем уравнение по x и получим выражение для p(x,t). В результате реше-

ние системы (1), (22), (23) будет иметь вид

u(x t)



U(t)xu

(t),



p x,t)



P t)



P t)

x p t),

(27)





0



x l





134

А.С. Мозохина, С.И. Мухин

где

S t)



U t)

U(t)





P t)

 

U t)U t)k





S(t)



S t)

(28)



u t)

P t)

 

u t)u t)U(t)k

8





S(t)





Для завершения решения необходимо дополнить эти формулы граничными

условиями, с помощью которых находятся пока не определенные функции

u₀(t) и p₀(t).

Рассмотрим некоторые варианты задания граничных условий.

Пусть на обеих границах задано давление

p(0,t)  p

(t), p(l,t)  p

(t), t  0.

(29)

Подставим выражение для давления из (27) во второе условие (29) и полу-

чим обыкновенное дифференциальное уравнение для скорости на левой

границе

(t)

u (t)  a(t)u

(t)  b(t)  0,

(30)

где



U t)

p t)

p t)

a(t)



U(t)

b t)



U t)U t)



(31)





S t)



S(t)



l

и из этого уравнения находим

(t).

Формулы (27), (28) и полученная из (30) функция

(t) определяют

решение задачи (1), (22), (29).

Рассмотрим частный случай граничных условий, соответствующих ра-

венству давлений на границах отрезка

p(0,t)  p(l,t)  p

(t), t  0.

(32)

В этом случае при постоянном коэффициенте кинематической вязкости ν

решение будет обладать свойством симметрии:

u(0,t)  u(l,t), t  0.

(33)

Подстановка функции скорости из (27) в равенство (33) даёт явное выраже-

ние для скорости жидкости на левой границе

U t)l

(t)



(34)

Такая функция

(t) обращает (30) в тождество, т.е. свойство симметрии

Некоторые точные решения задачи о течении жидкости ...

135

(33) позволяет избежать прямого решения уравнения (30). Формулы (27),

(28), (34) определяют решение задачи (1), (22), (32).

Полученные решения достаточно громоздки, и для произвольных функ-

ций S(t) анализ этих решений представляет собой весьма трудоемкую задачу.

Рассмотрим характер решения для простого, но вполне содержательно-

го случая.

Если сокращения (22) задаются синусоидальной функцией, то при ма-

лых значениях параметров и на малых временах такая функция может быть

приближена линейной

SS

 at ,

(35)

где a - скорость изменения сечения со временем, и представление о харак-

терных течениях в этом случае можно получить, анализируя решение систе-

мы с простейшим уравнением состояния (35). Заметим, что размерность па-

раметра а совпадает с размерностью коэффициента кинематической вязкости.

Рассмотрим задачу (1), (35), (32). Решение этой задачи определяется

формулами (27), (28), (34), которые с учётом (35) преобразуются к простому

виду







u x,t)











S at









(36)

a



p x,t)



(2ak)x



(2ak)lx  p t).



2(S



at)

2(S

at)



Решение (36), как и в общем случае (27), имеет линейный по x профиль ско-

рости и параболический по x профиль давления. Давление достигает экс-

тремального значения в точке x  l / 2 , и это значение определяется выра-

жением

a





4





(t) 

(37)

cryt

4S(t)

В зависимости от значения параметра a, который определяет знак коэффи-

циента (2a+k) = 2(a4π), возможны различные типы решений.

A. Пусть a < 0. В этом случае коэффициент (2a+k) отрицателен, гра-

фик давления представляет собой параболу с ветвями вниз. Площадь попе-

речного сечения убывает с течением времени, т.е. сосуд сжимается. При

этом давление растёт к середине отрезка, скорость направлена от его сере-

дины, максимальное давление достигается на середине отрезка и определя-

ется в соответствии с (37).

Пусть a > 0, что соответствует расширяющемуся сосуду. В этом случае

возможны два варианта течения в зависимости от величины а.

136

А.С. Мозохина, С.И. Мухин

B. При 0 < a < 4πν коэффициент (2a+k) < 0. Площадь поперечного се-

чения сосуда увеличивается с течением времени, давление в середине от-

резка достигает минимального значения (37), скорость направлена от гра-

ниц отрезка к его середине.

C. Третий вариант течения возникает при a > 4πν, когда (2a+k) > 0, что

соответствует «быстрому» увеличению площади поперечного сечения со-

суда. График функции давления представляет собой параболу с ветвями,

направленными вниз, максимального значения (37) давление достигает в

середине отрезка. В рассматриваемом случае давление в середине со време-

нем увеличивается, а скорость по-прежнему направлена от границ отрезка к

его середине - против градиента давления. Это решение представляется

достаточно интересным, поскольку его физическая интерпретация не оче-

видна. Тем не менее оно не является спецификой квазиодномерного подхо-

да. Например, в работе [11], в которой рассматривается течение в двумер-

ной пульсирующей трубке, описана похожая ситуация, однако авторы этой

работы сочли ее нефизической.

Как следует из рассмотренного примера, даже для простейшего закона

изменения сечения возможно (по крайней мере, формально) возникновение

нетривиальных течений.

Проведем сравнение точного аналитического и численного решений во

всех трех случаях. Расчётная область представляет собой три смежных от-

резка на одной прямой. На граничных отрезках уравнение состояния имеет

вид (10), на центральном отрезке уравнение состояния имеет вид (35). На

границах расчётной области задано постоянное давление. Численное реше-

ние получим по той же, что и в предыдущих расчетах, разностной схеме,

σ_i = 1, i = 1,2,3,4. Параметры сосудов приведены в табл.1. Результаты расчё-

та и соответствующие аналитические решения для вариантов А и В показа-

ны на рис.4а, 4б. Численное решение на центральном отрезке полностью

совпадает с аналитическим и качественно, и количественно, максимум мо-

дуля разности между значениями давления, полученными аналитически и

численно, и относительная погрешность приведены в табл.2.

Точное и численное решения для варианта С получены для сосудов боль-

шего сечения (скорость изменения просвета достаточно велика) и представ-

лены на рис.4в. Они также совпадают.

Таблица 2

вариант A

вариант B

вариант C

max



analyt

p

numeric



(мм рт.ст.)

0.003

0.0003







numeric

ma xanalyt

 *100 (%)

0.05

0.11

0.009







analyt



Некоторые точные решения задачи о течении жидкости ...

137

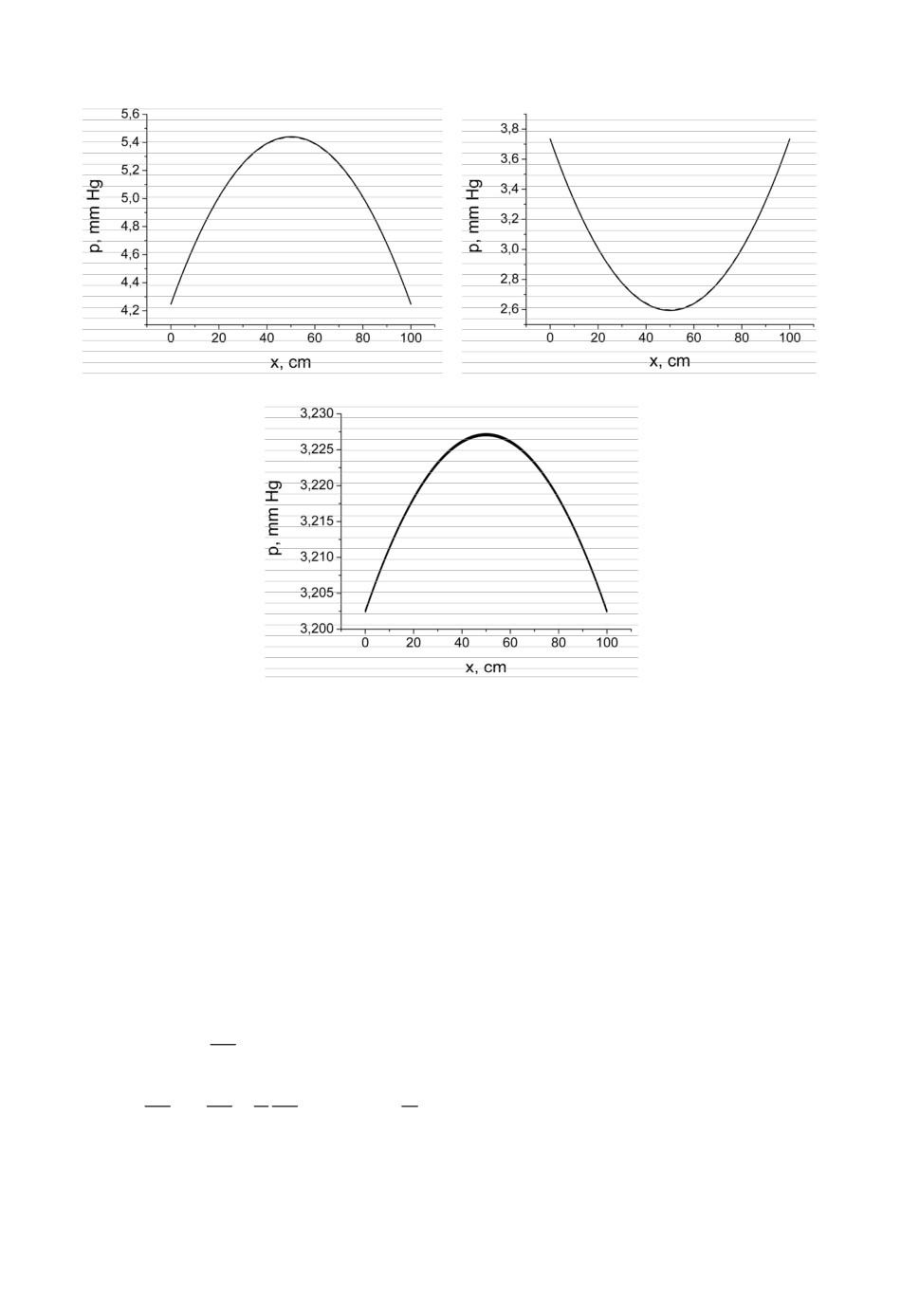
а)

б)

в)

Рис.4. Результаты численного решения (сплошная линия) нелинейной задачи о сокра-

щениях и сравнение их с аналитическим решением (пунктирная линия). а) Вари-

ант А: a = 104 см²/с (a < 0), развёртка по пространству при t = 1 c; б) Вари-

ант В: a = 104 см²/с (0 < a < 4πν), развёртка по пространству при t = 1 с; в) Вари-

ант С: a = 0.6 см²/с (a > 4πν), S = 2 см², развёртка по пространству при t = 0.2 c.

4.2. Интересным представляется точное решение рассматриваемой за-

дачи для течения с переменной вязкостью. Такая постановка задачи в даль-

нейшем может быть использована для моделирования течения в лимфати-

ческих сосудах с частыми клапанами, рассматриваемых как активно сокра-

щающиеся сосуды с преимущественным направлением тока жидкости.

Рассмотрим следующую неоднородную нелинейную систему:

dS

u



0,



x

u

u

p





8(u)

(38)

t

x

x



S  S t),



0

x l





138

А.С. Мозохина, С.И. Мухин

Такая постановка совпадает с рассмотренной ранее задачей (1), (22), (23),

только теперь коэффициент кинематической вязкости ν зависит от скорости

u(x,t). Решение задачи (38), (23) имеет вид



S

u(x t)



(t) 





















p x,t)



p t)





x



u t)

u t)



(39)











2













S

u t)

S



+8

8

I(,t)d,





где

I I x,







,t



d

(40)



В данном случае решение также имеет линейный по x профиль скоро-

сти. Функция давления содержит параболическую составляющую (как и ра-

нее) и часть, определяемую интегралом (40), порожденным переменной вяз-

костью. Представленное решение является многопараметрическим и суще-

ственно зависит от вида функции (u), однако доступно для аналитического

и численного исследования [24].

Заключение

В работе получены некоторые точные решения линеаризованных и не-

линейных уравнений гемодинамики, описывающих течения жидкости в со-

суде при вынужденных сокращениях в квазиодномерном приближении. Эти

решения позволяют получить представление о характере возникающих те-

чений. Кроме того, точные решения использованы в качестве тестовых и

показано, что применяемый авторами вычислительный алгоритм хорошо их

воспроизводит. Представленные результаты могут использоваться для соз-

дания простой модели сокращений лимфатических сосудов в рамках квази-

одномерного приближения.

СПИСОК ЛИТЕРАТУРЫ

1. Э.И. Борзяк, В.Я. Бочаров, М.Р. Сапин. Анатомия человека. - М.: Медицина, 1993, 560с.;

E.I. Borziak, V.Ia. Bocharov, M.R. Sapin. Anatomiia cheloveka. - M.: Meditsina, 1993, 560 s.

2. В.М. Петренко. Лимфатическая система. Анатомия и развитие. - Спб.: ДЕАН, 2010,

112с.;

V.M. Petrenko. Limfaticheskaia sistema. Anatomiia i razvitie. - Spb.: DEAN, 2010, 112 s.

3. N.P. Reddy, T.A. Krouskop, P.H.Jr. Newell. Biomechanics of a lymphatic vessel // Blood

vessels, 1975, v.12, №5, p.261-278.

Некоторые точные решения задачи о течении жидкости ...

139

4. C.M. Quick, A.M. Venugopal, A.A. Gashev, D.C. Zawieja, R.H. Stewart. Intrinsic pump-

conduit behavior of lymphangions // Am. J. Physiol. Regul. Integr. Comp. Physiol., 2007,

v.292, №.4, p.R1510-R1518.

5. C.D. Bertram, C. Macaskill, J.E.Jr. Moore. Simulation of a chain of collapsible contracting

lymphangions with progressive valve closure // J. Biomech. Eng., 2011, v.133, №1, p.011008.

6. A.J. Macdonald, K.P. Arkill, G.R. Tabor, N.G. McHale, C.P. Winlove. Modeling flow in

collecting lymphatic vessels: one-dimensional flow through a series of contractile elements

// Am. J. Physiol. Heart. Circ. Physiol., 2008, v.295, №1, p.305-313.

7. E. Rahbar, J.E.Jr. Moore. A model of a radially expanding and contracting lymphangion //

J. Biomech., 2011, v.44, №6, p.1001-1007.

8. S. Uchida, H. Aoki. Unsteady flows in a semi-infinite contracting or expanding pipe // J. Fluid

Mech., 1977, v.82, p.371-387.

9. M.G. Blyth, P. Hall, D.T. Papageorgiou. Chaotic flows in pulsating cylindrical tubes: a class

of exact Navier-Stokes solutions // J. Fluid Mech., 2003, v.481, p.187-213.

10. F.M. Skalak, C.Y. Wang. On the unsteady squeezing of a viscous fluid from a tube // J.

Austral. Math. Soc., 1979, v.21, p.65-74.

11. O.D. Makinde. Collapsible tube flow: a mathematical model // Rom. Journ. Phys, 2005,

p.493-506.

12. Д.В. Князев, И.Ю. Колпаков. Точные решения задачи о течении вязкой жидкости в

цилиндрической области с меняющимся радиусом // Нелинейная динамика, 2015,

т.11, №1, с.89-97;

D.V. Kniazev, I.Iu. Kolpakov. Tochnye resheniia zadachi o techenii viazkoi zhidkosti v

tsilindricheskoi oblasti s meniaiushchimsia radiusom // Nelineinaia dinamika, 2015, t.11,

№1, s.89-97.

13. С.А. Регирер. Квазиодномерная теория перистальтических течений // Изв. АН СССР.

МЖГ, 1984, №5, с.89-97;

S.A. Regirer. Kvaziodnomernaia teoriia peristalticheskikh techenii // Izv. AN SSSR,

MZHG, 1984, №5, s.89-97.

14. О.А. Дудченко. Перистальтический транспорт в биологических системах: базовые

модели и явные асимптотические решения.  М.: МФТИ, 2012, автореферат диссерт.

… канд. физ.-мат. наук;

O.A. Dudchenko. Peristalticheskii transport v biologicheskikh sistemakh: bazovye modeli i

iavnye asimptoticheskie resheniia. - M.: MFTI, 2012, avtoreferat dissert. … kand. fiz.-mat. nauk.

15. М.В. Абакумов, Н.Б. Есикова, С.И. Мухин, Н.В. Соснин, В.Ф. Тишкин, А.П. Фаворский.

Разностная схема решения задач гемодинамики на графе.  М.: Диалог-МГУ, 1998,

препринт, 16 с.;

M.V. Abakumov, N.B. Esikova, S.I. Mukhin, N.V. Sosnin, V.F. Tishkin, A.P. Favorskii. Raznos-

tnaia schema resheniia zadach gemodinamiki na grafe. - M.: Dialog-MGU, 1998, preprint, 16s.

16. М.В. Абакумов, И.В. Ашметков, Н.Б. Есикова, В.Б. Кошелев, С.И. Мухин, Н.В. Соснин,

В.Ф. Тишкин, А.П. Фаворский, А.Б. Хруленко. Методика математического моделирова-

ния сердечно-сосудистой системы // Математ. моделир., 2000, т.12, №2, с.106-117;

M.V. Abakumov, I.V. Ashmetkov, N.B. Esikova, V.B. Koshelev, S.I. Mukhin, N.V. Sosnin,

V.F. Tishkin, A.P. Favorskii, A.B. Khrulenko. Metodika matematicheskogo modelirovaniia

serdechno-sosudistoi sistemy // Matemat. modelir., 2000, t.12, №2, s.106-117.

17. И.В. Ашметков, С.И. Мухин, Н.В. Соснин, А.П. Фаворский, А.Б. Хруленко. Численное

140

А.С. Мозохина, С.И. Мухин

исследование свойств разностной схемы для уравнений гемодинамики.  М.: Диа-

лог-МГУ, 1999, препринт, 14 с.

I.V. Ashmetkov, S.I. Mukhin, N.V. Sosnin, A.P. Favorskii, A.B. Khrulenko. Chislennoe

issledovanie svoistv raznostnoi skhemy dlia uravnenii gemodinamiki. - M.: Dialog MGU,

1999, preprint, 14 s.

18. И.В. Ашметков, С.И. Мухин, Н.В. Соснин, А.П. Фаворский, А.Б. Хруленко. Анализ и

сравнение некоторых аналитических и численных решений задач гемодинамики //

Дифференциальные уравнения, 2000, т.36, №7, с.919-924;

I.V. Ashmetkov, S.I. Mukhin, N.V. Sosnin, A.P. Favorskii, A.B. Khrulenko. Analysis and

comparison of some analytic and numerical solutions of hemodynamic problems // Differ-

ential Equations. 2000, v.36, №7, p.1021-1026.

19. M.V. Abakumov, K.V. Gavrilyuk, N.B. Esikova, A.V. Lukshin, S.I. Mukhin, N.V. Sosnin,

V.F. Tishkin, A.P. Favorskii. Mathematical model of the hemodynamics of the cardio-vas-

cular system // Differential Equations, 1997, v.33, №7, p.895-901;

20. А.А. Самарский, Ю.П. Попов. Разностные методы решения задач газовой динамики.

 М.: Наука, 1992, 424 с.;

A.A. Samarskii, Iu.P. Popov. Raznostnye metody resheniia zagach gazovoi dinamiki.  M.:

Nauka, 1992, 424 s.

21. E.C. Dauenhauer, J. Majdalani. Unsteady Flows in Semi-Infinite Expanding Channels

with Wall Injection // 30th Fluid Dynamics Conference, Fluid Dynamics and Co-located

Conferences, 1999.

22. И.В. Ашметков, С.И. Мухин, Н.В. Соснин, А.П. Фаворский, А.Б. Хруленко. Частные

решения уравнений гемодинамики.  М.: Диалог-МГУ, 1999, препринт, 43 с.;

I.V. Ashmetkov, S.I. Mukhin, N.V. Sosnin, A.P. Favorskii, A.B. Khrulenko. Chastnye reshe-

niia uravnenii gemodinamiki. - M.: Dialog-MGU, 1999, preprint, 43 s.

23. А.Н. Тихонов, А.А. Самарский. Уравнения математической физики.  М.: Изд-во МГУ,

1999, 798 с.

A.N. Tikhonov, A.A. Samarskii. Uravneniia matematicheskoi fiziki.  M.: Izd-vo MGU,

1999, 798 s.

24. А.С. Мозохина, С.И. Мухин. О квазиодномерном течении жидкости с анизотропной

вязкостью в сокращающемся сосуде // Дифференциальные уравнения, 2018, т.54,

№7, с.956-962;

A.S. Mozokhina, S.I. Mukhin. Quasi-one-dimensional flow of a fluid with anisotropic vis-

cosity in a pulsating vessel // Differential Equations, 2018, v.54, №7, p.938-944.

Поступила в редакцию 20.06.2017

После доработки 29.05.2018

Принята к публикации 18.06.2018