МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 4, стр. 111-130
СКВОЗНОЙ МЕТОД РАСЧЕТА УРАВНЕНИЙ ПЕРЕНОСА
МНОГОКОМПОНЕНТНОЙ ГЕТЕРОГЕННОЙ СИСТЕМЫ
НА ФИКСИРОВАННЫХ ЭЙЛЕРОВЫХ СЕТКАХ
©
2019 г.
Ч. Чжан1, И.С. Меньшов1,2
1 Московский государственный университет им. М.В. Ломоносова
2 Институт прикладной математики им. М.В. Келдыша РАН
zhang-c@mail.ru; menshov@kiam.ru
DOI: 10.1134/S0234087919040075
Рассматривается новый численный метод для решения уравнений переноса много-
компонентной гетерогенной системы на фиксированных эйлеровых сетках. Система
состоит из произвольного числа компонент. Любые две компоненты разделены гра-
ницей (интерфейсом). Каждая компонента характеризуется характеристической
функцией - объемной долей, которая переносится в заданном поле скорости и опре-
деляет мгновенное распределение компоненты в пространстве. Особенность данной
системы состоит в том, что при её решении требуется выполнение двух условий.
Во-первых, объемная доля каждого компонента должна быть в интервале [0,1] и,
во-вторых, любая частичная сумма объемных долей не должна превышать единицы.
Для обеспечения этих условий мы вводим специальные характеристические функ-
ции вместо объемных долей и предлагаем решать относительно них уравнения пе-
реноса. Доказывается, что при таком подходе гарантировано выполнение указанных
выше условий. При этом метод совместим с различными TVD схемами (MINMOD,
Van Leer, Van Albada, Superbee) и способами разрешения межфазной границы (Lim-
ited downwind, THINC, Anti-diffusion, Artifical compression). Метод верифицируется
на расчетах ряда тестовых задач с использованием всех упомянутых выше схем.
Численные результаты показывают точность и надежность предложенного метода.
Ключевые слова: эйлеровая сетка, перенос, многокомпонентное течение, метод
разрешения межфазной границы.
CONTINUOUS METHOD FOR CALCULATING
THE TRANSPORT EQUATIONS
FOR A MULTICOMPONENT HETEROGENEOUS SYSTEM
ON FIXED EULER GRIDS
Ch. Zhang1, I.S. Menshov1,2
1 Lomonosov Moscow State University
2 Keldysh Institute of Applied Mathematics of RAS
A new numerical method for solving the transport equations of a multicomponent het-
erogeneous system on fixed Eulerian grids is considered. The system consists of an arbi-
112
Ч. Чжан, И.С. Меньшов
trary number of components. Any two components are separated by a boundary (inter-
face). Each component is characterized by a characteristic function - the volume fraction,
which is transported in a given velocity field and determines the instantaneous distribu-
tion of the component in space. The feature of this system is that it requires two condi-
tions to be satisfied. First, the volume fraction of each component should be in the inter-
val [0,1], and, secondly, any partial sum of volume fractions should not exceed unity. To
ensure these conditions, we introduce special characteristic functions instead of volume
fractions and propose to solve the transport equations with respect to them. We prove
that this approach ensures the fulfillment of the above conditions. The method is com-
patible with various TVD schemes (MINMOD, Van Leer, Van Albada, Superbee) and
interface-sharpening methods (Limited downwind, THINC, Anti-diffusion, Artifical
compression). The method is verified in the calculation of a number of test problems, us-
ing all the above schemes. Numerical results show the accuracy and reliability of the
proposed method.
Key words: eulerian grid, transport, multicomponent flow, interface-sharpening method.
Введение
Течение многоматериальных сред встречается в различных приложе-
ниях и прикладных задачах. Например, это - подводный взрыв, истечение
нефтепродуктов или природного газа из подводного трубопровода, задачи
высокоскоростного удара, динамические процессы в гетерогенных неодно-
родных средах и многое другое. В многоматериальном течении присутст-
вуют разные материалы, которые разделены межфазными границами (ин-
терфейсами), имеют различные физико-механические свойства и описыва-
ются разными уравнениями состояния. Прямое моделирование таких неод-
нородных течений включает расчет параметров течения во внутренних од-
нородных подобластях и положения межфазных границах на каждый мо-
мент времени. При сильных пространственных изменениях межфазных
границ подобласти однородного материала и сетки, связанные с ними, так-
же могут претерпевать сильные деформации, при которых точность расчета
падает настолько, что может привести к нефизичным результатам. Напри-
мер, такая ситуация возникает при моделировании неустойчивости Рихт-
майераМешкова, развивающейся на межфазной границе двух материалов
при прохождении ударной волны.
Чтобы обойти трудности прямого численного моделирования, связан-
ные с деформацией межфазной границы, существует альтернативный под-
ход, который называется в литературе методом диффузной границы. Суть
этого подхода состоит в том, что среда из разных материалов рассматрива-
ется как некоторая однородная эффективная среда, свойства которой зави-
сят от характеристических функций, определяющих пространственное рас-
Сквозной метод расчета уравнений переноса многокомпонентной ...
113
пределение составляющих компонент. Как правило, в качестве такой функ-
ции используется объемная доля компонента. Межфазная граница в этом
случае представляется зоной, где значение объемной доли меняется от нуля
до единицы.
Таким образом, методы расчета многоматериальных течений можно
разделить на две группы: методы прямого отслеживания межфазной грани-
цы [1-5] и методы диффузной межфазной границы [6-9]. В методах первой
группы межфазная граница выделяется специальным образом, и ее положе-
ние на каждом временном шаге рассчитывается. В методах второго типа
проводится сквозной расчет области без выделения границы. При этом
межфазная граница определяется подобластью, где объемная доля больше
нуля и меньше единицы. Точность моделирования при втором подходе на-
прямую зависит от размера зоны межфазной границы. Поэтому важнейшей
задачей является разработка вычислительных технологий, помогающих
максимально уменьшить размер зоны размазывания межфазной границы.
На сегодняшний день разработаны несколько таких методик. К ним отно-
сятся: метод LD (Limited Downwind) [10, 11], метод THINC [12], метод
AntiD (Anti-diffusion) [13,14], метод ACM (Artificial Compression Method)
[15, 16]. Эти методы были изначально разработаны для случая двух компо-
нент. Прямое обобщение их на случай с N (N≥3) компонент не проходит из-
за появления дополнительного ограничения на значения объемных долей -
условия совместности, а именно: не только объемная доля каждого компо-
нента должна находиться в диапазоне [0, 1], но и любая частичная сумма
объемных долей должна быть меньше единицы. Оценки показывают, что
даже схема MUSCL не гарантирует выполнения этого условия при простом
переносе трех и более компонент.
Выполнение условия совместности зависит от численного метода для
решения уравнений переноса объемных долей компонентов. Поэтому в на-
стоящей работе рассматриваются только уравнения переноса в заданном
поле скорости. Разработанные методы потом легко переносятся на полную
систему уравнений Эйлера.
Чтобы обеспечить выполнение условия совместности для объемных
долей в случае N≥3, S. Jaouen [10] модифицировал численный поток в ме-
тоде LD [11]. При этом была предложена сложная рекурсивная процедура,
которая работает исключительно со схемой LD.
В данной статье мы предлагаем новый подход, который в отличие от
[10] не привязан к конкретному численному методу решения уравнения пе-
реноса. Он совместим с любым из вышеупомянутых методов разрешения
114
Ч. Чжан, И.С. Меньшов
межфазной границы. Его суть состоит в следующем. Мы предлагаем вместо
объемных долей в уравнении переноса использовать специальные характе-
ристические функции, являющиеся нелинейными комбинациями объемных
долей, которые автоматически обеспечивали бы выполнение условия совме-
стности при условии, что базовая схема решения уравнения является TVD.
1. Постановка задачи
Рассматривается перенос в поле скорости u гетерогенной системы из N
z :
z uz
0,
i=1,2,3,,N
(1)
t i
i
В силу нормировки
N
z
1,
(2)
i
i1
только (N1) неизвестных независимы, и, соответственно, только (N1)
уравнение переноса надо решать. Не вошедшая в систему компонента будет
просто определяться из (2). Не ограничивая общности, будет рассматривать
следующую систему:
z uz
0,
i
2,3,,N
(3)
t i
i
Условия совместности объемных долей представляются следующими
неравенствами:
z
0,1,
(4)
i
и
z
1,
j
(5)
j
j
Если в начальный момент времени заданы начальные данные, удовле-
творяющие неравенствам (4) и (5), решение на последующих временных
слоях должны также удовлетворять этим неравенствам. Стандартная проти-
вопотоковая схема первого порядка обеспечивает выполнение условий со-
вместности. Однако при этом из-за большой численной вязкости происхо-
дит сильное «размазывание» разрывов объемных долей, из-за которого
трудно четко выделить межфазную границу. Схемы более высокого поряд-
ка, такие как схема Ван Лиира MUSCL с MINMOD ограничителем произ-
водных, основанные на нелинейной интерполяции, существенно уменьша-
ют зону размазывания, но при этом не гарантируют выполнения условий
Сквозной метод расчета уравнений переноса многокомпонентной ...
115
совместности. Причина заключается в том, что интерполированные значе-
ния объемных долей могут нарушать условия (4) и (5). Поясним суть про-
блемы следующим примером.
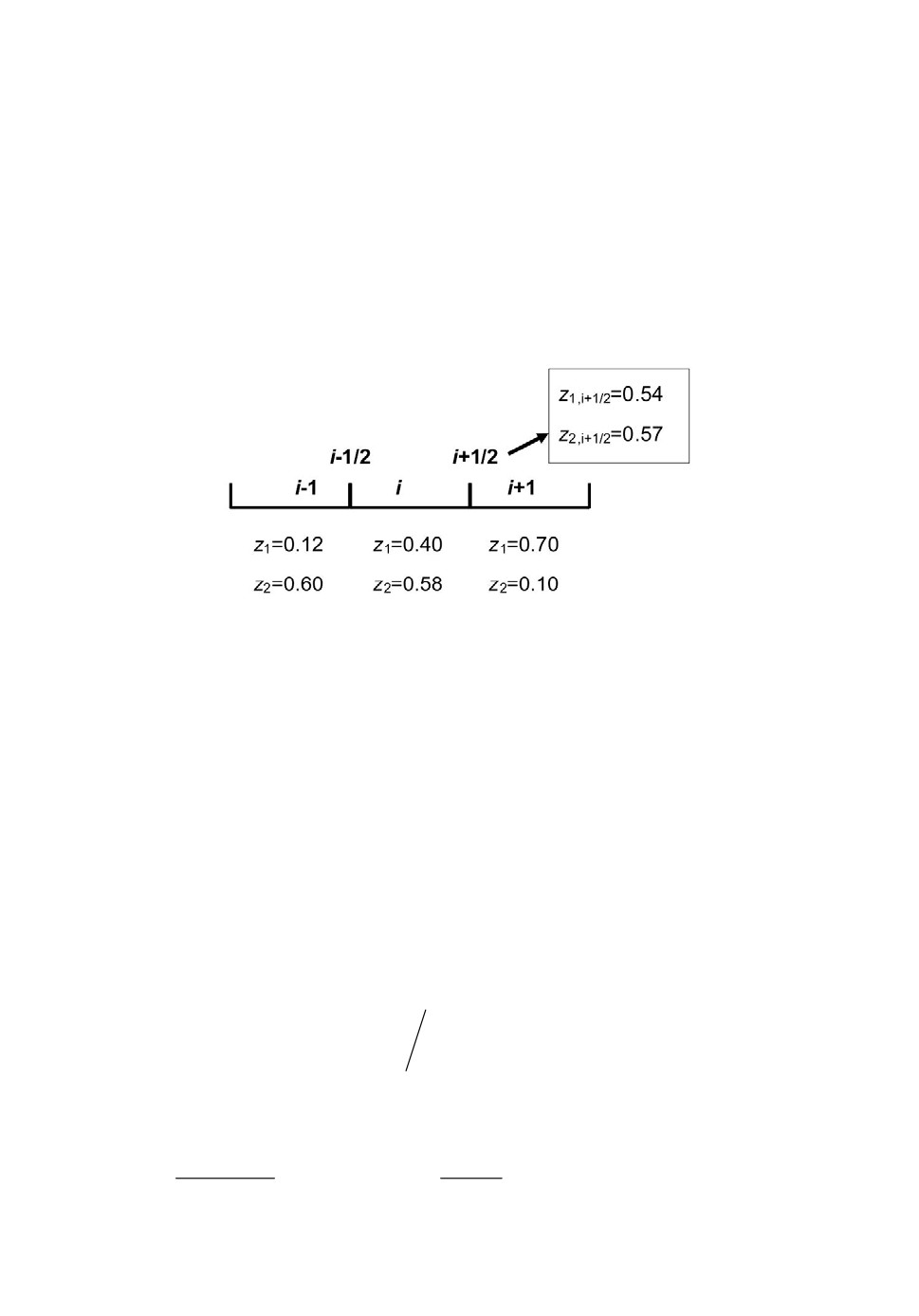
На рис.1 приведен пример MINMOD интерполяции для системы из
трех компонент. Интерполяции выполняется для значений объемных долей
на границе i+1/2 между двумя ячейками i и i+1. Хотя значения объемных
долей в ячейках удовлетворяют условиям (4) и (5), интерполированные зна-
чения на границе i+1/2 условие (5) нарушают. Такая же проблема возникает
при использовании других методов разрешения межфазной границы.
Рис.1. Пример интерполяции MINMOD для системы с тремя компонентами.
В схеме первого порядка условия совместности не будут нарушаться,
так как объемные доли на границе равняются усредненным объемным до-
лям либо левой ячейки, либо правой ячейки. Следовательно, на границе ус-
ловия автоматически выполняются.
2. Новые характеристические функции
Для того чтобы выполнить условия совместности при решении уравне-
ния (1) методом повышенного порядка точности, мы предлагаем ввести
специальные характеристические функции и решать относительно них
уравнения переноса:
f uf
0,
i
2,3,,N
,
(6)
t i
i
где
N
N
f
f
(z
, z
,, z
)
z
z
(7)
i
i
i1
i
N
k
k
ki
ki
1
В частном случае N=3 характеристические функции имеют следующий
вид:
z
z
z
2
3
3
f
z
z
,
f
2
2
3
3
z
z
z
z
z
1
2
3
2
3
116
Ч. Чжан, И.С. Меньшов
Лемма 1. Система уравнений (3) и система уравнений (6) эквивалент-
ны, если
z
0,
i
2,3,,N
i
Доказательство. Перепишем уравнение (6) следующим образом:
f
(z
, z
,
, z
)
u
f
(z
, z
,, z
)
t i
2
3
N
i
2
3
N
N
f
(z
, z
,,
z
)
(8)
i
2
3
N
(
z
uz
)
0.
t k
k
z
i2
k
После несложных вычислений найдем якобиан
f
/
z
f
/
z
f
/
z
2
2
2
3
2
N
f
/
z
f
/
z
f
/
z
3
2
3
3
3
N
1
J=
(9)
N1
N
z
k
f
/
z
f
/
z
f
/
z
N
2
N
3
N
N
i2
ki
Так как
z
0,
i
2,3,,N
, якобиан не равен нулю. Это значит, что
i
система уравнений (3) и система уравнений (6) эквивалентны.
■
Если одна компонента отсутствует в расчетной ячейке, и ее объемная
доля равна нулю, якобиан и характеристические функции приобретают син-
гулярность. Чтобы избежать такого вырождения, вводится малое значение η
(например, η=106), которое ограничивает компоненты от полного вырож-
дения. Таким образом, в рассматриваемой модели отсутствие компоненты
означает фактически наличие ее, но в пренебрежимо малом количестве.
Полное вырождение компоненты не допускается.
Так как система уравнений (3) и система уравнений (6) эквивалентны,
их точные решения совпадают. Поэтому при сходимости численной схемы
численные решения будут близки, и в пределе совпадать.
Лемма 2. Пусть имеются значения объемных долей, удовлетворяющие
условиям совместности (4) и (5), и интерполяционная схема, сохраняющая
монотонность при подсеточной реконструкции. Тогда применение такой
схемы к значениям характеристических функций (7) определяет интерпо-
лированные значения объемных долей, также удовлетворяющие условиям
совместности (4) и (5).
Доказательство. Так как усреднённые значения объемных долей удов-
летворяют условиям (4) и (5), то для усреднённых значений характеристи-
ческих функций имеем
f
0,1
,
(10)
i,
j
где i - индекс компонента, j - индекс ячейки.
Сквозной метод расчета уравнений переноса многокомпонентной ...
117
Если используется схема интерполяции, сохраняющая монотонность,
то новый экстремум не создается, т.е.
cf
f
0,1
,
(11)
i
где верхний индекс «cf» обозначает интерполированные значения. Интер-
полированные значения характеристических функций и объемных долей
связаны соотношением
N
N
cf
cf
cf
f
=
z
z
0,1
,
i
2,3,,N
,
(12)
i
k
k
ki
ki
1
откуда сразу получаем, что
N
N
N
cf
cf
cf
cf
0
z
z
z
z
1
(13)
N
k
k
k
kN
1
k
3
k
2
Неравенство (13) обеспечивает выполнение условий (4) и (5). ■
Таким образом, решив систему уравнений (6), можно найти численные
решения системы (3), удовлетворяющие требованиям (4) и (5). Для этого
надо выразить объемные доли через значения характеристических функций.
Решение (7) дает простые формулы для этого преобразования:
i
i
1
N
z
f
f
,
i
N,
z
f
(14)
i
k
k
N
k
k
2
k
2
k
2
Если используется схема TVD для решения уравнения переноса в ха-
рактеристических функциях, то их полные вариации будут убывать во вре-
мени, т.е.
n
1
n
TV(
f
)
TV(
f
)
,
(15)
i
i
где полная вариация определяется по следующей формуле:
TV
f
f
f
(16)
i
i
,
j1
i
,
j
j
Однако, не очевидно, что TVD характеристических функций гарантирует
также TVD свойство объемных долей. Монотонность характеристических
функций не обязана гарантировать монотонность объемных долей. Тем не
менее, можно доказать, что полная вариация объемной доли при этом остает-
ся ограниченной. Для этого нам нужно сначала доказать следующую лемму.
Лемма 3. Полная вариация произведения двух характеристических
функций ограничена следующим неравенством:
TV(
f
f
) TV(
f
)TV(
f
)
(17)
m l
m
l
118
Ч. Чжан, И.С. Меньшов
Доказательство.
TV(
f
f
)=
(
f
f
)
(
f
f
)
l m
l m j1
l m j
j
=
(
f
)
(
f
)
(
f
)
(
f
)
(
f
)
(
f
)
(18)
l j1
m j1
m j
m j l j1
l j
j
(
f
)
(
f
)
(
f
)
+
(
f
)
(
f
)
(
f
)
l j1
m j1
m j
m j l j1
l j
j
j
Так как
0
(
f
)
,(
f
)
1
, получим, что
l j1
m j
TV(
f
f
)
(
f
)
(
f
)
(
f
)
+
(
f
)
(
f
)
(
f
)
l m
l j1
m j
1
m j
m j l j1
l j
j
j
■ (19)
(
f
)
(
f
)
(
f
)
(
f
)
TV(
f
)TV(
f
).
m j
1
m j
l j1
l j
l
m
j
j
Лемма 4. Полная вариация объемной доли zi ограничена следующими
неравенствами:
n1
n
TV(
z
)
C
,
C
C
(20)
i
i
i
i
Доказательство. Используя уравнение (14) и лемму 3, получим
i
i1
TV(
z
)
TV(
f
)
TV(
f
)
C
,
i
N
(21)
i
k
k
i
k
2
k
2
N
N
и TV(
z
)TV
f
TV(
f
)
С
(22)
N
k
k
N
k
2
k
2
n
1
n
Из неравенства (15) следует, что
C
C
,
i
2,3,,N
■
i
i
Лемма 4 означает, что, хотя полная вариация объемной доли не убывает,
она, тем не менее, ограничена верхним пределом, убывающим во времени.
Замечание. Характеристические функции (7) не является единствен-
ным выбором. Следующие комбинации тоже гарантируют выполнение ус-
ловий совместности (4) и (5):
N
N
f
f
(z
,
z
,
, z
)
(
z
)
(
z
)
,
(23)
i
i
i
1
i
N
k
k
ki
ki
1
N
N
f
f
(z
,
z
,
, z
)
z
z
,
(24)
i
i
i
1
i
N
k
k
ki
ki
1
где монотонная функция (x)[0,1], x
[0,1]
. Например, (x) x ,
Сквозной метод расчета уравнений переноса многокомпонентной ...
119
3. Дискретизация
Явная схема и метод конечного объема используются для дискретиза-
ции системы уравнений (3) и (6):
n1
n
n
n
q
q
u(q
q
),
(25)
j1
2
j1
2
где =t x , Δt и Δx - шаг по времени и шаг по пространству, соответст-
венно, u скорость, верхние индексы n, n+1 обозначают соответствующий
номер шага по времени. Ниже индекс n опускается для простоты.
Мы анализируем два подхода, когда в качестве неизвестной величины
берется q = zi и q = fi соответственно. В обоих случаях характеристические
функции (7) используются для подсеточной интерполяции, чтобы удовле-
творять условиям совместности (4) и (5). Противопотоковая схема исполь-
зуется для вычисления численного потока, т.е.
u
u
u
u
q
q
q
,
(26)
j1
2
j1
2,L
j1
2,R
2
2
гдеqj12,L ,qj
- интерполированные значения q с левой и правой сто-
1
2,R
роны границы между ячейками j и j+1.
В следующем разделе мы сравниваем предложенный метод с методом
S. Jaouen [10], разработанным на основе схемы LD [11]. Последняя фактиче-
ски эквивалентна схеме Ultrabee для линейного уравнения переноса. Для того
чтобы удовлетворить условиям совместности, в [10] предлагается достаточно
громоздкая модификация численного потока LD. Рассматриваются уравне-
ния переноса для q=zi, и численный поток определяется следующим образом:
d
,
z
d
,
i,
j1
2
i,
j1
2
i,
j1
2
z
z
,
d
z
D
,
(27)
i,
j1
2
i,
j1
i,
j1
2
i,
j
1
2
i,
j1
2
D
,
z
D
i
,
j1
2
i,
j1
2
i
,
j1
2
m
min(
z
,
z
),
M
max(z
, z
),
i,
j1
2
i,
j
i,
j1
i
,
j
1
2
i,
j
i,
j1
z
M
z
m
i,
j
i
,
j
1
2
i,
j
i,
j1
2
b
M
,
B
m
,
(28)
i,
j1
2
i
,
j
1
2
i,
j
1
2
i,
j1
2
u
u
a
max(
b
,
m
),
A
min(B
, M
),
i,
j
1
2
i,
j
1
2
i,
j
1
2
i,
j
1
2
i,
j1
2
i,
j1
2
N
N
d
max
a
,1
A
,
D
min
A
,1
a
,
1,
j1
2
1,
j
1
2
l
,
j
1
2
1,
j
1
2
i,
j1
2
l,
j1
2
l
2
l
2
i
1
N
d
max
a
,1
z
A
,
i
2,3,
, N
1
,
i,
j
1
2
i,
j
1
2
l
,
j
1
2
l
,
j1
2
l
1
li
1
120
Ч. Чжан, И.С. Меньшов
i
1
N
D
min
A
,1
z
a
,
i
2,3,,N
1
i,
j1
2
i,
j1
2
l,
j1
2
l,
j1
2
l
1
li
1
Очевидно, что метод [10] намного сложнее предложенного в настоя-
щей работе подхода на основе характеристических функций. Кроме того, он
жестко привязан к схеме LD. Наш метод не предполагает какой-то специ-
альной схемы разрешения межфазной границы. Он совместим с любым из
указанных выше методов нелинейной интерполяции без внесения в них ка-
ких-либо модификаций.
4. Численные тесты
В этом разделе предложенный метод характеристических функций тес-
тируется на некоторых одномерных и двумерных задачах переноса. Рас-
сматриваются и сравниваются классические TVD схемы второго порядка,
такие как MUSCL c ограничителями производных MINMOD, Van Albada,
Superbee, а также специальные алгоритмы разрешения межфазной границы,
в том числе LD, AntiD, THINC, ACM. По умолчанию во всех расчетах число
Куранта равнялось 0.2.
4.1. Адвекция трехкомпонентной системы. Расчетная область пред-
ставляет собой интервал [0,1]. Начальные распределения компонент имеют
следующий вид:
(x)
0.4,0.6
z x)
,
z x)
x
1/2
,
z x)
1
z x)
z x),
(29)
1
2
3
1
2
2
1,
xI
,
где функция
x
I
0,
xI
Периодические граничные условия применяются на левой и правой
границах. Скорость адвекции u=1. В этом примере мы не рассматриваем
схемы AntiD, THINC и ACM, которые разработаны специально для разре-
шения межфазной границы, где происходит резкий переход z+→0, z→1 или
z+→1, z→0.
На рис.2 показано начальное распределение объемных долей каждой
компоненты и решение системы уравнений (3) по противопотоковой схеме
первого порядка. Видно, что происходит сильное искажение начальных
распределений из-за чрезмерной численной вязкости.
Схемы второго порядка уменьшают численную вязкость. Но если они
применяются к уравнению переноса для объемных долей, оператор нели-
нейной интерполяции может приводить к отрицательным значениям, как это
видно на рис.3, где приведены численные результаты решения по схемам
MUSCL-Superbee и LD.
Сквозной метод расчета уравнений переноса многокомпонентной ...
121
Рассмотрим теперь численные решения, которые получаются, если в
уравнении переноса использовать предложенные характеристические функ-
ции. Численные решения системы уравнений (6), полученные с использова-
нием схемы второго порядка MUSCL с различными ограничителями произ-
водных (Minmod, Van Leer, Van Albada, Superbee) и схемы LD, приведены на
рис.4, 5 и 6 соответственно. Результаты показывают, что получающиеся зна-
чения объемных долей удовлетворяют условиям совместности во всех рас-
четных вариантах; отрицательные объемные доли не появляются.
x
x
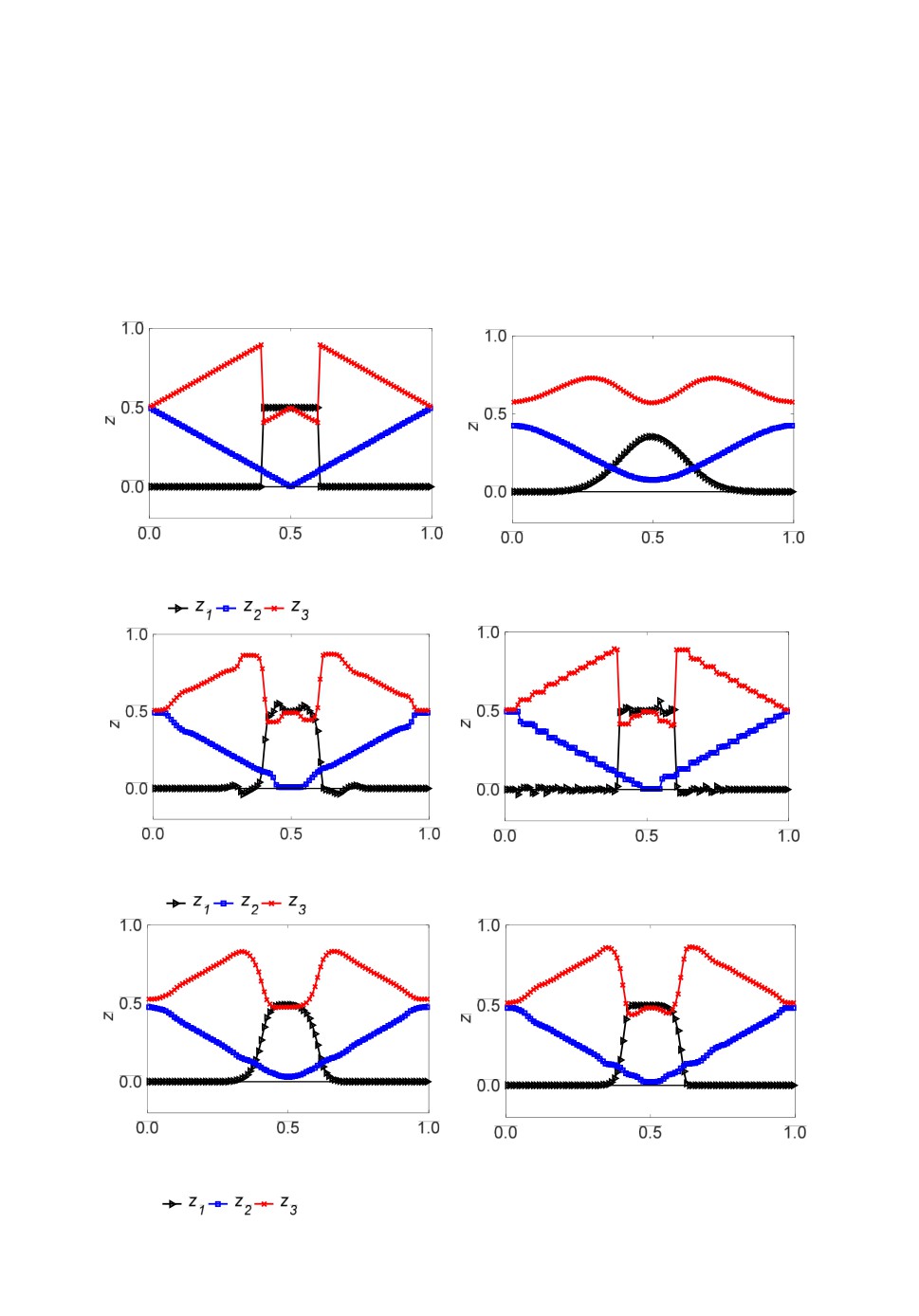
Рис.2. Начальные распределение объемных долей (слева) и численные результаты по
противопотоковой схеме первого порядка после одного цикла, t=1.0 (справа).
x
x
Рис.3. Численные результаты по схеме Superbee (слева) и LD (справа) после одного
цикла, t=1.0. Решение уравнений
(3) относительно объемных долей.
x
x
Рис.4. Численные результаты по схеме Minmod (слева) и Van Leer (справа) после одного
цикла, t=1.0. Решение уравнений (6) относительно характеристических функций.
122
Ч. Чжан, И.С. Меньшов
x
x
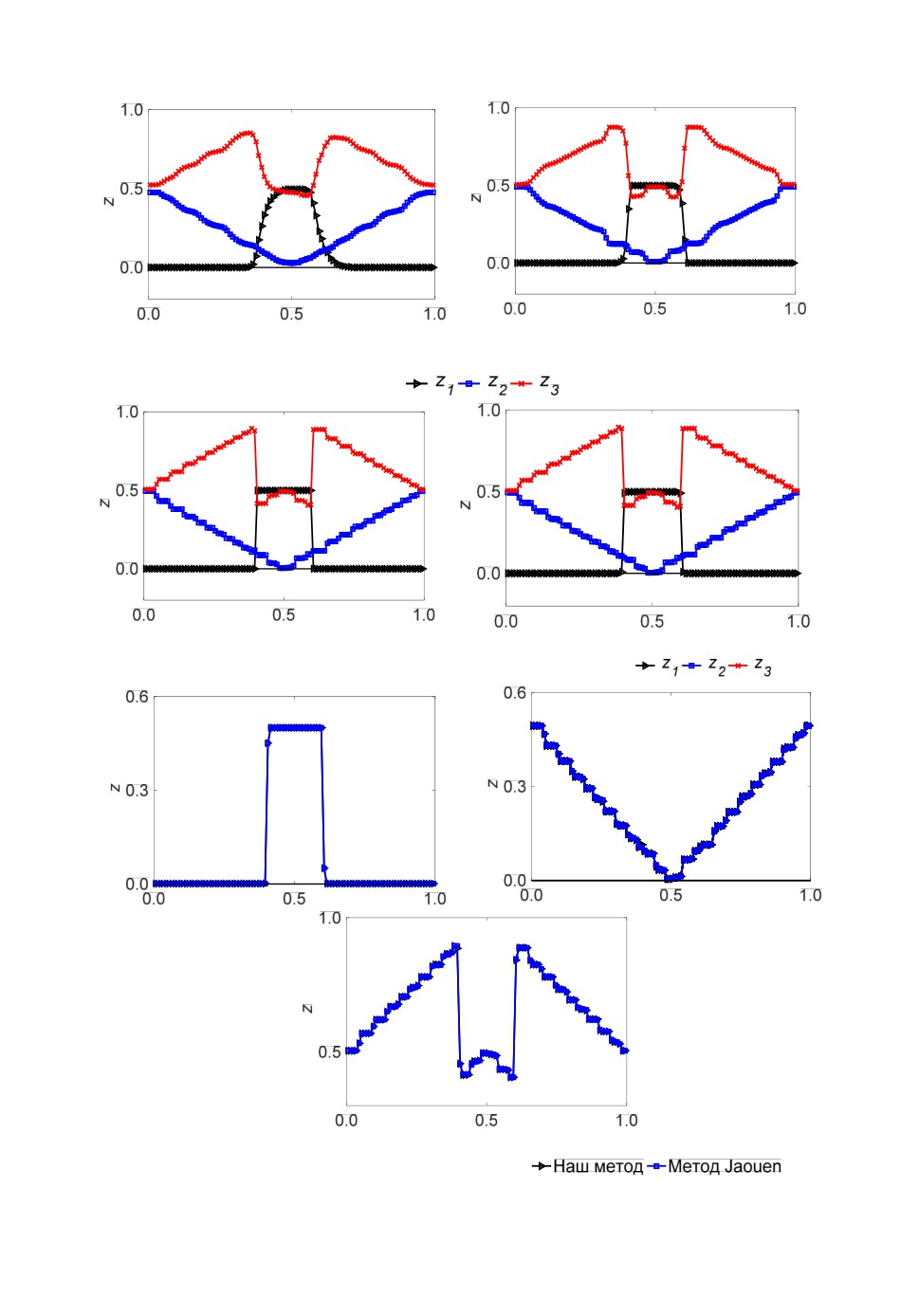
Рис.5. Численные результаты по схеме Van Albada (слева) и Superbee (справа)
после одного цикла, t=1.0. Решение уравнений (6) относительно харак-
теристических функций.
x
x
Рис.6. Численные результаты по схеме LD c характеристическими функциями (6) (слева)
и методом S. Jaouen [10] (справа) после одного цикла, t=1.0.
a)
б)
x
x
в)
x
Рис.7. Сравнение метода LD c характеристическими функциями и метода S. Jaouen [10].
Расчет 500 циклов, t=500: (а) z1, (б) z2, (в) z3.
Сквозной метод расчета уравнений переноса многокомпонентной ...
123
На рис.7 приведены результаты расчета 500 циклов (t=500) по схеме
LD с характеристическими функциями. Для сравнения также приведены
аналогичные результаты по методу S. Jaouen [10]. Результаты фактически
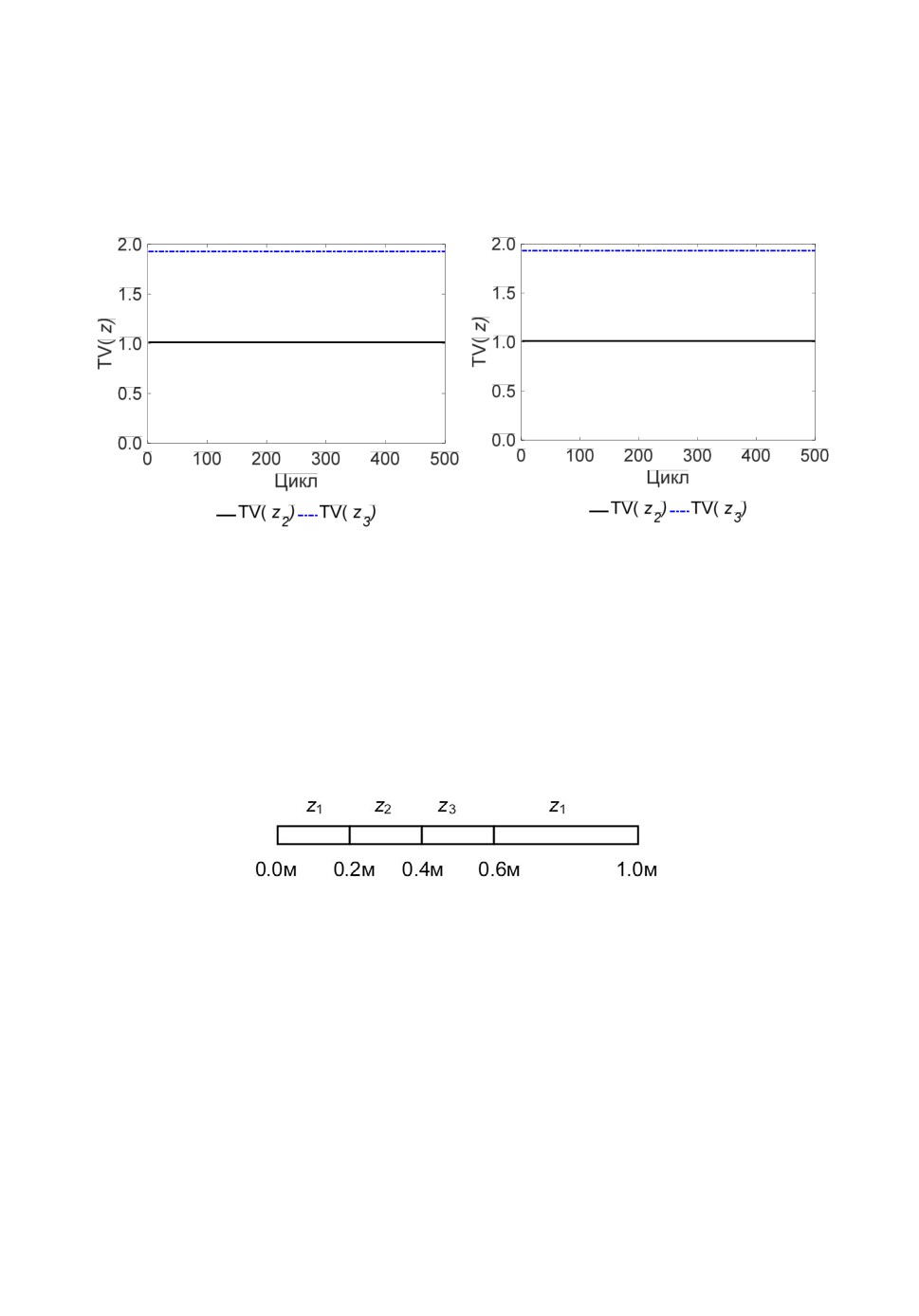
совпадают. Полные вариации показаны на рис.8. Видно, что полная вариа-
ция почти не меняется со временем и в нашем методе, и в методе [10].
Рис.8. Полные вариации численных решений в методе LD c характеристическими
функциями (слева) и методе S. Jaouen [10] (справа). Расчет 500 циклов (t=500).
4.2. Перенос межфазной границы. Эта задача моделирует движение
межфазных границ. Ее постановка схематично изображена на рис.9. Расчет-
ная область представляет собой отрезок [0.0м, 1.0м]. Внутри области заданы
интервалы I1= [0.0м, 0.2м], I2 = [0.2м, 0.4м], I3 = [0.4м, 0.6м], I4 = [0.6м, 1.0м],
в которых в начальный момент времени находятся 1-я, 2-я, 3-я и 1-я компо-
ненты трехкомпонентной системы. Число счетных ячеек составляет 100. Пе-
риодические граничные условия задаются на левой и правой границе.
Рис.9. Схема расчета задачи переноса межфазной границы.
Начальные данные задаются следующим образом:
z x)
(x),
z x)
(x),
z x)
(x).
1
I
1
I
4
2
I
2
3
I
3
6
110
,
xI,
где
(x)
I
6
1/(N
1)
10
,
xI
В этой задаче мы тестируем наш метод со схемами MINMOD, LD,
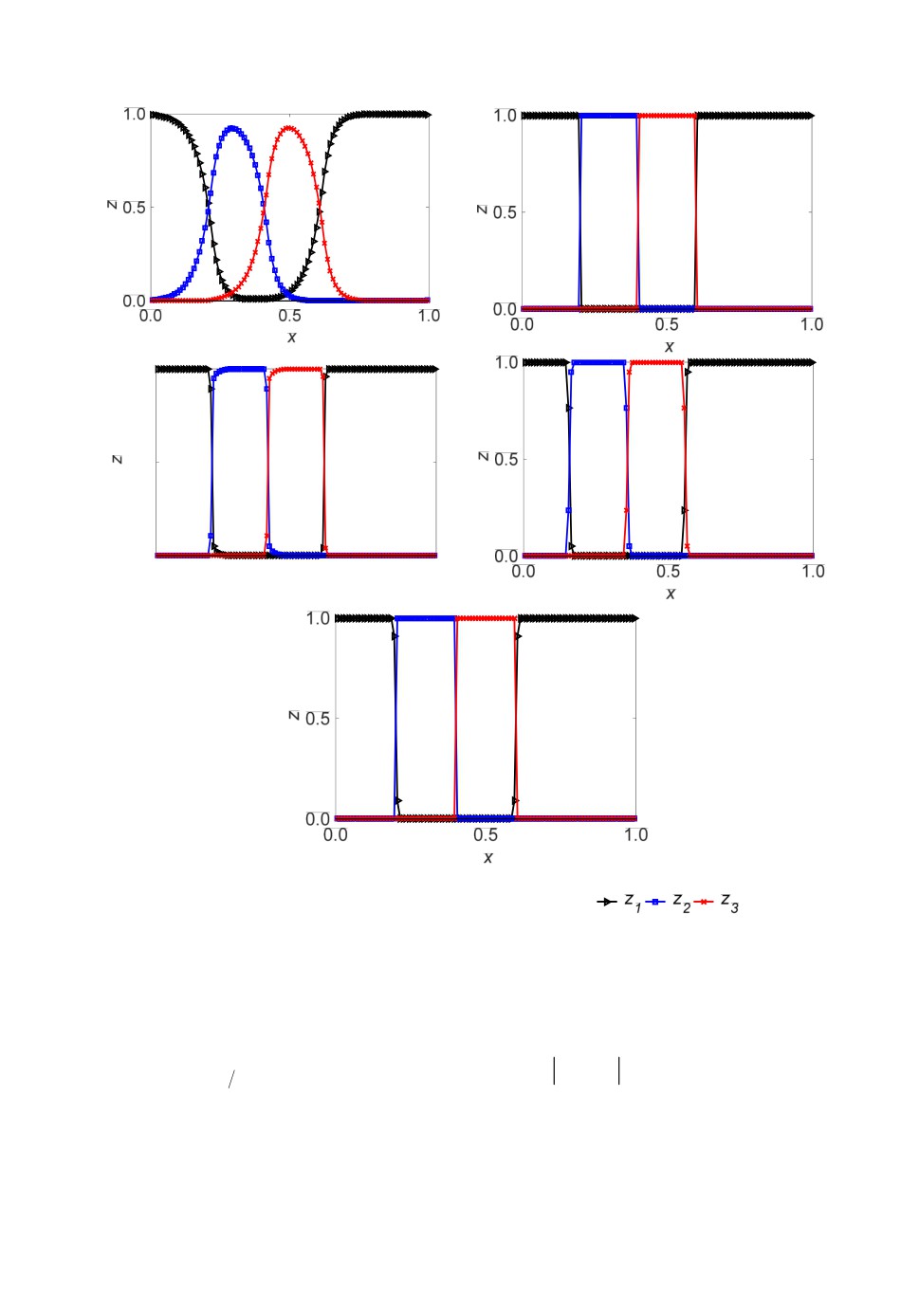
THINC, AntiD и ACM. Численные результаты после 10 циклов представле-
ны на рис.10. Видно, что за исключением MINMOD межфазные границы
имеют высокое разрешение в 2-3 счетных ячейках. При этом численных ос-
цилляций, связанных с нарушением условий совместности, не наблюдается.
124
Ч. Чжан, И.С. Меньшов
а)
б)
1.0
0.5
в)
г)
0.0
0.0
0.5
1.0
x
д)
Рис.10. Численные результаты задачи переноса межфазной границы: (а) схема Minmod,
(б) схема LD, (в) схема THINC, (г) AntiD, (д) ACM.
4.3. Перенос семи компонентов. Далее рассмотрим более сложную с
вычислительной точки зрения задачу перенос 7-компонентной системы. В
начальный момент каждая компонента задается распределением объемных
долей, которые удовлетворяют условиям совместности (4) и (5):
z x)
(x)
(1sin(2x))/10
,
z x)
x
1/2
,
1
0,1
2
2
2
z x)
1.5sin(0.72x)
/14,
z x)0.5exp
100(x1/2)
,
(30)
3
4
6
z x)
1
cos(10
x)
/14,
z x)
(x)
/7,
z x)1
z
(x).
5
6
0.7,1
7
k
k1
Сквозной метод расчета уравнений переноса многокомпонентной ...
125
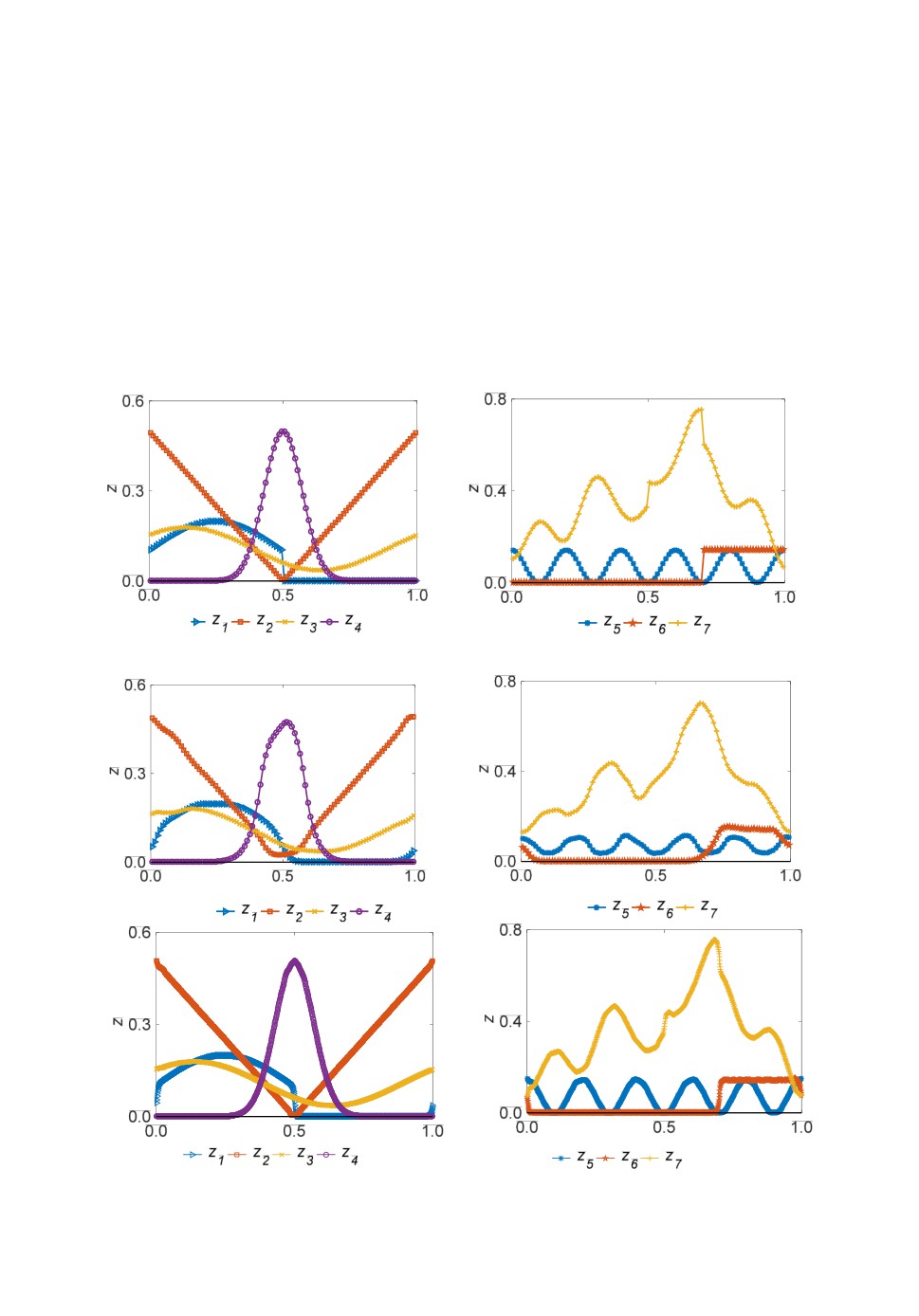
Начальное распределение показано на рис.11. Расчет проводится на
двух сетках с числом ячеек 100 и 1000, соответственно. Численные резуль-
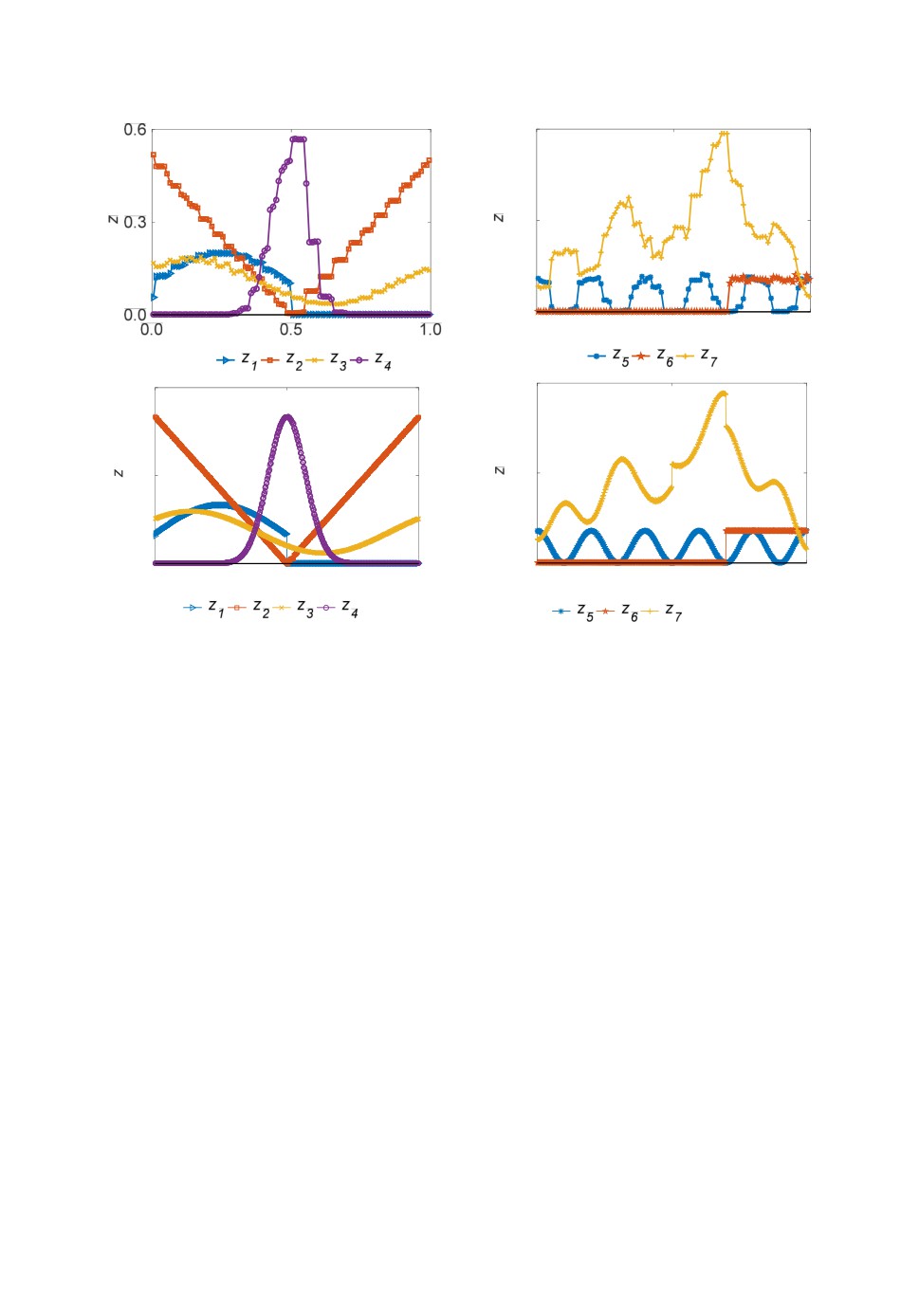
таты по схемам MINMOD и LD представлены на рис.12 и 13. Более дисси-
пативная схема MINMOD дает ожидаемое большее искажение в распреде-
лениях объемных долей по сравнению со схемой LD, которая показывает
отличную сходимость. Как видно из рис.13, на 1000 ячейках разрешение
разрывов в LD схеме составляет всего 1 точку. При этом наш метод харак-
теристических функций гарантированно обеспечивает свойство совместно-
сти (4) и (5) в численных решениях как в MINMOD, так и в LD схеме, на
разных сеточных разрешениях.
а)
б)
x
x
Рис.11. Начальное распределение объемных долей в задаче переноса
7-компонентной системы.
а)
б)
x
x
в)
г)
x
x
Рис.12. Численные результаты задачи переноса 7-компонентной системы
по схеме MINMOD: (а, б) число ячеек - 100, (в, г) число ячеек - 1000.
126
Ч. Чжан, И.С. Меньшов
0.8
а)
б)
0.4
x
0.0
x
0.0
0.5
1.0
0.8
0.6
в)
г)
0.3
0.4
0.0
0.0
x
x
0.0
0.5
1.0
0.0
0.5
1.0
Рис.13. Численные результаты задачи переноса 7-компонентной системы по схеме LD:
(а, б) число ячеек - 100, (в, г) число ячеек - 1000.
4.4. Двумерная задача переноса 4-компонентной системы. Рассмат-
ривается задача переноса 4-компонентной системы, которая изображена на
рис.14. Система в начальный момент представляется двумя окружностями
(O1, O2) и одной крестообразной областью (C), которые определяются сле-
дующими формулами:
O
B
1,1
, 0.5
,
1
O
B
1,1
, 0.7
,
2
C
0.8,1.2
0.4,1.6
0.4,1.6
0.8,1.2
Начальное распределение объемных долей компонент имеет вид
z
(x,
y
)
(x,
y
)
,
z
(x,
y)
(x,
y)
,
1
C
2
O
1
/C
3
z x,
y
)
(x,
y),
z x,
y
)
1
z x,
y).
3
O
2
/(CO
1
)
4
k
k 1
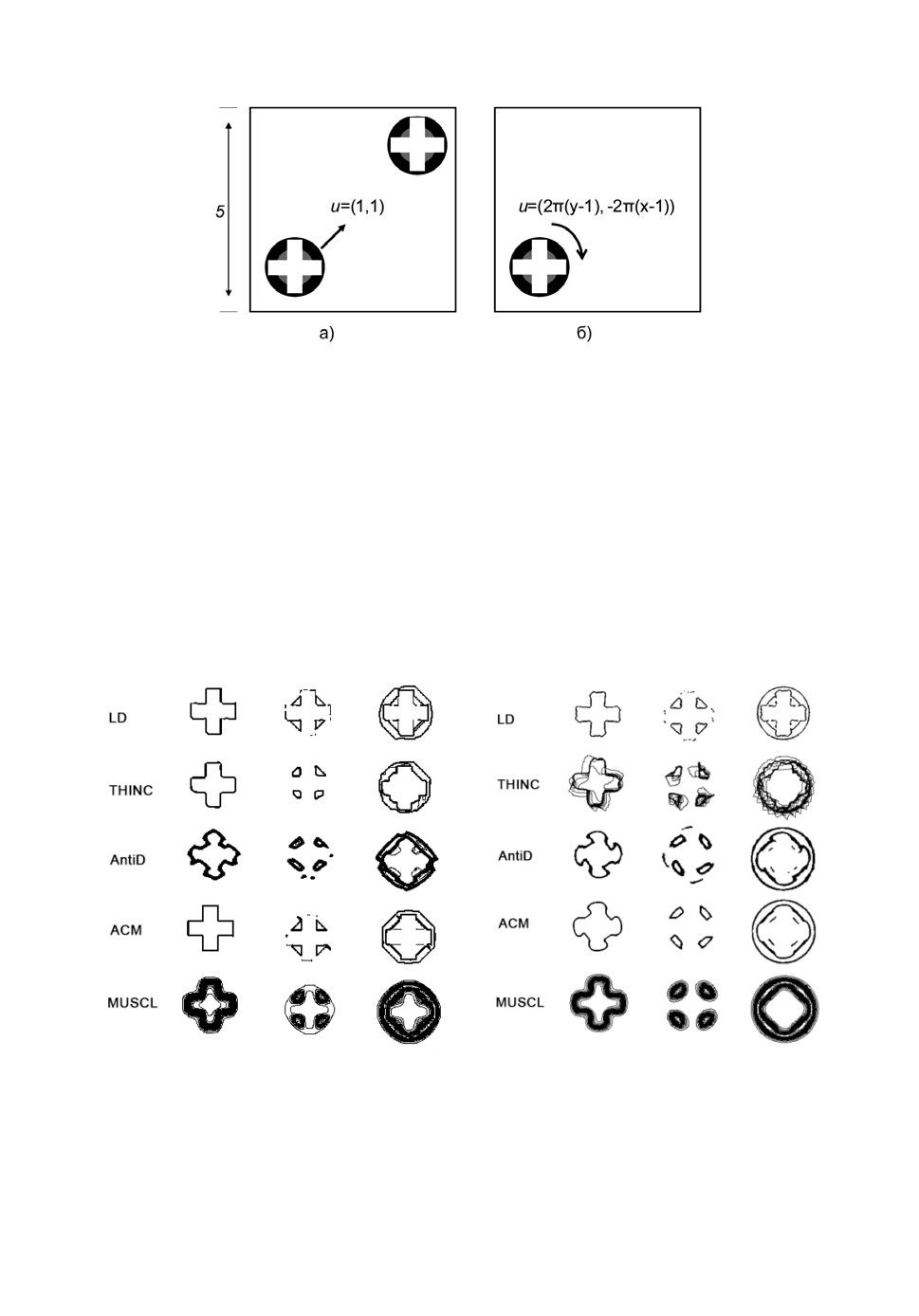
Рассматриваются следующие постановки: (а) трансляция материалов
вдоль диагонали со скоростью u = (1,1) и (б) вращение около точки (1,1).
Тестируются пять методов: (1) LD, (2) THINC, (3) AntiD, (4) ACM, (5)
MUSCL.
Сквозной метод расчета уравнений переноса многокомпонентной ...
127
Рис.14. Схема двумерной задачи переноса 4-х компонентной систе-
мы: (а) трансляция, (б) вращение.
Периодические граничные условия задаются на противоположных гра-
ницах. Вычисление проводится на сетке 400 × 400. Используется метод
Стрэнга (Strang) расщепления по направлению. Численные результаты по-
сле двух циклов (t = 10 с) переноса по диагонали представлены на рис.15а.
В результатах, полученных по смехе MUSCL, наблюдается сильное разма-
зывание межфазных границ. Другие методы разрешения межфазной грани-
цы эффективно уменьшают зону размазывания. Наиболее хорошее разре-
шение интерфейсов обеспечивается схемами LD и ACM.
z1
z2
z3
z1
z2
z3
а)
б)
Рис.15. Линии уровней объемных долей: (а) после двух циклов трансляции
вдоль диагонали, (б) после двух циклов вращения.
В схеме AntiD разрешение интерфейсов несколько хуже, чем в других
методах. Причем, распределение объемных долей искажается в результате
переноса. Можно уменьшить зону межфазной границы с помощью двойно-
128
Ч. Чжан, И.С. Меньшов
го применения схемы AntiD, но это приводит к еще более сильному иска-
жению ее формы.
Численные решения задачи в случае вращения, полученные после двух
циклов (t = 2c) по разным схемам, представлены на рис.15б. Как видно из
представленных результатов, точнее всего интерфейсы разрешаются здесь
также схемой LD. В распределениях объемных долей, полученных по схеме
THINC, наблюдаются осцилляции и достаточно сильное размазывание
межфазной границы. В распределениях объемных долей, полученных по
схемам AntiD и ACM, имеются сильные искажения формы границы.
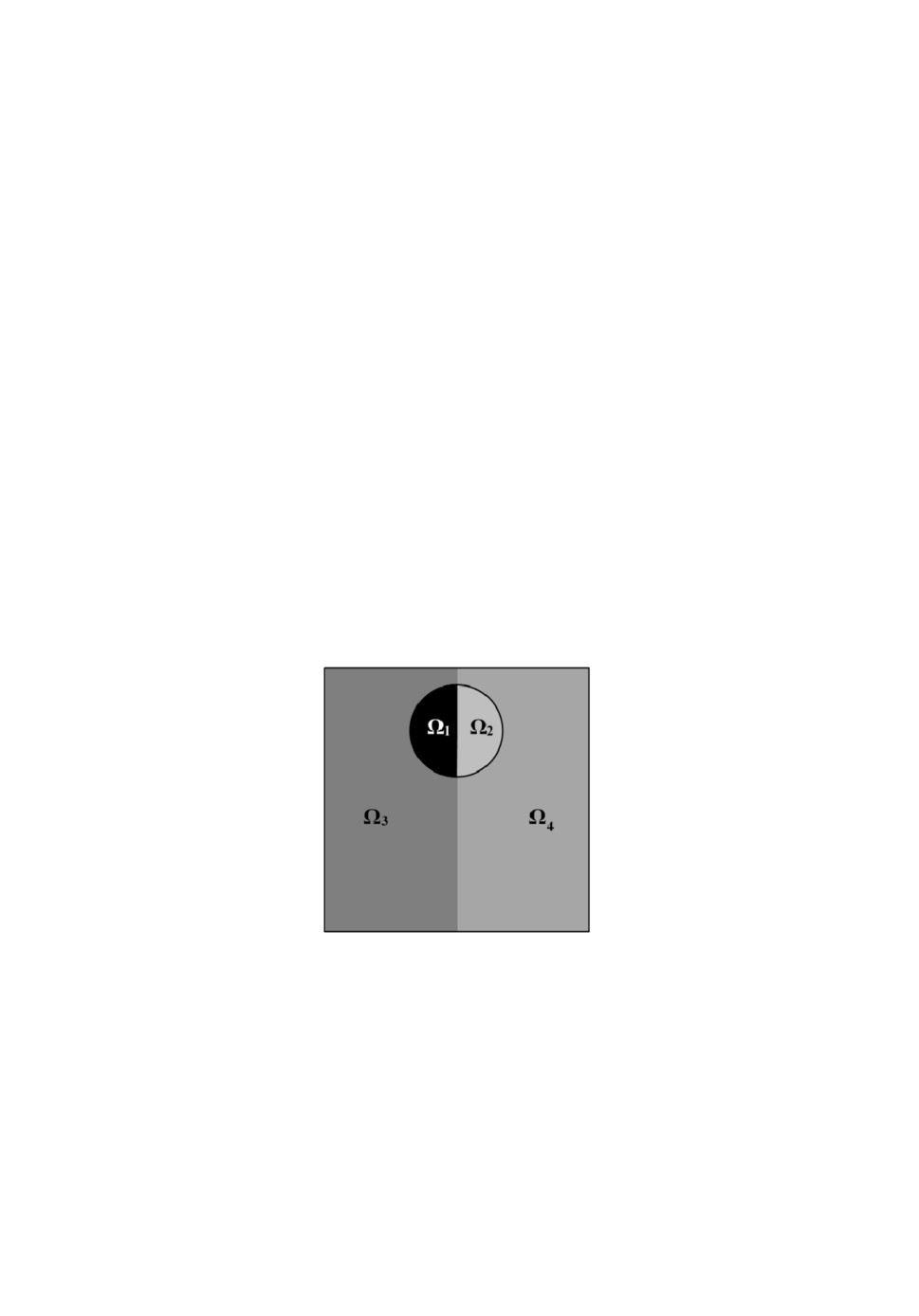
4.5. Перенос 4-компонентной системы в вихревом поле. В последнем
тесте мы рассматриваем перенос 4-компонентной системы вихревым полем
скорости. Начальное распределение компонент представлено на рис.16. Дли-
на стороны квадрата - 1.0. Центр окружности (Ω1+Ω2) - (0.50, 0.50), радиус -
0.15. В расчетной области в начальный момент находятся четыре разных
компонента. Объемные доли определяются по следующим формулам:
z x,
y)
(x,
y),
z x,
y)
(x,
y),
1
1
2
2
3
z (x, y)
(x,y), z (x,y)
1
z (x, y).
3
3
4
k
k 1
Рис.16. Схема задачи переноса в вихревом поле скорости.
Поле скорости сначала определяется вихревым распределением с на-
правлением по часовой стрелке,
2
2
u sin
(x)sin(2y), v sin
(y)sin(2x).
В момент времени t=1.0 направление вектора скорости мгновенно ме-
няется на противоположное, т.е. при t>1.0 распределение вектора скорости
становится
2
2
u sin
(x)sin(2y),
v sin
(y)sin(2x).
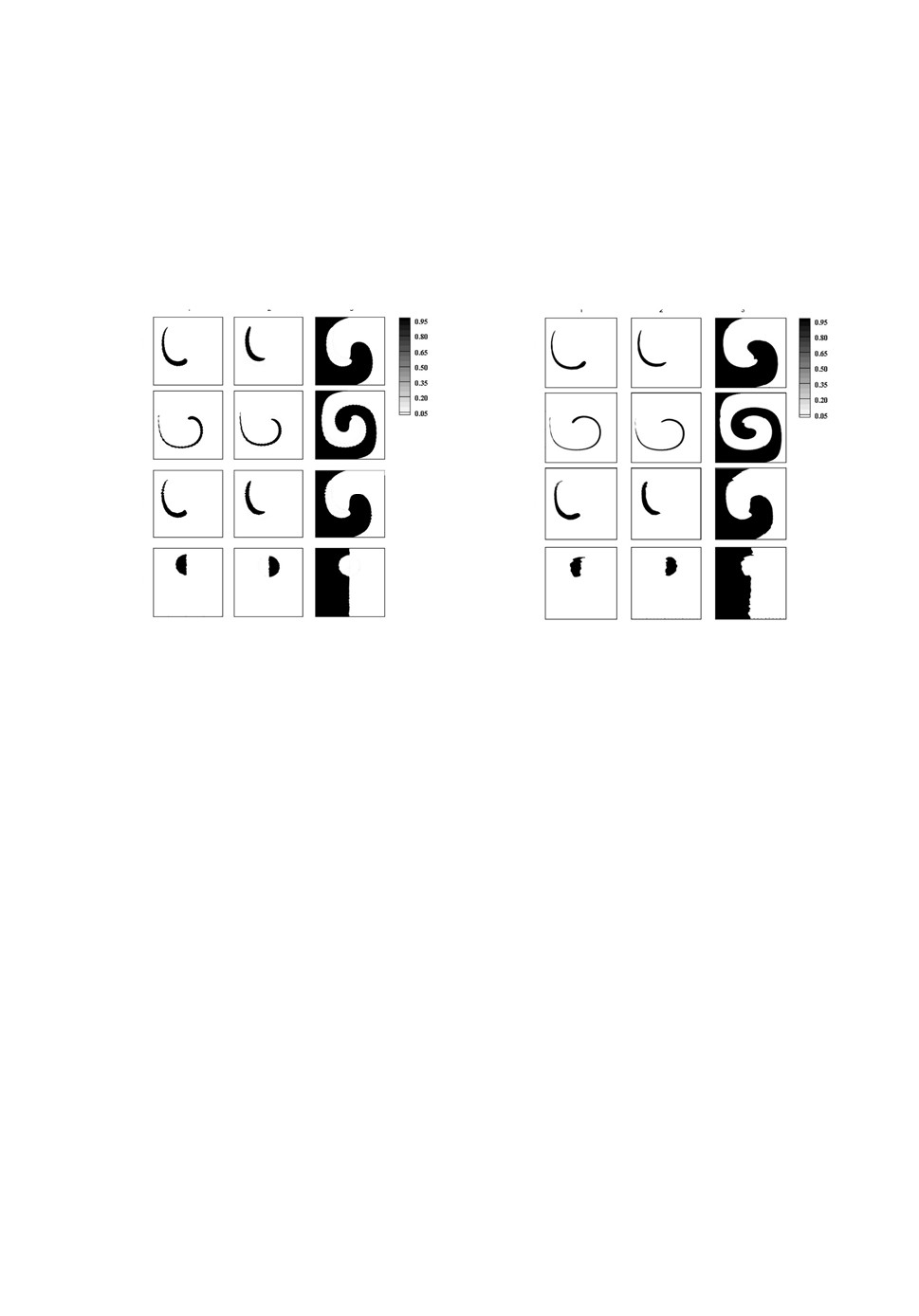
Сквозной метод расчета уравнений переноса многокомпонентной ...
129
Таким образом, к моменту времени t=2.0 система должна вернуться в
начальное состояние. В этом тесте мы тестируем только схемы LD и ACM,
которые наилучшим образом показали себя на предыдущих задачах. Вы-
числения проводятся на сетке 200×200. Численные результаты приведены,
соответственно, на рис.17а, б. Разрешение интерфейсов LD схемой почти
идеально. Метод ACM допускает искажение формы границы.
z1
z2
z3
z1
z2
z3
t=0.5
t=0.5
t=1.0
t=1.0
t=1.5
t=1.5
t=2.0
t=2.0
а)
б)
Рис.17. Распределения объемных долей, полученных в разные моменты времени:
t=0.5, 1.0, 1.5, 2.0: (а) методом LD, (б) методом ACM.
Заключение
В настоящей работе описан новый метод решения системы уравнений
переноса объемных долей многокомпонентной гетерогенной системы в за-
данном поле скоростей на неподвижных эйлеровых сетках. Метод гаранти-
рованно обеспечивает выполнение условий совместности объемных долей,
а именно: (1) объемная доля каждого компонента должна быть в диапазоне
[0,1] и (2) любая частичная сумма объемных долей не должна превышать
единицу. При этом метод совместим с разными TVD схемами и методами
разрешения межфазных границ. Метод прост и не требует существенных
изменений в расчетных схемах. Он протестирован на разных задачах со схе-
мами MUSCL (с ограничителями Minmod, Van Leer, Van Albada, Superbee),
THINC, LD, AntiD, AMC. Наилучшие свойства разрешения интерфейсов
были получены со схемой LD. Метод может быть применен к расчету
сквозным образом (на фиксированных эйлеровых сетках) несжимаемых и
сжимаемых течений многофазных сред с интерфейсами, что будет предме-
том наших будущих работ.
130
Ч. Чжан, И.С. Меньшов
СПИСОК ЛИТЕРАТУРЫ
1. Galera S., Maire P.H., Breil J. A two-dimensional unstructured cell-centered multi-
material ALE scheme using VOF interface reconstruction // J. Comput. Phys., 2010, v.229,
p.5755-5787.
2. Maire P.H., Abgrall R., Breil J., Ovadia J. A cell-centered Lagrangian scheme for two-
dimensional compressible flow problems // SIAMJ. Sci. Comput., 2007, v.29, p.1781-1824.
3. Glimm J., Li X.L., Liu Y.J., Xu Z.L., Zhao N. Conservative front tracking with improved
accuracy // SIAM J. Numer. Anal., 2003, v.41, p.1926-1947.
4. Terashima H., Tryggvason G. A front-tracking/ghost-fluid method for fluid interfaces in
compressible flows // J. Comput. Phys., 2009, v.228, p.4012-4037.
5. Mulder W., Osher S., Sethian J.A. Computing interface motion in compressible gas dynam-
ics // J. Comput. Phys., 1992, v.100, p.209-228.
6. Abgrall R. How to prevent pressure oscillations in multicomponent flow calculations: a
quasi-conservative approach // J. Comput. Phys., 1996, v.125, p.150-160.
7. Saurel R., Abgrall R. A multiphase Godunov method for compressible multifluid and mul-
tiphase flows // J. Comput. Phys., 1999, v.150, № 2, p.425-467.
8. Menshov I., Zakharov P. On the composite Riemann problem for multi-material fluid
flows // Int. J. Numer. Meth. Fluids, 2014, v.76, p.109-127.
9. Allaire G., Clerc S., Kokh S. A five-equation model for the simulation of interfaces be-
tween compressible fluids // J. Comput. Phys., 2002, v.181, p.577-616.
10. Jaouen S., Lagoutière F. Numerical transport of an arbitrary number of components //
Comput. Methods Appl. Math., 2007, v.196, p.3127-3140.
11. Després B., Lagoutière F. Contact discontinuity capturing schemes for linear advection,
compressible gas dynamics // J. Sci. Comput., 2001, v.16, p.479-524.
12. Xiao F., Honma Y., Kono T. A simple algebraic interface capturing scheme using hyper-
bolic tangent function // Int. J. Numer. Mech. Fluids, 2005, v.48, p.1023-1040.
13. So K.K., Hu X.Y., Adams N.A. Anti-diffusion method for interface steepening in two-phase
incompressible flow // J. Comput. Phys., 2011, v.230, p.5155-5177.
14. So K.K., Hu X.Y., Adams N.A. Anti-diffusion interface sharpening technique for two-phase
compressible flow simulations // J. Comput. Phys., 2012, v.231, p.4304-4323.
15. Harten A. The artificial compression method for computation of shocks and contact discon-
tinuities, I: single conservation laws // Commun. Pure Appl. Math., 1977, v.30, p.611-638.
16. Harten A. The artificial compression method for computation of shocks and contact dis-
continuities, III: self-adjusting hybrid schemes // Math. Comput., 1978, v.32, p.363-389.
Поступила в редакцию 18.06.2018
После доработки 18.06.2018
Принята к публикации 19.11.2018