МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 5, стр. 20-38
РАССЕЯНИЕ ЗВУКА ТЕРМОУПРУГИМ ШАРОМ
С НЕПРЕРЫВНО-НЕОДНОРОДНЫМ ПОКРЫТИЕМ
В ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
©
2019 г.
Н.В. Ларин, Л.А. Толоконников
Тульский государственный университет
Larinaelen@mail.ru
Исследование выполнено за счет гранта РНФ (проект 18-11-00199).
DOI: 10.1134/S0234087919050022
Решены прямая и обратная задачи дифракции плоской гармонической звуковой
волны на термоупругом шаре с покрытием в виде радиально-неоднородного тер-
моупругого сферического слоя, граничащем с невязкой теплопроводной жидко-
стью. Колебания шара с покрытием рассматриваются в рамках линейной модели
связанной термоупругости. Определены волновые поля в сферическом теле и вне
его. Представлены результаты расчетов частотной и угловой зависимостей ампли-
туды рассеянного акустического поля в дальней зоне. Показано существенное от-
личие характеристик рассеяния звука для термоупругого и упругого тел. Осущест-
влено моделирование покрытия, обеспечивающего наименьшее рассеяние звука в
заданных диапазоне частот и угловом секторе наблюдения. Построены функциона-
лы, выражающие интенсивность звукоотражения, и представлен алгоритм их ми-
нимизации, основанный на комбинации методов случайного поиска и покоорди-
натного спуска. Найдены законы неоднородности термоупругого покрытия с оп-
тимальными звукоотражающими свойствами.
Ключевые слова: прямая и обратная задачи дифракции, звуковая волна, термоуп-
ругий шар, неоднородный термоупругий слой, теплопроводная жидкость.
SOUND SCATTERING
BY THE THERMOELASTIC CONTINUOUSLY-INHOMOGENEOUS
COVERED SPHERE IN HEAT-CONDUCTING FLUID
N.V. Larin, L.A. Tolokonnikov
Tula State University, Tula region
In the project we solved direct and inverse problems of the plane harmonic acoustic wave
diffraction on the thermoelastic sphere covered with radially inhomogeneous thermoelas-
tic spherical layer, bounded by inviscid heat-conducting fluid. Coated ball vibrations are
considered in terms of the linear model of coupled thermoelasticity. The wave fields are
Рассеяние звука термоупругим шаром …
21
defined in a spherical body and outside it. The results of calculations of the frequency
and angular dependences of the amplitude of the scattered acoustic field in the far zone
are presented. We showed the essential difference between the characteristics of sound
scattering for thermoelastic and elastic bodies. In the project we modeled the coating,
which provides the smallest scattering of a sound in a given frequency range and angular
observation sector. Functionals expressing the intensity of sound reflection were con-
structed, as well as an algorithm for its minimization. The algorithm is based on the
combination of random search and coordinate descent methods. We discovered the in-
homogeneity laws of the thermoelastic coating with optimal sound-reflecting properties.
Key words: direct and inverse problems of diffraction, acoustic wave, thermoelastic
sphere, inhomogeneous thermoelastic layer, heat-conducting fluid.
1. Введение
Создание покрытий, обеспечивающих требуемые звукоотражающие
свойства тел, является актуальной проблемой. Моделировались различные
типы покрытий, наносимых на твердые тела. Например, в [1] рассмотрены
прямая и обратная задачи дифракции плоской звуковой волны на цилиндре
с перфорированным покрытием. В [2] обсуждаются задачи о нерассеиваю-
щем покрытии с протяженной реакцией, делающем тело акустически неви-
димым. В [3] выявлены условия, при которых совместный выбор импедан-
сов однородного покрытия и упругой цилиндрической оболочки позволяет
минимизировать рассеянное поле.
Требуемые звукоотражающие свойства тел, в том числе сферической
формы, можно получить с помощью непрерывно-неоднородного упругого
покрытия, если подобрать соответствующие законы неоднородности для
его механических параметров [4]. Такое покрытие можно моделировать
системой однородных упругих слоев [5]. В указанных выше работах тепло-
вые процессы в телах не учитывались.
Реальный процесс деформирования тела от воздействия на него звуко-
вой волны сопровождается изменением температурного поля. Изучению
процессов деформирования упругих тел при наличии температурных полей
(термоупругих тел) посвящены, например, работы [6, 7], в которых взаимо-
действие звуковых волн с термоупругими телами не рассматривалось. В [8]
показано, что характеристики рассеяния звука для термоупругого сфериче-
ского тела могут значительно отличаться от соответствующих характери-
стик для упругого тела.
В настоящей работе при моделировании покрытия шара с оптималь-
ными звукоотражающими свойствами учитывается взаимодействие процес-
сов деформирования и теплопроводности в упругом рассеивателе.
22
Н.В. Ларин, Л.А. Толоконников
2. Прямая задача
Рассмотрим однородный изотропный термоупругий шар радиуса r0,
плотность материала которого ρ0, упругие постоянные λ0 и μ0, температур-
0
0
ный коэффициент линейного расширения
, теплопроводность
, объ-
T
T
0
емная теплоемкость
. Начало сферической системы координат r, θ, φ сов-
c
падает с центром шара. Шар имеет покрытие в виде изотропного термоуп-
ругого сферического слоя с внешним радиусом r1. Полагаем, что модули
упругости λ и μ, температурный коэффициент линейного расширения αT и
теплопроводность λT материала покрытия являются дифференцируемыми
функциями координаты r, а плотность материала покрытия ρ и его объем-
ная теплоемкость cε - непрерывными функциями координаты r. Источники
тепла в теле отсутствуют. Окружающая тело жидкость - невязкая теплопро-
водная, ее равновесная плотность ρf, скорость звука c, отношение удельных
теплоемкостей при постоянных давлении и объеме γ, теплопроводность λT,
температуропроводность χT, коэффициент температурного расширения αT. В
невозмущенном состоянии тело и жидкость имеют одну и ту же постоян-
ную температуру T0.
Пусть из внешнего пространства на шар с покрытием падает плоская
звуковая волна. Без ограничения общности будем полагать, что волна рас-
пространяется в направлении θ=0. Тогда в сферической системе координат
потенциал скорости падающей волны имеет вид Ψ0 = Aexp[i(k1rcosθ - ωt)] и
может быть представлен разложением [8]
n
(r,,t) exp(
)
j
(k
r P (cos),
Ai
(2n1),
0
n n
1
n
n
n0
где A - амплитуда волны; k1 - волновое число звуковых волн в жидкости; ω -
круговая частота; t - время; jn(x) - сферическая функция Бесселя порядка n;
Pn(x) - многочлен Лежандра степени n.
При падении плоской звуковой волны, распространяющейся в невязкой
теплопроводной жидкости на термоупругое тело, в жидкости возникают
рассеянная звуковая и возбужденная тепловая волны. Само тело деформи-
руется, его температура изменяется.
Определим волновые поля вне термоупругого тела и внутри него.
Ввиду осевой симметрии задачи и свойств материалов шара и покры-
тия, искомые волновые поля не будут зависеть от координаты φ.
Определим волновые поля в жидкости, воспользовавшись полной сис-
темой линеаризованных уравнений гидродинамики вязкой теплопроводной
Рассеяние звука термоупругим шаром …
23
жидкости [9, 10], состоящей из уравнений: Навье-Стокса, неразрывности,
притока тепла и физического состояния, которые соответственно имеют вид
v
gradp
v
graddivv ,
f
t
3
s
divv
0,
t
T
s
T
,
t
t
2
p
с
s
T
,
f
t
t
t
где v - скорость частиц жидкости; ν и ς - коэффициенты вязкости; p, s и Θ -
акустические давление, сжатие и температура соответственно; βT - коэффи-
циент пропорциональности (1 + αT βT = γ). Так как рассматриваем устано-
вившийся режим колебаний с временным множителем exp(-iωt), то здесь и
далее дифференцирование по t в уравнениях заменяем умножением на -iω,
временной множитель опускаем. В предположении отсутствия вязкости
жидкости (ν = ς = 0) представим вектор скорости в виде
v grad(
),
0
1
2
где Ψ1 и Ψ2 - потенциалы рассеянной телом звуковой и возбужденной теп-
ловой волн соответственно. В результате из приведенной выше системы
уравнений приходим к уравнениям Гельмгольца
2
k
0,
q 1,2,
q
q q
где k2 - волновое число тепловых волн в жидкости. При этом в предполо-
жении выполнения условия ωχT/c2 << 1 будем иметь
1
2
k
,
k
(1i)
1
2
c
2T
Учитывая условия излучения на бесконечности, отвечающие уходя-
щим от тела волнам, функции Ψ1 и Ψ2 будем искать в виде
(r,)
V
h
(k r P (cos), q 1,2,
(1)
q
qn n q n
n0
где hn(x) - сферическая функция Ганкеля первого рода порядка n.
24
Н.В. Ларин, Л.А. Толоконников
Волновые поля в однородном изотропном шаре определим на основе
системы уравнений линейной связанной динамической задачи термоупру-
гости [6], состоящей из уравнения движения
0
0
0
0
0
0
0
0
0
0
2
2
u
(
)grad divu
(3
2
)
gradT
(
u/t
)
T
и уравнения теплопроводности
0
0
u
T
0
0
0
0
0
0
T
(3
2
)
T
div
c
,
T
T
0
t
t
где u0 и T0 - cмещение частиц и изменение температуры в шаре соответст-
венно. Из данной системы уравнений, с учетом представления
0
u
grad(
) rotФ
,
1
2
3
получаем уравнения Гельмгольца
2
2
0,
Ф
Ф
0
,
q 1,2,
q
q q
3
3
3
где κq (q = 1,2) и κ3 - волновые числа продольных термоупругих и попереч-
ных упругих волн соответственно. При этом
2
2
k
l
0
q
0
2
0 2
1(1
) (1)
12(1
)
(1
)
,
,
q
3
2
c
где
2
1
2
k
T
,
k
(1i),
k
,
T
l
k
2
c
l
T
l
2
1
2
1
2
0
0
0
0
0
0
0
(3
2
T
)T
0
2
T
0
c
,
,
,
,
l
0
c
0
0
0
0
0
T c
(
2
)c
kT и kl - волновые числа продольных тепловых и упругих волн соответст-
венно; cl и cτ - скорости продольных и поперечных упругих волн соответст-
венно; χT - температуропроводность; ε0 - параметр связанности.
В силу осевой симметрии задачи Φ3 = Φ3(r,θ)eφ, где eφ - единичный
вектор оси φ. Тогда векторное уравнение Гельмгольца сведется к одному
скалярному уравнению
2
2
Ф
(
1/sin
θ)Ф
0.
3
3
3
Рассеяние звука термоупругим шаром …
25
Учитывая условие ограниченности, функции Φ1, Φ2, Φ3 будем искать в виде
(r,),
(r,),
(r,)
1
2
3
(2)
d
W
j
(
r),W
j
(
r),W
j
(
r)
P
(cos).
1n n
1
2n n
2
3n n
3
n
d
n0
Волновые поля в неоднородном покрытии опишем системой уравне-
ний линейной связанной динамической задачи термоупругости неоднород-
ного изотропного тела [7], которая включает общие уравнения движения
сплошной среды
2
1
u
rr
r
r
1(2
ctg )
,
(3)
rr
r
2
r
r
r
t
2
1
u
r
1[(
)ctg3
r
]
2
r
r
r
t
и уравнение притока тепла
2
2
T
2
T
T
T
T
T
u
T
ctg
T
div
c
,
(4)
T
T
0
2
2
2
r
r
r
r
t
t
где штрихом обозначена производная по координате r. Компоненты тензора
напряжений σrr, σrθ, … связаны с компонентами тензора деформаций εrr, εrθ,
… и изменением температуры T в покрытии соотношениями Дюгамеля-
Неймана [7]
2
div
uT
k r,,
,
2
,
(5)
kk
kk
r
r
где
u
1
u
1
r
,
u
,
u
u
ctg
,
rr
r
r
r
r
r
1
1
u
u
r
u
,
divu
,
3
,
r
rr
2
r
r
ur и uθ - компоненты вектора смещения u в покрытии.
Функции ur, uθ и T будем искать в виде разложений
d
u r,),
u r,),
T r,)
U r),U r)
,U r)
P
(cos)
(6)
r
1n
2n
3n
n
d
n
0
26
Н.В. Ларин, Л.А. Толоконников
Подставляя ряды (6) в уравнения (3) и (4), получим систему линейных
обыкновенных дифференциальных уравнений второго порядка относитель-
но функций Umn(r) (m = 1,2,3) для каждого значения n = 0,1,2,…
A
U B
UC
U
0,
U
U
,U
,U
T,
(7)
n n
n n
n n
n
1n
2n
3n
где
A
diag
a
,a
,a
,
B
(b
)
,
C
(c
)
,
n
11
22
33
n
ms
n
ms
33
a
2 ,
a
,
a
,
11
22
33
T
2( )
b
2
,
b
n(n1)
,
b
,
11
12
13
r
r
2
2T
b
,
b
,
b
b
0
,
b
iT
,
b
,
21
22
23
32
31
0
33
T
r
r
r
2
2( )n(n
1)
2
n(n1)
3
c
,
c
,
c
,
11
2
12
13
r
r
r
r
1
2( )
2
2
c
,
с
n(n
1)
,
c
,
21
22
2
23
r
r
r
r
r
2iT
iT
0
0
c
,
c
n
(n 1)
,
c
n(
n1)T
31
32
33
2
r
r
r
Индекс n, которым должны быть снабжены элементы матриц, здесь и в
дальнейшем для простоты записи опускаем.
Граничные условия на внешней поверхности покрытия включают ра-
венство нормальных скоростей частиц термоупругой среды и жидкости, ра-
венство нормального напряжения и акустического давления, отсутствие
тангенциального напряжения, непрерывность акустической температуры и
теплового потока:
T
T
rr
iu
,
p
,
0
,
T ,
(8)
1:
r
r
rr
r
T r
r
На внутренней поверхности покрытия должны быть непрерывны ком-
поненты вектора смещения частиц взаимодействующих однородной и не-
однородной термоупругих сред, нормальные и тангенциальные напряже-
ния, температура и тепловой поток:
0
0
0
0
0
0
T
0
T
rr
u
u
,
u u
,
,
,
T T
,
(9)
0:
r
r
rr
rr
r
r
T
T
r
r
Рассеяние звука термоупругим шаром …
27
Нормальная компонента скорости частиц жидкости, акустическое дав-
ление и акустическая температура определяются выражениями
(
)
r
,
p i
(
),
r
0
1
2
f
0
1
2
i
1
(
)
(
)
0
1
2
0
1
2
T
2
c
В однородном шаре составляющие вектора смещения и изменение
температуры определяются выражениями
0
1
0
1
u
(
)
(sin
),
u
(
)
(r
)
,
r
1
2
3
1
2
3
r
rsin
r
r
2
0
0
0
2
T
k
(
) (
),
l
1
2
1
2
0
(3
2
)
0
0
T
0
0
а для компонентов тензора напряжений
,
остаются справедливыми
rr
r
соотношения (5), в которых функции λ, μ, αT следует заменить постоянными
0
λ0, μ0,
соответственно.
T
Из первого и четвертого граничных условий (8) находим выражения
для коэффициентов отражения V1n, V2n
1
1
T
rr
V
(D
E
)U
D
a ,
V
(V
,V
)
,
(10)
1:
n
n n n
n n
n
1n
2n
где
a
k
j
(k
r),
j
(k
r)T
,
D
(
d
)
,
E
(
)
,
n
1
n
1
1
n
1
n
n
q
22
n
e
m
23
2
k
i
q
d
k
h
(k r) ,
d
h
(k r),
,
q 1,2,
1q
q n q
2q
q n q
q
T
2
c
e
i,
e
e
e
e
0
,
e
1
11
12
13
21
22
23
Из оставшихся трех граничных условий (8) находим
rr
A
U F
U G
V b
,
(11)
1:
n n
n n
n n
n
где
T
T
b
i
j
(k
r),0,
k j
(k
r)
,
F
(
f
)
,
G
(g
)
,
n
f n
1
11
n
1
n
n
ms
n
mq
32
f
2
r,
f
n(n 1) r ,
f
,
11
12
13
28
Н.В. Ларин, Л.А. Толоконников
f
r,
f
r,
f
f
f
f
0
,
21
22
23
31
32
33
T
g
i
h
(k
r),
g
0,
g
k h
(k r), q 1,2.
1q
f n
q
2q
3q
q q n q
После подстановки выражения (10) в формулу (11) получаем краевые усло-
вия для системы дифференциальных уравнений (7) на внешней поверхности
покрытия
1
rr
A
U L
U c
,
(12)
1:
n n
n n
n
где
(1)
1
1
L
F
G
(D
E
),
c
b
(G
D
)a
n
n
n n n
n
n
n n
n
Теперь рассмотрим граничные условия (9). Из условий непрерывности
компонентов вектора смещения и температуры находим выражения для ко-
эффициентов Wmn (m = 1,2,3)
1
rr
W
T
U
,
W
W
,W
,W
T,
(13)
0:
n
n
n
n
1n
2n
3n
где
1
1
T
(
t
)
,
t
Z
,
t
n(n
1) Z
,
t
Z
,
n
ms
33
1q
1q
13
03
2
q
0q
r
r
0
0
1
2
2
2
t
Z
Z
,
t
Z
,
t
0
,
(k
),
23
03
13
3q
q
0q
33
q
l
q
0
0
0
r
(3
2
)
T
Z
j
( r),
Z
j
( r),
q 1,2, m 1,2,3.
0m n m
1m m n m
Из условий непрерывности компонентов тензора напряжений и теплового
потока находим
rr
A
U F
U Y
W ,
(14)
0:
n n
n n
n n
где
0
0
2
1
Y
(
y
)
,
y
2
Z
Z
,
y
n(n
1)
Z
Z
,
n
ms
33
1q
2
q
q
0q
13
03
13
r
r
0
2
1
0
1
y
Z
Z
,
y
2n
n1
Z
Z
,
2
q
1q
0q
23
03
23
2
r
r
r
0
y
Z
,
y
0
,
3q
T q
1q
33
0
2
0
0
2
2
2
(
2
)k
,
Z
j
(
r),
q1,2, m1,2,3.
q
q
l
2m m n m
Рассеяние звука термоупругим шаром …
29
После подстановки выражения (13) в формулу (14) получаем краевые усло-
вия для системы дифференциальных уравнений (7) на внутренней поверх-
ности покрытия
(0)
rr
A
U L
U
0,
(15)
0:
n n
n n
(0)
1
где
L
F
Y
T
n
n
n n
Таким образом, система уравнений для малых возмущений неоднород-
ного термоупругого покрытия сведена к краевой задаче (7), (12), (15), ре-
шив которую и определив по выражениям (10), (13) коэффициенты V1n, V2n,
W1n, W2n, W3n в рядах (1), (2), получаем возможность исследовать волновые
поля в термоупругом теле и вне его.
Рассмотрим дальнюю зону акустического поля. Используя асимптоти-
ческую формулу для сферической функции Ганкеля первого рода при
больших значениях аргумента, из равенства (1) при q = 1 находим
Ar
1
2
n1
(r,)
exp(ik
r)F(
,
F(
(i)
V
P
(cos),
(16)
1
1
1n n
2r
Ak
r
11
n0
где ϖ = k1r0 волновой размер шара без покрытия.
Были проведены расчеты амплитуды рассеяния звука |F(ϖ,θ)| для шара
радиуса r0=1 м с покрытием толщиной 0.1 м, находящегося в воде (ρf =
=1000 кг/м3, c = 1485 м/с, γ = 1.006, λT = 0.59 Вт/(м·K), χT=1.43·10-7 м2/c, αT =
= 2.1·10-4 1/K, T0 = 293 K). Амплитуда падающей волны полагалась равной
единице.
Расчеты проводились для неоднородных покрытий, физико-механичес-
кие характеристики которых менялись по толщине сферического слоя по
линейным законам
1
(r)
1
0.5(r r
) (r
r
)
,
0
1
0
1
1
1
1
1
(r)
,
(r)
,
(r)
,
(r
)
,
c (r) c
,
r
rr
,
T
T
T
T
0
1
1
1
1
где ρ1, λ1, μ1,
,
λ
c
- плотность, упругие постоянные, температурный
T
T ,
коэффициент линейного расширения, теплопроводность и объемная тепло-
емкость материала однородного покрытия соответственно.
Физико-механические характеристики материалов шара (алюминий) и
однородного покрытия (поливинилбутираль) приведены в табл.1. Здесь же
приведены значения параметра связанности εj для этих материалов.
30
Н.В. Ларин, Л.А. Толоконников
Таблица 1. Физико-механические характеристики материалов.
j
j
j
j
ρj, кг/м3
λj, Н/м2
μj, Н/м2
, 1/K
, Вт/(м·K)
, Дж/(м3·K)
εj
T
T
c
0
2700
5.3·1010
2.6·1010
25.5·10-6
236
2.3·106
0.035
1
1070
3.9·109
9.8·108
2.3·10-4
0.2
1.2·106
0.411
Для оценки влияния термоупругости материалов однородного шара и
его покрытия на рассеяние звука расчеты проводились также для упругого
шара с упругим покрытием и для упругого шара с термоупругим покрыти-
ем. При этом рассматривалось покрытие с плотностью ρ = ρ+(r).
Краевая задача (7), (12), (15) решена методом сплайн-коллокации [8].
На отрезке [r0, r1] введена равномерная сетка. Решение краевой задачи
ищется в виде трех кубических сплайнов дефекта 1 с узлами на введенной
сетке, приближающих функции U1n(r), U2n(r), U3n(r) соответственно. Сплай-
ны представляются в виде разложений по базису из нормализованных ку-
бических B-сплайнов. Полагалось, что искомые сплайны удовлетворяют
системе (7) и краевым условиям (12), (15) в узлах коллокации, совпадаю-
щих с узлами сетки. Для контроля точности приближенного решения крае-
вой задачи (для каждого значения n) расчеты проводились на сгущающихся
сетках, причем каждая следующая сетка была в два раза мельче предыду-
щей. Вычисления заканчивались, когда относительная погрешность значе-
ний Umn(rj) (m=1,2,3, j = 0,1) на последней паре сеток не превосходила 0.1%.
При суммировании ряда (16) индекс n изменялся до значения n=2[ϖ] +
+3, где [ ] - целая часть числа. Для рассматриваемых частот увеличение n
практически не сказывается на результатах расчетов.
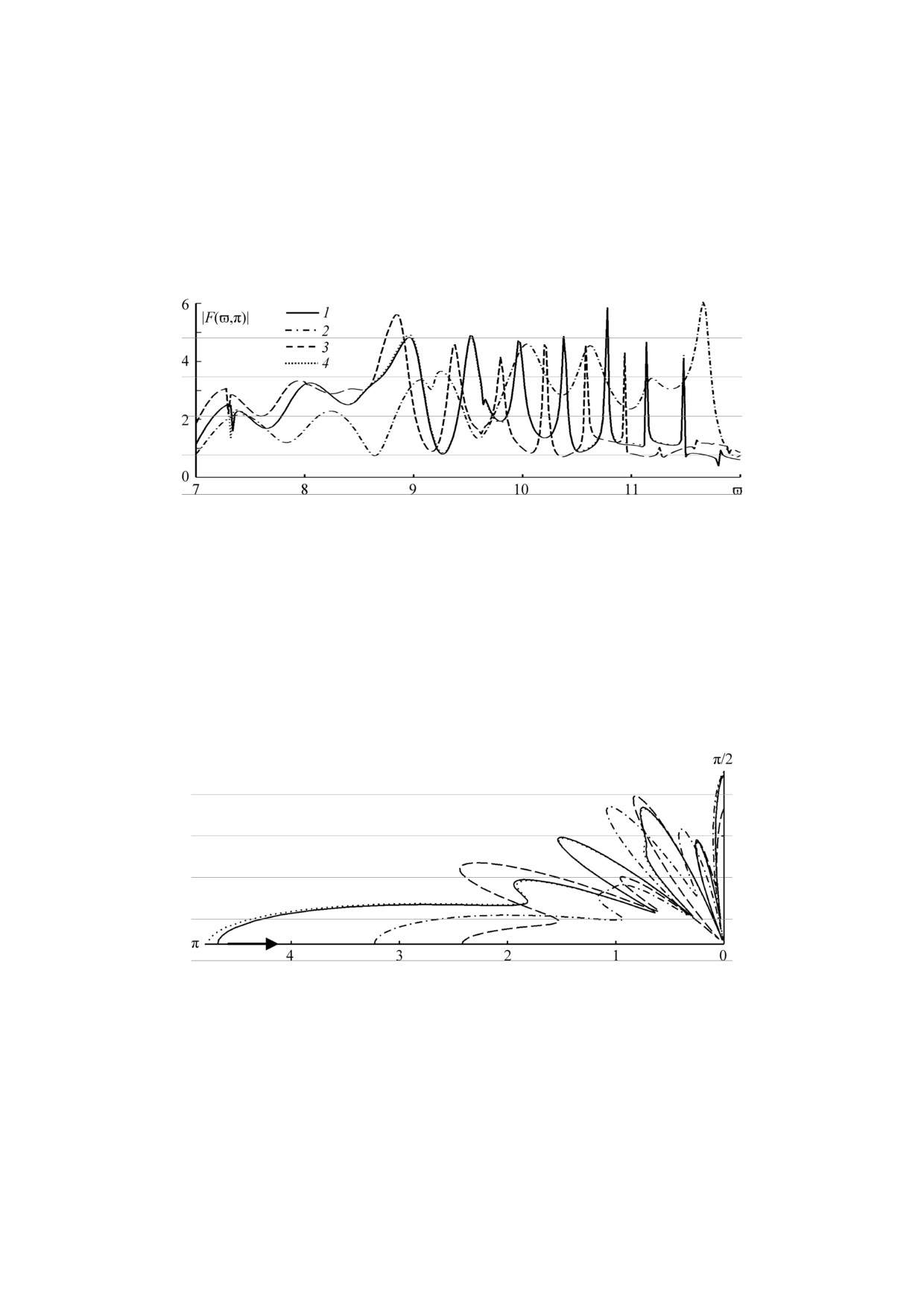
На рис.1 приведены графики зависимости амплитуды обратного рас-
сеяния звука от волнового размера шара (|F(ϖ,π)|) в интервале 7 ≤ ϖ ≤ 12.
Заметим, что расчеты в области ϖ < 7 показали, что как неоднородность ма-
терила покрытия, так и термоупругость рассматриваемых материалов шара
и его покрытия слабо влияют на величину |F(ϖ,π)|. Однако с увеличением
волнового числа картина заметно меняется, что видно из рис.1. Сравнение
кривых 1 и 2 показывает существенное различие частотных зависимостей
при разных законах неоднородности материала покрытия, а сравнение кри-
вых 1 и 3 - существенное различие частотных зависимостей в термоупру-
гом и чисто упругом случаях. Почти полное совпадение кривых 1 и 4 по-
зволяет сделать вывод, что основной вклад в совместное влияние термоуп-
ругости материалов шара и его покрытия на отраженное акустическое поле
вносит термоупругость материала покрытия. Это объясняется тем, что в ме-
Рассеяние звука термоупругим шаром …
31
таллическом шаре взаимовлияние полей деформации и температуры суще-
ственно слабее, чем в полимерном покрытии (значение параметра связанно-
сти для алюминия на порядок ниже, чем для поливинилбутираля (табл.1)).
Заметим, что в [6, 11] отмечалось, что для материалов, обладающих боль-
шим параметром связанности, могут существенно различаться решения свя-
занной и несвязанной динамических задач термоупругости.
Рис.1. Зависимость амплитуды обратного рассеяния звука от волнового размера шара:
1 (2) термоупругий шар с термоупругим покрытием с плотностью ρ = ρ+(r) (ρ
= ρ-(r)), 3 (4) упругий шар с упругим (термоупругим) покрытием с плотно-
стью ρ = ρ+(r).
На рис.2 представлены диаграммы направленности рассеянного аку-
стического поля в освещенной области (π/2 ≤ θ ≤ π) для частоты, соответст-
вующей волновому числу ϖ = 9. Стрелкой показано направление распро-
странения падающей плоской волны. Видно, что на рассматриваемой часто-
те неоднородность материала покрытия, а также учет термоупругости рас-
сматриваемых материалов шара и его покрытия заметно влияют на зависи-
мость |F| от угла θ.
Рис.2. Полярные диаграммы направленности рассеянного акустического поля
при ϖ = 9 (обозначения приведены на рис.1).
32
Н.В. Ларин, Л.А. Толоконников
3. Обратная задача
Для достижения заданных звукоотражающих свойств рассеивателя тре-
буется решить проблему определения законов неоднородности термоупру-
гого материала покрытия по известному акустическому полю, то есть при-
ходим к необходимости решать коэффициентную обратную задачу. Число
работ, в которых рассматривались коэффициентные обратные задачи термо-
упругости, невелико. В известных работах для нахождения параметров или
функций, характеризующих неоднородность, используется сопоставление
теоретических и измеряемых величин в некоторой области, например,
[12-15]. В [16] при решении обратной задачи предложен подход, использу-
ющий исключительно решение прямой задачи дифракции звука и не требую-
щий экспериментальных замеров акустических откликов. Такой способ при-
менен при решении обратных задач в [4, 17, 18] и будет использован ниже.
На основе решения прямой задачи определим законы неоднородности
материала покрытия, для которых будем иметь наименьшее рассеяние звука
в заданном диапазоне частот ϖ1 ≤ ϖ ≤ ϖ2, при фиксированном угле наблю-
дения θ = θ*, а также в заданном угловом секторе наблюдения θ1 ≤ θ ≤ θ2 при
фиксированной частоте ϖ = ϖ*.
Будем считать, что функции ρ(r), λ(r), μ(r), αT(r), λT(r), cε(r) аппрокси-
мированы многочленами второй степени относительно переменной r, то
есть будем рассматривать следующие параболические законы неоднород-
ности термоупругого материала покрытия:
1
(r)
(r)
,
(17)
где
(0)
(1)
(2)
2
(r)
r
r
,
(18)
η1 - характерная величина материала покрытия. Здесь и далее под симво-
лом η подразумеваем каждую из величин ρ, λ, μ, αT, λT, cε.
Построим функционалы I1 и I2 вида
2
1
2
,,
,
,
F(,
)
d,
(19)
1
T T c
2
1
1
2
1
2
,,
,
,
F(
,)
d,
2
T T c
2
1
1
определенные на классе параболических функций (17) и выражающие
усредненные интенсивности рассеяния звука в заданных диапазоне частот и
угловом секторе наблюдения соответственно.
Рассеяние звука термоупругим шаром …
33
Для каждого функционала найдем такие значения коэффициентов
функций (18), при которых он достигает минимального значения.
Для функций (18), определенных на отрезке [r0, r1], введем ограничения
C
(r) C
,
(20)
1
2
где C1η и C2η некоторые положительные константы.
Геометрически каждое из неравенств (20) задает в прямоугольной сис-
теме координат с осью абсцисс r и осью ординат f бесконечное множество
кривых, лежащих в прямоугольной области
(0)
(1)
(2)
(
,
,
) ={(r, f ): r
r r
,
C
f
C
},
0
1
1
2
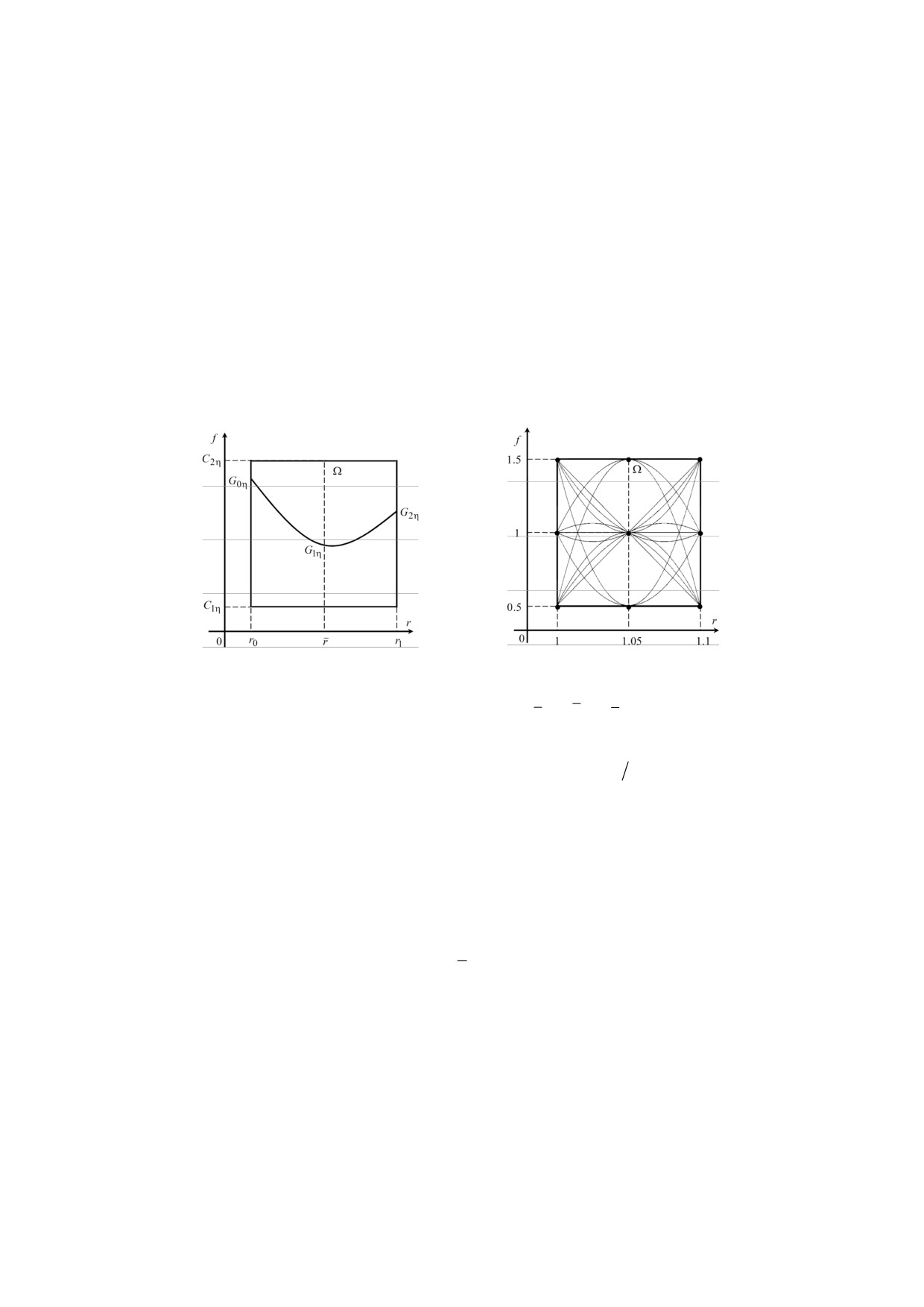
показанной на рис.3а
а
б
Рис.3. Область Ω(η(0), η(1), η(2)) = {(r, f): r0 ≤ r ≤ r1, C1η ≤ f ≤ C2η} и допустимые
параболические зависимости для функций (r) , (r) , (r) .
В области Ω(η(0), η(1), η(2)) каждую параболу будем определять тремя
точками G0η(r0, f0η),
G
(r, f
)
G2η(r1, f2η), где
r (r
r
) 2, fqη ϵ [C1η, C2η]
1
1
,
0
1
(q = 0,1,2).
Подставляя координаты точек G0η, G1η, G2η в выражение (18), приходим
к системе трех линейных уравнений с неизвестными η(0), η(1), η(2). Решая
полученную систему, находим
1
(0)
(1)
(2) T
η
R
f
,
η(
,
,
) ,
(21)
2
1
r
r
0
0
T
2
где
f
(f
,f
,f
)
,
R
1
r r
.
0
1
2
2
1
r
r
1
1
34
Н.В. Ларин, Л.А. Толоконников
Выбирая из отрезка [C1η, C2η] значения для ординат f0η, f1η, f2η и вычис-
ляя с помощью соотношений (21) значения коэффициентов η(0), η(1), η(2),
получаем параболические (линейные при η(2) = 0) законы неоднородности
материала покрытия. При этом не все параболические законы подлежат
рассмотрению. Если выполняется условие
(1)
(2)
r
/(2
)r
,
(22)
0
1
то это означает, что абсцисса вершины параболы принадлежит отрезку [r0, r1].
В этом случае параболу следует рассматривать только тогда, когда ордината
ее вершины принадлежит отрезку [C1η, C2η], то есть когда выполняется ус-
ловие
(0)
(1)2
(2)
C
/(4
)C
(23)
1
2
Нахождение значений неизвестных коэффициентов η(0), η(1), η(2) функ-
ций (18), удовлетворяющих условиям (20) и минимизирующих функцию
восемнадцати переменных
(0)
(1)
(2)
(0)
(1)
(2)
,
,
,...,c
,c
,c
min,
m 1,2,
(24)
m
осуществим с помощью алгоритма, предложенного в [17, 18].
Введем для ординаы fqη (q = 0,1,2) точки Gqη на отрезке [C1η, C2η] рав-
номерную сетку
(
l
q
)
f
C
l
h
,
q 0,1,2.
(25)
q
1
q q
Здесь lqη = 0,1,…,nqη - номер узла сетки, hqη = (C2η - C1η)/nqη - шаг q-й сетки,
nqη - количество равных частей, на которые разбит отрезок [C1η, C2η]. Таким
образом, построены двумерные сетки в каждой из шести областей Ω, соот-
ветствующих неравенствам (20). На этих сетках, используя выражения (21) и
условия (22), (23), рассчитываем наборы значений коэффициентов η(0), η(1), η(2).
Нахождение оптимального набора коэффициентов η(0), η(1), η(2) осуще-
ствим с помощью процедуры поиска минимума функции восемнадцати пе-
ременных (24). Вычислительная процедура построена на основе комбина-
ции методов случайного поиска и покоординатного спуска [19] и включает
два этапа. При этом в качестве восемнадцати искомых координат выступа-
ют не сами коэффициенты η(0), η(1), η(2), а соответствующие им наборы вели-
чин f0η, f1η, f2η, присутствующие в выражениях (21).
На первом этапе случайным образом выбирается начальная точка - со-
вокупность восемнадцати значений f0η, f1η, f2η
Рассеяние звука термоупругим шаром …
35
f
(
f
,
f
,
f
,...,
f
,
f
,
f
)
0
1
2
0c
1c
2c
из множества допустимых дискретных сочетаний на введенной многомер-
ной сетке.
На втором этапе в случайном порядке выбирается одна из координат и
выполняется поиск минимума Im (m = 1,2) при изменении значений этой ко-
ординаты в узлах введенной для нее сетки (25). При этом другие семна-
дцать координат сохраняют неизменные значения. Интегралы (19) вычис-
ляются численно. Это повторяется до исчерпания непросмотренных коор-
динат. По окончании второго этапа получаем значение локального мини-
мума функции Im и соответствующий набор координат f, по которому с по-
мощью формул (21) вычисляются искомые коэффициенты η(0), η(1), η(2).
Локальный минимум функции Im и соответствующий ему набор мате-
риальных параметров будут зависеть как от выбора начальной точки, так и
от порядка перебора координат при покоординатном спуске. Поэтому про-
цедура поиска локального минимума повторяется M раз. В качестве конеч-
ного решения выбирается набор коэффициентов η(0), η(1), η(2), обеспечиваю-
щий наименьшее значение Im среди локальных решений. Получаемое таким
образом оптимальное решение является приближенным, точность которого
зависит от выбора шага сетки hqη и числа M.
Ниже приведены результаты численной реализации описанного выше
алгоритма. Расчеты проводились для алюминиевого шара радиуса r0 = 1 м с
покрытием толщиной 0.1 м на основе поливинилбутираля, находящегося в
воде (см. п.1). При расчетах полагали, что неоднородность термоупругого
покрытия проявляется в изменении его плотности ρ(r) и модулей упругости
λ(r) и μ(r). При этом для функций (r) , (r) , (r) вводились ограничения
(20), в которых C1ρ=C1λ=C1μ=0.5, C2ρ= C2λ = C2μ = 1.5. Такие значения границ
неравенств (20) обеспечивают достаточно широкий диапазон изменения
функций ρ(r), λ(r), μ(r), когда максимально возможные значения функций
больше минимально допустимых значений в три раза.
В первой строке табл.2 приведены значения оптимальных коэффициен-
тов ρ(q), λ(q), μ(q) (q = 0,1,2), обеспечивающих наименьшее обратное (θ* = π)
рассеяние звука шаром с покрытием в частотном диапазоне, который опре-
деляется изменением волнового размера шара в интервале 11.5 ≤ ϖ ≤ 12.5.
При этом в каждой из трех областей Ω(ρ(0), ρ(1), ρ(2)), Ω(λ(0), λ(1), λ(2)), Ω(μ(0), μ(1),
μ(2)) строилась двумерная сетка для одинаковых шагов (hqρ=hqλ=hqμ=0.5, q =
0,1,2), отмеченная на рис.3б точками. Рассчитанные на этих сетках наборы
коэффициентов ρ(q), λ(q), μ(q) определяют в каждой из областей все допусти-
мые функции (r) , (r) , (r) для законов неоднородности материала по-
36
Н.В. Ларин, Л.А. Толоконников
крытия, показанные на рис.3б. Из этих законов в соответствии с изложенным
выше алгоритмом выбираются те, которым соответствует минимальное зна-
чение I1. Минимальному значению I1, найденному при M = 63 и равному
0.715, соответствует термоупругое покрытие со следующими свойствами:
9
2
(r) 1070(9.510r),
(r) 3.910
(116.5 215r 100r
),
8
2
4
(r)9.810
(441.5840r400r
),
2.310
,
T r)
6
0.2
,
c (r)1.210
T r)
Результаты, приведенные во второй строке табл.2, получены для слу-
чая фиксированной частоты, которой соответствует волновое число ϖ* = 12.
При этом угол наблюдения изменялся в интервале π/2≤θ≤π. Из табл.2 следу-
ет, что наименьшее рассеяние звука в освещенной зоне со значением I2=
=0.320 достигается при неоднородности материала покрытия, определяемой
зависимостями, которые отличаются от зависимостей, приведенных выше,
только законом изменения плотности
2
(r) 1070(114.5 215r 100r
).
Таблица 2. Оптимальные наборы коэффициентов.
ρ(0)
ρ(1)
ρ(2)
λ(0)
λ(1)
λ(2)
μ(0)
μ(1)
μ(2)
Im
−9.5
10
0
116.5
-215
100
441.5
-840
400
0.715 (m = 1)
−114.5
215
-100
116.5
-215
100
441.5
-840
400
0.320 (m = 2)
Для оценки эффективности покрытий с оптимальными звукоотражаю-
щими свойствами были рассчитаны значения величин I1, I2 и для термоуп-
ругого шара без покрытия, которые оказались равными 1.973 и 0.824 соот-
ветственно. Видно, что и в заданном диапазоне частот, и в определенном
секторе углов наблюдения покрытия с найденными оптимальными закона-
ми неоднородности уменьшают среднее значение интенсивности рассеяния
звука более чем на 60 процентов.
В заключение отметим, что непрерывно-неоднородное по толщине
термоупругое покрытие шара можно моделировать системой однородных
термоупругих слоев с различными значениями материальных констант по-
добно тому, как это сделано для непрерывно-неоднородного термоупругого
плоского слоя [20].
СПИСОК ЛИТЕРАТУРЫ
1. В.П. Иванов. Анализ поля дифракции на цилиндре с перфорированным покрытием //
Акустический журнал, 2006, т.52, №6, с.791-798;
Рассеяние звука термоупругим шаром …
37
англ. пер.: V.P. Ivanov. Analysis of the field diffracted by a cylinder with a perforated
coating // Acoustical Physics, 2006, v.52, №6, p.683-690.
2.
Ю.И. Бобровницкий, К.Д. Морозов, Т.М. Томилина. Периодическая поверхностная
структура с экстремальными акустическими свойствами // Акустический журнал,
2010, т.56, №2, с.147-151;
англ. пер.: Yu.I. Bobrovnitskii, K.D. Morozov, T.M. Tomilina. A periodic surface structure
with extreme acoustic properties // Acoustical Physics, 2010, v.56, №2, p.127-131.
3.
О.И. Косарев. Дифракция звука на упругой цилиндрической оболочке с покрытием //
Проблемы машиностроения и надежности машин, 2012, т.46, №1, с.34-37;
O.I. Kosarev. Difraktsiia zvuka na uprugoi tsilindricheskoi obolochke s pokrytiem // Prob-
lemy mashinostroeniia i nadezhnosti mashin, 2012, t.46, №1, s.34-37.
4.
Л.А. Толоконников, Н.В. Ларин, С.А. Скобельцын. Моделирование неоднородного
покрытия упругого шара с требуемыми звукоотражающими свойствами // Матема-
тическое моделирование, 2017, т.29, №11, с.89-98;
англ. пер.: L.A. Tolokonnikov, N.V. Larin, S.A. Skobel'tsyn. Modelling an inhomogeneous
coating of an elastic sphere with the required sound reflecting properties // Mathematical
models and computer simulations, 2018, v.10, №3, p.333-340.
5.
Л.А. Толоконников. Моделирование непрерывно-неоднородного покрытия упругого
шара системой однородных упругих слоев в задаче рассеяния звука // Прикладная
математика и механика, 2017, т.81, №6, с.699-707;
англ. пер.: L.A. Tolokonnikov. Modelling of a continuously inhomogeneous coating of an
elastic sphere by a system of homogeneous elastic layers in the problem of sound scatter-
ing // Journal of Applied Mathematics and Mechanics, 2017, v.81, №6.
6.
А.Д. Коваленко. Основы термоупругости. Киев: Наукова думка, 1970, 240 с.;
A.D. Kovalenko. Osnovy termouprugosti. Kiev: Naukova dumka, 1970, 240 s.
7.
Я.С. Подстригач, В.А. Ломакин, Ю.М. Коляно. Термоупругость тел неоднородной
структуры. М.: Наука, 1984, 368 с.;
Ia.S. Podstrigach, V.A. Lomakin, Iu.M. Koliano. Termouprugost tel neodnorodnoi struk-
tury. M.: Nauka, 1984, 368 s.
8.
Н.В. Ларин, Л.А. Толоконников. Рассеяние звука неоднородным термоупругим сфе-
рическим слоем // Прикладная математика и механика, 2010, т.74, №4, с.645-654;
англ. пер.: N.V. Larin, L.A. Tolokonnikov. Scattering of sound by an inhomogeneous ther-
moelastic spherical layer // J. of Applied Math. and Mechanics, 2010, v.74, №4, p.460-466.
9.
Дж.В. Стретт Лорд Рэлей. Теория звука. Т.2. М.: Гостехиздат, 1955, 475 с.;
J.W. Strutt Lord Rayleigh. The theory of sound. V.2. - NY. Dover Publications, Inc., 1945, 522p.
10. J.R. Allegra, S.A. Hawley. Attenuation of sound in suspensions and emulsions: Theory and
experiments // The J. of the Acoustical Society of America, 1972, v.51, №5, p.1545-1564.
11. Э.М. Карташов, Л.М. Ожерелкова. Новые модельные представления в проблеме те-
плового удара // Математическое моделирование, 2002, т.14, №2, с.95-108;
E.M. Kartashov, L.M. Ozherelkova. Novye modelnye predstavleniia v probleme teplovogo
udara // Matematicheskoe modelirovanie, 2002, t.14, №2, s.95-108.
12. В.А. Ломазов. Задачи диагностики неоднородных термоупругих сред. Орел: ОрелГТУ,
2002, 168 с.;
V.A. Lomazov. Zadachi diagnostiki neodnorodnykh termouprugikh sred. Orel: OrelGTU,
2002, 168 s.
38
Н.В. Ларин, Л.А. Толоконников
13. S.A. Lukasiewicz, R. Babaei, R.E. Qian. Detection of material properties in a layered body
by means of thermal effects // Journal of Thermal Stresses, 2003, v.26, №1, p.13-23.
14. А.О. Ватульян, С.А. Нестеров. Об особенностях идентификации неоднородного
предварительно напряженного состояния в термоупругих телах // Прикладная мате-
матика и механика, 2017, т.81, №1, с.103-110;
англ. пер.: A.O. Vatul'yan, S.A. Nesterov. Certain aspects of identification of the inhomo-
geneous prestressed state in thermoelastic bodies // Journal of Applied Mathematics and
Mechanics, 2017, v.81, №1, p.71-76.
15. А.О. Ватульян, С.А. Нестеров. Численная реализация итерационной схемы решения
обратных задач термоупругости для неоднородных тел с покрытиями // Вычисли-
тельные технологии, 2017, т.22, №5, с.14-26;
A.O. Vatulian, S.A. Nesterov. Chislennaia realizatsiia iteratsionnoi skhemy resheniia obrat-
nykh zadach termouprugosti dlia neodnorodnykh tel s pokrytiiami // Vychislitelnye
tekhnologii, 2017, t.22, №5, s.14-26.
16. Н.В. Ларин, С.А. Скобельцын, Л.А. Толоконников. Определение законов неоднород-
ности плоского упругого слоя с заданными звукоотражающими свойствами // Аку-
стический журнал, 2015, т.61, №5, с.552-558;
англ. пер.: N.V. Larin, S.A. Skobel'tsyn, L.A. Tolokonnikov. Determination of the inho-
mogeneity laws for an elastic layer with preset sound-reflecting properties // Acoustical
Physics, 2015, v.61, №5, p.504-510.
17. Н.В. Ларин, С.А. Скобельцын, Л.А. Толоконников. Моделирование неоднородного по-
крытия упругой пластины с оптимальными звукоотражающими свойствами // При-
кладная математика и механика, 2016, т.80, №4, с.480-488;
англ. пер.: N.V. Larin, S.A. Skobel'tsyn, L.A. Tolokonnikov. Modelling the inhomogeneous
coating of an elastic plate with optimum sound-reflecting properties // Journal of Applied
Mathematics and Mechanics, 2016, v.80, №4, p.339-344.
18. Л.А. Толоконников, Н.В. Ларин, С.А. Скобельцын. Моделирование неоднородного
покрытия упругого цилиндра с заданными звукотражающими свойствами // При-
кладная механика и техническая физика, 2017, т.58, №.4, с.189-199;
англ. пер.: L.A. Tolokonnikov, N.V. Larin, S.A. Skobel’tsyn. Modeling of an inhomogene-
ous coating of an elastic cylinder with given sound-reflecting properties // Journal of Ap-
plied Mechanics and Technical Physics, 2017, v.58, №4, p.733-742.
19. Ф.П. Васильев. Численные методы решения экстремальных задач. М.: Наука, 1988, 552с.;
F.P. Vasilev. Chislennye metody resheniia ekstremalnykh zadach. M.: Nauka, 1988, 552s.
20. Л.А. Толоконников, Н.В. Ларин. Прохождение звука через термоупругий дискретно-
неоднородный плоский слой, граничащий с теплопроводными жидкостями // При-
кладная механика и техническая физика, 2017, т.58, №1, с.108-116;
англ. пер.: L.A. Tolokonnikov, N.V. Larin. Sound propagation through a discretely inho-
mogeneous thermoelastic plane layer adjacent to heat-conducting liquids // Journal of Ap-
plied Mechanics and Technical Physics, 2017, v.58, №1. p.95-102.
Поступила в редакцию 04.06.2018
После доработки 06.11.2018
Принята к публикации 10.12.2018