МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 5, стр. 121-144
О ВЫЧИСЛЕНИИ ГРАДИЕНТА
В МЕТОДЕ КОРРЕКЦИИ ПОТОКОВ
©
2019 г.
П.А. Бахвалов
Институт прикладной математики им. М.В. Келдыша РАН, Москва
bahvalo@mail.ru
Статья подготовлена в ходе выполнения проекта РФФИ 16-31-60072 мол-а-дк.
DOI: 10.1134/S0234087919050083
Метод коррекции потоков является семейством рёберно-ориентированных схем
для решения гиперболических систем на неструктурированных сетках. Ключевое
место в этих схемах занимает вычисление градиентов от физических переменных в
сеточных узлах не менее чем со вторым порядком аппроксимации. Существуют
две известные процедуры, обеспечивающие выполнение этого условия. Первая ос-
нована на методе наименьших квадратов, а вторая - на спектральных элементах. В
настоящей работе проводится сравнение схем, получающихся при использовании
этих процедур, между собой и с другими рёберно-ориентированными схемами.
Ключевые слова: неструктурированная сетка, метод коррекции потоков, схема UFC.
ON GRADIENT CALCULATION IN FLUX CORRECTION METHOD
P.A. Bakhvalov
Keldysh Institute of Applied Mathematics of RAS
Flux Correction method is a family of edge-based schemes for solving hyperbolic
systems on unstructured meshes. The cruical operation there is a nodal gradient
calculation of physical variables with at least second order of accuracy. There are two
well-known procedures meeting this condition. One is based on Least Squares method
and the other one is based on spectral elements. In this paper we compare resulting
schemes and discuss their problems.
Key words: unstructured mesh, Flux Correction method, UFC scheme.
1. Введение
Рёберно-ориентированные схемы представляют собой особый класс
конечно-объёмных схем для решения гиперболических систем уравнений
на неструктурированных сетках. В этих схемах консервативные перемен-
ные определяются в сеточных узлах, а потоки, используемые для аппрокси-
122
П.А. Бахвалов
мации законов сохранения, вычисляются в серединах сеточных рёбер или
диагоналей элементов. Впервые эти схемы предложены в [1, 2]. Современ-
ное состояние этих схем представлено, главным образом, схемами с квази-
одномерной реконструкцией переменных [3-6] и схемами на основе метода
коррекции потоков (Flux Correction method - FC) [7-14].
Схема T. Barth [2] заключается в линейной реконструкции переменных
в середине ребра с использованием градиентов, вычисленных в сеточных
узлах. Она обладает 1-м порядком аппроксимации и на практике показывает
порядок точности от 3/2 до 2. Однако в [7] было замечено, что если эти гра-
диенты вычислять со вторым порядком аппроксимации, то и вся схема в
целом также будет обладать вторым порядком аппроксимации. Порядок
точности получаемой при этом схемы на нестационарных задачах остаётся
равным 2, однако на стационарных задачах часто наблюдается 3-й порядок
сходимости. Дальнейшее развитие этих схем заключалось в перенесении
этой сверхсходимости на нестационарные задачи [8-12], но это было дос-
тигнуто ценой существенного усложнения схемы и потери консервативно-
сти. Другим подходом является метод коррекции нестационарных потоков
[13, 14], который снижает порядок аппроксимации до первого, однако при
этом на практике позволяет улучшить точность стационарного метода при
ничтожных дополнительных затратах машинного времени.
Ключевое место в схемах на основе метода коррекции потоков занима-
ет процедура вычисления градиентов от физических переменных в сеточ-
ных узлах не менее чем со вторым порядком аппроксимации. Этого можно
добиться, например, вычисляя градиент от интерполяционного многочлена,
полученного методом наименьших квадратов (Least Squares Method, LSM).
Проблемой является возможность вырождения системы уравнений для на-
хождения коэффициентов многочлена. Кроме того, при использовании ани-
зотропной сетки в пристеночных областях число обусловленности системы
растёт с ростом анизотропии и кривизны поверхности.
Чтобы избежать этих проблем, в [8] предложено вычислять градиенты
по спектральным элементам. В этом случае расчётная сетка должна пред-
ставлять собой результат однократного естественного измельчения (см.
рис.1) некоторой другой расчётной сетки, элементы которой называются
спектральными. На каждом спектральном элементе интерполянт определя-
ется однозначно, после чего градиент в узле определяется как средний гра-
диент от таких интерполянтов, определённых в этом узле. При этом на рав-
номерной сетке схема получается неоднородной: часть сеточных узлов яв-
ляются вершинами спектральных элементов, а часть - не являются таковы-
О вычислении градиента в методе коррекции потоков
123
ми, и поэтому в них по-разному вычисляются градиенты. Метод вычисле-
ния градиентов по спектральным элементам к настоящему моменту казался
оптимальным. Однако, как будет показано ниже, неоднородность схемы
может приводить к странностям в поведении решения.
Рис.1. Естественное измельчение сеточных элементов в 2 раза.
В трёхмерном случае в пристеночных областях для вязких задач рас-
чётная сетка обычно имеет тип strand, то есть её топология представляет со-
бой декартово произведение двумерной неструктурированной сетки на од-
номерную сетку. В этом случае становится возможным ещё один способ
вычисления градиентов. Компонента градиента вдоль ребра, втыкающегося
в границу, вычисляется с использованием одномерной конечно-разностной
схемы, а касательные компоненты - с использованием только значения пе-
ременных на соответствующем слое, с применением одного из двух описан-
ных выше методов [10, 11]. Этот тип сеток мы в настоящей работе рассмат-
ривать не будем, ограничившись невязким случаем.
В настоящей работе на ряде тестовых задач проводится сравнение схем
на основе метода коррекции потоков, получающихся при использовании
разных процедур вычисления градиентов. Также эти схемы сопоставляются
по точности со схемами с квазиодномерной реконструкцией. Помимо этого
предлагается новый ограничитель наклонов для решения задач с разрывами
при помощи метода коррекции потоков.
2. Рёберно-ориентированные схемы
В настоящей работе будем рассматривать гиперболические системы
уравнений
Q
(Q)
0,
(1)
t
где
(F
,F
,F
). Условие гиперболичности означает, что для любого
x y z
вектора
n якобиан вектора потоков в этом направлении представим в виде
d
(Q)
1
SΛS
,
(2)
dQ
где Λ - диагональная матрица. В частности, такой вид имеет уравнение пере-
носа при Qu , au . Уравнения Эйлера для идеального газа имеют вид (1)
124
П.А. Бахвалов
T
T
2
при
Q
u,E)
,
(u,
uupI
,(
Ep u)
,
где
E u
/2,
I - еди-
ничная матрица, и замыкаются уравнением состояния идеального газа p
( 1). Всюду в настоящей работе используется показатель адиабаты 1.4 .
Построение конечно-объёмной схемы предполагает разбиение расчёт-
ной области на ячейки, для которых выписываются дискретные законы со-
хранения. Для схем с определением переменных в сеточных узлах роль ячеек
выполняют контрольные объёмы, каждый из которых построен вокруг сво-
его сеточного узла. Опишем их построение на примере треугольной сетки.
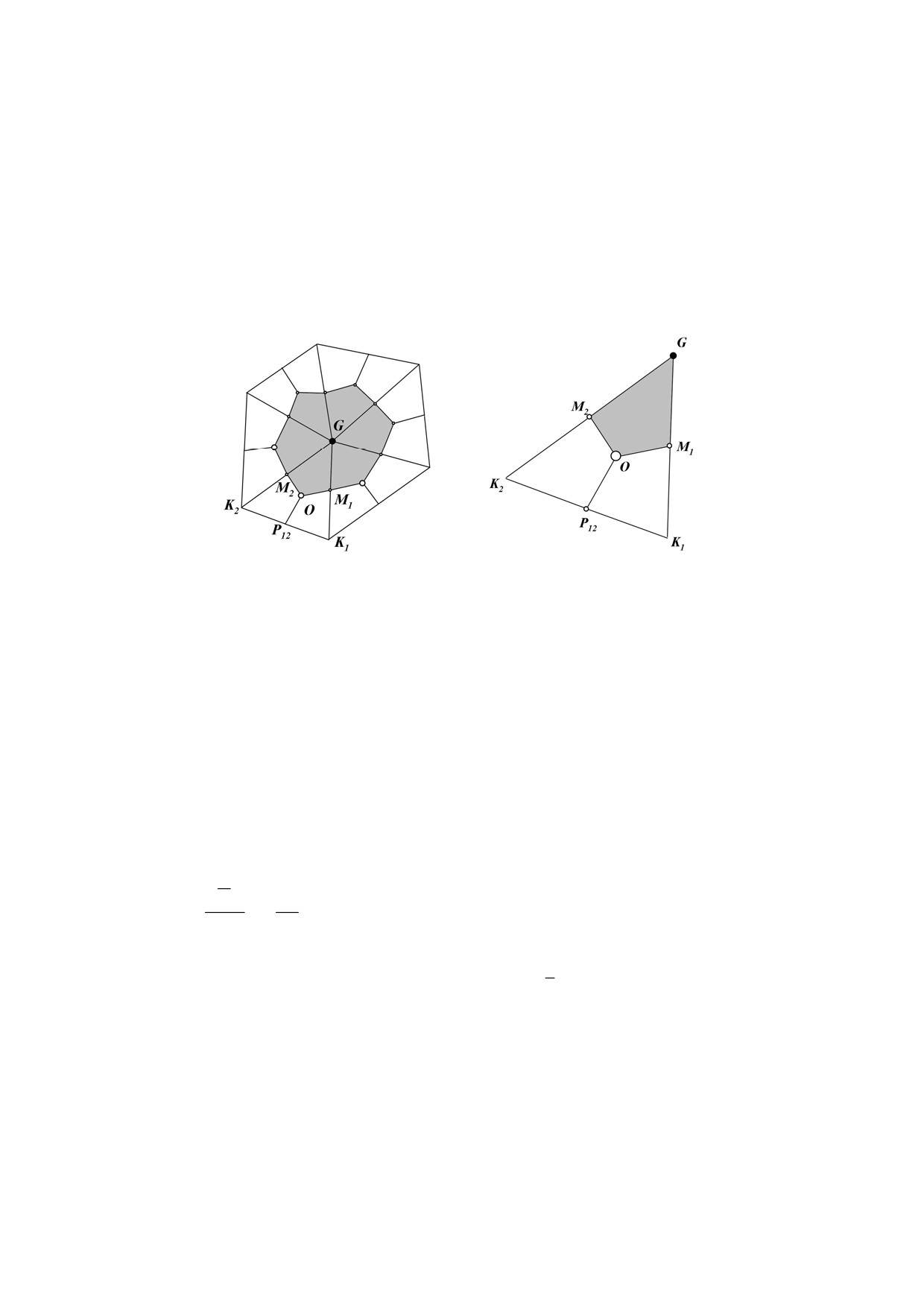
Рис.2. Двумерный медианный объём узла G (слева) и относящаяся к нему
часть треугольного сеточного элемента
GK
K
(справа).
1
2
Рассмотрим некоторый треугольник
GK
K
, изображённый на рис.2
1
2
справа. Середины рёбер
GK
,
GK
и
K
K
обозначим через
M
, M
и P12
1
2
1
2
1
2
соответственно, а центр треугольника через O. Треугольник
GK
K
раз-
1
2
бивается на три четырёхугольника:
GM
OM
(входит в контрольный объём
1
2
узла G),
K
M
OP (входит в контрольный объём узла
K
) и
K
M
OP (вхо-
1
1
1
2
2
дит в контрольный объём узла
K
). Контрольный объём узла G представля-
2
ет собой объединение таких четырёхугольников и изображён на рис.2 слева.
Если в качестве центра треугольника выбирается его центр масс, то полу-
чающиеся при этом ячейки называются медианными или барицентрически-
ми. Построение аналогичных ячеек в трёхмерном случае описано в [15, 16].
Закон сохранения вида (1) для ячейки G можно переписать в виде
dQ
1
G
n
ds,
(3)
dt
V
G C
гдеCG контрольный объём узла G,
V
|C
|
C
его
G G
граница, n внешняя единичная нормаль к ней,QG интегральное среднее
от Q по ячейкеCG .
О вычислении градиента в методе коррекции потоков
125
Поверхность ячейки может быть представлена в видеCG
C
,
GK
KN
1(
G
)
где
N
(G) множество узлов, соседних (то есть соединённым общим се-
1
C
общая поверхность ячеек G и K.
Введём обозначения
n
ndS,
n
n
/
n
GK
GK
GK
GK
C
C
G
K
Для аппроксимации (3) подставимQG (точечное значение Q в сеточ-
C
в (4) представим в виде
C
, и в каждом таком интеграле заменим поток
на некоторое значение, отнесённое к середине ребра. Имеем
dQ
1
G
h
n
,
(4)
GK
GK
dt
V
G K N1(G)
гдеhGK — численный поток, не менее чем с первым порядком аппроксими-
рующий
в середине ребра. Cхемы вида (4) называются рёберно-ори-
GK
ентированными (edge-based). При использовании медианных ячеек на сим-
плициальной сетке рёберно-ориентированные схемы обладают первым по-
рядком аппроксимации во внутренних узлах сетки [15]. Это свойство выте-
кает из точности вычисления правой части (4) на линейной функции, если
потокиhGK точны на линейной функции в серединах рёбер.
На гибридной сетке можно построить два типа контрольных объёмов:
полупрозрачные [16] и прямые [17, 16]. Полупрозрачные контрольные объ-
ёмы являются обобщением медианных: они сохраняют точность на линей-
ной функции на произвольной неструктурированной сетке (если потоки
точны на линейной функции в серединах рёбер), но ошибка аппроксимации
пропорциональна коэффициенту анизотропии. Прямые контрольные объё-
мы не сохраняют точность на линейной функции. На призматической сетке
в пристеночной области первый порядок аппроксимации, как правило, име-
ет место за счёт структурированности сетки в нормальном направлении,
однако теряется при переходе на неструктурированную сетку.
С целью обеспечения устойчивого счёта потоки обычно определяются
при помощи некоторого приближённого решения задачи о распаде разрыва,
например, схемы типа Куранта-Изаксона-Риса (см., например, [18]):
126
П.А. Бахвалов
(Q
) (Q
)
1
Q
Q
GK
GK
GK GK
h
S
1|
Λ|S
,
GK
GK
2
2
2
где матрицы S и Λ определены (2). Частным случаем этой схемы является
схема Роу [19]. В некоторых случаях используется поток более общего вида
F
F
Q
Q
GK GK
1
GK
GK
h
S
| Λ | S
(5)
GK
2
2
2
Независимое определение
F
позволяет добиться большего порядка точ-
ности на нелинейных задачах на равномерных сетках, хотя на практике это,
как правило, не очень заметно.
Определение конкретной рёберно-ориентированной схемы сводится к
определению значенийQK и
F
. Простейшей рёберно-ориентированной
схемой является «линейная» схема T. Barth [1]. В ней предраспадные значе-
ния вычисляются по формулам
r
r
r
r
K G
K G
Q
Q
·(Q
) ,
Q
Q
·(Q)
,
(6)
GK
G GK
G
GK
K KG
K
2
2
в качестве одного из вариантов определения
F
предлагается
F
(Q
)·
, а градиент функции в сеточном узле вычисляется процеду-
GK GK
рой Грина-Гаусса:
1
Q
Q
G K
Q
n
(7)
G
GK
V
2
G
KN1(G)
При решении задач с гладкими решениями коэффициентыGK иKG
полагаются равными 1. Для расчётов течений с разрывами они выбираются
независимо для каждой компоненты вектора Q таким образом, чтобы вы-
полнялось условие min{Q
,Q
}Q
max{Q
,Q
} [1].
G K
GK
G K
Другими примерами рёберно-ориентированных схем являются схема
Luo и др. [20], схема Eliasson [21], метод коррекции потоков (Flux Corrector
method, FC) [7-14] и построенные на его основе схемы H. Nishikawa [22,
23], схемы Mixed Element-Volume (MEV) [3, 24, 25] и схемы EBR (Edge-
Based Reconstruction) [3-6].
3. Метод коррекции потоков
Рассмотрим схему (6) для уравнения переноса u / t au 0. Пред-
положим, что градиент вычисляется со вторым порядком аппроксимации.
О вычислении градиента в методе коррекции потоков
127
Покажем, что при этом и вся схема (4)-(6) обладает вторым порядком ап-
проксимации во внутренних узлах на медианных ячейках на неструктури-
рованной сетке.
Поскольку точность на линейной функции имеет место в силу свойств
медианных ячеек, то чтобы убедиться во втором порядке аппроксимации,
c
достаточно рассмотреть функцию вида
u r)
(xx
)a(yy
)b(zz
)
G
G
G
при a + b + c = 2. Предраспадное значение со стороны узла G в центре ребра
GK вычисляется по формуле (6) и равно 0, поскольку
u(r
)
u(r
)
0
G
G
Рассмотрим предраспадное значение со стороны узла K. Проанализируем
его разложение в ряд Тейлора в окрестности точки rG. Штрихом будем обо-
значать производную по направлению ребра, а через h - длину ребра GK.
1
2
u
u(r
) u(r
)h u(x
)h
GK
G
G
G
2
1
1
h(u(x
)
hu(x
))
u(x
)
u(x
)
h
0.
G
G
G
G
2
2
Таким образом, на квадратичной функции предраспадное значение со стороны
K также равно 0. Следовательно, равен нулю и численный поток (5), и правая
часть равенства (4) в целом. Более подробно это доказательство см. в [7].
На неравномерных и неструктурированных сетках схемы часто обес-
печивают сходимость с большей скоростью, чем это предсказывается их
порядком аппроксимации (см., например, [26]). Это явление иногда назы-
вают сверхсходимостью (supra-convergence). Так, близкий ко второму поря-
док точности обычно показывает «линейная» схема T. Barth (4)-(7), хотя
известен пример, на котором решение по этой схеме сходится с порядком
3/2 [27]. Для метода коррекции потоков второй порядок аппроксимации ме-
тода обеспечивает второй порядок точности, когда схема устойчива, однако
при этом порядок сходимости оказывается тоже равным двум, то есть эф-
фект сверхсходимости отсутствует. Тем не менее, в [7] было обнаружено,
что сверхсходимость метода коррекции потоков наблюдается на задачах со
стационарными решениями. Поэтому схема (4)-(6) при условии вычисления
градиентов со вторым порядком аппроксимации была названа стационар-
ным методом коррекции потоков (steady Flux Correction method).
Исследования в области аппроксимации источникового члена, если та-
кой содержится в уравнении, вызвало дальнейшее развитие схем на основе
метода коррекции потоков: A. Pincock и A. Katz вместо (4) в [8] предложили
использовать разнесённую по пространству аппроксимацию производной
по времени:
128
П.А. Бахвалов
dQ
1
M
h
GK
GK
dt
V
K
K
G
KN
G
)
1(
Здесь hGK - поток типа (5). Коэффициенты MGK выбираются таким образом,
что сохраняется второй порядок точности на произвольной неструктуриро-
ванной сетке и обеспечивается третий порядок аппроксимации на трансля-
ционно-инвариантных сетках, однако теряется консервативность. Трансля-
ционно-инвариантными называются сетки в бесконечном пространстве, пе-
реходящие в себя при пространственной трансляции на вектор любого сво-
его ребра. Таковыми являются равномерные сетки из параллелепипедов или
их однородные разбиения на симплексы, см. рис.3. Теми же свойствами об-
ладает схема, полученная по методике, описанной в работе Nishikawa [28].
Различные варианты определения матрицы M подытожены в [12].
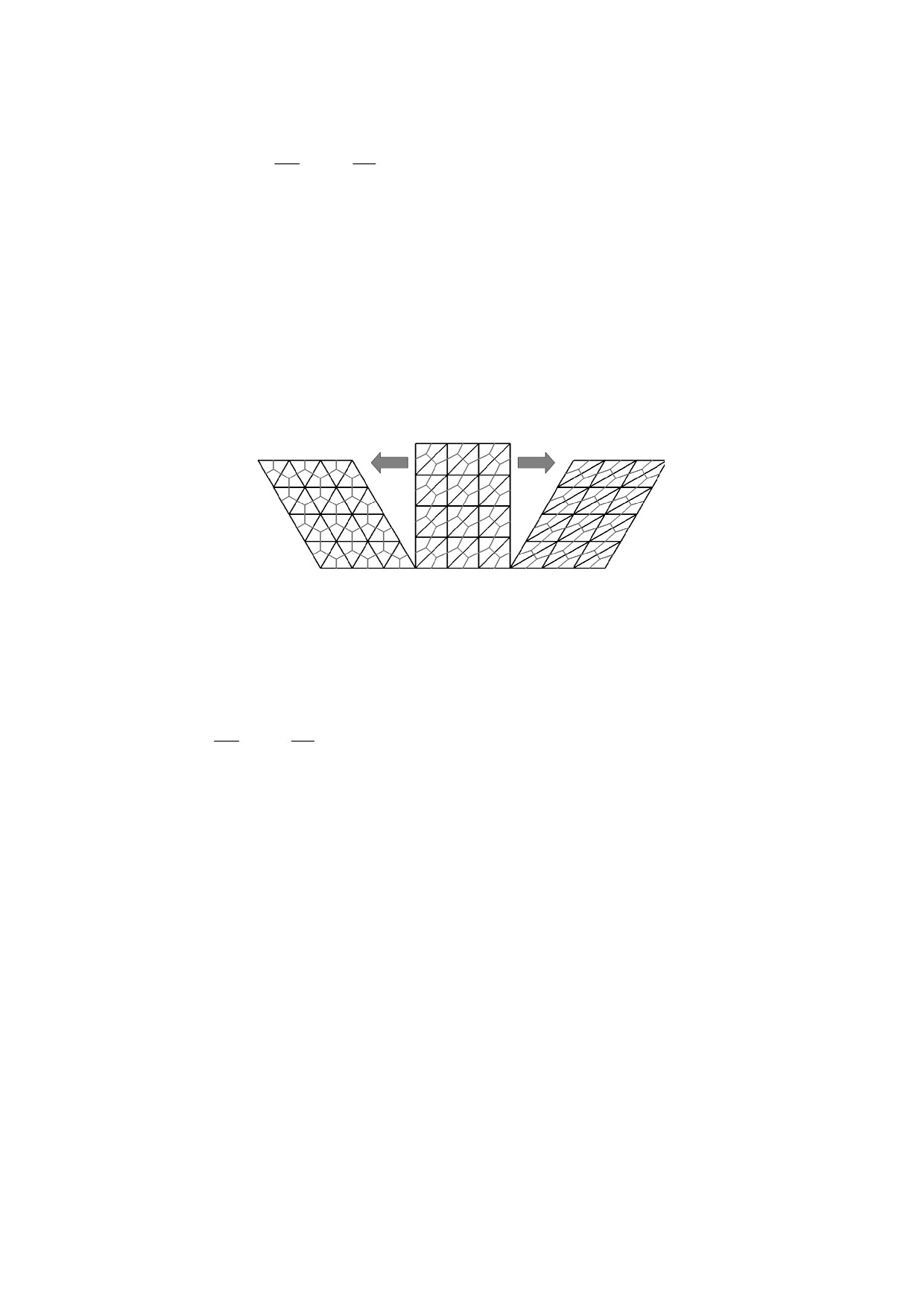
Рис.3. Треугольная трансляционно-инвариантная сетка (чёрные линии) и
медианные контрольные объёмы на ней (серые линии).
В [13] автором была предложена схема UFC, представляющая собой
другой алгоритм повышения точности решения нестационарных задач. Она
может быть представлена в виде
dQ
1
U
h
GK
KL
dt
V
G
G KN
(G
)
LN
(K)
1
1
Коэффициенты матрицы UGK подобраны таким образом, чтобы сохранить
консервативность исходной схемы и обеспечить 3-й порядок аппроксима-
ции на трансляционно-инвариантных сетках. Второй порядок аппроксима-
ции на неструктурированных сетках при этом, однако, теряется. В [13]
описано обобщение схемы UFC для гибридной сетки (не применимое, од-
нако, к задачам с анизотропной сеткой в пристеночном слое). Заметим, что
если методом коррекции потоков получено стационарное решение, то оно
является стационарным решением также и схемы UFC.
В нелинейном случае определение
F
(Q
)·
ограничивает
GK
GK GK
порядок аппроксимации на равномерных сетках вторым. Вместо этого в на-
О вычислении градиента в методе коррекции потоков
129
стоящей работе используется реконструкция потоковых переменных, ана-
логичная реконструкции консервативных:
r
r
r
r
K G
K G
F
F
·(F) ,
F
F
·(F)
,
GK G
G GK K
K
2
2
. Отметим, что в [8] была предложена аль-
тернативная процедура
r
r
dF
r
r
dF
K G
K G
F
F
·
(Q) ,
F
F
·
(Q)
,
GK G
G
GK
K
K
2
dQ
2
dQ
G
K
не требующая вычисления градиентов от потоковых переменных и за счёт
этого немного снижающая вычислительную стоимость.
4. Вычисление градиентов
Ключевое место в схемах на основе метода коррекции потоков занима-
ет процедура вычисления градиентов от физических переменных в сеточ-
ных узлах не менее чем со вторым порядком аппроксимации. Хорошо из-
вестны две процедуры, отвечающие этому требованию.
Наиболее простым способом вычисления узлового градиента со вто-
рым порядком является вычисление градиента от интерполяционного мно-
гочлена, полученного методом наименьших квадратов (Least Squares
method, LSM). Пусть требуется вычислить градиент в узле G. В качестве
шаблона выбирается, например, совокупность узлов, соединённых с узлом
G не более чем двумя рёбрами. Этот метод обладает двумя критическими
недостатками. Во-первых, возможно вырождение системы уравнений на
нахождение коэффициентов многочлена. Легко создать такую сетку искус-
ственно; на практике же это иногда случается в граничных или пригранич-
ных узлах, где соседей 2-го порядка меньше, чем для внутренних узлов. Во-
вторых, в пристеночных областях для моделирования высокорейнольдсо-
вых течений используется анизотропная сетка. Если граница области кри-
волинейная, то построение интерполяционных полиномов методом наи-
меньших квадратов было бы корректным, если бы базисные функции были
полиномами от переменных в криволинейной, связанной с границей систе-
ме координат. Если же использовать многочлены в декартовых координа-
тах, то такой подход может приводить к очень большому числу обуслов-
ленности системы и, как следствие, катастрофическим ошибкам.
Чтобы избежать этих проблем, в [8] предложено вычислять градиенты
по спектральным элементам. В этом случае расчётная сетка должна пред-
ставлять собой результат однократного естественного (см. рис.1) измельче-
130
П.А. Бахвалов
ния некоторой другой расчётной сетки, элементы которой называются спек-
тральными. Если измельчение проводилось в k раз по линейному размеру, то
спектральные элементы называются элементами k-го порядка. Спектраль-
ный треугольный элемент 2-го порядка содержит 6 узлов, что позволяет на
2
2
них однозначно определить многочлен вида
ax
bxy cy
dxey f по
значениям переменных в узлах. Четырёхугольный спектральный элемент 2-
го порядка содержит 9 узлов, что позволяет однозначно определить много-
2
2
2
2
2
2
член вида
ax
y
bx
ycx
dxy
exy fxgy
hy k . Аналогично, спек-
тральный тетраэдральный элемент 2-го порядка содержит 10 узлов, пира-
мидальный - 14 узлов, призматический - 18 узлов, гексаэдральный - 27 уз-
лов, что также позволяет однозначно определить многочлен с соответст-
вующим набором одночленов [14]. Определив многочлен, можно опреде-
лить и градиент от него. Далее, градиент в узле определяется как среднее от
градиентов в этом узле по всем спектральным элементам, содержащим этот
узел, с весом, равным объёму спектрального элемента. В [8] показано, что
использование спектральных элементов 3-го порядка приводит к неустой-
чивости около границ расчётной области, поэтому нужно использовать
спектральные элементы именно 2-го порядка.
Метод вычисления градиентов с использованием спектральных эле-
ментов имеет два недостатка. Во-первых, расчётная сетка обязательно
должна быть получена измельчением другой, «спектральной» сетки. В об-
ласти с криволинейной границей процедура измельчения сетки содержит
технические трудности, связанные с тем, что граничные узлы измельчённой
сетки должны быть смещены с рёбер и граней «спектральной» сетки на гра-
ницу истинной расчётной области. При наличии анизотропного пристеноч-
ного слоя такое смещение может привести к выворачиванию элементов и
поэтому потребовать смещения и части внутренних узлов. Во-вторых, на
равномерной сетке схема получается неоднородной: часть сеточных узлов
являются вершинами спектральных элементов, а часть - не являются тако-
выми, и поэтому в них по-разному вычисляются градиенты.
Несмотря на указанные выше недостатки, метод вычисления градиен-
тов по спектральным элементам (быть может, с использованием strand-
технологии) к настоящему моменту казался оптимальным. Однако, как бу-
дет показано ниже, неоднородность схемы, вызванная неоднородным спо-
собом вычисления градиентов, может приводить к частичному исчезнове-
нию численной диссипации и, как следствие, некорректному поведению
решения.
О вычислении градиента в методе коррекции потоков
131
5. Тестирование: линейная задача с периодическими условиями
Рассмотрим модельную задачу для уравнения переноса u/t u/x 0
2
2
с начальными условиями
u(0,x)exp(x
) при
ln2/(0.03)
и периоди-
ческими граничными условиями u(t,1/2) u(t,1/2). В качестве меры ошиб-
ки выберем максимум модуля разности численного решения на момент
времени Tmax = 20 и точного решения на этот момент времени.
Будем использовать расчётную сетку с шагами
h
h
h
,
1/2
3/2
min
h
h
h
,
h
h
h
и т.д., см. рис.4. Обозначим
Kh h
,
5/2
7/2
max
9/2
11/2
min
h(h
h
)/2.
max min
Рис.4. Расчётные сетки для одномерных тестов. Сверху вниз: K=1, K=1.2, K=2.
Для интегрирования по времени будем использовать метод Рунге-
Кутты 5-го порядка точности с CFL=0.5. Будем использовать следующие
схемы на основе метода коррекции потоков: 1) стационарный метод кор-
рекции потоков (2-го порядка точности), 2) неконсервативная модификация
Nishikawa [26], 3) неконсервативная модификация Pincock [25], 4) схема
UFC. Для схемы UFC рассматривается два способа вычисления градиентов:
путём дифференцирования интерполяционного многочлена Лагранжа 2-го
порядка и с использованием спектральных элементов; для остальных схем
используется только первый вариант. Результаты сопоставим с полученны-
ми по схемам EBR3 и SEBR5 [4].
Результаты всех расчётов на равномерных сетках и неравномерных
сетках при K=1.2 и K=2 сведены на рис.5. На равномерной сетке результаты
по схеме UFC накладываются на метод Pincock. Анализируя результаты,
можно сделать следующие выводы.
1. На всех сетках, включая равномерную, стационарный метод коррек-
ции потоков показывает второй порядок точности. Использование некон-
сервативных схем с нестационарным членом в форме как Nishikawa [28],
так и Pincock [8], улучшает порядок точности до 3-го, причём использова-
ние нестационарного члена в форме Nishikawa обеспечивает в несколько
раз меньшую величину численной ошибки.
2. На равномерных сетках, как и ожидалось, схемы EBR3 и SEBR5 по-
казывают, соответственно, 3-й и 5-й порядок точности. Схема UFC с 3-
точечной аппроксимацией градиента обладает третьим порядком точности.
Использование спектральных элементов для вычисления градиентов позво-
ляет получить четвёртый порядок точности. Объяснение этого факта непро-
132
П.А. Бахвалов
стое и будет изучено в дальнейшем. Четвёртый порядок точности на рав-
номерной сетке, с одной стороны, обеспечивает более высокую точность,
но, с другой стороны, вызывает опасения, поскольку старший член (член 4-
го порядка) накапливаемой со временем ошибки - фазовый, а не диссипа-
тивный.
3. На неравномерных одномерных сетках все варианты схемы UFC,
схемы EBR3 и SEBR5 обладают 1-м порядком аппроксимации и 2-м поряд-
ком точности. Однако величины численной ошибки существенно меньше,
чем у стационарного метода коррекции потоков, обладающего 2-м поряд-
ком аппроксимации.
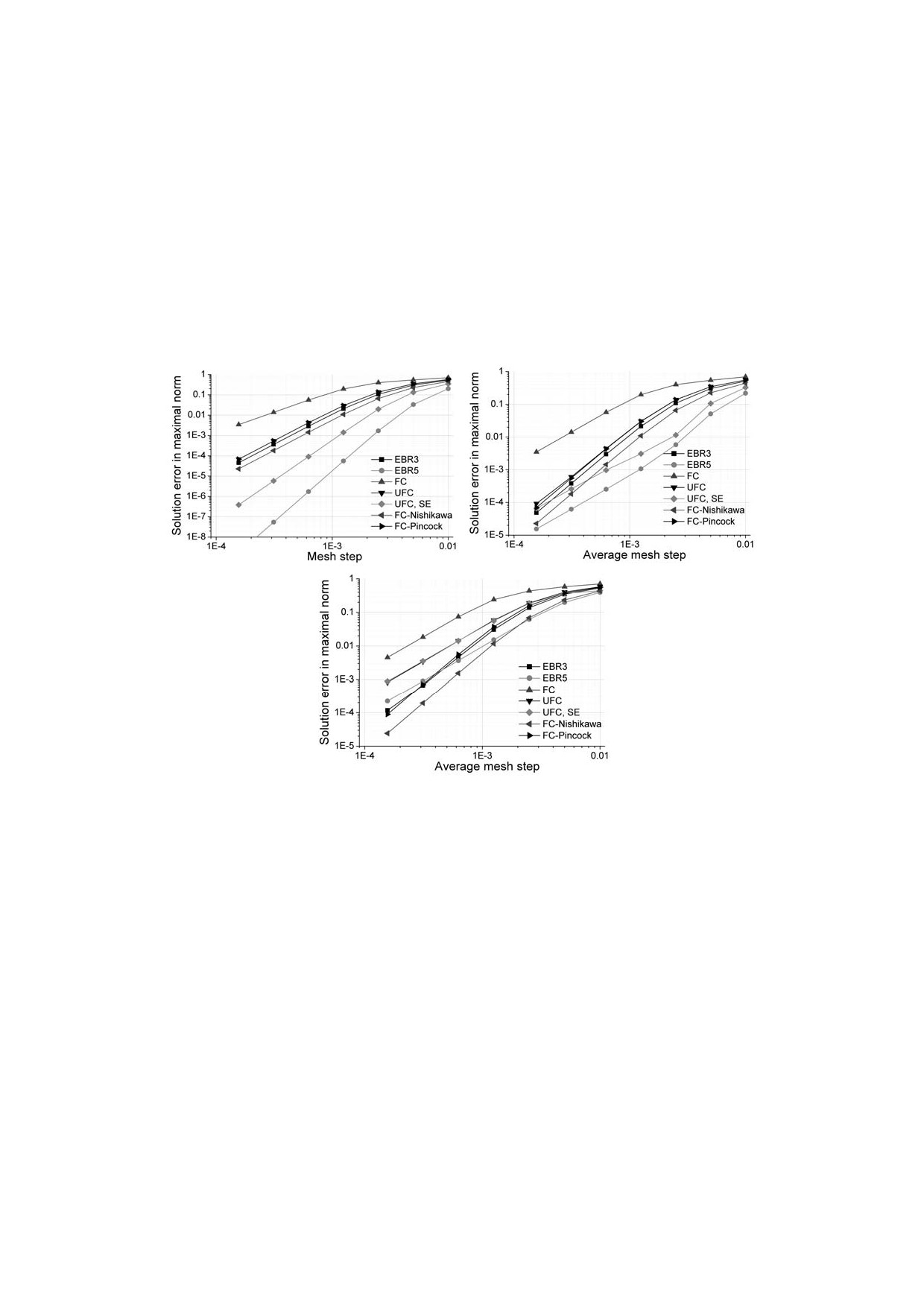
Рис.5. Точность различных FC- и EBR-схем на одномерном уравнении переноса. а) рав-
номерная сетка, б) неравномерная сетка с K=1.2, в) неравномерая сетка с K=2.
Результаты тестирования на многомерных линейных задачах с перио-
дическими условиями читатель может найти в [13]. На неструктурирован-
ной сетке оба способа вычисления градиентов - при помощи спектральных
элементов и на основе метода наименьших квадратов - как и в случае од-
номерной неравномерной сетки, дают близкие результаты. На трансляци-
онно-инвариантной сетке использование спектральных элементов даёт бо-
лее точные результаты, но, в отличие от одномерного случая, не приводит к
повышению порядка точности до четвёртого.
О вычислении градиента в методе коррекции потоков
133
6. Тестирование: потенциальное обтекание сферы
Теперь рассмотрим задачу о потенциальном обтекании сферы. Расчёт
будем проводить в рамках уравнений Эйлера для идеального газа при числе
Маха фонового потока M = 0.01. Расчёт проводится во внешности сферы ра-
диуса R = 0.5 с центром в начале координат; внешние границы расчётной
области удалены достаточно далеко, чтобы они не влияли на решение. На
поверхности сферы ставятся условия непротекания. В начальный момент
времени задаётся однородный поток, он же держится на внешних границах
расчётной области. Точное решение задачи при использовании гидроди-
намического обезразмеривания в пренебрежении членами порядка O(M4)
имеет вид
3
2
2
5
u
1
R
(3x
r
)/
r
;
3
5
v
3R
xy
/(2r
);
3
5
w
3
R
xz
/(2r
);
2
2
2
2
p
c
/
p',
p
'
(1
u
v
w
)/2;
2
1
p
'/
c
,
2
2
2
2
где
r
x
y
z
, а c
p / - скорость звука в невозмущённом потоке.
Хорошо известно, что при обтекании цилиндра в двумерной поста-
новке может устанавливаться не только безцируляционное обтекание, но и
циркуляционное обтекание с любой величиной циркуляции (см., например,
[29]). Аналогичный эффект имеет место и при обтекании сферы. Чтобы из-
бежать этого, расчётная сетка с характерным шагом h строилась следую-
щим образом. Вначале в четверти расчётной области (y >0, z >0) строилась
сетка, имеющая характерную длину ребра 2h на поверхности сферы и
разбег с коэффициентом 1.5. Затем сетка отражалась относительно плоскос-
тей y = 0 и z = 0. После этого сетка измельчалась вдвое, чтобы иметь спект-
ральные элементы, и узлы, которые должны лежать на поверхности сферы,
смещались на неё. Можно считать, что после измельчения коэффициент
разбега сетки от границы становился равным 1.5 . Однако расчёты показа-
ли, что, несмотря на симметричность сетки, арифметическая погрешность
накапливалась со временем и приводила к нарушению симметричности те-
чения. Поэтому на каждом шаге по времени течение искусственно симмет-
ризовалось.
Для более оптимального выбора численной диссипации вместо реше-
ния задачи о распаде разрыва по формуле (5) использовалась схема Роу с
предобуславливателем E. Turkel [30], см. также [6, 31].
134
П.А. Бахвалов
Результаты расчётов в сечении z=0 при y>0 на сетке с h=0.04 приведе-
ны на рис.6. Тонкими чёрными линиями отмечены изолинии точного, а се-
рыми толстыми - численного решения для p. Поток направлен слева напра-
во. Поскольку численное решение стационарное, расчёты по схеме UFC да-
ли бы в точности тот же результат, что и при помощи стационарного метода
коррекции потоков, и поэтому не проводились.
Видно, что на передней стороне сферы изолинии точного и численного
решений накладываются друг на друга, а на задней стороне сферы числен-
ное решение по давлению несколько меньше точного. Это является обыч-
ным результатом численной диссипации. Опыт автора показывает, что в
этой задаче определяющую роль играет диссипация в одной-двух слоях яче-
ек вблизи сферы. Из рис.6 видно, что у схемы SEBR5 диссипация меньше,
чем у метода коррекции потоков с полиномиальными градиентами (FC-
poly), но больше, чем у метода коррекции потоков с градиентами по
спектральным элементам (FC-SE). Более подробные результаты расчётов на
последовательности сеток приведены в табл.1.
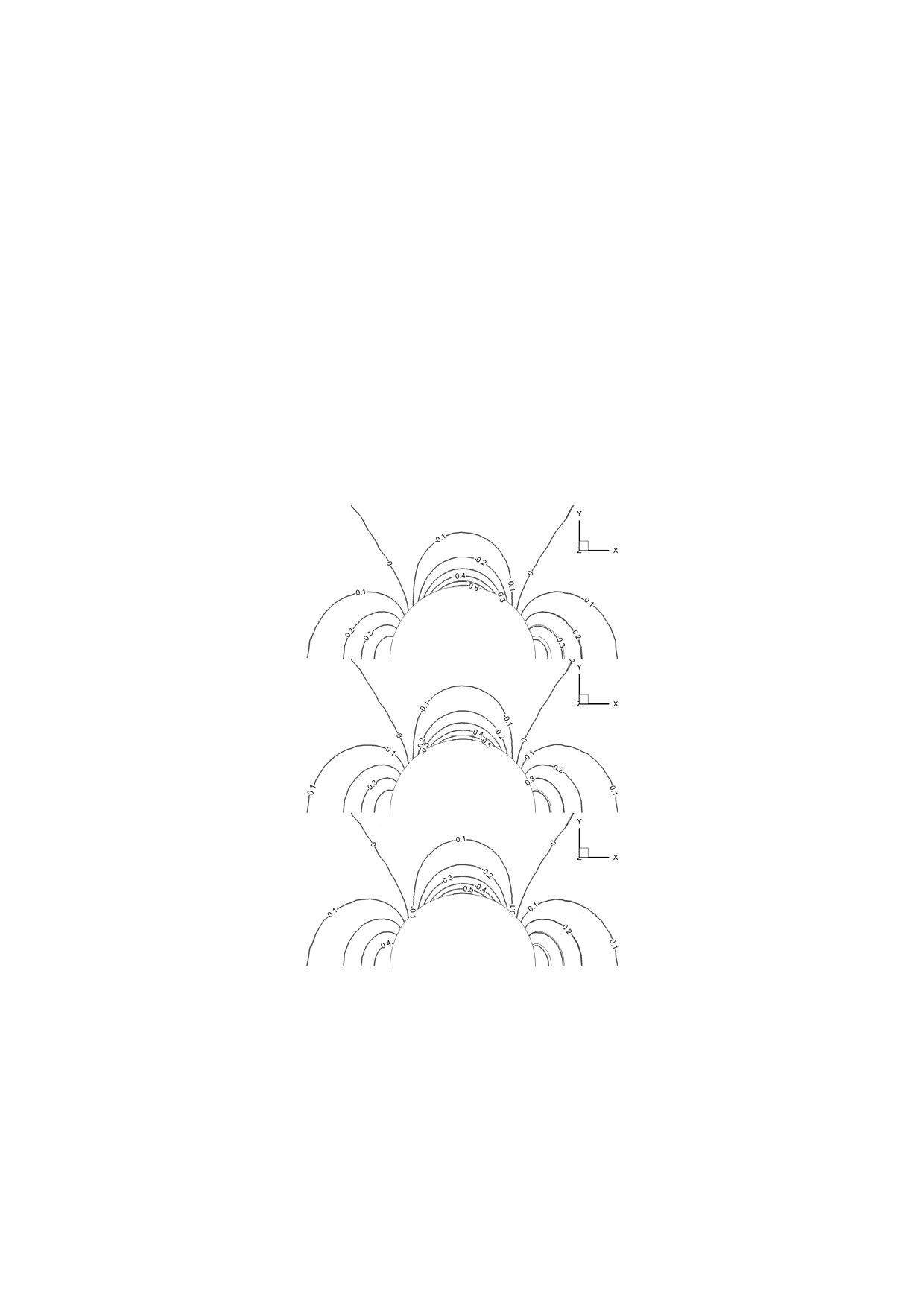
Рис.6. Изолинии пульсации давления в сечении z = 0, y > 0 на сетке с h = 0.04 в
сравнении с точным решением. Сверху вниз: FC с полиномиальными
градиентами, FC с градиентами по спектральным элементам, EBR5.
О вычислении градиента в методе коррекции потоков
135
Таблица 1. Численная ошибка решения задачи об обтекании сферы.
h
Схема
CD
на передней и
макс.
макс.
макс.
(точное
задней точках сферы
ошибка
ошибка
ошибка
знач. 0)
по p
по u
по v
(точное значение 5·105)
0.04
FC-SE
7.49 ·104
5.060 ·105
4.614 ·105
2.08 ·102
2.57 ·102
3.86 ·102
FC-poly
1.63 ·103
5.031 ·105
4.450 ·105
4.05 ·102
5.11 ·102
5.59 ·102
SEBR5
1.87 ·103
4.959 ·105
4.540 ·105
3.37 ·102
3.78 ·102
4.93 ·102
0.02
FC-SE
1.49 ·104
5.023 ·105
4.930 ·105
7.63 ·103
1.31 ·102
1.99 ·102
FC-poly
1.70 ·104
5.013 ·105
4.861 ·105
1.18 ·102
1.62 ·102
2.03 ·102
SEBR5
3.47 ·104
4.982 ·105
4.845 ·105
1.17 ·102
1.48 ·102
2.47 ·102
0.01
FC-SE
3.48 ·105
5.019 ·105
5.146 ·105
1.30 ·102
1.99 ·102
8.86 ·102
FC-poly
1.52 ·105
5.019 ·105
5.021 ·105
6.01 ·103
6.42 ·103
1.49 ·102
SEBR5
3.67 ·105
4.997 ·105
4.977 ·105
5.94 ·103
6.48 ·103
8.68 ·103
Из табл.1 видно, что решение по методу коррекции потоков с полино-
миальными градиентами и по схеме SEBR5 сходится к точному примерно
со скоростью O(h). Первый порядок сходимости по максимумам ошибки
связан с потерей точности рёберных схем на границе. Более высокая ско-
рость сходимости коэффициента сопротивления является неожиданным ре-
зультатом. Однако при использовании градиентов по спектральным элемен-
там решение вблизи задней точки сферы оказывается неверным. Поскольку
заниженное давление вблизи задней точки сферы обычно является следст-
вием избыточной численной взякости, можно предположить, что завышен-
ная плотность является следствием недостаточной численной вязкости.
7. Тестирование: гладкий двумерный вихрь
Теперь рассмотрим задачу о двумерном стационарном вихре в рамках
уравнений Эйлера. Профиль азимутальной скорости был задан в виде
r
u
(r)
. Давление и плотность определялись из условия стационар-
2
2
2
r
a
2
ности вихря
p/ru
/r
и постоянства энтропии с учётом граничных усло-
вий на бесконечности
1, p
1/ . Поскольку циркуляция (r)2ru (r)
2
2
2
(1a
/(
r
a
)) является монотонно возрастающей функцией, по крите-
рию Рэлея [32] это вихрь устойчив к радиальным возмущениям. Радиус вихря
был задан равным a = 0.001, а циркуляция на бесконечности - Г = 0.0005, что
соответствует максимальной окружной скорости вихря
u
(r)
0.0398
,max
Расчёты проводились на последовательности из пяти расчётных сеток.
Сетка строилась при помощи генератора GMSH [33] следующим образом. В
круге радиуса a строилась квазиравномерная неструктурированная тре-
угольная сетка с характерной длиной ребра 2h, где h = a/N, и N - условное
136
П.А. Бахвалов
количество узлов на радиус вихря. Далее в круге радиуса 10a шаг сетки
увеличивался с коэффициентом 1.05 и ограничивался размером 5h. Вне это-
го круга шаг увеличивался с коэффициентом 1.2 без ограничения на макси-
мальный шаг. Полученная при этом сетка измельчалась естественным обра-
зом (каждый треугольник делился на четыре).
Внешняя граница расчётной области - куба со стороной 2 - удалена
достаточно далеко от области интереса. На ней держались все физические
переменные в соответствии с точным решением.
Результаты расчётов на момент времени tmax = 0.02 сведены в табл.2.
«no data» означает, что расчёт не проводился.
Таблица 2. Численная ошибка решения задачи о покоящемся вихре.
Количе-
Steady
Steady
UFC, SE
UFC,
EBR3
EBR5
Тип
ство уз-
FC, SE
FC, poly
poly
ошиб-
лов на
ки
радиус
вихря
Макс.
5
6.12 ·105
1.51 ·104
6.11 ·105
1.66 ·104
1.84 ·104
9.88 ·105
ошибка
10
1.31 ·105
2.15 ·105
1.32 ·105
2.31 ·105
4.43 ·105
2.21 ·105
по дав-
20
2.48 ·106
2.99 ·106
2.45 ·106
2.47 ·106
6.92 ·106
6.44 ·106
лению
40
4.25 ·107
3.81 ·107
4.06 ·107
3.79 ·107
1.82 ·106
1.91 ·106
80
1.12 ·107
1.05 ·107
9.85 ·108
9.07 ·108
5.61 ·107
5.62 ·107
Макс.
5
5.37 ·104
2.20 ·103
5.24 ·104
2.48 ·103
2.63 ·103
7.35 ·104
ошибка
10
1.04 ·104
3.39 ·104
1.03 ·104
3.61 ·104
5.71 ·104
2.08 ·104
по ско-
20
1.59 ·105
4.88 ·105
1.59 ·105
4.36 ·105
8.77 ·105
3.81 ·105
рости u
40
4.08 ·106
5.43 ·106
3.98 ·106
5.39 ·106
1.77 ·105
1.48 ·105
80
8.51 ·107
8.50 ·107
8.55 ·107
8.54 ·107
2.87 ·106
3.22 ·106
Анализируя результаты расчётов, можно сделать следующие выводы.
Во-первых, результаты расчётов, полученные по схеме UFC, почти не отли-
чаются от результатов, полученных при помощи стационарного метода
коррекции потоков при использовании тех же градиентов. Этот результат
ожидаем, поскольку точное решение задачи является стационарным. Во-
вторых, порядок точности схемы FC лежит между 2 и 3. Это также ожидае-
мо, поскольку стационарный метод коррекции потоков обладает 2-м поряд-
ком аппроксимации; повышенная наблюдаемая скорость сходимости (до 3-
го порядка) на стационарных задачах также наблюдалась ранее [7-9]. В-
третьих, метод коррекции потоков обеспечивает меньшую от 1 до 4 раз
ошибку при использовании градиентов, основанных на спектральных эле-
ментах, чем при использовании полиномиальных градиентов. Этот резуль-
тат выше наблюдался на примере одномерного уравнения переноса. В-
четвёртых, схема EBR5 на грубых сетках превосходит по точности не толь-
О вычислении градиента в методе коррекции потоков
137
ко схему EBR3, но и схему FC с полиномиальными градиентами, однако на
подробных сетках результаты по схемам EBR3 и EBR5 близки и сущест-
венно хуже, чем даваемые методом коррекции потоков. Этот эффект связан
с преобладанием для схем EBR ошибки, пропорциональной второй произ-
водной от решения; эта составляющая хаотически меняется от узла к узлу,
ограничена константой, не растущей со временем, но при малых временах
счёта она преобладает и на неструктурированных сетках убывает медленнее
всего при измельчении сетки. В одномерном случае анализ структуры
ошибки проведён в [34].
Подводя итог, на проведённом тесте наилучший результат обеспечива-
ет метод коррекции потоков с использованием спектральных элементов.
Однако сравнительная характеристика схем изменится, если мы увеличим
время счёта: вместо tmax = 0.02 будем проводить расчёт до tmax = 1. Проведе-
ние тестов в этой постановке на последовательности сеток потребовало бы
существенных временных затрат, поэтому ограничимся сеткой с разреше-
нием 20 узлов на радиус вихря. Результаты расчётов по схеме EBR и FC с
полиномиальными градиентами показывают разглаживание профиля ази-
мутальной скорости, то есть численную диссипацию вихря. Этот результат
является физически корректным; если диссипация является избыточной,
она может быть уменьшена измельчением сетки и, в некоторой степени,
уменьшением параметра δ в формуле (5).
Иная картина получается при расчёте по схемам FC и UFC с градиента-
ми по спектральным элементам. Вначале возникает радиальная неустойчи-
вость: профиль азимутальной скорости приобретает паразитные осцилляции,
экспоненциально нарастающие со временем, и к t ~ 0.7 они становятся за-
метны на фоне начального вихря, см. рис.7. Примерно при t ~ 0.9 становится
отчётливо видно нарушение осевой симметрии течения, и к t ~ 1 ядро вихря
полностью разрушается. К моменту времени t ~ 4 решение практически пол-
ностью «забывает» своё начальное состояние. Результаты по схемам FC и
UFC в целом совпадают, немного меняется лишь момент развала вихря.
Таким образом, специфический характер диссипации 4-го порядка,
присущий схеме UFC-SE и наблюдавшийся выше на линейных задачах, на
задаче о вихре приводит к неверному решению, хотя оно и не «разваливает-
ся» в привычном понимании при возникновении неограниченно растущих
численных осцилляций. Поскольку на стационарных задачах дополнитель-
ные диссипативные члены, присущие стационарному методу коррекции по-
токов, зануляются, эта схема обладает тем же недостатком. Вероятно, эта
проблема является неустранимым недостатком вычисления градиентов, ос-
нованных на спектральных элементах второго порядка. При использовании
138
П.А. Бахвалов
спектральных элементов 3-го или более высокого порядка во внутренних
узлах этого эффекта не наблюдается, однако, как было отмечено в [8], воз-
никает неустойчивость на границе расчётной области.
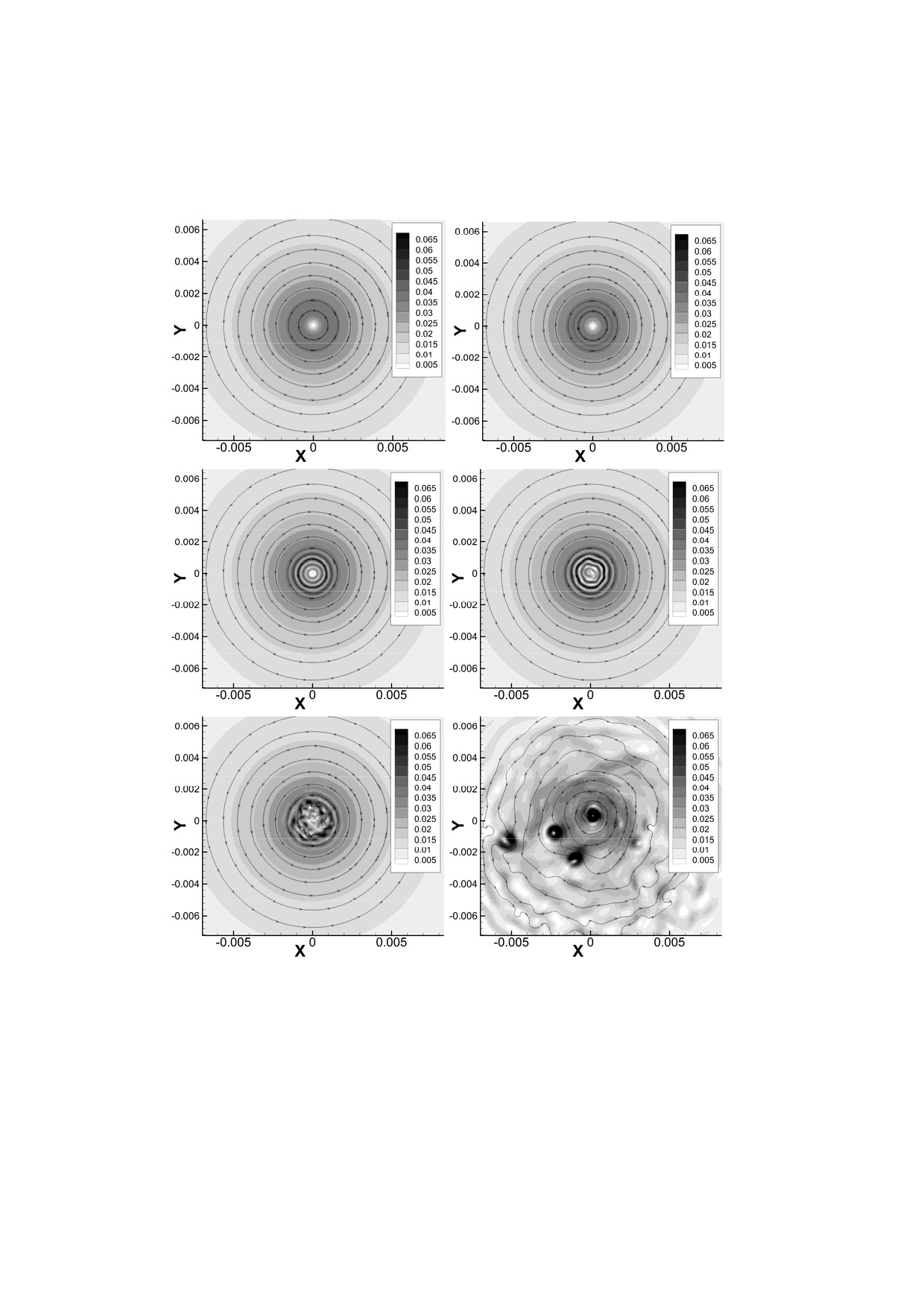
Рис.7. Распад вихря при расчёте по схеме FC с градиентами по
спектральным элементам. Сверху вниз и слева направо: t = 0.5, t = 0.7,
t = 0.9, t = 0.95, t = 1.0, t = 3.0. Цвет соответствует модулю скорости.
О вычислении градиента в методе коррекции потоков
139
8. Задачи с разрывными решениями
Поскольку основное развитие метода коррекции потоков было направ-
лено на создание неконсервативной схемы для гладких нестационарных
решений, показывающей третий порядок точности на неструктурированных
сетках [8-12], вопросу применимости метода коррекции потоков для реше-
ния задач с разрывными решениями уделялось мало внимания. В этом на-
правлении можно отметить работу [11]; в ней рассматриваются стационар-
ные задачи, на которых метод коррекции потоков является консервативным.
Для решения задач с разрывами в методе коррекции потоков исполь-
зуются ограничители наклона, так же, как и в других рёберно-ориентиро-
ванных схемах. Они заключаются в том, что в (6) значенияGK иKG вы-
бираются меньшими 1. В [11] был предложен ограничитель
3
u
u
K G
1
,
u
2(r
r
)·(Q)
(Q
Q
). (8)
GK
20
i
K G
i
K G
max{|u
| | u
|,10
}
K
G
Также рассмотрим другой ограничитель:
3
(u
u
) (u
/ e)
K G
G
1
max{l
,l
}
,
l
,
(9)
GK
K G
i
20
max{|u
u
|
|(u
/
e)
|,10
}
K G
G
где (u
/
e)G
- это производная по направлению ребра GK, умноженная на
длину этого ребра и рассчитанная с использованием данных в узле G и зна-
чения, интерполированного на продолжение этого ребра по аналогии со
схемой EBR3 [4]. Хотя в [11] ограничитель предлагается применять к кон-
сервативным переменным Q, мы будем применять (8) и (9) к характеристи-
ческим переменным SQ, где матрица S определена (2). Подробное описание
такой реконструкции характеристических переменных см. в [5].
В этом разделе мы ограничимся двумя тестами. В качестве первого
теста выберем задачу об обтекании прямого уступа в канале сверхзвуковым
потоком [35]. Начальными данными является однородный поток с парамет-
рами ρ = 1.4, p = 1, u = 3, v = 0. Расчёт проводится до времени tmax =4. Будем
проводить расчёты этой задачи на очень подробной неструктурированной
сетке, а именно, с характерным шагом h = 1/320, чтобы можно было наибо-
лее явно увидеть преимущество схем более высокой точности. Сетка по-
строена генератором GMSH [33].
На рис.8 представлены результаты расчётов по схемам EBR-minmod,
FC с ограничителями (8) и (9) и EBR-WENO. Во всех расчётах для их ста-
билизации использовалось переключение на поток Русанова на рёбрах, хотя
бы один узел которых лежит на границе. Для схемы EBR-WENO была
включена искусственная вязкость с искусственной теплопроводностью [36].
140
П.А. Бахвалов
Из рисунка видно, что ограничитель (9) позволяет добиться меньшей искус-
ственной диссипации на контактном разрыве в верхней части расчётной об-
ласти, чем ограничитель (8).
Теперь рассмотрим задачу с бесконечно гладким решением, чтобы оце-
нить влияние ограничителей. Выберем фоновое поле 1, u 0, p 1/ и
наложим на него пульсации, в начальный момент времени равные
2
r12.5(ie
je
ke
)
4
x
y
z
(0,r)
p(0,r)10
p
expln2
,
ijk
6
i
j
k
где ex, ey, ez - единичные векторы по соответствующим направлениям, а pijk =
= 1, если (i+j+k) - чётное, и 0 иначе.
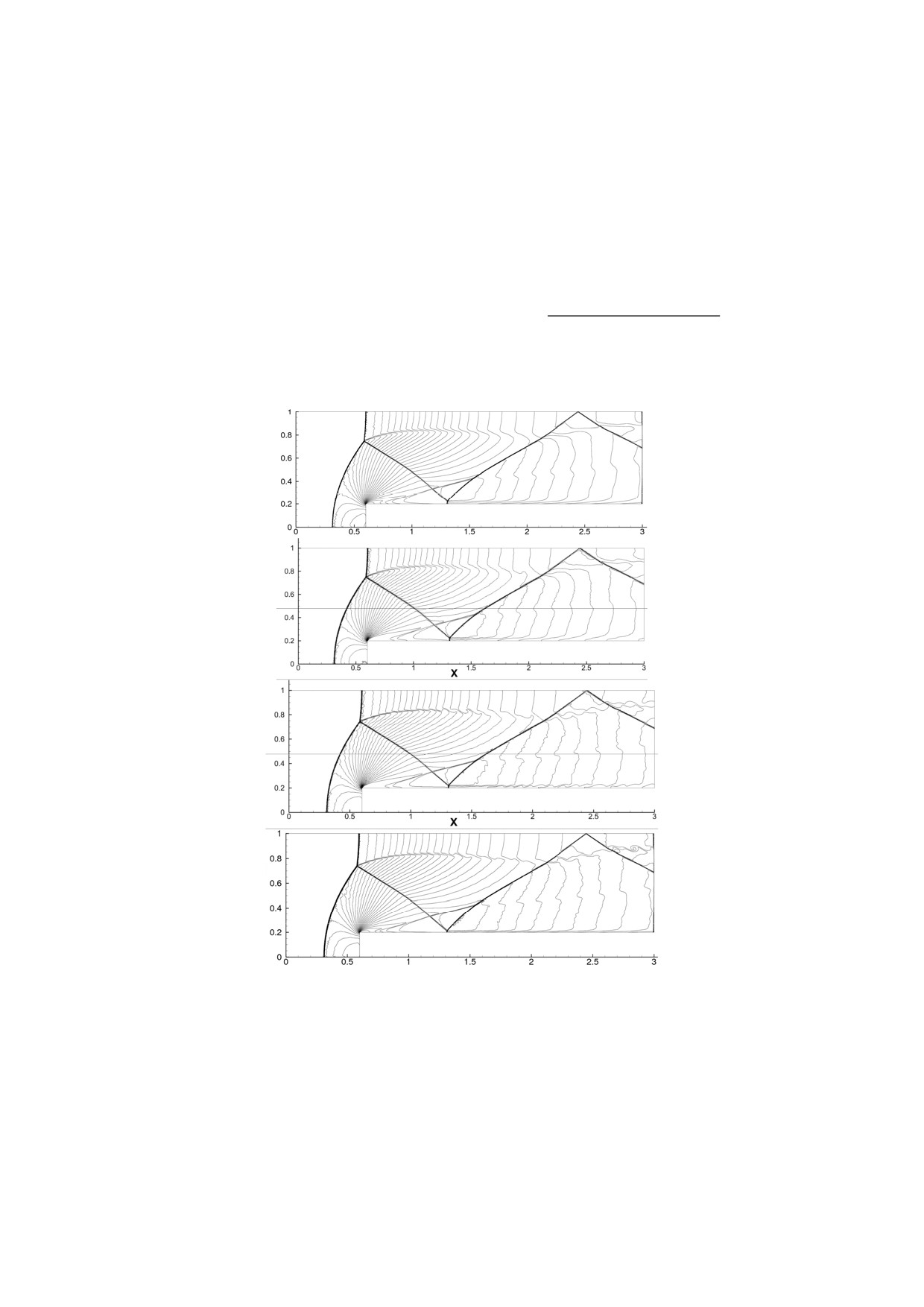
Рис.8. Решение задачи об обтекании уступа в канале на неструктурированной сетке.
Сверху вниз: EBR-minmod, FC с ограничителем (8), FC с ограничителем (9),
EBR-WENO5.
О вычислении градиента в методе коррекции потоков
141
Расчёт проведём в кубе с ребром 25 и периодическими условиями по
всем направлениям до времени tmax=20. Ограничимся случаем декартовой
сетки. Результаты сведены в табл.3. Видно, что предложенный ограничитель
в среднем позволяет добиться на 30-40% меньшей ошибки, чем (8), однако
результат остаётся в разы хуже, чем полученный по схеме EBR-WENO5.
Таблица 3. Численная ошибка решения акустической задачи на декартовой сетке.
Тип
Шаг
Steady FC,
Steady FC,
UFC,
UFC, огра-
EBR-
ошибки
сетки
ограничи-
ограничи-
ограничи-
ничитель
WENO5
тель (8)
тель (9)
тель (8)
(9)
Макс.
1
5.59 ·106
4.01 ·106
6.92 ·106
4.76 ·106
3.08 ·107
ошибка
0.5
1.50 ·106
1.05 ·106
1.44 ·106
1.06 ·106
1.86 ·108
по давле-
0.25
6.38 ·107
8.37 ·107
9.71 ·107
3.72 ·107
4.34 ·109
нию
9. Заключение
В настоящей работе рассмотрены различные модификации метода кор-
рекции потоков. Особое внимание было уделено способу вычисления гра-
диентов в сеточных узлах со вторым порядком аппроксимации.
На линейных задачах было замечено, что нестационарный метод кор-
рекции потоков при использовании градиентов, рассчитанных с использова-
нием спектральных элементов, даёт меньшую численную ошибку в сравне-
нии с другими модификациями и другими рёберно-ориентированными схе-
мами. Но за кажущимся повышением точности скрывается потеря диссипа-
ции и, как следствие, ошибочность решения. В частности, на вихре, кото-
рый должен быть устойчивым к радиальным возмущениям, эти возмущения
нарастают и, в конечном счёте, приводят к разрушению вихря.
Если же использовать градиенты от интерполяционных полиномов, по-
строенных методом наименьших квадратов, то многочисленные экспери-
менты показывают, что нестационарный метод коррекции потоков даёт ре-
зультаты, очень близкие к рассчитанным по схеме EBR5. Вычислительная
стоимость этих схем также сопоставима: время, затрачиваемое на один шаг
у метода коррекции потоков, в 0.85-1.5 раза выше, чем у EBR5. Это значе-
ние варьируется в зависимости от модификаций; замеры проводились при
решении двумерных уравнений Эйлера.
Проведённые выше расчёты задачи об обтекании прямого уступа пока-
зывают, что метод коррекции потоков полностью совместим с ограничите-
лями наклонов и с их помощью успешно справляется с задачами с разрыв-
ными решениями. Но на гладких решениях использование этих ограничите-
лей сказывается на точности сильнее, чем в схемах с квазиодномерной ре-
конструкцией. Численная ошибка, полученная методом коррекции потоков
142
П.А. Бахвалов
c различными ограничителями, лишь немногим лучше схемы с ограничите-
лем MinMod. Ещё большую точность даёт схема EBR-WENO. Таким обра-
зом, на задачах с разрывными решениями схемы с квазиодномерной рекон-
струкцией предпочтительнее.
Основной задачей, стоявшей перед настоящей работой, являлось реше-
ние вопроса о выборе основной рёберно-ориентированной схемы, исполь-
зуемой для расчётов в программном коде NOISEtte [37]. Проведённые рас-
чёты тестовых задач позволяют сделать вывод о том, что в настоящее время
такой схемой стоит считать схему семейства EBR. Возможно, у метода кор-
рекции потоков есть дальнейший потенциал развития в направлении некон-
сервативных схем. Этот вопрос является темой дальнейшего исследования.
СПИСОК ЛИТЕРАТУРЫ
1. B. Stoufflet, J. Periaux, F. Fezoui, A. Dervieux. Numerical simulation of 3-D hypersonic
Euler flows around space vehicles using adapted finite elements // AIAA Paper No. 87-0560.
2. T.J. Barth. Numerical aspects of computing high reynolds number flows on unstructured
meshes // AIAA Paper No. 91-0721.
3. B. Koobus, F. Alauzet, A. Dervieux. Numerical algorithms for unstructured meshes, In
Book: Computational Fluid Dynamics, F. Magoules (Editor), CRC Press, 2011, p.131-203.
4. I. Abalakin, P. Bakhvalov, T. Kozubskaya. Edge-based reconstruction schemes for unstruc-
tured tetrahedral meshes // International journal for numerical methods in fluids, 2016, v.81,
№6, p.331-356.
5. Pavel Bakhvalov, Tatiana Kozubskaya. EBR-WENO scheme for solving gas dynamics prob-
lems with discontinuities on unstructured meshes // Comput. Fluids, 2017, 157, p.312-324.
6. И.В. Абалакин, В.Г. Бобков, Т.К. Козубская. Разработка метода расчета течений с ма-
лыми числами Маха на неструктурированных сетках в программном комплексе
NOISETTE // Матем. моделирование, 2017, т.29, № 4, с.101-112;
Ilya Abalakin, Vladimir Bobkov, Vladimir Kozubskaya. Implementation of the Low Mach
Number Method for Calculating Flows in the NOISEtte Software Package // Math. Mod.
and Comp. Simul., 2017, 9(6), p.689-697.
7. A. Katz, V. Sankaran. An efficient correction method to obtain a formally third-order accurate
flow solver for node-centered unstructured grids // J. Sci. Comput., 2012, 51 (2), p.375-393.
8. B. Pincock, A. Katz. High-order flux correction for viscous flows on arbitrary unstructured
grids // J. Sci. Comput., 2014, 61 (2), p.454-476.
9. C.D. Work, A.J. Katz. Aspects of the flux correction method for solving the Navier-Stokes
equations on unstructured meshes // AIAA paper No.2015-0834.
10. A. Katz, D. Work. High-order flux correction/finite difference schemes for strand grids //
Journal of Computational Physics, 2015, 282, p.360-380.
11. O. Tong, Y. Yanagita, R. Shaap, S. Harris, A. Katz. High-Order strand grids methods for
shock-turbulence interaction // AIAA paper No. 2015-2283.
12. H. Nishikawa. Accuracy-preserving Source Term Quadrature for Third-Order Edge-Based
Discretization // Journal of computational physics, 2017, 344, p.595-622.
О вычислении градиента в методе коррекции потоков
143
13. P. Bakhvalov, T. Kozubskaya. Modification of Flux Correction method for accuracy im-
provement on unsteady problems // J. Comput. Phys., 2017, 338, p.199-216.
14. П.А. Бахвалов. Реализация метода коррекции потоков на гибридных неструктуриро-
ванных сетках // Препринт ИПМ, 2017, №38, 28 с.
P.A. Bakhvalov. Realizatsya metoda korrektsii potokov na gibridnyh nestrukturirovannih
setkah. - M.: IPM RAN, 2017, preprint №38, 28 s.
15. T.J. Barth. A 3-D upwind Euler solver for unstructured meshes // AIAA Paper No 91-1548.
16. П.А. Бахвалов, Т.К. Козубская. О построении реберно-ориентированных схем, обес-
печивающих точность на линейной функции, для решения уравнений Эйлера на гиб-
ридных неструктурированных сетках // ЖВММФ, 2017, т.57, № 4, с.92-111;
Pavel Bakhvalov, Tatiana Kozubskaya. Construction of Edge-Based 1-Exact Schemes for
Solving the Euler Equations on Hybrid Unstructured Meshes // Comp. Math. Math. Phys.,
2017, 57(4), p.680-697.
17. H. Nishikawa. Beyond Interface Gradient. A General Principle for Constructing Diffusion
Schemes // AIAA Paper No. 2010-5093.
18. А.Г. Куликовский, Н.В. Погорелов, А.Ш. Семенов. Математические вопросы числен-
ного решения гиперболических систем уравнений. М: Физматлит, МАИК, Наука/
Интерпериодика, 2001, 607 с.;
A.G. Kulikovsky, Nikolai V. Pogorelov, A.Yu. Semenov. Mathematical Aspects of Numeri-
cal Solution of Hyperbolic Systems // Taylor Francis Inc, United States (2000).
19. P.L. Roe. Approximate Riemann solvers, parameter vectors, and difference schemes//
Journal of Computational Physics, 1981, v.43, №2, p.357-372.
20. H. Luo, J.D. Baumt, R. Lohner. Edge-Based Finite Element Scheme for the Euler Equa-
tions // AIAA Journal, 1994, v.32, No. 6.
21. P. Eliasson. EDGE, a Navier-Stokes solver for unstructured grids, Tech. Rep. FOI-R-
0298-SE, FOI Swedish defence research agency // Division of Aeronautics, FFA, SE-172
90 STOCKHOLM (December 2001).
22. Y. Nakashima, N. Watanabe, H. Nishikawa. Hyperbolic Navier-Stokes solver for three-
dimensional flows // AIAA Paper No. 2016-1101.
23. H. Nishikawa. Alternative formulations for first-, second-, and third-order hyperbolic Na-
vier-Stokes schemes // AIAA Paper No. 2015-2451.
24. C. Debiez, A. Dervieux. Mixed-element-volume MUSCL methods with weak viscosity for
steady and unsteady flow calculations // Computers and Fluids, 2000, 29 (1), p.89-118.
25. C. Debiez, A. Dervieux, K. Mer, B. Nkonga. Computation of unsteady flows with mixed
finite volume/ finite element upwind methods // International journal for numerical method
in fluids, 1998, 27, p.193-206.
26. B. Diskin, J.-L. Thomas. Notes on accuracy of finite-volume discretization schemes on ir-
regular grids // Applied Numerical Mathematics, 2010, v.60, no. 3, p.224-226.
27. П.А. Бахвалов. О порядке точности рёберно-ориентированных схем на сетках специ-
ального вида // Препринт ИПМ им. М. В. Келдыша РАН, 2017, № 79, 32 с.;
P.A. Bakhvalov. O poryadke tochnosti reberno-orientirovannyh shem na setkah spet-
sial’nogo vida - M.: IPM RAN, 2017, preprint №79, 32 s.
28. H. Nishikawa, Divergence formulation of source term // Journal of Computational Physics,
2012, 231, p.6393-6400.
29. Л.Г. Лойцянский. Механика жидкости и газа. М.-Л.: Гостехиздат, 1950;
144
П.А. Бахвалов
L.G. Loitsyansky. Mechanics of Liquids and Gases // Pergamon Press, Oxford, UK, 1966,
804 p.
30. E. Turkel. Preconditioning Techniques in Computational Fluid Dynamics // Annual Re-
view of Fluid Mechanics, 1999, v.31, 385-416.
31. H. Guillard, C. Viozat C. On the behaviour of upwind schemes in the low Mach number
limit // Computers and Fluids, 1999, v.28, №1, p.63-86.
32. С.В. Алексеенко, П.А. Куйбин, В.Л. Окулов. Введение в теорию концентрированных
вихрей. Новосибирск: Институт теплофизики СО РАН, 2003, 504 с.;
S.V. Alekseenko, P.A. Kuibin, V.L. Okulov. Theory of Concentrated Vortices. Springer-
Verlag. Berlin Heidelberg: 2007. 487 p.
33. C. Geuzaine, J.-F. Remacle. Gmsh: a three-dimensional finite element mesh generator with
built-in pre- and post-processing facilities, 1997.
34. П.А. Бахвалов. Метод нестационарного корректора для анализа точности линейных
полудискретных схем // Препринт ИПМ им. М.В. Келдыша РАН, 2018, № 123, 38 с.;
P.A. Bakhvalov. Metod nestatsionarnogo korrektora dlya analiza tochnosti lineinyh polud-
iskretnyh shem. - M.: IPM RAN, 2018, preprint №123, 38 s.
35. P. Woodward, P. Colella. The Numerical Simulation of Two-Dimensional Fluid Flow with
Strong Shocks // Journal of computational physics, 1984, v.54, p.115-173.
36. И.Ю. Тагирова, А.В. Родионов. Применение искусственной вязкости для борьбы с
«карбункул»-неустойчивостью в схемах типа Годунова // Математическое модели-
рование, 2015, т.27, с.47-64;
I.Y. Tagirova, A.V. Rodionov. Application of the artificial viscosity for suppressing the car-
buncle phenomenon in Godunov-type schemes // Math. Models. Comput. Simul., 2015; 27,
p.47-64.
37. И.В. Абалакин, П.А. Бахвалов, А.В. Горобец, А.П. Дубень, Т.К. Козубская. Парал-
лельный программный комплекс NOISETTE для крупномасштабных расчетов задач
аэродинамики и аэроакустики // Вычислительные методы и программирование, 2012,
т.13, с.110-125;
I.V. Abalakin, P.A. Bakhvalov, A.V. Gorobets, A.P. Duben, T.K. Kozubskaia. Parallelnyi
programmnyi kompleks NOISETTE dlia krupnomasshtabnykh raschetov zadach aerodina-
miki i aeroakustiki // Vychislitelnye metody i programmirovanie, 2012, t.13, s.110-125.
Поступила в редакцию 20.08.2018
После доработки 20.08.2018
Принята к публикации 22.10.2018