МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 6, стр. 55-81
О РЕШЕНИИ ЛИНЕЙНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
ВТОРОГО ПОРЯДКА
2019 г.
А.В. Шильков
Институт прикладной математики им. М.В. Келдыша РАН, Москва
ale-shilkov@yandex.ru
Исследование выполнено за счет гранта Российского научного фонда №14-
11-00699.
DOI: 10.1134/S0234087919060042
Изложен метод решения внутренних граничных задач для эллиптических уравне-
ний второго порядка с помощью перехода к лучевым переменным. Область разби-
вается на ячейки, в пределах которых коэффициенты и источники имеют свойства
гладкости и непрерывности, необходимые для существования в ячейке регуляр-
ного классического решения. Конечные разрывы коэффициентов (если они есть)
проходят по границам ячеек. Регулярное решение в ячейке ищется в виде суперпо-
зиции вкладов объемных и граничных источников, размещенных на лучах, прихо-
дящих в данную точку от границ ячейки. Далее составляется конечно-аналитичес-
кая схема для численного нахождения обобщенного решения в области с разрыв-
ными коэффициентами и источниками посредством сшивки регулярных решений,
выходящих из ячеек на границах ячеек. В схеме отсутствует жесткая зависимость
точности аппроксимации от размеров и формы ячеек, присущая конечно-разност-
ным схемам.
Ключевые слова: эллиптические уравнения, граничная задача, метод лучевых пере-
менных, численные методы, конечно-аналитическая схема.
ON THE SOLUTION OF SECOND-ORDER LINEAR ELLIPTIC EQUATIONS
A.V. Shilkov
Keldysh Institute of Applied Mathematics, Russian Academy of Sciences, Moscow
A method for solving interior boundary value problems for second-order linear elliptic
equations by introducing ray variables is described. The region is divided into cells,
within which the coefficients and sources of the equations have the smoothness and con-
tinuity properties necessary for the existence of regular solutions in the cell. The finite
discontinuities of the coefficients (if any) pass along the cell boundaries. The regular so-
lution in a cell is sought in the form of a superposition of the contributions made by vol-
56
А.В. Шильков
ume and boundary sources placed on rays arriving at a given point from the cell bounda-
ries. Next, a finite-analytic scheme for the numerical solution of boundary value prob-
lems in a domain with discontinuous coefficients and sources is constructed by matching
the regular solutions emerging from cells at the cell boundaries. The scheme does not ex-
hibit the rigid dependence of the accuracy of approximation on the sizes and shape of the
cells, which is inherent in finite-difference schemes.
Keywords: elliptic equations, boundary value problem, method of ray variables, numeri-
cal methods, finite-analytic scheme.
1. Введение
В первой части работы найдены регулярные решения внутренних гра-
ничных задач для линейных эллиптических уравнений второго порядка с
помощью перехода к лучевым переменным. Решение ищется в виде супер-
позиции вкладов источников, размещенных на лучах, приходящих в данную
точку области от ее границ. На коэффициенты, источники и границу облас-
ти накладываются ограничения, необходимые для существования регуляр-
ного классического решения. Также на коэффициенты уравнений наклады-
ваются некоторые дополнительные ограничения. Метод лучевых перемен-
ных отличается от известных методов решения граничных задач, таких как
метод функций Грина и метод разделения переменных.
Во второй части работы составлена конечно-аналитическая схема для
численного нахождения обобщенного решения в области с разрывными ко-
эффициентами и источниками. Область разбивается на ячейки, в пределах
которых коэффициенты и источники уравнений имеют необходимые свой-
ства гладкости и непрерывности, а конечные разрывы коэффициентов (если
они есть) проходят по границам ячеек. Схема строится с помощью сшивки
регулярных решений, выходящих из ячеек на границах ячеек. Для составле-
ния схемы оказалось удобным использовать представление решений в лу-
чевых переменных. В сравнении с разностными схемами аналитические
схемы имеют ряд недостатков и ряд преимуществ. Наиболее важное пре-
имущество состоит в отсутствии жесткой зависимости точности аппрокси-
мации от размеров и формы ячеек.
Первые публикации [1-3], посвященные аналитическим схемам, появи-
лись позже публикаций, посвященных разностным схемам. Однако по вос-
поминаниям участников американского и советского атомных проектов пер-
воначально схемы применялись для решения одномерных задач наравне с
разностными схемами и методами Монте-Карло. Позднее, ввиду труднос-
тей переноса схем с одномерных задач на многомерные задачи, их развитие
замедлилось. Аналитическим схемам посвящено относительно мало работ
О решении линейных эллиптических уравнений второго порядка
57
(см. [1-15] и цит. литературу). В первых работах [2,3] схема называлась
«точной». Термин конечно-аналитическая схема дискретизации появился
позднее [8].
Определения. Пусть в ограниченной области V евклидова пространст-
ваEN некоторый процесс описывается системой линейных уравнений в ча-
стных производных:
i
F
u i
u
F
Y S,
i
i
0
r
(1)
ij
[A
Y]
ij w
w i
i
B
k
Y
F S
,
1i
N
j
j
0
r
ij
ji
ij
ij
ij
A
A
,
b
A
c
,
detB
0,
|B
|c
,
|Ω|1,
A
i
j
A
i
j
B
i
u
u
w
w
|S(r)|,|S
(r
)|c
,
|
(r)|,|
(r)|,|k
(r)|c
,
b
r)c
S
0
i
i
w
0 (
w
1
2
N
Здесь
r
(r
,r
,...,r
)
есть вектор координат, Y (r) - искомая скалярная
i
функция (далее - плотность),
(
)
F
r
- искомая векторная функция (поток),
i
S (r) и
(
)
S
r
- заданные скалярная и векторная функции (источники). В (1)
и последующих формулах подразумевается суммирование по повторяющим-
ся координатным индексам.Aij (r) иBij (r) - тензорные функции типа (2,0),
ij
A
– положительно определенная билинейная форма на ковекторах,Bij - не-
u
вырожденный тензор. Тензоры, источники и коэффициенты уравнений
,
0
u
w
w
,
,
k
ограничены положительными постоянными
b
,c
0
. Коэф-
i
0
i
()
()
w
фициент
принимает только положительные значения. ТензорBij можно
0
исключить из системы
ij w
i
kl w
ij
kl w
ij
w w ij
w
kl w
B
k
B
k
A
A
B
k
A
A ,
A
B
k
(2)
j
k
l
jk
l
j
j
j
jk
l
w
w
заменой векторного коэффициента
k
(r)
на коэффициент
(r). ЗдесьAij
i
i
ki
ki
i
j
– котензор (обратный тензор) тензораAij :
A
A
A
A
,
- сим-
jk
jk
j
k
вол Кронекера.
ij
i
Разбиение области на ячейки. Тензор
A
(r), источники S(r),
S
(r)
и
коэффициенты уравнений могут иметь конечные разрывы на некоторых по-
верхностях размерности N-1. Ограничимся решением задач, в которых об-
ласть V допускает разбиение на непересекающиеся подобласти (далее -
ячейки)Vm , m 1,..., M , такое, что ячейки плотно покрывают область, по-
58
А.В. Шильков
верхности разрывов (если разрывы есть) проходят по границам ячеек. Для
каждой ячейки выполнены условия, необходимые для существования в ней
ij
ij
u
u
w
w
i
регулярного решения. В частности,
A
,
B
,
,
,
S
- гладкие
0,
i
0 ,
i
функции в ячейке, S - непрерывная функция. Граница ячейкиm состоит
из гладких участков, на которых вектор нормали меняется непрерывно, а
ячейка видна под телесным углом (N) 2 , составляющим половину полно-
N/2
го телесного угла пространства
(N)
2
(N
2), (3) 4. В точках
пересечения участков ячейка видна под телесным углом, который больше
числа c и меньше
. На границеm каждой ячейкиVm на решения
c
системы (1) наложим условия
j
i
i
1
G
n
[F
F
]
[Y Y
],
r
,
(3)
ij
ext
ext
m
1
i
j
G
G
,
0b
G
c
,
|Ω|1,
0b
(r c
,
1 (r) 1.
ij
ji
G ij
G
i
G
(r),
(r), (r),
Y
(r
),
F
(r)
- заданные на гладких участках границы
ij
ext
ext
i
ограниченные кусочно-непрерывные функции,
(
)
n
r
- вектор внешней нор-
мали,Gij - положительно определенная билинейная форма на векторах.
Индекс ячейки m в обозначениях величин опущен. Функция имеет смысл
коэффициента отражения границы. При 0 отражение отсутствует. Если
на участке границы 1, то условия (3) переходят в граничные условия
A
ki
ki
i
(обратным тензором) тензораAij :
A
A
A
A
, то условия (3) соот-
jk
jk
j
ветствуют граничным условиям обобщенной задачи Неймана [16, с.436;
17, с.158; 18, с.16]. Случай 1 соответствует условиям классической зада-
A , 1 называют условием с косой производ-
ной. Общий случай называют смешанными граничными условиями. Далее
под термином граничные условия Дирихле понимается ситуация, когда на
участке границы поставлены условия Дирихле. Его следует отличать от
термина «граничная задача Дирихле», когда данный тип условий поставлен
на всей границе.
Если из второго векторного уравнения системы (1) выразить потокFi
и подставить в первое уравнение, то в ячейках (областях гладкости/непре-
рывности функций) система сводится к уравнению второго порядка:
О решении линейных эллиптических уравнений второго порядка
59
2
ij
w
ij
ij
[A
Y]
ln
[A
Y]
[B
Y]
u
0
w
k
(4)
i
j
j
j
i
j
i
r
r
r
r
r
w
i
k
S
u
w u ij w
w ij
j
w
u i
w
B k
B
Y
S
S
,
r V
0
0
i
j
0
0
i
0
m
i
w
i
w
r
r
0
0
A дифференциаль-
ный оператор уравнения (4) приводится локально (в точке) к оператору эл-
липтического типа [19, с.156].
Приведение системы к стандартному виду. Пусть в пределах каждой
ячейки поля векторных коэффициентовui иwi потенциальны, т.е. можно
u
w
подобрать скалярные функции
(r),
(r)
такие, что
u,w
u,
w
u,w
2
u,w
u,w
i
j
2
,
2
,
r V
(5)
i
m
i
j
i
i
j
r
r
r
r
r
u,w u,w
При постоянных коэффициентах в ячейке
const
искомые по-
i
m,i
u
,w
u,w
i
i
u,w
тенциалы -
r)
[r
r
]
2
. В случае линейной зависимо-
m,i
m
0
u,w
u,w
j
j
u,w
u
,
w
сти коэффициентов от координат:
r)
2P
[r
r
]
, где
P
i
ij
m m,i
ij
u
,
w
P
- постоянная билинейная форма:
ji
u,w
1
u,w
i
i
j
j
1
u
,w
i
i
u,w
P
[r
r
][r
r
]
[r
r
]
,
r V
ij
m
m
m
,i
m
0
m
2
2
Нетрудно указать и ряд других простых потенциалов, с помощью которых
(или их суперпозиции) задаются потенциальные коэффициенты. Это, на-
пример, функции, зависящие от расстояния до точки, прямой или плоскости
(множеств размерности от 0 до N-1).
Если выполнено (5), то замена искомых функций, тензора и коэффици-
ентов [15]
w u
i
u
w
u
w
U
i
i
ij
j
j
S
Y e ,
F
W
D
Ue
,
(6)
w
w
a
2
0
0
u
w u w u
w u
[
][
]
j
j
i
i
j
j
ij
ij
0
ij
ij
w
A
aD
,
D
D
,
,
u
w
i
w
w
0
a
4
r
2
0
0
преобразует систему уравнений (1), (2) в ячейке к стандартному виду
60
А.В. Шильков
i
W
UQ,
u
u i
i
i
u
w
r
i
S
S
QS
e
(7)
ij
w
i
w
[D
U]
r
i
0
0
W
0,
j
w
r
Здесь U - новая плотность,Wi - новый поток, a(r) , a 0 - ограниченная
положительная гладкая функция. Коэффициентw принимает положи-
тельные значения, коэффициентu может иметь любой знак. Граничные
условия (3) преобразуются в условия аналогичного вида:
w u
1
1
j
i
i
i
i
j
ik
G
n
[W
W
]
[UU
],
G
n
D
,
r
(8)
ij
ext
ext
w
kj
m
1
a
1
2
0
Уравнение (4) переходит в уравнение
ij
1
[D
U]
UQ,
r V
(9)
i
j
u
m
r
r
w
ij
ij
Выбором функции a(r) тензор
D r)
A
/a всегда можно нормировать
ij
так, чтобы один из его инвариантов de
D или
SpD
был равен заданной
гладкой функции в ячейке. Далее считаем, что след тензора равен единице:
ij
ij
ij
SpD r)
D
1
,
a r)
SpA
(r)
(10)
ij
ij
Нормировка делает тензор
(
)
D
r
в ячейке функцией относительно малой
вариации, близкой к постоянному тензору.
ji
Симметричный тензорDij
D
ортогональным преобразованием ло-
кальной системы координат можно привести к диагональному виду с поло-
жительными числами на диагонали. Если далее выполнить растяжение
вдоль ортогональных координатных осей, то уравнение (9) перейдет (ло-
кально) в стационарное уравнение Шредингера, в случае постоянных коэф-
фициентов - в уравнение Гельмгольца, в случае |
|
- в уравнение
u
w
Пуассона.
Необходимость разрешения уравнений (1), (3), (7), (8) возникает в ма-
тематическом моделировании многих проблем физики и техники. Это рас-
четы теплообмена в технических установках, процессов переноса нейтро-
нов в ядерных реакторах и теплового излучения в газах и плазме, протека-
ния химических реакций, распространения реагентов в природных средах,
колебаний конструкций и распространения электромагнитных волн.
О решении линейных эллиптических уравнений второго порядка
61
Существование и единственность решения. Вопросы существования
регулярного решения граничной задачи в одной ячейкеVm и обобщенного
решения в полной области V с разрывными коэффициентами обсуждаются в
работах [16-22]. Существование и поведение решений зависит от знака про-
. Коэффициентw принимает ограничен-
ные положительные значения:
b
(r)c
,
b
0. Поэтому для класси-
w w
w
w
фикации задач достаточно рассматривать знак коэффициентаu .
Дополним разбиение области V на ячейки так, чтобы ячейки были не
только областями непрерывности функций и коэффициентов, но и были од-
нородны относительно знака коэффициентаu . В результате разбиения мо-
гут возникать однородные ячейки трех типов. Ячейки А с положительным
коэффициентом, в которых
/
c
, гдеcu - малое положительное чис-
u
w u
ло 0
c
1. Ячейки Б с отрицательным коэффициентом:
/
c
u
u
w
u
Вырожденные ячейки В: |
|
c
. В вырожденной ячейке решение
u
w u
уравнений (7), (9) близко к решению уравнения Пуассона
i
W
Q,
i
ij
r
1
[D
U]
Q
,
r V
(11)
i
j
m
ij
[D
U]
r
w
r
i
W
0,
j
w
r
Представим регулярное решение задачи (7), (8) в ячейкеVm в виде сум-
i
i
i
i
мы:
UU
U
,
W
W
. Функции
U
,
W
удовлетворяют неодно-
0
0
W
0
0
2
родной задаче (7), (8) с источником
QQ
[
1 uU
; функции U ,Wi
удовлетворяют однородной граничной задаче
i
W
2
U
0,
i
u
r
j
i
1
G
n
W
U
,
ij
ij
1
m
[D
U
]
m
i
W
0,
j
w
r
где 0 - собственное число. Для регулярного решения граничной задачи
в ячейке имеет место альтернатива [16, с.443; 17, с.157; 18, с.17].
1) В ячейке А или В uw
c
) однородная задача решений не
u
i
имеет, кроме тривиального решения
0
U W
. Неоднородная задача (7), (8)
имеет единственное решение. Исключение составляет классическая задача
Неймана для уравнений (11) в вырожденной ячейке В, в которой плотность
62
А.В. Шильков
U определяется с точностью до постоянной. Задача разрешима, если полная
мощность источников Q равна полному потоку через границу ячейки.
2) Ячейка Б,uw
c
может иметь ряд собственных значений
u
1,
,... 0 и соответствующих им нетривиальных решений однородной зада-
2
чи, интерпретируемых как собственные колебания. Множество решений
однородной задачи состоит из линейных комбинаций собственных колеба-
ний. Пусть в ячейке возбуждена некоторая комбинация собственных ко-
лебаний. Тогда неоднородная граничная задача (7), (8) имеет единственное
решение, если выполнено условие ортогональности источника Q каждому
колебанию данной комбинации. Если условие ортогональности источника
не выполнено, то неоднородная задача решений не имеет. Если в ячейке нет
возбужденных собственных колебаний, то неоднородная граничная задача
имеет единственное решение.
Цель и структура работы. Некоторые регулярные решения граничных
задач в ячейке, полученные методом функций Грина или методом разделе-
ij
ния переменных при частном виде тензораDij
D
, источников, коэффи-
циентов, граничных условий и простой форме ячейки, приведены в
[17, с.125; 23, с.116; 24, с.492]. Коэффициенты и источники уравнений
обычно полагаются постоянными, ячейка имеет форму параллелепипеда
или плоского, цилиндрического, сферического слоя. Этих решений недос-
таточно для составления конечно-аналитических схем решения задач, возни-
кающих в практических исследованиях.
Цель работы состоит в нахождении регулярного решения неоднород-
ной граничной задачи (7), (8) в ячейкеVm произвольной формы при огра-
ничениях (12) на поведение коэффициентов уравнений и в составлении ко-
нечно-аналитической схемы для численного нахождения обобщенного ре-
шения в области V с разрывными коэффициентами и источниками. Регу-
лярное решение в ячейке ищется методом лучевых переменных [15]. Струк-
тура работы следующая. В разделе 2 вводятся лучевые переменные, в этих
переменных формулируется общее решение системы в ячейке. В разделе 3
приведены решения типичных задач. В разделе 4 исследуются некоторые
свойства решений. В разделе 5 обсуждены условия сшивки решений из раз-
ных ячеек и составлена конечно-аналитическая схема.
2. Метод лучевых переменных
Ограничения на тензор и коэффициенты. Вследствие (10) тензор
ij
D
близок к постоянному тензору в ячейке. Во многих практических зада-
О решении линейных эллиптических уравнений второго порядка
63
чах коэффициенты
(
)
и
(
)
подобны друг другу, так что их отноше-
u r
w r
ние
/
меняется значительно медленнее коэффициентов по отдельно-
u
w
сти. Будем считать, что производные тензора и отношения коэффициентов
равномерно ограничены в пределах ячейки малыми постояннымиcD иcR :
ij
D
i
i
u
c
,
c
,
|Ω|1,
r V
(12)
D w
R w
m
j
i
r
r
w
При постоянном тензоре и постоянном отношении
c
c
0
D R
Лучевые переменные. Определим в пределах ячейки гладкое римано-
во многообразиеRN с метрикой
g
(r)
D
- билинейной формой на век-
ij
ij
торах, где
D
(r)
- котензор тензораDij . Метрика задает локальный мас-
ij
штаб расстояния между точками многообразия и порождает совокупность
геодезических линий. Снабдим многообразие римановой связностью [25;
26, с.359]. Рассмотрим вEN точку ячейки r и прикрепленный к ней еди-
ничный вектор Ω , |Ω|1, принимающий произвольное направление в пре-
делах телесного угла . Через точку в заданном направлении Ω проходит
только одна геодезическая линия многообразияRN , вообще говоря, не яв-
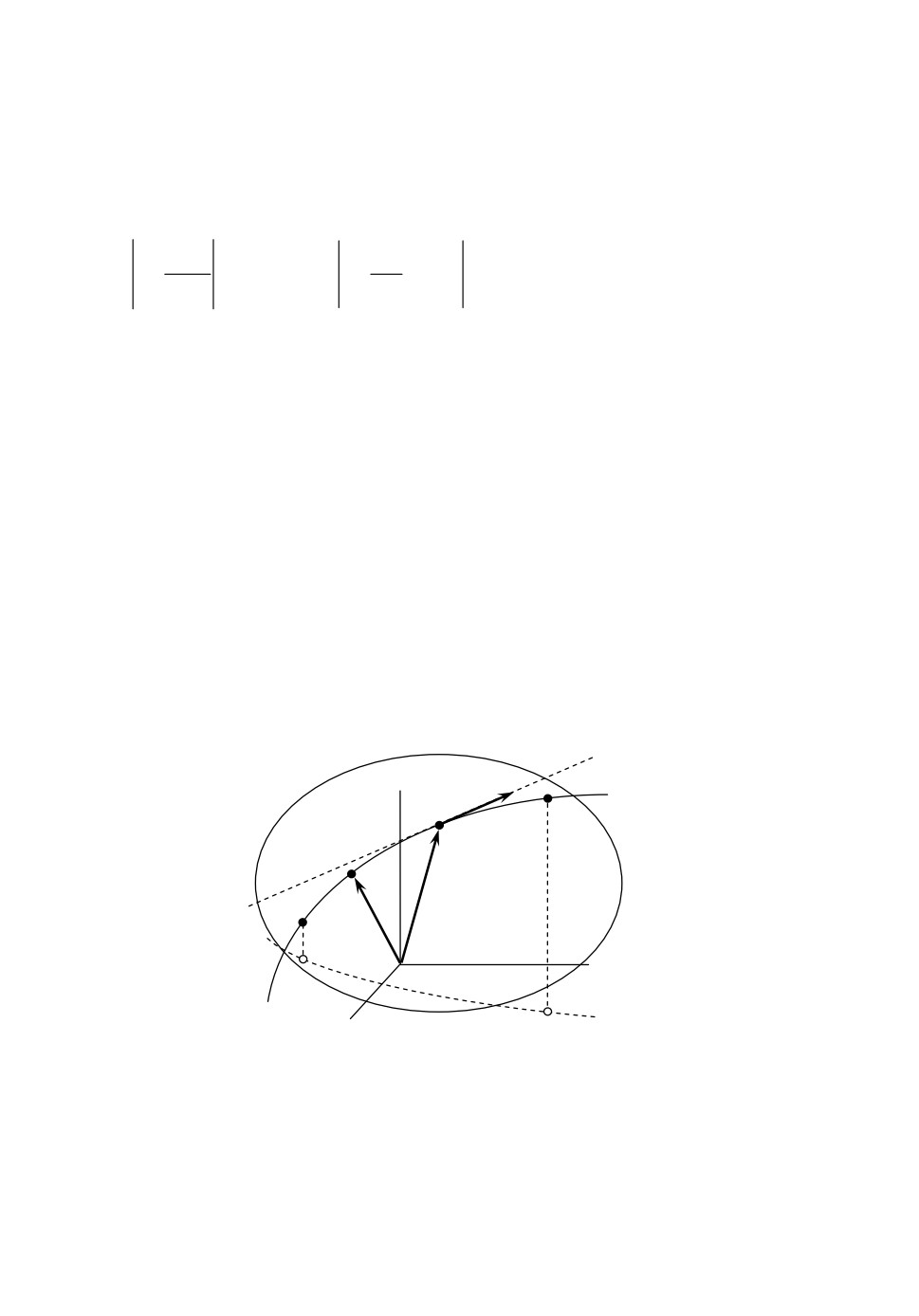
ляющаяся прямой. Назовем лучом направленный отрезок геодезической
r до точки выхода из ячейкиrout (рис.1).
3
V
r
m
Ω
l
l
out
0
r
l
in
0
r
2
r
1
r
l
, проходит
в направлении через точку наблюдения r с координатой l и покидает ячейку
l
. За начало отсчета принята точка
r
0
Зафиксируем на луче (r,Ω) начальную точку
r
и введем координату
0
p(r
,r)
- расстояние вдоль луча от точки
r
до точки r в масштабе, зада-
0
0
64
А.В. Шильков
ваемом метрикойgij , и натуральную координату
l(r
,r) - соответствующее
0
расстояние в масштабе длины пространстваEN . Дифференциалы расстоя-
ний и телесных углов связаны соотношениями
2
i
j
i
j
2
2
2
i
i
[dp]
g
dr
dr
D
[dl]
h
[dl]
,
dr
dl,
(13)
ij
ij
l
j
p
D
d
ij
dp hdl ,
p(
r r)
hdl,
,
d
,
0
i
R
r
h
e
0
i
j
N
ij
h r,Ω)
D
,
e r,Ω)
h
detD
ij
Здесь h есть длина единичного вектора Ω в масштабе длиныRN ; d - эле-
мент телесного угла в направлении Ω в пространствеEN ,
d
- его образ
R
вRN , e - масштабный множитель, de
D
- детерминант тензораDij . Кро-
ме размерной координаты
p(r
,r) введем на луче безразмерную лучевую
0
координату :
p
l
1
2
|
|
,
А, Б
u w
(
r r)
dp h dl
,
(r)
,
(14)
0
,
В
0
0
w
j
p
D
ij
d dp hdl ,
,
i
i
r
r
h
где (r) - положительный коэффициент, равный среднему геометрическо-
му коэффициентов |
|
иw . В вырожденной ячейке В полагаем
u
w
ij
При постоянном тензоре
D
const,
c
0
риманово многообразие
D
R
переходит в аффинное пространство с прямыми лучами (r,Ω), которые
N
совпадают с соответствующими лучами в евклидовом пространствеEN .
Масштабы длины h и телесного угла e зависят от направления луча. В слу-
ij
ij
чаеDij
N ,
SpD
1 многообразие становится евклидовым пространст-
вом с уменьшенным в N раз масштабом длины в сравнении сEN .
Основное решение. В общем случае решение уравнений (7), (11) в
ячейке строится с помощью функции Леви [16, с.232; 17, с.152; 18, с.24]. В
частном случае, когда выполняются условия (12), решение можно предста-
вить в ином, специальном виде, если перейти к лучевым переменным.
Будем искать регулярное решение системы (7) или (11) в точке ячейки
О решении линейных эллиптических уравнений второго порядка
65
rV
E в виде суперпозиции вкладов объемных и граничных источни-
m N
ков, размещенных на лучах, приходящих в точку от границы ячейки:
S
()
S
()
d
out
in
U(r)
[J
()
I
]
[J
()
I
]
,
(15)
in
in
out
out
X
X
i
C
()
C
()
d
i
out
in
W
(r)
[J
()
I
]
[J
()
I
]
,
in
in
out
out
h
X
X
out
1
d
1
d
J
()
S
()e()Q()
,
J
()
S
()e()Q()
(16)
in
in
out
out
e
e
in
Здесь h(r,Ω) , e(r,Ω) , X (r,Ω) - функции направления луча;
S
(),
C
(),
in
in
S
(),
C
()
- заданные функции лучевой координаты;
J
(),
J
()
-
out
out
in
in
интегралы от объемных источников, вычисляемые вдоль луча. Первый дает
вклад источников с отрезка лучаin
, второй - с отрезка
out
Индексами in и out обозначены величины, относящиеся соответственно к
точке входа и точке выхода луча из ячейки.
I r,Ω),
I
(r,Ω)
- свободные
in
out
параметры, определяемые для луча (r,Ω). Далее мы увидим, что это вклады
граничных источников. При обходе полного телесного угла вклад каждого
объемного источника и каждой точки границы учитывается дважды: один
раз на лучах (r,Ω) и второй раз на противоположных лучах (r,Ω). Функ-
ции лучевой координаты даются комбинациями элементарных функций:
sinh(
)
cosh(
)
w
in
in
S
()
,
(17)
in
in
sin(
)
cos(
)
in
in
cosh(
)
sinh(
)
in
in
C
()
,
in
in
cos(
)
sin(
)
in
w
in
sinh(
)
cosh(
)
w
out
out
S
()
,
out
out
sin(
)
cos(
)
out
out
cosh(
)
sinh(
)
out
out
C
()
,
out
out
cos(
)
sin(
)
out
w
out
S
()C
() C
()S
() const
X r,
Ω),
,
in
out
in
out
in
out
66
А.В. Шильков
sinh(
)
sinh(
)
w
out
in
out
in
X(r,Ω)
in out
sin(
)
sin(
)
out
in
w
out
in
cosh(
)
out
in
[
]
in
out
cos(
)
out
in
c , нижняя - к ячейке Б,
c
. В вырожденной ячейке В, |
|
c
функции (17) непре-
u w
u
u
w u
рывно переходят в функции
S
()
,
S
()
,
(18)
in
in
in
out
out
out
C
()
C
()
1,
X r,Ω)
,
in
out
out
in
in
out
где для вычисления лучевой координаты
используется коэффициент
(см. (14)). Функции лучевой координаты (17), (18) содержат сво-
w
бодные параметры
r,Ω),
(r,
Ω), определяемые (как и свободные па-
in
out
I
I
) для луча (r,Ω). Форма решения (15) получена в [15] рас-
пространением на многомерный случай решений одномерных задач [12].
Для доказательства того, что функции (15) удовлетворяют уравнениям
(7), (11), вычислим производные функций, пользуясь связями (13), (14):
i
i
W
C
()
C
()
d
out
in
[J
()I
]
[J
()I
]
in
in
out
out
i
i
r
r
h
X
X
Q
U
,
u
u
ij
D
U
S
()
S
()
d
ij
out
in
D
[J
()I
]
[J
()I
]
in
in
out
out
j
j
r
r
X
X
ij
D
i
i
U
W
j
w
w
r
j
i
Невязкиu ,iw зависят от величины производныхDij
r
,
[
]
w r
sinh(
)
out
C
()
[
hX]
d
out
[
J
()
I
]
u
in
in
out
X
sin(
)
hX
out
w
sinh(
)
C
()
[hX
]
d
in
in
[
J
()
I
]
,
out
out
in
X
sin(
)
hX
in
w
О решении линейных эллиптических уравнений второго порядка
67
ij
i
D
sinh(
)
S
()
Xd
i
out
w
out
U
[J
()I
]
w
j
in
in
hX
sin(
)
X
r
out
i
sinh(
)
in
S
()
Xd
w
in
[J
()I
]
,
out
out
hX
sin(
)
X
in
i
j
X
h
D
ij
w
[X
C
(
)
C
(
)]
,
in out in
out in out
2h
w
Если постоянныеcD ,cR в неравенствах (12) стремятся к нулю
,
0
c
c
,
D R
i
то модули невязок равномерно стремятся к нулю |
|,|
|
0
во внутренних
u w
точках ячейкиVm . Функции (15) в точности удовлетворяют уравнениям (7),
I
I
,in ,out . Лучи являются
отрезками прямых линий (см. комментарий к (14)). Если постоянныеcD ,cR
ij
j
i
и производные
D
/r
,
[
/
]/
малы, то функции (15) удовлетво-
w r
ряют уравнениям приближенно. Лучи могут немного искривляться в боль-
ших по размерам ячейках.
3. Регулярные решения граничных задач в ячейке
Смешанная граничная задача. Запишем основное решение (15) в точ-
ке гладкого участка границы, рассматривая ее как точку входа лучей в
ячейку
S
(
)
d
out in
in
U(r
)
2
I
[J
(
)
I
]
,
(19)
in
in
out in
out
X
X
Ωn0
i
C
(
)
1
d
i
out in
W
(r
)
2
I
[J
(
)
I
]
,
in
in
out in
out
h
X
X
Ωn0
и рассматривая ее как точку выхода лучей из ячейки:
S
(
)
d
out
in out
U(r
)
2
[J
(
)
I
]
I
,
(20)
out
in out
in
out
X
X
Ωn0
i
1
C
(
)
d
i
in out
W
(r
)
2
[J
(
)
I
]
I
out
in out
in
out
h X
X
Ωn0
В (19) интегрирование проводится по телесному углу /2, под которым вид-
на ячейка, и состоящему из направлений входа лучей в ячейку
:
0
Ω
Ωn
,
in
в (20) - по телесному углу /2, состоящему из направлений выхода лучей из
68
А.В. Шильков
ячейки
Ω:Ωn
0. Углы равны половине телесного угла пространства.
out
Здесьnin иnout - векторы внешней нормали в точке входа и соответствен-
но в точке выхода луча из ячейки. Подставим значения в граничные усло-
вия (8). В результате вычислений получим, что граничные условия будут
удовлетворены при следующих параметрах лучей:
i
j
i
j
1
G n
1
G
n
in
ij in
out
ij out
,
,
(21)
in
out
1
1
in
inh
out
outh
j
j
D
D
ext
ij
i
ext
ij
i
I
U
W
,
I
U
W
in
in
in
ext,in
out
out
out
ext,out
h
h
Параметры определены для лучей, которые начинаются и оканчиваются на
гладких участках границы. Решение неоднородной смешанной задачи в
ячейке в условиях его существования найдено.
Задача Дирихле. Граничные условия задачи Дирихле следуют из гра-
ничных условий (8) в результате перехода к пределу 1,
U
U(r
)
ext
на всей границе ячейки. Решение задачи Дирихле дается формулами (15)-
(21) при параметрах лучей
0,
I
U(r
),
I
U(r
),
r
,r
(22)
in
out
in
in
out
out
in out
m
Задача Неймана. Решение обобщенной задачи Неймана, если исхо-
дить из определения [17, с.158; 18, с.16], дается формулами (15)-(21) при
G
D
. Для нахождения решения классической задачи Неймана выпол-
ij
ij
i
i
ним в граничных условиях (8) переход к пределу 1,
W
W
(r
)
ext
Соответственно в (15)-(21) перейдем к пределу
,
:
in out
j
K
()
D
d
w
out
ij
i
U(r)
H
()
W
(r
)
(23)
in
in
L
(
)
h
out in
j
D
K
()
ij
d
w
in
i
H
()
W
(r
)
,
out
out
L
(
)
h
in out
i
L
()
d
i
out
i
W
(r)
H
() W
(r
)
in
in
L
(out in
)
h
i
L
()
d
in
i
H
() W
(r
)
,
out
out
L
(
)
h
in out
О решении линейных эллиптических уравнений второго порядка
69
out
1
d
1
d
H
()
K e()Q()
,
H
()
K
()e()Q()
,
in
in
out
out
e
e
in
cosh(
)
sinh(
)
cosh(
)
in
in
out
K
,
L
,
K
in
in
out
,
cos(
)
sin(
)
cos(
)
in
in
out
sinh(
)
out
L
out
.
sin(
)
out
Решение справедливо в ячейках А и Б и не относится к вырожденной ячей-
ке В. Решение классической задачи Неймана в вырожденной ячейке суще-
ствует, если источник удовлетворяет условию разрешимости задачи.
Для получения конечного ответа формулы (15)-(23) необходимо до-
полнить уравнениями для нахождения геодезических линий (если
ij
(
) const
D
r
), вычисления интегралов от источников вдоль лучей (16) и
вычисления интегралов по угловым переменным. Искривление геодезиче-
ских линий может проявляться в больших по размерам ячейках. Сведения о
геодезических линиях можно найти в литературе по дифференциальной
геометрии [25, с.54; 26, с.415].
Поведение решения вблизи изломов границы. Формулы решения на
границе (19), (20) допускают дальнейшее преобразование в случае, когда
точка
r
лежит вблизи точкиrA , принадлежащей пересечению гладких
in,
out
участков границы. Пусть
r
r
s, где s есть малый вектор перемеще-
in,
out
A
r вектор нормали не определен. Рассмотрим случай, когда
точкаrA лежит на ребре острого двугранного угла
/2, который не
in,out
превышает телесного угла полупространства. Разобьем интеграл в (19), (20)
на интеграл по телесному углу
r видна
in,
out
ячейка, и интеграл по дополнительному углу
/2
. Последний легко
in,out
вычислить в пределе s 0 и преобразовать (19) к виду
S
(
)
d
out in
in
ext
U(r
)
[1
]
I
[J
(
)
I
]
U
,
(24)
in
in
in
out in
out
in in
X
X
in
in
i
C
(
)
1
d
i
out in
i
W
(r
)
[1
]
I
[J
(
)
I
]
W
,
in
in
in
out in
out
in ext,in
h
X
X
in
in
70
А.В. Шильков
S
(
)
d
out
in out
ext
U(r
)
[1
]
[J
(
)
I
]
I
U
,
out
out
in out
in
out
out out
X
X
out
out
i
1
C
(
)
d
i
in out
i
W
(r
)[1
]
[J
(
)I
]
I
W
out
out
in out
in
out
out ext,out
h X
X
out
out
Здесь
12
/
,
есть доля дополнительного телесного
in,out
in,out
in,
out
угла в телесном угле полупространства. Интегрирование в (24) проводится
по телесному углу, под которым из точкиrA ,
r
r
, видна ячейка.
A in,
out
Если в точке границы
r
r
поставлены условия Дирихле (8),
in,
out
A
1 и параметры лучей (21) принимают значения (22), то формулы
in,out
(24) переходят в формулы
U(r
)
U(r
),
/2,
(25)
in,out
in
,out
in,out
i
C
(
)
1
d
i
out in
W
(r
)
U(
r
)
[J
(
)
I
]
,
in
in
out in
out
h
X
X
in
in
i
1
C
(
)
d
i
in out
W
(r
)
[J
(
)
I
]
U(
r
)
out
in out
in
out
h X
X
out
out
Если двугранный угол тупой и
/2, то формулы (19), (20) не
in,out
допускают упрощений.
Из (19), (20), (24), (25) следует, что при переходе с одной грани дву-
гранного угла на другую грань значение решения на границе может испы-
тывать конечный разрыв. Для острых углов
/2
разрыв может воз-
in,out
никать вследствие разрывности параметра луча
. Для тупых углов
in,
out
/2
к фактору разрывности параметра луча добавляется фактор ви-
in,out
димости границы ячейки. Конечный разрыв решения может возникать
вследствие того, что из точек, расположенных на разных гранях, видны
разные участки границы ячейки.
Если на гранях острого угла
/2
поставлены условия Дирих-
in,out
ле, то при переходе через ребро решение (25) меняется непрерывно. Если
угол тупой
/2, то из-за разной видимости границы может возни-
in,out
i
кать разрыв потока
W
(r
)
in
,out
Формулы (24), (25) обобщаются на точки границы, лежащие вблизи
О решении линейных эллиптических уравнений второго порядка
71
вершины трехгранного, многогранного или конического угла, опирающего-
ся на выпуклое основание.
4. Эквивалентные формы решения
Получим эквивалентные формы решения смешанной задачи (7), (8).
Ячейки А и Б. Пусть коэффициенты и источники системы уравнений
(7) - 2M раз дифференцируемые функции. Преобразуем систему (7):
i
i
i
[W
K
]
Q
K
0
0
U
,
u
i
i
r
r
u
(26)
ij
ij
D
Q
D
Q
ij
i
i
i
D
U
[W
K
]
K
j
w
0
j
w
0
r
r
u
u
i
Если определить поток
K
и источник
Q
в соответствии с формулами
0
1
ij
i
ij
1
D
Q
K
1
D
Q
i
0
K
(r)
,
Q
(r)
,
(27)
0
j
1
i
i
j
w
r
u
r
r
w
r
u
i
то мы получим эквивалентную задачу относительно функций
U
и
W
:
1
1
i
W
1
U
Q
,
u
1
1
i
U
UQ
,
r
1
U
(28)
ij
i
i
i
W
W
K
,
[D
U
1
]
i
1
0
W
0,
j
w
1
r
j
i
i
1
ext
G
n
[
W
W
]
[U
U
],
r
,
ij
1
1,ext
1
1
m
1
ext
ext
Q
i
i
i
U
U
,
W
W
K
1
1,ext
ext
0
u
Продолжим последовательно применять преобразование задач (26) в
задачи (28). Введем рекуррентно вычисляемые источники
ij
1
D
Q
i
0
i
Q
Q,
K
,
N
0
,
V
0,
(29)
0
0
j
0
0
r
w
u
i
ij
ij
K
1
D
Q
Q
1
[
D
N
]
0
i
1
0
i
1
Q
,
K
,
N
,
V
, … ,
1
1
1
1
i
j
j
r
w
r
u
u
w
r
72
А.В. Шильков
i
ij
n1
ij
K
1
D
Q
Q
1
[D
N
]
n1
i
n
k
i
n
Q
,
K
,
N
,
V
n
i
n
j
n
n
j
r
r
r
w
u
k0
u
w
ИсточникиQn , 0nM, определяют последовательность граничных задач:
i
W
n
U Q
,
u n
n
i
r
r V
,
(30)
m
ij
[D
U
]
n
i
W
0,
j
w n
r
1
UextUextN
j
i
i
ext
n
n
G
n
[W
W
]
[U
U
],
,
r
ij
n
n,ext
n
n
m
1
i
i
i
W
W
V
n,ext
ext
n
Решение задачи (7), (8) связано с решениями задач (30) соотношениями
n1
Q
Q Q
Q
1
k
U U
U
U
N
,
N
,
1
2
n
n
n
u
u
u
k0
u
ij
i
i
i
i
i
i
i
i
i
1
[D
N
n
]
W
W
K
W
K
K
W
V
,
V
1
0
2
0
1
n
n
n
j
w
r
Записывая формулы (15), (16), (21) для задач (30), получим эквивалентные
формы регулярного решения смешанной граничной задачи (7), (8):
S
()
S
()
d
out
(n)
(n)
in
(n)
(n
)
U(r)
N
(r)
[J
()
I
]
[J
()
I
]
,
(31)
n
in
in
out
out
X
X
i
C
()
C
()
d
i
i
out
(n)
(n)
in
(n)
(n)
W
(r)
V
(r)
[J
()
I
]
[J
()
I
]
,
n
in
in
out
out
h
X
X
out
1
d
1
d
(n)
(n)
J
()
S
()e()Q
()
,
J
()
S
()e()Q
()
,
in
in
n
out
out
n
e
e
in
j
j
D
D
(n)
ext
ij
i
(n)
ext
ij
i
I
U
W
,
I
U
W
in
n,in
in
n,ext,in
out
n,out
out
n,ext
,out
h
h
Аналогично можно получить формы решений частных задач (22), (23).
В практических приложениях форма решения (31) может оказаться бо-
лее удобной. В качестве примера рассмотрим ячейку А с постоянными ко-
О решении линейных эллиптических уравнений второго порядка
73
эффициентами
,
0, в которой распределение объемных источников
u w
Q задается многочленом второго порядка
2
i
i
u w
i
i
j
j
Q r)
R
R
[r
r
]
R
[r
r
][r
r
]
u
0
u w i
n
ij
n
n
2
Вычислим объемные источники:
Q
(r)
R
R
i
i
ij
ij
kj
jk
k
k
i
N
(r)
,
V
(r)
K
r)
D
R
D
[r
r
],
K
r)
0,
1
1
0
j
u
n
1(
2
u
Q
R
R
Q
Q
1
ij
ij
ji
(1)
1
(1)
1
D
const,
J
()
[C
() 1],
J
()
[C
()
1]
in
in
out
out
2
u
u
u
Полагая n 1, получим
Q Q
S
()
S
()
d
S
()
S
()
d
1
in
out
out
(1)
in
(1)
U(r)
1
I
I
,
in
out
X
X
X
u
u
i
i
Q
C
()C
()
d
C
()
C
()
d
i
i
1
in
out
out
(1)
in
(1)
W
(r)V
(r)
I
I
1
in
out
h
X
h
X
X
u
Регулярное решение смешанной граничной задачи в ячейке произвольной
формы выражается только через интегралы по угловым переменным.
Замечание. Эквивалентные формы решения (31) можно получить дру-
гим способом, если интегрировать по частям интегралы
J
(),
J
(
)
(16).
in
in
Вырожденная ячейка В. Введем объемные источники, вычисляемые
рекуррентным образом:
ij
i
1
D
Q
K
i
0
0
Q
(r) Q ,
K
(r)
,
Q
r)
,
(32)
0
0
1(
j
i
w
r
w
r
ij
1
D
Q
i
1
K
(r
)
, … ,
1
j
w
r
w
ij
1
D
Q
i
i
i
n
Q
(r)
K
/
r
,
K
(r)
,
0nM.
n
n1
n
j
r
w
w
Интегрируя по частям интегралы
J
(
),
J
()
(16), получим
in
out
74
А.В. Шильков
r
r
2k2
j
2k3
n1
D
n1
S
()
Q
(r)
ij
S
()
in
k
in
i
(n)
J
()
K
(r)
J
(),
(33)
in
k
in
[2k2]!
h
[2k3]!
k0
w
k0
r
in
r
in
r
r
2k2
j
2k3
n
1
D
n
1
S
()
Q
(r)
ij
S
()
out
k
out
i
(n)
J
()
K
(r)
J
(),
out
k
out
[2k2]!
h
[2k3]!
k
0
w
k
0
r
out
r
out
r
2n1
2n
2
1
S
()e()Q
()
S
()
Q
(r)
(n)
in
n
in
n
J
()
d
,
in
e
[2
n
1]!
[2n
2]!
w
r
w
in
in
r
out
2n1
2n2
1
S
()e()
Q
()
S
()
Q
(r)
(n)
out
n
out
n
J
()
d
,
0nM.
out
e
[2n
1]!
[2n
2]!
w
r
w
out
Подстановка (33) в (15) дает эквивалентные формы решения.
5. Конечно-аналитическая схема
Построим конечно-аналитическую схему для нахождения решения
системы уравнений (1), (3) или (7), (8) в области с разрывными коэффици-
ентами и источниками.
Конечно-аналитическая схема представляет собой дискретную аппрок-
симацию решения задачи, построенную с помощью сшивки регулярных ре-
шений в ячейках, на которые поделена область. Сшивка регулярных реше-
ний выполняется на границах ячеек, которые проходят по поверхностям ко-
нечных разрывов коэффициентов и источников уравнений (если таковые
имеются). Термин возник как аналог термина "конечно-разностная схема"
[8]. Заметим, что последняя есть дискретная аппроксимация задачи, постро-
енная с помощью сшивки конечных разностей решения в ячейках.
Как и в теории разностных схем, введем понятие шаблона. Шаблон по-
строенной далее конечно-аналитической схемы состоит из конечного набо-
ра точек, лежащих на гладких участках границы ячейки
r
r
,...,r
1,...,
p
S
. Точки шаблонов, лежащие на внешней границе области V, будем
m
называть «внешними» точками. Все остальные точки шаблонов будем на-
зывать «внутренними» точками области V. Любая внешняя точка принад-
лежит границе одной ячейки. Любая внутренняя точка лежит на общем уча-
стке границы, отделяющем две смежные ячейки.
Условия сшивки. Определим условия сшивки регулярных решений,
выходящих из ячеек. Первое условие сшивки под названием «выпуклость
О решении линейных эллиптических уравнений второго порядка
75
шаблонов» состоит в том, что из любой точки шаблона видны все осталь-
ные точки этого же шаблона. Для того чтобы шаблон был выпуклым, доста-
точно, чтобы ячейка была выпуклым множеством. Ограничимся построени-
ем аналитической схемы с выпуклыми ячейками.
Второе условие сшивки назовем условием «выравнивания шаблонов»
смежных ячеек. Желательно, чтобы точки шаблонов смежных ячеек, лежа-
щие на общем участке границы, совпадали. В противном случае схему не-
обходимо дополнить интерполяционными формулами для переноса значе-
ний решения из точки в точку вдоль общей границы. Интерполяция может
приводить к потерям точности.
Третье условие, назовем его «физическим» условием, состоит в пра-
вильном выборе сшиваемых величин. Выбор величин содержит долю про-
извола. При ответе на вопрос «что сшивать?» следует исходить из специфи-
ки прикладной задачи. Вместе с тем можно дать некоторые рекомендации.
Имеется довольно широкое многообразие систем (1), (3). При потенциаль-
ности векторных коэффициентов (5) они приводятся к стандартному виду
(7), (8). Поэтому искать сшиваемые величины целесообразно среди функ-
ций, входящих в уравнения (7), (8). Это могут быть линейные или нелиней-
ные комбинации функций.
Рассмотрим «естественные условия» сшивки, означающие, что во внут-
ренних точках области нет внешних источниковUext ,Wiext ; выбор сшивае-
мых величин определяется смыслом уравнений системы (7). Обратимся ко
второму уравнению. Оно выражает условие статического равновесия сил -
отклик системы в виде потокаWi и градиента величиныDijU на действие
внешней силыSi (см. (1),(6)). Пусть внутренняя точка p лежит на гладком
участке границы, отделяющем ячейкиVm иVk . Запишем проекцию условия
равновесия сил на направление нормали к границе. Из него следуют соот-
ношения детального баланса:
i
i
i
i
i
i
i
n
(m)W
(m)
n k)W k)
n
(m)[W
(m)
W k)]
0,
(34)
p
p
p
p
p
p
p
ij
i
j
ij
i
j
D
(m)n
(m)n
(m)U
(m)
D k)
n k)n k)U
(k) ,
n k)
n
(m)
p
p
p
p
p
p
p
p
p
p
Первое условие выражает равенство компонентов потока, нормальных к эле-
менту границы, второе выражает равенство соответствующих компонентов
тензора давления. Учтено, что векторы внешней нормали ячеек противопо-
ложны по направлению. Обращаем внимание, что второе условие инвари-
антно относительно нормировки тензораDij (см. (10)).
76
А.В. Шильков
Замечание. Естественные условия сшивки (34) в равной мере имеют
отношение и к разностным схемам, и к схемам метода конечных элементов.
В работах, посвященных разработке схем переноса энергии излучением или
переноса нейтронов в ядерных реакторах, можно встретить подмену второ-
го условия (34) более простым условием
U
(m)
U
(k). Это верно лишь в
p
p
ij
ij
случае
D
/N , т.е. когда используется так называемое диффузионное
приближение. В общем случае вызываемые подменой погрешности невели-
ки. Но они могут быть источником появления расхождений при выполне-
нии сравнения с результатами других расчетов или с точным решением.
Уравнения конечно-аналитической схемы. В каждой точке шаблона
r
определим свою подходящую квадратурную формулу для вычисления
p
интегралов по углуp , |
| /2 , под которым видна ячейка
V
:
p
m
d
2
f
(Ω)
f
(Ω
),
Ω
,
n Ωqp
0
,
1
(35)
qp
qp
qp
p
qp
q p
qp
p
Здесь f (Ω) - ограниченная интегрируемая функция,Ωqp - узлы квадратур-
ной формулы, представляющие собой направляющие векторы лучей, при-
ходящих в точку p из других точек q p шаблона,qp - веса квадратурной
формулы,np - вектор внешней нормали.
Запишем решение смешанной задачи (30), (31) для ячейки m в точке
шаблона p с помощью квадратурной формулы (35). За начало отсчета на лу-
че примем точку q:
j
D
qp p
ext
ij
qp
i
i
(n)
U
(m)
U
N
[W
V
]
J
(
)
p
q
n,q q
ext,q n
,q
q
p
X
h
qp
qp
qp
(36)
j
S
(
)
D
S
(
)
ext
q p
i
i
ij
qp q p
[U
p
N
n,p
]
qp
[W
ext,
p n
V
, p
]
qp p
N
n,p
,
X
h
X
qp
qp
qp
qp
qp
i
i
qp
i
i
qp ext
(n)
W
(m)
[W
V
]
[
U
N
J
(
)]
p
q ext
,q
n
,q
q
n,q
q
p
X
h
qp qp
qp
(37)
i
C
(
)
C
(
)
ext
qp q p
i
i
q p
i
[U
N
]
[W
V
]
V
,
p
n,p
qp
ext,p n,p
qp p
n,
p
h
X
X
qp
qp
qp
qp
qp
О решении линейных эллиптических уравнений второго порядка
77
(q)
j
i
( p)
j
i
1
G
n
1
G
n
i
j
q ij q qp
p ij
p
qp
h
D
,
,
,
qp
ij
qp
qp
q
p
1
1
q
q qph
p
p qph
lp
l
p
(n)
1
d
(r
,r
)
h
dl,
h
dl,
J
(
)
S e()Q
()
,
p p q p
qp
qp
q
p
q
n
e
0
0
0
sinh
cosh
cosh
sinh
W
S
()
sin
cos
,
C
()
cos
sin
,
q
q
q
q
W
1
1
0
sinh
sinh
cosh
p
p
p
W
X
sin
sin
[
] cos
qp
p
q p
p
q
p
p
W
0
1
p
Для составления конечно-аналитической схемы необходимо сшить ре-
шения (36), (37), выходящие из смежных ячеекVm иVk во внутренних точ-
ках области. Ограничимся схемой с естественными условиями сшивки (34).
В этом случае во всех внутренних точках области должны быть поставлены
условия Дирихле, а во внешних точках области V, лежащих на границе -
смешанные граничные условия (8). Соответственно, для внутренних точек
ext
p, q в формулах (36), (37) выполним замену (22):
0,
U
U
. В ре-
p,q
p,q
p,q
зультате из уравнений (36), (37) исключаются внешние источникиUext ,
i
W
во внутренних точках области. Уравнение (36) связывает плотность
ext
U
(m)
со значениями плотности
U
(m)
в остальных точках шаблона q p.
p
q
i
Уравнение (37) связывает поток
W
(m)
со значениями плотности
U
(m)
во
p
q
всех точках шаблона, включая данную точку. Исключим из первого условия
i
i
(34) потоки
W
(m),
W
(k)
в общей точке p с помощью уравнения (37).
p
p
Проделаем это для всех внутренних точек области. Полученные уравнения
вместе с (36) и вторым условием сшивки (34) составят полную систему ал-
гебраических уравнений относительно плотностей
(
)
U
m
в точках шабло-
p
нов. Конечно-аналитическая схема составлена.
Нахождение решения. Пусть система алгебраических уравнений ко-
нечно-аналитической схемы разрешима. Решение системы может быть най-
дено алгоритмами вычислительной линейной алгебры [27] или иными ме-
тодами. Далее по известным значениям плотности
(
)
U
m
с помощью соот-
p
78
А.В. Шильков
i
ношений (37) вычисляются потоки
(
)
W
m
. Часто значений решения в точ-
p
ках шаблонов бывает достаточно для ответов на запросы прикладной зада-
чи. Напомним, что точки шаблонов лежат на границах ячеек.
Если требуется найти решение внутри ячеек, то выполняется второй
этап. Пусть r есть некоторая точка внутри ячейки. Выпустим из нее лучи
так, чтобы они пришли в точки шаблона. Продолжим лучи назад до пересе-
чения с границей ячейки в некоторых точках. Эти точки могут не совпасть с
точками шаблона. Определим новый шаблон, включив в него точки старого
шаблона и новые точки. Затем построим квадратурную формулу для вы-
числения интегралов по угловым переменным. Эта формула аналогична
формуле (35) с тем отличием, что интегрирование выполняется по полному
телесному углу . Узлами формулы являются направляющие векторы лу-
чейΩqp , приходящих из точек нового шаблона. Дискретизация уравнений
(15), (16) или (32) с помощью квадратурной формулы дает искомое решение
в выбранной точке. Процедура повторяется для других точек области, пока
не будет достигнута необходимая степень детализации решения.
В сравнении с разностными схемами и схемами метода конечных эле-
ментов аналитические схемы имеют ряд недостатков и ряд преимуществ.
Наиболее важное преимущество состоит в отсутствии жесткой зависимости
точности аппроксимации от размеров и формы ячеек. В аналитической схе-
ме требования на размеры ячеек сводятся к условиям (5), (12). Это условия
совсем иного типа, чем требования аппроксимации разностных схем. Они
гораздо мягче и зависят от исходных, физических параметров задачи.
Имеется широкий класс задач численного моделирования ядерных ре-
акторов, защиты от излучений, радиационной газовой динамики, переноса
излучений в атмосфере, задач пограничного слоя, в которых разностные
схемы столкнулись с большими трудностями. Рассмотрим распространение
излучений - нейтронов или фотонов электромагнитного излучения. Если
решать задачу с физическими (настоящими) сечениями взаимодействия из-
лучений с веществом, то ячейки оказываются прозрачными для излучений
одних энергий и одновременно непрозрачными для излучений других энер-
гий. Непрозрачностью называется выполнение условия
1,
out
in
когда приведенная длина отрезка луча от точки входа до точки выхода из
ячейки больше единицы. Непрозрачность возникает вблизи резонансов по-
глощения и испускания, где резко увеличиваются коэффициенты уравнений
,
. Типичное отношение коэффициента при энергии резонанса к зна-
u
w
О решении линейных эллиптических уравнений второго порядка
79
чению этого же коэффициента между резонансами (среднему фону) может
2
5
3
5
составлять
10
10
. Число сильных резонансов может составлять
10
10
Разностные схемы аппроксимируют уравнения, если ячейки прозрачны
для излучений всех энергий. Т.е. требуется сильно измельчать пространст-
венную сетку. Поэтому современные детерминистические транспортные
коды решают не физические, а модельные уравнения со сглаженными на
интервалах сетки энергий коэффициентами. Сглаживание выполняется
применением многогруппового приближения, метода функций пропуска-
ния, другими методами. Лучшие транспортные коды, использующие разно-
стные схемы, на многомерных пространственных задачах достигли отметки
100-200 интервалов-групп по сетке энергий. Так что для проведения расче-
тов с физическими не сглаженными коэффициентами требуется еще на не-
сколько порядков увеличить мощность современных суперкомпьютеров.
Схожие трудности, связанные с требованием сильно уменьшать шаг конеч-
но-разностных схем в целях сохранения аппроксимации, возникают при
моделировании пограничного слоя [4, 5, 10].
Конечно-аналитические схемы измельчать пространственную сетку не
требуют. Это преимущество схемы показали, например, при решении од-
номерных задач переноса излучений [6, 7, 12, 14].
СПИСОК ЛИТЕРАТУРЫ
1. Владимиров В.С. Численное решение кинетического уравнения для сферы // Выч.
математика, сб. 3. Ред. А.А. Абрамов. - М.: Изд-во АН СССР, 1958, с.3-33;
Vladimirov V.S. Chislennoe reshenie kineticheskogo uravneniia dlia sfery // Vych. mate-
matika, sb. 3. Red. A.A. Abramov. - M.: Izd-vo AN SSSR, 1958, s.3-33.
2. Тихонов А.Н., Самарский А.А. Однородные разностные схемы высокого порядка точ-
ности на неравномерных сетках // Ж. вычисл. матем. и матем. физ., 1961, т.1(3),
с.425-440;
Tikhonov A.N., Samarskii A.A. Homogeneous difference schemes of a high degree of accu-
racy on non-uniform nets // USSR Comput. mathematics and math. physics, 1962, v.1(3),
p.465-486.
3. Самарский А.А. Введение в теорию разностных схем. - М.: Наука, 1971;
Samarskii A.A. Vvedenie v teoriiu raznostnykh skhem - M.: Nauka, 1971.
4. Ильин А.М. Разностная схема для дифференциального уравнения с малым парамет-
ром при старшей производной // Матем. заметки, 1969, т. 6(2), с.237-248;
Il'in A.M. Differencing scheme for a differential equation with a small parameter affecting
the highest derivative // Math. notes of the Acad. of sciences of the USSR, 1969, v.6(2),
p.596-602.
5. Емельянов К.В. Разностная схема для трехмерного эллиптического уравнения с ма-
лым параметром при старших производных // Свердловск: Труды Ин-та матем. и ме-
ханики Уральского научн. центра АН СССР, 1973, №11, с.30-42;
80
А.В. Шильков
Emelyanov K.V. Raznostnaia skhema dlia trekhmernogo ellipticheskogo uravneniia s ma-
lym parametrom pri starshikh proizvodnykh // Sverdlovsk: Trudy In-ta matem. i mekhaniki
Uralskogo Nauchn. Tsentra AN SSSR, 1973, №11, p.30-42.
6. Куликов Ю.Н., Четверушкин Б.Н. Неявный разностный метод определения темпера-
туры в задачах радиационной газовой динамики // Ж. вычисл. матем. и матем. физ.
1973, т.13(1), с.136-146;
Kulikov Yu.N., and Chetverushkin B.N. An implicit difference method for temperature de-
termination in problems of radiation gas dynamics // USSR Comput. mathematics and
math. physics, 1974, v.13(1), p.174-186.
7. Чарахчъян А.А. Расчет нестационарных, сферически симметричных течений излуча-
ющего серого газа // Динамика излучающего газа. Вып. 1. Ред. В.В. Александров. -
М.: ВЦ АН СССР, 1974, с.54-74;
Charakhchyan A.A. Raschet nestatsionarnykh, sfericheski simmetrichnykh techenii izlu-
chaiushchego serogo gaza // Dinamika izluchaiushchego gaza. Vyp. 1. Red. V.V. Aleksan-
drov. - M.: VTs AN SSSR, 1974, s.54-74.
8. Chen C.J., Naseri-Nashet H., and Ho K.S. Finite analytic numerical solution of heat trans-
fer in two dimensional cavity flow // J. Numer. heat transfer, 1981, v.4(2), p.179-197.
9. Sun Y., and Militzer J. The piecewise parabolic finite analytic method. Part I: Theory //
Appl. math. modelling, 1992, v.16, p.576-588.
10. Chen C.J., Bernatz R.A., Carlson K.D., Lin W., and de Vahl D.G. Finite analytic method in
flows and heat transfer // Appl. mech. rev., 2002, v.55(2), p.B34-B34.
11. Pontaza J.P., Chen H.C., and Reddy J.N. A local-analytic-based discretization procedure
for the numerical solution of incompressible flows // Num. methods in fluids, 2005,
v.49(6), p.657-699.
12. Шильков А.В. Четно-нечетные кинетические уравнения переноса частиц. 2: Конечно-
аналитическая характеристическая схема для одномерных задач // Матем. моделиро-
вание, 2014, т.26, №7, с.33-53;
Shilkov A.V. Even and odd parity kinetic equations of particle transport. 2: A finite analytic
characteristic scheme for one dimensional problems // Math. models and computer simula-
tions, 2015, v.7, №1, p.36-50.
13. Шильков А.В. Четно-нечетные кинетические уравнения переноса частиц. 3: Конечно-
аналитическая схема на тетраэдрах // Матем. моделирование, 2015, т.27, №2, с.34-62;
Shilkov A.V. Even and odd parity kinetic equations of particle transport. 3: Finite analytic
schemes on tetrahedral // Math. models and computer simul., 2015, v.7, №5, p.409-429.
14. Basko M.M., and Tsygvintsev I.P. A hybrid model of laser energy deposition for multidi-
mensional simulations of plasmas and metals // Comp. physics communications, 2017,
v.214, p.59-70.
15. Шильков А.В. Решение эллиптических уравнений методом лучевых переменных. -
М.: ИПМ им. М.В. Келдыша, 2017, препринт № 119, 35 с.;
Shilkov A.V. Reshenie ellipticheskikh uravnenii metodom luchevykh peremennykh. - M.:
IPM im. M.V. Keldysha, 2017, preprint № 119, 35 s.
16. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных мате-
матической физики. - М.: Высшая школа, 1970;
Koshlyakov N.S., Gliner E.B., and Smirnov M.M. Uravneniia v chastnykh proizvodnykh
matematicheskoi fiziki. - M.: Vysshaia shkola, 1970.
17. Бабич В.М., Капилевич М.Б., Михлин С.Г. и др. Линейные уравнения математической
физики. Справочник. - М.: Наука, 1964;
Babich V.M., Kapilevich M.B., and Mikhlin S.G. Lineinye uravneniia matematicheskoi fizi-
ki. Spravochnik. - M.: Nauka, 1964.
18. Миранда К. Уравнения с частными производными эллиптического типа. - М.: ИЛ, 1957;
О решении линейных эллиптических уравнений второго порядка
81
Miranda С. Partial differential equations of elliptic type. Transl. from the ital. - Berlin-
Heidelberg: Springer, 1970. XII.
19. Курант Р., Гильберт Д. Методы математической физики, т.2. - М.: Гостехиздат, 1945;
Courant R., and Hilbert D. Methods of mathematical physics, v.2. Partial differential equa-
tions. - New York: Wiley Interscience, 1962.
20. Ландис Е.М. Уравнения второго порядка эллиптического и параболического типов. -
М.: Наука, 1971;
Landis E.M. Second order partial differential equations of elliptic and parabolic type.
AMS, Transl. of math. monographs, 1998, v.171.
21. Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллипти-
ческого типа. - М.: Наука, 1973.
Ladyzhenskaya O.A., and Uraltseva N.N. Lineinye i kvazilineinye uravneniia ellip-
ticheskogo tipa. - M.: Nauka, 1973.
22. Михлин С.Г. Линейные уравнения в частных производных. - М.: Высшая школа, 1977.
Mikhlin S.G. Linear equations of mathematical physics. - Holt, Rinehart and Winston, 1967.
23. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике.
4-е изд. - М.: Физматлит, 2004;
Budak B.M., Samarskii A.A., and Tikhonov A.N. A Collection of problems in mathematical
physics. - Oxford: Pergamon Press, 1964.
24. Полянин А.Д. Справочник по линейным уравнениям математической физики. - М.:
Физматлит, 2001.
Polyanin A.D., and Nazaikinskii V.E. Linear partial differential equations for engineers and
scientists. 2nd ed. Boca Raton. CRC Press, 2016.
25. Бураго Ю.Д., Залгаллер В.А. Введение в риманову геометрию. - СПб.: Наука, 1994;
Burago Iu.D., and Zalgaller V.A. Vvedenie v rimanovu geometriiu. - SPb: Nauka, 1994.
26. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967;
Rashevsky P.K. Vvedenie v rimanovu geometriiu. - M.: Nauka, 1967.
27. Деммель Дж. Вычислительная линейная алгебра. Теория и приложения. - М.: Мир,
2001.
Demmel J.W. Applied numerical linear algebra. SIAM, Philadelphia, PA, USA, 1997.
Поступила в редакцию 19.11.18
После доработки 19.11.18
Принята к публикации 10.12.18