МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

2019 год, том 31, номер 7, стр. 45-57



РАЗНОСТНАЯ СХЕМА С АНАЛИЗАТОРОМ СИММЕТРИИ

ДЛЯ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ



2019 г.

А.В. Колдоба¹, Г.В. Устюгова^1,2

¹Московский физико-технический институт (ГУ)

²Институт прикладной математики им. М.В.Келдыша РАН

koldoba@rambler.ru, ustyugg@rambler.ru

Работа выполнена при финансовой поддержке РФФИ, грант 18-02-00907.

DOI: 10.1134/S0234087919070037

Предлагается анализатор симметрии как элемент вычислительного алгоритма для

численного интегрирования двумерных уравнений идеальной газовой динамики.

Анализатор симметрии - алгоритм, позволяющий по сеточным данным отдать

предпочтение тем или иным (в настоящей работе декартовым или полярным)

компонентам векторного поля для его реконструкции на грани расчетной сетки и

последующего расчета потоков консервативных переменных. Построен вычис-

лительный алгоритм, использующий расчетную сетку полярного типа и вклю-

чающий анализатор симметрии. Алгоритм легко переносится на трехмерные рас-

четные сетки цилиндрического типа.

Ключевые слова: разностная схема годуновского типа, анализатор симметрии.

DIFFERENCE SCHEME WITH A SYMMETRY ANALYZER

FOR EQUATIONS OF GAS DYNAMICS

A.V. Koldoba¹, G.V. Ustyugova^1,2

¹Moscow Institute of Physics and Technology (SU)

²Keldysh Institute of Applied Mathematics RAS

The paper proposes a symmetry analyzer as an element of the computational algorithm

for the numerical integration of two-dimensional equations of ideal gas dynamics. A

symmetry analyzer is an algorithm that allows using grid data to give preference to one

or another (in the present work, Cartesian or polar) components of a vector field for its

reconstruction on the cell interfaces of a computational grid and subsequent calculation

of fluxes of conservative variables. A computational algorithm was constructed using a

polar-type computational grid and including a symmetry analyzer. The algorithm is eas-

ily transferred to the three-dimensional computational grids of cylindrical type.

Key words: Godunov type difference scheme, symmetry analyzer.

А.В. Колдоба, Г.В. Устюгова

1. Введение

Постоянное усложнение задач вычислительной гидродинамики приво-

дит к появлению новых и совершенствованию ранее предложенных вычис-

лительных алгоритмов для численного интегрирования уравнений, в част-

ности, идеальной газовой динамики [1]. Даже если ограничиться схемами

конечно-объемного типа [2], то можно указать различные способы построе-

ния приближенных решений задачи Римана [3,4], использование адаптив-

ных (статических и/или динамических) [5] и/или неструктурированных рас-

четных сеток [6], различные типы контроля схемной вязкости [7] и ограни-

чителей антидиффузии [8]. Конечно, указанные подходы не ограничивают-

ся только задачами газовой динамики, диапазон их применения гораздо

шире. Каждый из них сам по себе не приводит к «идеальному» вычисли-

тельному алгоритму и в ряде случаев требует адаптации к специфике рас-

сматриваемого класса задач.

В некоторых задачах гидродинамики основное течение, на которое

накладываются дополнительные возмущения, обладает осевой симметрией

(например, см. [9]). Часто для решения таких задач используются полярные

(в двумерном случае) или цилиндрические (в трехмерном случае) координа-

ты. При моделировании течений в полярных или цилиндрических коорди-

натах возникает ряд проблем, связанных с аппроксимацией уравнений гид-

родинамики в окрестности оси, которая порождает геометрическую особен-

ность. Если течение обладает осевой симметрией, то использование поляр-

ных или цилиндрических координат является естественным (мы не касаем-

ся вопроса понижения размерности задачи в этих случаях). Если же течение

не обладает осевой симметрией, то использование таких координат может

привести к значительным ошибкам. Кроме того, использование подробной

сетки по азимутальному углу приводит к сильно вытянутым пространст-

венным ячейкам сетки в окрестности оси и сильному ограничению времен-

ного шага интегрирования в случае использования явных разностных схем.

В случае если течение обладает трансляционной симметрией в каком-либо

направлении, то для аппроксимации уравнений газовой динамики естест-

венно использовать декартовы координаты. Выбор расчетной сетки, на ко-

торой аппроксимируются дифференциальные уравнения (в данном случае

газовой динамики), и выбор способа представления векторных величин (в

данном случае скорости): декартовыми, полярными или другими компонен-

тами, вообще говоря, не связаны между собой. Хотя во многих случаях вы-

бор системы координат предопределяет как представление векторных ве-

личин, так и вид расчетной сетки. Конечно, и сами газодинамические пере-

Разностная схема с анализатором симметрии для уравнений газовой динамики

менные, и их потоки могут быть пересчитаны из полярных (цилиндричес-

ких) координат в декартовы и обратно. Но для расчета потоков между рас-

четными ячейками в рамках годуновского подхода следует задать газоди-

намические величины с двух сторон грани, разделяющей эти ячейки. Пере-

нос векторных величин из ячеек на грани можно выполнить различными

способами и в зависимости от выбранного способа получить различные

данные для решения задачи Римана или ее аппроксимаций [2-4].

В настоящей работе предлагается вычислительный алгоритм для чис-

ленного интегрирования уравнений газовой динамики, содержащий анали-

затор симметрии течения. Вычислительный алгоритм основан на конечно-

объемной схеме годуновского типа с приближенным решением задачи Ри-

мана [3,4], что, впрочем, не является принципиальным. Вместо уравнения

баланса энергии используется уравнение баланса энтропии. Это обстоятель-

ство также не является принципиальным для предлагаемого алгоритма, но

ограничивает его применимость непрерывными решениями. В настоящей

работе уравнения газовой динамики аппроксимируются на сетке полярного

типа, а поле скорости представляется декартовыми компонентами. Расчет-

ная сетка состоит из нескольких круговых блоков (концентрических колец)

с различным разрешением по азимутальному углу. Во внутреннем блоке

азимутальное направление разрешено шестью ячейками. В каждом следу-

ющем блоке число ячеек в азимутальном направлении удваивается. Во всех

блоках сетка равномерна по азимутальному углу. С одной стороны, исполь-

зование такой сетки позволяет избежать искусственных (связанных с гео-

метрией) ограничений на шаг интегрирования по времени. С другой сторо-

ны, в окрестности оси сетки разрешение по азимутальному углу является

грубым, в то время как различие между плоско- и осесимметричными век-

торными полями проявляется наиболее рельефно. На такой сетке примене-

ние анализатора симметрии дает наибольший положительный эффект. Если

для аппроксимации уравнений использовать расчетную сетку с фиксиро-

ванным (по всем блокам) азимутальным разрешением, то использование ана-

лизатора симметрии, по-видимому, не приведет к существенному улучше-

нию качества численного решения. В этом случае вычислительные проб-

лемы обусловлены другими факторами. В настоящей работе для аппрокси-

мации уравнений импульса используется декартова система координат, т.е.

плотность импульса и соответствующие потоки представляются декарто-

выми компонентами. Такой подход избавляет от необходимости аппрокси-

мировать слагаемые, обусловленные кривизной системы координат. Предпо-

лагается, что течения либо преимущественно однородные (плоскосиммет-

А.В. Колдоба, Г.В. Устюгова

ричные), либо преимущественно осесимметричные (относительно оси сет-

ки). Для реконструкции векторных переменных используется анализатор

симметрии, позволяющий локально отнести течение к одному из указанных

типов. В зависимости от того, к какому типу будет отнесено векторное поле,

для его реконструкции используются соответствующие компоненты векто-

ров. Такой подход позволяет более аккуратно воспроизводить особенности

течения на грубой сетке в окрестности оси.

2. Вычислительный алгоритм с анализатором симметрии

Опишем алгоритм с анализатором симметрии для численного интегри-

рования двумерных уравнений идеальной газовой динамики. На трехмер-

ный случай алгоритм переносится без изменений. Как уже отмечалось,

уравнения баланса импульса рассматриваются в декартовой системе коор-

динат, а вместо уравнения баланса энергии интегрируется уравнение балан-

са энтропии



v



=0,

t

x

y

v

(v



v

vx y



= 0,

(1)

t

x

y

v

(v



y x



=0,

t

x

y

S

Sv



t

x

y

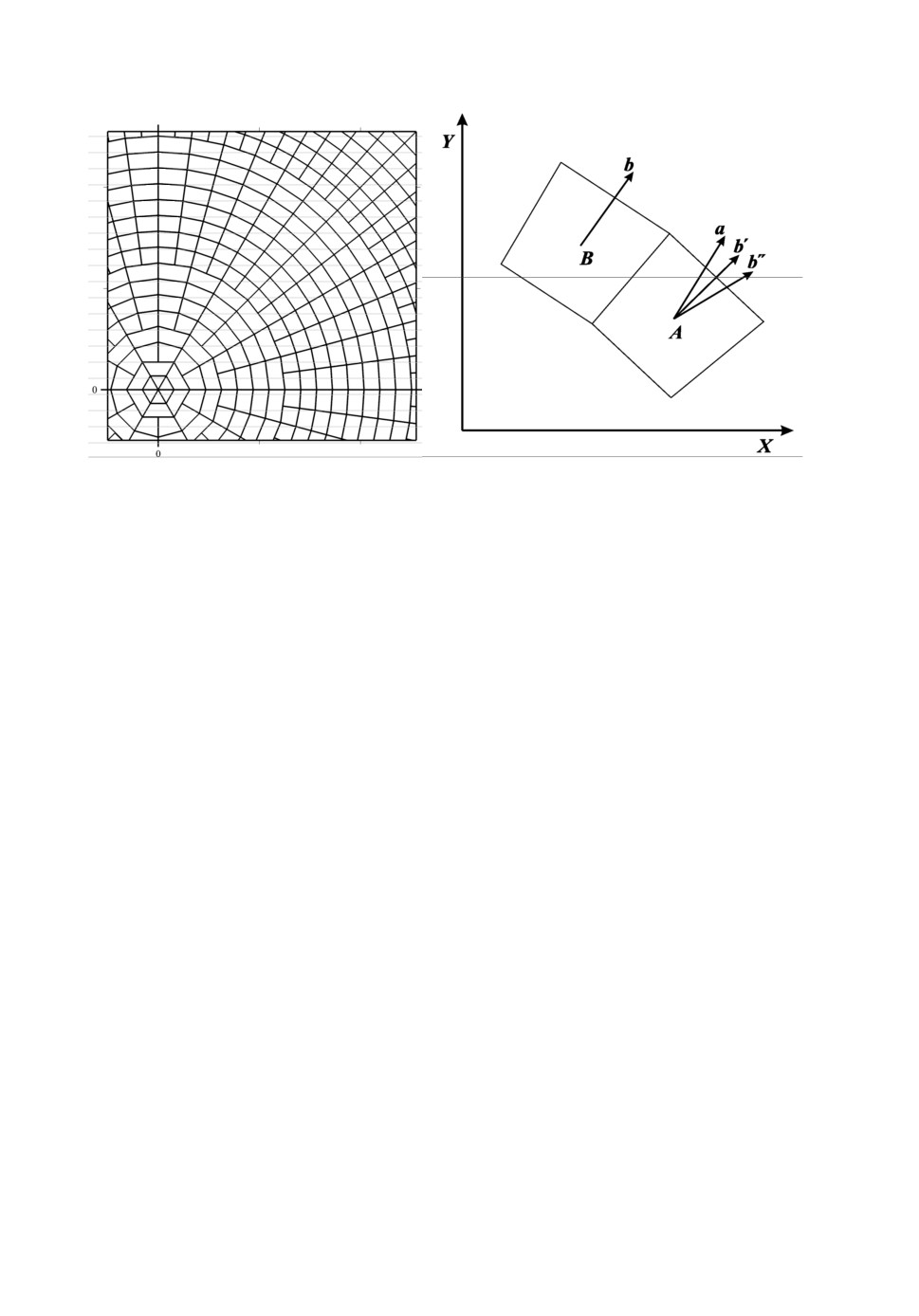
Расчетная сетка состоит из нескольких блоков (концентрических колец), в

каждом из которых разрешение по азимутальному направлению различно:

при переходе от предыдущего (внутреннего) блока к следующему (внешне-

му) подробность разрешения увеличивается вдвое. Использование таких

сеток позволяет сделать расчетные ячейки примерно равносторонними и из-

бежать дробления шага интегрирования по времени, обусловленного гео-

метрией расчетной сетки в окрестности оси (рис.1).

Для численного интегрирования системы уравнений (1) используется

явная разностная схема годуновского типа «третьего порядка аппроксима-

ции» по времени и пространству с приближенным HLLC-решением задачи

Римана [10] и ограничителем антидиффузии [3,4]. Имеется в виду, что ре-

конструкция переменных на грани расчетной сетки выполняется по алго-

Разностная схема с анализатором симметрии для уравнений газовой динамики

ритму, который в одномерном случае и на достаточно гладких решениях

обеспечивает третий порядок аппроксимации по пространственным пере-

менным. Реконструкция выполняется для давления, удельной энтропии и

выбранных анализатором симметрии компонент вектора скорости. Ограни-

читель диффузии имеет вид



при





(2 /1)x

при



x||

(x,



  0.5.

/6

при



|

||

| 4|



при



|



Применительно к реконструкции давления в радиальном направлении анти-

диффузионные поправки дают следующие величины на противоположных

гранях ячейки (i, j) блока l :











i, j,l

i1, j,l

i1, j,l

i, j,l

i j,l

 p

(d

)

 p

(d

)

i j,l

Непосредственно вычисляемыми величинами являются: плотность мас-

сы  , плотность энтропии S и декартовы компоненты вектора плотности

потока импульса

v

,v

, отнесенные к ячейкам расчетной сетки. Через эти

величины рассчитываются другие переменные, необходимые для реконст-

рукции функций и решения задачи Римана на гранях между ячейками сет-

ки. Для решения задачи Римана на грань между ячейками подается два на-

бора переменных, содержащих плотность, давление и полярные компонен-

ты векторных полей скорости, имеющие смысл состояний по обе стороны

грани. Использование полярных компонент при построении решения задачи

Римана (на используемых в настоящей работе расчетных сетках) естест-

венно, так как они являются нормальными и тангенциальными составля-

ющими векторов относительно граней расчетной сетки. Алгоритм расчета

этих величин будет представлен ниже. В результате приближенного реше-

ния задачи Римана через грань вычисляются потоки массы, энтропии и

вектора импульса (заданного полярными компонентами). Векторы потока

импульса на гранях пересчитываются в декартову систему координат для

расчета изменения вектора импульса в ячейках, заданного декартовыми

компонентами.

Для численного интегрирования уравнений по времени используется

трехстадийный метод Рунге-Кутта, более конкретно - метод Хойна третьего

порядка аппроксимации [11]. Время на промежуточных стадиях вычисля-

ется по правилу Рунге.

А.В. Колдоба, Г.В. Устюгова

Рис.1. Фрагмент расчетной сетки.

Рис.2. Перенос вектора b из точки B

в точку A с сохранением декартовых

компонент - b и с сохранением

полярных компонент - b .

Для расчета потоков консервативных переменных между расчетными

ячейками (например, A и B , см.рис.2) в рамках годуновского подхода не-

обходимо решить (точно или приближенно) задачу Римана о распаде разры-

ва между состояниями с двух сторон грани, разделяющей ячейки A и B. Га-

зодинамические величины, описывающие эти состояния, получают, приме-

няя ту или иную процедуру реконструкции функций (плотности, компонент

вектора скорости и др.) по сеточным данным. Применительно к реконст-

рукции векторных величин возникает вопрос: какие компоненты векторно-

го (сеточного) поля предпочесть - декартовы или полярные (или какие-либо

другие)? Для ответа на этот вопрос в настоящей работе используется ана-

лизатор симметрии - алгоритм, позволяющий по сеточным данным отдать

предпочтение декартовым или полярным (другие варианты не рассматрива-

ются) компонентам векторного поля для проведения его реконструкции на

грани расчетной сетки. Анализ проводится для каждой грани отдельно, так

что на части граней для реконструкции могут использоваться декартовы ком-

поненты векторов, а на другой части - полярные.

Для анализа типа векторного поля был принят следующий алгоритм.

Рассматривается два двумерных вектора a и b в (x, y) -плоскости, заданных

в двух точках A и B (например, векторы скорости в «центрах» двух сосед-

них ячеек, помечаемых теми же буквами), отличающихся только азимуталь-

ной координатой. Цель анализа симметрии - классифицировать это вектор-

ное поле (состоящее из двух векторов) как плоскосимметричное или осе-

Разностная схема с анализатором симметрии для уравнений газовой динамики

симметричное (азимутально-симметричное). Анализ симметрии устанавли-

вает близость этих векторов при перенесении их в одну общую точку, на-

пример, в точку A (рис.2). Рассматривается два способа переноса вектора b

из точки B в точку A:

1) вектор b переносится с сохранением своих декартовых компонент

, b ;

x y

2) вектор b переносится с сохранением своих полярных компонент

b^.

В результате этих операций в точке A, помимо вектора a, определены

два вектора b и b, полученные в результате применения двух указанных

способов переноса вектора. В обоих случаях длины этих векторов равны

длине вектора b. Близость векторов a и b,b



оценивается по величине

угла между ними. Так как при переносе длины векторов не менялись, срав-

ниваются модули z -компонент векторных произведений [a,b

]z

и [a,b

]_z

Если |[a,b] ||[a,b]

| , то принимается, что векторное поле, представлен-

ное векторами a и b , приблизительно плоскосимметричное. В противном

случае поле считается приблизительно осесимметричным. В соответствии с

отнесением поля к одному из указанных классов выполняется интерполяция

векторного поля на грани ячеек сетки. В первом случае для интерполяции

используются декартовы компоненты векторов, во втором - полярные.

Как уже отмечалось, для численного интегрирования уравнений балан-

са импульса используются декартовы компоненты векторов. Если в точках

A и B заданы только декартовы компоненты векторов, то:

1) вычисляются полярные компоненты векторов a и b



cos



sin

a

sin



cos

A y



A y

b A)=

b B) =b cos

b

sin

b A)=

b B)=

b

sin

b

cos

B y



B y

где_A и_B - азимутальные координаты точек A и B;

2) вычисляются z -компоненты векторных произведений

[a,b] =

b a

x y

y x

[a,b] =

ba b=(a

b a

)sin  (

b a

) cos ,



x x

y y

x y

y x

где



- азимутальный угол между направлениями на точки A и B

=AB

(шаг сетки по азимуту в соответствующем блоке);

А.В. Колдоба, Г.В. Устюгова

3) на основании сравнения величин [a,b

]z

и [a,b

]_z

реконструкция по-

ля скорости на соответствующую грань выполняется с использованием де-

картовых или полярных компонент поля скорости. Еще раз подчеркнем, что

алгоритм анализа симметрии применяется локально, т.е. для одних пар яче-

ек заданные в них векторы классифицируются как относящиеся к плоско-

симметричному типу, а для других - к осесимметричному типу.

После того как выполнена реконструкция переменных на грани рас-

четной сетки, для расчета потоков консервативных переменных через неко-

торую грань используется HLLC-алгоритм приближенного решения задачи

Римана о распаде разрыва между состояниями, реконструированными на

сторонах этой грани. Принимается, что решение содержит три разрыва: рас-

пространяющиеся налево и направо «ударные волны» (быть может разре-

жения) и тангенциальный разрыв, разделяющие области постоянного тече-

ния. Скорости «ударных волн» принимались равными D 1.1c , где c - ско-

рость звука перед ударной волной. Скорость вещества между «ударными

волнами» определяется из законов сохранения импульса с учетом того, что

на тангенциальном разрыве нормальная к фронту скорость непрерывна, а

тангенциальная компонента потока импульса равна нулю. Удельная энтро-

пия переносится через «ударные волны» без изменений.

3. Перенос переменных между блоками

Перенос переменных между блоками выполняется для удобства расче-

та потоков консервативных переменных через грани между соседними ячей-

ками, которые принадлежат разным блокам. Будем нумеровать блоки ин-

дексом l, самый внутренний блок l = 0. К каждому блоку присоединяются

слои фиктивных ячеек, которые имеют радиальные индексы i = 0, i = 1 (для

внутренних слоев) и

N l)1,

N l)

(для двух внешних слоев),

N l)

- количество ячеек в радиальном направлении в блоке с номером l. В

радиальном направлении фиктивные ячейки имеют такие же размеры, как

расчетные ячейки соседнего блока, на который они налагаются. Например,

фиктивные ячейки блока l с радиальным индексом i = 0 накладываются на

расчетные ячейки блока l - 1 с радиальным индексом

(

l

, фиктив-

ные ячейки блока l с радиальным индексом

N l)

1 накладываются на



расчетные ячейки блока l +1 с радиальным индексом i = 1. Расчетной ячей-

ке блока l - 1 с азимутальным индексом j соответствуют фиктивные ячейки

блока l с азимутальными индексами 2 j 1 и 2 j . Алгоритм переноса ска-

лярных и векторных величин одинаков за исключением того, что при пере-

носе векторных величин выполняется анализ симметрии.

Разностная схема с анализатором симметрии для уравнений газовой динамики

Для расчета, например, давления в фиктивных ячейках i = 0 блока l

рассчитывается азимутальная производная давления в блоке

i=N

(l1)

слоя

l - 1. Для этого используются величины давления в расчетных ячейках

(l1),

j k),(N

(l j,k),(N

(l1),

j1,k)

блока l - 1. Для подавле-

ния возможных осцилляций применяется анализатор гладкости

= minmod(p



;



)

j1,l1

j,l1

j1,l1

Здесь индексы

(l1),

k опущены и учтено, что сетка в азимутальном

направлении однородна в пределах каждого блока. Далее вычисляется дав-

ление в фиктивных ячейках:





j1,l

j,l1

2j,l

j,l1

Величины во внешних фиктивных ячейках блока l рассчитываются как

средние арифметические величин в соответствующих расчетных ячейках

блока l 1. Например,



j,l



j1,l1

2j,l1



4. Тестирование алгоритма

Для оценки эффективности предложенного алгоритма были проведены

тестовые расчёты. Во всех расчетах использовалась расчетная сетка, состо-

ящая из пяти радиальных блоков. Количество радиальных слоев в блоках

составляло: 4 (во внутреннем блоке), 4, 8, 16, 32 (во внешнем блоке), всего

64 слоя. Разрешение по азимутальному углу в блоках: 6 ячеек (во внут-

реннем блоке), 12, 24, 48, 96 (во внешнем блоке). Шаг интегрирования по

времени выбирался автоматически из условия: число Куранта = 0.4.

Плоскопараллельное течение. Рассматривалось течение на фоне по-

стоянного давления, в котором компоненты вектора скорости и плотность

зависят от переменной

  rsin()v

t :



exp(

2

coscos2

sin



sincos2

cos

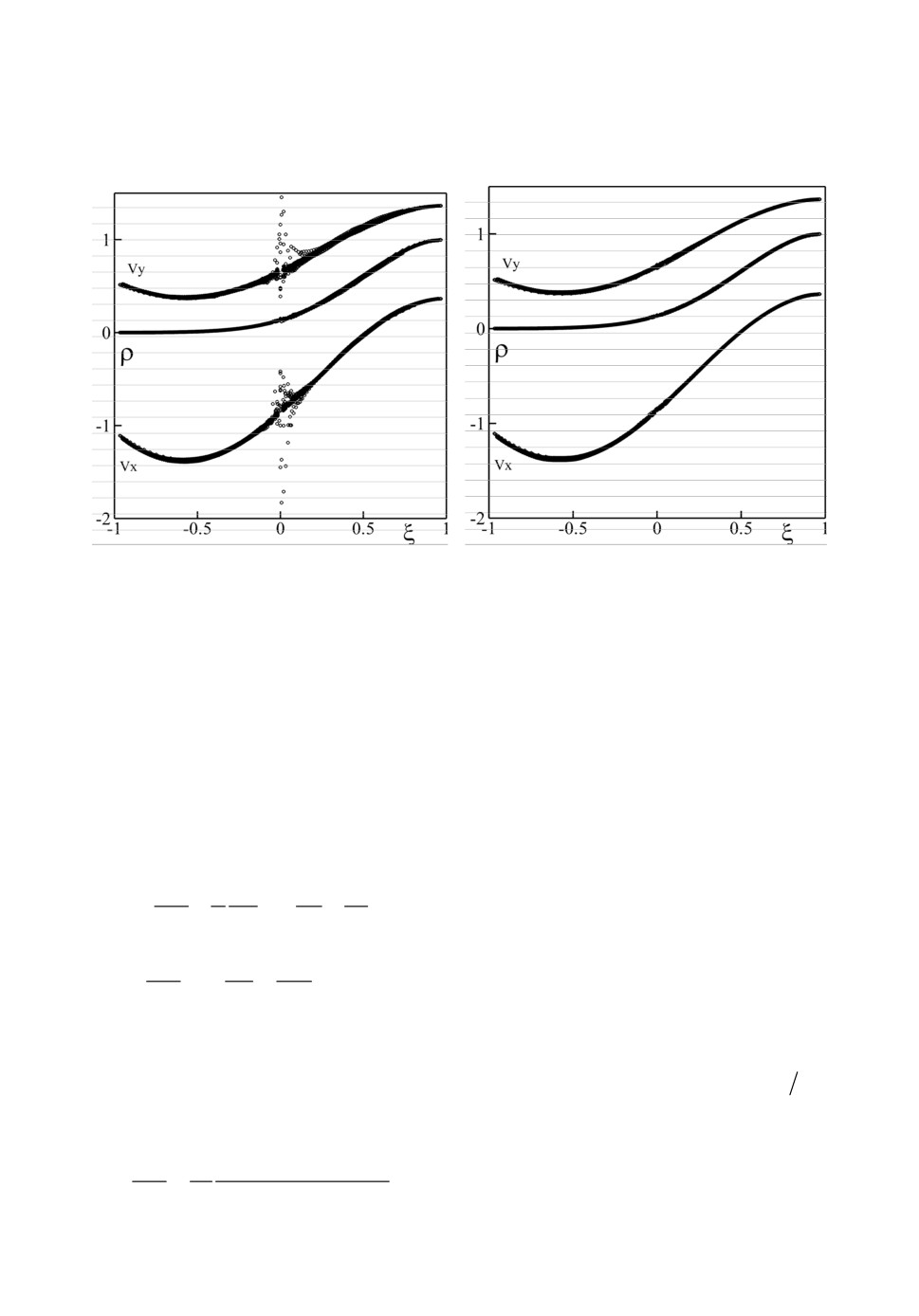
На рис.3a,b представлены результаты моделирования этого течения при

следующих параметрах течения: 30,



=1,

= 1,



1 для двух

вариантов реконструкции векторных переменных. На рис.3а - для реконст-

рукции поля скорости используются ее полярные компоненты, на рис.3b -

компоненты, выбранные анализатором симметрии в зависимости от вида

А.В. Колдоба, Г.В. Устюгова

течения, которые в случае данного течения совпадают с выбором декарто-

вых компонент для реконструкции поля скорости. Шаг сетки по радиусу,

одинаковый во всех блоках, составлял h  0.015 .

Рис.3a. Решение тестовой задачи о плоско-

Рис.3b. Решение тестовой задачи о плос-

параллельном течении (показаны все

копараллельном течении (пока-

точки расчетной сетки), полученное

заны все точки расчетной сетки),

при реконструкции поля скорости по

полученное при реконструкци

полярным компонентам. Показаны

поля скорости анализатором сим-

компоненты вектора скорости и

метрии. Показаны компоненты

плотность.

вектора скорости и плотность.

Осесимметричное течение. В качестве второго теста для предложен-

ного алгоритма рассматривается цилиндрическое течение Бонди - аккреция

на гравитирующий центр массы M . Это одномерное осесимметричное ста-

ционарное изоэнтропическое течение описывается системой уравнений

dP M l







(2)



d

v



v



(3)



с учетом сохранения энтропии P /





const

и удельного момента вращения



v r const 

. Комбинируя (2) и (3) с учётом

dp  c

d, где

 p  -

скорость звука, получаем



rl



(4)

c

Разностная схема с анализатором симметрии для уравнений газовой динамики

В звуковой точке

c

M

l

Условия сохранения энтро-

1

пии и потока массы приводят к соотношению





cr*/vr



. Для по-

строения решения, описывающего стационарную аккрецию на гравитиру-

ющий центр, задавались: масса гравитирующего центра M 1, положение

звуковой точки



1, удельный момент вращения l  0.25, при этом ско-

рость звука в звуковой точке составляла

 0.968 . Зависимость

(r)

по-

лучается интегрированием (5) от звуковой точки в обе стороны (до внут-

реннего радиуса

 0.12 и внешнего радиуса

 3.32 расчетной области)

на достаточно подробной сетке.

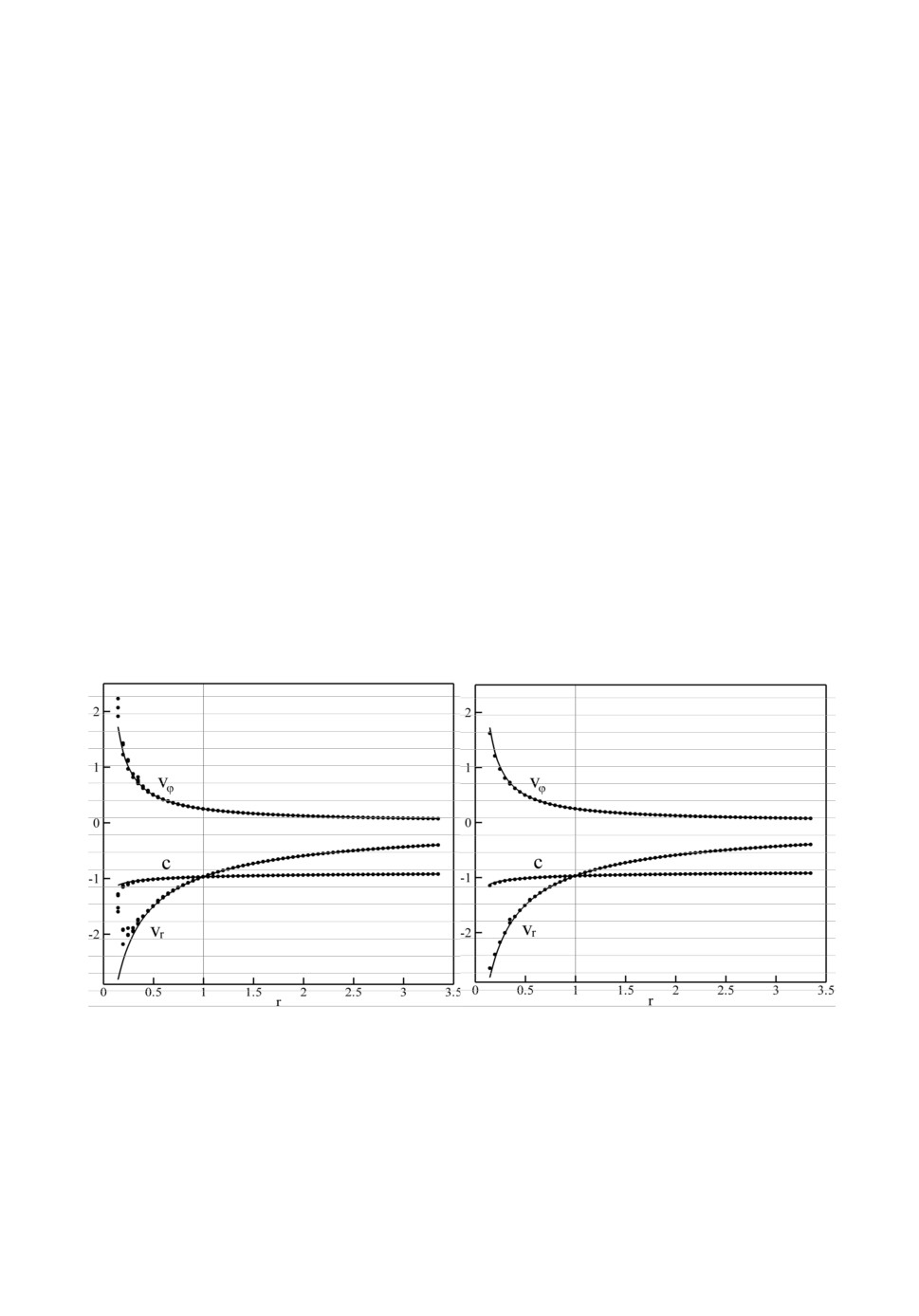
На рис.4a,b представлены «точное», полученное интегрированием (4),

и численные решения, полученные интегрированием системы (1) по схеме

третьего порядка аппроксимации, в зависимости от радиуса. На рис.4a пока-

заны азимутальная и радиальная компоненты вектора скорости и скорость

звука, полученные с помощью реконструкции поля скорости по ее декарто-

вым компонентам, на рис.4b - решение, полученное с использованием ана-

лизатора симметрии. Сплошной линией показано «точное» решение, точка-

ми - численные решения во всех ячейках двумерной расчетной сетки. Шаг

сетки по радиусу, одинаковый во всех блоках, составлял h = 0.05.

Рис.4a,b. Решение тестовой задачи об осесимметричной аккреции

на гравитирующий центр (показаны все точки расчетной сетки),

Сравнение результатов тестовых расчетов показывает, что для разного

типа течений анализатор симметрии выбирает наиболее подходящие компо-

ненты скорости для ее реконструкции на границах расчетных ячеек. Чис-

ленное решение, полученное для плоскопараллельного течения с помощью

реконструкции полярных компонент скорости, имеет большую ошибку из-

А.В. Колдоба, Г.В. Устюгова

за потери аппроксимации уравнений в окрестности оси расчетной сетки.

Аналогично, большую ошибку имеет численное решение, полученное для

осесимметричного течения с помощью реконструкции декартовых компо-

нент скорости. В то же время анализатор симметрии во всех случаях выби-

рает подходящие компоненты для реконструкции поля скорости, что приво-

дит к хорошему совпадению численного и точного решений.

Таким образом, можно сделать вывод, что использование анализатора

симметрии позволяет улучшить качество численного решения задач, в кото-

рых преимущественная симметрия течения в окрестности оси расчетной сет-

ки может менять тип в силу тех или иных причин.

5. Заключение

Предложен вычислительный алгоритм для численного интегрирования

уравнений газовой динамики, содержащий анализатор симметрии течения.

Вычислительный алгоритм основан на конечнообъемной схеме годуновско-

го типа с приближенным HLLC-решением задачи Римана. Выполненные

тестовые расчеты продемонстрировали целесообразность предложенного

подхода применительно к некоторым задачам газовой динамики.

СПИСОК ЛИТЕРАТУРЫ

1. В.М. Головизнин, Б.Н. Четверушкин. Алгоритмы нового поколения в вычислитель-

ной гидродинамике // ЖВМ и МФ, 2018, т.58, №8, с.20-29;

V.M. Goloviznin, B.N. Chetverushkin. New generation algorithms for computational fluid

dynamics // Comput. Math. Math. Phys., 2018, v.58, №8, p.1217-1225

2. С.К. Годунов и др. Численное решение многомерных задач газовой динамики. - М:

Наука, 1976, 400 с.;

S.K. Godunov i dr. Chislennoe reshenie mnogomernykh zadach gazovoi dinamiki. - M.:

Nauka, 1976, 400 s.

3. А.Г. Куликовский, Н.В. Погорелов, А.Ю. Семенов. Математические вопросы числен-

ного решения гиперболических систем уравнений. - М.: ФИЗМАТЛИТ, 2001, 608 с.;

A.G. Kulikovskii, N.V. Pogorelov, A.Yu. Semenov. Mathematical Aspects of Numerical So-

lution of Hyperbolic Systems, 2001, Boca Raton, Chapman & Hall.

4. E.F. Toro. Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical In-

troduction. - Springer, Berlin, 1997.

5. П.В. Бреславский, В.И. Мажукин. Моделирование взаимодействия ударных волн на

динамически адаптирующихся сетках // Математическое моделирование, 2007, т.19,

№11, с.83-95;

P.V. Breslavski, V.I. Mazhukin. Modelirovanie vzaimodeistviia udarnykh voln na dinami-

cheski adaptiruiushchikhsia setkakh // Matematicheskoe modelirovanie, 2007, t.19, №11,

s.83-85.

6. В.А. Гасилов, С.В. Дьяченко. Квазимонотонная двумерная схема МГД для неструкту-

Разностная схема с анализатором симметрии для уравнений газовой динамики

рированных сеток // Математическое моделирование, 2005, т.17, №12, с.87-109;

V.A. Gasilov, S.V. Diachenko. Kvazimonotonnaia dvumernaia schema MGD dlia nestruk-

turirovannykh setok // Matematicheskoe modelirovanie, 2005, t.17, №12, s.87-109.

7. И.В. Попов, И.В. Фрязинов. Конечно-разностный метод решения уравнений газовой

динамики с введением адаптивной искусственной вязкости // Математическое моде-

лирование, 2008, т.20, №8, с.48-57;

I.V. Popov, I.V. Fryazinov. Finite-difference method for computation of the gas dynamics

equations with artificial viscosity // Math. Models Comput. Simul., 2009, v.1, №4, p.493-502.

8. М.Е. Ладонкина, О.А. Неклюдова, В.Ф. Тишкин. Построение лимитера для разрывно-

го метода Галеркина на основе усреднения решения // Математическое моделирова-

ние, 2018, т.30, №5, с.99-116;

M.E. Ladonkina, O.A. Nekliudova, V.F. Tishkin. Postroenie limitera dlia razryvnogo me-

toda Galerkina na osnove usredneniia resheniia // Matematicheskoe modelirovanie, 2018,

t.30, №5, s.99-116.

9. О.Б. Бочарова, М.Г. Лебедев, И.В. Попов, В.В. Ситник, И.В. Фрязинов. Отражение

ударной волны от оси симметрии в неравномерном потоке с образованием циркуля-

ционной зоны // Математическое моделирование, 2013, т.25, №8, с.33-50;

O.B. Bocharova, M.G. Lebedev, I.V. Popov, V.V. Sitnik, I.V. Fryazinov. Shock wave reflec-

tion from the axis of symmetry in a nonuniform flow with the formation of a circulatory

flow zone // Math. Models Comput. Simul., 2014, v.6, №2, p.142-154.

10. A. Harten, P.D. Lax, B. van Leer. Upstream differencing and Godunov-type schemes for

hyperbolic conservation laws // SIAM Review, 1983, v.25, p.35-61.

11. И.Б. Петров, А.И. Лобанов. Лекции по вычислительной математике. - М.: Интернет-

Университет Информационных Технологий, 2006, 523 с.;

I.B. Petrov, A.I. Lobanov. Lektsii po vychislitelnoi matematike. - M.: Internet-Universitet

Infomatsionnykh Tekhnologii, 2006, 523 s.

Поступила в редакцию 12.11.18

После доработки 28.02.19

Принята к публикации 11.03.19