МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2019 год, том 31, номер 7, стр. 109-126
ГИСТЕРЕЗИСНЫЕ ПРЕОБРАЗОВАТЕЛИ
СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
©
2019 г.
С.В. Борзунов1, М.Е. Семенов1,2,3, Н.И. Сельвесюк4,
П.А. Мелешенко1,5
1 Воронежский государственный университет
sborzunov@gmail.com
2 Воронежский государственный технический университет
3 ФГБУН Федеральный исследовательский центр «Единая геофизическая
служба Российской академии наук»
4 ФГУП «Государственный научно-исследовательский институт авиационых
систем»
5 ВУНЦ ВВС «ВВА им. проф. Н.Е. Жуковского и Ю.А. Гагарина»
DOI: 10.1134/S0234087919070074
Предложен новый класс моделей гистерезисных преобразователей, обобщающий
классическое определение люфта на случай, когда геометрическое расположение
определяющих его кривых зависит от случайного параметра. Выход стохастичес-
кого преобразователя в этой ситуации трактуется как случайный процесс. Доказана
корректность определения соответствующего преобразователя в терминах специ-
альной предельной конструкции, позволяющей определить выход на произвольном
непрерывном входе. Исследованы свойства введенного преобразователя, получены
аналитические соотношения, определяющие первую и вторую моментные функции
выхода, приведены иллюстративные примеры.
Ключевые слова: гистерезис, люфт, гистерезисные свойства.
HYSTERETIC CONVERTERS WITH STOCHASTIC PARAMETERS
S.V. Borzunov1, M.E. Semenov1,2,3, N.I. Sel’vesyuk4, P.A. Meleshenko1,5
1 Voronezh State University
sborzunov@gmail.com
2 Voronezh State Technical University
3 Geophysical Survey of Russia Academy of Sciences
4 State Research Institute of Aviation Systems
5 Zhukovsky-Gagarin Air Force Academy
A new class of models of hysteretic converters which generalizes the classical definition
of backlash to the case when the curves defining it are non-deterministic and have a
random distribution is proposed. In this case an output of stochastic converter is defined
as a random process. The correctness of the definition of the corresponding converter in
110
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
terms of a special limit construction is proved. Using such a definition it is possible to
determine the output at an arbitrary continuous input. The properties of introduced
сonverters are investigated and explicit analytic relations determining the first and second
moment (as functions of the corresponding parameters) are presented together with
illustrative examples.
Keywords: hysteresis, backlash, hysteresis properties.
1. Введение
Изучение и моделирование сложных технических систем приводит к
необходимости представлять в формальном виде нетипичные нелинейнос-
ти, в том числе и гистерезисной природы. Известно, что многие физические,
физико-химические, биологические и экономические системы демонстри-
руют гистерезисное поведение, что обуславливается либо их внутренней
структурой, либо динамическими особенностями протекающих в таких сис-
темах процессов [1-6].
В настоящее время существуют два основных подхода к описанию гис-
терезисных явлений: конструктивные модели, например, люфт, неидеаль-
ное реле, преобразователь Прейзаха, модель Ишлинского [1, 7-11], и фено-
менологические модели, такие как модели Боука-Вена [12], Дьюема, Айва-
на и другие [13-15].
В работах М.А. Красносельского [1, 16] для анализа систем с гистере-
зисом был развит математический аппарат, основанный на идентификации
элементарных носителей гистерезиса (гистеронов). Гистероны - это преоб-
разователи с пространствами состояний, определенные посредством соот-
ветствий вход-выход и вход-состояние. Корректное определение гистерона
основано на реализации классической трехэтапной конструкции. На первом
шаге гистерон определяется на монотонных входах, на втором - с помощью
полугруппового тождества на кусочно-монотонных входах. На третьем эта-
пе осуществляется переход к произвольным непрерывным входам. Именно
эта конструкция была использована для определения люфтов и упоров в [1].
Конструктивные модели гистерезисных преобразователей вполне ус-
пешно применялись для анализа физических систем различной природы
[17-20]. В частности, в [17] рассмотрена задача стабилизации перевернутого
маятника с вертикально осциллирующей точкой подвеса, находящегося под
воздействием гистерезисного управления, и найдены критерии устойчивос-
ти для линеаризованного уравнения движения. В [19] исследовано влияние
электромагнитных актюаторов на частотную характеристику консольных
балок. Результаты численного моделирования демонстрируют возможность
наблюдения гистерезисных явлений и сдвига частоты вынужденных коле-
Гистерезисные преобразователи со случайными параметрами
111
баний под действием сил электромагнитной природы. Отметим, кроме того,
ряд работ, посвященных моделированию различных физических систем с
гистерезисной нелинейностью, формализуемой посредством преобразовате-
ля Прейзаха [21-23], а также большое количество публикаций, в которых гис-
терезисные свойства моделировались посредством феноменологических со-
отношений, отвечающих широко известной модели Боука-Вена [12,13,24-28].
В указанных выше моделях гистерезисных преобразователей все опре-
деляющие их параметры, а также входы и отвечающие им выходы пред-
полагались детерминированными. В этой связи отметим ряд работ, посвя-
щенных изучению отклика системы с гистерезисным звеном на случайный
или зашумленный сигнал [5, 23, 29, 30].
Однако характеристики, в том числе и гистерезисных блоков могут
быть известны лишь с некоторой точностью и не допускают возможности
идентификации в условиях неразрушающего контроля. Именно такая ситуа-
ция имеет место, когда люфты возникают в механических составляющих в
процессе длительного функционирования. Более того, параметры носителей
гистерезисных свойств могут испытывать регулярные или нерегулярные
изменения, связанные со старением материалов или варьироваться за счет
воздействия иных неконтролируемых факторов. В связи с этим возникает
необходимость обобщения конструктивных моделей гистерезисных преоб-
разователей, учитывающих вероятностный характер определяющих их
параметров.
Настоящая статья посвящена обобщению одной из основных моделей
гистерезиса люфта на класс преобразователей, характеристики которых
определяются случайными параметрами.
2. Постановка задачи. Люфт со случайными параметрами
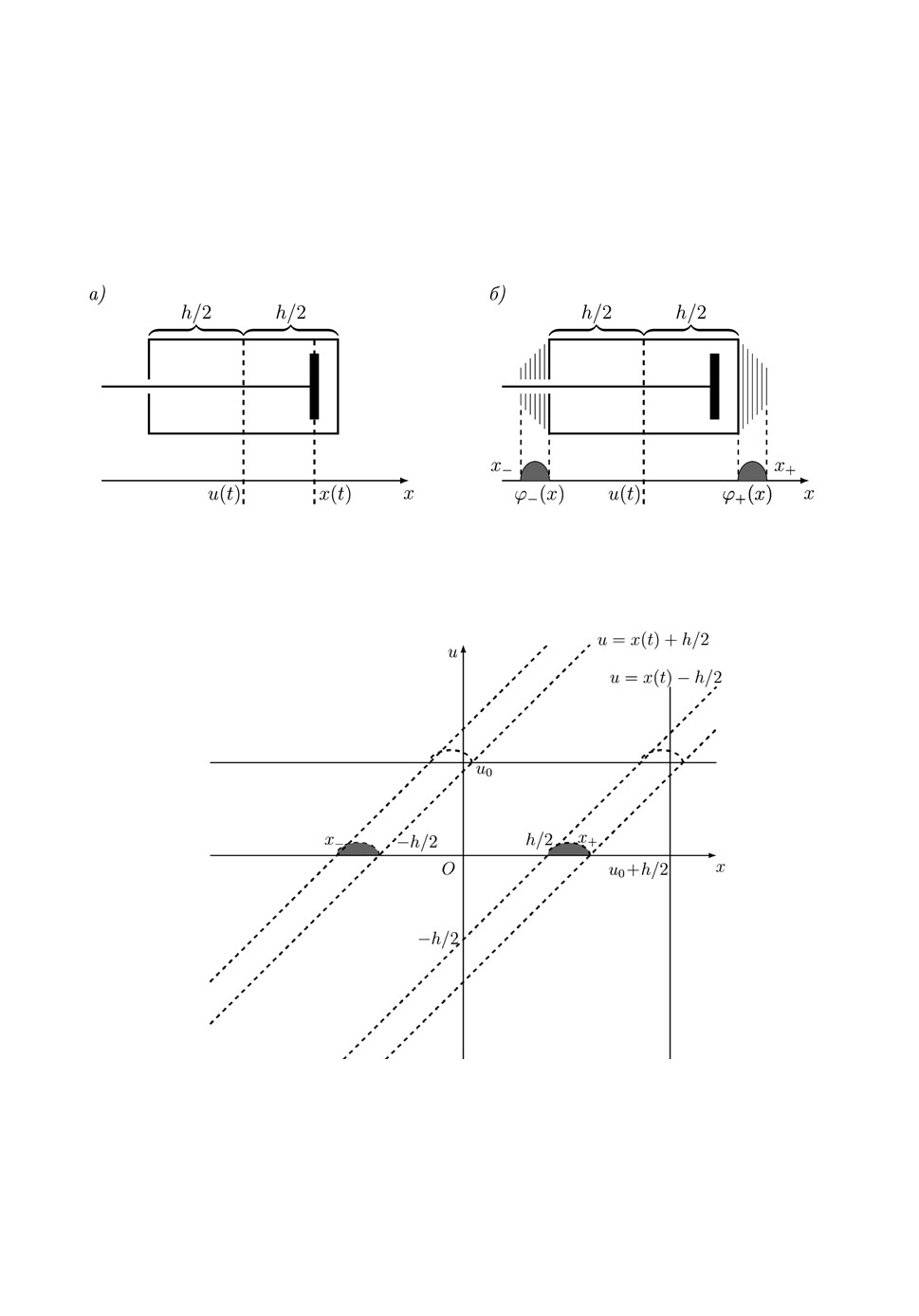
Физическая модель люфта представляет собой систему, состоящую из
цилиндра длины h и поршня, которые могут перемещаться в горизонталь-
ном направлении (рис.1а). Положение поршня будем считать входной коор-
динатой, а положение цилиндра выходной. Вход системы в зависимости
от времени на конечном интервале
t[t
,T] обозначим через x(t), выход
0
через u(t) .
Если считать положения левой и правой стенок цилиндра распределен-
ными по случайному закону, то соответствующий преобразователь естест-
венно назвать люфтом со случайными параметрами. Ниже предполагаются
заданными функции (x) и (x) , трактуемые как плотности вероятнос-
ти, соответствующие положениям левой и правой границ цилиндра соответ-
112
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
ственно. Будем считать, что носители функций (x) и (x) расположе-
ны на непересекающихся множествах, а именно (x) принимает ненуле-
вые значения только на промежутке (x , h / 2) , а
(x)
тождественно не
равна нулю на интервале (h / 2, x ) (рис.1б). Выход преобразователя-люфта
со случайными параметрами будем считать случайным процессом u(t) с
функцией распределения P{u(t) <u}
Рис.1. Схематическое изображение люфта. Панель a) люфт с детерминированными
параметрами, б) люфт со стохастическими параметрами. Серой заливкой
выделены для области под кривыми (x) и (x) , определяющими плотность
вероятности левой и правой границ цилиндра соответственно.
Рис.2. Люфт со случайными параметрами. Серой заливкой выделены
области под (x) и (x) .
Следуя классической схеме [1], определим сначала выход на моно-
тонных входах. Случайный процесс u(t) в каждый момент времени t под-
чиняется операторному соотношению
Гистерезисные преобразователи со случайными параметрами
113
u t)=
L[u
, x
;
,
x(t),
t
tT,
(1)
0
0
l
r
0
где
x
=x(t
) и
u
=u(t
) начальные значения функций входа и выхода со-
0
0
0
0
ответственно. Здесьl ,r определяющие кривые люфта:
: u
=
x
и
l
l
: u
=
x
,
,
случайные величины с плотностями вероятности
r
r
l
r
(x)
и (x) соответственно (см. рис.2).
Функцию распределения случайного процесса определим на монотон-
но возрастающих входах x(t) следующим образом:
P{u(t) <u}=
(uu
),
x t)<
u
h
/ 2;
0
0
0,
u<u0,
=
(u,x(t)),
u
u x t)h
/ 2,
u
h
/2
x t)
x u
;
(2)
0
0
0
1,
u
>
x t) h
/ 2;
0,
u<u0,
(u x(t)
x u
),
x u
),
u
u x t)h
/ 2,
x t)>
x
u
0
0
0
0.
1,
u
>
x t) h
/ 2;
Здесь введено обозначение:
uu
h/2
x
0
(u,x(t)) =
()
()
,
(3)
h/2
x t)u
0
следствием которого являются равенства
uu h/20
(u,
x u
)=
()
,
(4)
0
h
/2
u x(t)
x
)
h
/2
(u x(t)
x u
),
x u
)=
()
,
(5)
0
0
h
/2
и использована ступенчатая функция Хевисайда (x) .
Аналогично, обозначив через
x x t)u0
h/2
(u,x(t)) =
()
()
,
(6)
x
x t)
114
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
для монотонно убывающих входов имеем
P{u(t) <u}=
(uu
),
x t)>
u
h
/ 2;
0
0
1,
u>u0,
(u,x(t)),
x t)
h
/2uu
,
0
=
,
x u
x t)
u
h
/ 2;
(7)
0
0
0,
u
<
x t)
h
/ 2;
1,
u>u0,
(u x(t)
x u
),
x u x(t)
h
/2
uu
,
x t)<
x u
0
0
0
0
0,
u
<
x t)
h
/ 2;
Несмотря на громоздкость соотношений (2) и (7), они допускают впол-
не ясную интерпретацию: вероятность P(u) P{u(t) <u}
определяется на-
чальным положением цилиндра
u
и координатой поршня x(t) в текущий
0
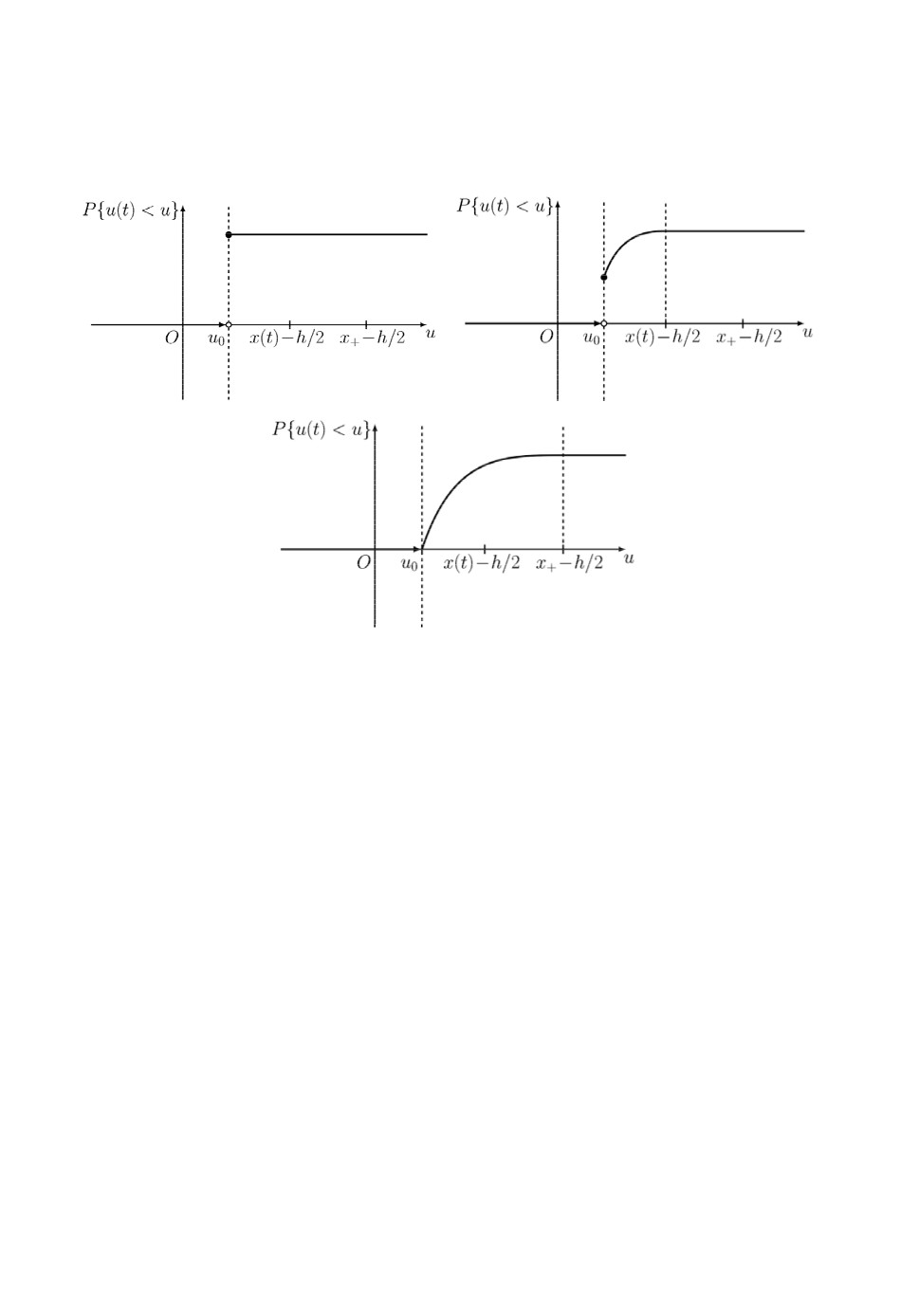
момент времени. Рассмотрим три случая, отвечающих различным соотно-
шениям между
u
и x(t) (рис.3).
0
1) Если
x(t) < u
h /2, то поршень расположен левее правой границы
0
цилиндра. Следовательно, координата u не менялась за прошедший про-
межуток времени, и P(u) = 1 при
uu
, P(u) = 0 при
u
<
u
. В этом случае
0
0
функция P(u) очевидным обрaзом совпадает с функцией Хевисайда:
P(u) = (u u
).
0
2) Если выполняются неравенства
u
h/2
x(t) x
u
, то поршень
0
0
находится на промежутке, в пределах которого плотность вероятности пра-
вой границы люфта отлична от нуля. Из физических свойств системы сле-
дует, что событие
u
<
u
невозможно, а событие u > x(t) h / 2 достовер-
0
но. Для u из интервала
[u
,x(t) h / 2] вероятность противоположного
0
uu
0
h/2
x
события, как следует из рис.2, равна
()
( )
. Ве-
h/2
x t)u
0
личина P(u) с увеличением u монотонно возрастает до единицы.
3) Если
x(t) > x
u
, то поршень при движении вправо с вероят-
0
ностью, равной единице, достигает правой стенки цилиндра. Этот случай
сводится к предыдущему посредством простой замены координаты
u=u(x(t) x u
))
0
Гистерезисные преобразователи со случайными параметрами
115
Соотношение (7) для монотонно убывающих входов вводится на осно-
ве аналогичных рассуждений с очевидным изменением пределов интегри-
рования в соотношении (3).
а)
б)
в)
Рис.3. Эволюция функции распределения P(u) = {u(t) <
u}
для монотонно возраста-
ющих входов. Панель a)
x(t) < u
h / 2, панель б)
u
h/2
x(t) x
u
,
0
0
0
панель в)
x(t) > x
u
0
Отметим, что для монотонно возрастающих входов соотношение (2)
может быть записано в более лаконичной форме:
(uu
),
x t)<
u
h
/ 2;
0
0
0,
u<u0,
(u ,x(t) ),
P u(t)<u}=
(8)
u
u x t)h
/ 2,
x t)
u
h
/ 2,
0
0
1,
u
>
x t)h
/ 2;
где введено обозначение
=(x(t) x u
)(x(t) x
u
). Аналогичным
0
0
образом преобразуется соотношение (7). Кроме того, с использованием
функции Хевисайда, последнее соотношение запишется как:
P{u(t) <u}= (u
u
)
0
(uu
)(x(t)u
h /2)(x(t)uh /2)
1
(u
,x(t)
)
=
0
0
116
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
x t)u
0
=(uu
)(uu
)(x(t)u
h
/2)(x(t)uh
/2)
()
,
(9)
0
0
0
uu
h
/2
0
а соответствующая плотность распределения определяется как
dP{u(t)<u}
(u)=
(uu
)
0
du
x t)u
0
(uu x(t)
u
h
/ 2)(x(t) uh
/ 2)
( )
0
0
uu
h
/2
0
x t)u
0
(uu x(t)
u
h
/ 2)(x(t) uh
/ 2)
( )
0
0
uu
0
h
/2
(uu
)(x(t)u
h /2)(x(t)uh /2)
(uu
h/2
),
(10)
0
0
0
где введено стандартное обозначение (u) для дельта-функции Дирака.
Первая и вторая моментные функции. Настоящий раздел посвящен
идентификации характеристик случайного процесса - выхода люфта со
случайными параметрами, а именно вычислениям моментных функций
2
2
u
(t) =
u(u)du
и
u
(t) =
u
(u)du
Теорема 1. Первая и вторая моментные функции определяются соот-
ношениями:
x t)u
0
u
(t)=
u
(x(t)u
h
/ 2)
(uh
/ 2)
(u
)du
,
(11)
0
0
h
/2
x t)u
0
2
2
2
2
u t)=
u
(x(t)u
h
/ 2)
((uu
h
/ 2)
u
)
(u )du
(12)
0
0
0
0
h
/2
Доказательство.
u
(t)=
u u)du u
u(uu x(t)u
h
/ 2)(x(t) uh
/ 2)
0
0
0
x t)u
0
( )ddu
u(uu x(t)
u
h
/ 2)(x(t)
uh
/ 2)
0
0
uu
h
/2
0
x t)u
0
( )ddu
u
(uu x(t)
u
h
/ 2)(x(t)
uh
/ 2)
0
0
uu
0
h
/2
Гистерезисные преобразователи со случайными параметрами
117
x t)u
0
(uu
h
/2)du uu x(t)u
h
/ 2)
()
0
0
0
h/2
x t)u
0
(x(t)u
h
/ 2)
u
( u
h
/2)
0
0
u
0
Произведя замену переменной
u' u
h/2,
получим
0
x t)u
0
u
(t)=
u
(x(t)u
h
/ 2)
(u'
h
/ 2)
(u')du'.
0
0
h
/2
Вторая моментная функция
2
2
2
u
(t) =
u
(u)du
u
((u u
)
(uu
)(x(t)u
h /2)
0
0
0
x t)u
0
(x(t)
uh
/ 2)
()
(
uu
)(x(t)
u
h
/ 2)
0
0
uu
0
h
/2
x t)
u
(x(t)uh
/ 2)
0
( )
(uu x(t)
u
h
/ 2)(x(t)uh
/ 2)
uu
h
/2
0
0
0
2
2
x(t)u0
(uu
h
/2
))du u
(x(t)
h
/2u
)u
(u
)du
0
0
0
0
h/2
x(t)u0
2
(x(t)
h
/2
u
)
u
( u
h
/2
)
h/2
0
После указанной замены получим
x t)
u
0
2
2
2
2
u t)=
u
(x(t)
h
/2
u
)
((u'
u
h
/ 2)
u
)
(u')du'.
■
0
0
0
0
h
/2
Определение выхода на кусочно-монотонных входах. Для реализа-
ции следующего этапа - определения выхода на кусочно-монотонных вхо-
дах необходимо определить соответствующий выход в ситуации, когда
начальное значение выхода является случайной величиной.
Пусть начальное значение
u
представляет собой случайную величину,
0
распределенную с плотностью вероятности
(
)
u
. Определим функцию
U
0
распределения следующим образом:
(u x(t)
h
/ 2)),
x t)>
u h
/ 2;
0,
u
<
x t)h
/ 2,
P u(t)<u}=
(13)
u
0
u
x t)
u h
/ 2,
(
u)du,
u x t)h
/ 2,
U
0
118
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
где u верхняя граница носителя
(u)
U
0
Перепишем последнее соотношение в виде
P u(t)<u}=(u x(t)h/2))[1(x(t)(u h/2))
()
].
(14)
u
0
U
0
u
Соответствующая плотность распределения равна
d
(u)=
P u(t)<u}=
u
0
u
0
du
(u x(t)h/2))[1(x(u h
/2))
()
]
U0
u
(u x(t) h
/ 2))(x(t)(u h
/ 2))
(u).
(15)
U
0
Плотность распределения p(u) в ситуации, когда
u
также является
0
случайной величиной, определяется как свертка (10) и (15):
p u)=
(us s)
)
ds
(16)
u
0
L в
Отметим, что оператор люфта со случайными параметрами
(1)
удовлетворяет полугрупповому тождеству
L[t
,u
,x
]x(t) = L[t
,L[t
,u
,x
]x(t
),x(t
)]x(t)
(17)
0
0
0
1
0
0
0
1
1
для произольного момента времени t1[t
,T].
0
L на кусочно-монотонных входах в случае
Для определения оператора
конечного значения t выполним разбиение промежутка
[0,T ] вида
[0,t
]
[
t
,t
]
[t
,
t
][t
,T ]
на промежутки монотонности и опре-
1
1
2
n1
n
n
делим на каждом из них соответствующий оператор как оператор на моно-
тонном входе. Начальное состояние при этом определяется как состояние в
момент времени перехода на следующий промежуток монотонности.
t t T имеет место равномерная схо-
димость последовательности кусочно-монотонных функций {x t)}, n=1,2,
n
…, к функции
x
(t):
*
x t)
x t)
t [
t
,T ].
(18)
n
*
0
Тогда выход представляет собой случайный процесс, сходящийся по рас-
пределению к случайному процессу
Гистерезисные преобразователи со случайными параметрами
119
u
(t) = L[u
,x
]x
(t).
(19)
*
0
0
*
Доказательство. Сходимость последовательности n, n=1,2,…, по рас-
d
пределению к (обозначениеn ) означает, что для произвольной огра-
ниченной непрерывной функции f=f(x) выполняется предельный переход
lim
f
(
)
=
f
() ,
(20)
n
n
где
отвечает усреднению по функции распределения [31].
Выходу
x
(t) сопоставляется случайный процесс с функцией распреде-
*
ления
P{u<
u t)} как предел
P u<
u t)}
*
limn
n
d
1. Докажем, что
u t)
u t)
выполняется для монотонных функций
n
*
x t)
n
Для этого рассмотрим модуль разности математических ожиданий
D=|<
f
(u t)) >
<
f
(u t)) >|
и убедимся, что
> 0 = () > 0: при
n
*
|
x t)
x t)|<
справедливо условие D< . В самом деле, используя (10),
n
*
получим
1
1
D
=
|
f u)dP u<
u
}
f u)dP u<u
}|
=
|
f u)
(u)du
f u)
(u)du |. (21)
n
*
n
*
0
0
Имеет место оценка
D
=|
f u)(
(u)
(u))du |
n
*
n
x t)u
0
(
n
x t))
|
f u)((uu
)(
x t)
u
h/2)(
x t) h/2)
( )
0
n
0
n
uu
h/2(
x t))
0
n
*
x t)
u
0
(
*
x t))
(uu
)(
x t)u
h
/ 2)(
x t)
uh
/ 2)
()
0
*
0
*
uu
h
/2
(
x t))
0
*
n
x t)
u
0
(
n
x t))
(uu
)(
x t)
u
h
/ 2)(
x t)
uh
/ 2)
( )
0
n
0
n
uu
h
/2(
x t))
0
n
x t)
u
(
x t))
*
0
(uu
)(
x t)
u
h
/ 2)(
x t)
uh
/ 2)
()
0
0
uu
0
h
/2
(
x t))
(uu
)(
x t)
u
h/2)(
x t)
uh/2)
(uu
h/2
(
x t)))
0
n
0
n
0
n
(uu
)(
x t)
u
h
/2)(
x t)
uh
/2)
(uu
h
/2
(
x t))) |
du
0
0
0
*
120
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
n
x t)u
0
(
n
x t))
|
f
(u
)((
x t)u
h
/ 2)
( )
0
n
0
h/2
(
x t))
n
x t)u
0
(
x t))
*
*
(
x t)u
h
/ 2)
()
)
*
0
h/2(
x t))
*
n
x t)u
0
(
n
x t))
(
uu
)(
x t)u
h/2)(
x t)uh/2)
( )
0
n
0
n
uu
h/2(
x t))
0
n
x t)u
(
x t))
*
0
(
uu
)(
x t)u
h/2)(
x t)uh
/2)
()
0
0
uu
0
h
/2
(
x t))
(
uu
)(
x t)u
h/2)(
x t)uh/2)
(
uu
h/2(
x t)))
0
n
0
n
0
n
(uu
)(
x t)u
h
/2)(
x t)uh
/2)
(uu
h
/2(
x t))) |
du
0
0
0
*
x t)u
(
x t))
n
0
n
=
|
f
(u
)(
(
x t)u
h
/ 2)
(
)
0
n
0
h/2
(
n
x t))
x t)
u
(
x t))
*
0
*
(
x t)
u
h
/ 2)
()
n
0
h/2(
x t))
*
x t)
u
(
x t))
*
0
*
(
x t)
u
h
/ 2)
()
n
0
h/2(
x t))
*
x t)
u
(
x t))
*
0
*
(
x t)
u
h
/ 2)
( )
)
*
0
h/2(
x t))
*
n
x t)u
0
(
n
x t))
(
uu
)(
x t)u
h
/ 2)(
x t)uh
/ 2)
()
0
n
0
n
uu
0
h
/2
(
n
x t))
x t)
u
(
x t))
n
0
(uu
)(
x t)
u
h
/ 2)(
x t)uh
/ 2)
( )
0
0
uu
0
h
/2
(
x t))
(
uu
)(
x t)
u
h
/2)(
x t)uh/2)
(
uu
h
/2(
x t)))
0
n
0
n
0
n
(
uu
)(
x t)
u
h
/2)(
x t)uh
/2)
(
uu
h
/2
(
x t))) |
du
0
0
0
n
x t)x t)(
(
x t))
(
x t)))
*
n
*
n
=
|
f
(u
)((
x t)u
h
/ 2)
(
)
0
n
0
(
(
x t))
(
n
x t)))
*
Гистерезисные преобразователи со случайными параметрами
121
x t)u
(
x t))
*
0
*
x t)u
h
/ 2)(
x t)u
h
/ 2))
()
)
*
0
n
0
h/2(
x t))
*
x t)u
(
x t))
n
0
n
(uu
)(
x t)
u
h
/ 2)(
x t)
uh
/ 2)
( )
0
n
0
n
uu
0
h
/2(
n
x t))
(22)
x t)
u
(
x t))
*
0
(uu
)(
x t)
u
h
/ 2)(
x t)uh
/ 2)
()
0
0
uu
h
/2
(
x t))
0
(uu
)(
x t)
u
h/2)(
x t)uh/2)
(uu
h
/2(
x t)))
0
n
0
n
0
n
(uu
)(
x t)
u
h/2)(
x t)uh/2)
(uu
h
/2(
x t))) |du
0
0
0
*
Принимая во внимание непрерывность функции f (u) и с учетом
x t)
x t), на основании непрерывности определенного интеграла как
n
*
функции пределов интегрирования [32] получаем, что D < , следовательно,
d
u t)
u t)
n
*
2. Перейдем к рассмотрению кусочно-монотонных входов x(t) для
t
tT . Обозначим
y t)=
f u)dP u<
u
}
. Докажем, что последова-
0
n
n
тельность {
y
} является фундаментальной на отрезке
[t
,T]:
n
0
>0N
:
m,n N t
[
t
,T ] |
y t)
y t)|<
(23)
0
m
n
Действительно, получим следующую оценку:
|
y t)
y t)|
m
n
y t)
u
(
y t))
m
0
m
|
f u)(
(uu
)(
y t)u
h/2)(
y t)
h
/2)
()
0
m
0
m
uu
0
h/2
(
m
y t))
n
y t)
u
0
(
y
n
(t))
(uu
)(
y t)
u
h
/ 2)(
y t)
uh
/ 2)
( )
0
n
0
n
uu
0
h
/2
(
n
y t))
m
y t)
u
0
(
m
y t))
(uu
)(
y t)
u
h
/ 2)(
y t)
uh
/ 2)
()
0
m
0
m
uu
h
/2
(
y t))
0
m
y t)
u
(
y t))
n
0
n
(uu
)(
y t)
u
h
/ 2)(
y t)
uh
/ 2)
( )
0
n
0
n
uu
0
h
/2
(
n
y t))
(uu
)(
y t)
u
h
/ 2)(
y t)
uh
/2)
(
uu
h
/2
(
y t)))
0
m
0
m
0
m
(uu
)(
y t)
u
h
/ 2)(
y t)
uh
/ 2)
(
uu
h
/2
(
y t)))du|
0
n
0
n
0
n
122
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
m
y t)u
0
(
m
y t))
|
f
(u
)((
y t)u
h
/ 2)
( )
0
m
0
h/2
(
y t))
m
0
y t)
(
y t))
n
n
u
(
y t)u
h
/ 2)
()
)du |
n
0
h/2(
n
y t))
y t)u
(
y t))
m
0
m
|
(uu
)(
y t)u
h
/ 2)(
y t)uh
/ 2)
( )
0
m
0
m
uu
0
h/2(
m
y t))
n
y t)u
0
(
n
y t))
(
uu
)(
y t)
u
h
/ 2)(
y t)uh
/ 2)
()ddu |
0
n
0
n
uu
0
h/2
(
n
y t))
|
(uu
0
)(
m
y t)u
0
h
/ 2)(
m
y t)
uh
/2)
(
uu
0
h/2(
m
y t)))
(
uu
)(
y t)
u
h
/ 2)(
y t)uh
/ 2)
(
uu
h
/2
(
y t)))du
|.
0
n
0
n
0
n
Следовательно, последовательность {
y
}
имеет предел:
Y t)=
{y
}
n
limn
n
Докажем, что
Y t)=
limn
f
(u t))
n
Рассмотрим на промежутке
t
t T произвольную последователь-
0
ность кусочно-монотонных функций
x t), обладающую свойством
n
(1)
x t)
x t). Соответствующая последовательность интегралов
y t)=
n
*
n
(1)
=
f
(
x t))du
сходится равномерно к функции
y
(t).
n
*
Чередуя слагаемые
y t)
и
y t), построим вспомогательную после-
n
n
(1)
(1)
(1)
довательность
z t)={
y t),
y t),
y t),
y t),
,
y t),
y t),}. Очевид-
n
1
1
2
2
n
n
но, что она также является фундаментальной и имеет тот же предел
y
(t).
*
Тем самым доказано, что для произвольного непрерывного на
[t
,T]
0
входа x(t) определен случайный процесс u(t) , трактуемый как выход гисте-
резисного преобразователя со случайными параметрами на произвольном
непрерывном входе.
■
Иллюстративные примеры. Рассмотрим люфт с направляющими
прямыми
:
u
=
x
и
:
u
=
x
,
,
равномерно распределен-
l
l
r
r
l
r
ные на интервалах ( x , h / 2 ) и (h / 2, x ) соответственно случайные вели-
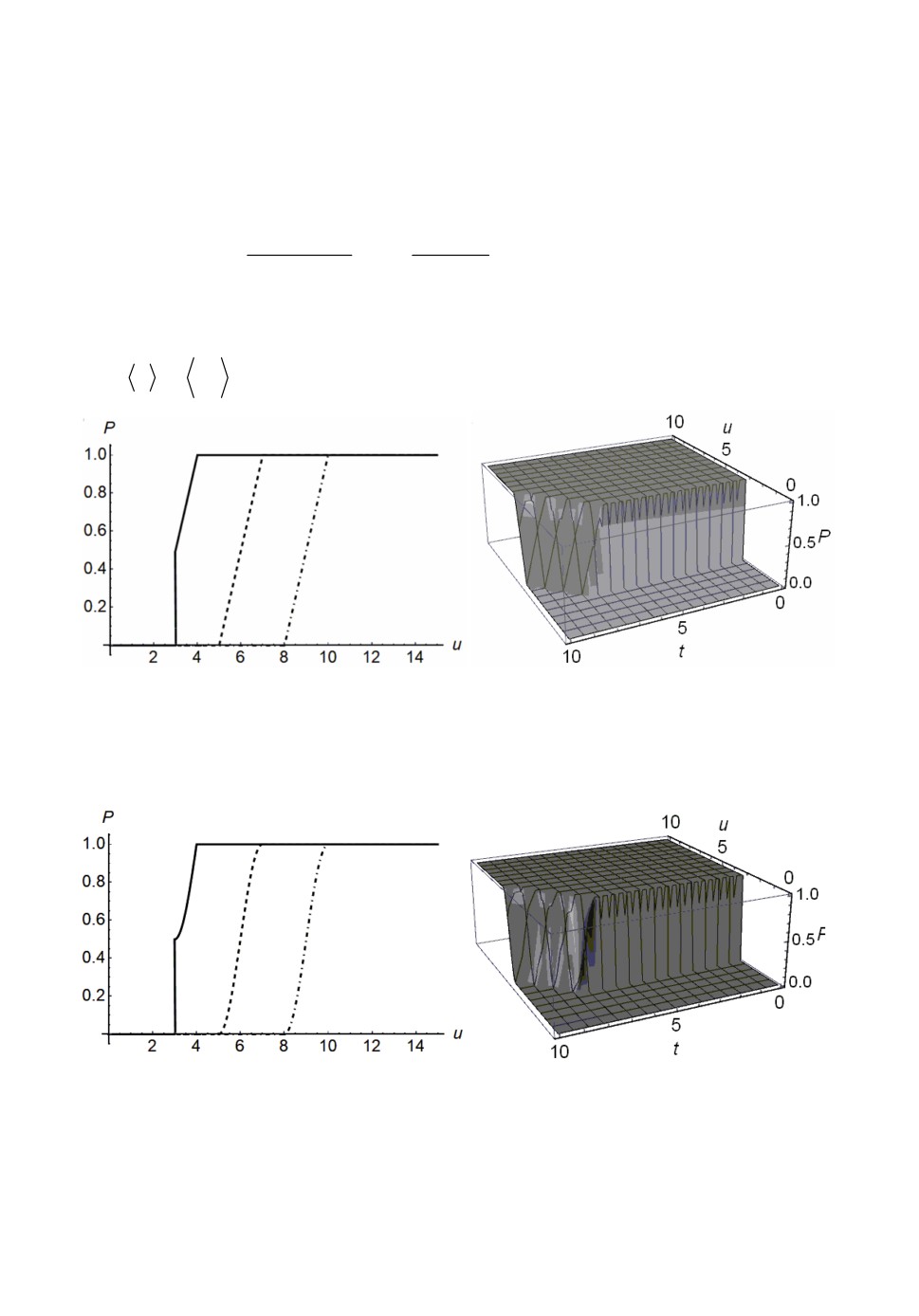
чины. Динамика изменения функции распределения P(u) = P{u(t) <u}
для
монотонно возрастающего входа x(t) t 1 в зависимости от u приведена
на рис.4, правая граница является равномерно распределенной случайной
Гистерезисные преобразователи со случайными параметрами
123
величиной, значения параметров равны h/2=5, x
=7,
u
= 3, t =8 (сплош-
0
ная кривая), t = 11 (пунктирная кривая), t = 14 (штрих-пунктирная кривая).
Рис.5 иллюстрирует эволюцию функции распределения в ситуации,
когда правая граница является случайной величиной с плотностью распре-
xh/2
деления
(x)=
sin
) , значения пара-
при (h/2,x
2(x h/2)
x h
/2
метров равны h / 2 = 5, x
=7,
u
=3.
0
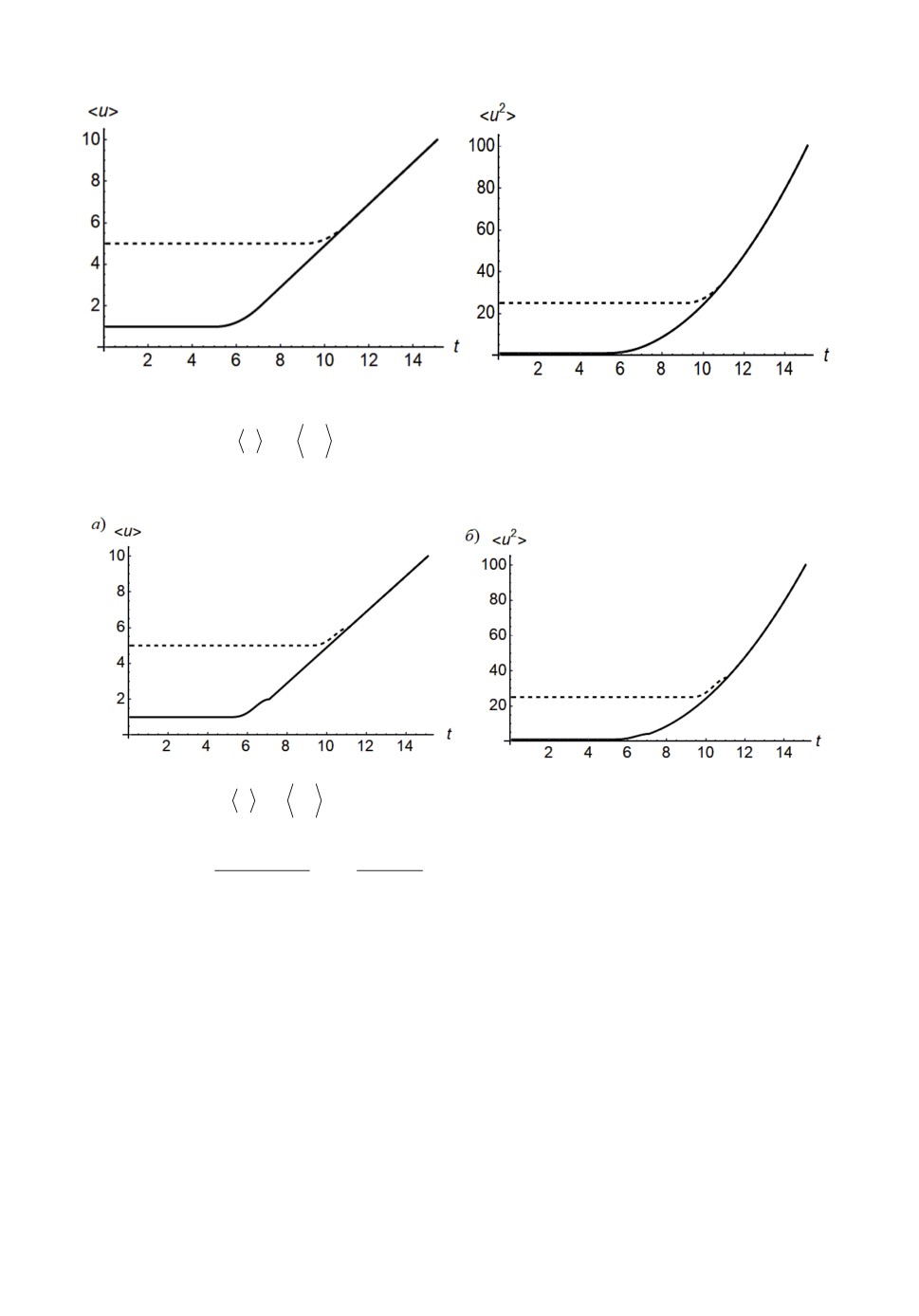
Результаты численного эксперимента определения моментных функ-
2
ций
u
и
u
приведены на рис.6, 7.
а)
б)
Рис.4. а) Динамика эволюции функции распределения P(u) = P{u(t) < u} для входа
x(t) t 1, сплошная линия соответствует моменту времени t = 8, пунктирная -
t =11, штрих-пунктирная - t =14, б) Функция распределения
P u)=
P u(t)<
}
u
t
а)
б)
Рис.5. а) Функция распределения P(u) = P{u(t) < u} для входа x(t) t 1, t =8 (сплошная
кривая), t =11 (пунктирная кривая), t =14 (штрих-пунктирная кривая), б) Функ-
ция распределения
P u)=
P u(t)<
}
u
t
124
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
а)
б)
2
Рис.6. Моменты
u
и
u
для входа x(t) t 1 при
u
=1 и
u
= 3, правая граница
0
0
является равномерно распределенной случайной величиной, значения парамет-
ров равны h / 2 = 5 , x
=7
2
Рис.7. Моменты
u
и
u
для входа x(t) t 1 при
u
=1 и
u
=3,
0
0
правая граница является случайной величиной с плотностью распределения
xh/2
(x) =
sin(
)
при x (h/2, x ) ,
2(
x h
/ 2)
x h
/2
значения параметров равны h/2=5 , x
=7
3. Заключение
В работе предложен новый класс моделей гистерезисных преобразова-
телей, обобщающий классическое определение люфта на случай, когда оп-
ределяющие его кривые зависят от случайного параметра. Такие преобразо-
ватели естественным образом возникают при изучении моделей динамичес-
ких систем, содержащих люфты, параметры которых невозможно иденти-
фицировать без разрушающего контроля. Предложенный математический
аппарат позволяет определить выходы соответствующих преобразователей
как случайный процесс.
Гистерезисные преобразователи со случайными параметрами
125
Доказана корректность определения введенных преобразователей в
терминах специальной предельной конструкции, позволяющей определить
выход на произвольном непрерывном входе. Приведены явные выражения
для первой и второй моментных функций выхода. Полученные выражения
иллюстрируются результатами численного моделирования.
СПИСОК ЛИТЕРАТУРЫ
1. М.А. Красносельский, А.В. Покровский. Системы с гистерезисом. - М.: Наука.
Главная редакция физико-математической литературы, 1983, 272 с.;
M.A. Krasnosel'skii, A.V. Pokrovskii. Systems with hysteresis. Springer-Verlag, Berlin,
Heidelberg, 1989, 410 p.
2. I.D. Mayergoyz, G. Bertotti (eds.) The Science of Hysteresis (3-volume set), 2005, 2097 p.
3. F. Ikhouane, J. Rodellar. Systems with Hysteresis Analysis, Identification and Control
Using the Bouc-Wen Model. Chichester: John Wiley & Sons, 2007, 222p.
4. W. Lacarbonara, D. Bernardini, F. Vestroni. Nonlinear thermomechanical oscillations of
shape-memory devices // International Journal of Solids and Structures, 2004, v.41 (5-6),
p.1209-1234.
5. L.A. Rios, D. Rachinskii, R. Cross. A model of hysteresis arising from social interaction
within a firm // Journal of Physics: Conference Series, 811(1), p.012011.
6. A. Fahsi, M. Belhaq, F. Lakrad. Suppression of hysteresis in a forced van der Pol-Duffing
oscillator / Communications in Nonlinear Sci. & Numer. Simul., 2009, 14 (4), 1609-1616.
7. R. Cross, H. McNamara, A. Pokrovskii, D. Rachinskii. A new paradigm for modelling hys-
teresis in macroeconomic flows // Physica B: Condensed Matter, 2008, v.403, Iss.2-3,
p.231-236.
8. W. Lacarbonara, F. Vestroni. Nonclassical Responses of Oscillators with Hysteresis //
Nonlinear Dynamics, 2003, v.32, p.235-258.
9. M.A. Janaideh, R. Naldi, L. Marconi, P. Krejčí. A hybrid model for the play hysteresis
operator // Physica B 430, 2013, p.95-98.
10. B. Carboni, W. Lacarbonara. Nonlinear dynamic characterization of a new hysteretic
device: experiments and computations // Nonlinear Dynamics, 2016, 83, p.23-39.
11. M.E. Semenov, A.M. Solovyov, M.A. Popov, P.A. Meleshenko. Coupled inverted pendu-
lums: stabilization problem // Archive of Applied Mechanics, 2018, v.88, p.517-524.
12. F. Ikhouane, J. Rodellar. On the Hysteretic Bouc-Wen Model // Nonlinear Dynamics,
2005, v.42, p.63-78.
13. W.D. Iwan. A distributed-element model for hysteresis and its steady-state dynamic res-
ponse // Journal of Applied Mechanics, Transactions ASME, 1966, 33(4), 1966, p.893-900.
14. M.F.M. Naser, F. Ikhouane. Consistency of the Duhem Model with Hysteresis.
Mathematical Problems in Engineering, 2013. Article ID 586130, 16 p.
15. C.-J. Lin, P.-T. Lin. Tracking control of a biaxial piezo-actuated positioning stage using
generalized Duhem model // Comp. and Math. with Applications, 2012, v.64, p.766-787.
16. М.А. Красносельский, Б.М. Даринский, И.В. Емелин, П.П. Забрейко, Е.А. Лифшиц,
А.В. Покровский. Оператор-гистерант // Докл. АН СССР, 1970, 190:1, c.34-37.;
126
С.В. Борзунов, М.Е. Семенов, Н.И. Сельвесюк, П.А. Мелешенко
M.A. Krasnosel'skii, V.M. Darinskii, I.V. Emelin, P.P. Zabreiko, E.A. Lifshitz, A.V. Pok-
rovskii. Operator-hysteron // Dokl. AN SSSR, 1970, 190, p.29-33.
17. M.E. Semenov, D.V. Shevlyakova, P.A. Meleshenko. Inverted pendulum under hysteretic
control: stability zones and periodic solutions // Nonlinear Dynamics, 2014, v.75, N1-2.
p.247-256.
18. M.E. Semenov, P.A. Meleshenko, A.M. Solovyov, A.M. Semenov. Hysteretic nonlinearity in
inverted pendulum problem. В сборнике: Springer Proceedings in Physics Сер. "Structu-
ral Nonlinear Dynamics and Diagnosis Selected papers from CSNDD 2012 and CSNDD
2014", 2015, p.463-506.
19. M. Belhaq, A. Bichri, J. Der Hogapian, J. Mahfoud. Effect of electromagnetic actuations
on the dynamics of a harmonically excited cantilever beam. International Journal of Non-
Linear Mechanics, Elsevier, 2011, 10.1016/j.ijnonlinmec.2011.03.001
20. W. Lacarbonara, M. Talò, B. Carboni, G. Lanzara. Tailoring of Hysteresis Across Diffe-
rent Material Scales. In Collection: M. Belhaq (ed.), Recent Trends in Applied Nonlinear
Mechanics and Physics, Springer Proceedings in Physics 199, p.227-250.
21. D. Rachinskii. Realization of Arbitrary Hysteresis by a Low-dimensional Gradient Flow,
2015, arXiv:1506.03842v1 [math.DS].
22. I.D. Mayergoyz. Mathematical models of hysteresis // Physical Review Letters, 1986,
v.56(15), p.1518-1521.
23. I.D. Mayergoyz, M. Dimian. Stochastic aspects of hysteresis // Journal of Physics:
Conference Series, 2005, v.22, p.139-147.
24. R. Bouc. Forced vibration of mechanical systems with hysteresis. Proceedings of the
Fourth Conference on Nonlinear Oscillation. Prague, Czechoslovakia, 1967, p. 315.
25. R. Bouc. Modèle mathématique d'hystérésis: application aux systèmes à un degrè de
liberté. Acustica [in French], 1971, v.24, p.16-25.
26. Y.K. Wen. Method for random vibration of hysteretic systems. Journal of Engineering
Mechanics. American Society of Civil Engineers, 1976, 102 (2), p.249-263.
27. A.E. Charalampakis, V.K. Koumousis. A Bouc-Wen model compatible with plasticity
postulates. Journal of Sound and Vibration, 2009, v.322, p.954-968.
28. A.K. Kottaria, A.E. Charalampakis, V.K. Koumousi. A consistent degrading Bouc-Wen
model. Engineering Structures, 2014, v.60, p.235-240.
29. S.A. Belbas. New hysteresis operators with applications to counterterrorism // Applied
Mathematics and Computation, 2005, v.170, p.425-439.
30. A.E. Charalampakis, V.K. Koumousis. Identification of Bouc-Wen hysteretic systems by a
hybrid evolutionary algorithm // J. of Sound and Vibration, 2008, 314 (3-5), p.571-585.
31. А.Н. Ширяев. Вероятность-1. - М.: МЦНМО, 2007. 552 с.;
A.N. Shiryaev. Probability-1. Springer, 2016, 486 p.
32. В.А. Зорич. Математический анализ. Часть 1. - М.: МЦНМО, 2017, 576 с.;
V.A. Zorich. Mathematical Analysis I. Berlin, Heidelberg, Springer, 2015, 616 p.
Поступила в редакцию 20.12.2018
После доработки 20.12.2018
Принята к публикации 11.03.2019