МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

2019 год, том 31, номер 8, стр. 101-119



ГРАФЫ ЗАДАЧ ДЛЯ РЕПЛИКАТОРНЫХ УРАВНЕНИЙ

И "ТРАГЕДИЯ ИСЧЕРПАНИЯ ОБЩЕГО РЕСУРСА"

2019 г. Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

Российский университет транспорта (МИИТ)

navolosova@yandex.ru, alya01@yandex.ru, konstantinvolosov@yandex.ru,

k-gdsu@mail.ru

DOI: 10.1134/S0234087919080069

Появились активные пользователи, которым необходимо решение обратных задач

на графе в условиях неопределённости для моделирования процессов в экономиче-

ской сфере. Такие задачи ранее математиками не рассматривались. В данной рабо-

те найдена аналогия с математическими моделями, которые описываются реплика-

торной системой (РС) уравнений, связанной с темой «трагедии исчерпания общего

ресурса» (ТИОР). Построены точные и асимптотические решения в случае «жёст-

ких» РС. Обнаружены эффекты «apriori» вымирающего клона и эффект погранич-

ного слоя, которые наблюдаются при численных расчётах. Проведена аналогия с

некоторыми похожими по свойствам объектами, реально существующими в эко-

номике. Описан эффект существования «теневых, невидимых» сверхпотребителей.

Ключевые слова: исчерпание общего ресурса, репликаторные системы, реальные

структуры в экономике.

GRAPHS FOR THE REPLICATOR EQUATIONS

AND "TRAGEDY OF COMMON RESOURCE"

N.K. Volosova, A.K. Volosova, K.A. Volosov, S.P. Vakulenko

Russian University of Transport

Appeared active users, which require the solution of inverse problems on the graph with

uncertainty for modeling processes in the economic sphere. Such tasks earlier mathema-

ticians were not considered. There was provided a connection replicator systems of equa-

tions (RS) with the stated theme. The exact and asymptotic solutions were developed in

the case of a «hard» RS equations. The effect of «a priori» dying clone and boundary

layer for small values of time were discovered. There was the analogy with similar struc-

tures in the economy the effect of the existence of "shadow invisible" super-consumers

described was.

Key words: tragedy of common resource, the replicator systems of equations, real struc-

tures in economy.

102

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

1. Введение

Примеры модельных систем и их значение в методологии науки опи-

саны, например, в [1, гл.1]. Роль маломерных моделей описана также в [2,

гл.3]. К ним относятся и ниже рассмотренные примеры. Первоначально в

[3] была предложена модель гиперциклов. В гиперцикле более примитив-

ные цепочки РНК кооперируются и привлекают примитивные полипептид-

ные ферменты. Возникает синергетический эффект, и количество информа-

ции передаваемое следующим поколениям, увеличивается. Как следствие,

увеличивается их выживаемость. Таким образом, в [3] моделируется гипо-

тетическая стадия эволюции, которая могла следовать за квазивидами. Реп-

ликаторная система (РС) уравнений давно заняла своё базисное место в ма-

тематической теории отбора и эволюции РНК молекул на Земле.

Этой теории посвящены, например, работы [3-8]. В большом потоке

публикаций в «мире РНК» с разных позиций предпринимаются попытки

объяснить условия и причины возникновения жизни и объяснить способ-

ность молекул хранить информацию и катализировать реакции, ведущие к

воспроизводству и их усложнению. В данной работе обсуждается другой

аспект этой темы.

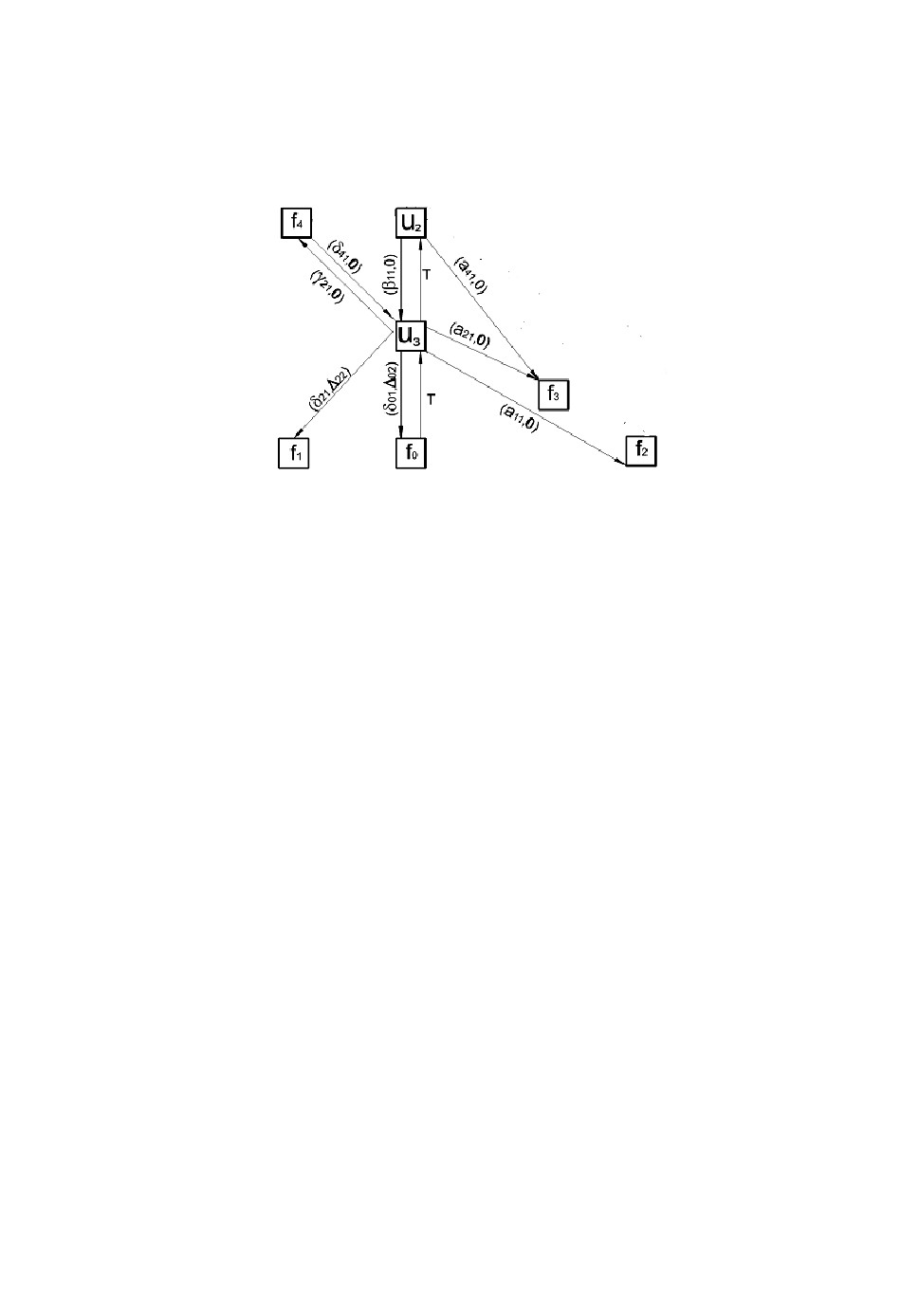
Постановка обратной задачи на графе в условиях неопределённос-

ти. Пусть дана часть ориентированного графа, а именно известны только

вершины

и некоторые компоненты вектора весов на

дугах, заказчики также дают некоторую априорную информацию о задаче.

Задача состоит в том, чтобы, во-первых, восстановить гипотетический

граф, не противоречащий экономическому смыслу задачи, а, во-вторых,

сделать оценку недостающих значений весов (потоков соответствующих

ситуации на рынке в некоторый промежуток времени), см. рис.1. Мы свя-

зываем эту задачу с темой «трагедии исчерпания общего ресурса» (ТИОР).

Задача не имеет единственного решения, и один из вариантов, который

вполне удовлетворил заказчика, описан в разд. 4.

Сначала мы рассмотрим, как решалась проблема ТИОР¹ в природе в

некоторых случаях. Модели в экономике похожи на биологические, но они

более изощрённые, так как строятся человеком.

Замечание 1. В случае с молекулами РНК нет информации об их попу-

ляциях, количестве таких различных популяций, о законе размножения,

скорости роста их количества и т.д., то есть того, что обычно известно о по-

¹ Мы беседовали со скептиками, однако выяснили, что они не пьют воду из водопровода,

избегают потребления пальмового масла и других факторов, приводящих к загрязнению

своих кровеносных сосудов и т.д.

Графы задач для репликаторных уравнений и ...

103

пуляциях в макромире. Поэтому и была предложена репликаторная модель

на основе динамических систем. Это моделирование процессов, с помощью

которых решалась в прошлом в природе проблема ТИОР.

Рис.1. Исходные данные для решения обратной задачи на графе

в условиях неопределённости.

Символьный результат часто позволяет глубоко вникнуть в ход реше-

ния и выявить внутренние связи в задаче, которые при нагромождении чи-

сел не очевидны. Раньше исследователи большинство своих вычислений

проводили в символьном виде и только в конце выполняли подстановку чи-

сел. После распространения компьютеров оказалось, что наиболее просто

можно использовать численные методы, нежели символьные вычисления.

Использование символьных вычислений требует от исследователей более

глубоких знаний математики [8]. Молодые исследователи целиком положи-

лись на численные расчёты, а символьные вычисления просто исчезли из

списка инструментов. На самом деле авторы данной работы считают, что

надо комбинировать оба подхода.

Распространено заблуждение о том, что РС не поддаются аналитиче-

скому анализу. В работах по этой теме сразу используются численные ме-

тоды [3-7]. Аналитическое исследование простых репликаторных моделей,

точные и асимптотические решения, приведённые ниже, позволяют выявить

общие важные подробности и свойства моделей, а именно: эта возможность

связана с введением малого параметра при старшей производной и, следо-

вательно, с «жёсткими» системами.

Одна молекула РНК выжить не может. Ей нужна энергия и обмен ве-

ществом с внешней средой. После взаимодействия с другими молекулами у

неё возникает новое качество на макроскопическом уровне [1]. Возникает

синергетическое самозарождение нового смысла, рождение новых качеств

на макроскопическом уровне. Когда «исчерпывается общий ресурс» для од-

104

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

ной комбинации взаимодействия с партнерами, может выжить другая ком-

бинация взаимодействия. Как следствие, в природе наблюдается большое

разнообразие различных РНК и множество биологических видов в макро-

мире.

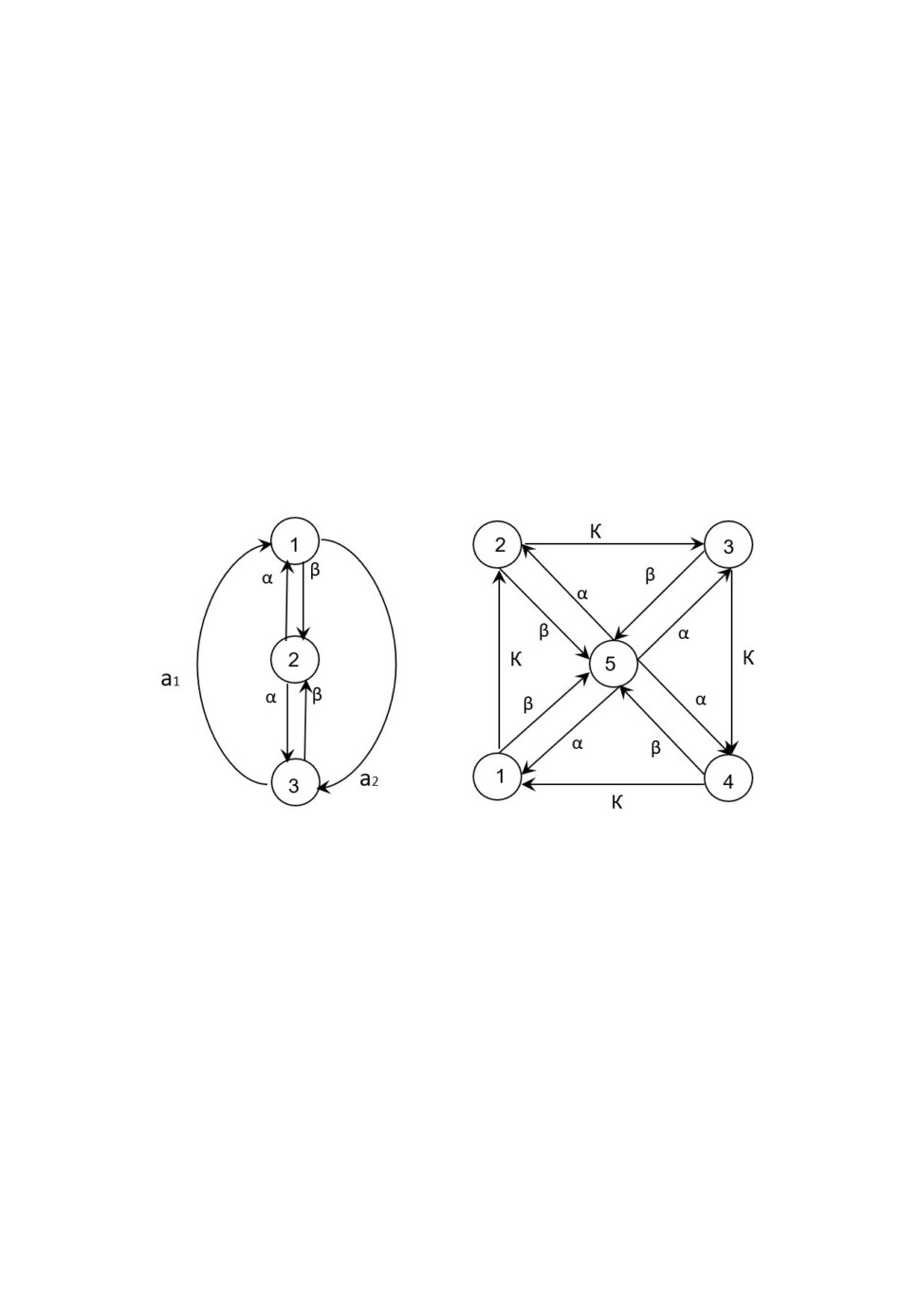
2. Репликаторные модели (РС)

Общие постановки задачи для РС даны, например, в [47]. Для наших

целей, чтобы попутно объяснить метод, в данной работе рассмотрим снача-

ла наиболее простую систему, состоящую из трех молекул. Соответствую-

щий ориентированный граф приведен на рис.2. Направление стрелок на ду-

ге означает знак слагаемого в правой части динамической системы. Знак

«плюс» соответствует «источнику», а знак «минус» соответствует «дисси-

пации» («стоку»). Везде ниже предположим, что все функции являются не-

прерывно дифференцируемыми необходимое число раз в своих областях

определения.

Рис.2. Графы для задачи «муравейник 3» и «муравейник 5».

Замечание 2. Совершенно очевидно, что подход в нашей работе не

вполне удовлетворителен. Но и без учёта фактора случайности простые мо-

дели позволяют выявить важные свойства модели, см. [1].

С нарастанием числа переменных связи и взаимодействие вершин в

графе становятся всё сложнее, и тогда ничего не остается кроме использо-

вания асимптотических и численных методов. В данной работе найдены от-

веты на ряд вопросов, освещенных ниже.

В РС все зависит от распределения истоков и стоков (диссипации) в

правой части динамической системы. В [3-6] и в цитируемых там работах

по этой теме рассматривались разнообразные варианты. Мы коснемся толь-

ко двух типов таких моделей.

В этом разделе основное внимание уделим модели, называемой "мура-

Графы задач для репликаторных уравнений и ...

105

вейник". Молекулы номер 1 и номер 2 (обмениваются между собой) катали-

зируют друг друга и взаимодействуют с молекулой номер 3 (левая схема на

рис.2). В цитируемых работах константы



i1, 2, и







0, в

правой части динамической системы с этими коэффициентами записывают-

ся источники. Функция

f  f(u

)  0 называется в этой теории функцией

фитнеса и описывает диссипацию в условиях неопределенностей, существо-

вавших в далёком прошлом. Соотношения на симплексе являются результа-

том процедуры обезразмеривания задачи на суммарную максимальную кон-

центрацию молекул в единице объема

u t)

1,

ut)





(1)

i1

u t)





1, ..., N,





Для модели «муравейник 3» N  3, а для модели «муравейник 5» N  5.

Уточним, что функция фитнеса

f (u

) имеет смысл средней приспо-

собляемости и именно в ней собрана вся диссипация (сток) в системе. Она

определяется из второго соотношения в (1), которое является следствием

первого равенства в (1). Такой выбор этой функции в значительной мере оп-

ределяет и свойства всей РС. Роль молекулы номер N в такой модели по-

добна роли матки в муравейнике или пчелином улье в макромире. Структу-

ра муравейника, например, повторяет на следующей, более высокой, стадии

развития с новым смыслом (информацией) модель РС. Молекула, концен-

трация которой обозначена через u₃, ведет себя «взвешено», получает от ис-

точника и отдает энергию и вещество, что моделируется с помощью дисси-

пации (стока) f. Молекулы номер 1 и 2 в цитируемых работах называют

«альтруистами». Их «жизнь и смерть» полностью зависит от соотношения

источников и стоков. Начальные условия для РС также удовлетворяют ус-

ловиям (1):

(0)





1,...,N,





l1

Первое обыкновенное дифференциальное уравнение (ОДУ, N=3) РС имеет

вид

u(t)  u

(t) (a

(t)  u

(t)  f (u

(t), u

(t))).

(2)

В (2) подробно записаны все аргументы, однако далее, для краткости, будем

их опускать. Объясним здесь более подробно, как строится первое уравне-

ние. Для молекулы номер 1 и с точки зрения

два первых слагаемых

106

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

(t)  u

(t) в уравнении (2) являются для

источниками (см. неравен-

ства в (1)). Аналогично записываются второе ОДУ и третье ОД уравнение

РС, они имеют вид

u (t)  u

(t) (a

(t)  u

(t)  f (u

)) ,

(3)

u (t)  u

(t)



(u

u

) f (u

)



(4)

Замечание 3. Вторым, распространенным в цитируемой литературе,

предельным случаем является модель, которую называют кратко - «пара-

зит». Для демонстрации этой модели можно использовать тот же граф на

рис.2, если положить вес дуг   0 . Здесь молекулу номер 3 в литературе

принято называть «эгоистом» (сверхпотребитель) потому, что она ничего не

отдает другими и забирает все ресурсы себе. В этой модели «альтруисты»

гибнут через некоторое время.

Вычислим функцию фитнеса f >0. Подставляем во второе равенство (1)

выражения производных функций

1,2,3

u

i

, из уравнений (2)(4) и полу-

чим

, u

)



(

)u

u





()u



(5)

1u

u

Такой самосогласованный выбор функции диссипации со всеми уравнения-

ми РС является важным и определяет её свойства и существование точных

и асимптотических решений.

Проведем анализ задачи (1)(5) с точки зрения, отличающейся от из-

ложенной в [3-8].

Вычислим неподвижную точку. Положим равными нулю производные

1,2,3

u

l

, в уравнениях (2)(4). Решение этой системы и следующие

из него неравенства (ограничения на параметры) обозначим







/



a

( a

)

/







()  a

(



(6)



/(a





/(a



)



или

a

/(a

a

),

0a

/(a

a

Неравенства в (6) следуют из требования



в (1). Если

a

/(a

a

то

limu t)



, и в данной задаче



(



) называем «apriori» выми-

t

рающим клоном.

Графы задач для репликаторных уравнений и ...

107

Замечание 4. Предполагаем, что и в далёком прошлом происходила

смена сезонов, были приливы и отливы, шторма, извержения вулканов и

т.п. То есть благоприятные условия существовали конечный период време-

ни T . Когда общий ресурс исчерпан, происходит мутация, эволюция делает

следующий шаг. Существует возможность введения в модели малого пара-

метра 0    1,   1/, если   1. Отметим, что для изучения нелинейного

случая используются методы [9]. Асимптотические решения уравнений с

малым параметром при старшей производной изучались в [10, 11].

Рассмотренная задача типа «муравейник» (1)(5) имеет следующее

свойство РС, а именно она имеет точное решение, но которое описывает

главный член асимптотического решения. Главный член не зависит от па-

раметров задачи , . Докажем это в следующих ниже теоремах.

Для краткости текста, чтобы не писать фактически одни и те же фор-

мулы два раза, в теореме 1 попутно объясним алгоритм построения точных

и далее асимптотических решений.

Теорема 1. Пусть дана задача Коши для РС (1)-(5). Тогда задача (1)-

(5) имеет точное решение, которое не зависит от параметров задачи

,

. Эта функция в то же время описывает главный член асимптотиче-

ского решения задачи (1)-(5) по параметру 0    1,   1/  .

Точное решение задачи (1)-(5) ищем в виде

1

u t)

Y t)/

Y t),

u t)



Y t)/(a

a

(7)

u t)





u t)



u t).

Константа

определяется начальными условиями и параметрами задачи.

Функция Y (t) является решением нелинейного ОДУ (нелинейное об-

общение уравнения Абеля первого рода) второго порядка:

Y t)/



Y t)/





Y t)



Y t)







Y t)



Y t)







Y t)



 (a

)

(

) 





2())





(



)





)



()



)/(Dn

)



Y t)





(2

1)







)a

(

a

2

)



/(Dn





(8)

Dn   Y(a C  a Y

Замена Y(t)P Y(t),

Y t)



даёт нелинейное ОДУ Риккати с коэффици-

ентами, которые зависят от q

108

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

P q)

F q)

P q)

F q)

P q)





F q)

 (a

)

() 





2())





)



)

(

)



)/(z

)

F q

(21)



(2)

(1



2

)







(9)





 

Асимптотическое решение уравнения (9) имеет вид

P(q) Y

(q)    (q) O(1/ 

 1/ 1.

(10)

При (q)  0 точное решение уравнения (9), не зависящее от параметров

,

, имеет вид

P q)

q

(

a

q

) a

(11)





Главный член асимптотического решения уравнения (8) в исходных пере-

менных

(t) при  1/1 следует из (10) и определяется из неявного

уравнения





Y t)



a



Y t)



) exp



(tC

)



(12)

В частности, при

a

явный вид главного члена асимптотического ре-

шения вычисляется и функция

(t) в (7) имеет вид

u t)



2exp





)





(



(13)





4 exp (

(

t C

))





При

a

/2 явный вид главного члена асимптотического решения (10)

выражаются через функции

2/a

1/3

2/3

Y t





(

)

(

)

/ (3

)









exp



(t C

)/2





(14)





27exp (a

(t C

)).

Функция для поправки в (10) (q)  1/W (q) приводит к линейному ОДУ

первого порядка

Графы задач для репликаторных уравнений и ...

109

W (q)G(q)W q)

G q)

a₂

G q)

(a



)

G q)



(a

)

(1)



)(a

1)a

)q



(15)









(2a



 



(

2(1))

(a



)

/



q

a

Решение уравнения первого порядка (15) и интеграл

(q)  exp(G(q)dq),

как известно, имеют вид

W q)

С

exp





G q)dq





I q)

I q)G q)dq,



I q) exp(

(3

)/a

)Arcth

(

2a

)

a

))/(

)



(16)



1 2



1

)/(2a

)

q



(2a



)



)

Доказательство. В [12] введен термин «скрытая ключевая» перемен-

ная, который мы можем употребить и в данном случае. А именно, можно

все функции выразить через одну. Но есть выбор. Можно получить одно

уравнение на одну из функций

(t) или

(t). Выберем в качестве «клю-

чевой» переменной функцию

(t) .

Поделив уравнение (3) на функцию

(t), а уравнение (2)  на функ-

цию

(t) и вычитая полученные соотношения, получим

(t)  a

(t)  u(t) / u

(t) u (t) / u

(t)  0,

(17)

(t) Y(t) /Y(t).

(18)

Интегрируя это соотношение, получим выражение функции

(t) через

(t), см. (7). Анализ случая



приводит к равенству

(t)  u

(t) и к

противоречию. Поэтому на этом случае останавливаться не будем.

Подставив (7) и (5) в (4) и в (3), исключив

(t) 1u

(t) u

(t), полу-

чим не два, а одно и то же «жёсткое» нелинейное интегро-дифференциаль-

ное уравнение (ИДУ) относительно функции

(t) с малым параметром

при старшей производной. Оно громоздкое, и его привести в статье нет воз-

можности.

Однако после замены

(t) Y(t) /Y(t) ИДУ упрощается и получается

нелинейное обыкновенное дифференциальное уравнение (ОДУ) второго по-

рядка (8). Далее сделаем замену переменных Y(t)  P(Y (t)), Y (t)  q и по-

110

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

лучим нелинейное ОДУ Риккати с коэффициентами, которые зависят от

функции Y (t)  q [13]. Точное решение уравнения (9) имеет вид (12).

Далее делаем обратные замены, следующие из (9), (18). Из (11) полу-

чим нелинейное ОДУ первого порядка

Yt)

Y t)

a

(

Y t))

(a

a Y(t))



(19)



/



Это уравнение интегрируется точно. Функция Y (t ) определяется из неявно-

го уравнения

ln(

Y t))(1/

) ln

a

(

Y t))

tC

(20)





Отсюда следует (12). Заметим, что при некоторых очевидных соотношениях

междуa_i из неявного вида решения (12) следуют явные решения. Приведе-

ны конкретные примеры (13), (14). Если точное решение не удается вычис-

лить из-за нелинейности и большого числа переменных в модели, то проще

построить асимптотическое решение.

После вычисления главного члена асимптотического решения, не зави-

сящего от параметров ,  , построим уравнение на поправку (q) (10). По

этой поправке вычисляется функция (10) и, следовательно, сначала функ-

цию

в (7) с поправкой, а потом и остальные функции в (7). Решение ли-

нейного уравнения (15) полностью здесь не приводим в силу его очевиднос-

ти  по формулам (16).

Отметим, что аналогично изложенному, можно построить асимптоти-

ческое решение по параметру   1/ , если   1. Теорема 1 доказана.

Отметим, что числитель в (6) для концентрации третьего вида обраща-

ется в нуль при некотором соотношении параметров. То есть этот вид мо-

жет исчезнуть, выродиться.

Замечание 5. Таким образом, выявлены эффекты: главный член асим-

птотического разложения вычисляется точно; при введении малого пара-

метра   1/   1 или   1/   1 при малых значениях t формируется по-

граничный слой; описан эффект в РС моделях, который назовём «apriori»

вырождающимся элементом.

Кратко опишем модель «муравейник 5», следуя цитируемой литерату-

ре. На правой фигуре 5 показан граф, соответствующий РС этой модели.

Задача рассматривается на симплексе (1), где N=5. В этой модели сде-

лано некоторое упрощение по сравнению с моделью «муравейник 3», а

именно предположена равной интенсивность источников

1,...,4

k

i

см. веса на дугах графа на правом рис.2.

Графы задач для репликаторных уравнений и ...

111

Исходная РС уравнений имеет вид

u (t)  u

(t) (k u

(t)  u

(t)  f ) ,

(21)

u (t)  u

(t) (k u

(t)  u

(t)  f ) ,

(22)

u (t)  u

(t) (k u

(t)  u

(t)  f ) ,

(23)

u (t)  u

(t) (k u

(t)  u

(t)  f ) ,

(24)

u t)



u t)(

u t)



(25)



i1

Функция фитнеса следует после подстановки производных (21)-(25) во вто-

рое соотношение (1)







ku



)



()

u t)

u t).

(26)



i i1











1

Начальные условия также удовлетворяют условиям (1). Справедлива

Теорема 2. Пусть дана РС (1), (21)-(26). Тогда неподвижная точка

описывается соотношениями

u t)



/(4()

k),

1,...,4,

(27)





)/(4(

)



и справедливы соотношения

(t)  S(t) / S(t),

(t)  H (t) / H(t),

(28)

(t)  u

exp (ku

(t)dt) exp(k u

(29)





u t)



u t)/(ku

)

  t)/(ku

u t)1

(30)







i1



Комментарии к доказательству

Соотношения в неподвижной точке (27) получены тривиально. В дан-

ной задаче

называем «apriori» вымирающим клоном. Делим уравнение

(21) на функцию u₁, а уравнение (22)  на функцию u₂ и вычитаем получен-

ные соотношения. Отсюда следует (30). Делим уравнение (23) на функцию

u₃, а уравнение (22)  на функцию

и вычитаем полученные соотношения

u (t) / u

(t)  k u

(t)  k u

(t)u /u

112

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

После интегрирования следует (29). Подставляем (26), (29), (30) в уравне-

ния (21) - (25) и получим пять ИДУ, четыре из которых одинаковые в силу

выбора вида функции (26). Их не приводим из-за громоздкости. Все выра-

жено через «скрытые ключевые» переменные

Выбираем вид этих

функций в виде (27). В итоге получим два нелинейных «жестких» ОДУ для

функций S (t) , H (t) . Можно построить асимптотическое решение по пара-

метру 0    1, если   1/   1. Здесь не приводим эти формулы, так как

они не дают ничего нового для понимания проблемы.

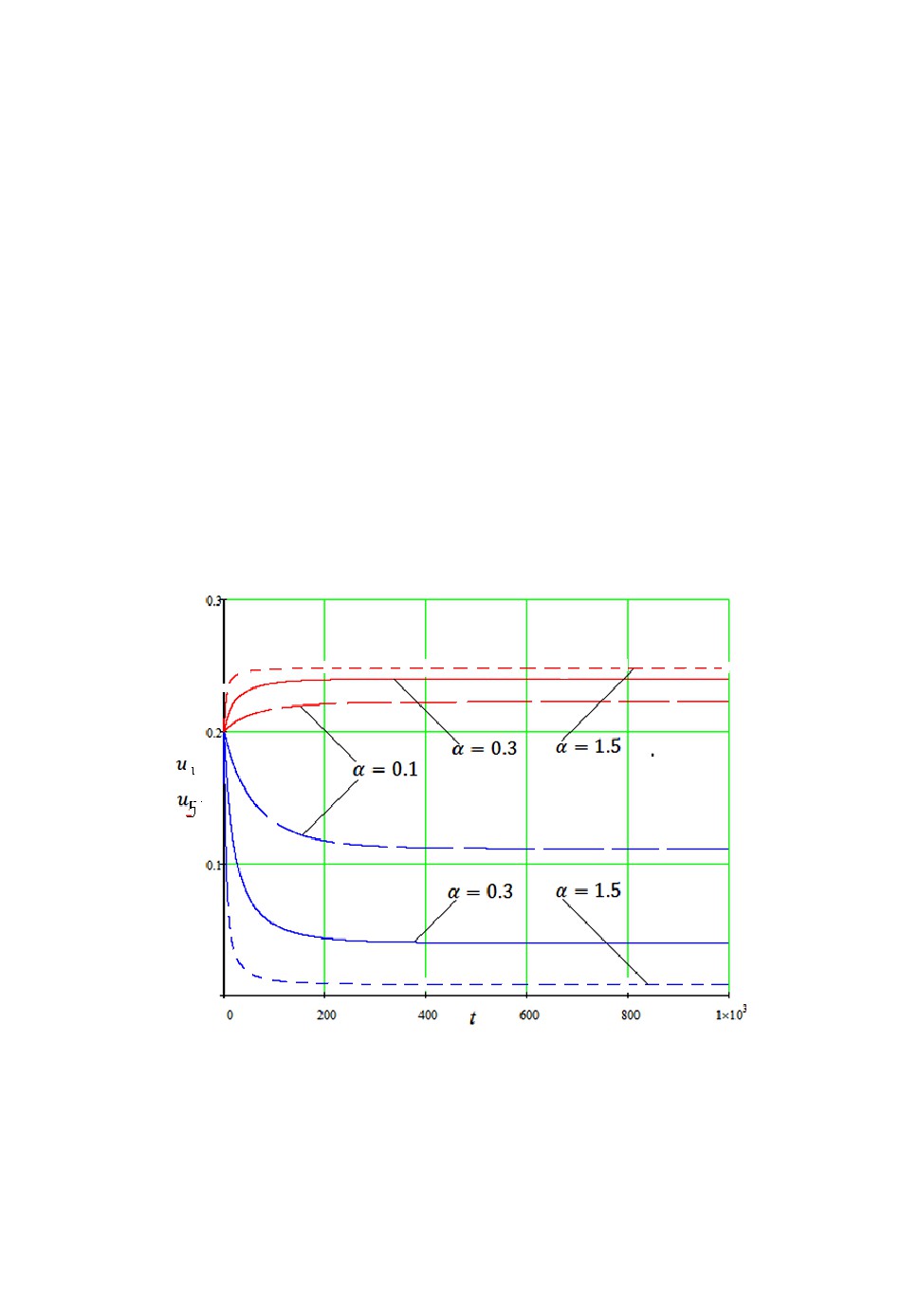
Эти результаты подтверждаются численными расчетами. На рис.3 по-

казано формирование пограничного слоя при =1/ >1. Аналогично асимп-

тотическое решение РС может быть получено при 4  k  1/   1 по мало-

му параметру 0   1.

Аналогичные результаты изложенным методом вычислены авторами

для модели «муравейник 4». С увеличением размерности РС идет усложне-

ние формул, в которые входят специальные функции, но остаётся возмож-

ность построения асимптотического решения.

Рис.3. Формирование пограничного слоя в задаче «муравейник 5».

3. Комментарии к статье [14]

В работах, перечисленных в [14], рассмотрены разные модели популя-

ций, элементы в которых обобщенно называют клонами. Будем также ис-

пользовать этот обобщающий термин. В [14] рассмотрена модель ресурс-

потребитель Кракауэра. В этой работе дан обзор и приведены результаты

Графы задач для репликаторных уравнений и ...

113

статей других авторов, которые рассматривают ряд примеров «исчерпания

общего ресурса». Приведем кратко список некоторых ситуаций в разных

областях деятельности человека: например, классический, давно известный

случай истощения скотом пастбищ на общинных землях (15 век, Англия,

политика «огораживания»), загрязнение окружающей среды свалками му-

сора, проблемы питьевой воды, истребление животных, рыбы и т.д. (эко-

цит), эволюция миксомицету (Distiostelium discoideum) [1], перенаселение

территорий людьми, проблема «трёх вокзалов» в Москве в контексте РЖД,

глобальное потепление, явления ядерной зимы и ядерной ночи [15], финан-

совые пирамиды, подпольные банкиры и многое другое. В ряде работ, ци-

тируемых в [14], их авторы приходят к выводу, что «трагедии исчерпания

общего ресурса» избежать не удастся. В качестве выхода из этой ситуации

предлагается создать такие системы самоуправления, которые не допускают

чрезмерного использования общих ресурсов. Предлагается регламентиро-

вать способы использования ресурса и установить наказание в случае нару-

шения установленных правил. Авторы [14] регулируют в правой части ди-

намической системы соотношения между источниками и стоками (диссипа-

цию), чтобы избежать коллапса системы, и они ввели понятия «альтруи-

стов» и «сверхпотребителей». Динамические системы исследуются, в част-

ности, методами [9].

Замечание 6. В выводах автор [14] делает приятные, оптимистичные

для читателя и своих работодателей выводы, что государство будет осуще-

ствлять поощрение «альтруистов» и наказывать «сверхпотребителей» нели-

нейно. То есть с ростом потребления ресурса должно расти и наказание

«сверхпотребителей». С точки зрения авторов данной работы, такие выводы

являются наивными, если иметь в виду, что в государстве именно «сверхпо-

требители» принимают законы и именно они осуществляют надзорные и

контролирующие функции в государстве (cм., например, статьи в [16]). Су-

ществует термин «эгоизм элит».

Мы не будем давать каких-либо оценок, чтобы не выходить из плоско-

сти «математического моделирования», но изложим описание модели ре-

ально существующих экономических структур в упрощённом виде допол-

нительных предположений, а выводы делать читателю. Описанная выше

модель РС наводит на аналогии со структурой связки фирм (клонов), зани-

мающихся торгово-закупочной деятельностью как самой простой для ана-

лиза дискретной модели. В экономических математических моделях среди

факторов не учитывают, с точки зрения авторов данной работы и [16, 17],

один из главных, а именно: алчность и жадность, заложенные в генотип

114

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

людей. Как ответить на вопрос: «возможно ли их обуздать и как учесть их в

математической модели»? Не понятны причины отсутствия попыток анали-

за таких моделей, хотя описанный ниже объект существует и известен спе-

циалистам в мире десятки лет. Отсутствие анализа таких моделей приводит

к возможности искажения статистических данных в разных целях, что и

происходит в действительности. Одна из точек зрения на «алчную эконо-

мику» изложена в [16, разд.2.4] и с другой позиции описана в данной рабо-

те. В.П. Маслов в [16, c.20] приводит цитату Д.И. Менделеева, сказанную

более ста лет назад: «Мне говорят, ведь вы химик, а не экономист, зачем же

вы входите не в своё дело? На это необходимо ответить тем, что истинного,

правильного решения экономических вопросов можно ждать впереди толь-

ко от приложения опытных приемов естествознания».

4. Клоны в экономике

Один из возможных вариантов локальных схем реализации алгоритма

для решения обратной задачи это решение на графе в условиях неопреде-

лённости. Наблюдение и сбор данных о реально существующих структурах

дает возможность провести беспристрастный математический анализ их

упрощённой математической модели на графе. «Хорошая теория сложных

систем должна представлять собой лишь хорошую «карикатуру» на эти

системы, утрирующую те свойства их, которые являются наиболее типич-

ными, и умышленно игнорирующую все остальные  несущественные

свойства» [2, c.71]. Будем называть составляющие их структуры, фирмы и

объединение физических лиц клонами, следуя [14]. Эти структуры облада-

ют свойствами, похожими на биологические объекты. Они размножаются и

усложняются, но более изощренно, чем в природе, так как строятся челове-

ком. Одиночный клон не может существовать в реальной экономической

«рыночной среде» из-за большой реальной финансовой нагрузки и челове-

ческого фактора, о котором указывалось выше. В данном случае не природа

и эволюция, а разум человека позволяет создать более эффективную струк-

туру клонов.

Рассмотрим только один цикл возможной деятельности структуры, по-

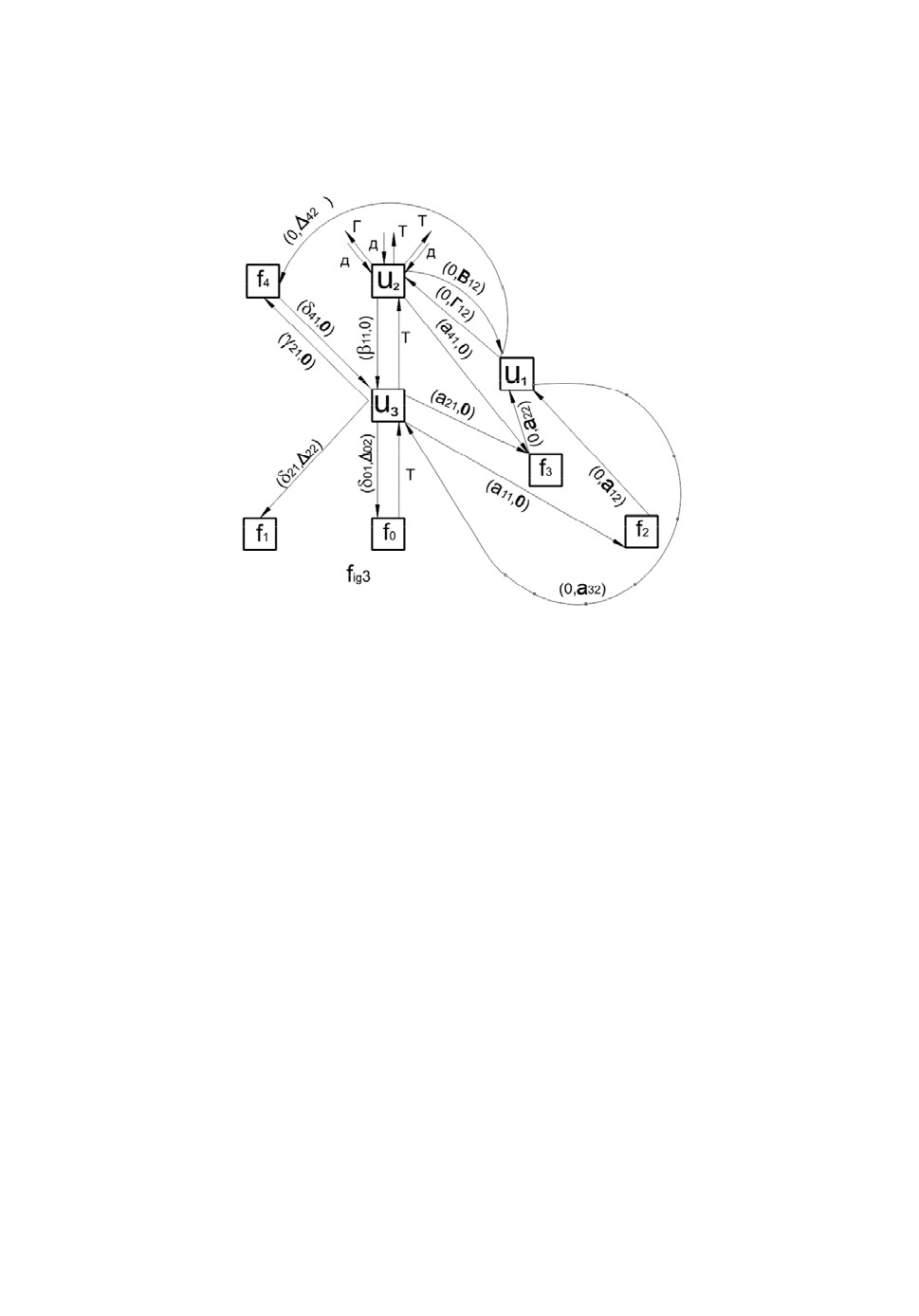
казанной в виде ориентированного графа на рис.4. (просьба сравнить с

рис.1). Цель функционирования описываемой структуры  уменьшение из-

держек и увеличение прибыли для

В теории поля в физике известна теория «хромодинамика» и определе-

ние «цветового заряда». Аналогично, давно известно, что деньги характери-

Графы задач для репликаторных уравнений и ...

115

зуются двумя цветами. На рис.4 веса на графе заданы векторами, которые

имеют две компоненты: «белую» и «черную» с соответствующим хорошо

известным, не только специалистам, смыслом.

Рис.4. Граф для задачи раздела 4.

«Сверхпотребитель» (одно или несколько физических лиц, объединён-

ных общими интересами, обозначим его через клон u₁), оставаясь в тени ор-

ганизует структуру, в простейшем случае две фирмы-клона

, u

, исполь-

зуя экономические и другие методы. Клон

осуществляет фактическое

руководство

, u

через назначенных директоров  ответственных лиц.

Клон

вообще представлен только одним директором. Таких клонов

в реальных условиях может быть несколько и они занимаются параллель-

ными проектами, но для простоты анализа взаимоотношений объектов в

модели рассмотрим только один клон. Ответственное перед

лицо дейст-

вует по доверенности от учредителя (который даже, иногда, может не знать

в деталях, что происходит). Клон

выполняет необходимые экономиче-

ские действия, но не выполняет и не собирается выполнять никаких требо-

ваний законодательства. Опишем функционирование структуры в один

цикл деятельности, который занимает время T.

Аналог пограничного слоя здесь тоже существует. Все участники

структуры заинтересованы материально в минимизации времени T. Дирек-

тор

и сотрудники

получает «разноцветные» премии из источников

( 0,Г₁₂ ), (0,a₃₂ ), а

получает маржу. Через веса на дугах графа обозначе-

116

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

ны потоки (0,Г₁₂ ), (0,a₃₂ )  затраты на регистрацию, создание и функцио-

нирование

Директор

заинтересован также в скорейшем прекращении деятель-

ности клона и уничтожении всех материальных фактов деятельности. После

окончания цикла ответственное лицо

просто прекращает все связи с уч-

редителем клона, меняет телефоны и адреса. Клон

после окончания цик-

ла превращается брошенную «фирму-однодневку».

Это поможет ему после окончания цикла затеряться среди других ана-

логичных клонов. По аналогии с введением в «макромире экономики» на-

блюдается большое количество брошенных клонов

, телефоны которых

не отвечают, а по зарегистрированному адресу никого нет, в том случае, ес-

ли существует сам адрес регистрации. Представители разных социальных

групп в своих интересах трактуют статистические данные о «фирмах-одно-

дневках». При переходе к следующими циклу при необходимости легко бу-

дет создан другой аналогичный клон.

Клон

представлен директором, бухгалтерами и рядом сотрудников.

В целом клон

выполняет все требования законодательства и осуществля-

ет все необходимые платежи во все инстанции государства и фонды и мо-

жет существовать достаточно долго. Для внешнего наблюдателя и структур

контроля наблюдаются только не зависимые друг от друга клоны

, u

которые относятся к малому и среднему бизнесу.

Таким образом «сверхпотребитель» маскируется под «альтруиста», но

он ведёт себя взвешено, что похоже на модель «муравейник», оставаясь не-

наблюдаемым со стороны. Это подробней описано в разделе 1.

Оборотные средства (

0) и некоторая часть расходов

на создание

41,

и функционирование

и закупку товара оформляется как кредит от ком-

мерческого банка

. Специалистам хорошо известно, что банки легко ме-

няют цвет денег (0,



) на противоположный за некоторый процент в дан-

ный конкретный момент времени в зависимости от экономической ситуа-

ции, по достигнутому соглашению на соответствующем уровне. Выполнено

очевидное неравенство





Сотрудники u₃ находят на восточных рынках оптового продавца f₀ поль-

зующегося спросом товара (т) и покупают его

(

,

) . При этом перечис-

ляют все необходимые платежи. Заранее планируется логистика, и u₃ за-

ключает договоры на подготовку договоров с f₃ и f₂ о покупке товара у f₀,

продаже всей партии на реализацию u₂ с небольшой наценкой, и договоры

об аренде складов, охране, ж.д. и автотранспорта, погрузке и разгрузке и т.д.

Графы задач для репликаторных уравнений и ...

117

Для простоты модели в f₂ объединены все обслуживающие услуги, та-

кие как услуги аренды складов, уборка территорий и офисов, подготовка

помещений для проведения встреч и переговоров, обучение персонала. В f₂

также объединим услуги по перевозке с помощью РЖД и перевозке авто-

транспортом и легковым транспортом с водителем и т.д.

Услуги по составлению документов, договоров, актов, нотариальные

услуги и т.д. для простоты модели сосредоточены в f₃.

Все отчисления разнообразных налогов, таможенных пошлин, отчис-

ления во все фонды из

обозначены

(

,

) и для простоты модели со-

средоточены в f₁.

Клон

продает товар по максимально возможным, договорным це-

нам и рассчитываются с

по договору купли-продажи товара. На рис.4 то-

вар обозначен через «т», а деньги, поступающие в

от сторонних покупа-

телей, обозначен через «D». Наценка заранее вычисляется такой, чтобы бы-

ли покрыты издержки

и осталась небольшая прибыль. Обратный поток

расчета за товар разбивается на две части



,0) в

и (0, B₁₂ ) в

. Спе-

циалисты утверждают, что часто для уменьшения времени T расчет за то-

вар в потоке



,0) проводится за счёт средств из (0,Г₁₂). Как только весь

товар развезён по складам сторонних фирм, клон

бросают. Деньги за товар

у сторонних фирм можно собирать и потом (в моменты времени t>T) и вер-

нуть потом в

в потоке (0, B₁₂ ).

В свою очередь от f₃ и f₂ идет обратный поток (0,a₁₂ ), (0,a₂₂ ) в

. Это

осуществляется в связи с договорённостями о разделе финансового потока

при заключении договоров.

Можно провести аналогию и с процессом перехода к модели «пара-

зит», описанной в разд.1. При завершении цикла клон u₂ ликвидируется (см.

комментарии в начале разд.4).

Замечание 7. Коротко опишем алгоритм решения. По известным дан-

ным составляется недоопределённая СЛАУ. Восстанавливаем предполага-

емый граф, делая предположения, соответствующие экономическому смыс-

лу задачи. Дописываем необходимые уравнения с неизвестными параметра-

ми. Восстанавливаем неизвестные предполагаемые значения потоков. Под-

бираем их так, чтобы получить решение, не противоречащее экономическо-

му смыслу задачи и известным данным. Проблема обсуждалась на конфе-

ренциях [18,19].

Выводы

Чтобы не повторяться, сошлёмся на замечание 6, где приведены важ-

ные аргументы. При описанном механизме цены на товары никогда не бу-

118

Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко

дут снижаться. Никакой конкуренции в описанной схеме нет. Есть только

жажда получить максимальную прибыль и платить минимальные налоги.

Клон u₁ остается невидимым для стороннего наблюдателя, а u₃ маски-

руется под фирму, ведущую «честный малый бизнес». ТИОР избежать не

получится, можно лишь попытаться отодвинуть её по времени. Фактически

на графе решена спекулятивная задача оптимального управления с миними-

зацией затрат и максимальной прибылью.

Выражаем благодарность В.Г. Данилову, А.С. Братусю, О.С. Розано-

вой, В.П. Маслову за полезные обсуждения.

СПИСОК ЛИТЕРАТУРЫ

Г. Хакен. Синергетика от прошлого к будущему.  М.: Мир, 2005, 248 с.

Н. Haken. Information and self-organization. A macroscopic approach to complex systems

// Theoretical, Mathem.&Comp. Physics, Springer-Vertag.  Berlin: 2005.

И.В. Андрианов, Р.Г. Баранцев, Л.И. Маневич. Асимптотическая математика и синер-

гетика.  М.: Едиториал УРСС, 2004, 308 с.;

I.V. Andrianov, R.G. Barantsev, L.I. Manevich. Asimptoticheskaia matematika i siner-

getika.  M.: Editorial URSS, 2004, 308 s.

М. Эйген, П. Шустер. Гиперцикл. Принципы самоорганизации.  М.: Мир, 1982, 270 с.;

M. Eigen, P. Schuster. The hypercycle. A principle of natural self-organization. Part:

Emergence of the hypercycle // Naturwissenschaften, 1977, 64 (11), p.541-565.

N. Lehman, N. Vaidya, M.L. Manapat. Spontaneous network formation among cooperative

RNA replications // Nature, 2012.

А.С. Братусь, АС. Новожилов, А.П. Платонов. Динамические системы и модели в

биологии.  М.: Физматлит, 2010, 230 с.

A.S. Bratus, A.S. Novozhilov. A note on the replicator equation with explicit space and

global regulation // Mathematical Biosciences and Engineering, 2011, v.8, №3.

J. Hofbauer, K. Sigmund. Evolutionary Games and Population dynamics. Cambridge Uni-

versity Press, 1998.

W. Jansen. A permanence theorem for replicator and Lotka-Volterra systems. Mathemati-

cal biology, 1987, v.25, p.411-427.

А.К. Волосова. Математическое моделирование нелинейной динамики открытой сис-

темы гиперцикла.  М.: МИИТ, 2011, автореферат диссерт…. канд.физ.-мат.наук

http://www.dissercat.com

A.K. Volosova. Matematicheskoe modelirovanie nelineinoi dinamiki otkrytoi sistemy

gipertsikla.  M.: MIIT, 2011, avtoreferat dissert…. kand.fiz.-mat.nauk http://www. dis-

sercat.com

Н.Н. Баутин, Е.А. Леонтонович. Методы и приемы качественного исследования ди-

намических систем на плоскости. 2-е изд.  М.:ФИЗМАТЛИТ, 2003, 296 с.

N.N. Bautin, E.A. Leontonovich. Metody i priemy kachestvennogo issledovaniia dinami-

cheskikh sistem na ploskosti. 2-e izd.  M.: FIZMATLIT, 2003, 296 s.

10. К.А. Волосов. Методика анализа эволюционных систем с распределенными парамет-

Графы задач для репликаторных уравнений и ...

119

рами.  М.: МИЭМ, 2007, автореф. диссерт. …. докт. физ.-мат.наук. http://eq world.

ipmnet.ru dis volosov Doc2007.pdf

K.A. Volosov. Metodika analiza evoliutsionnykh sistem s raspredelennymi parametrami. 

M.: MIEM, 2007, avtoref. dissert. …. dokt. fiz.-mat. nauk. http://eq world.ipmnet.ru dis

volosov Doc2007.pdf

11. В.П. Маслов, В.Г. Данилов, К.А. Волосов. Математическое моделирование процессов

тепломассопереноса (эволюция диссипативных структур) с добавлением Н.А. Коло-

бова.  М.: Наука,1987, 352 с.;

V.G. Danilov, V.P. Maslov, K.A. Volosov. Mathematical Modeling of Heat and Mass

Transfer Processes. Kluver Academic publishers. Dordrecht /Boston/London 1995.

12. G.P. Karev. The HKV method of solving of replications and models of biological popula-

tions and communities. National Center for Biotechnology Information, National Institute

of Health, Bidg. 38 A, Rm. N 511N, 8600 Rockville Pike, Bethesda, MD 20894, USA.

13. В.Ф. Зайцев, А.Д. Полянин. Справочник. Обыкновенные дифференциальные уравне-

ния.  М.: Физматлит, 2001, 576 c.;

A.D. Polyanin and V.F. Zaitsev. Handbook of Nonlinear Partial Differential Equations,

Chapman&Hall/CRC Press, Boca Raton-London, 2004.

14. F.K. Berezovskaya, L.G. Kareva, G.P. Karev. Is it possible to prevent the "Tragedy of

Common Resource"? // Math. Biolog. Bioinform., 2012, v.7, Issue 1, p.30-44.

15. Н.Н. Моисеев. Быть или не быть человечеству?  М.: Ульяновский Дом печати, 1999,

288 с.;

N.N. Moiseev. Byt ili ne byt chelovechestvu?  M.: Ulianovskii Dom pechati, 1999, 288 s.

16. В.П. Маслов. Квантовая экономика.  М.: Наука 2006, 92 c.;

V.P. Maslov. Kvantovaia ekonomika.  M.: Nauka 2006, 92 s.

17. А.В. Щербаков. Экономика Чернавского // Компьютерные исследования и моделиро-

вание, 2017, т.9, № 3, с.397-417;

A.V. Shcherbakov. Ekonomika Chernavskogo // Kompiuternye issledovaniia i modeliro-

vanie, 2017, t.9, № 3, s.397-417.

18. Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко. К вопросу о «трагедии

исчерпания общего ресурса». LXXI Межд. конф. «Герценовские чтения». Россий-

ский госуд. педагогический университет им. А.И. Герцена.  С.-П.: 2018, с.60-74;

N.K. Volosova, A.K. Volosova, K.A. Volosov, S.P. Vakulenko. To the question of "the trag-

edy of exhaustion of the common resource". LXXI international conf. "Herzen readings"/

Herzen Russian state pedagogical University.  St.-Petersburg: 2018, 9-13.04, p.60-74.

19. Н.К. Волосова, А.К. Волосова, К.А. Волосов, С.П. Вакуленко. К вопросу о «трагедии

исчерпания общего ресурса» / Тезисы докладов. Межд. конференция по дифферен-

циальным уравнениям и динамическим системам. г. Суздаль, 2018, 6-11 июля, с.63;

N.K. Volosova, A.K. Volosova, K.A. Volosov, S.P. Vakulenko. To the question of "the trag-

edy of exhaustion of the common resource" / Thesis of reports. International conference on

differential equations and dynamical systems. Suzdal, 2018, 6-11 July, p.63.

Поступила в редакцию 12.03.2018

После доработки 01.04.2019

Принята к публикации 08.04.2019