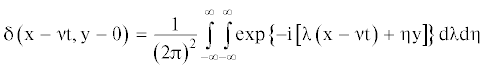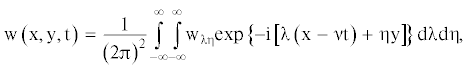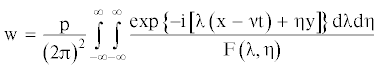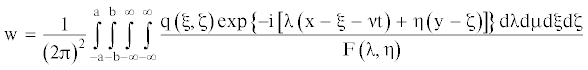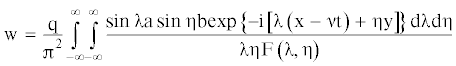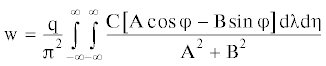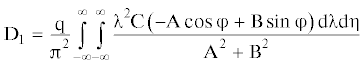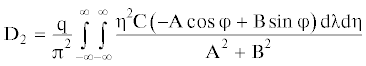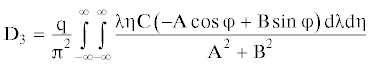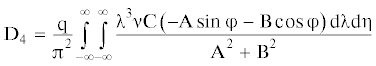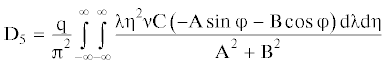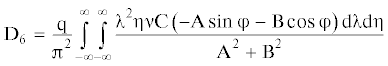1. Введение. Известно, что основным средством для разрушения ледяного покрова является ледокольный флот. Однако, большие энергетические затраты на разрушение льда, невозможность его использования на малых глубинах из-за большой осадки ледоколов, а также для разрушения заторов и зажоров заставляют искать новые способы борьбы со льдом. В этом направлении перспективы открываются благодаря открытой в Канаде способности СВП разрушать ледяной покров при их движении по льду со скоростью резонансных ИГВ [1]. При такой скорости частота изгибных волн, распространяющихся в свободной плавающей пластине, совпадает с частотой гравитационных волн на поверхности чистой воды, т.е. возникают условия для их резонансного взаимодействия. В этом случае архимедовы силы (силы плавучести) полностью уравновешиваются гидродинамическими силами и вода перестает поддерживать ледяной покров, т.е. его равновесие достигается только за счет внутренних сил упругости, возникающих в самой пластине. Это приводит к резкому увеличению амплитуды возбуждаемых изгибно-гравитационных волн (ИГВ), что значительно повышает энергоэффективность разрушения льда по сравнению с известными методами. На основании этого метод разрушения ледяного покрова путем возбуждения резонансных ИГВ был назван резонансным [2].
Резонансный метод разрушения ледяного покрова (РМРЛ) может осуществляться любым транспортным средством, обладающим возможностью перемещаться по ледяному покрову с достаточной скоростью и создающим необходимую для разрушения льда нагрузку. Так, разрушение льда резонансными ИГВ наблюдалось при движении автомашин, танков, поездов по ледяным переправам, при использовании ледяного покрова в качестве взлетно-посадочных полос для самолетов и автомобильных трасс.
При решении ледотехнических задач на замерзающих водоемах с использованием резонансного метода необходимо возбуждать ИГВ значительной амплитуды. Для этого потребуются транспортные средства массой в десятки и сотни тонн и способные безопасно двигаться надо льдом с большой скоростью. В настоящее время этим требованиям удовлетворяют только СВП. Кроме того, их вездеходные качества позволяют разрушать ледяной покров на акваториях любой глубины. Обладая большой скоростью, маневренностью и амфибийными свойствами, СВП могут быстро перемещаться в районы с ледовыми осложнениями. Преимуществами СВП являются также отсутствие непосредственного контакта судна со льдом (это повышает надежность их эксплуатации), проходимость над заснеженным и заторошенным ледяным покровом, безопасность движения над подводными островами, битым льдом, возможность выхода со льда на чистую воду и наоборот, на необорудованный берег. Это позволяет решать ряд задач по продлению навигации на внутренних водных путях, использовать СВП для быстрого (с резонансной скоростью 20–25 км/ч [2]) разрушения льда на больших площадях с целью более раннего вскрытия рек и водохранилищ. В периоды ледостава и ледохода для предотвращения разрушительных наводнений приходится разрушать ледяные заторы и зажоры. В этих случаях РМРЛ окажется более эффективным по сравнению с традиционными технологиями.
2. Краткий обзор экспериментальных исследований нагружения ледяного покрова движущимися нагрузками. Первое упоминание об экспериментальных исследованиях грузоподъемности пресноводного ледяного покрова и определения предельных нагрузок с целью транспортировки по нему грузов относится к середине 20-х годов прошлого столетия [3–5]. Записи колебаний ледяного покрова от действия импульсной нагрузки при посадке на лед самолета и его пролете на предельно малой высоте и их анализ приведены в работе [6]. Волновой характер колебаний льда под действием движущейся нагрузки описан в работах [7, 8]. Автором было высказано предположение о возможности проявления опасных явлений резонанса. Анализируя данные о волнообразных колебаниях ледяного покрова при перемещении грузов, авторы работы [9] пришли к выводу о существовании определенной скорости, превышение которой может привести к разрушению ледяного покрова. В 1949 г. были проведены экспериментальные исследования деформаций ледяного покрова от движущихся нагрузок, что позволило установить, как скорость перемещения нагрузки влияет на величину и характер прогиба льда [10]. При выполнении экспериментальных исследований по возбуждению в ледяном покрове волн сравнительно низкой частоты были обнаружили недиспергирующие волны [11]. Позднее были опубликованы результаты натурных наблюдений за естественными колебаниями льда арктических и антарктических морей [12, 13]. Записи профиля резонансных ИГВ, генерируемых в ледяном покрове, при посадке и маневрировании самолетов приведены в работе [14]. Экспериментальным исследованиям колебаний ледяного покрова посвящены работы [15, 16]. Автор работы [17] проводил исследования на озерном льду толщиной порядка 0.5 м при перемещении транспортных средств массой от 3.8 до 7.7 тонн со скоростью от 2.8 до 8.9 м/с, а работы [18] – замерил параметры волнения в дрейфующих льдах. Результаты замеров свободных и вынужденных колебаний ледяного покрова приведены в работе [19]. Спектры естественного фона вертикальных колебаний ледяного покрова приводятся в работе [20]. При изучении опыта использования ледяного покрова для транспортировки грузов с помощью колесной и гусеничной техники было установлено, что при резонансной скорости движения прогибы льда возрастали в два раза [21]. Во время испытаний канадского СВП “Voyageur” были обнаружены его ледокольные качества, при этом на его резонансной скорости 6.2 м/с судно непрерывно разрушало ледяной покров толщиной 0.38 м [1]. Экспериментальные исследования по распространению волн в ледяном покрове для определения его напряженно-деформированного состояния (НДС) и физико-механических свойств проводились в ААНИИ [22, 23]. С помощью датчиков давления, закрепляемых на границе раздела лед–вода, изучались колебания ледяного покрова, вызванные движущейся нагрузкой [24]. На льду озера Дифенбейкер при помощи датчиков вертикальных перемещений проведена серия экспериментов по записи профилей взволнованной поверхности льда толщиной от 0.50 до 0.73 м от движения транспортных средств [25]. В работе [26] опубликованы экспериментальные данные, полученные с помощью 1200 тензодатчиков. Они были установленны на расстоянии 1 км от взлетно-посадочной полосы, расположенной на морском льду пролива Макмердо. На озере Сарома (Хоккайдо, Япония) были проведены экспериментальные исследования по изучению деформаций ледяного покрова при движении по нему нагрузки. Автором с высокой точностью были записаны профили взволнованной поверхности льда [27]. В работе [28] исследовались режимы движения нагрузки по льду. Испытания проходили на озерах Канады при различных глубинах и толщинах льда от 0.4 до 0.6 м. Была установлена зависимость резонансной скорости движения нагрузки от ледовых условий. Также на озере Сарома были проведены дополнительные полевые испытания при наличии снежного покрова. В результате исследований были выявлены пять режимов деформирования ледяного покрова [29–31]. Эксперименты по определению динамических деформаций льда от ветровой и движущийся нагрузок, были проведены с использованием тензометрических датчиков. В качестве движущейся нагрузки использовалось автотранспортное средство. В результате было определено значение резонансной скорости движения. Отмечено, что при этой скорости прогибы льда возрастали в 2.2 раза по сравнению со статически приложенной нагрузкой [32, 33]. Также была проведена крупная серия полевых испытаний на морском льду для определения параметров возбуждаемых ИГВ. Глубина акватории составляла от 350 до 450 м. Молодой ледяной покров толщиной 1.6 м имел ровную, гладкую поверхность с одинаковыми физико-механическими свойствами. В качестве транспортных средств использовались грузовой автомобиль массой 2100 кг и самолет LC-130 Hercules массой около 50000 кг [34]. Эксперименты с использованием грузового автомобиля проводились вдоль ледяной дороги протяженностью 6 км. В процессе их выполнения исследованы вопросы поведения морского и озерного льда при действии на него движущихся нагрузок. Авторами выполнена серия экспериментов на антарктической станции McMurdo Sound, в которых сделаны записи деформаций ледяного покрова на различных расстояниях от ледовой трассы [35]. Для имитации воздействия самолета на естественный ледяной покров при его взлете и посадке была произведена серия полунатурных экспериментов с использованием двухместного мотодельтаплана [36].
3. Обзор теоретических исследований по деформированию ледяного покрова ИГВ. К одному из первых исследований колебаний ледяного покрова можно отнести работу [37], в которой была установлена зависимость фазовой скорости поверхностных волн в плавающей тонкой однородной упругой пластине от волнового числа.
В период Великой Отечественной войны интерес к исследованиям динамики ледяного покрова повысился в связи с эксплуатацией ледовой трассы “Дорога жизни” на льду Ладожского озера. Теоретические исследования влияния волновых движений жидкости на НДС ледяного покрова от приложенной ко льду подвижной и импульсной нагрузок опубликованы в работе [38]. Автором также были описаны физические процессы, сопровождающие распространение ИГВ. В работе [39] рассмотрено распространение упругих волн в плавающем ледяном слое конечной толщины и получено характеристическое уравнение, связывающее волновое число с частотой. Влияние сжимаемости воды на распространение упругих волн во льду оценено в работе [40]. Сопоставляя результаты теоретических исследований с экспериментальными данными, авторы пришли к выводу, что при длинных волнах, для которых справедлива теория слабого изгиба тонких пластин, влияние сжимаемости воды пренебрежимо мало. Вопросы динамики ледяного покрова наиболее полно и глубоко были проработаны в работе [41]. Автор разработал математическую теорию волновых процессов в плавающем на воде ледяном покрове, им решен ряд нестационарных задач динамики ледяного покрова в случае бассейна неограниченной глубины. Рассмотрел влияние неупругих свойств льда на характер изгиба в зависимости от режима нагружения. Исследования влияния ледяного покрова и вязкости жидкости на длинные волны, вызываемые периодическими давлениями, отражены в работе [42]. Вынужденные колебания бесконечной упругой пластины на упругом основании винклеровского типа под действием гармонически изменяющейся во времени сосредоточенной силы рассмотрены в работе [43]. На примере плоских установившихся волн, возникающих в ледяном покрове от действия движущейся области поверхностных давлений, исследовано влияние неоднородностей ледяного покрова и жидкости на развитие волновых движений [44]. Вопросами влияния слоя снега на характеристики ледяного покрова посвящена работа [45]. Автор статьи [46] предложил использовать введение в дифференциальные уравнения колебаний ледяного покрова нелинейных членов, что позволило избежать неограниченный рост амплитуды волны при резонансных скоростях движения нагрузки. Зависимости для расчета НДС ледяного покрова в случае движения по нему нагрузки при разных граничных условиях на контуре ледяного поля и законах ее движения получены в работе [47]. В работах [49, 50] рассмотрены вопросы дифракции поверхностных волн краем плавающей упругой полубесконечной пластины для конечной и бесконечной глубины жидкости. Авторы работ [51, 52] исследовали стационарное и нестационарное движение нагрузок по ледяному покрову. Решения ряд прикладных задач динамики ледяного покрова приведены в работе [53]. Авторы [54] рассмотрели ряд задач динамики ледяного и снежного покровов. Решение распространения волн в прямоугольном канале конечной и малой глубины для ледяного покрова, прикрепленного к его стенкам, получено в работе [55]. Влияние физико-механических характеристик ледяной пластины, режимов взлета и посадки самолета на НДС ледяного покрова установлено в работе [56]. Авторами [57] исследована задача о распространении ИГВ в покрытом льдом канале прямоугольного сечения. В работе [58] исследовано влияние гидростатического и гидродинамического давлений на колебания ледяного покрова в канале под действием движущейся нагрузки. В рамках линейной теории исследовались установившиеся колебания ледяного покрова и жидкости, вызванные локальной областью периодического по времени давления [59]. В работах [60–62] решены задачи о взаимодействии поверхностных волн и ИГВ с вертикальной преградой, о поведении полубесконечного ледяного покрова на поверхности жидкости конечной глубины под действием нагрузки, движущейся с постоянной скоростью вдоль кромки покрова и по свободной поверхности жидкости. Автором [63, 64] получено решение линейной гидроупругой задачи об установившихся вынужденных колебаниях полубесконечного ледяного покрова под действием локализованной внешней нагрузки. Исследовано поведение ледяного покрова в зависимости от частоты внешней нагрузки и граничных условий на краю пластины. В работе [65] изучено влияние снежного покрова на распространение ИГВ, генерируемых в сплошном ледяном поле под действием периодической перемещающейся системы давлений и начальных деформаций. Исследованы неустановившиеся колебания сплошного ледяного покрова, возникающие под действием атмосферных возмущений в условиях ледового сжатия и скорости дрейфа льда и многие другие вопросы. Изучению влияние битого льда на образование гравитационных волн, вызванных движением внешней нагрузки вдоль канала, решению нестационарной задачи об ИГВ на поверхности замороженного ледового канала, вызванных движением внешней нагрузки, исследованию реакции ледяного покрова на нагрузку, движущуюся по замерзшему каналу, посвящены работы [66–68].
4. Цель работы. Выполненный обзор экспериментальных работ по деформированию ледяного покрова движущимися нагрузками и теоретических исследований по возбуждению ИГВ в ледяном покрове говорит о глубокой изученности и все возрастающем интересе к этим вопросам. Уже более 100 лет решаются различные теоретические и прикладные задачи в этих направлениях. Связано это с тем, что проблемы освоения регионов с суровыми климатическими условиями и богатыми природными ресурсами были и остаются актуальными. Однако, несмотря на большой объем выполненных экспериментально-теоретических исследований известные решения не могут быть использованы для достижения цели, поставленной в работе: исследовать закономерности разрушения ледяного покрова резонансным методом. Объясняется это тем, что все они получены для случаев деформирования ледяного покрова, когда не происходит его полного разрушения. Под полным разрушением далее будем понимать такую стадию нагружения ледяного покрова, когда его деформации приводят не только к изгибным напряжениям, превышающим его предел прочности, но и к раскрытию образовавшихся вследствие этого трещин.
В работе поставлена задача разработать зависимости для определения толщины ледяного покрова, который способны разрушить резонансным методом существующие (построенные), спроектированные СВП или выбрать параметры СВП, предназначенных для разрушения резонансным методом ледяного покрова заданной толщины.
5. Выполненные экспериментальные исследования разрушения ледяного покрова резонансным методом. Теория волновых колебаний ледяного покрова пока еще не разработана настолько, чтобы дать ответы на все практические вопросы разрушения льда ИГВ. Для этого необходимо установить зависимость параметров нагрузки от толщины разрушаемого ледяного покрова.
Натурные исследования поведения ледяного покрова под действием движущихся нагрузок весьма трудоемки. Нестабильность во времени и многообразие свойств ледяного покрова, зависимость их от погодных условий и влияние на них различных факторов создают дополнительные трудности в получении достоверных результатов. Уменьшение их затрат достигалось с помощью модельных экспериментов. Они проводились в ледовом бассейне (рис. 1), в котором для намораживания льда использовались естественные низкие температуры [69].
Когда размеры имеющегося бассейна оказывались недостаточными для имитации бесконечного ледяного поля (при увеличении толщины намораживаемого льда его площадь значительно возрастает), то опыты проводились в полевых условиях на льду открытых водоемов рек и озер. В таких случаях в их толстом ледяном покрове при помощи ледорезного инструмента приготавливались каналы необходимых размеров, т.е. для проведения экспериментов создавались своеобразные ледовые “бассейны”. Ледяной слой необходимой толщины намораживался на их поверхности за счет естественного холода (рис. 2).
Рис. 2.
Ледовый “бассейн” размерами 8.0 × 3.0 × 2.5 м, созданный в ледяном покрове озера толщиной 0.8 м.

Трудности, связанные с получением естественного бесконечного ледяного поля, т.е. необходимость в бассейнах больших размеров (для уменьшения влияния отраженных волн, граничных условий и возможности получения установившегося режима движения), а также желание уменьшить влияние масштабного эффекта обусловили целесообразность проведения экспериментов с крупномасштабными моделями СВП на замерзающих акваториях (рис. 3). Следует отметить, что для этих целей студентами Комсомольского-на-Амуре политехнического института была построена модель СВП “КнАПИ”.
Исследования ледоразрушающих свойств возбуждаемых ИГВ также проводились с использованием катеров на воздушной подушке (рис. 4) и СВП береговой охраны (рис. 5).
Рис. 4.
Разрушение ледяного покрова катерами на воздушной подушке: (а) –“Тайфун – 1”; (b) – “Тайфун – 2”.

Особой трудоемкостью отличались эксперименты с натурными СВП (рис. 6), т.к. кроме испытуемых объектов для технического обеспечения экспериментов приходилось привлекать водоизмещающие суда (для очистки акватории от битого льда после проведения экспериментов с целью намораживания очередного ледяного поля) и вертолет МИ-8 (для получения пространственной картины разрушения ледяного покрова).
Цель выполненных экспериментов заключалась в определении минимальных нагрузок, движущихся по льду с резонансной скоростью и приводящих к полному разрушению ледяного покрова. Под полным разрушением далее будем понимать такую стадию нагружения ледяного покрова, когда его деформации приводят не только к изгибным напряжениям, превышающим его предел прочности, но и к раскрытию образовавшихся вследствие этого трещин. При этом технологии экспериментов отличались в зависимости от условий их проведения. Так, в ледовых бассейнах вначале намораживался лед определенной толщины. После этого неоднократно начинали с резонансной скоростью буксировать модель с увеличивающейся массой. Если при очередном проходе модели начиналось полное разрушение льда, то опыты прекращали. В результате определялась минимальная масса нагрузки при известной площади ее распределения (интенсивности), достаточная для полного разрушения ледяного покрова заданной толщины и прочности. При проведении опытов в натурных условиях, когда параметры СВП заранее были известны, вначале проходы СВП с резонансной скоростью начинали на тонком льду с последующим ростом его толщины. Эксперименты прекращали, когда после очередного прохода непрерывного и полного разрушения льда не происходило. Результаты экспериментов по определению минимальной толщины разрушаемого льда, а также данные испытаний СВП “Voyageur” [1] приведены в табл. 1.
6. Теоретические зависимости для расчета напряженно-деформированного состояния ледяного покрова от движущихся нагрузок. При решении ледотехнических задач лед обычно рассматривается как упругий изотропный материал, а для изучения его НДС привлекается аппарат теории изгиба упругих пластин. В действительности, ледяная пластина обладает анизотропией вследствие градиента температуры по толщине, различного химического состава, ориентации кристаллов по слоям, наличия примесей, истории ледостава и др. В вопросах волновых колебаний ледяного слоя эти факторы учитываются путем рассмотрения трансверсально-изотропной модели льда с последующим переходом к изотропной, но с приведенным модулем упругости.
Соотношения между напряжениями и деформациями во льду носят вязко-упругий характер и зависят от режима нагружения. Учет этих свойств в условиях изгибно-гравитационного резонанса (ИГР) позволит избавиться от неопределенности в теоретических решениях и получить реальную картину НДС ледяного покрова в месте приложения нагрузки.
Известные исследования показывают, что для описания волновых колебаний льда при ИГР можно принять закон деформирования упруго-запаздывающей среды Кельвина–Фойгта [41]. Тогда дифференциальное уравнения вязко-упругих колебаний ледяного покрова при установившемся движении сосредоточенной силы Р с постоянной скорость v будет иметь вид:
(6.1)
$\begin{gathered} \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}\left( {1 + {{{{\tau }}}_{{\text{Ф}}}}\frac{\partial }{{\partial {\text{t}}}}} \right){{\nabla }^{4}}{\text{w}} + \left( {{{{{\rho }}}_{{\text{L}}}}{\text{h}} + {{{{\rho }}}_{{\text{c}}}}{{{\text{h}}}_{{\text{c}}}}} \right)\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {{{\text{t}}}^{2}}}} + {{{{\eta }}}_{{\text{c}}}}{{{\text{h}}}_{{\text{c}}}}\frac{\partial }{{\partial {\text{t}}}}{{\nabla }^{2}}{\text{w}} + {{{{\rho }}}_{{\text{V}}}}{\text{gw}} + {{{{\rho }}}_{{\text{В}}}}{{\left. {\frac{{\partial {\text{Ф}}}}{{\partial {\text{t}}}}} \right|}_{{{\text{Z}} = 0}}} = \\ = Р\delta \left( {x - \nu t,y - 0} \right){\text{\;\;}} \\ \end{gathered} $Для бесконечной области дельта–функции Дирака в этом случае может быть представлена двойным интегралом Фурье:
Тогда прогиб льда w и потенциал движения жидкости Ф будем искать в виде:
Окончательное выражение для w получено в виде:
где(6.4)
$\begin{gathered} {\text{F}}\left( {{{\lambda }},{{\eta }}} \right) = \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}{{({{{{\lambda }}}^{2}} + {{{{\eta }}}^{2}})}^{2}} - {{{{\lambda }}}^{2}}{{{{\nu }}}^{2}}{{{{\rho }}}_{{\text{L}}}}{\text{h}} + {{{{\rho }}}_{{\text{V}}}}{\text{g}} - \\ - \frac{{{{{{\rho }}}_{{\text{V}}}}{{{{\lambda }}}^{2}}{{{{\nu }}}^{2}}}}{{{\text{th}}({\text{H}}\sqrt {{{{{\lambda }}}^{2}} + {{{{\eta }}}^{2}}} )\sqrt {{{{{\lambda }}}^{2}} + {{{{\eta }}}^{2}}} }} + {\text{i}}\frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}{{{{\tau }}}_{{\text{Ф}}}}{{\lambda \nu }}{{({{{{\lambda }}}^{2}} + {{{{\eta }}}^{2}})}^{2}} \\ \end{gathered} $Линейная постановка задачи позволяет с помощью принципа суперпозиций перейти от полученного решения для сосредоточенной силы к случаю движения по льду ограниченной в плане нагрузки, распределенной по площади прямоугольника со сторонами 2а, 2в. Тогда прогиб ледяного покрова определится после интегрирования по переменным ξ, ζ:
При равномерном распределении нагрузки по площади прямоугольника получим:
где q = P/4abВведем обозначения:
Выделяя действительную часть выражения (7), получим:
Выражения изгибающих моментов запишутся так:
(6.8)
$\begin{gathered} {{{\text{M}}}_{{\text{x}}}} = - \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}\left( {1 - {{{{\tau }}}_{{\text{Ф}}}}\frac{\partial }{{\partial {\text{t}}}}} \right)\left( {\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {{{\text{x}}}^{2}}}} + {{\mu }}\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {{{\text{y}}}^{2}}}}} \right) \\ {{{\text{M}}}_{{\text{y}}}} = - \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}\left( {1 - {{{{\tau }}}_{{\text{Ф}}}}\frac{\partial }{{\partial {\text{t}}}}} \right)\left( {\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {{{\text{y}}}^{2}}}} + {{\mu }}\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {{{\text{x}}}^{2}}}}} \right) \\ {{{\text{M}}}_{{{\text{xy}}}}} = \frac{{{\text{G}}{{{\text{h}}}^{3}}\left( {1 - {{\mu }}} \right)}}{3}\left( {1 + {{{{\tau }}}_{{\text{Ф}}}}\frac{\partial }{{\partial {\text{t}}}}} \right)\frac{{{{\partial }^{2}}{\text{w}}}}{{\partial {\text{x}}\partial {\text{y}}}} \\ \end{gathered} $После взятия производных выражения для изгибающих моментов окончательно перепишутся в виде:
(6.9)
$\begin{gathered} {{{\text{M}}}_{{\text{x}}}} = - \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}\left[ {{{{\text{D}}}_{1}} + {{\mu }}{{{\text{D}}}_{2}} + {{{{\tau }}}_{{\text{Ф}}}}\left( {{{{\text{D}}}_{4}} + {{\mu }}{{{\text{D}}}_{5}}} \right)} \right] \\ {{{\text{M}}}_{{\text{y}}}} = - \frac{{{\text{G}}{{{\text{h}}}^{3}}}}{3}\left[ {{{{\text{D}}}_{2}} + {{\mu }}{{{\text{D}}}_{1}} + {{{{\tau }}}_{{\text{Ф}}}}\left( {{{{\text{D}}}_{5}} + {{\mu }}{{{\text{D}}}_{4}}} \right)} \right] \\ {{{\text{M}}}_{{{\text{xy}}}}} = \frac{{{\text{G}}{{{\text{h}}}^{3}}\left( {1 - {{\mu }}} \right)}}{3}\left( {{{{\text{D}}}_{3}} + {{{{\tau }}}_{{\text{Ф}}}}{{{\text{D}}}_{6}}} \right) \\ \end{gathered} $Максимальные погонные (отнесенные к единице длины) напряжения определятся из зависимостей:
(6.10)
${{{{\sigma }}}_{{\text{x}}}} = \frac{{6{{{\text{M}}}_{{\text{x}}}}}}{{{{{\text{h}}}^{2}}}};\quad {{{{\sigma }}}_{{\text{y}}}} = \frac{{6{{{\text{M}}}_{{\text{y}}}}}}{{{{{\text{h}}}^{2}}}};\quad {{{{\tau }}}_{{{\text{xy}}}}} = \frac{{6{{{\text{M}}}_{{{\text{xy}}}}}}}{{{{{\text{h}}}^{2}}}}$7. Критерий для оценки ледоразрушающей способности ИГВ. В большинстве известных расчетов предельных нагрузок, разрушающих ледяной покров при их движении, используется уровень напряжений. При этом ледяной покров считается разрушенным, если напряжения превышают соответствующий предел прочности. Такой подход можно считать приемлемым, когда для безопасного использования ледяного покрова в качестве ледяных переправ необходим запас его несущей способности, а его разрушение считают нежелательным. При решении поставленных в работе задач такой подход не приемлем. Это объясняется тем, что возникновение в сплошном ледяном покрове предельных напряжений, т.е. появление во льду сквозных трещин и даже их раскрытие не приводит к полной утрате его несущей способности. В опытах с катерами на воздушной подушке, натурными СВП и их изготовленными крупномасштабными моделями установлено, что нагрузка, гарантирующая его полное разрушение (рис. 7,а), может в несколько раз превышать нагрузку, вызывающую появление трещин (рис. 7,b).
Рис. 7.
Стадии разрушения ледяного покрова ИГВ: (а) – полное разрушение; (b) – достижение предела прочности льда на изгиб.

Причиной сохранения несущей способности ледяного покрова, разделенного трещинами на отдельные куски в области возникновения ИГВ наибольшей амплитуды, являются контактные напряжения на берегах трещин. Несмотря на нарушение сплошности ледяной пластины, кинематическая и силовая связь растрескавшейся области с кромками сплошного ледяного поля (своеобразный арочный эффект) не позволяет распасться растрескавшемуся льду на отдельные куски. Несущая способность ледяного покрова будет полностью исчерпана, когда произойдет разрушение образовавшейся блочной конструкции и она не сможет нести нагрузку, превышающую силу плавучести ее обломков, т.е. Архимедовых сил (такая стадия разрушения представлена на рис. 7,а).
Процесс нагружения ледяного покрова ИГВ приводит к трещинообразованию с одновременным частичным “самозалечиванием” трещин (вода, попадая в переохлажденный лед полностью не раскрытых трещин, сразу замерзает, т.е. трещина исчезает) или последующим их раскрытии при достижении определенных амплитуд ИГВ. Раскрытие трещин в ледяном покрове связано с несколькими механизмами и с различной энергетикой. Это не только растяжение, но и сжатие с потерей устойчивости и надвиганием блоков льда друг на друга. Все это влияет и на удельную энергетику в целом. Кроме этого, происходит смятие и скол острых кромок, а часть энергии ИГВ затрачивается на поворачивание обломков льда. Колебания ледяного покрова сопровождаются диссипаций энергии в воде, ледяной пластине и снежном покрове. Энергия ИГВ также рассеивается в присоединенных массах воды, колеблющихся вместе со льдом, при частичном отражении и преломлении волн в трещинах, в виде акустического излучения, вследствие дифракции, интерференции, трансформации параметров ИГВ и др. Из-за сложной геометрии разлома, густоты сетки не раскрытых трещин затруднительно определить энергию даже на образование во льду свободных поверхностей. Относительно строгому анализу поддается лишь определение условий для их спонтанного роста (критерий Гриффитса).
Учесть влияния вышеперечисленных процессов на предельное деформирование ледяного покрова практически не возможно. Поэтому для оценки ледоразрушающей способности ИГВ была принята такая интегральная характеристика, как энергия изгибно-гравитационных колебаний ледяного покрова. Ее величина равна сумме потенциальной энергии изгиба ледяной пластины, кинетической энергии ее изгибных колебаний и сопутствующих им гравитационных волн в воде. Очевидно, что две последних составляющих в общем балансе энергии при предельных деформациях ледяного покрова ИГВ малы по сравнению с первой. Поэтому определение энергии ИГВ, полностью разрушающих ледяной покров, производилось по потенциальной энергии изгиба ледяной пластины. Таким образом, в качестве критерия ледоразрушающей способности ИГВ была принята теоретическая плотность потенциальной энергии изгиба U, достижение которой приводит к началу непрерывного (полного) разрушения льда. Величина U определялась по теоретическим напряжениям, соответствующим этой стадии разрушения ледяного покрова.
Для пластины бесконечных размеров потенциальная энергия изгиба определяется выражением [70]:
(7.1)
${\text{U}} = \frac{{\text{h}}}{{4{\text{G}}(1 + {{\mu }})}}\mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_{ - \infty }^\infty [{{\sigma }}_{x}^{2} + {{\sigma }}_{y}^{2} - 2{{\mu }}{{{{\sigma }}}_{{\text{x}}}}{{{{\sigma }}}_{{\text{y}}}} + 2\left( {1 + {{\mu }}} \right){{\tau }}_{{xy}}^{2}]{\text{dxdy}}$Нормальные σx, σy и касательные напряжения τxy находились по зависимостям (6.10).
Разрушение льда ИГВ от движущихся нагрузок носит локальный характер и происходит в месте ее приложения, т.е. в области возникновения максимальных деформаций. Поэтому рассчитывалась погонная потенциальная энергия, приходящаяся на длину фронта волны, равную h, и на длину волны максимальных напряжений λσ (необходимость в таком подходе была связана с желанием найти единообразный параметр для оценки ледоразрушающей способности ИГВ, возбуждаемых в различных ледовых условиях). Тогда плотность потенциальной энергии изгиба ледяной пластины определится выражением:
(7.2)
${\text{U}} = \frac{1}{{4{\text{G}}{{{{\lambda }}}_{{{\sigma }}}}\left( {1 + {{\mu }}} \right)}}\mathop \smallint \limits_0^{{{{{\lambda }}}_{{{\sigma }}}}} [{{\sigma }}_{x}^{2} + {{\sigma }}_{y}^{2} - 2{{\mu }}{{{{\sigma }}}_{x}}{{{{\sigma }}}_{y}} + 2\left( {1 + {{\mu }}} \right){{\tau }}_{{xy}}^{2}]{\text{dx}}$Результаты расчетов U для толщин ледяного покрова, разрушаемого минимальными нагрузками при их движении с резонансной скоростью, показали относительно стабильные ее значения (см. табл. 1). Для этих расчетов необходимые параметры выбирались из базы данных экспериментов, полученных: в ледовых бассейнах; с использованием крупномасштабных моделей СВП в полевых условиях; катеров и натурных судов на воздушной подушке. Следует отметить, что на параметры ИГВ, т.е. их ледоразрушающую способность, безусловно влияли: наличие подледного течения; температура воздуха; глубина водоема и ее изменение; близость берега к месту проведения экспериментов; структура льда и наличие в нем примесей; скорость нагружения льда движущимися нагрузками; масштабный фактор (зависимость прочностных свойств льда от его толщины); наличие на льду снежного покрова (правда, при проведении экспериментов снежный покров практически отсутствовал); внутренняя напряженность льда; история ледостава и др. Однако, в условиях изгибно-гравитационного резонанса, когда происходит резкое (резонансное) увеличение изгибных напряжений, влияние ранее перечисленных и этих факторов при полном разрушении льда оказалось незначительным. Это подтверждается результатами расчетов U в различных ледовых условиях. Их устойчивость позволила в качестве критерия ледоразрушающей способности ИГВ, возбуждаемых распределенными движущимися с резонансной скоростью нагрузками, принять относительную теоретическую плотность потенциальной энергии изгиба ледяной пластины. Ее значение, соответствующее стадии полного разрушения льда по результатам проделанных опытов (при ее вычислении предполагалось, что ледяной покров сохраняет свою целостность), оказалось равным примерно 650 дж/м3. Из этого следует заключение, что, если теоретическая плотность относительной потенциальной энергии изгиба ледяного покрова ИГВ окажется равной или большего найденного значения, то за нагрузкой, возбуждающей такие волны, будет происходить полное разрушение ледяного покрова.
Таблица 1.
Результаты расчетов U
| Вид нагрузки | Длина, м | Ширина, м | Масса, кг | Толщина льда, см | U, Дж/м3 |
|---|---|---|---|---|---|
| Модель СВП | 0.23 | 0.19 | 2.85 | 0.42 | 690 |
| 1.20 | 0.27 | 560 | |||
| 2.10 | 0.34 | 750 | |||
| 2.35 | 0.44 | 560 | |||
| 4.80 | 0.56 | 770 | |||
| СВП “КнАПИ” | 3.7 | 2.1 | 340 | 2.5 | 690 |
| “Косатка” | 5.1 | 2.6 | 400 | 2.8 | 670 |
| “Тайфун-1” | 7.4 | 3.6 | 2100 | 6.0 | 670 |
| “Тайфун-2” | 10.2 | 4.6 | 5200 | 8.2 | 550 |
| “Гепард” | 6.9 | 3.2 | 18 000 | 7.5 | 570 |
| “Скат” | 17.0 | 7.4 | 20 500 | 26.0 | 700 |
| “Мурена” | 30.0 | 13.0 | 120 000 | 60.0 | 660 |
| “Voyageur” | 20.0 | 8.0 | 40 800 | 38.0 | 640 |
| Среднее значение плотности потенциальной энергии изгиба | 650 | ||||
Следует отметить, что при расчетах ледовой ходкости судов, ледовых нагрузок на гидротехнические сооружения при ледоходах или подвижках льда, при определении несущей способности ледяных переправ или грузонесущих платформ и решении других ледотехнических задач влияние вышеперечисленных различных факторов на разрушающую лед нагрузку, безусловно, следует учитывать [5, 10].
8. Результаты расчетов основных параметров СВП, достаточных для разрушения ледяного покрова резонансным методом. Основными параметрами, определяющими способность СВП разрушать лед резонансным методом, как показали экспериментально-теоретические исследования, являются нагрузка на лед от силы тяжести судна, т.е. его масса М, и ее интенсивность, т.е. давление в воздушной подушке Рvp. Форма и соотношение размеров воздушной подушки в плане, используемые у существующих судов, существенного влияния на их ледоразрушающую способность не оказывают [2]. В качестве исходных данных для получения этих зависимостей от толщины ледяного покрова, полностью разрушаемого резонансным методом, были взяты результаты выполненных экспериментов. Зависимость М = f(h, Pvp) для параметров построенных и перспективных СВП, охватывающая весь диапазон интересующих значений h, определялась с помощью предложенного выше критерия оценки ледоразрушающей способности ИГВ. Принимая во внимание теоретическое значение предельной плотности потенциальной энергии изгиба ледяной пластины ИГВ (U = 650 дж/м3) и выполняя численные расчеты по зависимостям (10, 12) для интересующих нас диапазонов изменения массы СВП М и давления в воздушной подушке Рvp была получена их зависимость толщины разрушаемого льда. Следует заметить, что полученная зависимость М = f(h, Pvp ) позволяет определить минимально достаточную для разрушения льда величину М при заданном Pvp. Результаты этих расчетов для чистого от снега ледяного покрова (эксперименты проводились при его отсутствии и среднесуточной температуре – (10–15)°С ), при резонансной скорости движения нагрузки для наиболее вероятных физико-механических характеристик пресноводного льда в различных ледовых условиях [71] и с учетом влияния масштабного эффекта [72] представлены на рис. 8.
Рис. 8.
Зависимость массы СВП и давления в воздушной подушке от толщины разрушаемого ледяного покрова (T/кПа).
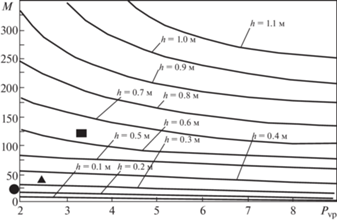
Работоспособность этих зависимостей подтверждается нанесенными на график символами, соответствующими параметрам использованным в экспериментах натурных СВП с указанием максимальных толщин ледяного покрова, разрушаемого ими резонансным методом (⚫ – “Скат” (M = 20.5 т; Рvp = 1.8 кПа; h = 26 см; ▲ – “Voyager” (M = 38.0 т; Рvp = 2.4 кПа; h = 38 см; ◼ – “Мурена” (M = 120.0 т; Рvp = 3.3 кПа; h = 60 см).
9. Заключение. Основным результатом работы является определение взаимосвязи между толщиной разрушаемого льда и параметрами СВП, как основным средством реализации резонансного метода разрушения ледяного покрова. Она установлена на основании обработки результатов экспериментальных исследований, выполненных в условиях модельного, полунатурного и натурного экспериментов и соответствующих теоретических исследований. Полученные результаты позволяют определить ледоразрушающую способность СВП при их использовании в качестве ледокольных средств при решении различных ледотехнических задач. Это делает возможным в ряде случаев возникновения ледовых осложнений решать задачи по разрушению льда СВП, когда использование традиционных ледокольных технологий и средств затруднительно или вообще невозможно. С помощью полученных результатов также можно оценивать целесообразность использования СВП для разрушения ледяного покрова резонансным методом, т.е. его энергоэффективность.