ВВЕДЕНИЕ
В начале XXI в. в центре внимания научных разработок находятся функциональные и многофункциональные материалы, способные открыть новые возможности для разработки технологий и аппаратуры в химической промышленности, металлургии, тепло- и электроэнергетике, ядерной энергетике [1–9]. В последнее время значительно вырос интерес к исследованию и применению фазовых диаграмм в различных областях промышленности в связи с изысканием и получением новых материалов и композиций из металлов, сплавов, полупроводников, сверхпроводников, огнеупорных и керамических материалов. В настоящее время известно большое число функциональных материалов, применяемых в различных фазовых состояниях. Помимо индивидуальных простых веществ и соединений широкое применение нашли функциональные материалы на основе солевых смесей из двух и более компонентов [10–15].
Изучение фазового комплекса стабильных элементов древа фаз четырехкомпонентной взаимной системы из фторидов и хроматов лития, калия и рубидия представляет интерес как в теоретическом, так и в практическом плане. Ранее эта система не изучалась. Описание физико-химического взаимодействия в многокомпонентной взаимной системе является важной задачей физико-химического анализа и физической химии. Полученные низкоплавкие составы на основе компонентов данной системы могут быть использованы для получения новых расплавляемых электролитов в химических источниках тока как среды для синтеза монокристаллов или для электролитического выделения металлов из расплавов.
Цель настоящей работы – исследование фазового комплекса стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 четырехкомпонентной взаимной системы Li+, K+, Rb+||F–, ${\text{CrO}}_{4}^{{2 - }},$ включающее изучение 3D-модели и построение на ее основе политермических и изотермических сечений, а также экспериментальное изучение методом дифференциального термического анализа (ДТА) фазовых равновесий.
Аналитическое изучение фазового комплекса четырехкомпонентной взаимной системы Li+, K+, Rb+||F–, $CrO_{4}^{{2 - }}$
Фазовый комплекс четырехкомпонентной взаимной системы Li+, K+, Rb+||F, ${\text{CrO}}_{{\text{4}}}^{{{\text{2}} - }}$ включает в себя совокупность многокомпонентных систем. Геометрический образ этих систем – двухмерная или трехмерная фигура составов. Обзор литературных данных об элементах огранения системы Li+, K+, Rb+||F, ${\text{CrO}}_{{\text{4}}}^{{{\text{2}} - }}$ [13–27] позволил определить положение стабильных диагоналей и стабильных секущих в тройных и тройных взаимных системах, входящих в данную систему. Эта информация стала основой для разбиения системы на стабильные элементы древа фаз (рис. 1).
Рис. 1.
Развертка тригональной призмы составов системы Li+, K+, Rb+||F, ${\text{CrO}}_{4}^{{2 - }}.$

В работе составы представлены в процентах, выраженных в эквивалентных долях (экв. % или %), температура – в градусах Цельсия (°С).
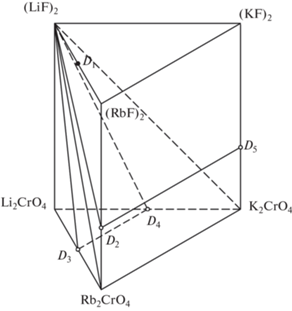
На рис. 2 изображена схема призмы составов с нанесенными на нее секущими элементами, которые позволили произвести разбиение с помощью 3D-модели. Соединение D1 не принимает участия в разбиении, поскольку в трехкомпонентной системе Li+, K+, Rb+||F– данное соединение “выклинивается”, т.е. фаза LiRbF2 исчезает ниже температуры выклинивания по фазовой реакции P450: ж + LiRbF2 ⇄ LiF + (KxRb1–xF)ss, где фаза (KxRb1–xF)ss – ограниченный твердый раствор на основе непрерывного ряда твердых растворов (НРТР) состава KxRb1–xF, в котором растворен LiF [28].
В результате разбиения получен набор стабильно сосуществующих фаз – стабильных элементов и построено древо фаз (рис. 3), имеющее линейное строение. Оно состоит из двух стабильных пентатопов, стабильного тетраэдра и двух стабильных секущих треугольников. Каждый элемент древа фаз является независимой физико-химической системой. На рис. 3 также указаны кристаллизующиеся фазы для каждого стабильного элемента.
Характеристика фазового комплекса стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4
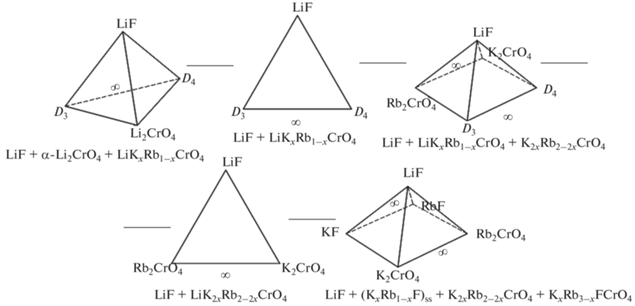
Теоретическое исследование фазового комплекса стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 предполагает анализ элементов огранения с целью прогнозирования фазовых равновесий внутри системы. В двух ограняющих системах – стабильном треугольнике LiF–LiRbCrO4–LiKCrO4 и Li2CrO4–LiRbCrO4–LiKCrO4 отсутствует нонвариантное равновесие, и для них характерно образование НРТР LiKxRb1–xCrO4. В стабильных треугольниках LiF–Li2CrO4–LiKCrO4 и LiF–Li2CrO4–LiRbCrO4 наблюдаются эвтектические равновесия и протекают следующие реакции: E 397 ж ⇄ LiF + α-Li2CrO4 + β-LiKCrO4; E 400 ж ⇄ LiF + α-Li2CrO4 + γ-LiRbCrO4 соответственно [26]. Развертка граневых элементов тетраэдра с ранее исследованными стабильными треугольниками представлена на рис. 4.
Рис. 4.
Развертка граневых элементов стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 системы Li+, K+, Rb+||F, ${\text{CrO}}_{4}^{{2 - }}.$

В системе прогнозируется фазовая реакция с моновариантным равновесием ж ⇄ LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss, где фаза (LiKxRb1 –xCrO4)ss – ограниченный твердый раствор на основе НРТР состава LiKxRb1–xCrO4, в котором растворены LiF и Li2CrO4, которая описывается линией, соединяющей две тройные эвтектики Е 397–Е 400. Прогнозируется образование точки экстремума данного фазового равновесия.
Экспериментальное исследование фазовых равновесий в стабильном тетраэдре LiF–LiRbCrO4–Li2CrO4–LiKCrO4
Экспериментальное изучение фазовых равновесий в многокомпонентных системах в настоящей работе основано на использовании проекционно-термографического метода при планировании эксперимента [29] и дифференциального термического анализа в качестве основного инструментального метода изучения фазовых равновесий [30–33]. На основе анализа развертки граневых элементов (рис. 4) для исследования было выбрано политермическое сечение a[LiF – 20%; LiRbCrO4 – 80%]–b[LiF – 20%; LiKCrO4 – 80%]–c[LiF – 20%; Li2CrO4 – 80%] в объеме кристаллизации фторида лития (рис. 4, 5).
Рис. 5.
Схема расположения разреза N–L в политермическом сечении a–b–c тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4.

В сечении a–b–c экспериментально исследован политермический разрез L[LiF – 20%; LiRbCrO4 – 40%; Li2CrO4 – 40%;]–N[LiF – 20%; LiKCrO4 – 40%; Li2CrO4 – 40%], который представлен на рис. 6. На T–x-диаграмме разреза N–L экспериментально установлена стабильность фазы твердого раствора (LiKxRb1–xCrO4)ss и наличие четверного минимума на линии моновариантного фазового равновесия ж ⇄ LiF + + (LiKxRb1–xCrO4)ss +α-Li2CrO4.
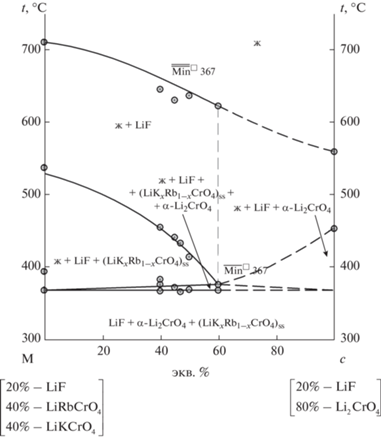
Для выявления состава четверного минимума Min◻ 367 был выбран политермический разрез M[LiF – 20%; LiRbCrO4 – 40%; LiKCrO4 – 40%]–c [LiF – 20%; Li2CrO4 – 80%], диаграмма состояния которого представлена на рис. 7. Ветви вторичной кристаллизации сходятся в точке ${{\overline {{\text{Min}}} }^{\square }}{\text{\;}}367,$ которая является проекцией точки Min◻ 367 на плоскость секущего треугольника a–b–c.
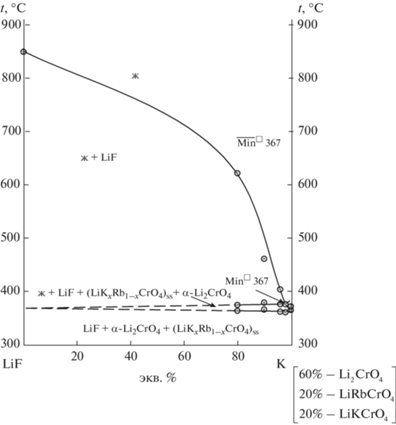
Для выявления состава четверного минимума Min◻ 367 изучен политермический разрез LiF–K, проходящий через точку ${{\overline {{\text{Min}}} }^{\square }}{\text{\;}}367.$ На рис. 8 представлена Т–х-диаграмма данного разреза. Из разреза выявлен состав и температура четверного минимума Min◻ 367: LiF – 2%, Li2CrO4 – 58.8%, LiRbCrO4 – 19.6%, LiKCrO4 – 19.6% или 2% LiF + + 78.4% Li2CrO4 + 9.8% Rb2CrO4 + 9.8% K2CrO4, tпл = 367°С [34].
3D-моделирование фазового комплекса стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4
Экспериментальные исследования подтвердили теоретический прогноз фазового комплекса системы, что позволило построить компьютерную 3D-модель фазового комплекса стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 (рис. 9). Модель представляет собой проекцию гиперповерхности ликвидуса на тетраэдр составов четырехкомпонентной системы. Построение модели выполнено в программе КОМПАС 3D [35]. Компьютерная модель демонстрирует фазовые превращения в системах. С помощью этих моделей можно прогнозировать процессы кристаллизации для любого состава систем. Базовые геометрические элементы модели представлены в табл. 1 [36].
Рис. 9.
Проекция модели стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 четырехкомпонентной взаимной системы Li+, K+, Rb+||F–, ${\text{CrO}}_{4}^{{2 - }}$ на плоскость.
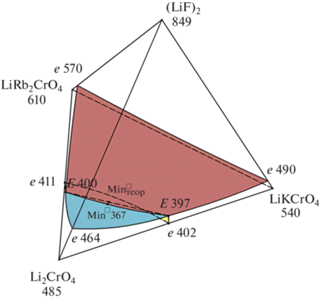
Таблица 1.
Фазовые равновесия, протекающие в стабильном тетраэдре LiF–Li2CrO4–LiRbCrO4–LiKCrO4
| Фазовое состояние | Количество фаз | Степень свободы | Геометрический элемент | Тип равновесия |
|---|---|---|---|---|
| ж ⇄ LiF | 2 | 3 | Объем | Тривариантное |
| ж ⇄ Li2CrO4 | 2 | 3 | Объем | Тривариантное |
| ж ⇄ (LiKxRb1–xCrO4)ss | 2 | 3 | Объем | Тривариантное |
| ж ⇄ LiF + Li2CrO4 | 3 | 2 | Поверхность | Дивариантное |
| ж ⇄ LiF + (LiKxRb1–xCrO4)ss | 3 | 2 | Поверхность | Дивариантное |
| ж ⇄ Li2CrO4 + (LiKxRb1–xCrO4)ss | 3 | 2 | Поверхность | Дивариантное |
| ж ⇄ LiF + Li2CrO4 + (LiKxRb1–xCrO4)ss | 4 | 1 | Линия | Моновариантное |
Для пересчета из координат состава некоторой фигуративной точки i в концентрационном тетраэдре квазичетверной системы LiF–Li2CrO4–LiRbCrO4–LiKCrO4 (барицентрическая система координат) в декартовую систему координат 0xyz, которая используется программой КОМПАС 3D и для обратного пересчета используются матричные уравнения, приведенные в [37].
3D-модель позволила спрогнозировать состав четверного минимума Min◻ 367, которому соответствует точка ${\text{Min}}_{{{\text{теор}}}}^{\square }$ (рис. 9), – 2.8% LiF + + 57.7% Li2CrO4 + 19.7% LiRbCrO4 + 19.7% LiKCrO4. Выдвинуто предположение, что данная точка располагается посередине линии Е 397–Е 400 в 3D-модели. При сравнении с экспериментальными значениями рассчитали относительную ошибку моделирования состава искомой точки по формуле (с учетом аддитивного вклада каждого компонента смеси):
где j – компонент в смеси, k – число компонентов; ${{{{\delta }}}_{j}} = \frac{{\left| {x_{j}^{'} - {{x}_{j}}} \right|}}{{{{x}_{j}}}}$ – относительная ошибка по содержанию j-ого компонента; xj – мольное содержание (в %) j-ого компонента, полученное экспериментально; $x_{j}^{'}$ – мольное содержание (в %) j-ого компонента, полученное теоретически при помощи моделирования.Полученное значение δош = 2.19% указывает на адекватность моделирования фазового комплекса данной системы при помощи 3D-модели для прогноза фазовых равновесий.
Выполнен количественный и качественный прогноз кристаллизующихся фаз для данной точки. Для этого составлено уравнение материального баланса в эквивалентном соотношении (2), которое будет иметь вид:
(2)
$\begin{gathered} {\text{ж(}}2{\text{LiF}} + 78.4{\text{L}}{{{\text{i}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{4}} + \\ + \,\,9.8{\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + 9.8{{{\text{K}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{4}}) = \\ = a{\text{LiF}} + b{\text{Li}}{{{\text{K}}}_{x}}{\text{R}}{{{\text{b}}}_{{1--x}}}{\text{Cr}}{{{\text{O}}}_{4}} + c\alpha {\text{ - L}}{{{\text{i}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{4}}. \\ \end{gathered} $Здесь для упрощения расчета вместо фазы (LiKxRb1 –xCrO4)ss использована фаза LiKxRb1 –xCrO4 без содержания компонентов фторида лития и хромата лития. Далее для выявления значений a, b, c и x составлена и решена система уравнений ионного баланса системы [27]:
(3)
$\left\{ \begin{gathered} {\text{L}}{{{\text{i}}}^{ + }}{\text{:}}~\,\,158.8 = a + b + 2c \hfill \\ {\text{R}}{{{\text{b}}}^{ + }}{\text{:}}~~19.6 = b\left( {1 - x} \right) \hfill \\ {{{\text{K}}}^{ + }}{\text{:}}~\,\,19.6 = bx \hfill \\ {{{\text{F}}}^{ - }}{\text{:}}~~2 = a \hfill \\ {\text{CrO}}_{4}^{{2 - }}{\text{:}}~~98 = b + c. \hfill \\ \end{gathered} \right.$В результате решения системы уравнений (3) составлена фазовая реакция для фигуративной точки Min◻ 367:
(4)
$\begin{gathered} {\text{ж(}}2{\text{LiF}} + 78.4{\text{L}}{{{\text{i}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + \\ + \,\,9.8{\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{4}} + 9.8{{{\text{K}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{4}}) = \\ = 2{\text{LiF}} + 39.2{\text{Li}}{{{\text{K}}}_{{0.5}}}{\text{R}}{{{\text{b}}}_{{0.5}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{ }}58.8\alpha {\text{ - L}}{{{\text{i}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}. \\ \end{gathered} $Для изучаемой системы LiF–Li2CrO4–LiRbCrO4–LiKCrO4 построены 3D-модели изотермических сечений при температуре четырехкомпонентного минимума Min◻ 367 (рис. 10) и при чуть более высокой температуре – 370°С (рис. 11). Данные модели носят прогностический характер. В табл. 2 и 3 представлено описание пространственных фазовых областей. Фазовая область моновариантного равновесия в четырехкомпонентных системах для изотермического сечения, согласно правилу фаз Гиббса и понятию “базовый геометрический элемент для фазовой области” [36, 38], представляет собой тетраэдр (четыре точки однозначно описывают геометрию фазовой области). Однако стоит отметить, что при температуре минимума существует вырожденная четырехфазная область моновариантного равновесия ж ⇄ LiF + Li2CrO4 + (LiKxRb1 –xCrO4)ss, представляющая собой критический коннодный треугольник. За состав равновесной жидкой фазы отвечает точка минимума Min◻ 367. При повышении температуры в системе область жидкости приобретает локальный объем, который описывается фигурой (табл. 3), моновариантное равновесие описывается двумя четырехфазными областями – тетраэдрами (рис. 11).
Рис. 10.
Концентрационный тетраэдр изотермического сечения при 367°С системы LiF–Li2CrO4–LiRbCrO4–LiKCrO4.

Рис. 11.
Концентрационный тетраэдр изотермического сечения при 370°С системы LiF–Li2CrO4–LiRbCrO4‒LiKCrO.

Таблица 2.
Фазовые области в концентрационном тетраэдре LiF–Li2CrO4–LiRbCrO4–LiKCrO4 при 367°С (рис. 10)
| Фазовая область | Количество фаз | Степень свободы | Базовые геометрические элементы | Дополнительные геометрические элементы, фигура области |
|---|---|---|---|---|
| ж + LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss | 4 | 0 | Четыре точки: (LiF)2, Li2CrO4, a, Min□ 367 | Треугольник (LiF)2–Li2CrO4–a |
| LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss | 3 | 1 | Три линии: LiKCrO4–a, LiF*, Li2CrO4* |
Фигура LiKCrO4–a–(LiF)2–Li2CrO4, схожая с тетраэдром |
| LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss | 3 | 1 | Три линии: LiRbCrO4–a, LiF*, Li2CrO4* |
Фигура LiRbCrO4–a–(LiF)2–Li2CrO4, схожая с тетраэдром |
| LiF + (LiKxRb1–xCrO4)ss | 2 | 2 | Две поверхности: LiKCrO4–a–LiRbCrO4–b– LiKCrO4 и (LiF)2** |
Фигура LiKCrO4–a–LiRbCrO4– b–LiKCrO4–(LiF)2, схожая с тетраэдром |
| α-Li2CrO4 + + (LiKxRb1–xCrO4)ss | 2 | 2 | Две поверхности: LiKCrO4–a–LiRbCrO4–c– LiKCrO4 и Li2CrO4** |
Фигура LiKCrO4–a–LiRbCrO4– c–LiKCrO4–(LiF)2, схожая с тетраэдром |
| (LiKxRb1–xCrO4)ss | 1 | 3 | Один объем | Фигура тетрагональная бипирамида a–b–c–LiKCrO4–LiRbCrO4 |
Таблица 3.
Фазовые области в концентрационном тетраэдре LiF–Li2CrO4–LiRbCrO4–LiKCrO4 при 370°С (рис. 11)
| Фазовая область | Количество фаз | Степень свободы | Базовые геометрические элементы | Дополнительные геометрические элементы, фигура области |
|---|---|---|---|---|
| ж + LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss(a) | 4 | 0 | Четыре точки: (LiF)2, Li2CrO4, a, d | Тетраэдр (LiF)2–Li2CrO4–a–d |
| ж + LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss(b) | 4 | 0 | Четыре точки: (LiF)2, Li2CrO4, a, c | Тетраэдр (LiF)2–Li2CrO4–a–c |
| ж + LiF + Li2CrO4 | 3 | 1 | Три линии: (LiF)2*; Li2CrO4*; (c–e–d) | Фигура, похожая на тетраэдр (LiF)2, Li2CrO4, c–e–d |
| ж + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss (a–b) | 3 | 1 | Три линии: Li2CrO4*; (c–g–d); (a–b) | Фигура, похожая на тетраэдр Li2CrO4; (c–e–d); a, b |
| ж + LiF + + (LiKxRb1–xCrO4)ss (a–b) | 3 | 1 | Три линии: (LiF)2*; (c–f–d); (a–b) | Фигура, похожая на тетраэдр (LiF)2, (c–f–d), a, b |
| LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss (LiKCrO4 – a) | 3 | 1 | Три линии: (LiF)2*; Li2CrO4*; LiKCrO4 –a | Фигура, похожая на тетраэдр (LiF)2, Li2CrO4, LiKCrO4, a |
| LiF + α-Li2CrO4 + + (LiKxRb1–xCrO4)ss (LiRbCrO4 – b) | 3 | 1 | Три линии: (LiF)2*; Li2CrO4*; LiRbCrO4 –b | фигура, похожая на тетраэдр (LiF)2*, Li2CrO4*, LiRbCrO4, b |
| LiF + α-(LiKxRb1–xCrO4)ss | 2 | 2 | Две поверхности: (LiF)2** и LiKCrO4–i–LiRbCrO4–b–a –LiKCrO4 | Фигура, ограниченная тремя поверхностями: LiKCrO4–i–LiRbCrO4–b–a–LiKCrO4;
LiF –LiRbCrO4–b–
a–LiKCrO4–LiF; LiF–LiRbCrO4–i– LiKCrO4–LiF |
| Α-Li2CrO4 + (LiKxRb1–xCrO4)ss | 2 | 2 | Две поверхности: Li2CrO4** и LiKCrO4–h–LiRbCrO4–b–a –LiKCrO4 | Фигура, ограниченная тремя поверхностями: LiKCrO4–h–LiRbCrO4–b–a–LiKCrO4; Li2CrO4–LiRbCrO4–b–a–LiKCrO4–Li2CrO4; Li2CrO4–LiRbCrO4–h–LiKCrO4–Li2CrO4 |
| ж | 1 | 3 | Локальный объем | Фигура c–e–d–f–c–g–d |
| (LiKxRb1–xCrO4)ss | 1 | 3 | Локальный объем | Фигура LiKCrO4–LiRbCrO4–b–a–LiKCrO4 –i–LiRbCrO4–h–LiKCrO4 |
ЗАКЛЮЧЕНИЕ
1. Выполнен литературный обзор по элементам огранения четырехкомпонентной взаимной системы Li+, K+, Rb+||F, ${\text{CrO}}_{4}^{{2 - }}.$ Все ограняющие системы изучены ранее.
2. Проведено разбиение фазового комплекса системы на стабильные элементы, получено древо фаз, спрогнозированы кристаллизующиеся фазы. Система характеризуется образованием непрерывных рядов твердых растворов между парами солей KF и RbF, K2CrO4 и Rb2CrO4, LiKCrO4 и LiRbCrO4, K3FCrO4 и Rb3FCrO4, что, по всей видимости, обусловлено изоструктурными строением веществ и близостью значений ионных радиусов атомов калия и рубидия.
3. Методом ДТА изучен фазовый комплекс стабильного тетраэдра LiF–Li2CrO4–LiRbCrO4–LiKCrO4 четырехкомпонентной взаимной системы Li+, K+, Rb+||F–, ${\text{CrO}}_{4}^{{2 - }}.$ Определены состав и температура плавления четверного минимума моновариантного фазового равновесия ж ⇄ LiF + + α-Li2CrO4 + (LiKxRb1–xCrO4)ss. Даны количественные характеристики кристаллизующихся фаз.
4. Построена 3D-модель фазового комплекса системы по данным элементов огранения, которая позволяет строить изотермические и политермические сечения. В работе приведены два изотермических сечения.
5. Спрогнозирован состав четверного минимума на основе 3D-модели системы. Сравнение полученных данных с экспериментальными значениями дает относительную ошибку 2.19%, что указывает на хорошую сходимость результатов.