Письма в ЖЭТФ, том 109, вып. 1, с. 65 - 71

Ангармонические эффекты 3-го порядка в ядерной квантовой

теории многих тел

С. П. Камерджиев¹⁾, М. И. Шитов

Национальный Исследовательский Центр “Курчатовский Институт”, 123182 Москва, Россия

Поступила в редакцию 25 октября 2018 г.

После переработки 14 ноября 2018 г.

Принята к публикации 15 ноября 2018 г.

Квантовая теория ангармонических эффектов 3-го порядка по амплитуде рождения фонона, раз-

витая В.А. Ходелем, обобщается для ядер со спариванием и для случая более точного описания низко-

энергетических коллективных фононов. Получено выражение для амплитуды перехода между двух-

фононным и однофононным состояниями. Выполнено сравнение полученного выражения с решением

аналогичной задачи, рассмотренной в рамках квазичастично-фононной модели. Показано, что рассмат-

риваемый нами подход содержит ряд новых эффектов, включая трех- и четырех-квазичастичные кор-

реляции в основном состоянии (backward-going graphs).

DOI: 10.1134/S0370274X19010132

1. Введение. Ангармонические эффекты, кото-

ческих ядер, основанная на методе ФГ и теории

рые количественно изучались в ядерной физике низ-

конечных ферми-систем (ТКФС) [13] и использую-

ких энергий, т.е. при энергиях возбуждения до 30-

щая условия согласования между средним полем и

40 МэВ, можно разделить на 2 вида: эффекты 2-го

эффективным ядерным взаимодействием, что поз-

и 3-го порядков по амплитуде рождения фонона g,

волило избежать введения новых параметров. Ис-

если предполагается относительно слабый ангармо-

ходным положением здесь является использование

низм, когда существует малый параметр по ампли-

МХФ (точнее, приближения Бора-Моттельсона для

туде g (в дальнейшем эффекты g² и g³). Это озна-

амплитуды g) и эффектов так называемого фонон-

чает, что задача решается поэтапно: сначала можно

ного тэдпола (tadpole), который, по определению, со-

построить фононы, а затем рассматривать их вза-

держит величину δ₁g₂ ≡ g₁₂, где δ₁g₂ есть вариация

имодействия. Указанный параметр существует для

амплитуды рождения фонона 2 в поле другого фо-

магических ядер [1] и для полумагических ядер [2].

нона 1 (подробнее см. [14]).

Ангармонические поправки g² для магических

В анализе эффектов g² было показано, что для

ядер изучались давно в рамках теории ядерных по-

квадрупольных моментов фононов [7] и вероятностей

лей (TЯП) [1, 3], метода функций Грина (ФГ) [4].

переходов между однофононными состояниями [15] в

Для ядер со спариванием они изучались в рамках

магических и полумагических ядрах роль КОС коли-

ТЯП [5], метода ФГ [6, 7] и в рамках квазичастично-

чественно велика и разумное согласие с эксперимен-

фононной модели (КФМ) [8-10], подробнее см. [7].

том получается только за счет одновременного учета

В [7] впервые было сказано о новом эффекте трех-

эффектов КОС и ядерной поляризуемости, описыва-

квазичастичных корреляций в основном состоянии

емой в рамках МХФ, точнее ТКФС. Главное отли-

(КОС), которые, как оказалось, велики (в отличие

чие от КФМ [9] заключалось в учете КОС, в КФМ

от двухквазичастичных КОС, имеющихся в стан-

согласие с экспериментом получалось также за счет

дартном (квазичастичном) методе хаотических фаз

примешивания двухфононных компонент к волновой

((К)МХФ)) и объясняют половину эффекта. Следу-

функции рассматриваемого однофононного состоя-

ет отметить, что эти новые КОС в g² подходе фак-

ния, т.е. в выходе за рамки (К)МХФ подхода при

тически учитывались в рамках TЯП [5] и метода ФГ

описании фононов.

[6, 11], но количественно они не выделялись и не на-

Совершенно другая ситуация сложилась с ангар-

зывались.

моническими эффектами 3-го порядка - это воз-

Большую роль в изучении эффектов второго и

буждение трехфононных состояний, переходы меж-

третьего порядков сыграла работа [12] для маги-

ду двухфононными и однофононными состояниями и

др. Насколько мы знаем, они рассматривались лишь

¹⁾e-mail: kamerdzhiev_sp@nrcki.ru

в рамках КФМ и, как увидим, без учета КОС. По-

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

С. П. Камерджиев, М. И. Шитов

требность рассмотрении этих эффектов состоит не

M⁽³⁾ = V₀GGg₁Gg₂Gg₃ + V₀GGg₁₂Gg₃ + V₀GGg₁₂₃,

только в том, что есть (см. [9]) или планируется полу-

(2)

чить [10] соответствующие экспериментальные дан-

где g₁₂₃ = δ₁δ₂g₃ = δ₁g₂₃. В формулах мы нигде не

ные, прежде всего для вероятностей переходов, но

выписываем слагаемые, отличающиеся перестанов-

и в необходимости обоснования гипотезы Бринка-

кой фононов. Здесь и в дальнейшем величина g рас-

Акселя [16, 17] (подробнее см. [18]), на использова-

сматривается в рамках МХФ, точнее ТКФС:

нии которой фактически основана вся система рас-

g = FAg,

(3)

чета радиационных ядерных данных для реакторов

и астрофизики.

здесь F - эффективное взаимодействие нуклонов,

По этим причинам представляет интерес более

A - частично-дырочный пропагатор, представляю-

подробно и на современном языке рассмотреть под-

щий собой интеграл от двух ФГ G. То есть, в отличие

ход Ходеля [12] для эффектов 3-го порядка, что-

от [12], приближение Бора-Моттельсона для ампли-

бы понять специфику такого подхода, впервые вы-

туды g не используется.

делить вклад КОС и, по возможности, сравнить с

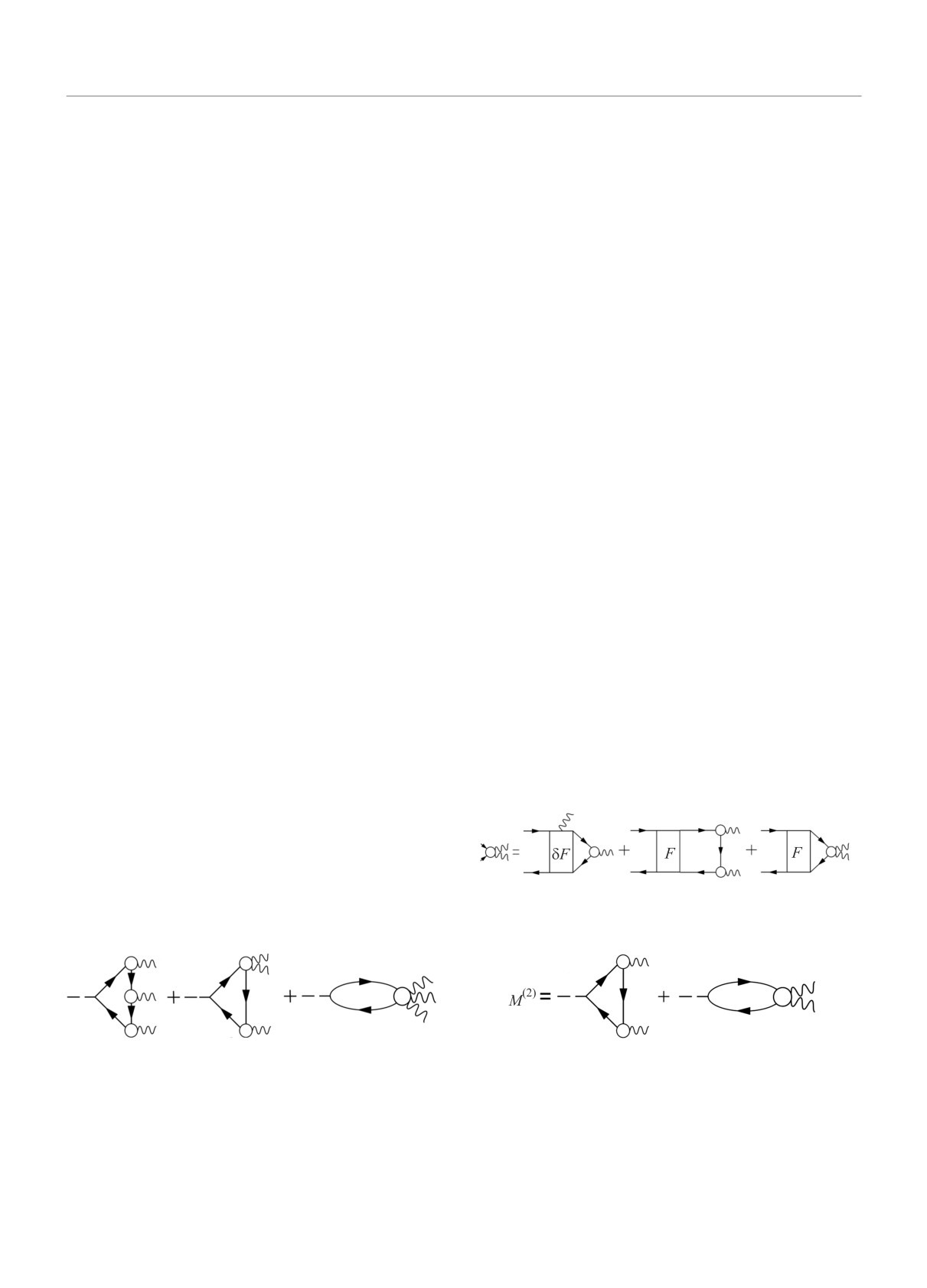
В формулу (2) (рис.1) входят “четырехугольник”

имеющимися подходами. Это является первой зада-

с тремя фононами, “треугольник” с амплитудой g₁₂

чей настоящей работы. Поскольку в работе [12] рас-

(эффекты фононного тэдпола), которые содержат,

сматривались только магические ядра и использова-

соответственно, интегралы от 4-x и 3-x ФГ и третий

лось приближение Бора-Моттельсона для амплиту-

график с блоком g₁₂₃, удовлетворяющим сложному

ды g, желательно избавиться от этих приближений и

интегральному уравнению с большим количеством

обобщить подход на случай ядер со спариванием. Это

свободных членов.

является второй задачей настоящей работы и выпол-

Проще пояснить смысл дальнейшего вывода для

няется впервые. Обобщение на спаривание позволит

M⁽³⁾ на примере более простой задачи ангармониче-

сравнить этот подход с конкретной задачей перехода

ских поправок 2-го порядка для величины M⁽²⁾, в

между двухфононным и однофононым состояниями,

которую входит только g₁₂. Для амплитуды перехо-

рассмотренной ранее в рамках КФМ [9].

да для двух фононов под действием внешнего поля

2. Диаграммный анализ эффектов 3-го по-

имеем (см. рис. 3):

рядка. Исходная амплитуда перехода M⁽³⁾ для воз-

M⁽²⁾ = V₀δ²G = V₀Gg₁Gg₂G + V₀GGg₁₂,

(4)

буждения внешним полем V₀ трех фононов выража-

ется через вариацию одночастичной ФГ под действи-

где

ем трех фононов [12], которые в этом разделе мы

обозначим для простоты как 1, 2, 3, где 1 - набор

g₁₂ = δ₁FAg₂ + F(δ₁A)g₂ + FAg₁₂.

(5)

квантовых чисел фонона с энергией ωs1 : Is1 , Ms1 и

Уравнение (5) получается вариацией уравнения

т.д.:

(3) для g в поле фонона, оно показано на рис. 2.

M⁽³⁾ = V₀δ³G = V₀δ₁δ₂δ₃G,

(1)

где, например, δ₃G = Gg₃G и g₃ - амплитуда рожде-

ния фонона. Последовательное варьирование в фор-

муле (1) приводит к символическому выражению для

M⁽³⁾, правую часть которого можно записать на язы-

ке диаграм Фейнмана в виде, представленном на

Рис. 2. Уравнение (5) в диаграммном виде

рис. 1.

Рис. 1. Правая часть формулы (2) в диаграммном ви-

Рис. 3. Выражение (4) в диаграммном виде

де. Пунктир означает внешнее поле V0, кружки с од-

ной волнистой линией обозначают амплитуду рожде-

Итерируя (5) по эффективному взаимодействию F,

ния фонона g, кружки с двумя и тремя волнистыми

получаем следующее выражение для g₁₂

линиями обозначают, соответственно, величины g12 и

g123, линии со стрелками - функции Грина

g₁₂ = Γ(δ₁A)g₂ + (δ₁Γ)Ag₂,

(6)

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

Ангармонические эффекты 3-го порядка в ядерной квантовой теории многих тел

где величины Γ и δ_LΓ удовлетворяют интегральным

уравнениям [12]

Γ = F + FAΓ,

(7)

δ_LΓ = δ_LF + FAδ_LΓ.

(8)

Подставим (6) в (4) и воспользуемся соотношением

между амплитудой Γ и вершиной V [13]

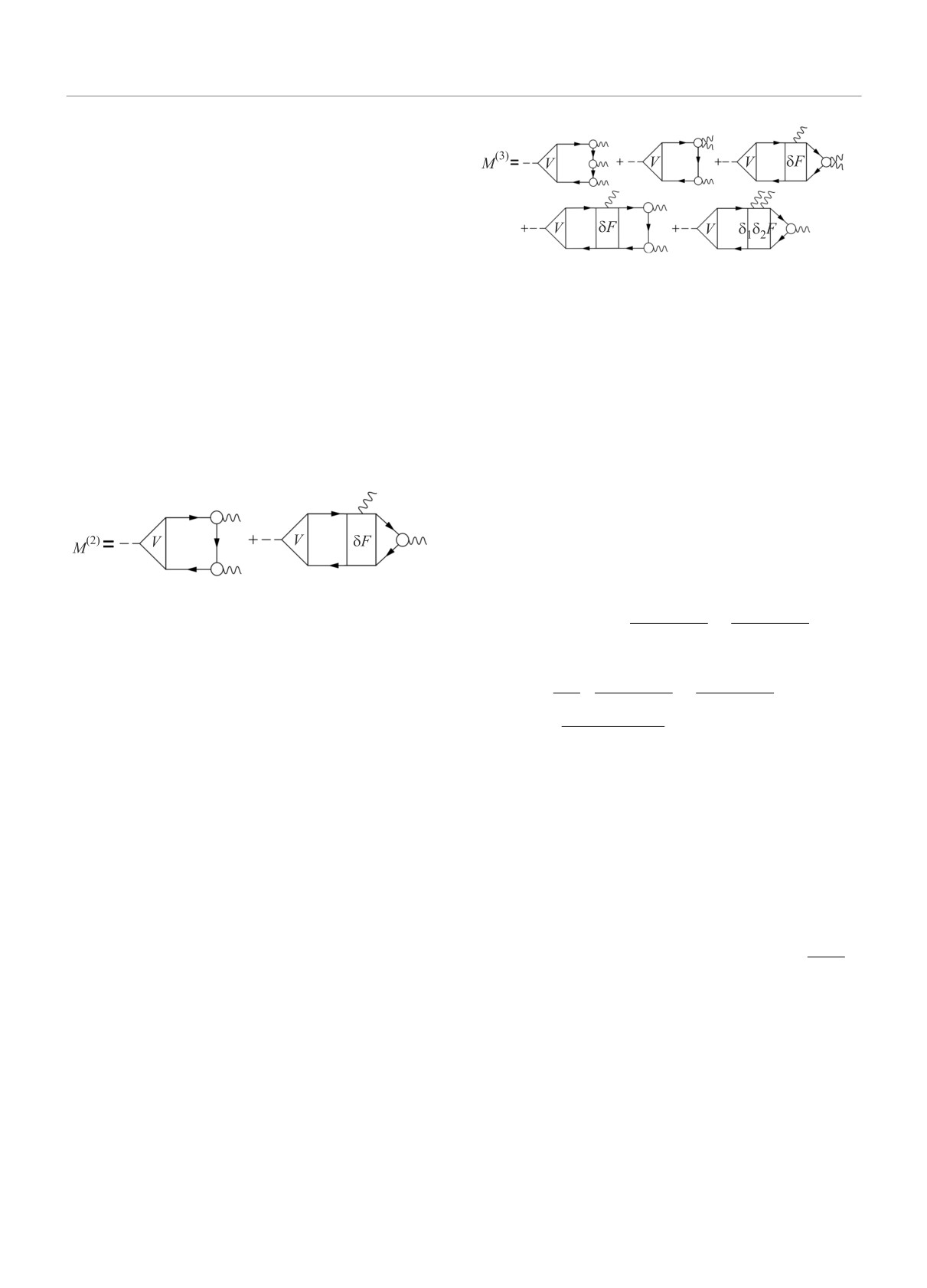
Рис. 5. Выражение (12) в диаграммном виде

V = V₀ + ΓAV₀.

(9)

По аналогии с результатами о малости графиков

с δF, полученными в [7], можно думать что третий,

Учитывая соотношение V₀GGδ₁Γ = V GGδ₁F , полу-

четвертый и пятый графики на рис. 5, содержащие

чаемое из уравнения (8) умножением на V GG, нахо-

δF, δ₁δ₂F, также дают малый вклад. Второй график

дим окончательное выражение для M⁽²⁾:

на рис. 5 с g₁₂, который содержит эффекты фонон-

ного тэдпола, насколько мы знаем, нигде не обсуж-

M⁽²⁾ = V GGGg₁g₂ + V GGδ₁FGGg₂,

(10)

дался, и в дальнейшем для нашей задачи с тремя

которое представлено на рис. 4.

фононами мы рассматриваем только первый график

с четырьмя ФГ на рис. 5. Для задачи с тремя равно-

правными фононами, рассмотренной в [12], необхо-

димо учитывать перестановки фононов.

3. Обобщение на спаривание. Чтобы на язы-

ке ФГ рассмотреть ядра со спариванием, следует ис-

пользовать четыре ФГ: G, G^h, F⁽¹⁾, F⁽²⁾ [13],

Рис. 4. Выражение (10) в диаграммном виде. Треуголь-

u²¹

v²¹

ник с пунктиром означает эффективное поле V , опре-

G₁(ε) = G^h1(-ε) =

деляющее поляризуемость ядра

ε - E₁ + ıδ

ε + E₁ - ıδ

F⁽¹⁾¹(ε) = F⁽²⁾¹(ε) =

(13)

[

]

Таким образом, окончательное выражение для

Δ₁

M⁽²⁾ содержит эффект поляризуемости ядра, описы-

2E₁

ε - E₁ + ıδ

ε + E₁ - ıδ

ваемый в рамках RPA, точнее ТКФС (первое слагае-

√

мое), и второе слагаемое с δF . Как показали расчеты

где E₁ =

(ε₁ - µ)² + Δ²¹, u²¹ = (E₁ + ε₁ - µ)/ 2E₁ =

в [7], вклад второго слагаемого мал.

= 1-v²¹. Действуя по аналoгии с нашей работой для

Чтобы получить аналогичную формулу для M⁽³⁾,

задачи со спариванием [7], запишем первый график

надо рассмотреть более сложное интегральное урав-

для M⁽³⁾ с учетом этих ФГ. При этом, как и в [7],

нение для g₁₂₃, которое получается варьированием

учитываем только ph-вершины в уравнении для эф-

уравнения (5):

фективного поля и не учитываем pp- и hh-вершины,

которые обычно дают малый вклад, их учет привел

g₁₂₃ = δ₁δ₂FGGg₃ + δ₁FGg₂Gg₃G + δ₁FGGg₁₂ +

бы к огромному усложнению задачи. Итак, в случае

+ FGg₁₂Gg₃G + FGg₁Gg₂Gg₃G + FGGg₁₂₃

(11)

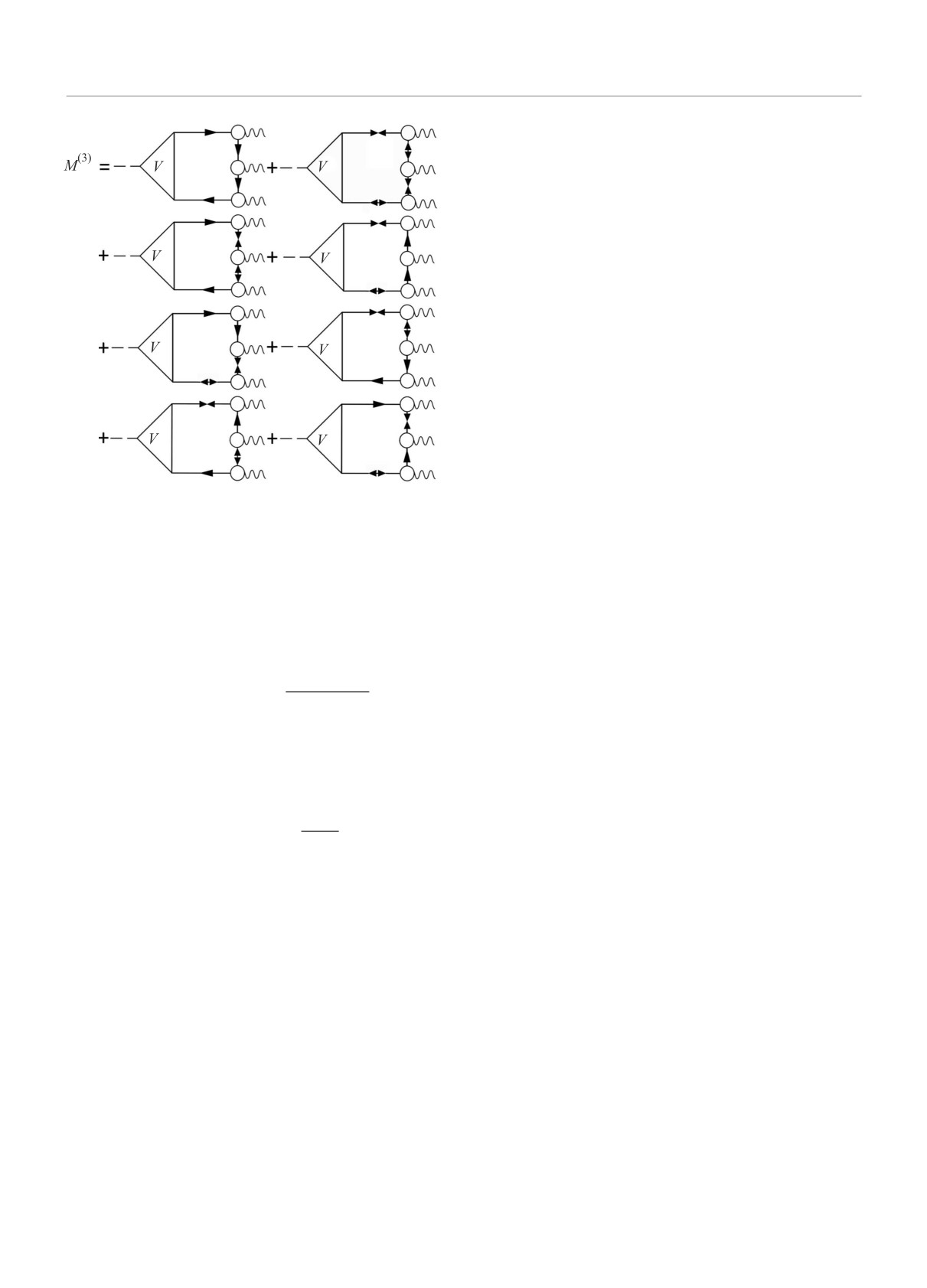
спаривания необходимо рассмотреть 7 типов графи-

ков. Все они, кроме графика с четырьмя аномальны-

и содержит 5 (а не 2, как в g₁₂ (5)) различных свобод-

ми ФГ, содержат произведения ФГ F⁽¹⁾¹F⁽²⁾² и инте-

∫

ных членов, не считая подобных от перестановки фо-

гралы вида

GGF⁽¹⁾F⁽²⁾dǫ с множителямиΔ1Δ² и_4E

1E2

нонов. Повторяя по аналогии вывод для получения

представлены на рис. 6 для M⁽³⁾ вместе с графика-

M⁽²⁾, после длительного вывода находим выражение

ми, содержащими четыре ФГ G и четыре аномаль-

для M⁽³⁾:

ных ФГ.

Из (13) следует что в наши интегралы от 4-х ФГ

M⁽³⁾ = V Gg₁Gg₂Gg₃G + V Gg₁₂Gg₃G +

всегда входят произведения квадратов коэффициен-

+ V GGδ₁FGGg₁₂ + V GGδ₁FGg₁Gg₂G +

тов Боголюбова v²¹ и u²¹. Комбинации коэффициен-

+ V Gδ₁δ₂FGg₃G.

(12)

тов v₁ и u₁ используются в других подходах, преж-

де всего в КФМ. Поэтому полезно знать (и мы бу-

На языке диаграмм Фейнмана его можно записать в

дем использовать) соответствующие формулы “при-

виде, показанном на рис. 5.

ведения к квадратам”. Например, общий множитель

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

5^∗

С. П. Камерджиев, М. И. Шитов

(n₁, j₁, l₁, m₁), Ai - интегралы от 4-х ФГ, вершина

V и амплитуда gsi удовлетворяют, соответственно,

уравнениям (9) и (3), в которых следует уже учесть

спаривание, см. [13]. Соответствующие 8 графиков

без перестановок фононов показаны на рис.6.

Представляет интерес рассмотреть конкретный

случай перехода между двухфононным и однофо-

нонным состояниями, для которого имеются экспе-

риментальные данные и расчеты в рамках других

моделей. В частности, в [9] была рассмотрена задача

о Е1 переходе между конкретными двух-фононным

и однофононным состояниями в ядрах со спаривани-

ем. Авторы вывели формулу (10), рассчитали веро-

ятность наблюдаемых Е1 переходов между двухфо-

нонным 1^- состоянием, состоящем из низколежащих

однофононных 2⁺- и 3^- состояний, и однофононным

2⁺ состоянием в трех ядрах Sn, Sm, Nd, и получи-

ли хорошее согласие с экспериментом. По аналогии

с [9] рассмотрим переход между конкретным двух-

Рис. 6. Амплитуда перехода в ядрах со спариванием,

фононным состоянием [1 × 2] → 4 на однофононное

полученная при учете лишь первого слагаемого в (12),

состояние 4. В формулу (10)[9] входит общий множи-

рис. 5. Линии с двумя входящими и двумя выходящими

тель u⁺¹²u⁺¹³u⁺²⁴u⁺⁴³ (u⁺¹² ≡ u₁v₂ + v₁u₂), который про-

стрелками означают ФГ F⁽¹⁾ и F⁽²⁾ (см. текст)

исходит от множителя u⁺¹² в (10) [9] и содержится в

определениях для амплитуд ψ, φ оператора рожде-

u⁺¹²u⁺¹³u⁺²⁴u⁺⁴³, где u⁺¹² = u₁v₂ + v₁u₂, входящий в фо-

ния фонона, описываемого в рамках КМХФ. Соот-

мулу (10) [9], выражается через v²¹ и u²¹ так:

ветствующее приведение к квадратам определяется

формулой (14).

u⁺¹²u⁺¹³u⁺²⁴u⁺⁴³ =

В результате интегрирования 4-х ФГ G

Δ₁Δ₂Δ₃Δ₄

=u²¹v²²v²³u²⁴ + v²¹u²²u²³v²⁴ +

∫

2E₁E₂E₃E₄

A^(1)1234 = G₁(ε)G₂(ε - ω) ×

C₁₂(u²³v²⁴ + v²³u²⁴) + C₁₃(u²²v²⁴ + v²²u²⁴) +

C₁₄(u²²v²³ + v²²u²³) + C₂₃(u²¹v²⁴ + v²¹u²⁴) +

× G₃(ε - ω₁)G₄(ε - ω + ω₂)dε

(16)

+ C₂₄(u²¹v²³ + v²¹u²³) + C₃₄(u²¹v²² + v²¹u²²) ≡

с законом сохранения (ω - энергия перехода)

≡u²¹v²²v²³u²⁴ + v²¹u²²u²³v²⁴ + b₁₂₃₄,

(14)

ω=ω₁ +ω₂ -ω₄

(17)

и b₁₂₃₄.

E1E2

4. Общая схема расчета. Сравнение с

получаются 14 слагаемых. В том числе, 6 слагаемых

квазичастично-фононной моделью. В случае

содержат по два множителя вида u²u² или v²v² и в

равноправных фононов [12], следует рассматривать

пределе отсутствия спаривания соответствуют слу-

шесть (число сочетаний) графиков, содержащих

чаю, когда две частицы (дырки) находятся выше по-

ФГ G. Для задачи со спариванием необходимо

верхности Ферми, а две дырки (частицы) находят-

добавить 7 × 6 = 42 графика с аномальными ФГ

ся ниже поверхности Ферми. Из них 2 слагаемых с

F⁽¹⁾, F⁽²⁾, итого 48 диаграмм с 48 интегралами от

числителями u²¹v²²v²³u²⁴ и v²¹u²²u²³v²⁴, как видно из фор-

4-х ФГ, каждый из которых имеет весьма сложный

мулы “приведения” (14), содержатся в формуле (10)

алгебраический вид. Формула для амплитуды M⁽³⁾,

[9]. 4 слагаемых с иным наборам коэффициентов Бо-

квадрат которой определяет вероятность перехода,

голюбова, а именно [v²¹u²²v²³u²⁴ + u²¹v²²u²³v²⁴ + b₁₂₃₄] и

имеет следующий общий вид:

[v²¹v²²u²³u²⁴ + u²¹u²²v²³v²⁴ + b₁₂₃₄] отсутствуют в формуле

∑

(10) [9]. Эта группа 4-х слагаемых содержит знамена-

M⁽³⁾ =

A^(i)1234(ω, ωs1 , ωs2 ωs3 ).

i=1-48,1234

тели (E₁₂ ± ω), где 1, 2-индексы вершины V , и более

(15)

сложные знаменатели с суммой энергий двух квази-

В этом выражении нижние индексы 1 обознача-

частиц и двух фононов. По аналогии с [7, 15] мы на-

ют полный набор одночастичных квантовых чисел

зываем их четырех-квазичастичными корреляциями

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

Ангармонические эффекты 3-го порядка в ядерной квантовой теории многих тел

в основном состоянии (КОС), они, как будет видно,

ветствующих интегралов от 4-х ФГ и отделению уг-

отсутствуют в формуле (10) [9].

ловых переменных получаем следующие результаты

Кроме слагаемых типа u²u²v²v² в результате ин-

для приведенного матричного элемента от амплиту-

тегрирования 4-х ФГ G в (16) получаются 8 сла-

ды EL-перехода M⁽³⁾ из двухфононного состояния с

гаемых с одним из двух коэффициентов Боголюбо-

моментом I₃ на однофононное состояние с моментом

ва и тремя другими коэффициентами типа u²v²v²v²

I₄, которую надо сравнивать с формулой (10) [9]:

или u²u²u²v², а именно [v²¹u²²u²³u²⁴ + u²¹v²²v²³v²⁴ + ...],

[u²¹v²²u²³u²⁴ +v²¹u²²v²³v²⁴ +...], [v²¹v²²u²³v²⁴ +u²¹u²²v²³u²⁴ +...] и

〈[s₁ × s₂]I3 ∥ M⁽³⁾ ∥ s₄〉 =

∑

[v²¹v²²v²³u²⁴ + u²¹u²²u²³v²⁴ + ...]. В пределе отсутствия спа-

(-1)^J ×

ривания они соответствуют случаю, когда одна ча-

1234

стица (дырка) находится выше поверхности Ферми

× (u²¹v²²v²³u²⁴ + v²¹u²²u²³v²⁴ + b₁₂₃₄) ×

и три дырки (частицы) находятся ниже поверхности







j₂

j₁



Ферми. Как видно из (14), таких слагаемых нет в

j₄

j₃

I₄

формуле (10)[9].

×



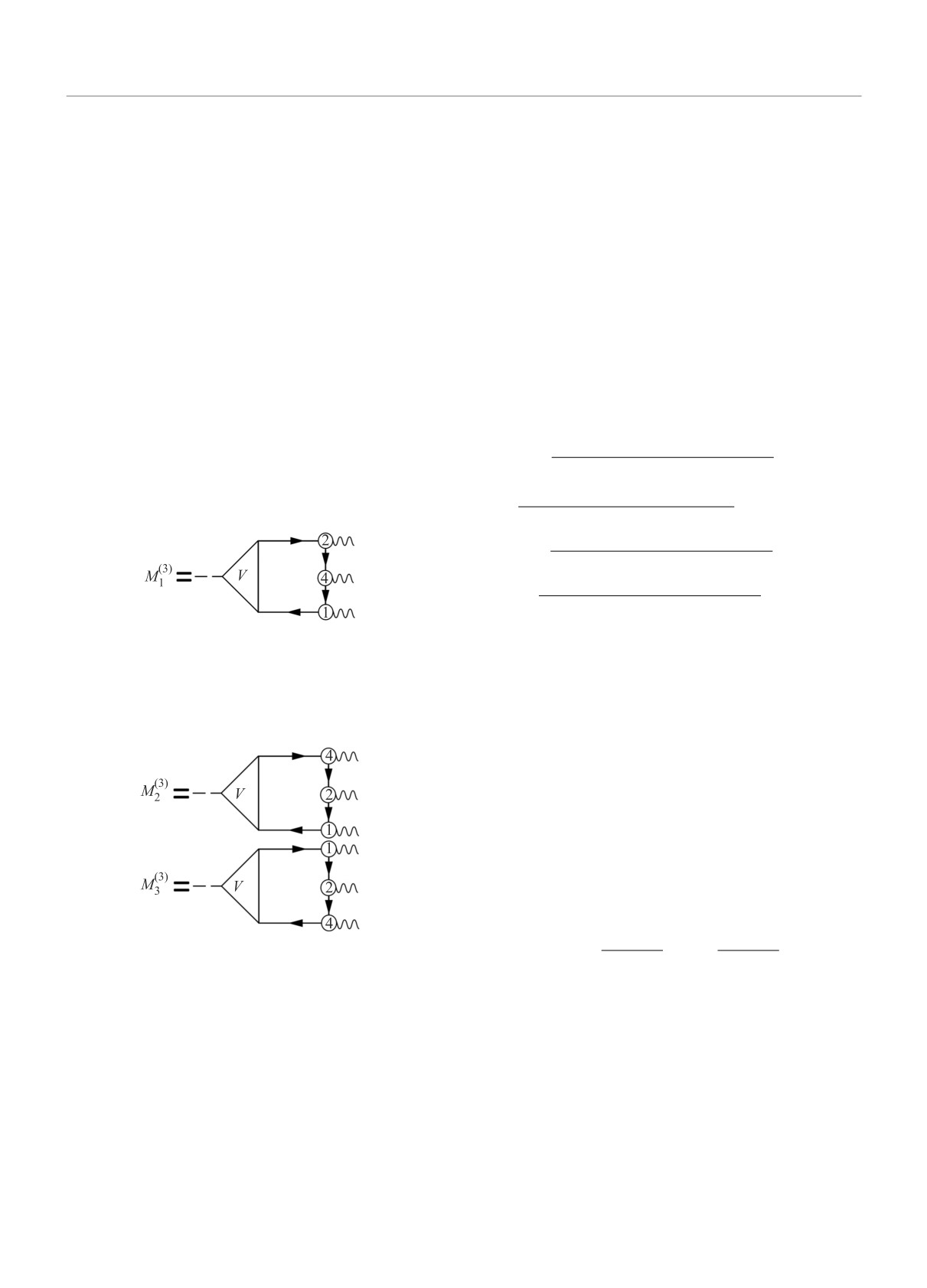
Учитывая, как уже говорилось, только первый

I₂

I₁

график на рис. 5, для нашей конкретной задачи со

[(

спариванием на языке ФГ следует рассмотреть 3 гра-

(E₁₃ + ω₁)(E₂₄ + ω₂)(E₃₄ + ω₄)

фика с ФГ G (аналог задачи без спаривания): гра-

)

фик, показанный на рис. 7, и графики с перестав-

×δI3J +

(E₁₃ - ω₁)(E₂₄ - ω₂)(E₃₄ - ω₄

(

(E₁₃ + ω₁)(E₂₄ - ω₂)(E₃₄ - ω₄)

)

13 - ω1)(E24 + ω2)(E34 + ω4)

{

}]

L I₄

I₃

Рис. 7. Пример диаграммы, порождающей группу гра-

× (2J + 1) ·

+ [GSC] + [uvvv], (18)

I₁

I₂

фиков, приводящих к получению первого слагаемого в

формуле (10) [9], см. текст

где V₁₂, g

- приведенные матричные элементы.

Здесь (кроме индексов при энергиях фононов ω_i)

индексы 1 означают набор одночастичных кванто-

вых чисел (n₁, j₁, l₁) для сферического ядра. Сла-

гаемое с первой круглой скобкой c 9j-символом и

фактором δI3J соответствует первому слагаемому с

9j-символом, а второе слагаемое со второй круглой

скобкой с 9j- и 6j-символами второму слагаемому с 9j-

и 6j-символами в формуле (10) [9], поскольку вели-

чины ψ^s12 и φ^s12 в операторе рождения КМХФ фонона

в КФМ имеют вид (с точностью до нормировки):

u⁺¹²

ψ^s12 ∼

,φ^s12 ∼

(19)

Рис. 8. Пример диаграмм, порождающих группу гра-

E₁₂ - ω_s

E₁₂ + ω_s

фиков, приводящих к получению второго слагаемого в

формуле (10) [9], см. текст

Группа из 16 графиков типа рис. 7, но без КОС,

определяет первое слагаемое в формуле (10) [9], со-

ленными фононами 2 → 4 и 1 → 4, показанные на

держащее 9j-символ, если при отделении угловых пе-

рис. 8. Далее следует добавить такие же графики с

ременных для суммы 4-х коэффициентов Клебша-

перестановками фононов 1 и 2, а также, для учета

Гордана воспользоваться формулой (A.165) из книги

спаривания, к каждому из вышеупомянутых доба-

А.Л. Барабанова [19]. Группа из 32 графиков типа

вить еще аналогичные 7 графиков, рис. 6, с аномаль-

рис. 8, но без КОС, дает второе слагаемое в форму-

ными ФГ F⁽¹⁾, F⁽²⁾ - всего 6 + 6 · 7 = 48 графи-

ле (10) [9], содержащее 9j- и 6j-символы. Выписанная

ков. После длительных вычислений по взятию соот-

часть в (18) полностью соответствует формуле (10)

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

С. П. Камерджиев, М. И. Шитов

[9]. Невыписанные и значительно более длинные ча-

рен частный случай перехода между двух-фононным

сти, обозначенные как [GSC] и [uvvv], соответствуют

и одно-фононным состояниями. При этом показано,

указанным выше КОС (4 слагаемых в интеграле (16)

что, если не учитывать четырех-(квази)частичные

и 8 слагаемых с [uvvv]). Половина из них содержит

КОС как в магических ядрах, так и в ядрах со спа-

знаменатели (E₁₂ ± ω), характерные для изученных

риванием, получается случай, аналогичный изучен-

ранее КОС 2-го порядка [7, 15].

ному ранее в рамках метода КФМ [9, 10]. В нашем

Таким образом, формула (10) [9] получается в

подходе последовательно учитывается эффект ядер-

рассматриваемом нами подходе, если в первом гра-

ной поляризуемости и, следовательно, соответствую-

фике на рис. 6 не учитывать:

щих эффективных зарядов [15], см. об этой проблеме

1) указанные четырех-квазичастичные КОС, в

в [10].

том числе, четыре слагаемых типа u²u²v²v²;

Предложенный подход позволит уточнить описа-

2) все 8 слагаемых типа u²v²v²v² или u²u²u²v².

ние низколежащих возбуждений ядер на языке фо-

И на рисунке 5 не учитывать:

нонов с помощью микроскопических расчетов раз-

1) графики с g₁₂ (вторые на рис.5), которые

личных характеристик двух-фононных состояний и,

содержат как эффекты тэдпола, так и и трех-

в частности, прояснить известную задачу о распад-

квазичастичные КОС;

ных характеристиках двух-фононного 3^-1 × 3^-1 муль-

2) слагаемые с δF и δ₁δ₂F, которые, видимо, ма-

типлета в²⁰⁸Pb [10] на одно-фононное состояние.

лы. Вышесказанное остается справедливым и для за-

Они также дают возможность проверить гипотезу

дачи без спаривания, рассмотренной в работе [10],

Бринка-Акселя в рамках последовательного количе-

если заменить коэффициенты Боголюбова на соот-

ственного подхода. Численный анализ этих и других

ветствующие числа заполнения. Для графиков на

задач выходит за рамки настоящей работы

рис. 6, содержащих аномальные ФГ, следует выпол-

Авторы благодарят В.А. Ходеля за обсуждение

нить аналогичные процедуры.

результатов работы и В.Ю. Пономарева за обсужде-

ния вопросов, связанных с КФМ. Работа поддержана

Каждый из этих пунктов применим для многих

физических случаев - по мультипольности и энергии

грантом РНФ # 16-12-10155.

переходов, характеристикам фононов и т.п. Иначе го-

воря, появляется много новых физических вариантов

1. О. Бор, Б. Моттельсон, Структура атомного ядра,

изучения ангармонических эффектов 3-го порядка.

Мир, М. (1977), т. 2.

К этому следует добавить факт наличия в форму-

2. А. В. Авдеенков, С. П. Камерджиев, ЯФ 62,

563

лах (12) (рис. 5), (15) вершины V , описывающей по-

(1999) [Phys. Atom. Nucl.

62, 563 (1999)].

ляризуемость ядра под действием внешнего поля V₀,

3. I. Hamamoto, Phys. Rep. 10, 63 (1974).

которая определяется эффективным взаимодействи-

4. P. Ring and J. Speth, Nucl. Phys. A 235, 315 (1974).

ем нуклонов. Как показано ранее [7,15], для случая

5. R. A. Broglia, R. Liotta, and V. Paar, Phys. Lett. B 38,

эффектов 2-го порядка наблюдаемые данные объяс-

480 (1972).

няются только при совместном учете вкладов от

6. B. L. Birbrair, Phys. Lett. B 32, 165 (1970).

КОС и ядерной поляризуемости. Можно думать, что

то же самое вместе с вкладом от графиков с g₁₂ бу-

7. D. Voitenkov, S. Kamerdzhiev, S. Krewald,

дет важным и для ангармонических эффектов 3-го

E. E. Saperstein, and S. V. Tolokonnikov, Phys.

Rev. C 85, 054319 (2012).

порядка.

8. В. Г. Соловьев, Теория атомного ядра. Квази-

5. Заключение. В рамках квантовой теории

многих тел выполнен общий анализ ангармониче-

частицы и фононы, Энергоатомиздат, М. 1989).

ских эффектов 3-го порядка. Впервые указано (и на

9. V. Yu. Ponomarev, Ch. Stoyanov, N. Tsoneva, and

M. Grinberg, Nucl. Phys. A 635, 470 (1998).

качественном уровне пояснено): 1) на существование

четырех-(квази)частичных КОС и 2) на появление

10. J. Enders, E von Neumann-Cosel, V. Yu. Ponomarev,

новых эффектов, определяемых вторым графиком

and A. Richter, Nucl. Phys. A 612, 239 (1997).

на рис. 5, который содержит одновременно эффекты

11. A. P. Platonov, Sov. J. Nucl. Phys. 36, 491 (1982).

и фононного тэдпола g₁₂, и трех-(квази)частичных

12. В. А. Ходель, ЯФ 24, 704 (1976) [Sov. J. Nucl. Phys.

КОС. Впервые в рамках метода ФГ: 1) выполнено

24, 367 (1976)].

обобщение квантовой теории ангармонических эф-

13. А. Б. Мигдал, Теория конечныых ферми-систем и

фектов 3-го порядка на ядра со спариванием, приме-

свойства атомных ядер, Наука, М. (1965).

нимо только для коллективных фононов, 2) с исполь-

14. V. A. Khodel and E. E. Saperstein, Phys. Rep. 92, 183

зованием только первого графика на рис.5 рассмот-

(1982).

Письма в ЖЭТФ том 109 вып. 1 - 2

2019