Письма в ЖЭТФ, том 109, вып. 2, с. 131 - 138

Обобщенные модели Калоджеро и Тоды

Ю. Черняков^+∇1), С. Харчев^+◦, A. Левин^+∗, M. Ольшанецкий^+◦, А. Зотов^+∗×

⁺Институт теоретической и экспериментальной физики им. А.И. Алиханова,

НИЦ “Курчатовский институт”, 117218 Москва, Россия

^∗Национальный исследовательский университет “Высшая школа экономики”, НИУ ВШЭ, 119048 Москва, Россия

^×Математический институт им. В.А. Стеклова РАН, 119991 Москва, Россия

^◦Институт проблем передачи информации им. А.А. Харкевича РАН, 127994 Москва, Россия

^∇Объединенный Институт Ядерных Исследований,

Лаборатория теоретической физики им. Н.Н. Боголюбова, 141980 Дубна, Россия

Поступила в редакцию 16 ноября 2018 г.

После переработки 16 ноября 2018 г.

Принята к публикации 16 ноября 2018 г.

Рассматривается система Калоджеро-Сазерленда с двумя типами взаимодействующих спиновых пе-

ременных. Система описана, используя подход Хитчина и квази-компактную структуру. Полная инте-

грируемость устанавливается с помощью уравнения Лакса, заданного на сингулярной кривой, а также

классической r-матрицы, зависящей от спектрального параметра. Также рассмотрены обобщенные си-

стемы Тоды. Приведено описание их фазовых портретов.

DOI: 10.1134/S0370274X19020139

1. Обобщенные системы Калоджеро. Одно-

их свойством является полная интегрируемость как

мерные системы частиц с интегрируемым потенци-

на классическом, так и на квантовом уровне.

алом взаимодействия широко известны в математи-

Как уже говорилось, мы рассматриваем частицы,

ческой физике. В этой статье рассматриваются два

обладающие внутренними степенями свободы, назы-

типа таких систем - модели типа Калоджеро [1] и

ваемые спином. В оригинальных работах [3, 4] спины

полные симметрические системы Тоды, обобщающие

принадлежали орбитам O коприсоединенного дей-

трехдиагональные системы Тоды, отвечающие по-

ствия простой комплексной группы G^C. Иначе го-

тенциалам с экспоненциальной зависимостью от рас-

воря, это элементы алгебры, двойственной к алгеб-

стояний [2]. Мы рассматриваем частицы в системах

ре Ли g^C = Lie(G^C), c фиксированными значения-

типа Калоджеро с дополнительными внутренними

ми функций Казимира. Например, для g^C = sl(N, C)

степенями свободы (классическим спином), введен-

(бесследовые комплексные матрицы размера N ×N)

ные в [3, 4]. Еще точнее, будут описаны обобщенные

элементы орбиты - бесследовые матрицы с фиксиро-

системы Калоджеро с двумя типами спинов. В слу-

ванными собственными значениями. На орбитах су-

чае тодовских взаимодействий рассматриваются си-

ществует невырожденная линейная скобка Пуассо-

стемы с большим числом степеней свободы.

на, определяемая структурными константами алгеб-

Описание системы. Модели Калоджеро [1] - это

ры g^C. Пусть R = {α} - система корней, отвечаю-

одномерные системы попарно взаимодействующих

щая простой комплексной алгебре Ли g^C, v, u ∈ h^C -

частиц с потенциалами, зависящими от расстояния

элементы ее картановской подалгебры, которые мы

между частицами или от более сложной линейной

отождествляем с импульсами и координатами час-

∑

функции от координат, заданной корнями простых

тиц, а S =_α∈R S_αE_α - разложение спина S ∈ g^C

алгебр Ли [5]. Потенциалы могут быть рациональ-

по корневому базису {E_α}. В этих терминах квадра-

ными, тригонометрическими либо эллиптическими

тичный гамильтониан систем Калоджеро имеет вид:

функциями.

∑

Эти модели имеют много приложений как в тео-

H =

(v, v) + U(S, u), U(S, u) =

S_αS_-αV (u_α),

ретической физике, так и в математике. Важнейшим

α∈R

(1)

¹⁾e-mail:

chernyakov@itep.ru;

kharchev@itep.ru;

где ( , ) - инвариантное скалярное произведение на

alevin2@hse.ru; olshanet@itep.ru; zotov@mi-ras.ru

h^C, u_α = (α, u), а V (u_α) - некоторая рациональная,

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

131

9^∗

132

Ю. Черняков, С. Харчев, A. Левин, M. Ольшанецкий, А. Зотов

тригонометрическая [6, 7] либо эллиптическая функ-

где S_ij , Tij - матричные элементы антисимметрич-

ция. Скобки Пуассона между координатами частиц

ных матриц S и T (S_jk = -S_kj , T_jk = -T_kj ) со

и их импульсов канонические {v_k, u_j} = δ_jk, а пуас-

скобками Пуассона-Ли, отвечающими прямой сумме

сонова структура для спиновых переменных дается

двух алгебр so(N) ⊕ so(N):

дираковскими скобками. Они получаются из скобки

Пуассона-Ли после введения связей Project S|_hC = 0

{S_ij, S_kl} = -

(S_ilδ_kj - S_kj δ_il - S_ikδ_lj + S_lj δ_ik) ,

и фиксации калибровки по отношению к присоеди-

ненному действию картановской подгруппы на спи-

новые переменные. Потенциал является гамильтони-

{T_ij, T_kl} =

(T_ilδ_kj - T_kj δ_il - T_ikδ_lj + T_lj δ_ik) ,

аном волчка Эйлера-Арнольда [8], построенного по

группе G^C с тензором инерции, зависящим от коор-

{S_ij, T_kl} = 0.

динат взаимодействующих частиц. В частности, для

G^C = SL(N, C)

(5)

Таким образом, гамильтониан и скобки описывают, в

∑

U (S, u) =

S_jkS_kjV (u_j - u_k).

(2)

частности, два взаимодействующих волчка Эйлера-

j=k

Арнольда на группе SO(N) с моментами инерции,

зависящими от координат частиц.

Было доказано, что системы (1) являются вполне ин-

Размерность фазового пространства равна (N -

тегрируемыми по Лиувиллю.

- 1)(N + 2) - 2[N/2]. Мы предъявляем необходи-

В этой работе рассматривается модификация та-

мое для интегрируемости число независимых инте-

ких систем Калоджеро, сохраняющая интегрируе-

гралов движения. Их инволютивность следует из су-

мость. Модификация заключается в замене спино-

ществования классической r-матрицы, которую мы

вых переменных, принадлежащих орбитам, на пе-

явно строим.

ременные P , являющиеся сечениями кокасательных

В случае N = 2 алгебра so(2) коммутативна, и мы

расслоений T^∗X к однородным пространствам X =

можем зафиксировать значения спинов. Тогда из (4)

= K\G^C. Здесь K - максимальная компактная под-

получаем гамильтониан с двумя константами

группа G^C. Пространство X называется симметриче-

ским пространством. Для G^C = SL(2, C), K = SU(2)

v²

m²¹ + m²² - 2m₁m₂ cosh(2u)

H =

(6)

и X =SU(2)\SL(2,C) - пространство Лобачевского.

sinh²(2u)

Кокасательное расслоение T^∗X - пуассоново много-

образие с невырожденной скобкой.

Можно показать, что он совпадает с моделью КС ти-

Ниже мы опишем классический тригонометриче-

па BC₁ [5]. Его квантовая версия рассматривалась в

ский случай, обобщающий вещественную спиновую

[14].

модель Калоджеро-Сазерленда (КС) (2)

Так же, как и модель КС (2), двухспиновое обоб-

щение переносится на произвольные простые алгеб-

∑

S_jkS_kj

ры Ли с сохранением полной интегрируемости. У

H^CS =

v^2j +

(3)

sinh²(u_j - u_k)

произвольной простой комплексной алгебры Ли g

j=1

j<k

имеется единственная с точностью до изоморфизма

∑

Здесь v_j , u_k ∈ R, переменные S =_jk S_jkE_jk в моде-

вещественная форма g^R ⊂ g^C и максимальная ком-

ли КС - элементы орбиты группы SL(N, R), т.е. соб-

пактная подалгебра k ⊂ g^C [15]. Максимальная ком-

ственные значения матриц S фиксированы. Кроме

пактная подалгебра алгебры g^R - алгебра u = k ∩ g^R.

того, наложена связь diagS = 0, и матричные эле-

Пусть h^R - картановская подалгебра алгебры g^R, и

менты S_jk и S_jk exp(x_j - x_k) для всех x_k ∈ R счи-

R⁺ - система положительных корней по отношению

таются эквивалентными. До наложения связей пере-

h^R. Тогда интегрируемое обобщение гамильтониана

менные S идентифицируются с угловыми моментами

(4) имеет вид

SL(N, R) волчка.

Обобщение модели КС выглядит следующим об-

∑

S^2α + T^2α - 2S_αT_α cosh(u_α)

H =

(v, v) + 2

(7)

разом [9-13]. Гамильтониан (3) обобщается до

(α, α) sinh²(u_α)

α∈R⁺

∑

S^2jk + T^2jk - 2S_jkT_jk cosh(u_j - u_k)

Скобки Пуассона-Ли для угловых моментов S, T

H =

v^2j +

sinh²(u_j - u_k)

j=1

j<k

определены на компактной подалгебре u (нижняя

(4)

строка табл.1).

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

Обобщенные модели Калоджеро и Тоды

133

Таблица 1. Нормальные формы g^R и компактные подалгебры

ство модулей решений уравнений Хитчина, есть ги-

k, u простых комплексных алгебр g^C

перкэлерово многообразие. В частности, координаты

A_N-1

B_N

C_N

D_N

частиц и их импульсы описывают модули решений

gC sl(N, C)

so(2N + 1, C)

sp(N, C)

so(2N, C)

уравнения Хитчина. Отметим также, что уравнения

gR sl(N, R)

so(N, N + 1)

sp(N, R)

so(N, N)

Хитчина появляются естественным образом в четы-

su(N)

so(2N + 1)

sp(N)

so(2N)

рехмерной твистованной суперсимметричной N = 4

so(N) so(N + 1)⊕so(N)

u(N)

so(N)⊕so(N)

теории Янга-Миллса [18].

G₂

F₄

E₆

E₇

E₈

Спиновые переменные есть вычеты поля Хиггса в

g^C2

f^C4

e^C6

e^C7

e^C8

особых точках. С точки зрения четырехмерной тео-

g^R2

f^R4

e^R6

e^R7

e^R8

рии, особые точки - это точки пересечения рима-

g^R2

f^R4

e^R6

e^R7

e^R8

новой поверхности Σ с двумерными поверхностями

su(2)⊕su(2) sp(3)⊕su(2) sp(4) su(8) so(16)

C, трансверсальными к Σ. Спиновые переменные же

в этом подходе - это переменные в сигма-модели

C → O, взаимодействующей с системой Хитчина

Можно показать, что эта модель эквивалентна

[19]. Фазовое пространство такой сигма-модели тоже

следующей модели с квадратичным Гамильтонианом

гиперкэлерово. Это означает, что отвечающие этой

сигма-модели так называемые поверхностные опера-

∑

P_αP_-α

H =

v^2j +

(8)

торы (surface operators) не нарушают N = 4 супер-

sinh²(u_α)

j=1

α∈R⁺

симметрию.

На самом деле для построения фазового про-

Здесь по-прежнему v_j , u_k ∈ R - координаты и им-

странства интегрируемых систем вместо простран-

пульсы частиц, а переменные P - сечение кокаса-

ства модулей решений уравнений Хитчина использу-

тельного расслоения T^∗X^R, где X^R = U\G^R - сим-

ется пространство модулей расслоений Хиггса. Рас-

метрическое пространство. Это фактор простран-

слоение Хиггса описывается антиголоморфной ком-

ство группы G^R (Lie G^R = g^R) - нормальной веще-

понентой вектор потенциала и голоморфной компо-

ственной формы группы G^C. Группа U есть ее макси-

нентой поля Хиггса, принимающими значение в ком-

мальная компактная подгруппа (Lie U = u). Сечения

плексной алгебре g^C. Эти два пространства моду-

P могут быть определены как сопряжения элемента

лей почти эквивалентны, и мы рассматриваем вто-

ζ ∈g^R

рое из них. В таком подходе поле Хиггса оказывает-

P = Ad^-1gζ.

ся оператором Лакса интегрируемой системы. Кро-

Здесь g ∈ X^R. Пусть σ - инволютивный автомор-

ме того, такая конструкция позволяет ввести зависи-

физм группы G^R, чьи неподвижные точки - под-

мость оператора Лакса от спектрального параметра

группа U. Тогда g может быть представлена в виде

L = L(z) (z ∈ Σ). В свою очередь, с помощью опера-

g = ff^†, где † = σ^-1, f ∈ G^R. Кроме того, наложены

тора Лакса можно строить полный набор интегралов

связи P|_hR = 0, ζ|_u = 0.

движения.

Обобщенные модели КС как системы Хитчина.

Важным ингредиентом нашей конструкции яв-

Обобщенную КС систему можно построить, исполь-

ляется так называемая квази-компактная структура

зуя подход Хитчина [16, 17]. Оператор Лакса инте-

калибровочной группы. Ее наличие означает, что ка-

грируемых систем Хитчина удовлетворяет так назы-

либровочные преобразования в сингулярных точках

ваемым уравнениям Хитчина. Эти уравнения возни-

базовой кривой редуцируются к унитарной группе (в

кают из уравнения самодуальности в четырех изме-

стандартном подходе системы Хитчина могут иметь

рениях после редукции на двумерную риманову по-

квази-параболического структуру, т.е. в сингуляр-

верхность Σ. А именно, вместо R⁴ рассматривает-

ных точках калибровочные преобразования редуци-

ся четырехмерное пространство R² × Σ, где Σ иг-

руются к борелевским подгруппам). В результате мы

рает роль базовой спектральной кривой. Состав по-

заменяем описанную выше сигма-модель на модель

лей системы Хитчина определяется четырехмерны-

C → T^∗X^C, где X^C - симметрическое пространство

ми вектор-потенциалами, принимающими значение

SU(N)\SL(N, C). В общем же случае это симметри-

в компактной алгебре su(N) (k в общем случае, см.

ческое пространство XC = K\GC, где K ⊂ GC -

табл. 1). Они зависят только от координат на Σ. По-

максимальная компактная подгруппа. Фазовое про-

сле редукции два из четырех вектор-потенциалов

странство этой сигма-модели не является гиперкэле-

превращаются в скалярные поля - поля Хиггса. Фа-

ровым, что приводит к нарушению суперсимметрии

зовое пространство систем Хитчина, т.е. простран-

в соответствующей четырехмерной теории.

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

134

Ю. Черняков, С. Харчев, A. Левин, M. Ольшанецкий, А. Зотов

С точки зрения динамических систем, фазовое

пространство систем с квазикомпактной структу-

рой плохо определено, так как часть описывающих

его переменных, относящаяся к сигма-модели, веще-

ственная, а другая часть - комплексная. Мы пере-

ходим к вещественным переменным, используя под-

ход, предложенный для гладких кривых [20]. Пред-

положим, базовая спектральная кривая Σ допус-

кает антиголоморфную инволюцию, которая в ло-

кальных координатах выглядит как ı

: z

→ z.

Одновременно рассмотрим инволютивный автомор-

физм σ алгебры g^C (σ2 = 1) такой, что инвари-

антная подалгебра инволюции является веществен-

ной нормальной формой g^R алгебры Ли g^C. Эти

подалгебры приведены в табл. 1. Рассмотрим одно-

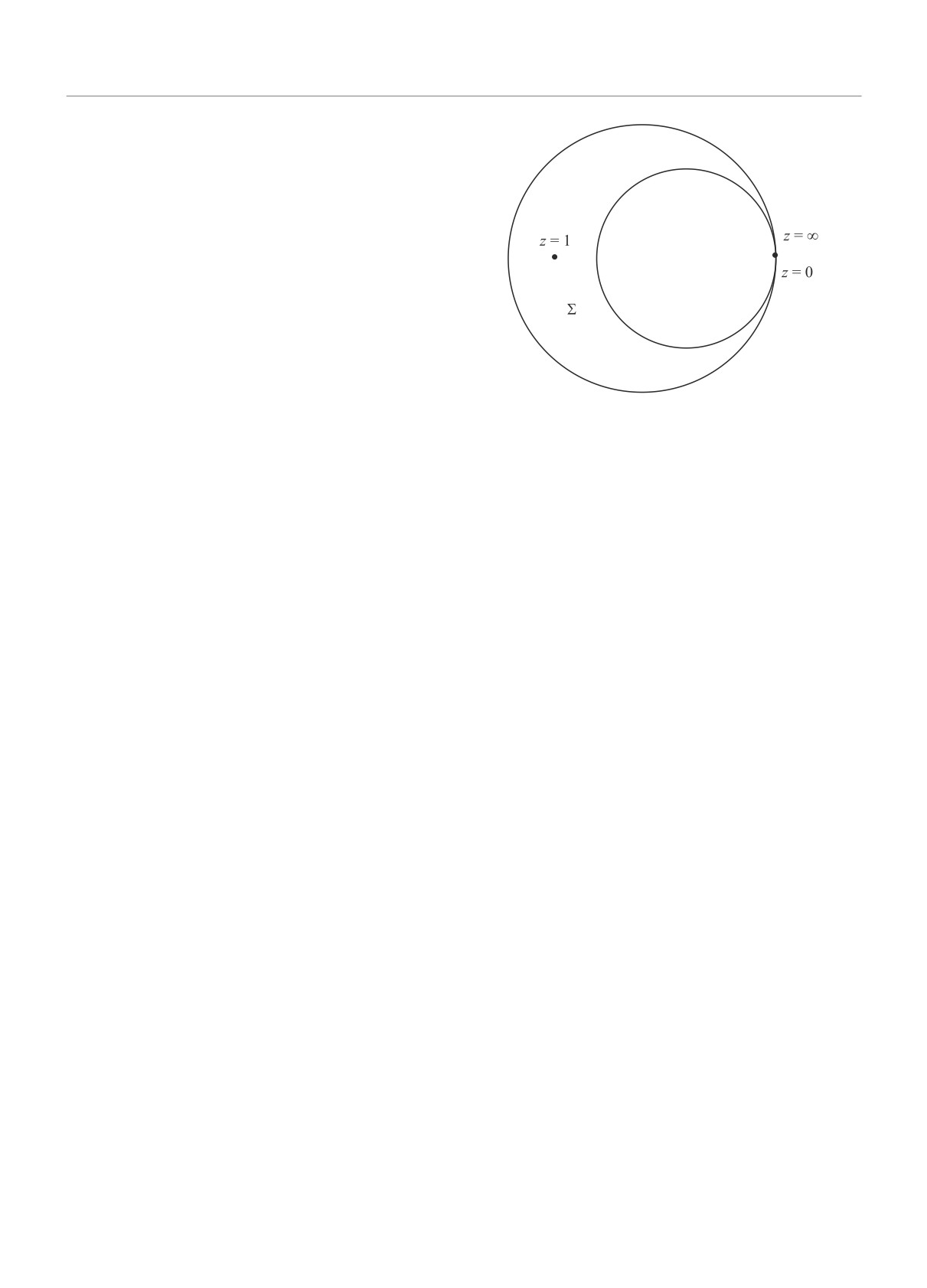
Рис. 1. Базовая спектральная кривая Σ = CP¹

временное действие этих инволюций L(z) → L^σ(z).

Инвариантное подмножество такого действия опре-

деляет оператор Лакса вещественной интегрируе-

этой системы см. [30, 31]; схема Адлера-Костанта-

мой системы. Его аргументом является веществен-

Симса была развита в [32-34].

ная кривая S - инвариант действия ı. Таким обра-

Можно поставить вопрос о геометрических свой-

зом, мы переходим к вещественной интегрируемой

ствах такой системы на произвольной группе. В част-

системе.

ности, в нашей работе [35] был описан фазовый порт-

В нашем случае, как и в случае системы КС, кри-

рет такой системы на действительной специальной

вая Σ сингулярна. На рисунке 1 изображена базовая

линейной группе (в более абстрактных терминах, на

спектральная кривая для обобщенной системы КС.

действительных формах A_n серий). Было также по-

Это комплексная проективная кривая CP¹, в кото-

казано, что он может быть идентифицирован с диа-

рой отождествлены точки 0 и ∞. Для модели КС

граммой Хассе порядка Брюа на соответствующей

сингулярная точка это точка z = 1 на CP¹. Отли-

группе Вейля. Этот результат обобщает, в некотором

чие системы КС от обобщенной системы КС в том,

смысле, классический результат работы [36]; он по-

что вычет оператора Лакса в точке z = 1 в пер-

явился, как попытка дать точную математическую

вом случае лежит в коприсоединенной орбите груп-

интерпретацию результатов [37] (см. также [38, 39]).

пы G^C, а во втором - в кокасательном пространстве

Вопрос описания фазового портрета заключает-

X^C = K\G^C. Отметим, что системы Хитчина на осо-

ся в исследовании асимптотического поведения си-

бых кривых (и, в частности, система КС) изучались

стемы. Аналогия - абсолютно упругое столкновение

ранее в [21, 22].

двух бильярдных шаров, один из которых покоится,

При переходе к вещественной интегрируемой си-

а другой движется с импульсом p. После столкно-

стеме кривая Σ на рис.1 заменяется на окружность

вения шары обмениваются импульсами. То же явле-

S¹, а оператор Лакса L(x) в точке x = 1 имеет по-

ние происходит и в трехдиагональной системе Тоды.

люс с коэффициентом, принадлежащем веществен-

Например, в случае матрицы Лакса ранга 2, мат-

ному симметрическому пространству X^R = U\G^R.

рица Лакса вырождается в диагональную матрицу

Алгебры Ли групп G^R и U приведены во второй и

(+λ, -λ) при t → -∞, а после взаимодействия при

последней строчках табл. 1.

t → +∞ в диагональную матрицу (-λ, +λ), где λ

2. Фазовые портреты обобщенной системы

- импульсы. В случае матрицы Лакса более высо-

Тоды. Система Тоды (или цепочка Тоды) впервые

кого ранга, вопрос асимптотического поведения си-

была рассмотрена в работах [2, 23], в работе [24] были

стемы уже не такой простой, и в этом и заключает-

найдены n функционально независимых интегралов

ся задача - получить картину всех возможных тра-

движения, а в работах [25-27] была доказана инволю-

екторий системы. Для решения этой задачи мы бу-

тивность этих интегралов. Известно (см. [28, 29]), что

дем использовать свойства обобщенной системы То-

система Тоды имеет в качестве обобщения интегри-

ды: во-первых, градиентность потока на соответству-

руемую систему на произвольной полупростой груп-

ющем многообразии флагов, существование функ-

пе Ли. Эта система называется обобщенная (полная

ции Морса и невырожденных критических точек, и,

симметричная) система Тоды. Об интегрируемости

во-вторых, существование достаточно большого ко-

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

Обобщенные модели Калоджеро и Тоды

135

личества полуинвариантов - координат Плюккера.

го способов, которыми система Тоды может быть

Заметим, что, когда матрица Лакса вырождается в

определена на классических простых группах или,

диагональную матрицу собственных значений, такая

скорее, на соответствующих алгебрах Ли (факти-

матрица отвечает критической точке в фазовом про-

чески можно говорить об индуцированной системе

странстве. Идея решения этой задачи заключается

на соответствующих пространствах флагов G/B⁺).

в следующем. Так как система градиентная, имеет

Например, можно дать точные формулы для мат-

функцию Морса, значит каждая траектория должна

риц L и M в терминах канонической системы кор-

идти от одной критической точки к другой, следо-

ней (см. [29]): для любого базиса Картана-Вейля

вательно, для каждой критической точки мы можем

H₁, . . ., H_r, Eα1 , . . ., Eαn-r , где r = rkg, n = dimg,

описать локальное пространство входящих и исходя-

пусть Δ⁺ определяет подмножество положительных

щих траекторий. Чтобы понять, какие траектории

корней (относительно данного базиса), тогда

связывают две критические точки, мы высаживаем

нашу систему на минорные поверхности - полуин-

∑

L= a_iH_i +

b_α(E_α + E_-α),

варианты с нулевым значением (M = 0, см. [40]),

i=1

α∈Δ⁺

∑

сохраняющиеся потоком Тоды. То есть траектории

(9)

M =

b_α(E_α - E_-α),

будут лежать на этих поверхностях или их пересече-

α∈Δ

нии. Оказывается, этих минорных поверхностей до-

L^′ = [L, M].

статочно, чтобы выделить одну траекторию между

двумя критическими точками, но бывает и так, что

Другой возможный подход состоит в том, чтобы при-

две критические точки вообще не соединяются ни-

менить схему Адлера-Костанта-Симса, мы получим

какой траекторией. В систематизации траекторий и

следующие матричные представления:

состоит задача. И, повторим, оказывается, что траек-





тории соединяют критические точки в соответствии

a₁₁

a₁₂

a_1n

с диаграммой Хассе порядка Брюа на соответствую-







a₁₂

a₂₂

a_2n



щей группе Вейля. О порядке Брюа см. [41, 42].



,

(10)





3. Фазовые портреты потоков Тоды на





Sp(4, R), на действительной форме G₂ и на вы-

a_1n a_2n ... a_nn

рожденных орбитах. Настоящая заметка основы-





вается на наших работах [42, 43]. Наши рассуждения

a₁₂

a₁₃

a_1n

строятся на немного измененных методах, которые







−a₁₂

a₂₃

a_2n



мы использовали в предыдущей работе [35], однако,









применение этих методов к группам, отличающимся



−a₁₃

-a₂₃

a_3n





,

от SL(n, R), оказывается довольно сложным. При-









чина этого состоит в том факте, что определение си-







a_n-1n



стемы Тоды на группах Ли обычно основывается на

−a_1n

-a_2n

-a_3n ...

-a_n-1n

рассмотрении корней и базисов Шевалье, в то время

как наше исследование фазового портрета основано

где L₊ и L_- - верхняя и нижняя диагональные ча-

на большом множестве инвариантных относительно

сти L, соответственно, а B = L₊ - L_-. В настоящей

потоков подпространств, которые могут быть описа-

работе мы выбираем такую точку зрения на обоб-

ны в терминах пространства флагов и матричных

щенную систему Тоды, которая была использована

представлений групп.

в работе [38] (см. также [29]). Она основана на сле-

Чтобы решить эту задачу, нужно было найти

дующей идее, обобщающей схему Адлера-Костанта-

подходящую переформулировку системы Тоды, что-

Симса: если мы вкладываем группу G в подходящую

бы матричное представление группы могло быть ис-

SL(n, R) так, что подалгебра Картана отобража-

пользовано. Оказалось, что такая переформулировка

ется в диагональные матрицы и корневые векто-

действительно существует; она была дана, в частно-

ра соответствуют верхней и нижней треугольным

сти, в работе [29]. Фактически, можно показать, что

матрицам, так что матрицы, соответствующие

существует вложение полупростой группы G в специ-

+α и -α векторам транспонируются друг в дру-

альную линейную группу подходящей размерности,

га, тогда матрица Лакса L дается формулой (10)

такое, что G сохраняется системой Тоды на SL(n, R);

и принадлежит пересечению симметрической мат-

тогда система Тоды на G эквивалентна ограниче-

рицы и образа g ⊂ sl_n, а M дается ограничением

нию системы, определенной на SL(n, R). Есть мно-

процедуры антисимметризации на L.

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

136

Ю. Черняков, С. Харчев, A. Левин, M. Ольшанецкий, А. Зотов

Как уже говорилось, важным свойством систе-

ориентацию, - сохраняет данную невырожденную

мы Тоды является то, что она также имеет струк-

антисимметрическую билинейную форму J. Если мы

туру градиентного потока. Есть много способов опи-

хотим вложить Sp(4, R) в SL(4, R) так, чтобы по-

сать это (см., например, [28, 44]). Рассмотрим вложе-

ложительные корни перешли в верхние треугольные

ние (вещественную форму) G в SL(n, R), как объяс-

матрицы, нам следует выбрать J антидиагональной.

нялось выше. Тогда максимальная компактная под-

Вследствие этого вложения подалгебра Картана ал-

группа в G будет отображена внутрь группы орто-

гебры sp(4, R) диагональна. Матрица Лакса - сим-

гональных матриц SO(n, R). Кроме того, из уравне-

метрическая матрица в sp(4, R): L = UΛU^-1. Здесь

ния (9) следует, что собственные значения матрицы

Λ - диагональная матрица собственных значений L,

Лакса сохраняются потоком Тоды. Поскольку каж-

а U - матрица из U(2) = Sp(4,R)

⋂SO(4,R), макси-

дая вещественная симметрическая матрица L может

мальная компактная подгруппа группы Sp(4, R). M

быть представлена в форме ΨΛΨ^t, где Ψ - ортого-

матрица из уравнения (9) равна M = (UΛU^-1)_>0 -

нальная и Λ - диагональная матрица собственных

- (UΛU^-1)_<0. Зафиксируем собственные значения L

значений, мы можем использовать это же разложе-

как 0 < λ₁ < λ₂, так что соответствующий элемент в

ние. Тогда Ψ будет матрицей из максимальной ком-

алгебре Картана есть λ₁h₁ +λ₂h₂. Поскольку система

пактной подгруппы K_G ⊂ G, и Λ будет матричной

Тоды на Sp(4, R) дается ограничением уравнения (9)

формой подгруппы Картана группы G. Так как мат-

из SL(4, R), можно описать критические точки пото-

рица Λ не меняется под действием потока Тоды, фик-

ка на пространстве флагов; они даются классами эк-

сируя ее, мы получим динамическую систему на Ψ

вивалентности ортогональных матриц в Sp(4, R), т.е.

⋂

Sp(4, R) = U(2), которые

из пересечения SO(4, R)

dΨ

= MΨ, M = (ΨΛΨ^t)₊ - (ΨΛΨ^t)_-.

(11)

сохраняют подалгебру Картана Sp(4, R). Существует

восемь перестановочных матриц

s_i, которые попада-

Эта система (11), в определенном смысле, эквива-

ют в U(2). Используем формулы из [29], которые вы-

ражают функцию Морса системы Тоды на симплек-

лентна потоку Тоды (поток Тоды получен из при-

соединенного действия Ψ(t) на Λ). Можно рассмот-

тических флагах в терминах корней Sp(n, R). Вы-

числяем квадратичную часть функции Морса F_n на

реть эту систему на пространстве флагов, ассо-

Sp(n, R) в особых точках в терминах локальных ко-

циированном с G, которое эквивалентно F (G)

ординат, перенесенных из алгебры Ли. Чтобы восста-

= K_G/(K_G

⋂H), где H есть выбранная максималь-

новить точную картину траекторий, соединяющих

ная коммутативная подгруппа. Теперь можно пока-

зать, что уравнения (11) в самом деле заданы гра-

особые точки, делаем перечень минорных поверхно-

стей, к которым они принадлежат, см. [43]. Сравни-

диентным потоком на K_G (или на F (G)). Для этого

введем инвариантную евклидову структуру на so_n

вая индексы Морса точек и множества точек внут-

ри различных инвариантных подмногообразий (ми-

(подходящая деформация формы Киллинга), и про-

должим ее до римановой на SO(n, R); эта структура

норных поверхностей), получим следующий рисунок:

является тогда ограничением на K_G, вложенным в

ортогональную группу, как объяснялось выше. То-

гда можно показать, что уравнение (11) имеет фор-

му градиентного потока следующей функции отно-

сительно выбранной римановой структуры F_G(Ψ) =

= Tr(ΨΛΨ^tN), где Λ - матрица собственных значе-

ний, и N - подходящая диагональная матрица (пред-

ставляющая элемент в выбранной подгруппе Карта-

на). Список таких элементов для различных групп

можно найти, например, в работе [28].

Другим важным свойством системы (11) явля-

ется то, что может быть найдено много многообра-

зий в SO(n, R), сохраняющихся этой системой. Важ-

ное большое семейство таких инвариантных многооб-

разий образовано так называемыми минорными по-

верхностями (подробнее см. в [40]).

Эта диаграмма 1-параметрических семейств траек-

Система на Sp(4, R). Напомним, что Sp(2n, R) -

торий, соединяющих особые точки, которые соответ-

группа линейных преобразований R²ⁿ, сохраняющих

ствуют

s_i. Как можно видеть, она совпадает с диа-

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

Обобщенные модели Калоджеро и Тоды

137

граммой порядка Брюа для группы Вейля группы

Sp(4, R), см. [41]. Также отметим, что индексы осо-

бых точек совпадают с длинами соответствующих

элементов Вейля; такой факт также имел место во

всех предыдущих ситуациях, которые мы рассмат-

ривали в работе [35].

Случай G₂. Наименьшей спорадической группой

из классификационного списка простых групп Ли яв-

ляется группа G₂. Существует много способов вве-

сти ее. Например, как подгруппу в SL(7, R), которая

сохраняет данную симметрическую 2-форму и куби-

ческую форму на R⁷. Наше рассмотрение основано

на описании G₂, данном Гроссом в [45]. Нужно вло-

жить эту группу в SL(7, R) так, чтобы все необхо-

Рис. 3. (Цветной онлайн)

1-мерные траектории на

димые для анализа условия, перечисленные выше,

SO(4)/(SO(2) × SO(2))

оставались в силе. Схема в этом случае похожа на

схему в предыдущем случае, трудность была в вы-

Система на Gr₂(4, R). Рассмотрим две пары

боре правильного представления для корневых век-

совпадающих собственных значений матрицы Лак-

торов, что было достигнуто определенным выбором

са ранга 4. Тогда динамическая система (11) на

ортогональной матрицы сопряжения P , подробности

Ψ ∈ SO(4,R) определена на грассманиане Gr₂(4,R),

см. в [43]. Алгебра Картана в этом случае (мы полу-

так как Ψ определена с точностью до действия то-

чаем ее, сопрягая алгебру Картана, рассмотренную в

ра. В этом случае рассмотрим расслоение с базой

[45], матрицей P ) состоит из диагональных матриц,

SO(4)/(SO(2) × SO(2)) и слоем, изоморфным тору.

и можно получить точные матричные представления

Пространство расслоения - SO(4). Наверху (над ба-

элементов группы Вейля в этом представлении, что

зой) количество особых точек - 24, на базе - 6. Каж-

и было сделано. После вычисления функции Мор-

дая особая точка на базе - проекция (результат слия-

са и анализа минорных поверхностей, мы получили

ния) целого непрерывного множества (тора) точек из

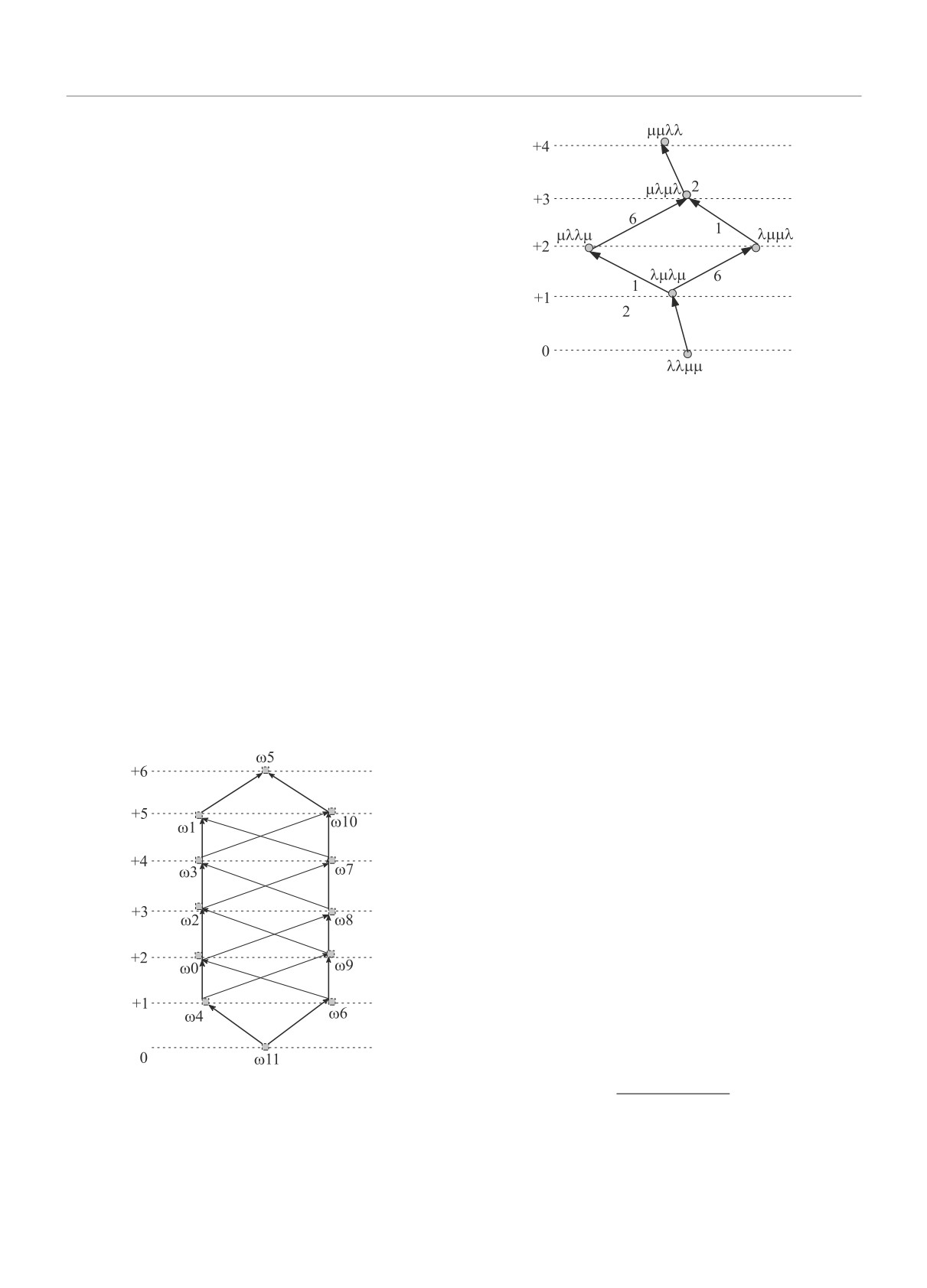
рис. 2. Этот рисунок совпадает с диаграммой Хассе

SO(4), которое соответствует диагональной матрице

порядка Брюа группы G₂ с точностью до перестано-

с двумя парами совпадающих собственных значений

вок элементов.

(одной из 6). Граничные точки этого множества на-

верху - 4 особые точки, связанные преобразованием

из SO(2) × SO(2). В работе [42] мы показываем, что

все необходимые свойства такой системы Тоды для

анализа фазового портрета сохраняются, и в резуль-

тате мы получаем рис. 2, который совпадает с диа-

граммой Хассе для порядка Брюа на перестановках

с повторениями.

Работа выполнена при частичной поддерж-

ке грантами РФФИ

#18-02-01081 (А.Левин,

М. Ольшанецкий, Ю. Черняков),

#18-01-00926

(А. Зотов) и

#18-01-00460 (С.Харчев). Работа

А. Левина выполнена при поддержке Лаборато-

рии зеркальной симметрии НИУ ВШЭ, грант

Правительства РФ, Договор # 14.641.31.0001. Ис-

следование А. Зотова финансировалось в рамках

государственной поддержки ведущих университетов

Российской Федерации “5-100”.

Рис. 2. (Цветной онлайн) 1-мерные траектории, соеди-

няющие две особые точки, которые не накрываются

траекториями высших размерностей

1. F. Calogero, J. Math. Phys. 10, 2191 (1969).

2. M. Toda, J. Phys. Soc. Japan 22(2), 431 (1967).

Письма в ЖЭТФ том 109 вып. 1 - 2

2019

138

Ю. Черняков, С. Харчев, A. Левин, M. Ольшанецкий, А. Зотов

J. Gibbons and T. Hermsen, Physica D: Nonlinear

25.

H. Flaschka, Phys. Rev. B 9(4), 1924 (1974).

Phenomena 11, 337 (1984).

26.

H. Flaschka, On the Toda lattice. II. Prog. Theor.

S. Wojciechowski, Phys. Lett. A 111, 101 (1985).

Phys. 51(3), 703 (1974).

M. A. Olshanetsky and A. M. Perelomov, Inventiones

27.

С. В. Манаков, ЖЭТФ 40(2), 269 (1975).

mathematicae 37(2), 93 (1976).

28.

A.M. Bloch, R. W. Brockett, and T. S. Ratiu, Comm.

B. Sutherland, Phys. Rev. A 4(5), 2019 (1971).

Math. Phys. 147, 57 (1992).

B. Sutherland, Phys. Rev. A 5(3), 1372 (1972).

29.

Y. Kodama and J. Ye, Comm. Math. Phys. 178(3),

В. И. Арнольд, Математические методы классиче-

765 (1996).

ской механики, Наука, М. (1979).

30.

P. Deift, L. C. Li, T. Nanda, and C. Tomei, CPAM 39,

L. Fehér and B. G. Pusztai, Nuclear Physics B 734[FS],

183 (1986).

304 (2006).

31.

N. Ercolani, H. Flaschka, and S. Singer, Integrable

10.

L. Fehér, An application of the reduction method

Systems, v. 115 of Progress in Mathematics,

to Sutherland type many-body systems, Geometric

Birkhauser, Boston (1993), p. 181.

Methods in Physics, Birkhauser, Basel (2013), p. 109.

32.

M. Adler, Invent. Math. 50, 219 (1979).

11.

L. Fehér, arXiv:1809.01529 [math-ph].

33.

B. Kostant, Adv. in Math. 34, 195 (1979).

12.

S. Kharchev, A. Levin, M. Olshanetsky, and A. Zotov,

34.

W. W. Symes, Invent. Math. 59(1), 13 (1980).

JETP Lett. 106(3), 179 (2017).

35.

Yu. B. Chernyakov, G. I. Sharygin, and A. S. Sorin,

13.

S. Kharchev, A. Levin, M. Olshanetsky, and A. Zotov,

Commun. Math. Phys. 330, 367 (2014).

J. Math. Phys. 59(10), 103509 (2018).

36.

P. Deift, T. Nanda, and C. Tomei, SIAM J. Numer.

14.

Н. Я. Виленкин, Специальные функции и теоря

Anal. 20, 1 (1983).

представлений групп, Наука, М. (1991), гл VI.5.

37.

P. Fre and A. S. Sorin, Nucl. Phys. B 815, 430 (2009).

15.

S. Helgason, Differential geometry, Lie groups and

38.

P. Fre, A. S. Sorin, and M. Trigiante, JHEP 1204, 015

symmetric spaces, Academic press, San Diego (1978).

(2012).

16.

N. Hitchin, Proceedings of the London Mathematical

39.

Y. Kodama and L. Williams, arXiv:1308.5011.

Society 1, 59 (1987).

40.

Yu. B. Chernyakov and A. S. Sorin, Lett. Math. Phys.

17.

N. Hitchin, Duke Math. J. 54(1), 91 (1987).

104, 1045 (2014).

18.

A. Kapustin and E. Witten, arXiv hep-th/0604151

41.

A. Bjorner and F. Brenti, Combinatorics of Coxeter

(2006).

groups, Springer, N.Y. (2005).

19.

S. Gukov and E. Witten, arXiv hep-th/0612073 (2006).

42.

Yu. B. Chernyakov, G. I. Sharygin, and A. S. Sorin,

20.

D. Baraglia and L. P. Schaposnik, Adv. Theor. Math.

SIGMA 12, 084 (2016).

Phys. 20(3), 525 (2016); arXiv:1309.1195 [math.AG].

43.

Yu. B. Chernyakov, G. I. Sharygin, and A. S. Sorin,

21.

N. Nekrasov, Commun. Math. Phys. 180, 587 (1996).

Theor. Math. Phys. 193(2), 1574 (2017).

22.

D. V. Talalaev and A.V. Chervov, Theoret. and Math.

44.

F. De Mari and M. Pedroni, J. Geom. Anal. 9(4), 607

Phys. 140(2), 1043 (2004).

(1999).

23.

M. Toda, J. Phys. Soc. Japan 23(3), 501 (1967).

45.

K.I. Gross, Transactions Amer. Math. Soc. 132, 411

24.

M. Henon, Phys. Rev. B 9, 1921 (1974).

(1968).

Письма в ЖЭТФ том 109 вып. 1 - 2

2019