Письма в ЖЭТФ, том 109, вып. 4, с. 231 - 235

Формирование складок в двумерной гидродинамической

турбулентности

Е. А. Кузнецов^+∗×1), Е. В. Серещенко^×◦∇

⁺Физический институт им. П. Н. Лебедева РАН, 119991 Москва, Россия

^∗Институт теоретической физики им. Л. Д. Ландау РАН, 119334 Москва, Россия

^×Новосибирский государственный университет, 630090 Новосибирск, Россия

^◦Дальневосточный федеральный университет, 690950 Владивосток, Россия

^∇ Институт теоретической и прикладной механики им. С. А. Христиановича Сибирского отделения РАН, 630090 Новосибирск,

Россия

Поступила в редакцию 28 ноября 2018 г.

После переработки 28 ноября 2018 г.

Принята к публикации 6 декабря 2018 г.

Для вырождающейся двумерной гидродинамической турбулентности поле ротора завихренности

B = rotω благодаря тенденции к опрокидыванию сосредоточено в окрестности линий, соответствующих

положению квази-шоков завихренности. На стадии формирования квази-шоков максимальное значение

ротора завихренности Bmax растет экспоненциально во времени, при этом толщина ℓ(t) максимальной

области в поперечном направлении к вектору B сужается во времени также экспоненциально. Численно

показано, что Bmax(t) зависит от толщины степенным образом: Bmax(t) ∼ ℓ-α(t), где показатель α ≈ 2/3.

Такое поведение свидетельствует в пользу формирования складок для бездивергентного векторного по-

ля ротора завихренности.

DOI: 10.1134/S0370274X19040052

1. Введение. В двумерной развитой гидроди-

Отображение r = r(a, t), как решение этих урав-

намической турбулентности (при числах Рейнольдса

нений, является сжимаемым, поскольку в ситуации

Re ≫ 1), как было выяснено в работах [1-4], фор-

общего положения div v_n = 0. Сжимаемость этого

мирование прямого каскада - каскада Крейчнана [5]

отображения также следует из уравнения Лиувилля

с постоянным потоком энстрофии - обязано появ-

для якобиана отображения J (как меры изменения

лению квази-шоков завихренности, благодаря сжи-

дифференциально малого элемента площади):

маемости непрерывно распределенных линий поля

ротора завихренности B = rotω (по-английски -

= div v_n · J.

“ divorticity”). Это свойство следует непосредственно

Таким образом, якобиан J может принимать произ-

из уравнения для B,

вольные значения, в том числе и нулевые. Именно в

∂B

этом кроется причина сжимаемости непрерывно рас-

= rot[v × B], div v = 0,

(1)

∂t

пределенных линий divorticity и, соответственно, тен-

которое имеет вид уравнения вмороженности. Из

денции к опрокидыванию, в результате чего проис-

этого уравнения немедленно следует, что B меняется

ходит формирование квази-шоков завихренности.

только благодаря компоненте скорости v_n, перпенди-

В случае вырождающейся турбулентности этот

кулярной вектору divorticity (в силу векторного про-

процесс является доминирующим, приводящим к

изведения). Из-за вмороженности B компонента ско-

сильной анизотропии спектров турбулентности из-за

рости v_n определяет изменение положения силовых

наличия джетов, порождаемыми квази-шоками [1-3].

линий этого поля с помощью лагранжевых траекто-

Этот процесс оказывается самым быстрым, в резуль-

рий, которые находятся из решения уравнений

тате чего спектр турбулентности прямого каскада да-

же при наличии накачки, как показывают численные

= v_n(r, t) = 0, r|_t=0 = a.

эксперименты [6], приобретает практически с само-

го начала степенную зависимость от волнового чис-

¹⁾e-mail: kuznetso@itp.ac.ru

ла k с крейчнановским показателем: E_k ∼ k^-3 (см.

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

231

232

Е. А. Кузнецов, Е. В. Серещенко

оригинальную работу Крейчнана [5]). При этом фор-

ной с колмогоровским поведением. Объединяет оба

мирование квази-шоков завихренности носит экспо-

этих случая - формирование трехмерных вихревых

ненциальный характер; в соответствии с этим обла-

структур блинного типа и квази-шоков завихренно-

сти максимального ротора завихренности сужаются

сти для двумерных течений, вмороженность как по-

в направлении, перпендикулярном линиям постоян-

ля завихренности в трехмерном уравнении Эйлера,

ной завихренности. Как показывает численный экс-

так и поля divorticity. Несмотря на несжимаемость

перимент [1-4], для типичных начальных условий

поля скорости, оба поля - трехмерная завихренность

рост ротора завихренности составляет 2-2.5 поряд-

и поле divorticity - являются сжимаемыми (см. [11]).

ка, а поперечный размер максимальной области B

По-видимому, благодаря этому свойству вморожен-

существенно уменьшается. Объяснение этого роста

ных полей можно ожидать, что закон 2/3 является

связано с возможностью частичного интегрирования

универсальным для любых полей этого типа.

уравнения (1) в терминах отображения r = r(a, t):

2. Результаты численных экспериментов. В

данной работе при численном интегрировании дву-

(B₀(a) · ∇_a)r(a, t)

B(r, t) =

(2)

мерных уравнений Эйлера, записанных в терминах

завихренности (уравнение Гельмгольца),

где B₀(a) - начальное значение поля B, представля-

∂ω

ющее собой аналог инварианта Коши. Аналогичная

+ (v∇)ω = 0,

(3)

∂t

формула для трехмерного уравнения Эйлера явля-

мы используем алгоритм, подробно изложенный в

ется основной для так называемого представления

наших предыдущих публикациях [3, 4, 6]. Область

вихревых линий [7, 8]. Ключевым здесь для понима-

интегрирования уравнения (3) представляла собой

ния является сжимаемость поля ротора завихренно-

квадрат с размерами 2π ×2π, граничные условия бы-

сти - возможность обращения J в нуль. Как извест-

ли периодическими по обеим координатам. Скорость

но, опрокидывание в газовой динамике возникает за

v и завихренность ω находилась через функции тока

счет сжимаемости газа. При подходе к точке опроки-

ψ по стандартным формулам. По заданному значе-

дывания происходит формирование квазидвумерных

нию ω находилась функция тока, обращая оператор

каустик (см., например, [9]). Аналогично этому про-

Лапласа с помощью быстрого преобразования Фу-

исходит формирование квази-шоков завихренности.

рье, а затем определялась скорость. Как и ранее,

В данной работе нами исследован вопрос, как

в качестве начальных условий использовались два

максимальное значение divorticity меняется в зави-

набора вихрей гауссовой формы с положительной

симости от толщины максимальной области, чтобы

и отрицательной завихренностью с нулевой общей

выяснить, можно ли рассматривать этот процесс как

завихренностью. Размер каждой пары был случай-

формирование складки (что такое складка - см.,

ным в диапазоне 0.2-0.6, расположение вихрей тоже

например, [10]). В результате численного моделиро-

было случайным. В отличие от предыдущих работ

вания на сетке 16384 × 16384 мы обнаружили, что

между максимальным значением B_max и толщиной

ℓ на стадии экспоненциального роста возникает сте-

пенная зависимость: B_max

∼ ℓ^-α, где показатель

α близок к 2/3. Следует отметить, что такого ро-

да зависимость была обнаружена при формирова-

нии вихревых структур блинного типа, возникающих

для невязких трехмерных течений [11]. Этот резуль-

тат свидетельствует о том, что формирование квази-

шоков можно рассматривать как процесс образова-

ния складки для бездивергентного векторного поля -

поля ротора завихренности. Если для трехмерного

уравнения Эйлера появление степенной зависимости

Рис. 1. Распределение |B| при t = 12

между максимальной завихренностью ω_max и толщи-

ной блина ℓ вида ω_max ∼ ℓ^-2/3 можно было бы от-

[3, 4] мы ограничили число вихрей 8 (4 положитель-

нести к соотношению колмогоровского типа, то за-

ных и 4 отрицательных), чтобы более точно опреде-

висимость B_max ∼ ℓ^-2/3 свидетельствует о том, что

лить требуемые зависимости - поле B и его геомет-

в двумерной гидродинамике Эйлера мы имеем де-

рические характеристики: положения максимумов,

ло с образованием именно складки, никак не связан-

продольные и поперечные размеры квази-шоков и

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

Формирование складок в двумерной гидродинамической турбулентности

233

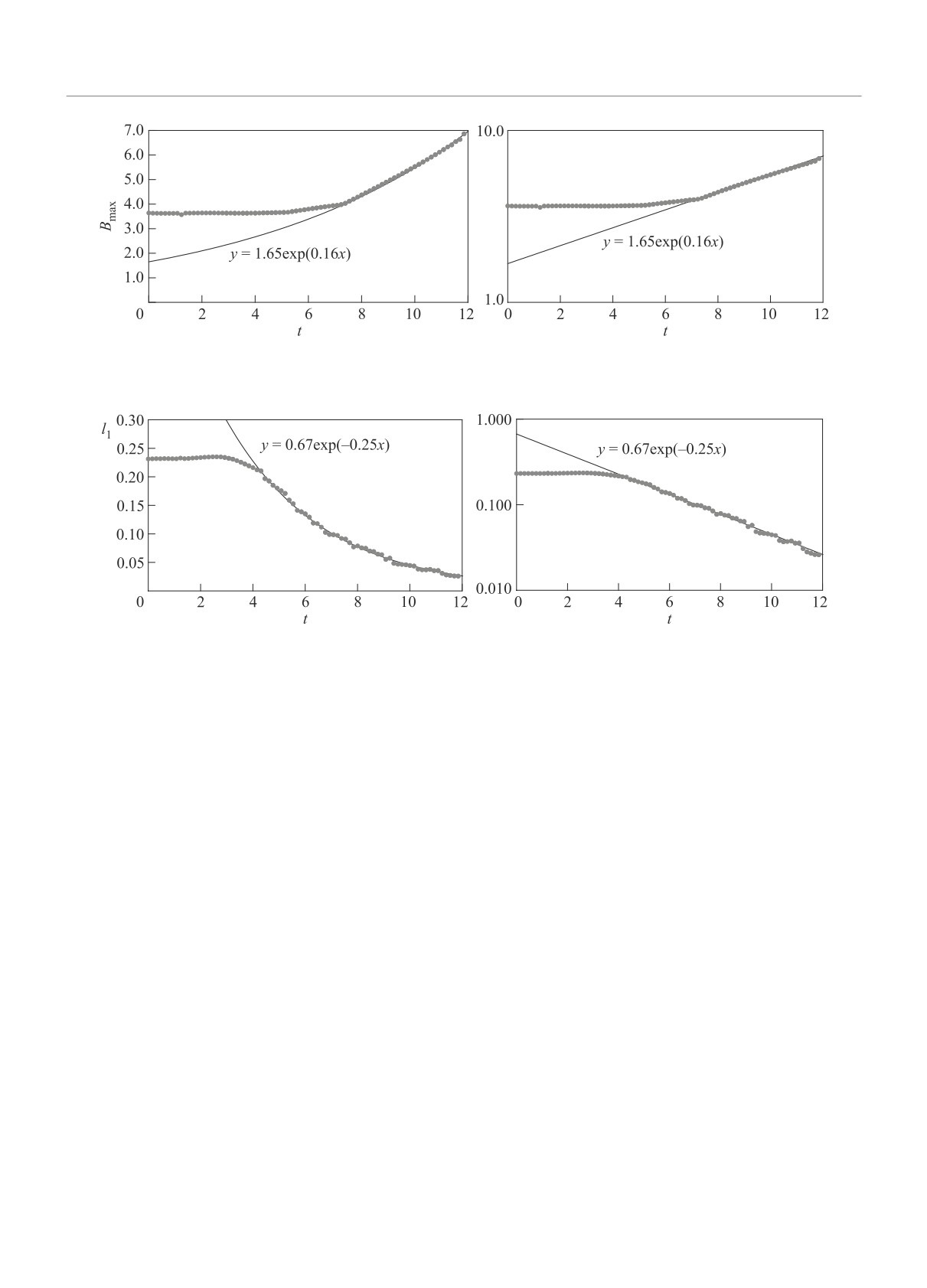
Рис. 2. Зависимость максимума ротора завихренности от времени (слева - обычный масштаб, справа - логарифмиче-

ский). Точки соответствуют численным результатам, а линия - экспоненте

Рис. 3. Зависимость толщины ℓ1 от времени (слева - обычный масштаб, справа - логарифмический). Точки соответ-

ствуют численным результатам, а линия - экспоненте

т.д. Вначале численно находились пространственно-

на временах от t = 4 до t = 12 с инкрементом, рав-

временные зависимости завихренности, а затем опре-

ным 0.16. Для нахождения поперечного размера в

делялась временная эволюция поля ротора завихрен-

окрестности максимума B_max вычислялась матрица

ности. Анализ распределения поля ротора завихрен-

Гессиана ∂_i∂_j |B| в максимальной точке и затем по ее

ности (divorticity) показал, что основная его масса

собственным значениям находились поперечный (по

сосредоточена в малых окрестностях линий с мак-

отношению к ленте) размер ℓ₁ (≡ ℓ) и продольный ℓ₂

симальным значением |B| в виде сужающихся дву-

как ℓ_i = (2|λ_i|/B_max)^1/2, где λ_i - собственные зна-

мерных лент, которые формируют сложную паутину,

чения матрицы ∂_i∂_j |B|. На рисунке 3 представлена

при больших временах - турбулентную. На рисунке 1

зависимость ширины ℓ₁ от времени: вначале ℓ₁ прак-

приведена структура |B| при t = 12. Вставка (zoom)

тически не меняется, а далее, начиная с t = 4, идет

показывает, что между максимальными линиями ро-

экспоненциальное сужение до t = 14 с декрементом

тора завихренности значения |B| существенно мень-

0.25.

ше максимальных. Для завихренности этому соот-

При t = 14 число точек на толщине было порядка

ветствует террасы со ступеньками переменной высо-

20. При больших временах это число уменьшается.

ты. Каждая из таких ступенек представляет собой

Так при t = 20 ширина достигает значения 0.00045,

квази-ударную волну завихренности. Как уже отме-

сопоставимого с размером сетки 2π/16384 = 0.00038,

чалось, максимум амплитуды ротора завихренности

т.е. последующий анализ становится уже некоррект-

B_max на начальном этапе растет по экспоненциально-

ным. Следует отметить, что при t > 14 экспоненци-

му закону, а затем после достижения своего максиму-

альный рост B_max прекращается - возникает насы-

ма претерпевает небольшие осцилляции вблизи этого

щение с небольшими осцилляциями (ср. с [1, 3]).

максимума. На рисунке 2 представлена зависимость

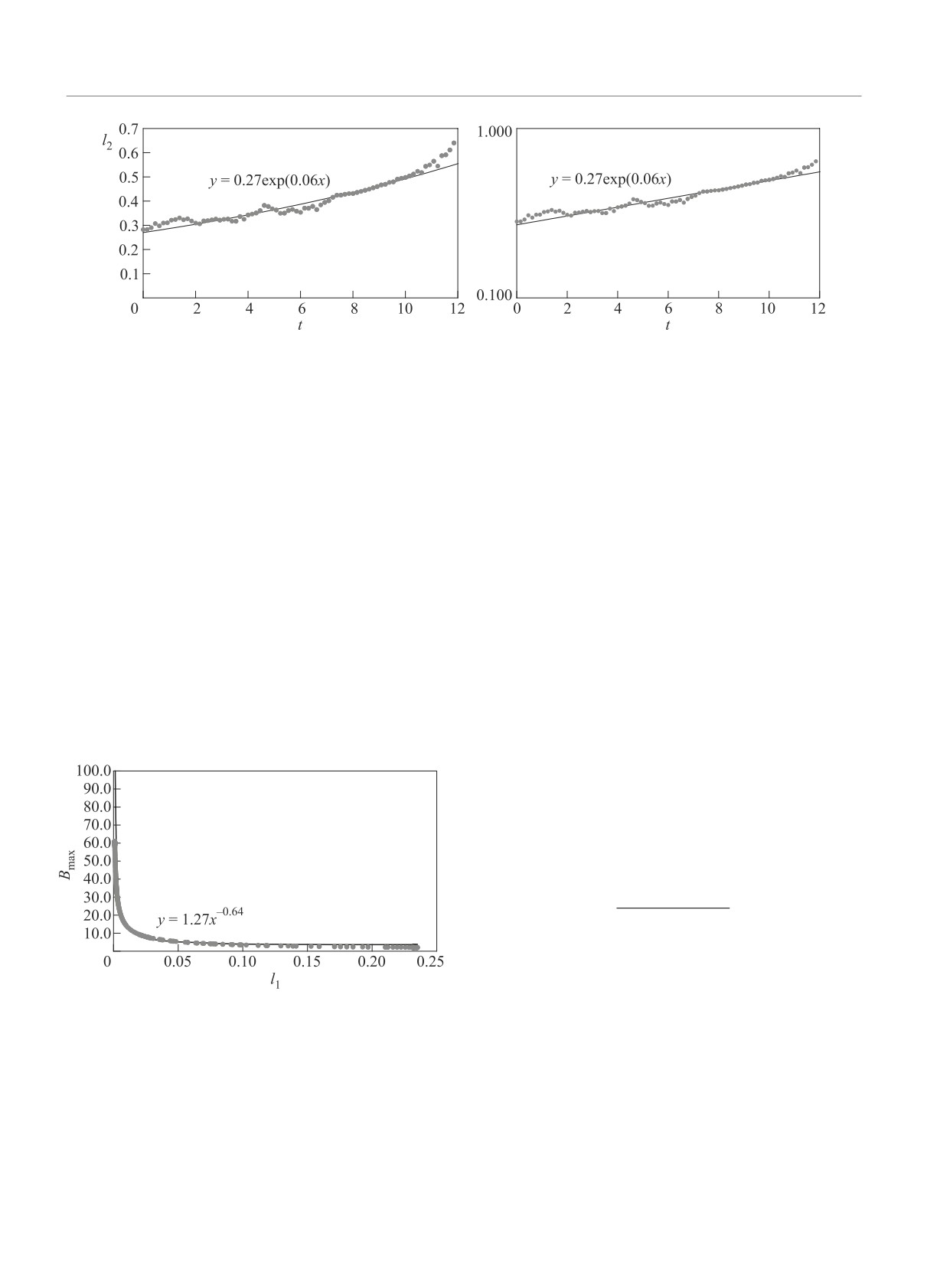
Что касается продольного масштаба ℓ₂, то он

B_max от времени на начальном этапе. Как видно из

вплоть до t = 14 растет экспоненциально с инкремен-

этих графиков, экспоненциальный рост наблюдается

том 0.06 (см. рис.4). При больших временах ℓ₂ рост

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

234

Е. А. Кузнецов, Е. В. Серещенко

Рис. 4. Зависимость продольного размера ℓ2 от времени (слева - обычный масштаб, справа - логарифмический). Точки

соответствуют численным результатам, а линия - экспоненте

прекращается, а далее наблюдается даже экспонен-

считать, что указанное соотношение можно рассмат-

циальное падение, которое, по нашему мнению, свя-

ривать как универсальное.

зано с дискретностью сетки и является некоррект-

3. Заключение. Основной вывод этой работы

ным.

состоит в том, что формирование степенной зависи-

Важно отметить, что до t = 14 суммарное зна-

мости B_max от ширины ℓ - закон 2/3 - можно рас-

чение декремента ℓ₁ и инкремента ℓ₂ отрицательно:

сматривать как проявление формирования складки,

-0.25 + 0.06 = -0.19, что свидетельствует о сжима-

подчеркнем, для бездивергентного векторного поля -

емости области максимального значения B_max. Ана-

ротора завихренности. Как уже отмечалось во вве-

логичное поведение масштабов наблюдается при об-

дении, такой же скейлинг был обнаружен при фор-

разовании вихревых структур блинного типа в трех-

мировании вихревых структур блинного типа для

мерной гидродинамике [12].

трехмерной гидродинамики Эйлера [12, 11]. В этом

Полученные зависимости для B_max и ширины ℓ

случае скейлинг 2/3 был установлен между макси-

показывают, что на экспоненциальной стадии меж-

мальной завихренностью и толщиной блина: ω_max ∼

ду этими величинами имеется степенная зависимость

ℓ^-2/3. Объединяет оба этих явления вмороженность

B_max

= Cℓ^α c показателем α = 0.16/(-0.25) =

поля завихренности для трехмерных течений и ро-

= -0.64 ≈ -2/3, C - константа (см. рис.5). Следует

тора завихренности для двумерной гидродинамики.

Является ли этот закон универсальным для лю-

бых вмороженных полей для несжимаемых течений?

Этот вопрос остается пока открытым, особенно он

интересен для магнитной гидродинамики, где маг-

нитное поле в бездиссипативном пределе является

вмороженным.

Данная работа выполнялась при поддержке гран-

та Российского научного фонда # 14-22-00174.

1. E. A. Kuznetsov, V. Naulin, A. H. Nielsen, and

J. J. Rasmussen, Phys. Fluids 19, 105110 (2007).

2. E. A. Kuznetsov, V. Naulin, A. H. Nielsen, and

J. J. Rasmussen, Theor. Comput. Fluid Dyn. 24, 253

(2010).

Рис. 5. Зависимость максимума ротора завихренности

от толщины ℓ. Точки соответствуют численным резуль-

3. А. Н. Кудрявцев, Е. А. Кузнецов, Е. В. Серещенко,

Письма ЖЭТФ 96, 783 (2012) [JETP Lett. 96, 699

татам, а линия - степенной зависимости Bmax ∼ ℓ-2/3

(2013)].

4. Е. А. Кузнецов, Е. В. Серещенко, Письма ЖЭТФ

отметить, что это поведение B_max от ℓ в виде закона

102, 870 (2015) [JETP Lett. 102(11), 760 (2015)].

2/3 было проверено нами также для других началь-

5. R. Kraichnan, Phys. Fluids 11, 1417 (1967).

ных условий (напомним, что положение вихрей и их

6. Е. А. Кузнецов, Е. В. Серещенко, Письма ЖЭТФ

размеры были случайными). Это дает основание нам

105, 70 (2017) [JETP Lett. 105, 83 (2017)].

2019

Письма в ЖЭТФ том 109 вып. 3 - 4