Письма в ЖЭТФ, том 109, вып. 4, с. 236 - 241

Нелокальный турбофорез частиц в логарифмическом слое

пристенной турбулентности

Д.Ф.Сиковский¹⁾²⁾

Институт теплофизики им. С. С. Кутателадзе Сибирского отделения РАН, 630090 Новосибирск, Россия

Новосибирский государственный университет, 630090 Новосибирск, Россия

Поступила в редакцию 21 ноября 2018 г.

После переработки 3 декабря 2018 г.

Принята к публикации 6 декабря 2018 г.

С помощью стохастического лагранжева моделирования исследована динамика высокоинерционных

частиц в логарифмическом слое пристенного турбулентного течения. Вследствие линейного изменения

турбулентного масштаба времени с расстоянием от стенки в логарифмическом слое наблюдается тур-

бофорез - миграция частиц к стенке, имеющая нелокальный характер в пристенной области из-за су-

щественного вклада баллистического движения частиц. Получены профили концентрации и второго

момента скорости частиц для произвольного параметра инерционности частицы и различных значений

коэффициента восстановления скорости частиц при отскоке от стенки. Показано наличие “тяжелых хво-

стов” функции плотности вероятности скорости частиц в пристенной области, приобретающих степенное

поведение в режиме неупругого коллапса траекторий частиц, наблюдаемого при значениях коэффици-

ента восстановления ниже критического значения 0.163 в соответствии с результатами Belan et al., Phys.

Rev. E 93, 052206 (2016).

DOI: 10.1134/S0370274X19040064

Турбулентные течения с взвешенными частица-

ν - кинематическая вязкость среды. Формирование

ми встречаются во многих сферах человеческой де-

степенной сингулярности концентрации происходит

ятельности, природных и космических явлениях.

при участии больших выбросов скорости среды, про-

Статистические модели динамики частиц в турбу-

исходящих на границе вязкого подслоя с ядром по-

лентной среде в последнее время являются объек-

тока и вызванных когерентными вихревыми струк-

том многочисленных исследований, главным обра-

турами пристенной турбулентности. Частицы, полу-

зом, благодаря явлению кластеризации частиц [1-3],

чившие благодаря таким выбросам большую отрица-

связанному с их инерцией. Большинство практи-

тельную (направленную к стенке) скорость, достига-

чески важных турбулентных газо-дисперсных пото-

ют стенки благодаря своей инерции по баллистиче-

ков ограничено твердыми стенками, вблизи которых

ским траекториям без существенного влияния турбу-

имеет место еще одно вызванное инерцией частиц яв-

лентных флуктуаций среды, резко затухающих при

ление: аккумуляция частиц в пристенной зоне. При-

движении частицы вглубь вязкого подслоя. Если им-

чиной аккумуляции традиционно считается турбо-

пульса влетающей в подслой частицы недостаточно,

форез частиц [4, 5] - миграция частиц против гради-

чтобы после столкновения со стенкой отскочить и

ента турбулентных напряжений частиц (второй мо-

вылететь в ядро потока, частица остается в подслое

мент флуктуации скорости частиц), принимающего

на достаточно долгое время. Несмотря на описанный

наибольшие значения в вязком подслое - прилега-

нелокальный баллистический механизм формирова-

ющей к стенке тонкой области, в которой скорость

ния пристенного пика концентрации частиц в вяз-

среды падает до нуля на стенке. Как показано в [6],

ком подслое, статистический режим скорости час-

профиль концентрации частиц в вязком подслое под-

тиц, формирующих такой пик, является локально-

чиняется степенному закону с отрицательным по-

равновесным вплоть до чисел Стокса τ₊

∼ 0.2ρ,

казателем, зависящим от параметра инерционности

где ρ - отношение плотностей частицы и среды, что

частиц - числа Стокса τ+ = v2ττ/ν, где τ - вре-

позволяет получить простые аналитические решения

мя релаксации частиц, v_τ - динамическая скорость,

для концентрации частиц в вязком подслое [6-8].

В то же время для высокоинерционных частиц в

¹⁾D.Ph. Sikovsky.

ядре потока с числами Стокса 10² и более, характер-

²⁾e-mail: dphs@mail.ru

ная длина пробега частиц превышает толщину вязко-

236

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

Нелокальный турбофорез частиц в логарифмическом слое пристенной турбулентности

237

го подслоя. Такие частицы, сталкиваясь со стенкой,

поверхности [13], в котором взвешены инерционные

проводят в вязком подслое малое время, поэтому их

частицы с временем релаксации τ. Поскольку тече-

динамика определяется главным образом турбулент-

ние статистически однородно в параллельных стенке

ностью в логарифмическом слое, занимающем основ-

направлениях, ниже будет рассматриваться движе-

ную часть пристенной зоны потока при больших чис-

ние частиц в нормальном к стенке направлении y,

лах Рейнольдса [9]. Определяющими параметрами

подчиняющееся уравнениям y˙_p = v, v = (v_f - v_p)/τ,

для турбулентности логарифмического слоя являют-

где v_p - скорость частицы, v_f - скорость среды вдоль

ся динамическая скорость и расстояние до стенки y,

траектории частицы, которую необходимо моделиро-

поэтому интенсивность флуктуаций скорости среды

вать исходя из заданных статистических характери-

в нем постоянна [10]. Вблизи стенки лагранжев мас-

стик движения среды в логарифмическом слое. К та-

штаб времени меньше времени релаксации частицы,

ковым прежде всего относятся интенсивность флук-

из-за чего степень вовлечения инерционных частиц

туаций нормальной к стенке компоненты скорости

в турбулентное движение и интенсивность флукту-

v_f,rms = (〈v^2f〉)^1/2 и характерное время декорреляции

аций их скорости становится меньше интенсивности

флуктуаций скорости среды - лагранжев интеграль-

флуктуаций скорости среды, в то время как вдали от

ный масштаб времени T_L, которые в соответствии

стенки лагранжев масштаб времени превышает вре-

с теорией подобия пристенной турбулентности [10]

мя релаксации и скорость частицы стремится к ско-

имеют вид

рости среды (предел пассивной примеси [1, 11]). В

v_f,rms = av_τ , T_L = κ_Ly/v_τ ,

(1)

результате интенсивность флуктуаций скорости час-

тиц при приближении к стенке падает, что вызыва-

где a = 1.13, κL = 0.356 - коэффициенты, явля-

ет миграцию частиц по направлению к стенке. В [1]

ющиеся универсальными в пределе больших чисел

получены соответствующие решения для концентра-

Рейнольдса. Здесь значение a получено из результа-

ции и интенсивности флуктуаций скорости частиц в

тов прямого численного моделирования турбулент-

логарифмическом слое на основе уравнений перено-

ного течения в плоском канале при большом числе

са вторых моментов скорости частиц, выведенных

Рейнольдса [14], а также использовано соотношение

из кинетического уравнения для функции плотно-

κ_L = κa^-2Pr^-1t, связывающее коэффициент турбу-

сти вероятности (ФПВ) скорости и местоположения

лентной диффузии в логарифмическом слое с посто-

частиц с использованием квазиравновесных гипотез

янной Кармана κ = 0.41 и турбулентным числом

замыкания для третьих и четвертых моментов. Од-

Прандтля P r_t = 0.9 [10]. В качестве модели скоро-

нако, применимость квазиравновесных соотношений

сти среды вдоль траектории частицы используется

для замыкания моментных уравнений в данном слу-

нормализованная ланжевеновская модель [15], в ко-

чае вызывает вопросы, поскольку характерная длина

торой скорость среды нормируется на свою интен-

пробега частиц v_τ τ вблизи стенки превышает рассто-

сивность: u = v_f /(〈v^2f〉)^1/2 , а для нормализованной

яние до нее. За время декорреляции скорости час-

скорости u записывается стохастическое дифферен-

тицы статистический режим скорости среды вдоль

циальное уравнение (СДУ) в смысле Ито

ее траектории существенным образом меняется, что

свидетельствует о нелокальном механизме турбофо-

du = [u_d(y_p) - G(y_p)u] dt + [2G(y_p)]^1/2 dW,

(2)

реза и аккумуляции частиц в логарифмическом слое,

где W (t) - стандартный винеровский процесс, для

отличающемся от локально-равновесного механизма

которого 〈(dW (t))²〉 = dt, G(y_p) - обратное время де-

аккумуляции в вязком посдлое. Аналогичная нело-

корреляции скорости среды, u_d(y) - скорость дрей-

кальность механизма кластеризации высокоинерци-

фа, определяемая из выражений

онных частиц обнаружена в однородно-изотропной

турбулентности [12].

d(f_vv_f,rms)

u_d =

, f_v =

(3)

В настоящей работе проведено статистическое

1+τG

моделирование динамики частиц в логарифмическом

Для однородной турбулентности с G, v_f,rms = const

слое с помощью стохастической лагранжевой моде-

СДУ (2) описывает процесс Орнштейна-Уленбека

ли турбулентности, преимуществом которой перед

с гауссовой ФПВ и корреляционной функцией

квазиравновесными моделями замыкания уравнений

〈u(0)u(t)〉

= exp(-Gt), что позволяет вычислить

переноса моментов является прямое моделирование

лагранжев интегральный масштаб времени скорости

нелокального транспорта частиц.

среды вдоль траектории частиц

Рассматривается турбулентное течение в лога-

рифмическом слое вдоль неограниченной плоской

G=T^-1Lp.

(4)

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

238

Д.Ф.Сиковский

Для однородно-изотропной турбулентности связь

весом, пропорциональным времени пребывания час-

между T_Lp и интегральным лагранжевым масшта-

тицы в каждом из 200 интервалов Δη_i, на которые

бом времени турбулентности среды T_L задается

разбивалась расчетная область (со сгущением к стен-

аппроксимацией [16]

ке). Сбор статистики велся после начального периода

[

]

времени Δt_in = 3 · 10⁵, в течении которого устанав-

T_L

0.644

ливался стационарный статистический режим дви-

T_Lp =

(5)

0.356

(1 + St_E )^0.4(1+0.01StE⁾

жения частицы. При выходе частицы из расчетной

области она симметрично отражалась от плоскости

где St_E = 0.356τ/T_L. Для произвольного неоднород-

η = η_max, возвращаясь обратно, при этом знаки v и

ного турбулентного течения связать обратное время

u менялись на противоположные.

декорреляции с интегральным масштабом времени

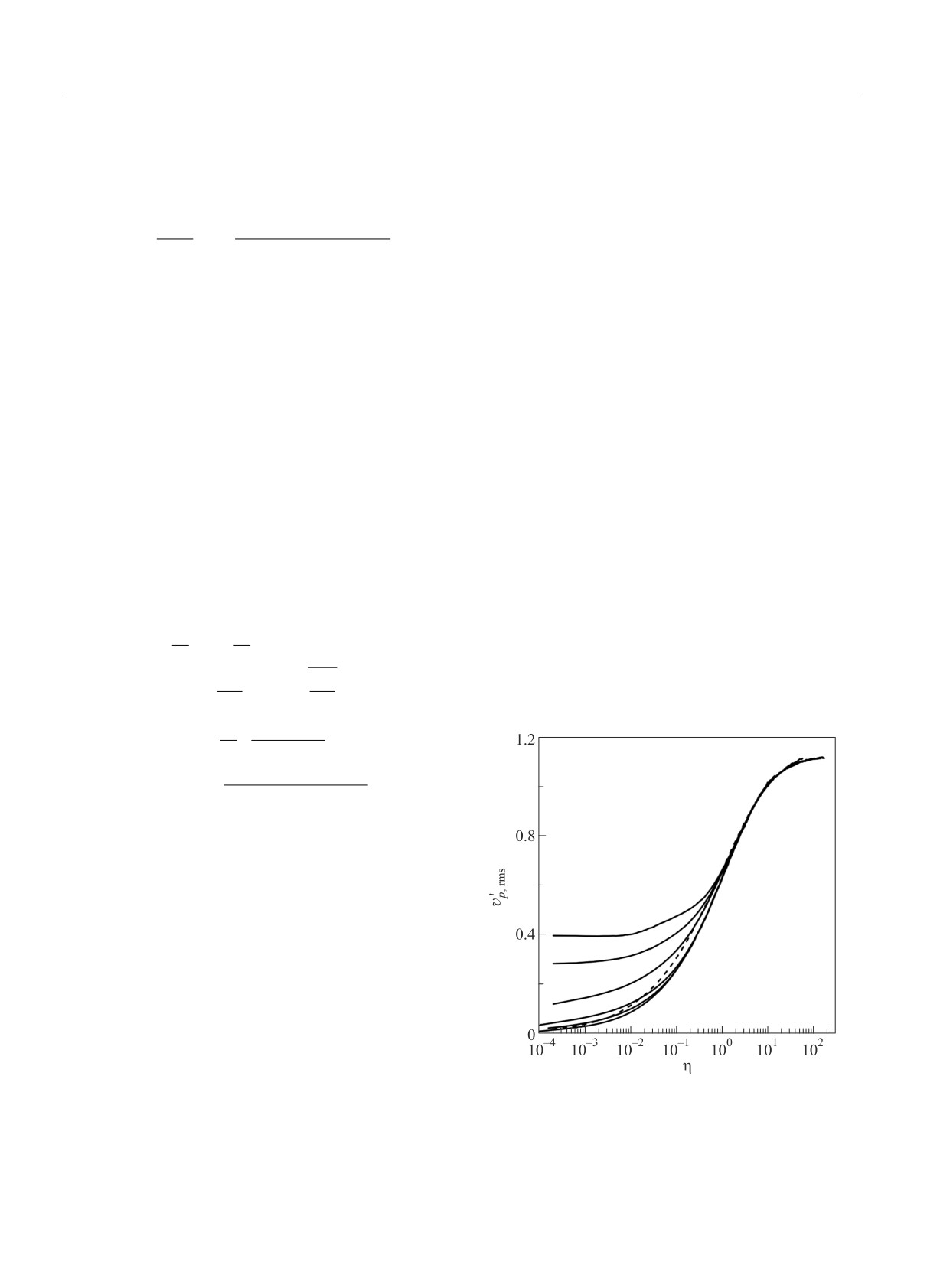
На рисунке 1 представлена интенсивность флук-

не удается, можно лишь показать, что соотношение

туаций скорости частицы для различных значений

(4), а также первое соотношение (3), являются глав-

коэффициента восстановления. При η > 1 профили

ными приближениями некоторого разложения по па-

интенсивности близки к равновесному, определяемо-

раметру неравновесности для квазиравновесных те-

му соотношением Чена [18]

чений [15]. Для рассматриваемого неравновесного те-

чения в логарифмическом слое выражения (3)-(5)

v_rms = v_f,rms[1 + T^-1Lp]^-1/2 = a[1 + T^-1Lp]^-1/2,

(11)

могут рассматриваться, как разумная аппроксима-

ция, дающая неплохие результаты при моделирова-

При η

< 1 локальность связи между v_rms и

нии динамики частиц с преобладанием баллистиче-

T_Lp нарушается. Так, например, поскольку на стенке

ских механизмов переноса [15].

турбулентный масштаб времени равен нулю, в равно-

Поскольку единственными определяющими пара-

весном случае скорость частиц, согласно (11), долж-

метрами задачи являются динамическая скорость и

на обращаться в ноль и столкновения частиц со стен-

время релаксации частицы, удобно привести уравне-

кой должны отсутствовать. Однако, по данным рас-

ния модели (2)-(5) к безразмерному виду

четов столкновения имеют место при любых e_y, что

связано с преобладающей ролью баллистического пе-

dη

= v,

+ v = au,

(6)

реноса в пристенной области, за счет которого час-

√

тицы достигают стенки с расстояний η ∼ 1.

(

)

Как видно из рис.1, интенсивность флуктуаций

du = u_d -

dt +

dW,

(7)

T_Lp

скорости частиц вблизи стенки падает с уменьше-

[

]

T_Lp(η)

u_d(η) = a

(8)

dη

1 + T_Lp(η)

[

]

0.644

T_Lp(η) = η

(9)

(1 + 1/η)^{0.4(1+0.01/η)}

где η = y_p/(v_τ τ), v = v_p/v_τ и время t теперь обезраз-

мерено на время релаксации τ.

Ниже будет рассмотрен случай неупругого взаи-

модействия частиц со стенкой, характеризуемого ко-

эффициентом восстановления e_y (0 < e_y ≤ 1)

v(t_c + 0) = -e_yv(t_c - 0),

(10)

где t_c - время столкновения частицы со стенкой.

Задача (6)-(10) решалась численно с использова-

нием метода Хойна второго порядка точности [17]

для расчетной области [0; η_max], η_max = 200. Инте-

грировалось уравнение движения для одной частицы

в течении длительного времени t_comp = 2 · 10⁷, в те-

чение которого ее траектория достаточно плотно за-

Рис. 1. Интенсивность флуктуаций скорости частиц в

полняет доступное фазовое пространство, после чего

логарифмическом слое. Коэффициент восстановления

профили концентрации и статистических моментов

ey: 0.02 (нижняя), 0.163, 0.3, 0.5, 0.8, 1 (верхняя). Пунк-

тир - равновесная зависимость (11)

скорости частицы вычислялись путем осреднения с

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

Нелокальный турбофорез частиц в логарифмическом слое пристенной турбулентности

239

нием e_y, что связано с диссипацией энергии в хо-

соответствующее степенной сингулярности концен-

де столкновений со стенкой. При e_y

< 0.5 про-

трации

фили интенсивности флуктуаций скорости частиц

Φ∼η^2/3-2γ.

(14)

приближаются к равновесному и могут быть ниже

Кроме того, в пределе η → 0 ФПВ скорости частиц

его. При этом в распределении концентрации час-

также стремится к степенному закону

тиц (рис. 2) происходит качественная перестройка:

P ∼ |v|^-3γ.

(15)

Коэффициент γ в (13)-(15) зависит только от коэф-

фициента восстановления и определяется из соотно-

шения

sin(πγ) - sin[π(γ - 2/3)]

=e^3(γ-2/3)y,

(16)

sin(2π/3)

Решение (13) имеет физический смысл только при

0 < e_y < e_y,cr, где критическое значение коэффи-

√

3) ≃

циента восстановления равно e_y,cr = exp(-π/

≃ 0.163. В этом интервале коэффициента восстанов-

ления происходит так называемый неупругий кол-

лапс траектории частицы, когда ее скорость в резуль-

тате последовательности столкновений стремится к

нулю, а сама частица стремится к стенке [19].

Как видно из рис.2, степенной закон (14) с рас-

считанными из (16) величинами γ(e_y) хорошо со-

гласуется с данными численного моделирования для

Рис. 2. Концентрация частиц в логарифмическом слое.

ey < ey,cr, в то время как при ey > ey,cr наблю-

Значения ey - см. рис. 1, верхней кривой соответствует

наименьшее значение ey. Пунктирные линии - степен-

дается отклонение от степенного закона. В соответ-

ной закон (14)

ствии с приведенными на рис.3 расчетными функ-

циями плотности вероятности скорости частиц вбли-

при e_y < 0.163 вблизи стенки отчетливо формирует-

зи стенки (в расчетах - на расстояниях y < 10^-4),

ся степенная сингулярность концентрации, в то вре-

при e_y < e_y,cr также происходит переход к степенно-

мя как для e_y > 0.163 концентрация, по-видимому,

му закону (15). Эти результаты иллюстрируют экс-

стремится к конечному пределу при η → 0, хотя по-

тремальную перемежаемость скорости частиц вбли-

следний не всегда достигается в численных расчетах

зи стенки в режиме неупругого коллапса e_y < e_y,cr,

с конечным разрешением, особенно для значений e_y,

когда ФПВ скорости состоит практически из сплош-

близких к критическому e_y,cr = 0.163.

ных степенных “тяжелых хвостов” (15) [19]). При

Причину такого поведения помогает понять ме-

e_y > e_y,cr “хвосты” ФПВ остаются “тяжелыми” вбли-

тод, развитый в [19]. Поскольку вблизи стенки тур-

зи стенки, но уже не имеют выраженных степенных

булентный масштаб времени стремится к нулю, тур-

асимптотик. Вдали от стенки при η ≫ 1, как упо-

булентные флуктуации скорости среды можно заме-

миналось выше, скорость частицы стремится к ско-

нить в первом приближении белым шумом, что поз-

рости среды, которая в соответствии с моделью (2)

воляет с учетом (1),(9) записать для ФПВ скорости

имеет гауссову статистику (рис. 4).

частиц P (v, η) уравнение Фоккера-Планка

Полезно обсудить отличия динамики инерцион-

ных частиц в двух разных областях пристенного тур-

v∂_ηP - ∂_v(vP) = a²η∂^2vP.

(12)

булентного потока: логарифмическом слое и в вяз-

ком подслое (см. [6, 8]). В обоих случаях наблюдает-

Вследствие преобладания баллистического переноса

ся степенная сингулярность концентрации частиц на

частиц при η ≪ 1 вторым членом в левой части (12)

стенке, однако в вязком подслое она имеет место при

можно пренебречь. Получившееся уравнение, как по-

любом числе Стокса, которое однозначно определяет

казано в [19], имеет автомодельное решение

величину показателя степени, в то время как в лога-

рифмическом слое степенная сингулярность концен-

P ∼ η^-2γh(ζ), ζ =

(13)

трации имеет место только для коэффициентов вос-

9a²η²

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

240

Д.Ф.Сиковский

Рис. 3. (Цветной онлайн) Функция плотности вероятностей отрицательных скоростей частиц вблизи стенки. Линии -

степенной закон (15)

становления, меньших критического значения пере-

нальному расстоянию до стенки [6], и связаны с бал-

хода к неупругому коллапсу, причем показатель сте-

листическими частицами из ядра потока.

пени однозначно определяется коэффициентом вос-

Таким образом, в логарифмическом слое наблю-

становления. За пределами режима неупругого кол-

дается миграция частиц к стенке, направленная про-

лапса концентрация частиц на стенке имеет конечное

тив градиента масштаба времени турбулентности.

значение. Отличие наблюдается и в поведении “тя-

Профили концентрации и статистических моментов

желых хвостов” ФПВ скорости частиц вблизи стен-

скорости частиц однозначно определяются автомо-

ки: если в логарифмическом слое они наблюдаются

дельной координатой η и коэффициентом восстанов-

для всех e_y и имеют степенной вид при неупругом

ления e_y. Координата η характеризует близость ста-

коллапсе, то в вязком подслое хвосты ФПВ возника-

тистики скорости частиц к локально-равновесной,

ют только во втором порядке асимптотического раз-

отклонение от которой растет при уменьшении η.

ложения по параметру неравновесности, пропорцио-

Вблизи стенки баллистический перенос частиц ста-

Письма в ЖЭТФ том 109 вып. 3 - 4

2019

Нелокальный турбофорез частиц в логарифмическом слое пристенной турбулентности

241

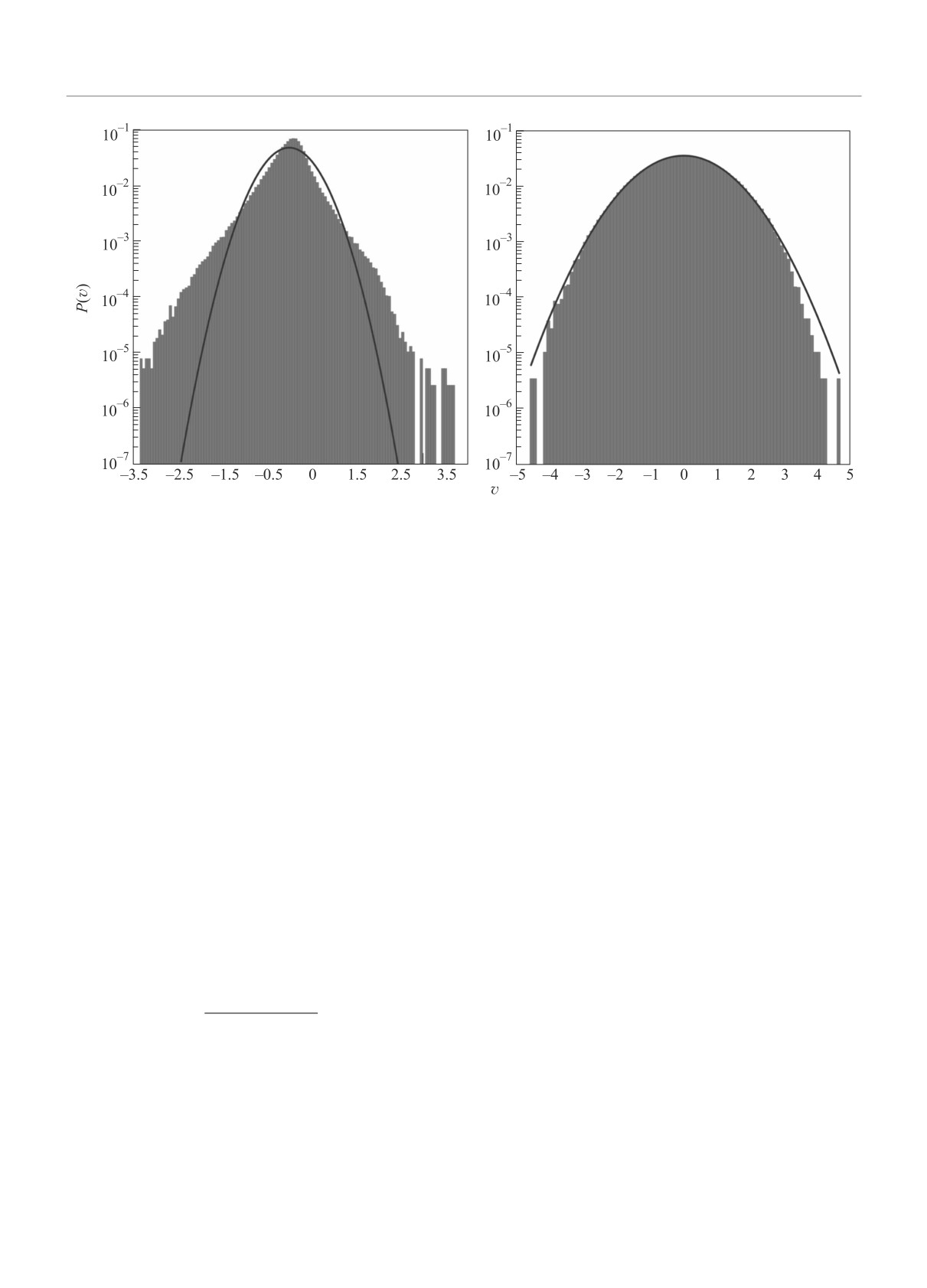
Рис. 4. (Цветной онлайн) Функция плотности вероятностей скоростей частиц с упругим отскоком (ey = 1) вблизи

стенки η = 0.1 (a) и вдали от нее η = 200 (b). Линии - гауссова ФПВ

новится преобладающим, нарушая локальность тур-

3. K. Gustavsson and B. Mehlig, Adv. Phys. 65, 1 (2016).

булентного переноса частиц и приводя к появлению

4. M. W. Reeks, J. Aerosol Sci. 92, 729 (1983).

“тяжелых хвостов” ФПВ скорости частиц в пристен-

5. M. Caporaloni, F. Tampieri, F. Trombetti, and

ной области. При значениях коэффициента восста-

O. Vittori, J. Atmos. Sci. 32, 565 (1975).

новления ниже критического значения перехода к

6. D. Ph. Sikovsky, Flow Turb. Comb. 92, 41 (2014).

неупругому коллапсу, ФПВ скорости частиц приоб-

7. S. Belan, I. Fouxon, and G. Falkovich, Phys. Rev. Lett.

ретает степенные “тяжелые хвосты”, свидетельству-

112, 234502 (2014).

ющие об экстремальной перемежаемости скорости

8. S. Belan, Physica A 443, 128 (2016).

частиц. Концентрация частиц на стенке растет при

9. S. B. Pope, Turbulent Flows, Cambridge Univ. Press

уменьшении коэффициента восстановления и при-

(2000).

ближении его к критическому значению и расходит-

10. А. С. Монин, А. M. Яглом, Статистическая гидро-

ся по степенному закону при значениях коэффици-

механика, Гидрометеоиздат, СПб. (1992), т. 1.

ента восстановления ниже критического в режиме

11. D. F. Sikovskii, Fluid Dynamics 45, 74 (2010).

неупругого коллапса траекторий частиц.

12. A. D. Bragg, P. J. Ireland, and L. R. Collins, J. Fluid

Автор благодарен С. А. Белану, Г. Е. Фальковичу

Mech. 780, 327 (2015).

и В.В. Лебедеву за полезные обсуждения.

13. Л. Д. Ландау, Е. M. Лифшиц, Гидродинамика, Наука,

Работа выполнена при поддержке гранта Россий-

М. (1986), пп. 42.

ского научного фонда (проект # 14-19-01685). Чис-

14. M. Lee and R. D. Moser, J. Fluid Mech. 774, 395 (2015).

ленные методы стохастического моделирования раз-

15. D. Ph. Sikovsky, Flow Turb. Comb. 95, 561 (2015).

работаны в рамках государственного задания Инсти-

16. L.-P. Wang and D. E. Stock, J. Atmos. Sci. 50, 1897

(1993).

тута теплофизики Сибирского отделения РАН.

17. J.-P. Minier, E. Peirano, and S. Chibbaro, Monte Carlo

Methods Appl. 9, 93 (2003).

1. Л. И. Зайчик, В. M. Алипченков, Статистические

18. И. О. Хинце, Турбулентность, Изд-во физ.-мат. лит.,

модели движения частиц в турбулентной жидко-

М. (1963).

сти, Физматлит, М. (2007).

19. S. Belan, A. Chernykh, V. Lebedev, and G. Falkovich,

2. M. W. Reeks, Flow. Turb. Combust. 92, 3 (2014).

Phys. Rev. E 93, 052206 (2016).

Письма в ЖЭТФ том 109 вып. 3 - 4

2019