Pis’ma v ZhETF, vol. 109, iss. 5, pp. 292 - 293
© 2019
March 10
A note on reflection positivity in nonlocal gravity
M. Christodoulou1), L. Modesto1)
Department of Physics, Southern University of Science and Technology, 518055 Shenzhen, China
Submitted 17 December 2018
Resubmitted 17 December 2018
Accepted 25
December 2018
DOI: 10.1134/S0370274X19050023
∫ ∞
Reflection positivity. Reflection positivity is one
21-D
G(|x|) =
du uD-3 F (u2 σ)
of the axioms laid out by Osterwalder and Schrader in
πD/2
0
]
their seminal works [1, 2], and an important test for any
[D
1
0
F1
;-
u2|x|2
(4)
attempt to quantize Einstein’s theory in the quantum
2
4
field theory framework. It is a necessary and sufficient
where we have introduced the radial coor-
condition in order for Euclidean Green’s functions to
√
dinate in momentum space u
=
k2, and
(uniquely) define a Wightman quantum field theory in
0
F1(a; z)
=
0F1(a; z)/Γ(a) is the regularized con-
Minkowski space. Recently, concerns were raised [3] that
fluent hypergeometric function.
weakly nonlocal theories fail to pass the basic test of per-
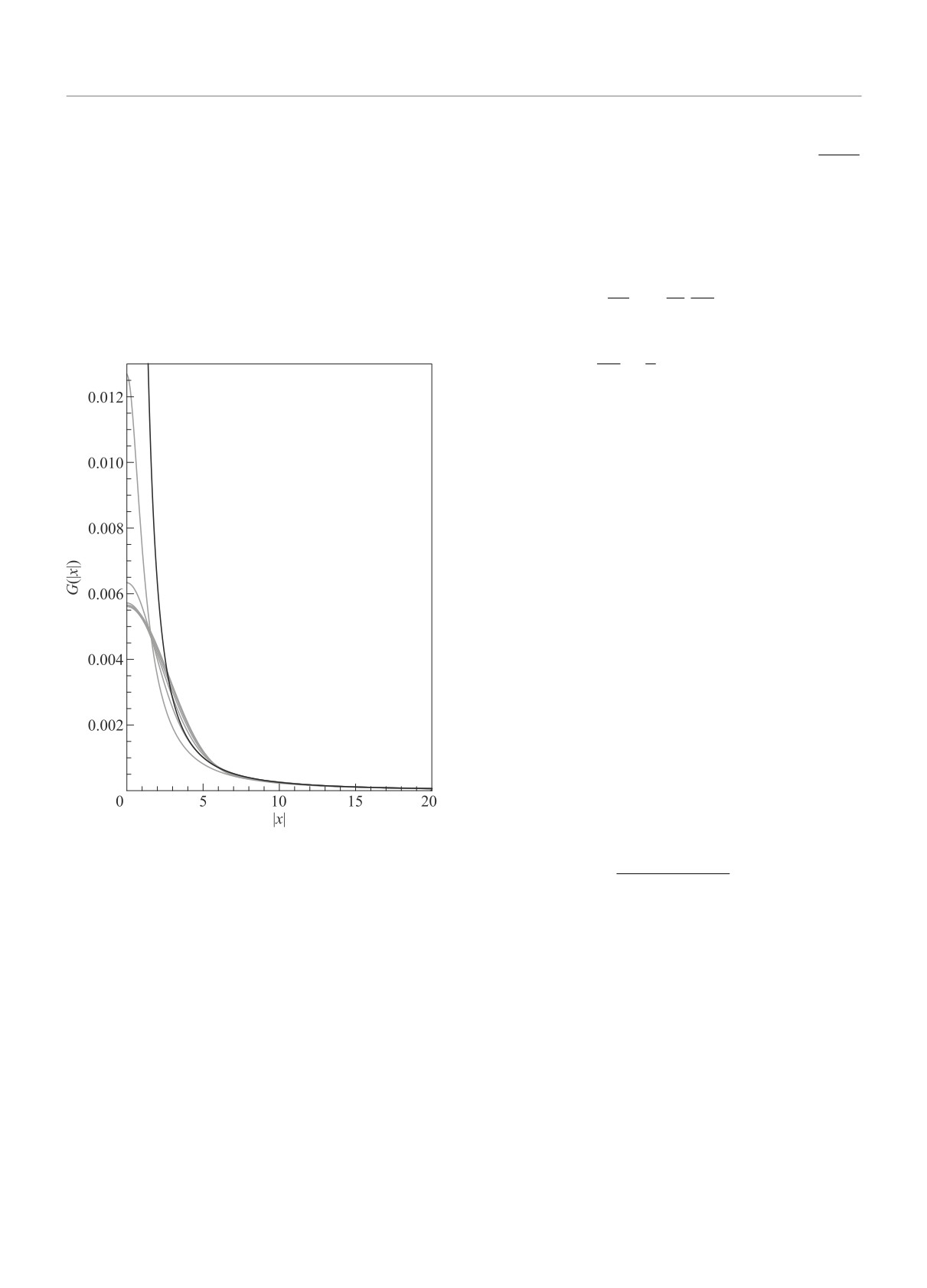
From the form (4) of the propagator we can prove
turbative reflection positivity in the coincidence limit.
the following statement. For any form factor F (u) that
In this note we show that this issue does not arise for
is a bounded positive monotonically decreasing function
massless scalar field theories.
of the non-negative variable u, the propagator G(Y ) is
A Euclidean quantum field theory is said to satisfy
positive for any Euclidean vector Y . This is our main
reflection positivity when the following statement holds.
technical result. It follows from the following integral
For any functional F[φ] of the fields whose support in-
inequality [6]. For any bounded positive real function
cludes only points that have positive Euclidean time
F (u) that is monotonically decreasing on the positive
τ > 0, we have
< 0 and 0 < F < ∞ for u ∈ (0,∞)),
real axis (that is, F′
and for any J(u) that satisfies
〈(ΘF[φ])F[φ]〉 ≥ 0,
(1)
∫ u
dt J(t) > 0,
∀u ∈ (0, ∞),
(5)
where ΘF[φ] denotes complex conjugation and reflec-
0
tion with respect to the τ = 0 (hyper) plane.
we have that
Considering only one “charge” [4] at fixed position
∫ ∞
X is physically equivalent to studying the properties of
du F (u)J(u) > 0.
(6)
the propagator in the coincidence limit. Then, a simple
0
necessary (but not sufficient) condition for perturbative
Restricting to four dimensions, we show that a suf-
reflection positivity is
ficient condition for perturbative reflection positivity in
the coincidence limit is simply that the form factor F
G(θX - X) ≥ 0.
(2)
is a monotonically decreasing function
This is in fact equivalent to the requirement that the
F′ < 0.
(7)
propagator itself is positive for any vector Y
Theories concerned. Two popular classes of theo-
G(Y ) ≥ 0
∀ Y.
(3)
ries concerned by the above are those with form factors
F ≡ e-H(σ□) such that
Propagator. We simplify the expression for the
HK(z) = α [log (z) + Γ (0, z) + γE] , Re z > 0,
(8)
propagator G(x) for a general form factor F ≡ exp -H
1
[
(
)
(
)
]
using similar manipulations as in [5], to arrive at
HT (p) =
log
p2
+Γ
0, p2
+γE
, Re p2 > 0. (9)
2
1)e-mail: christod.marios@gmail.com;
Here, α is an integer, p is a polynomial of degree n in the
lmodesto1905@icloud.com
variable z ≡ σ□ and γE is the Euler-Mascheroni con-
292
Письма в ЖЭТФ том 109 вып. 5 - 6
2019
A note on reflection positivity in nonlocal gravity
293
stant. The parameters α and n must satisfy the super-
son that the propagator can be negative for the massive
renormalizability conditions
case is that when m = 0, there is an extra facto
2+m2
in the integral, which is equal to unit when m = 1.
α > D - 1, n > D - 1,
(10)
This function is monotonically increasing in the inter-
val u ∈ (0, ∞).
respectively. We also consider form factors that are
Returning to the massless case, for form factors as
asymptotically exponential and are of the form, see
in Eq. (9) we have that
Fig. 1
F =e-H =e-(-σ□)n, n∈N+.
(11)
dF
dp dH
=-
F.
(12)
du
du dp
Such form factors have been studied in the context of
string theory and gauge theories.
Since
)
dH
α(
=
1-e-p2 ,
(13)
dp
p
the inequality (7), and thus also (3), is automatically
satisfied whenever p is a monomial, which includes the
case of Eq.(8). Then, (3) and by extension (2) is shown
to hold for these cases as well.
Conclusions. We gave a simple proof for the posi-
tivity of the propagator for a large class of massless non-
local theories in four dimensions. As a consequence, a
basic test for unitarity, perturbative reflection positivity
in the coincidence limit, was shown to hold. This result
covers theories defined by exponential form factors as
well as form factors that have the properties required of
candidates for a well defined quantum gauge or gravita-
tional theory. Furthermore, we have provided numerical
evidence that the same is true also for higher dimen-
sions and for nonlocal theories not covered by the proof
given here. Our results show that the results in [3] do
not imply a generic violation of perturbative reflection
positivity in the coincidence limit for weakly nonlocal
field theories, including quantum gravity or gauge the-
ories. We have shown here that this issue does not arise
for the massless case.
Full text of the paper is published in JETP Letters
Fig. 1. The propagators for the form factor of Eq. (11) for
journal. DOI: 10.1134/S0021364019050011
D = 4 and n = 1/2,1,3/2,2,5/2,3 (gray). The propaga-
tor for General Relativity is drawn for comparison (black).
The propagators for the non-local theory are positive and
1. K. Osterwalder and R. Schrader, Commun. Math. Phys.
well behaved in the ultraviolet, including the coincidence
31, 83 (1973).
limit |x| = 0. The infrared behaviour is identical as that
2. K. Osterwalder and R. Schrader, Commun. Math. Phys.
of General Relativity. We note that as n increases, G(0)
42, 281 (1975).
converges to the value ∼ 6 · 10-3. The nonlocality scale σ
3. M. Asorey, L. Rachwal, and I. Shapiro, Galaxies 6(1),
has been set to unit here
23 (2018); arXiv:1802.01036 [hep-th].
4. A. Uhlmann, Czechoslovak Journal of Physics B 29(1),
All form factors of the form (11) satisfy the above.
117 (1979).
This result shows that the violation of perturbative re-
5. G. V. Efimov, Nonlocal Interactions [in Russian], Nauka,
flection positivity noticed in [3], where such form factors
M. (1977).
and the test (2) were considered for massive scalar field
6. W. T. Sulaiman, Advances in Pure Mathematics 01(03),
theories, does not arise for the massless case. The rea-
63 (2011).
Письма в ЖЭТФ том 109 вып. 5 - 6
2019