Письма в ЖЭТФ, том 109, вып. 6, с. 423 - 428

Переход типа Изинг-XY в трехмерных фрустрированных

антиферромагнетиках с коллинеарным спиновым упорядочением

А. О. Сорокин¹⁾

Национальный исследовательский центр “Курчатовский институт”, Петербургский институт ядерной физики,

188300 Гатчина, Россия

Поступила в редакцию 21 ноября 2018 г.

После переработки 24 января 2019 г.

Принята к публикации 25 января 2019 г.

Методом Монте-Карло исследуется критическое поведение в двух моделях фрустрированных XY ан-

тиферромагнетиков с коллинеарным спиновым упорядочением и дополнительным двукратным вырож-

дением основного состояния. Рассматривается классический антиферромагнетик на объемноцентриро-

ванной кубической решетке с дополнительным обменным взаимодействием между спинами, следующими

за ближайшими, а также ферромагнетик на простой кубической решетке с дополнительным антиферро-

магнитным внутрислойным обменом. Найдено, что в обоих моделях переход как по дискретному, так и

по непрерывному параметрам порядка происходит одновременно в виде перехода первого рода. В случае

примерного равенства величин конкурирующих обменов наблюдается псевдоскейлинг с показателями,

согласующимися с известными показателями XY магнетиков с планарным спиновым упорядочением

типа антиферромагнетика на слоисто-треугольной решетке и спиральных магнетиков, принадлежащих

тому же симметрийному классу. Также мы предлагаем возможное объяснение наблюдающемуся псев-

доскейлинговому поведению.

DOI: 10.1134/S0370274X19060146

Критические явления во фрустрированных маг-

ный, то при рассмотрении систем малого размера

нитных системах чрезвычайно интересны из-за реа-

и/или при отклонении от критической температуры

лизации в них множества различных сценариев на-

переход становится неотличим от перехода второго

рушения симметрии [1, 2]. На протяжении несколь-

рода. То есть в критическом поведении наблю-

ких десятилетий обсуждалась возможность того, что

дается кроссовер между степенным поведением в

магнетики с планарным спиновым упорядочением

области параметров, где корреляционная длина

типа антиферромагнетика на слоисто-треугольной

мала, и поведением, характерным для перехода

решетке и спиральных магнетиков [3] принадлежат

первого рода. В терминах РГ подобный кроссовер

новому классу универсальности, характеризующему-

может объясняться тем, что соответствующая РГ-

ся набором показателей, отличных от показателей

траектория проходит через область РГ- диаграммы,

обычной O(N)-модели. Большое количество числен-

характеризующейся очень медленным РГ-потоком.

ных и экспериментальных результатов, в которых

Наглядным примером модели с переходом слабого

наблюдается скейлинговое и почти универсальное

первого рода и псевдоскейлинговым поведением

поведение в критической точке, подтверждают эту

служит двумерная 5-позиционная модель Поттса

гипотезу (для обзора см. [4]). Однако наиболее на-

[17]. В недавней работе [18] для данной модели

дежные результаты указывают [5-7], что в физиче-

подобный кроссовер был детально исследован.

ски интересных случаях XY (N = 2) и изотропных

Псевдоуниверсальность также может быть

(N = 3) спинов переход слабого первого рода. Это

объяснена в терминах РГ в случае, когда область

также подтверждается методами ренормгруппы (РГ)

замедления потока оказывается притягивающей для

[8-15].

РГ-траекторий, стартующих с достаточно обширной

Наблюдаемое (псевдо)скейлинговое поведение,

области начальных параметров. Одна из ситуаций,

имитирующее характерные для перехода второго

когда подобная притягивающая область может по-

рода сингулярности, типично для перехода слабого

явиться, связана с неподвижной точкой с комплекс-

первого рода [16]. Если переход почти непрерыв-

ными координатами, но небольшой мнимой частью.

Именно такая ситуация реализуется в O(N) ⊗ O(2)-

¹⁾e-mail: aosorokin@gmail.com

модели, описывающей фрустрированные магнетики

Письма в ЖЭТФ том 109 вып. 5 - 6

2019

423

424

А. О. Сорокин

с планарным спиновым упорядочением, для случаев

N = 2 и N = 3 [8-10,14,15]. Однако для случая

N = 2, которым мы интересуемся в данной работе,

область, в которой РГ-поток существенно замед-

ляется, довольно велика, и поэтому наблюдается

широкий разброс в значениях псевдоиндексов для

различных решеточных моделей. Более того, в неко-

торых моделях из рассматриваемого симметрийного

класса наблюдается ярко выраженный переход

первого рода (см., например, [19]).

Случай N = 2 O(N) ⊗ O(2)-модели выделен тем,

Рис. 2. Обменные взаимодействия в слоисто-J1-J2 мо-

что упорядоченная фаза описывается двумя пара-

дели. Приведены две конфигурации противоположной

метрами: дискретным и непрерывным. В общем слу-

киральности, которые нельзя свести друг к другу с по-

чае нарушается O(N)/O(N - 2) симметрия, что для

мощью глобальных поворотов спинов и инверсии

N = 2 сводится к группе O(2) = Z₂⊗SO(2), отвечаю-

щей симметрии относительно глобальных поворотов

центрированной кубической [24, 25], гексагональной

спинов и инверсии. В данной работе мы рассматрива-

плотноупакованной [26, 27] и слоисто-треугольной

ем две модели фрустрированных XY антиферромаг-

решеток [28, 29]. Для этих моделей дополнительное

нетиков с коллинеарным спиновым упорядочением и

вырождение основного состояния трехкратно, и пе-

дополнительным нарушением Z₂ подгруппы группы

реход ярко выраженного первого рода происходит с

симметрии решетки, так что нарушенной симметри-

нарушением Z₃ ⊗ SO(2) симметрии.

ей также оказывается группа Z₂ ⊗SO(2). Первая мо-

В данной работе мы покажем, что в обеих мо-

дель - это антиферромагнетик на объемноцентриро-

делях для широкого диапазона отношения величин

ванной кубической решетке с дополнительным об-

обменов наблюдается переход слабого первого ро-

менным взаимодействием между спинами, следую-

да одновременно по обоим параметрам порядка с

щими за ближайшими. Вторая модель - это так на-

псевдоскейлинговым поведением. Более неожиданно,

зываемая слоисто-J₁-J₂ модель, описывающая фер-

что критические показатели имеют значения, близ-

ромагнетик на простой кубической решетке с допол-

кие к показателям, наблюдающимся в треугольном

нительным внутрислойным обменом. На самом деле,

антиферромагнетике и спиральных магнетиках (см.

эти модели эквивалентны двум взаимодействующим

табл. 1). Основываясь на РГ-анализе [30], мы предла-

антиферромагнитным подрешеткам и имеют допол-

гаем возможное объяснение наблюдающемуся псев-

нительное бесконечное вырождение основного состо-

доскейлингу.

яния, которое снимается температурными флуктуа-

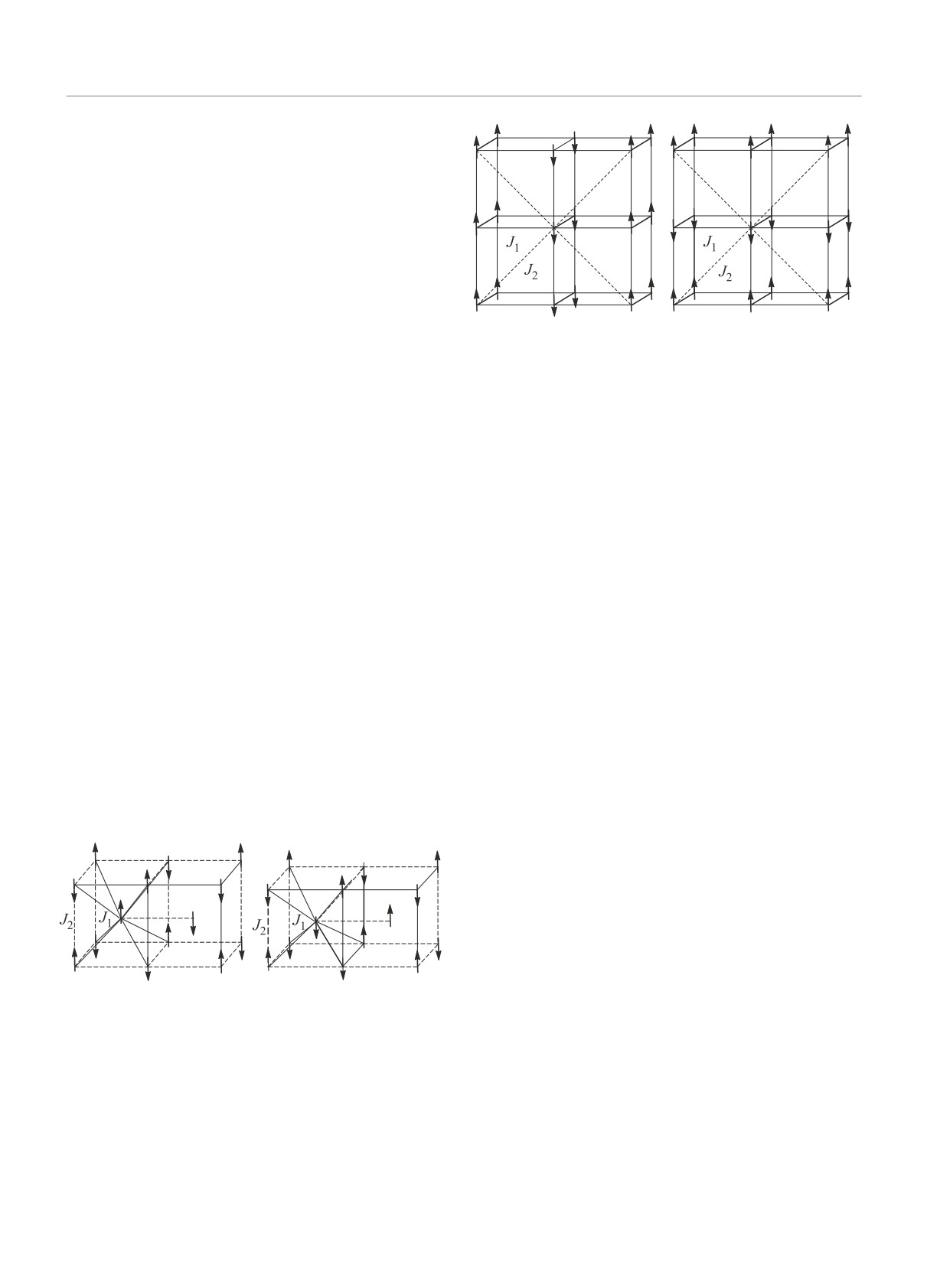
Модель антиферромагнетика на объемноцентри-

циями так, что только остаются только две неэквива-

рованной кубической решетке (для краткости - ОЦК

лентные конфигурации (рис. 1, 2) [20, 21]. Отметим,

модель) описывается гамильтонианом

∑

H =J₁

S_iS_j + J₂

S_kS_l,

(1)

где сумма ij перечисляет все пары ближайших спи-

нов на решетке, сумма kl перечисляет все пары

спинов, следующих за ближайшими (рис. 1). Спин

S - классический 2-компонентный вектор, J₁, J₂ >

> 0. При J₂ < 2J₁/3 основное состояние эквива-

Рис. 1. Обменные взаимодействия в ОЦК модели. При-

лентно двум ферромагнитным подрешеткам, взаимо-

ведены две конфигурации противоположной кирально-

действующим антиферромагнитно, и фрустрации не

сти, которые нельзя свести друг к другу с помощью

возникает. Но при J₂ > 2J₁/3 подрешетки становят-

глобальных поворотов спинов и инверсии

ся антиферромагнитными. Два неэквивалентных ос-

новных состояния показаны на рис. 1.

что модели классических фрустрированных XY ан-

Слоисто-J₁-J₂ модель описывается гамильтониа-

тиферромагнетиков с коллинеарным спиновым упо-

ном

∑

рядочением исследовались ранее для других реше-

H = -J₁

S_iS_j + J₂

S_kS_l,

(2)

ток, например, простой кубической [22, 23], гране-

Письма в ЖЭТФ том 109 вып. 5 - 6

2019

Переход типа Изинг-XY в трехмерных фрустрированных антиферромагнетиках...

425

∑

где сумма ij перечисляет все пары ближайших спи-

S_x+a (S_x - Sx+e1 - Sx+e2 - Sx+e3+

нов простой кубической решетки, а сумма kl перчис-

8L³

ляет все пары следующих за ближайшими спинов

+ Sx+e1+e2 + Sx+e1+e3 + Sx+e2+e3 - Sx+e1+e2+e3) , (5)

внутри слоев (рис. 2). При J₂ < J₁/2, основное со-

стояние упорядочено ферромагнитно. При J₂ > J₁/2

где a = (¹² ,¹² ,¹² ) - вектор сдвига антиферромагнит-

основному состоянию соответствуют два типа кон-

ных подрешеток.

фигураций: волновыми векторами q = (π, 0, 0) и

Для оценки температуры перехода по одному из

q = (0,π,0). Данная модель эквивалентна двум про-

параметров порядка p = m,k, а также для оценки

стым тетрагональным антиферромагнитным подре-

точности определения этой температуры использу-

шеткам с векторами решетки (1, 1, 0), (1, -1, 0) и

ется метод пересечения кумулянтов Биндера [37, 38]

(0, 0, 1), встроенным друг в друга, и сдвинутым отно-

〈p⁴〉

сительно друг друга на вектор (1, 0, 0). Причем, об-

U_p = 1 -

(6)

3〈p²〉²

мен J₂ отвечает внутреннему взаимодействию в под-

решетках, а J₁ - взаимодействие между подрешет-

Критический показатель ν оценивается с помощью

ками. В двух измерениях данная модель численно

следующего кумулянта [39]

исследовалась в [31], где было найдено, что перехо-

(

)

ды по непрерывному и дискретному параметрам по-

∂

p²E

V_p =

ln〈p²〉 = L²

- 〈E〉

(7)

рядка происходят при разных температурах. Вообще

∂(1/T )

〈p²〉

говоря, в двумерных моделях из того же симметрий-

ного класса переходы происходят либо при различ-

причем оценка показателей проводится для обоих па-

ных температурах, либо одновременно в виде пере-

раметров порядка. Основные скейлинговые соотно-

хода первого рода [32, 33, 34].

шения:

Предлагаемые модели (1) и (2) исследуются мето-

max (V_p) ∼ L^ν ,

p|_T=T

∼L-ν, χ_p|

∼L^ν,

(8)

дом Монте-Карло с помощью сверхрелаксационного

T =Tc

алгоритма [35, 36]. Для определения рода перехода

где χ_p - восприимчивость, соответствующая тому

мы используем метод анализа гистограмм. Термали-

или иному параметру порядка p [37]

зация проводится за 2·10⁵ шагов алгоритма на спин,

а вычисление термодинамически усредненных вели-

L^d

χ_p =

p2 , T ≥Tc.

(9)

чин за 3.4 · 10⁶ шагов. Используются периодические

граничные условия, и рассматриваются решетки раз-

Основной результат моделирования заключается

меров 16 ≤ L ≤ 100. Выбираются следующие значе-

в том, что в обеих моделях наблюдается один пере-

ния соотношения обменов: J₂/J₁ = 0.7, 0.8, 0.9, 1,1.5,

ход первого рода одновременно по обоим параметрам

2 и 10.

порядка. Чтобы увидеть скачок внутренней энергии,

Магнитный (непрерывный) параметр порядка в

типичный для переходов первого рода, мы рассмат-

обоих моделях определяется через введение четырех

ривали большие решетки размера L = 80, 90 и 100.

подрешеток

Схожие размеры решеток использовались для опре-

деления рода перехода в треугольном антиферромаг-

∑

√1

нетике [7] и спиральных магнетиках [40, 41]. Двухпи-

m_i =

Sxi ,

〈m²ⁱ〉,

(3)

L³

i=1

ковая структура распределения по энергии в крити-

ческой точке, показанная на рис. 3, указывает на на-

где x_i пробегает все узлы i-й подрешетки, L³ - объ-

личие внутренней теплоты перехода. Отметим, что

ем системы (число спинов в ОЦК модели равно 2L³).

первый род перехода становится слабее с ростом от-

Киральность в слоисто-J₁-J₂ модели определяется

ношения величин обменов J₂/J₁.

следующим образом

Первый род перехода был также найден в [30] с

∑

помощью алгоритма Вонга-Ландау. К тому же, это

(S_x - Sx+e1+e2 ) (Sx+e1 - Sx+e2) ,

подтверждается РГ-анализом непрерывного предела

4L³

решеточных моделей (1) и (2), описываемого функ-

ционалом Гинзбурга-Ландау

k= 〈|k|〉,

(4)

∫

(

где e_µ - единичный вектор вдоль соответствующе-

F = d³x

(∂_µφ₁)² + (∂_µφ₂)² + r(φ²¹ + φ²²) +

го направления решетки. В ОЦК модели киральный

(

)

параметр порядка определен как

φ⁴¹ + φ⁴²

+ 2w(φ₁φ₂)² + 2vφ²¹φ²²

(10)

Письма в ЖЭТФ том 109 вып. 5 - 6

2019

426

А. О. Сорокин

Таблица 1. Сравнение критических (псевдо)показателей, полученных в данной работе для J₂/J₁ = 1 (помечены как [∗]), с

известными показателями других классов универсальности. Обозначения: Helix - спиральные магнетики, STA - антиферро-

магнетик на слоисто-треугольной решетке, SJJ - слоисто-J₁-J₂ модель, BCC - ОЦК модель, FSS - типичные показатели для

перехода первого рода в теории конечноразмерных систем

Class G/H

Model

Ref.

ν_k

β_k/2

γ_k + β_k

Z₂

Ising

[47]

0.630

0.327

1.236

SO(2)

O(2)

[47]

0.671

0.348

1.317

SO(4)/SO(3)

O(4)

[47]

0.75

0.39

1.47

Tricritical

Mean-field

0.5

0.25

1.00

First order

FSS

0.33

1.00

Z₂ ⊗ SO(2)

Helix

[40]

0.55

0.56

0.25

0.21

1.16

1.29

Z₂ ⊗ SO(2)

STA

[44]

0.54

0.55

0.25

0.23

1.13

1.22

Z₂ ⊗ SO(2)

SJJ

[∗]

0.565(8)

0.572(10)

0.260(6)

0.251(8)

1.18(4)

1.22(5)

Z₂ ⊗ SO(2)

BCC

[∗]

0.568(10)

0.571(9)

0.262(7)

0.258(10)

1.18(5)

1.20(8)

Рис. 3. Гистограмма распределения внутренней энер-

Рис. 4. (Цветной онлайн) Оценка показателя νp с ис-

гии для L = 90 в окрестности критической темпера-

пользованием кумулянта

(7) для обеих моделей с

туры в слоисто-J1-J2 модели с J2/J1 = 1

J2/J1 = 1. SJJ обозначает слоисто-J1-J2 model, BCC -

ОЦК модель

где u > 0, w < 0, u + v + w > 0, а φ1,2 - N-

компонентное векторное поле. В случае N = 2 в об-

ласти w < 0, отвечающей коллинеарному основному

состоянию φ₁||φ₂, неподвижные точки отсутствуют.

Тем не менее, первый род перехода оказывает-

ся слабым при J₂/J1 ≳ 0.8, а потому можно на-

блюдать псевдоскейлинговое поведение (пример на

рис. 4). Данное поведение не универсально, и значе-

ния псевдопоказателей зависят от отношения обме-

нов J₂/J₁. Подобная зависимость показана на рис. 5.

Отметим, что для больших J₂/J₁, когда решеточ-

ные модели сводятся к двум слабо взаимодейству-

ющим антиферромагнитным подрешеткам, показа-

тели имеют значения, близкие к показателям O(2)-

Рис. 5. Зависимость показателя ν от отношения обме-

модели. Однако, и это более неожиданно, что вда-

нов J1/J2 для слоисто-J1-J2 модели

ли от маргинальных значений отношения обменов

(т.е. при J₂/J1 ≈ 1) критическое поведение похо-

же на известные результаты для треугольного анти-

ное сравнение критических показателей приведено в

ферромагнетика и спиральных магнетиков. Подроб-

табл. 1.

Письма в ЖЭТФ том 109 вып. 5 - 6

2019

Переход типа Изинг-XY в трехмерных фрустрированных антиферромагнетиках...

427

Как обсуждалось выше, для O(N) ⊗ O(2)-модели

точке, но они могут приводить к кроссоверу между

псевдоскейлинговое поведение может быть объясне-

трикритическим и критическим поведением, замет-

но в терминах РГ, если РГ-траектория (стартующая

ному при моделировании на решетках конечного раз-

из точки, отвечающей решеточной модели) проходит

мера. Отметим, что подобный кроссовер наблюдался

через область с очень медленным РГ-потоком. Обыч-

в cхожей модели в двух измерениях [46].

но такая область соответствует окрестности непо-

Данная работа поддержана Российским Фондом

движной точки, даже если данная точка имеет ком-

Фундаментальных Исследований грантами # 14-02-

плексные координаты. На границе рассматриваемой

31448 и 16-32-60143.

области w < 0 находятся три неподвижных точ-

ки (НТ): гейзенберговская НТ, отвечающая O(4)-

D. Loison, in Frustrated Spin Systems, ed. by H.T. Diep,

модели; несвязанная НТ, отвечающая двум невзаи-

World Scientific, Singapore (2004), ch. 4, p. 177.

модействующим O(2)-моделям; и биконическая НТ

A. O. Sorokin and A. V. Syromyatnikov, Solid State

[30]. Несвязанная НТ описывает критическое пове-

Phenom. 190, 63 (2012).

дение при больших J₂/J₁, когда w ≈ 0. Но ни одна

H. Kawamura, J. Appl. Phys. 63, 3086 (1988).

из этих точек не объясняет показатели, наблюдаю-

B. Delamotte, D. Mouhanna, and M. Tissier, Phys. Rev.

щиеся в случае J₂/J₁ ≈ 1 (см. табл. 1), включая би-

B 69, 134413 (2004).

коническую НТ, расположенную при N = 2 очень

M. Itakura, J. Phys. Soc. Jpn. 72, 74 (2003).

близко к несвязанной НТ [42, 43].

A. Peles, B. W. Southern, B. Delamotte, D. Mouhanna,

В случае N = 2 имеется две неподвижных точки

and M. Tissier, Phys. Rev. B 69, 220408 (2004).

с комплексными координатами. Вещественная часть

V. . Ngo and H.T. Diep, J. Appl. Phys. 103, 07C712

координат попадает на подмногообразие v = u - w

(2008).

и w > 0, отвечающее O(N) ⊗ O(2)-модели. Преды-

G. Zumbach, Phys. Rev. Lett. 71, 2421 (1993).

дущие исследования этой модели для N = 2 с ис-

G. Zumbach, Phys. Lett. A 190, 225 (1994).

пользованием непертурбативной РГ [8-10, 14, 15] по-

10.

G. Zumbach, Nucl. Phys. B 413, 771 (1994).

казали, что область замедления РГ-потока достаточ-

11.

S. A. Antonenko, A.I. Sokolov, and K. B. Varnashev,

но широка и не имеет ярко выраженного центра, ас-

Phys. Lett. A 208, 161 (1995).

социируемого с локальным минимумом РГ-потока (в

12.

A. Pelissetto, P. Rossi, and E. Vicari, Nucl. Phys. B

отличие от случая N = 3). Более того, данная об-

607, 605 (2001).

ласть включает окрестность гейзенберговской НТ с

13.

P. Calabrese and P. Parruccini, Nucl. Phys. B 679, 568

w = 0, соответствующей O(4)-модели. Это объясняет

(2004).

разброс в значениях псевдопоказателей, наблюдаю-

14.

M. Tiesser, B. Delamotte, and D. Mouhanna, Phys. Rev.

щийся в численных исследованиях и эксперименте

Lett. 84, 5208 (2000).

(для обзора см. [4]). Показатели могут принимать

15.

M. Tiesser, B. Delamotte, and D. Mouhanna, Phys. Rev.

значения, близкие как к кавамуровским индексам

B 67, 134422 (2003).

для треугольного антиферромагнетика [44], так и к

16.

A. I. Larkin and S. A. Pikin, Sov. Phys. JETP 29, 891

показателям O(4) модели. Мы полагаем, что область

(1969).

замедления РГ-потока заходит и в сектор w < 0. Та-

17.

P. Peczak and D. P. Landau, Phys. Rev. B. 39, 11932

кая обширная область может включать траектории,

(1989).

на которых имитируемый скейлинг описывается по-

18.

S. Iino, S. Morita, A.W. Sandvik, and N. Kawashima,

казателями, близкими к результатам Кавамуры, но

arXiv 1801.02786.

без универсальности.

19.

D. Loison and K. D. Schotte, Eur. Phys. J. B 5, 735

Когда w достаточно мало, возможно и дру-

(1998).

гое объяснение наблюдаемой псевдоуниверсально-

20.

E. F. Shender, Sov. Phys. JETP 56, 178 (1982).

сти, связанное с трикритическим поведением. Та-

21.

C. L. Henley, Phys. Rev. Lett. 62, 2056 (1989).

кая возможность уже обсуждалась для треугольного

22.

C. Pinettes and H. T. Diep, J. Appl. Phys. 83, 6318

антиферромагнетика в [45]. В таблице 1 приведены

(1998).

значения показателей трикритической точки, кото-

23.

V. T. Ngo, D. T. Hoang, and H. T. Diep, Phys. Rev. E

рые оказываются близкими к показателям для си-

82, 041123 (2010).

стем с нарушенной Z₂ ⊗SO(2) симметрией. Посколь-

24.

C. L. Henley, J. Appl. Phys. 61, 3962 (1986).

ку член функционала (10) w(φ₁φ₂)² мал, скейлинг

25.

H. T. Diep and H. Kawamura, Phys. Rev. B 40, 7019

будет определяться членами типа w₆(φ₁φ₂)³. Обыч-

(1989).

но подобные члены не существенны в критической

26.

H. T. Diep, Phys. Rev. B 45, 2863 (1992).

Письма в ЖЭТФ том 109 вып. 5 - 6

2019