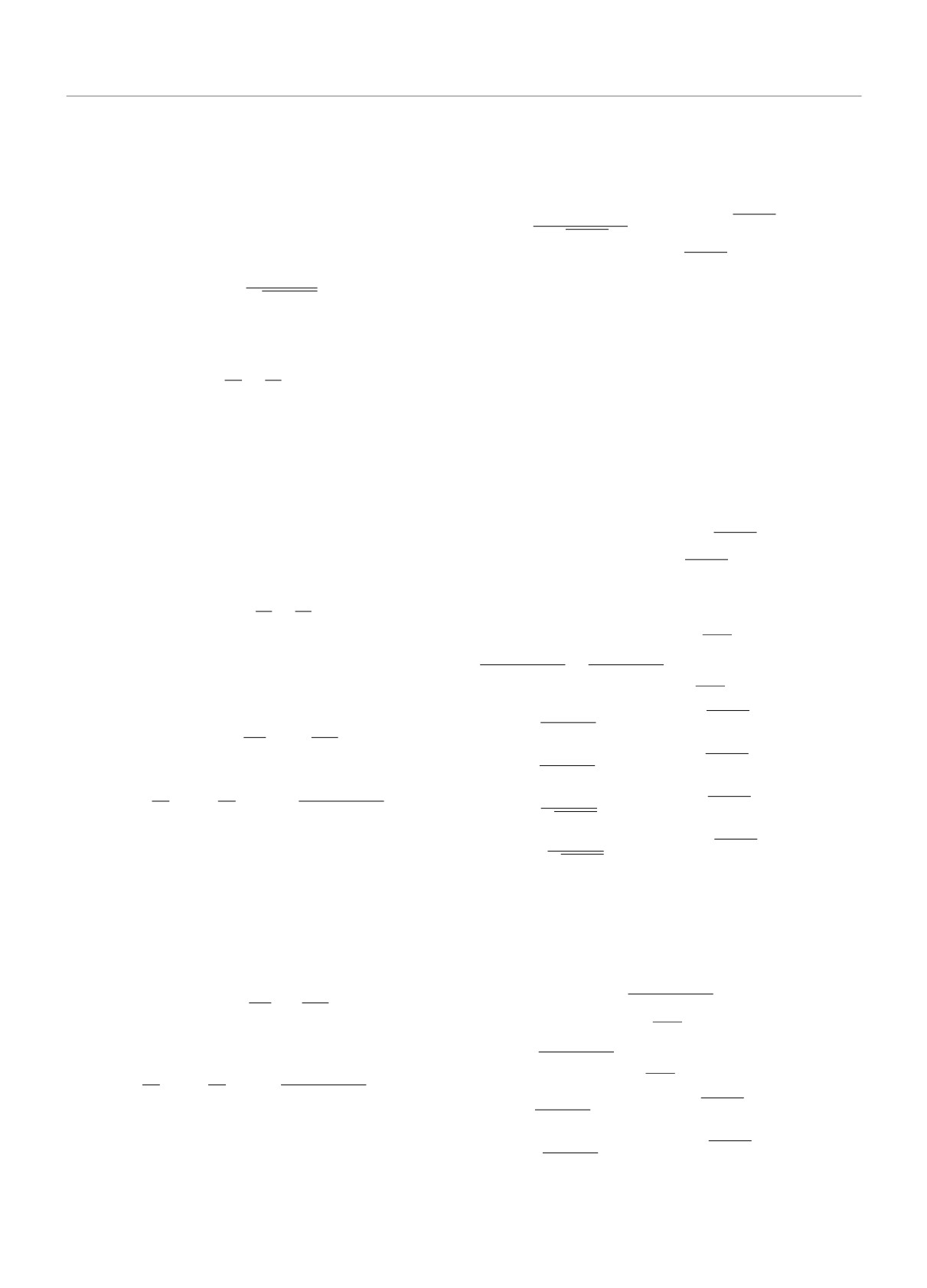Письма в ЖЭТФ, том 109, вып. 7, с. 500 - 503
© 2019 г. 10 апреля
О подвижных неоднородностях нелинейного уравнения
Клейна-Гордона
Р. К. Салимов1)
Башкирский государственный университет, 450076 Уфа, Россия
Поступила в редакцию 9 января 2019 г.
После переработки 24 января 2019 г.
Принята к публикации 7 февраля 2019 г.
Рассмотрена система из точечной материальной частицы и поля, описываемого нелинейным уравне-
нием Клейна-Гордона. Частица создает неоднородность поля и взаимодействует с ним. Показано, что
при учете релятивистких эффектов, в некоторых случаях, для такой системы невозможен устойчивый
минимум энергии при нулевой скорости. Подобное поведение интересно с точки зрения построения со-
литонных моделей частиц с собственным не нулевым моментом количества движения или солитонных
моделей частиц с осциллирующей массой.
DOI: 10.1134/S0370274X19070130
В современной нелинейной волновой теории боль-
нения интегрируемости, т.е. рассматривают некото-
шое внимание уделяется нахождению пространствен-
рое обобщение УСГ. Обычно при рассмотрении урав-
но локализованных и периодических по времени
нений Клейна-Гордона с различными неоднородно-
решений для большого количества моделей и различ-
стями или примесями, примеси считаются стацио-
ных размерностей (см., например, [1-6]). Такие про-
нарными. Неоднородности или примеси в таких зада-
странственно локализованные решения имеют ко-
чах моделируют различные дефекты, например, для
нечную энергию и соответствуют статическим ча-
уравнения синус-Гордона дефекты в магнитных ма-
стицеподобным объектам или различным бегущим
териалах [8,17-21]. Ранее в [22-24] численно была по-
волнам. Хотя, как известно, не существует стаци-
казана возможность существования в области при-
онарных локализованных решений Лоренц инвари-
меси долгоживущих 2D-пульсонов и 2D-солитонов,
антных полевых уравнений для пространственной
структура и динамические свойства которых зависят
размерности более одной, не исключено существо-
от параметров примеси.
вание локализованных решений при наличии раз-
С более общей точки зрения было бы интересно
личных неоднородностей или притягивающих при-
рассмотреть систему подвижных неоднородностей,
месей. Одним из часто исследуемых по данному
взаимодействующих с полем. Интерес к таким систе-
вопросу интегрируемых нелинейных дифференци-
мам вызван тем, что на притягивающих неоднород-
альных уравнений является (1 + 1) уравнение синус-
ностях возможны локализованные состояния. Если
Гордона (УСГ). Оно имеет много приложений в раз-
же подвижную притягивающую неоднородность до-
личных областях физики, включая гидродинамику,
статочно сильно ускорить, то естественно предполо-
физику конденсированного состояния, теории поля
жить, что локализованное состояние поля не удер-
и т.д. [7-10]. Делаются попытки нахождения точных
жится на неоднородности. Если неоднородность име-
аналитических решений (в том числе и локализо-
ет некоторую массу, то состояние примеси с локали-
ванных) (n + 1) размерных моделей (см., например,
зованным на ней полем будет добавлять к этой мас-
[11-15]). В [16] найдено численное доказательства су-
се некоторую эффективную поправку. Далее, в за-
ществования долгоживущего, хотя и имеющего ко-
висимости от величины ускорения таких неоднород-
нечное время жизни, пространственно локализован-
ностей можно предположить два состояния с двумя
ного и сферически симметричного (3+1) размерного
разными эффективными массами таких неоднород-
бризероподобного, объекта, названного “пульсоном”.
ностей и переходы между этими состояниями.
Другим направлением исследований является добав-
Для рассмотрения подвижных неоднородностей
ление слагаемых в нелинейное уравнение для сохра-
или дефектов будем считать, что неоднородность со-
здается частицей с массой m, координату которой
1)e-mail: salemsrkk@yandex.ru
обозначим как z, ее скорость как v = Ż. Гамильто-
500
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
О подвижных неоднородностях нелинейного уравнения Клейна-Гордона
501
ниан неоднородности, взаимодействующей с полем
областью , которую можно выразить через функции
u, запишем в следующем виде (рассматриваем од-
Хевисайда, а W = 2 cos2(u/2).
номерный случай).
q(x, z, v)W (u) =
H =Hdef +Hu +Hint,
(1)
√
U02 cos2(u/2)
=
√
(θ(x - (z - l
1-v2) -
2
1-v
где Hdef - энергия частицы,создающей неоднород-
√
ность.
- θ(x - (z + l
1 - v2)).
(10)
m
Hdef =
√
,
(2)
(1 - v2)
Здесь релятивистское изменение потенциала при
движении его источника, т.е. частицы, принимает-
Hu - энергия скалярного поля.
ся аналогичным изменению электростатического по-
∫∞
)
тенциала φ в релятивистском случае, например, из-
(u2x
u2
t
Hu =
+
+ V (u) dx.
(3)
менению потенциала движущегося заряда. То есть
2
2
−∞
значение потенциала при движении для покоящего-
ся наблюдателя становиться больше, а область его
Hint - энергия взаимодействия скалярного поля и
действия сужается. Запаздыванием при этом прене-
частицы, создающей неоднородность
брегаем. Такой потенциал взаимодействия приводит
к уравнениям движения для поля
∫∞
Hint =
q(z, v, x)W (u)dx.
(4)
uxx - utt = u + 2u3
-
-∞
√
- U0 sin(u)(θ(x - (z - l
1-v2)-
√
Функция V (u) в выражении (3) записывалась в
- θ(x - (z + l
1 - v2))
(11)
виде
2
u
u4
и для частицы
V (u) =
+
(5)
2
2
√
z+l
∫
1-v2
Из условия сохранения гамильтониана (1), диф-
mv v
U0v v
ференцируя его по времени, получаем уравнения
+
2 cos2(u/2)dx -
(1 - v2)(3/2)
(1 - v2)3/2
движения для поля и для частицы.
√
z-l
1-v2
√
∫
∞
(
)
U0v vl
−
2 cos2(u(z - l
1 - v2)/2)) -
∂V
∂W
(1 - v2)
uxuxt + ututt +
ut + q
ut dx +
∂u
∂u
√
U0v vl
−∞
−
2 cos2(u(z + l
1 - v2)/2)) =
∫∞
(
)
(1 - v2)
∂q
∂q
mv v
√
U0 Ż
+
W
Ż+W
v dx +
= 0. (6)
=
√
2 cos2(u(z - l
1 - v2)/2)) -
∂z
∂v
(1 - v2)(3/2)
−∞
1-v2
√
U0 Ż
-
√
2 cos2(u(z + l
1 - v2)/2)).
(12)
Далее, интегрируя
1-v2
∫
∞
∫
∞
Причем Ż = v. Выразим эффективную массу или ко-
uxuxtdx = - uxxutdx
(7)
эффициент meff в уравнении движения
−∞
-∞
meff v = Feff,
(13)
и считая, что выполняется уравнение движения для
поля u
m
∂V
∂W
meff =
+
-uxx + utt +
+q
= 0,
(8)
(1 - v2)(3/2)
∂u
∂u
√
z+l
∫
1-v2
получаем уравнение движения для частицы
U
0
+
2 cos2(u/2)dx -
∫
∞
(1 - v2)3/2
√
∂q
∂q
mv v
z-l
1-v2
(W
Ż+W
v)dx +
= 0.
(9)
∂z
∂v
√
(1 - v2)(3/2)
U0l
−∞
−
2 cos2(u(z - l
1 - v2)/2)) -
(1 - v2)
Рассмотрим далее случай взаимодействия Hint, где
U0l
√
1 - v2)/2)).
(14)
область действия потенциала q(z, v, x) ограничена
- (1 - v2)2cos2(u(z+l
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
502
Р. К. Салимов
Из выражения (14), в частности, следует, что для
решения вида u = 0 эффективная масса равна обыч-
ной, т.е. если поле не захватывается неоднородно-
стью, то уравнение движения для частицы совпада-
ет с уравнением движения без учета поля u. Далее
система уравнений (11) и (12) решалась численно.
Здесь следует выделить 2 основных случая. В пер-
вом случае, когда масса покоя m велика, решение
будет стремиться к стационарному решению с поко-
ящейся частицей. Например, численное решение при
m = 50, U0 = 20, l = 0.5 представленное на рис.1.
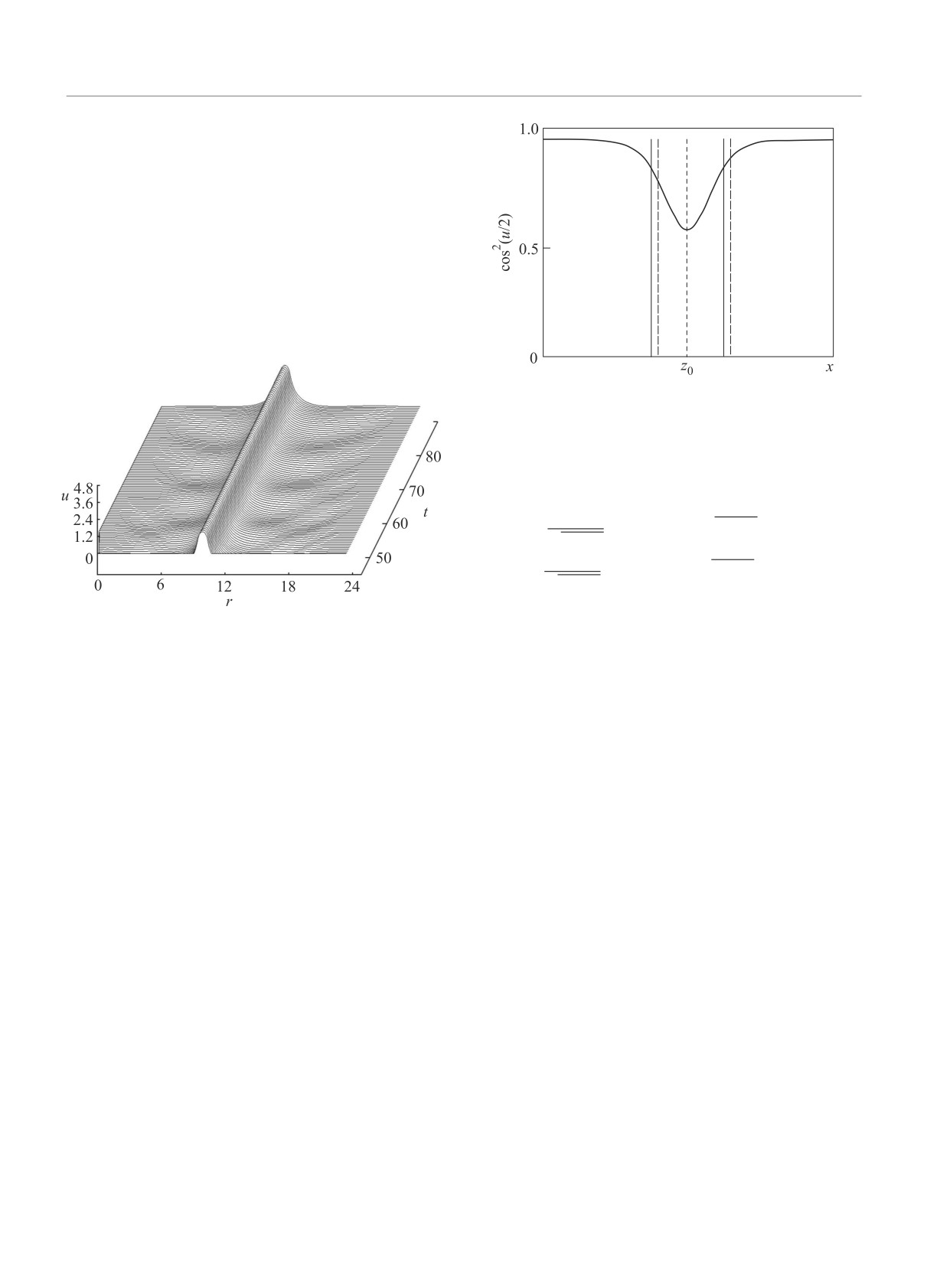
Рис. 2. Сплошными вертикальными линиями обозначе-
но положение границ действия потенциала z0 ±l стаци-
онарного решения, пунктирными - положение границ
действия потенциала при небольшом смещениии час-
тицы относительно центра стационарного решения z0
√
U0
Feff =
√
2 cos2(u(z - l
1 - v2)/2)) -
1-v2
√
U0
−
√
2 cos2(u(z + l
1 - v2)/2))
(17)
1-v2
будет отрицательной. Значение эффективной массы
Рис. 1. Численное решение системы уравнений (11) и
(14) при небольших смещениях и малых m также
(12) для поля u при m = 50, колебания на периферии
останется отрицательным и частица получит прира-
с течением времени затухают, и решение стремиться к
щение скорости в сторону смещения. Другими сло-
стационарному. Значения энергий в (8) и (9) взяты при
вами, для представленной системы при малой массе
t > 200
покоя m не будет существовать состояния устойчи-
вого равновесия, при скорости v = 0. Так как этот
Для этого численного решения значения интегралов
вывод верен для всех инерциальных систем отсчета,
в (14) равны, соответственно
получим, что в состоянии с минимальной энергией
z+l
частица также не может устойчиво двигаться с по-
стоянной скоростью. То есть устойчивым состояни-
U0
2 cos2(u/2)dx = 15.22,
(15)
ем для частицы в такой системе будет некое, в об-
z-l
щем случае, ускоренное движение. Таким образом,
представленная модель при малой массе покоя час-
U0l(2 cos2(u(z-l)/2)+2 cos2(u(z+l)/2)) = 21.78. (16)
тицы, описывает постоянно движущуюся с некото-
Покажем теперь невозможность подобного устой-
рым ускорением частицу. Если подобное движение
чивого стационарного решения для малых значений
будет инфинитным, с периодически колеблющейся
массы покоя m. Допустим, что при малых m (по
около ненулевой скорости значением, то ее эффек-
сравнению с разницей выражений (16) и (15), 6.56)
тивная масса также будет осциллировать. В этом
существует стационарное решение с покоящейся ча-
случае для подобной системы, как для солитонной
стицей. Тогда решение c минимальной энергией для
модели частиц, уместны некие аналогии с нейтрино.
поля будет иметь стационарный вид, рис. 1. Эффек-
В случае финитного движения частицы в двумерном
тивная масса (14) при этом будет отрицательной. По-
и трехмерном случае, подобная система будет иметь
добное решение будет неустойчиво при небольшом
некоторый не нулевой момент количества движения.
смещении координаты z относительно центра стаци-
В этом случае подобную систему уместно рассмат-
онарного решения z0. Покажем это более подробно.
ривать как солитонную модель спина. Возможность
Как видно из рис.2 при небольшом положительном
существования подобных решений далее предполага-
смещении z - z0 эффективная сила
ется исследовать численно для всего диапазона зна-
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
О подвижных неоднородностях нелинейного уравнения Клейна-Гордона
503
чений малых масс покоя m. Для уже проведенного
7.
Л. А. Тахтаджан, Л. Д. Фаддеев, ТМФ 21(2), 160
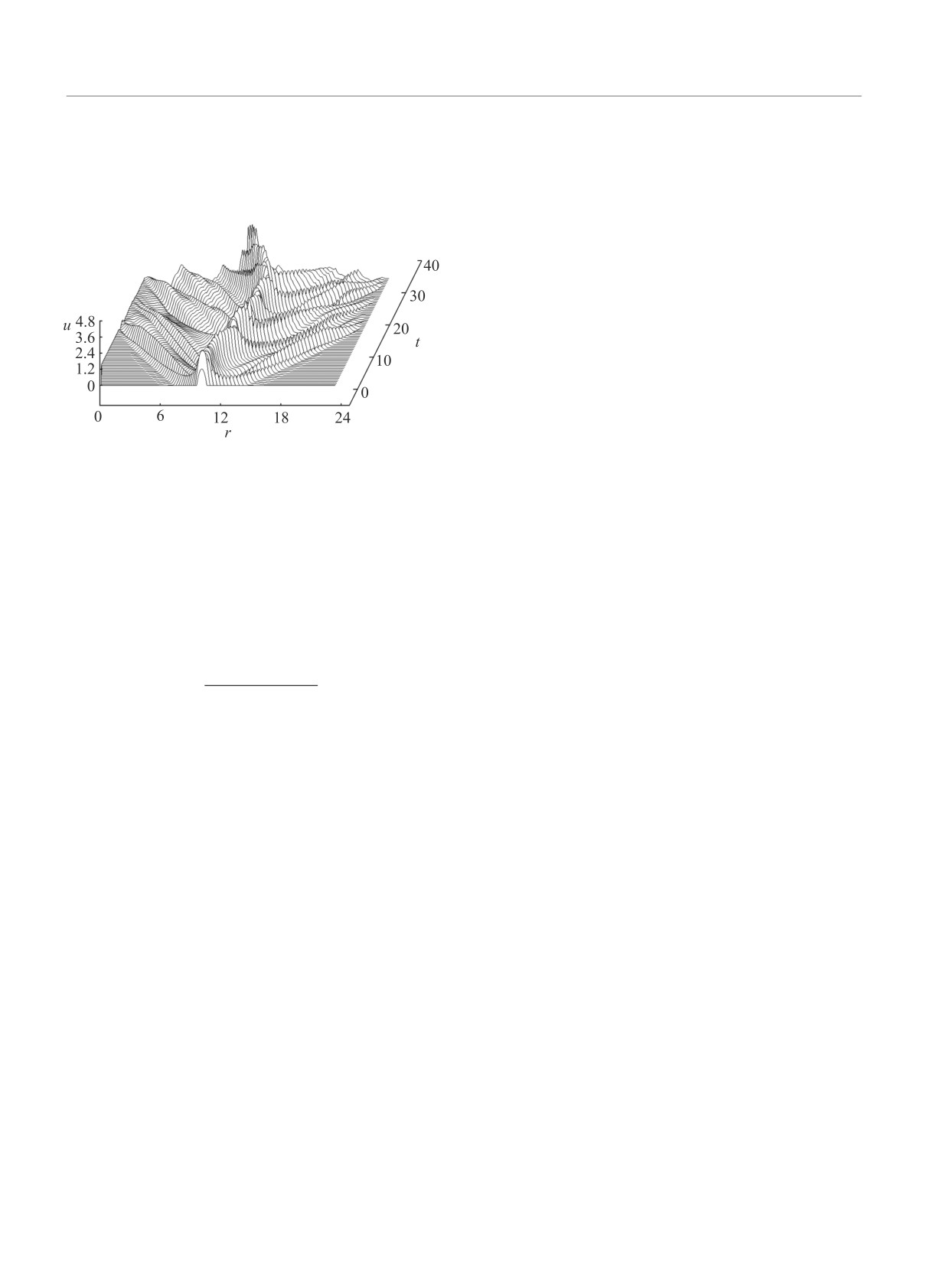
численного решения (11) и (12) при m = 1 видно, что
(1974).
решение не стремиться к стационарному, см. рис. 3.
8.
М. А. Шамсутдинов, В. Н. Назаров, И. Ю. Ломакина,
Для этого решения значение эффективной массы ко-
Ферро- и антиферромагнитодинамика. Нелинейные
колебания, волны и солитоны, Наука, М. (2009).
9.
J. Cuevas-Maraver, P. G. Kevrekidis, and F. Williams,
Physics 10, 263 (2014).
10.
T. Dauxois and M. Peyrard, Physics of solitons,
Cambridge University Press, N.Y. (2010).
11.
A. Wazwaz, J. Appl. Math. Informatics 30(5),
925
(2012).
12.
S. Johnson, P. Suarez, and A. Biswas, Mathematics and
Mathematical Physics 52(1), 98 (2012).
13.
Э. Л. Аэро, А. Н. Булыгин, Ю. В. Павлов, ТМФ
158(3), 98 (2009).
14.
M. Qing, H. Binb, and R. Weiguob, Journal of Computer
Mathematics 87(3), 591 (2010).
Рис. 3. Численное решение уравнений (11) и (12) для
15.
Е. Г. Екомасов, Р. К. Салимов, Журнал вычислитель-
ной математики и математической физики 56(9),
поля u при m = 1
1628 (2016).
16.
I. L. Bogoluvskii and V.G. Makhankov, JETP Lett.
леблется около нуля. Случай, в котором эффектив-
24(12), 107 (1977).
ная масса частицы будет оставаться положительной,
17.
Е. Г. Екомасов, А. М. Гумеров, Р. В. Кудрявцев,
также интересен с точки зрения существования со-
Письма в ЖЭТФ 101(12), 935 (2015).
стояний с двумя различными эффективными масса-
18.
E. G. Ekomasov, R. R. Murtazin, and V. N. Nazarov,
ми, зависящих от энергии движения частицы. Кроме
J. Magn. Magn. Mater. 385, 217 (2015).
того, данная модель обладает достаточной новизной
19.
Е. Г. Екомасов, Р. Р. Муртазин, Ш. А. Азаматов, Фи-
и достойна изучения с методологической точки зре-
зика твердого тела 54(8), 1487 (2012).
ния.
20.
Е. Г. Екомасов, Ш. А. Азаматов, Р. Р. Муртазин,
А. М. Гумеров, А.Д. Давлетшина, Известия Россий-
ской академии наук. Серия физическая 74(10), 1520
1. Encyclopedia of Nonlinear Science, ed. by A. Scott,
(2010).
Routledge, N.Y. (2004).
21.
Т. Б. Шапаева, Р. Р. Муртазин, Е. Г. Екомасов, Изве-
2. X. Jiang, Z. Fan, Z. Chen, W. Pang,and Y. Li, Phys.
стия Российской академии наук. Серия физическая
Rev. A 93, 023633 (2016).
78(2), 155 (2014).
3. B. A. Malomed, Phys. J. Special Topics 225,
2507
22.
E. G. Ekomasov, A. M. Gumerov, and R. R. Murtazin,
(2016).
Math. Meth. Appl. Sci., DOI:
10.1002/mma.3908
4. G. Fodor, P. Forgacs, Z. Horvath, and A. Lukacs, Phys.
(2016).
Rev. D 78, 025003 (2008).
23.
Е. Г. Екомасов, Р. Р. Муртазин, Ш. А. Азаматов,
5. J. Cuevas, P. G. Kevrekidis, B. A. Malomed, P. Dyke,
А. Е. Екомасов, Физика металлов и металловедение
and R. G. Hulet, New J. Phys. 15, 063006 (2013).
122(3), 227 (2011).
6. Е. Г. Екомасов, Р. К. Салимов, Письма в ЖЭТФ 102,
24.
Е. Г. Екомасов, Ш. А. Азаматов, Р. Р. Муртазин, Фи-
135 (2014).
зика металлов и металловедение 108(6), 556 (2009).
Письма в ЖЭТФ том 109 вып. 7 - 8
2019