Письма в ЖЭТФ, том 109, вып. 8, с. 516 - 520

Особенности Вигнеровских времен задержки медленных электронов

потенциальной ямой с появляющимися в ней дискретными уровнями

М. Я. Амусья^+∗1), A. С. Балтенков^×

⁺Институт Физики им. Рака, Еврейский Университет, 91904 Иерусалим, Израиль

^∗Физико-технический институт им. А. Ф. Иоффе, 194021 С.-Петербург, Россия

^×Институт Ионно-плазменных и лазерных технологий им. У. А. Арифова, 100125 Ташкент, Узбекистан

Поступила в редакцию 18 марта 2019 г.

После переработки 18 марта 2019 г.

Принята к публикации 18 марта 2019 г.

Мы исследовали здесь специфические особенности в поведении Вигнеровских времен задержки мед-

ленных s-электронов, рассеивающихся сферически-симметричными прямоугольными потенциальными

ямами. Мы рассмотрели потенциальные ямы, небольшое изменение параметров которых ведет к появ-

лению в них связанных состояний. Было показано, что время задержки частицы мелкой потенциальной

ямой, не имеющей связанных состояний, всегда положительно при малых энергиях электрона и ме-

няет знак после появления уровня. Было установлено, что в момент появления первого и следующих

s-уровней в яме время задержки ею медленных электронов испытывает скачки от положительных зна-

чений к отрицательным. Амплитуды этих скачков тем больше, чем меньше импульс электрона k.

DOI: 10.1134/S0370274X19080046

1. Мы описываем здесь особенности в Вигнеров-

Целью настоящего Письма является исследова-

ском времени задержки в упругом рассеянии мед-

ние связи фазового сдвига δ₀(k) и EWS-времени за-

ленных электронов потенциальной ямой, вариация

держки τ_s(k) с параметрами ямы, используя в каче-

параметров которой ведет к образованию связанных

стве примера простую прямоугольную потенциаль-

s-состояний. А именно, мы показываем, что в мо-

ную яму V (r) с радиусом R и глубиной U.

мент появления в яме s-уровня, время задержки, как

В статье [7] мы исследовали парциальные EWS-

функция параметров ямы, испытывает скачок от по-

времена задержки медленных электронов, упруго

ложительной величины к отрицательной.

рассеивающихся на фуллеренах С₆₀, и нашли, что

Айзенбуд, Вигнер и Смит (Eisenbud, Wigner and

знак парциального времени задержки зависит от

Smith (EWS)) впервые интерпретировали производ-

присутствия первого дискретного уровня с соответ-

ную от фазы рассеяния по энергии частицы E, как

ствующим орбитальным моментом l в потенциаль-

время задержки центральным потенциалом рассеи-

ной яме фуллереновой оболочки. Мы обнаружили,

вающегося им волнового пакета [1-3]. Они ввели в

что l^th время задержки положительно, когда нет дис-

рассмотрение EWS-время задержки, как квантово-

кретных l-уровней в яме, и оно отрицательно, когда

динамическую наблюдаемую при резонансном рас-

подобный уровень существует. Можно ожидать по-

сеянии частиц. В настоящее время эксперименталь-

добного же поведения времени задержки в момент

ное изучение этих времен стало возможно. Атто-

появления в яме не только первого но, также и вто-

секундные лазерные импульсы позволили экспери-

рого, третьего и т.д. дискретных уровней. Для того

ментально наблюдать времена задержки в процес-

чтобы выяснить, носит ли эта особенность в поведе-

сах фотоионизации, и сейчас это быстро развиваю-

нии EWS-времени задержки универсальный харак-

щаяся область исследований (см., например, [4-6] и

тер, мы исследуем здесь τ_s(k) как функцию пара-

ссылки там). Однако почти все внимание в этой об-

метров ямы.

ласти сосредоточено на фотоионизационных процес-

2. Зависимость фаз рассеяния δ_l(k) и, следова-

сах. В противоположность этому, здесь мы концен-

тельно, EWS-времен τ_l(k) от параметров функции

трируемся на процессах упругого рассеяния электро-

V (r) может быть в латентной или явной форме. По-

нов.

лагая V (r) прямоугольной ямой с радиусом R и глу-

биной U, мы получим желаемые зависимости в явном

виде, дополняя аналитическое рассмотрение некото-

¹⁾e-mail: amusia@vms.huji.ac.il

рыми численными расчетами.

516

Письма в ЖЭТФ том 109 вып. 7 - 8

2019

Особенности Вигнеровских времен задержки медленных электронов потенциальной ямой...

517

Парциальное EWS-время задержки [2] электрона

Парциальное EWS-время задержки связано с

потенциальным полем определяется следующим об-

производной δ^′0 следующим образом:

разом [7]

dδ₀

dδ₀ dk

dδ_l(E)

τ_s(k, U, R) = 2

δ^′0(k, U, R).

(8)

τ_l(E) = 2

(1)

dk dE

Фаза s-рассеяния δ₀ для прямоугольной потенциаль-

Мы ввели глубину потенциальной ямы U и ее ради-

ной ямы описывается следующим выражением (для

ус R как аргументы в формуле (8), чтобы подчерк-

детали см. в [8] уравнение (17), где параметр D_l ≡ 0)

нуть, что производная (6) и время задержки (8) есть

функции трех переменных, а именно k, U и R. Для

k tan qR - q tan kR

tan δ₀ =

(2)

малых энергий электрона E = k²/2, согласно Вигне-

q + ktanqRtankR

ровскому пороговому закону [10], s-фазовый сдвиг

√

пропорционален k, δ₀(k → 0) ∼ k. Поэтому s-тое

Здесь вектор q =

2U + k² есть волновой вектор

EWS-время задержки (8) вблизи порога стремится к

электрона внутри потенциальной ямы²⁾. Перепишем

бесконечности, как τ_s(k, U, R)_k→0 ∝ ±1/k. Далее мы

формулу (2) в тождественном виде [9]

будем рассматривать функции (6) и (7) при малых,

но конечных величинах электронных энергий.

q cotqR = k cot(kR + δ₀)

(3)

3. Начнем с численного исследования поведе-

и применим оператор ∂/∂k к обеим частям этого

ния s-парциального EWS-времени задержки, пола-

уравнения. Тогда мы получаем следующее выраже-

гая, что глубина потенциальной ямы U переменна,

ние

тогда как ее радиус R постоянен, и равен двум атом-

ным единицам, R = 2. Условие появления в яме дис-

q^′ cotqR + q(cotqR)^′ = cot(kR + δ₀) +k[cot(kR + δ₀)]^′,

кретного s-уровня описывается следующим выраже-

(4)

нием (см. уравнение (12) в [8]):

где штрих обозначает дифференцирование по k. Про-

(2n - 1)²π²

изводные в уравнении (4) равны

U⁽ⁿ⁾ =

(9)

8R²

q^′ =

; (cot qR)^′ = -

;

Здесь n - номер s-уровня в яме. Величины пер-

q sin² qR

вых трех критических глубин в потенциальной яме с

(R + δ^′0)

R = 2 есть, соответственно

[cot(kR + δ₀)]^′ = -

(5)

sin²(kR + δ₀)

π²

9π²

U⁽¹⁾ =

≈ 0.308; U⁽²⁾ =

≈ 2.776;

После простых преобразований получаем следую-

щую общую формулу для производной δ^′0

25π²

U⁽³⁾ =

≈ 7.711.

(10)

∂δ₀

sin 2(kR + δ₀)

δ^′0 =

= -R +

∂k

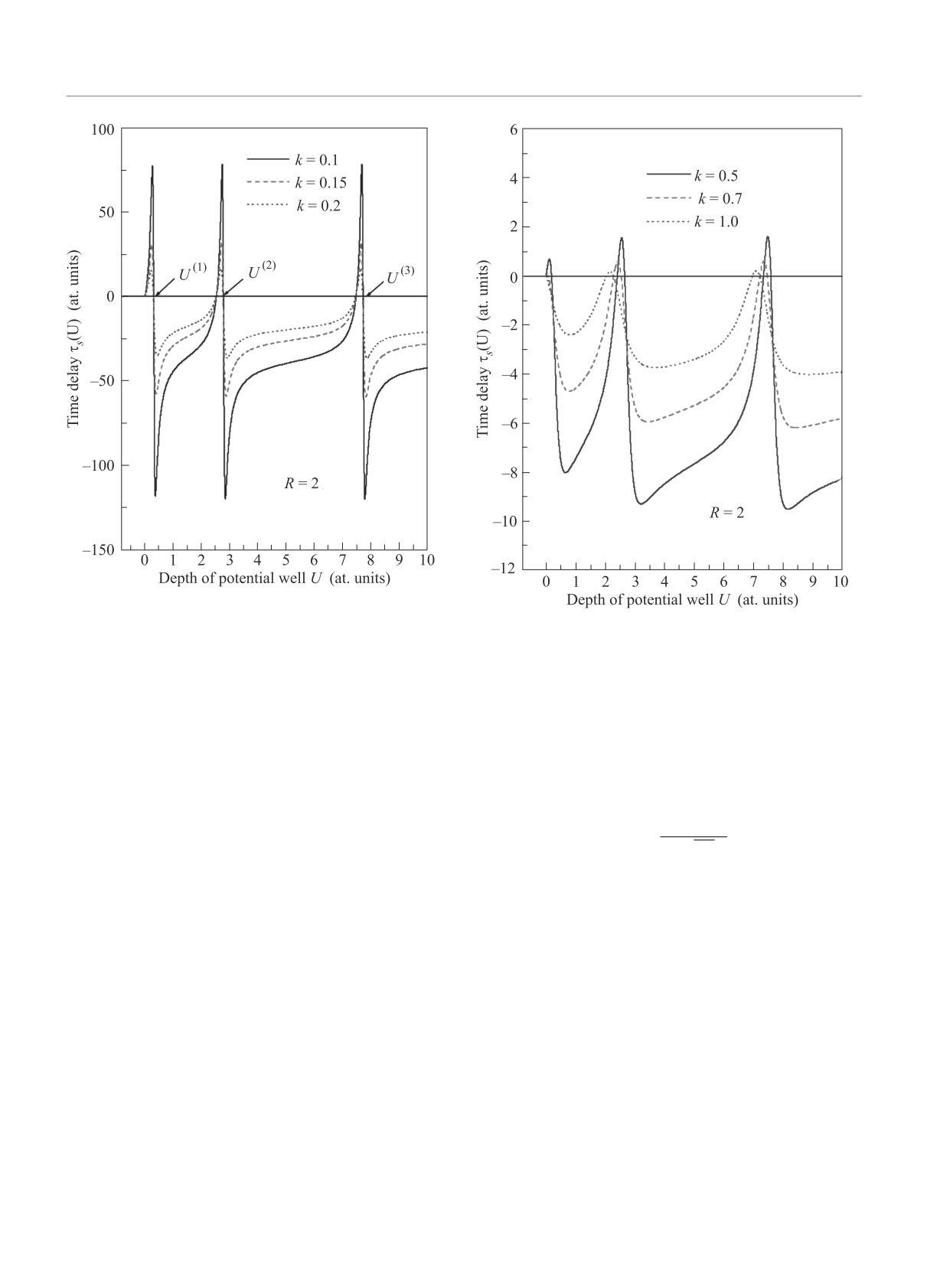
Рисунок 1 представляет EWS-время задержки

(

)

τ_s(U) как функцию U для трех малых величин элек-

sin²(kR + δ₀)

sin 2qR

(6)

тронного волнового вектора k. Для потенциальных

sin² qR

2qR

ям с отсутствием связанных уровней (интервал 0 <

Сравним уравнение (6) с формулой (5a) в статье [2]

< U < U⁽¹⁾) время задержки положительно и ме-

няет знак после появления первого s-уровня в яме

sin 2(kR + δ₀)

с ростом ее глубины U. Итак, малые изменения па-

δ^′0 > -R +

(7)

раметров потенциальной ямы (в данном случае это

глубина ямы U) в окрестности критического значе-

согласно которой, существует общее ограничение

на поведение фазовых производных, обусловлен-

ния U⁽¹⁾, ведут к скачку функции τ_s(U). Эта спе-

цифическая особенность в поведении EWS-времени

ное принципом причинности. Последний утверждает,

задержки имеет универсальный характер, поскольку

что “рассеянная волна не может покинуть рассеива-

мы можем наблюдать такую же картину в окрест-

тель до того, как падающая волна достигает его” [2].

ностях других критических величин переменной U.

Далее мы будем использовать формулы (1), (6) и (7)

Амплитуды резонансов кривых, представленных на

в наших численных расчетах.

рис. 1, быстро убывают с ростом величины k. Когда

²⁾В статье мы используем атомную систему единиц (at. un.).

волновой вектор увеличивается в два раза от k = 0.1

Письма в ЖЭТФ том 109 вып. 7 - 8

2019

518

М. Я. Амусья, A. С. Балтенков

Рис. 1. (Цветной онлайн) Время задержки τs(U) из

уравнений (1), (6), как функция параметра U при ма-

Рис. 2. (Цветной онлайн) Время задержки τs(U) из

лых волновых векторах электронов k = 0.1, 0.15 и 0.2.

уравнений (1), (6), как функция U для электронных

Величины первых критических глубин потенциальной

волновых векторов k = 0.5, 0.7 и 1.0. Радиус потенци-

ямы с радиусом R = 2 есть: U⁽¹⁾ ≈ 0.308; U⁽²⁾ ≈ 2.776;

альной ямы по-прежнему R = 2

U⁽³⁾ ≈ 7.711

глубина потенциальной ямы U постоянна. Условие

до 0.2, амплитуды соответствующих кривых в пер-

появления s-дискретных уровней в потенциальной

вой рассчитанной точке после критического значе-

яме V (r) определяется следующим соотношением

ния U⁽¹⁾ отличаются более, чем на порядок.

(см. уравнение (12) в [8])

Относительно простое резонансное поведение

функции τ_s(U) для очень малых волновых чисел

(2n - 1)π

R⁽ⁿ⁾ =

√

(12)

k меняется с ростом импульса электрона, что ил-

люстрируется рис. 2, где представлены результаты

Здесь n, как и выше, является номером s-уровня в

расчета функции τ_s(U) при k = 0.5, 0.7 и 1.0. Мы

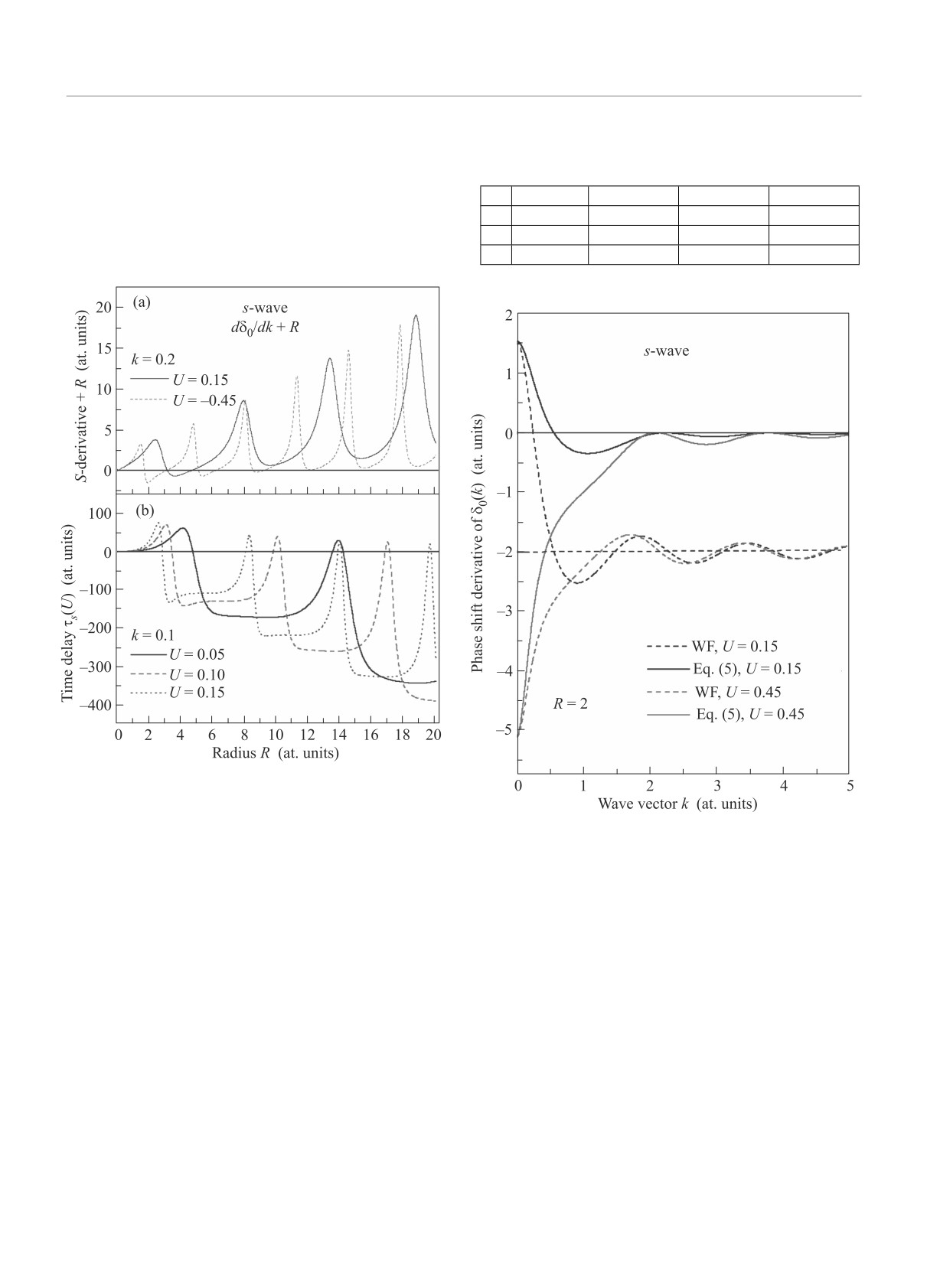
яме. На рисунке 3 изображены производные фазо-

наблюдаем здесь значительно более сложную кар-

вого сдвига и EWS-времена задержки, как функции

тину. Обратим внимание на существенно различный

R для фиксированных электронных волновых чисел

масштаб осцилляций кривых на рис. 1 и 2. В первом

k и глубин ямы U. На верхней панели этого рисун-

случае интервал вариаций времен задержки поряд-

ка представлена сумма δ^′0(R) + R. Согласно общему

ка от ∼ -100 до +100 ат. ед., тогда как на втором

ограничению δ^′0(R) + R > 0 (см. уравнение (2) в [2]),

рисунке этот интервал много меньше: от ∼ -4 до

кривые на этой панели не должны “проникать” че-

+2 ат.ед. Это есть иллюстрация следующего общего

рез ось R в нижнюю отрицательную полуплоскость,

поведения производной от фазового сдвига [11]

поскольку центр рассеяния имеет конечный радиус,

δ^′0(k → ∞) → 0.

(11)

так что условие причинности может быть примене-

но. Но согласно [2], волновая природа частиц допус-

Исследуем теперь поведение s-парциального

кает некоторые нарушения этого ограничения, и мы

EWS-времени, предполагая, что радиус потенциаль-

можем видеть это в начале кривых. Эти нарушения

ной ямы R является переменной, в то время как

исчезают с ростом R.

Письма в ЖЭТФ том 109 вып. 7 - 8

2019

Особенности Вигнеровских времен задержки медленных электронов потенциальной ямой...

519

Таблица 1. Сравнение позиций нулей кривых при изменени-

Как и на рисунках 1 и 2, время задержки τ_s(R)

ях параметров U и R. Критические величины радиусов R⁽ⁱ⁾

представляет собой знакопеременную функцию, по

взяты из уравнения (12). Положения нулей кривых на рис. 3

крайней мере, вблизи порога при малых энергиях

даются в скобках. Все параметры даны в атомных единицах

электронов. Однако если в случае U-зависимости

R⁽¹⁾

R⁽²⁾

R⁽³⁾

R⁽⁴⁾

критические значения глубин потенциальной ямы

0.05 4.967 (4.72) 14.902 (14.22)

24.836 (-)

34.771 (-)

U⁽ⁱ⁾ совпадают с нулями кривых на рис.1, то на

0.1

3.512 (3.42) 10.537 (10.27) 17.562 (17.15)

24.587 (-)

рис. 3 мы видим близость, а не совпадение нулей кри-

0.15 2.868 (2.82)

8.604

(8.45)

14.339 (14.10) 20.075 (19.74)

Рис. 3. (Цветной онлайн) R-зависимость производной

s-того фазового сдвига (уравнение (6)) и времена за-

держки (1), (6) для электронных импульсов k = 0.1

Рис. 4. (Цветной онлайн) Производные s-тых фазовых

и 0.2 при следующих глубинах потенциальных ям:

U = 0.05, 0.1, 0.15 и 0.45. Верхняя панель есть сумма

сдвигов при рассеянии электрона потенциальной ямой

с глубиной U до появления в ней первого s-уровня

dδ0/dk + R, тогда как нижняя - EWS-время задерж-

(U = 0.15) и после появления этого уровня (U = 0.45).

ки τs(R). Все параметры на рисунке даны в атомных

Критическое значение для глубины ямы U⁽¹⁾ при R = 2

единицах

- это U⁽¹⁾ = 0.308. Сплошные линии - результат рас-

чета с уравнением (6); пунктирные линии - результат

вых с критическими значениями R⁽ⁱ⁾. Это иллюстри-

расчета с уравнением (5a) из статьи Вигнера [2]

руется табл. 1, где корреляция между позициями ну-

лей кривых на оси R и значениями R⁽ⁱ⁾ несомненна.

На рисунке 4 представлено EWS-время задерж-

по формуле (6) (сплошные линии) есть также функ-

ки τ_s(k), как функция волнового вектора k. На этом

ции Вигнера (WF), рассчитанные по формуле (7)

рисунке две пары кривых. Первая из них, с глу-

(пунктирные линии). Производная фазового сдвига

биной ямы U = 0.15 и радиусом R = 2, соответ-

для рассеяния медленных электронов на потенци-

ствует случаю, когда в яме нет дискретных уров-

альной яме без связанного s-уровня положительна,

ней. Вторая пара соответствует потенциальной яме

и меняет знак после появления первого дискретно-

с первым появившимся s-уровнем (U

= 0.45 при

го уровня в яме [8]. Как и на рис.3, отрицательные

R = 2). В дополнение к этим кривым, рассчитанным

части пунктирных кривых есть проявления волно-

Письма в ЖЭТФ том 109 вып. 7 - 8

2019

520

М. Я. Амусья, A. С. Балтенков

вой природы рассеивающей частицы. Тем не менее,

няет при малой энергии электрона производную s-

ограничение δ^′0(R)+R > 0 сохраняется и в квантовой

фазы от отрицательных Хартри-Фоковских значе-

теории. Это справедливо, в частности, для больших

ний до положительных. Это изменение приводит к

импульсов k [2].

появлению широко известных минимумов Рамзауэ-

Суммируя результаты численных расчетов,

ра в сечении рассеяния медленных электронов ато-

можно сделать вывод, что EWS-задержка времени

мами благородных газов. Этот эффект, однако, не

τ_s(k, U, R) является знакопеременной функцией от-

связан с образованием дополнительного дискретно-

носительно всех трех аргументов с очень интересным

го электронного уровня. Было бы очень интересно, и

поведением.

это является одним из текущих направлений нашей

4. Мы исследовали EWS-времена задержки для

деятельности, раскрыть возможную связь между мо-

медленного s-рассеяния электрона на прямоуголь-

дификациями атомного поля и переходами на пути

ных потенциалах притяжения в зависимости от их

от благородного атома к его ближайшему соседу, ко-

параметров: глубины ямы U и ее радиуса R. Мы со-

торый способен образовывать отрицательной ион.

средоточились на таких параметрах потенциальных

Интересно было бы измерить временную задерж-

ям, которые близки к их критическим значениям,

ку в процессах рассеяния. В настоящее время экс-

при которых в них появляются s-состояния с нулевой

периментальная деятельность в этой области, как

энергией связи. Мы рассмотрели глубины и радиу-

упомянуто в начале Письма, сосредоточена на ис-

сы ям, при которых потенциал поддерживает произ-

следовании временной картины фотоионизации ато-

вольное количество s-уровней.

мов и молекул с помощью высокоинтенсивных атто-

Представленный выше анализ позволяет отме-

секундных импульсов. В этом случае кратковремен-

тить некоторые специфические особенности в пове-

ность светового импульса из-за принципа неопреде-

дении времени задержки, которые являются универ-

ленности приводит к большому разбросу энергии фо-

сальными, а именно: i) функции τ_s(U), τ_s(R) и τ_s(k)

тонов. Отметим, что описанные в этом Письме эф-

при медленном рассеянии электронов мелкой потен-

фекты требуют для своего наблюдения высокого раз-

циальной ямой без связанного s-уровня всегда поло-

решения для энергии рассеивающихся электронов,

жительны; они меняют свой знак после появления

таким образом, накладывая сильное ограничение на

первого дискретного уровня, ii) небольшие измене-

точность измерений временной задержки.

А. С. Балтенков благодарен за поддержку Грант

ния параметров потенциальной ямы в окрестностях

появления первого и любых других s-уровней при-

фонда Узбекистана OT-Ф2-46.

водят к мгновенным скачкам функции τ_s(U) с по-

ложительного значения на отрицательное. Амплиту-

1. L. E. Eisenbud, Ph. D. thesis, Princeton University,

да этих скачков увеличивается с уменьшением вол-

Princeton, USA (1948).

нового числа электронов k (см. также рис. 1 в [8]).

2. E. P. Wigner, Phys. Rev. 98, 145 (1955).

Это специфическое поведение функции τ_s(U), соот-

3. F. T. Smith, Phys. Rev. 118, 349 (1960).

ветствующей нулевому орбитальному моменту l = 0,

4. R. Pazourek, S. Nagele, and J. Burgdörfer, Rev. Mod.

и оно связано с расходимостью s-времени вблизи по-

Phys. 87, 765 (2015).

рога (см. рис. 1 в [8]). Для орбитальных моментов

5. A. S. Kheifets, Phys. Rev. A 87, 063404 (2013).

l > 0 EWS-задержка времени стремится к нулю вбли-

6. P. Hockett, E. Frumker, D. M. Villeneuve, and

зи порога как τ_l(k) ∝ k^2l-1, и поэтому функции τ_l(U)

P. B. Corkum, J. Phys. B 49, 095602 (2016).

плавно меняют знак вблизи критических точек на

7. M. Ya. Amusia and A. S. Baltenkov, J. Phys. B 52,

оси U, как показано на рис.2 в [8]. Функции τ_s(R)

015101 (2019).

меняют знак также как и функции τ_s(U), но переме-

8. M. Ya. Amusia and A. S. Baltenkov, e-print ArXive

1901.00411 (2019).

ны знака происходят без скачков.

9. L. D. Landau and E. M. Lifshitz, Quantum Mechanics,

Отдельной и важной проблемой является оцен-

Non-Relativistic Theory, Pergamon Press, Oxford

ка фазовых сдвигов и времен задержки не для про-

(1965).

стой модели, а для определения временной задержки

10. E. P. Wigner, Phys. Rev. 73, 1002 (1948).

в процессах рассеяния электронов на атомах. Многое

11. M. Wellner, Am. J. Phys. 32, 787 (1964).

известно о фазах рассеяния. Для них существуют от-

12. M. Ya. Amusia, L. V. Chernysheva, and V. G. Yarzhem-

носительно надежные результаты ab-initio расчетов

sky, Handbook of theoretical Atomic Physics, Data for

[12], включающие также рассеяние при низких энер-

photon absorption, electron scattering, and vacancies

гиях электронов. В ряде случаев добавление притя-

decay, Springer, Berlin (2012), 812 p.

гивающего поляризационного взаимодействия изме-

Письма в ЖЭТФ том 109 вып. 7 - 8

2019