Письма в ЖЭТФ, том 109, вып. 8, с. 521 - 524
© 2019 г. 25 апреля
Оптимальная динамика сферического сквирмера
в Эйлеровом описании
В.П.Рубан1)
Институт теоретической физики им. Л. Д. Ландау РАН, 142432 Черноголовка, Россия
Поступила в редакцию 8 февраля 2019 г.
После переработки 8 февраля 2019 г.
Принята к публикации 21 февраля 2019 г.
Проблема оптимизации цикла касательных деформаций поверхности сферического объекта (микро-
сквирмера), самопередвигающегося в вязкой жидкости при малых числах Рейнольдса, представлена в
неканонической гамильтоновой форме. Получена эволюционная система уравнений для коэффициентов
разложения поверхностной скорости по присоединенным полиномам Лежандра P1n(cos θ). Система имеет
квадратичную нелинейность, но в случае трех-модовой аппроксимации оказывается интегрируемой. Это
позволяет теоретически интерпретировать численные результаты, полученные ранее для такой задачи.
DOI: 10.1134/S0370274X19080058
Введение. Гидродинамика плавающих микроор-
например, [2, 7-10] и ссылки там). Несколько иной
ганизмов в настоящеее время выделилась в отдель-
тип плавания осуществляется за счет касательных
ную ветвь науки на стыке биологии и механики (см.
деформаций поверхности тела без изменения его гео-
обзор [1] и многочисленные ссылки там). Кроме то-
метрической формы [11-15]. Такого типа модельный
го, интерес к данной области имеется и со стороны
микроорганизм называется сквирмером (squirmer).
создания медицинских нанороботов. Задачей гидро-
Простейший сквирмер имеет сферическую форму и
динамики в этой связи является количественное опи-
допускает простое и точное решение задачи в терми-
сание движения жидкости и погруженных в нее ак-
нах присоединенных полиномов Лежандра [11, 12].
тивных объектов. Микроорганизмы используют для
А именно, если в системе координат, связанной со
своего перемещения разнообразные приспособления
сферой, касательное поле скорости раскладывается
и приемы жгутики, реснички, деформации поверх-
в ряд
ности и др. Решающее упрощение теории обусловле-
∑
но тем фактом, что течения жидкости происходят
an(t)P′n(cosθ)
uθ(θ, t) = sinθ
,
(1)
при очень малых числах Рейнольдса [2], когда эф-
n(n + 1)
n=1
фекты инерции в высокой степени несущественны по
сравнению с вязкостью (режим Стокса). Поэтому по-
то скорость самого сквирмера вдоль оси его симмет-
ле скорости практически мгновенно и однозначно ре-
рии по отношению к покоящейся на бесконечности
агирует на любое изменение формы тела, сдвигая его
жидкости есть просто Usq(t) = a1(t)/3. Поскольку
при этом в пространстве. Важно, что если объект из-
поверхностная скорость uθ(θ, t) обусловлена движе-
меняет свое состояние периодически по времени, то
нием некоторых лагранжевых маркеров θ0, то фак-
его смещение за цикл может быть отличным от нуля
тически
только при условии наличия “петли” в пространстве
∂θ(θ0, t)
параметров, характеризующих форму тела. Отсюда
uθ(θ, t) =
(2)
∂t
θ0=θ0(θ,t)
следует, что таких меняющихся во времени парамет-
ров - внутренних степеней свободы - должно быть
не меньше двух. Был предложен ряд упрощенных
Периодическое по времени (взаимно однозначное)
моделей, которые позволили исследовать механику
отображение θ(θ0, t) и определяет ту “петлю” в про-
вязкого плавания во всех подробностях. Например,
странстве конфигураций сквирмера, которая приво-
хорошо известны “три бусинки” с двумя перемычка-
дит к его перемещению.
ми переменной длины [3-6]. Изучались и другие, в
Здесь сразу же встает вопрос об оценке эффек-
том числе значительно более сложные модели (см.,
тивности любого заданного цикла с точки зрения
энергозатрат. Если учитывать только диссипацию
1)e-mail: ruban@itp.ac.ru
механической энергии в окружающей жидкости и
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
521
522
В.П.Рубан
не касаться внутренних энергозатрат, то мгновенный
оказывается интегрируемой, что полностью выявля-
темп диссипации дается выражением вида
ет структуру соответствующего решения.
Гамильтонова механика оптимизации. Нам
∑
Dn
Q∝
a2n,
(3)
будет удобно использовать стандартный язык кон-
2n + 1
n
сервативной динамики. Ввиду соотношения (8), наи-
более эффективный цикл сквирмера должен достав-
где D1 = 1, а остальные коэффициенты определяют-
∫
лять минимум функционалу “действия” A =
Ldt с
ся формулой [11, 12]
лагранжианом
2n + 1
∫1 (1
)
Dn =
,
n ≥ 2.
(4)
n(n + 1)
L[v] =
v Dv + λv dx, v = - ∂x0/∂t
,
(9)
-1
2
∂x0/∂x
Мы далее рассматриваем общий случай произволь-
где λ представляет собой неопределенный множи-
ных Dn > 0, за исключением численных примеров.
тель Лагранжа, а оператор
D дается формулой
Задачу оптимизации цикла удобно переформули-
ровать в других переменных [16]. Пусть x = cos θ,
∑
а лагранжево отображение поверхности есть x(x0, t).
Dv = - Dkak(t)P′k(x).
(10)
Тогда соответствующее поле скорости будет
k=1
∑
)-1
Варьированием действия по δx0(x, t) легко составить
( d
v(x, t) = - sin θuθ =
an(t)
Pn(x),
(5)
соответствующее динамическое уравнение Эйлера-
dx
n=1
Лагранжа и после простых преобразований получить
где
из него следующее уравнение:
)-1
( d
(1 - x2)P′n(x)
Pn(x) = -
(6)
∂p
∂
∂v
dx
n(n + 1)
=-
(vp) - p
,
(11)
∂t
∂x
∂x
При этом
∫
где введен канонический импульс p(x, t) = δL[v]/δv.
(2n + 1)
В нашем случае
an(t) = -
P′n(x)v(x, t)dx,
(7)
2
ˆv + λ.
p=
(12)
∫
a1(t)
1
Обратим внимание, что лагранжево отображение са-
Usq(t) =
=-
v(x, t)dx.
(8)
3
2
мо по себе здесь не фигурирует, и что порядок урав-
нения (11) по временной производной не второй, а
Оптимальный цикл должен обеспечить максималь-
ное смещение сферы за период при ограничении
всего лишь первый. Так проявляется упомянутая
ранее симметрия переобозначений при переходе от
энергозатрат. Такой цикл был найден численно в ра-
боте [16] в терминах отображения x(x0, t) путем гра-
лагранжева к эйлерову описанию.
диентной максимизации отношения 〈a1〉2/〈Q〉, где уг-
Стоит отметить, что уравнение (11) обладает
неканонической гамильтоновой структурой. Если
ловые скобки означают усреднение по периоду. Одна-
ко временные зависимости для коэффициентов an(t)
определить функционал Гамильтона H[p] стандарт-
ным образом как преобразование Лежандра от
были получены лишь опосредованно, уже после ре-
шения уравнения движения на x(x0, t). Интерпрети-
лагранжиана L[v], то тогда v = δH/δp и уравнение
(11) перепишется как
ровать поведение старших мод оказалось довольно
затруднительно. В целом, аналитическая сторона во-
∂p
∂ (
δH)
∂ δH
проса осталась не до конца исследованной.
=-
p
-p
(13)
∂t
∂x
δp
∂x δp
Целью данной работы является дополняющий по
∫
отношению к [16] теоретический анализ проблемы
Вариационный принцип δ
Ldt = 0 для таких дина-
оптимизации сферического сквирмера с учетом име-
мических систем имеет несколько необычный вид:
ющейся симметрии переобозначений лагранжевых
∫
маркеров x0 = x0(ξ0). Как будет показано далее, за-
L=-
√p∂-1x∂t√p dx - H[p].
(14)
дача допускает получение системы уравнений дви-
жения непосредственно в терминах an(t). К тому же,
Независимо от вида гамильтониана, имеется закон
эти уравнения имеют всего лишь первый порядок по
сохранения
∫
времени и разрешены относительно временной про-
√p dx = S = const.
(15)
изводной. Более того, трех-модовая аппроксимация
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
Оптимальная динамика сферического сквирмера в Эйлеровом описании
523
Остается под вопросом случай, когда p(x, t) - знако-
“Испортится” также интеграл движения (15). Одна-
переменная функция.
ко польза от таких приближений все же будет, если
Уравнения для коэффициентов. Подставим
только удастся найти такие их решения, на которых
теперь в уравнение (11) разложения (5) и (10), затем
последние моды содержат лишь малую часть от пол-
умножим на (d/dx)-1Pm(x) и проинтегрируем по x.
ной “энергии”. В этой связи необходимо отметить слу-
В результате получим бесконечную систему обыкно-
чаи N = 3 и N = 5. При N = 3 уравнения выглядят
венных дифференциальных уравнений вида
следующим образом:
∑
∑
2D1
4λ
4
2Dm
a1 = -
a2 +
a2D1a1 -
am = 2λ Ωmnan + WmnkanDkak, (16)
3
15
15
2m + 1
n
n,k
4
2
−
a2D3a3 +
a3D2a2,
(22)
35
7
где элементы антисимметричной матрицы Ω даются
2D2
4λ
4λ
4
выражениями
a2 =
a1 -
a3 -
a1D1a1 +
5
15
35
15
∫1
)-1
4
4
2
( d
Ωmn = -Ωnm = -
Pn(x)
Pm(x)dx.
(17)
+
a1D3a3 +
a3D1a1 +
a3D3a3,
(23)
dx
35
35
105
-1
2D3
4λ
2
a3 =
a2 -
a1D2a2 -
Используя свойства полиномов Лежандра, нетрудно
7
35
7
понять, что отличны от нуля только элементы между
4
2
−
a2D1a1 -
a2D3a3.
(24)
соседними модами, причем
35
105
У этой системы имеется еще один интеграл движения
2
Ωm,m-1 =
(18)
вида F (a1, a3) = C, поскольку в правых частях пер-
(2m + 1)(2m - 1)
вого и третьего уравнений множитель a2 выносится
Тензор квадратичной нелинейности W также анти-
за скобки. Их отношение не содержит переменной a2
симметричен по своим первым двум индексам. После
и соответствует автономной линейной неоднородной
интегрирования по частям он приводится к виду
системе с особой точкой в виде фокуса. Фазовая тра-
[
]
ектория оказывается пересечением эллипсоида (21) и
1
1
Wmnk =
-
Jmnk,
(19)
поверхности из семейства F (a1, a3) = C (предполага-
m(m + 1)
n(n + 1)
ется, что фокус находится за пределами эллипсоида).
∫1
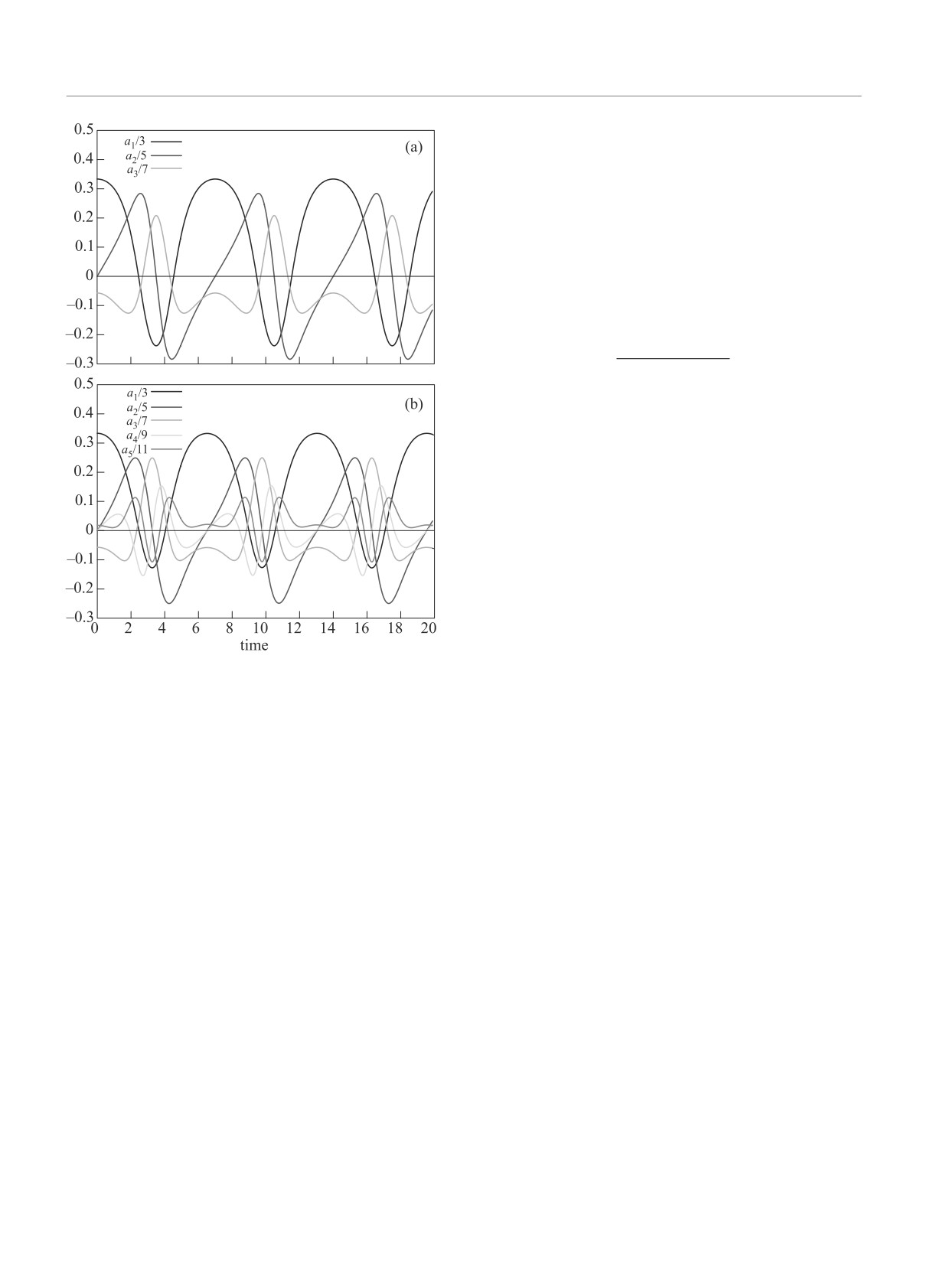
Пример динамики трех мод показан на рис. 1a. В слу-
Jmnk =
(1 - x2)P′m(x)P′n(x)Pk (x)dx.
(20)
чае же N = 5 удается без особого труда подобрать
−1
такие начальные условия, что фазовая траектория
Очевидно, что здесь отличны от нуля только такие
оказывается близкой к периодической и проходит че-
элементы, для которых сумма трех индексов явля-
рез относительно малые a4 и a5, как это показано
ется четным числом: m + n + k = 2s. Кроме того,
на рис. 1b. В качественном отношении эта картин-
должно выполняться условие (m+n) ≥ k. Несколько
ка очень похожа на рис. 6 из работы [16]. Но коли-
первых элементов W равны: W1,2,1 = 4/15, W1,2,3 =
чественно рис. 1b представляет другой оптимальный
= -4/35, W1,3,2 = 2/7, W2,3,1 = 4/35, W2,3,3 = 2/105.
цикл, поскольку локальных минимумов функциона-
По причине антисимметрии Ω и W темп диссипа-
ла действия на самом деле много, как было отмечено
ции на оптимальном цикле оказывается интегралом
авторами работы [16].
движения, то есть константой во времени,
Что касается систем с N > 5, то для них алго-
∑ Dm
ритм численного поиска подходящих периодических
a2m = E = const.
(21)
2m + 1
решений автором пока не разработан. Метод же проб
m
и ошибок ничего не дал.
Таким образом, движение происходит на эллипсоиде
Необходимо подчеркнуть, что задача оптимиза-
в многомерном фазовом пространстве.
ции не заканчивается на решении динамической си-
Конечно-модовые аппроксимации. Числен-
стемы (16). Еще необходимо отобрать те решения,
ные результаты работы [16] свидетельствуют о том,
на которых перемещение действительно максималь-
что на оптимальном решении амплитуды an убывают
но. Однако вполне может оказаться, что при уче-
экспоненциально с ростом номера n. Если оборвать
те дополнительных ограничений на свойства лагран-
цепочку уравнений (16), положив an = 0 при n > N,
жевых отображений некоторые не вполне оптималь-
то полученная таким образом конечномерная дина-
ные решения могут оказаться предпочтительнее. На-
мическая система перестанет быть гамильтоновой.
пример, если наиболее оптимальное решение дикту-
Письма в ЖЭТФ том 109 вып. 7 - 8
2019
524
В.П.Рубан
сти на поверхности. Найденные приближенные ре-
шения и их расположение в фазовом пространстве
позволяют лучше понять поведение нескольких наи-
более важных первых мод.
Аналогичный подход может быть использован и
для других осесимметричных сквирмеров. Только
разложение поля скорости v(x, t) нужно будет вести
по подходящим наборам функций, в зависимости от
геометрической формы объекта.
Работа выполнена в рамках госзадания # 0033-
2019-0003.
1. E. Lauga and T. R. Powers, Rep. Prog. Phys. 72, 096601
(2009).
2. E. M. Purcell, Am. J. Phys. 45, 3 (1977).
3. A. Najafi and R. Golestanian, Phys. Rev. E 69, 062901
(2004).
4. R. Golestanian and A. Ajdari, Phys. Rev. E 77, 036308
(2008).
5. F. Alouges, A. DeSimone, and A. Lefebvre, Eur. Phys. J.
E 28, 279 (2009).
6. R. Zargar, A. Najafi, and M. Miri, Phys. Rev. E 80,
026308 (2009).
7. J. E. Avron, O. Gat, and O. Kenneth, Phys. Rev. Lett.
93, 186001 (2004).
8. E. Gauger and H. Stark, Phys. Rev. E 74, 021907
(2006).
Рис. 1. (Цветной онлайн) (a) - Трех-модовая аппрокси-
9. D. Tam and A. E. Hosoi, Phys. Rev. Lett. 98, 068105
мация. (b) - Пяти-модовая аппроксимация
(2007).
10. D. Takagi, Phys. Rev. E 92, 023020 (2015).
ет слишком большие смещения лагранжевых марке-
11. M. J. Lighthill, Commun. Pure Appl. Math. 5,
109
ров по углу θ, которые невозможны по внутреннему
(1952).
устройству реального сквирмера, то пригодятся ре-
12. J. R. Blake, J. Fluid Mech. 46, 199 (1971).
шения с меньшей амплитудой.
13. O. S. Pak and E. Lauga, J. Eng. Math. 88, 1 (2014).
Заключение. Таким образом, переход к эйлеро-
14. M. Theers, E. Westphal, G. Gompper, and
ву описанию оптимальной динамики сферического
R. G. Winkler, Soft Matter 12, 7372 (2016).
сквирмера выявил ее неканоническую гамильтонову
15. D. Papavassiliou and G. P. Alexander, J. Fluid Mech.
структуру и позволил вывести удобные для числен-
813, 618 (2017).
ного решения уравнения движения непосредственно
16. S. Michelin and E. Lauga, Physics of Fluids 22, 111901
в терминах коэффициентов разложения поля скоро-
(2010).
Письма в ЖЭТФ том 109 вып. 7 - 8
2019