Письма в ЖЭТФ, том 109, вып. 9, с. 589 - 594

Квантово-оптический модовый затвор для неклассического

сжатого света

В.В.Сухарников⁺¹⁾, О.В.Тихонова^+∗

⁺Московский государственный университет им. М. В. Ломоносова, Физический факультет, 119991 Москва, Россия

^∗Московский государственный университет им. М. В. Ломоносова,

Научно-исследовательский институт ядерной физики им. Д. В. Скобельцына, 119234 Москва, Россия

Поступила в редакцию 6 марта 2019 г.

После переработки 20 марта 2019 г.

Принята к публикации 20 марта 2019 г.

В формализме мод Шмидта и операторов фотонов в этих модах разработан теоретический подход

для описания спектральных свойств света, получаемого в нелинейном процессе генерации суммарной

частоты. Детально описан особый режим, при котором частотные корреляции фотонов в выходных пуч-

ках подавляются. В данном режиме продемонстрировано управление модовым составом и спектраль-

ными свойствами неклассического сжатого света, использованного в качестве подсветки сигнального

канала, с возможностью генерации сжатого вакуума в моде суммарной частоты.

DOI: 10.1134/S0370274X19090030

1. Введение. Неклассические состояния света

Для генерируемых ярких сжатых световых полей

имеют ряд замечательных квантовых свойств, кото-

характерны сильная перепутанность фотонов друг

рые находят широкое применение в быстро развива-

с другом и существенно многомодовый спектраль-

ющихся современных областях физики. Для реше-

ный состав. Эти особенности затрудняют теоретиче-

ния задач в области квантовых измерений крайне

ский анализ таких состояний света. Наиболее удоб-

перспективными оказываются так называемые сжа-

но проводить теоретический анализ таких состоя-

тые состояния света [1, 2]. Под “сжатием” понимает-

ний в базисе так называемых широкополосных мод

ся уменьшение неопределенности одной квадратуры

Шмидта [8-10, 12]. В работах [13, 14] нелинейное вза-

поля по сравнению с вакуумной, что сопровождает-

имодействие анализировалось в терминах операто-

ся увеличением неопределенности в сопряженной ей

ров рождения фотонов в модах Шмидта. В [8, 10] в

квадратуре. Для задач в области квантовой инфор-

представлении Гейзенберга были решены уравнения

мации, в свою очередь, очень важны перепутанные

для таких операторов, что позволило теоретически

состояния фотонов [3-5]. При этом именно в ярких

предсказать целый ряд важных эффектов, обнару-

сжатых состояниях света имеет место сильная скор-

женных экспериментально. Одной из важных про-

релированность большого числа фотонов друг с дру-

блем, не решенных на сегодняшний день, являет-

гом.

ся контролируемое изменение относительных весов

Основной способ генерации сжатых некласси-

мод Шмидта, характеризующих генерируемый сиг-

ческих световых полей - нелинейные оптические

нал, что фактически означает ослабление сигнала в

процессы, например, квадратично нелинейный про-

одной или нескольких модах. Также возникает необ-

цесс параметрического рассеяния (PDC - parametric

ходимость поиска способов управления спектраль-

down-conversion) [6, 7]. В процессе PDC поле накачки

ными свойствами неклассического сжатого света, ко-

взаимодействует со средой с квадратичной нелиней-

торые бы сохранили его квантовые свойства. Это до-

ностью. В результате рождаются сигнальный и холо-

статочно нетривиальная задача, так как сжатое со-

стой фотоны меньшей частоты на выходе кристал-

стояние света очень хрупкое, поэтому при использво-

ла. Интерес также представляет процесс генерации

вании обычных оптических приборов оно разрушит-

суммарной частоты (SFG - sum-frequency generation),

ся из-за вносимых потерь и шумов. В связи с этим

для которого помимо накачки нужна еще подсветка

необходимы квантово-оптические методы, позволяю-

в сигнальном канале.

щие контролируемо изменять модовый и спектраль-

ный состав сжатого света.

¹⁾e-mail: sukharnikov.vv14@physics.msu.ru

Письма в ЖЭТФ том 109 вып. 9 - 10

2019

589

590

В.В.Сухарников, О.В.Тихонова

В данной работе предлагается метод такого

коллинеарное распространение полей (т.е. пренебре-

управления, основанный на особом режиме процесса

гаем поперечными компонентами волновых векто-

генерации суммарной частоты с подсветкой сжа-

ров), что позволяет заменить интеграл по простран-

тым светом. Разработан теоретический подход для

ству волновых векторов на интеграл по частотам в

квантового описания процесса генерации суммарной

(2) и (3).

частоты в терминах мод Шмидта и операторов

Считаем, что на длине кристалла L восприимчи-

фотонов в этих модах. В рамках данного подхода за

вость слабо зависит от пространственной перемен-

рамками теории возмущений анализируется схема,

ной, т.е. χ⁽²⁾(r) ≈ χ⁽²⁾⁰. С учетом закона сохранения

во многом аналогичная квантовому светоделите-

энергии, при котором фотон накачки с частотой ω и

лю, предложенному в [11, 12]. Для данной схемы

сигнальный фотон частоты ω_s рождают фотон сум-

обнаружена возможность блокировки одной из

марной частоты ω_o = ω_s + ω, гамильтониан (1) при-

мод Шмидта подсвечивающего сжатого вакуума.

водится к виду:

∫

Продемонстрировано, что эффект частичной или

H = iℏΓ dω_sdωo F(ω_s,ω_o)aωsa^†

+ h.c.,

(4)

полной блокировки сигнала в одной из мод Шмидта

ωo

приводит к значительному перераспределению отно-

где Γ ∼ χ⁽²⁾⁰E₀ · L - эффективная константа взаимо-

сительных весов входящих мод Шмидта. На основе

действия внутри кристалла, L - длина кристалла, а

этого эффекта впервые продемонстрирована воз-

F (ω_s, ω_o) - бифотонная амплитуда рассматриваемо-

можность существенного изменения спектрального

го процесса, имеющая вид:

и временного профилей сигнала сжатого вакуума на

( Δk_zL)

выходе.

F (ω_s, ω_o) = CΦ(ω_s - ω_o)sinc

(5)

2. Генерация суммарной частоты. Рассмот-

где C - постоянная нормировки, а Δk_z = k_p(ω_p) +

рим первоначально процесс генерации суммарной

+ k_s(ω_s) - k_o(ω_o) - расстройка волновых векторов

частоты. Пусть на кристалл с квадратично нелиней-

внутри кристалла. Считая, что нулевой порядок за-

ной восприимчивостью χ⁽²⁾(r) падает два световых

нуляется настройкой кристалла, главная часть рас-

сигнала: поле накачки E_p и поле подсветки E_s в сиг-

стройки имеет вид:

нальном канале. На выходе будет преобразованная

подсветка и сгенерированный сигнал суммарной час-

[

]

Δk_z ≈

k^′p(ω_p) - k^′o(2ω_p)

· (ω_o - 2ω_p).

(6)

тоты E_o. Такому квадратично нелинейному оптиче-

скому процессу соответствует следующий гамильто-

Аппроксимируя функцию sinc гауссианой [9], приве-

ниан:

дем бифотонную амплитуду (5) к виду:

∫

[

]

(ω_o - 2ω_p)²

H ∼ drχ⁽²⁾E^(+)p(r,t)E^(+)s(r,t)E^(-)o(r,t) + h.c.

(1)

F (ω_s, ω_o) = CΦ(ω_s - ω_o) exp -

(7)

2A²

Поле накачки будем считать классическим. Ампли-

где спектральная ширина A:

туду поля накачки обозначим как E₀, а нормирован-

ное спектральное распределение через Φ(ω). Счита-

A∼

(8)

L · |k^′p(ω_p) - k^′o(2ω_p)|

ем, что спектр накачки ограничен, центрирован на

частоте ω_p и имеет характерную ширину σ. В свою

имеет физический смысл обратного времени группо-

очередь, для квантованных полей сигнала и суммар-

вого запаздывания внутри кристалла (так как про-

ной частоты используем разложение по плоским вол-

изводная волнового вектора есть обратная групповая

нам:

скорость пакета), и зависит только от характеристик

∫

кристалла и его дисперсионных свойств. Заметим,

E^(+)s(r, t) = dk_s Cks e+i(ksr-ωst)aks ,

(2)

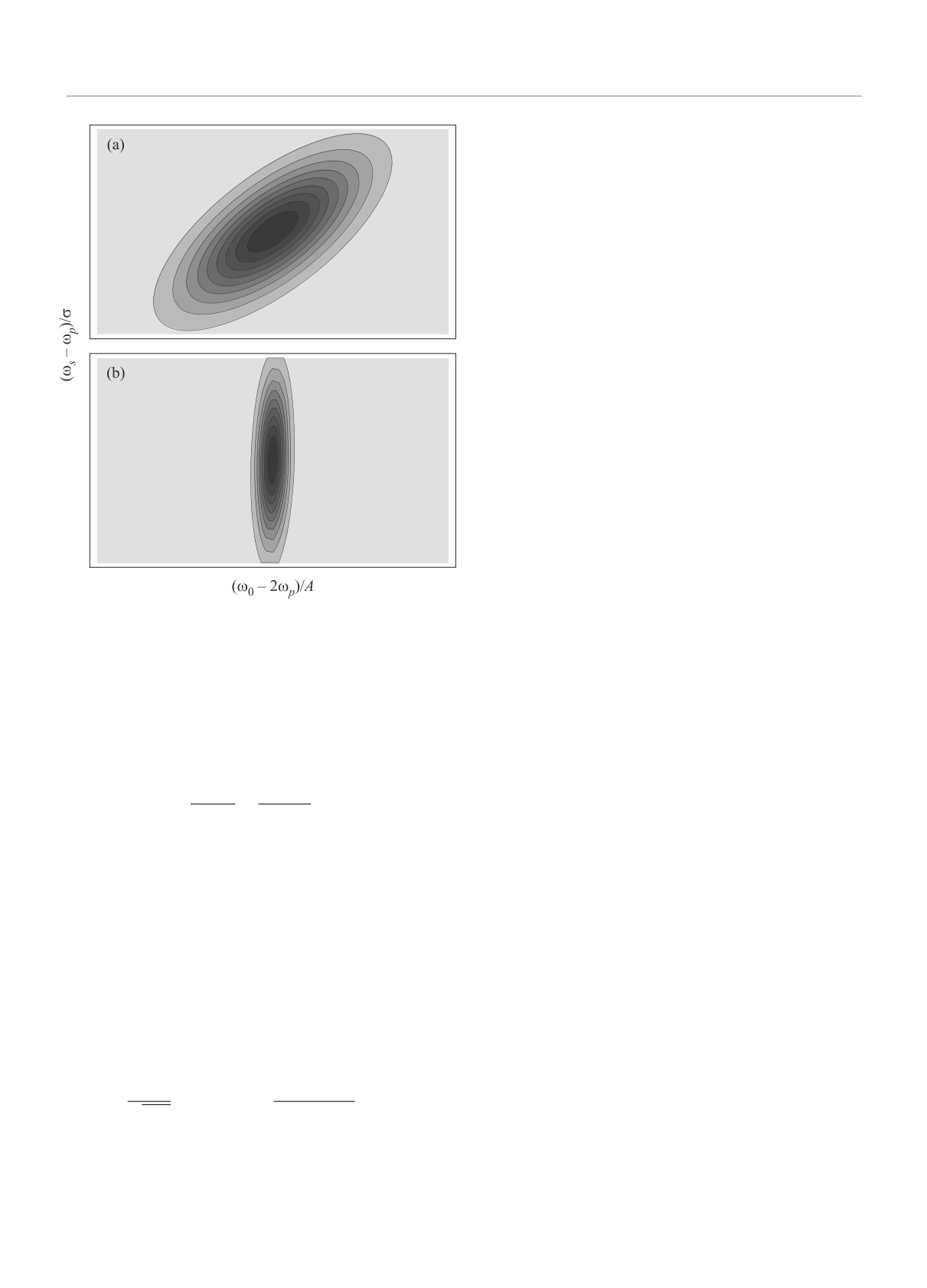
что структура бифотонной амплитуды (7) показыва-

∫

ет частотное перепутывание фотонов на выходе, по-

E^(-)o(r, t) = dk_o Cko e-i(kor-ωot)a^† .

(3)

скольку отсутствует частотная факторизация отно-

сительно ω_o и ω_s. Однако в случае широкого спектра

Пусть поле сигнала также центрировано на часто-

накачки σ ≫ A происходит частотная факторизация

те ω_p, как и поле накачки (вырожденный режим).

(рис. 1), поскольку значения ω_o находятся в очень уз-

Однако отметим, что они имеют разные поляриза-

кой окрестности 2ω_p:

ции: поле накачки имеет обыкновенную поляриза-

[

]

цию, а сигналы в сигнальном канале и канале сум-

(ω_o - 2ω_p)²

F (ω_s, ω_o) ≈

√

Φ(ω_s) exp -

(9)

марной частоты - необыкновенную [11]. Рассмотрим

πA²

2A²

Письма в ЖЭТФ том 109 вып. 9 - 10

2019

Квантово-оптический модовый затвор...

591

которые удовлетворяют стандартным коммутацион-

ным соотношениям [C, C^†] = [D, D^†] = 1, причем

операторы разных мод коммутируют между собой

[C, D^†] = 0. Гамильтониан (4) перепишется в виде:

H = iℏΓ(C^†D - D^†C).

(13)

Отметим, что такой вид гамильтониана совпадает с

гамильтонианом квантового светоделителя.

Изучим преобразование операторов сигнальной

моды (12) и моды суммарной частоты (11) в резуль-

тате взаимодействия в кристалле, для чего использу-

ем картину Гейзенберга. Начальные состояния опе-

раторов (до взаимодействия) будем обозначать при-

ставкой in (оно будет отвечать значению соответ-

ствующего оператора в картине Шредингера), после

взаимодействия - приставкой out. Все средние зна-

чения наблюдаемых рассчитываются по состоянию,

которое представляет собой тензорное произведение:

|Ψ〉 = |ψ〉_s ⊗ |0〉_o,

(14)

где |0〉_o - вакуум для моды суммарной частоты, а

|ψ〉_s - квантовое состояние фотонов поля подсветки

на входе кристалла.

Решение уравнений Гейзенберга, дающее преоб-

разование операторов в результате взаимодействия,

Рис. 1. (Цветной онлайн) Профили бифотонной амплиту-

можно записать в матричном виде, который совпа-

ды F(ωs, ωo). (а) - В обычном режиме. (b) - В режиме

дает с матрицей светоделителя [1]:

A ≪ σ. Поворот и сужение профиля говорит о подавле-

(

)

(

)(

)

нии частотных корреляций между сигналами на выходе

C^out

cosΘ sinΘ

Cⁱⁿ

кристалла

(15)

D^out

− sinΘ cosΘ Dⁱⁿ

∫

С физической точки зрения условие σ ≫ A нала-

где Θ =

dtΓ - параметр, зависящий от амплитуды

гает ограничения на ширину группового синхрониз-

накачки, который, следуя аналогии, будем называть

ма:



углом светоделителя.



Из структуры гамильтониана (13) видна динами-

L·

τ,

(10)

≫

v_p(ω_p)-

v_o(2ω_p)

ка нелинейного процесса: фотоны в сигнальной моде

где v_p(ω_p) = 1/k^′p(ω_p) и v_o(2ω_p) = 1/k^′o(2ω_p), а τ =

уничтожаются, что сопровождается рождением фо-

= 1/σ - характерная длительность накачки.

тонов в моде суммарной частоты.

Отметим, что в рамках рассматриваемого режи-

Введем наблюдаемые операторы числа фотонов

ма σ ≫ A в бифотонной амплитуде (9) множитель с

в моде суммарной частоты N_C = C^†C и в сигналь-

суммарной частотой всегда имеет такой вид и опре-

ной моде N_D = D^†D. Вначале отметим, что дина-

деляется только настройкой кристалла, а частотный

мика системы будет происходить таким образом, что

множитель фотонов подсветки определяется спек-

суммарное число фотонов, задействованное во взаи-

тром накачки.

модействии, не изменяется, т.е. [H, N_C + N_D] = 0, и

Подставим это выражение в гамильтониан (4) и

следовательно:

определим широкополосные спектральные операто-

〈N^inC + N^inD〉 = 〈N^outC + N^outD〉,

(16)

ры моды суммарной частоты и сигнальной моды со-

ответственно:

– интеграл движения. Средние значения наблюдае-

∫

[

]

мых операторов числа фотонов в широкополосных

(ω_o - 2ω_p)²

C =

√

dω_o exp -

aωo ,

(11)

модах вычисляются как:

πA²

2A²

〈N^outC〉 = sin² Θ · 〈N^inD〉,

(17)

∫

D = dωs Φ(ω_s)aωs,

(12)

〈N^outD〉 = cos² Θ · 〈N^inD〉.

(18)

Письма в ЖЭТФ том 109 вып. 9 - 10

2019

592

В.В.Сухарников, О.В.Тихонова

Таким образом, в случае вакуума в моде суммар-

- дисперсия одной квадратуры меньше вакуумной, а

ной частоты и отсутствия подсветки в сигнальную

другая превышает ее (в зависимости от знака G) та-

моду, процесс генерации суммарной частоты не про-

ким образом, что произведение этих дисперсий дает

исходит. При наличии подсветки сигнала, та ее часть,

1/4.

которая перекрывается только с частотной сигналь-

Полное спектральное распределение определя-

ной модой Φ(ω), участвует во взаимодействии, ча-

ется как сумма произведений веса каждой моды

стично или полностью конвертируясь в моду суммар-

Шмидта на квадрат модуля соответствующей функ-

ной частоты. Полная конвертация отвечает случаю

ции Эрмита-Гаусса:

Θ = (k + 1/2)π, где k - целое число. Тогда в пере-

∑

крывающейся части подсветки образуется вакуум, и

Nⁱⁿ(ω) =

|u_n(ω)|²Λⁱⁿⁿ,

(25)

все фотоны переводятся в суммарную частоту. Такая

n=0

схема называется квантово-оптическим модовым за-

твором [11, 12]. Чтобы получить конкретные резуль-

где Λⁱⁿⁿ - относительный вес n-й моды в in-состоянии,

таты, нужно задать квантовое состояние подсветки.

т.е. вероятность обнаружить ее:

3. Подсветка сжатым светом в модах

〈A^in†nAⁱⁿⁿ〉

Шмидта. Выберем в качестве подсветки некласси-

Λⁱⁿⁿ =

(26)

∑

ческий сжатый свет, сгенерированный в результате

〈A^in†kA^ink〉

процесса параметрического рассеяния в вырож-

k=0

денном коллинеарном случае. Квантовое состояние

На рисунке 2 представлено распределение весов мод

подсветки представляет собой сжатый вакуум и

Шмидта (26) и спектральный сигнал яркого сжато-

задается как [10]:

|ψ〉_s = S(G)|0〉,

(19)

где S(G) - оператор сжатия, зависящий от парамет-

ра сжатия G:

{

}

∑

√

(

)

S(G) = exp G

λ_n

A^†2n - A²ⁿ

(20)

n=0

Здесь A_n - операторы в модах Шмидта,

√λ_n - соб-

ственные значения Шмидта [8, 10]. Операторы в мо-

дах Шмидта определены как:

∫

A_n = dω_s u_n(ω_s)aωs,

(21)

где u_n(ω_s) - функции Эрмита-Гаусса, и операторы

Шмидта удовлетворяют коммутационным соотноше-

ниям [A_n, A^†m] = δ_nm.

Вычислим средние значения операторов числа

фотонов в каждой моде Шмидта на входе в кристалл

SFG:

(

√ )

〈A^in†nAⁱⁿⁿ

〉 = sinh2 2G

λ_n

(22)

Рис. 2. Распределение весов мод Шмидта (a) и норми-

рованный на максимум спектральный сигнал (b) ярко-

Полевые квадратуры для каждой моды Шмидта

A_n + A^†n

A_n - A^†n

го сжатого вакуума, рассчитанные для вырожденного

X_n =

√

и P_n =

√ имеют следующие

параметрического рассеяния на длине волны 800 нм в

кристалле BBO длиной L = 3 мм при длительности

дисперсии [1]:

импульса накачки 1 пс и коэффициенте параметриче-

(

√ )

ского усиления 11 (G = 25). Частота отсчитывается от

D[Xⁱⁿⁿ] =

exp

+4G

λ_n

(23)

центра спектра накачки для процесса SFG в единицах

(

√ )

ее спектральной ширины σ

D[Pⁱⁿⁿ] =

exp

-4G

λ_n

(24)

Письма в ЖЭТФ том 109 вып. 9 - 10

2019

Квантово-оптический модовый затвор...

593

го вакуума (25), рассчитанные для типичных значе-

ний реальных параметров эксперимента по вынуж-

денному параметрическому рассеянию света в режи-

ме большого усиления [15].

Подсветим кристалл, в котором проходит процесс

генерации суммарной частоты в режиме подавления

частотных корреляций, неклассическим сжатым све-

том, состояние которого определено в (19).

Рассмотрим случай, когда спектр сигнальной мо-

ды полностью совпадает с какой-либо n-й модой

Шмидта подсветки, т.е. Φ(ω) ≡ u_n(ω). В этом случае

мы можем отождествить операторы D и A_n. Так как

операторы несовпавших мод коммутируют с гамиль-

тонианом, то они никак не преобразуются. Совпав-

шая мода преобразуется согласно уже полученному

решению (15):

A^outn = Aⁱⁿⁿ cosΘ - Cⁱⁿ cosΘ,

(27)

что дает число фотонов в этой моде на выходе из

кристалла:

(

√ )

Рис. 3. Полное блокирование нулевой моды Шмидта из

〈A^out†nA^outn〉 = cos² Θ · sinh²

λ_n

(28)

подсветки. (a) - Перенормировка весов Λ^outn вследствие

блокирования фотонов из нулевой моды. (b) - Соот-

а число фотонов в моде суммарной частоты, согласно

ветствующее изменение нормированного на максимум

(15):

распределения частотного сигнала на выходе N^out(ω)

(

√ )

〈C^out†C^out〉 = sin² Θ · sinh²

λ_n

(29)

Изучим, что происходит с дисперсиями квад-

Частичная (или полная конвертация) совпавшей мо-

ратур совпавшей моды Шмидта. В общем случае

ды Шмидта приводит к перераспределению весов

дисперсии будут уже отвечать не идеальному сжа-

мод (26):

тию (сжатому вакууму), которое было до взаимодей-

〈A^out†mA^outm〉

ствия, а имеют следующие значения:

Λ^outm =

(30)

∑

〈A^out†kA^outk〉

k=0

{

√

}

[

]

λn

X^outn

· sin² Θ + cos² Θ · e^+4G

(31)

При углах светоделителя, равных π(k + 1/2) (где

{

√

}

k - целое число), совпавшая мода полностью кон-

[

]

λn

P^outn

· sin² Θ + cos² Θ · e^-4G

(32)

вертируется в сигнал суммарной частоты, т.е. после

взаимодействия в этой моде образуется вакуум, без

какого-либо влияния на другие моды. В этом и за-

Пусть G > 0. При значениях угла светоделителя

ключается принцип действия квантово-оптического

π(k + 1/2) дисперсии квадратур соответствуют зна-

модового затвора. Важно отметить, что зануление

чениям для вакуума, что отражает факт полной кон-

веса какой-нибудь моды Шмидта сопровождается

вертации из данной моды в моду суммарной частоты.

перераспределением весов остальных мод, что поз-

В промежуточных значениях угла дисперсия коор-

воляет управлять вкладами мод Шмидта. Измене-

динатной квадратуры превышает вакуумную, а для

ние вкладов мод Шмидта позволяет манипулировать

импульсной квадратуры - меньше вакуумной. Таким

спектром выходного сигнала. Этот эффект носит су-

образом, свет остается сжатым, однако произведение

щественный характер, что демонстрируется на рис.3

дисперсий может теперь превышать 1/4:

на примере блокирования нулевой моды Шмидта из

подсветки. На центральной частоте образуется “впа-

дина” (по сравнению с рис. 2), соответствующая об-

(

√ )sin2_2Θ

нулению вклада нулевой моды Шмидта.

D[X^outn] · D[P^outn] =

+ sinh²

λ_n

(33)

Письма в ЖЭТФ том 109 вып. 9 - 10

2019

594

В.В.Сухарников, О.В.Тихонова

Заметим, что для дисперсий квадратур X_C и P_C

случае полной конвертации, оказывается сжатым ва-

моды суммарной частоты можно получить следую-

куумом.

щие значения:

Исследование выполнено за счет гранта Россий-

{

}

ского Научного Фонда, проект # 19-42-04105.

[

]

√

λn

X^outC

· cos² Θ + sin² Θe^+4G

(34)

{

√

}

M. O. Scully and M. S. Zubairy, Quantum Optics,

[

]

λn

P^outC

· cos² Θ + sin² Θe^-4G

(35)

Cambridge U.P., N.Y. (1997).

N. Corzo, A. M. Marino, K. M. Jones, and P. D. Lett,

следовательно, сигнал суммарной частоты также яв-

Opt. Express. 19, 21358 (2011).

ляется сжатым. При углах полной конвертации π(k+

G. Brida, L. Caspani, A. Gatti, M. Genovese, A. Meda,

+1/2) свет в моде суммарной частоты является сжа-

and I. R. Berchera, Phys. Rev. Lett. 102, 213602 (2009).

тым вакуумом. То есть, предложенная схема может

N. Agafonov, M. V. Chekhova, and G. Leuchs, Phys.

рассматриваться как конвертер по частоте для сжа-

Rev. A 82, 011801 (2010).

того вакуума.

B. Brecht, D. V. Reddy, C. Silberhorn, and

4. Заключение. Таким образом, на основе фор-

M. G. Raymer, Phys. Rev. X 5, 041017 (2015).

мализма мод Шмидта был разработан теоретический

T. Iskhakov, M. V. Chekhova, and G. Leuchs, Phys. Rev.

подход для описания частотных свойств света, полу-

Lett. 102, 183602 (2009)

чаемого в процессе генерации суммарной частоты,

K. Yu. Spasibko, T. Sh. Iskhakov, and M. V. Chekhova,

Opt. Express. 20, 7507 (2012).

за рамками теории возмущений. Проанализировано

влияние спектра накачки на свойства полей, участ-

Lemieux, M. Manceau, P. Sharapova,

O. V. Tikhonova, R. W. Boyd, G. Leuchs, and

вующих в процессе генерации суммарной частоты,

M. V. Chekhova, Phys. Rev. Lett. 117, 183601 (2016).

а также выделен особый режим подавления частот-

M. V. Fedorov, Yu. M. Mikhailova, and P. A. Volkov,

ных корреляций фотонов в выходных пучках. Этот

J. Phys. B: At. Mol. Opt. 42, 175503 (2009).

режим пригоден для управления модовым составом

10.

P. Sharapova, O. V. Tikhonova, S. Lemieux,

сжатого света в модах Шмидта в случае его исполь-

R. W. Boyd, and M. V. Chekhova, Phys. Rev. A

зования в качестве подсветки для процесса генера-

97, 053827 (2018).

ции суммарной частоты. Фактически, рассмотрен-

11.

A. Eckstein, B. Brecht, and C. Silberhorn, Opt. Express.

ная схема квантово-оптического затвора позволяет

19, 13770 (2011).

управлять модовым составом яркого сжатого света,

12.

B. Brecht, A. Eckstein, A. Christ, H. Suche, and

варьировать веса входящих мод Шмидта, а также

C. Silberhorn, New J. Phys. 13, 065029 (2011).

контролируемым образом изменять спектральный и

13.

A. Christ, K. Laiho, A. Eckstein, K. N. Cassemiro, and

временной сигнал сжатого света за счет вовлечения

C. Silberhorn, New J. Phys. 13, 033027 (2011).

определенной моды Шмидта в процесс суммарной

14.

A. Eckstein, A. Christ, P. J. Mosley, and C. Silberhorn,

частоты. Замечательно то, что свет не только оста-

Phys. Rev. Lett. 106, 013603 (2011).

ется сжатым, но и генерируемый свет в моде сум-

15.

T. Iskhakov, A. Pérez, K. Spasibko, M. Chekhova, and

марной частоты также является сжатым, причем в

G. Leuchs, Opt. Lett. 37, 1919 (2012).

Письма в ЖЭТФ том 109 вып. 9 - 10

2019