Письма в ЖЭТФ, том 110, вып. 1, с. 34 - 46

Магнитные состояния и переход металл-изолятор

в сильно коррелированных системах

(Миниобзор)

В.Ю.Ирхин¹⁾, П.А.Игошев

Институт физики металлов им. M. Н. Михеева Уральского отделения РАН, 620108 Екатеринбург, Россия

Уральский федеральный университет им. Б. Н. Ельцина, 620002 Екатеринбург, Россия

Поступила в редакцию 17 мая 2019 г.

После переработки 17 мая 2019 г.

Принята к публикации 23 мая 2019 г.

Анализируются различные подходы вспомогательных частиц для рассмотрения электронных корре-

ляций в многоэлектронных моделях, в том числе в приложении к слоистым медно-оксидным системам.

Рассматриваются магнитные фазовые диаграммы основного состояния в рамках t-t^′ модели Хаббар-

да и s-d обменной модели для квадратной и кубических решеток в зависимости от заполнения зоны

и параметра взаимодействия с учетом коллинеарных ферро-, антиферромагнитных и несоразмеримых

(спиральных) магнитных фаз, а также магнитного разделения фаз. Используется обобщенное прибли-

жение Хартри-Фока и подход вспомогательных бозонов, учитывающий корреляции. Последний дает

корректный учет вклада в энергию числа дважды занятых узлов и адекватное описание парамагнитной

фазы. В рамках численных расчетов и аналитического разложения по интегралу переноса между вто-

рыми соседями t^′ и прямой антиферромагнитной щели Δ получен критерий перехода металл-изолятор.

В случае квадратной решетки род перехода изменяется со второго на первый при увеличении t^′ при

малом t^′ ∼ 0.05t, что связано с наличием сингулярности ван Хова вблизи центра зоны. Для простой и

объемноцентрированной кубических решеток переход из изоляторного антиферромагнитного состояния

происходит в фазу антиферромагнитного металла и является переходом второго рода; за ним следует

переход в парамагнитный металл. Эти результаты видоизменяются при учете межузельного гейзенбер-

говского взаимодействия, которое может приводить к смене рода перехода на первый.

DOI: 10.1134/S0370274X19130071

1. Введение. Электронные и магнитные свой-

интерес представляет переход металл-изолятор в

ства сильно коррелированных соединений переход-

системах взаимодействующих электронов. Он может

ных металлов и их связь с легированием, геомет-

быть реализован в рамках двух сценариев [9, 10]:

рией решетки, зонной структурой и параметрами

моттовский переход (для систем с сильными

взаимодействия - перспективный раздел современ-

корреляциями при высоких температурах) и сл-

ной физики твердого тела. В последние десятилетия

этеровский сценарий (реализуется для зонного

активно исследуется двумерный (2D) случай, тесно

антиферромагнетика при низких температурах).

связанный с проблемой высокотемпературной сверх-

Присутствие сингулярностей ван Хова в плотности

проводимости в купратах [1, 2] и пниктидах желе-

электронных состояний вблизи поверхности Ферми

за [3]. Недавно интерес к этому случаю дополнитель-

может существенно изменить физические свойства,

но вырос в связи с открытием крайне узкой кор-

в частности, термодинамику фазового перехода

релированной зоны в двухслойном графене [4] (см.

[6, 8, 11-13].

также [5]).

В последнее время интенсивно изучаются так-

Основное состояние сильно коррелированных

же необычные возбуждения и экзотические состоя-

систем характеризуется конкуренцией ферромаг-

ния в сильно коррелированных твердых телах и дру-

нитного (ФМ) и антиферромагнитного (АФМ)

гих конденсированных средах, например, различные

упорядочения, которая может приводить к воз-

типы спиновых жидкостей, состояния с топологиче-

никновению спирального упорядочения

[6] или

ским и квантовым порядком [2, 14].

магнитного фазового расслоения

[6-8]. Особый

В данном обзоре мы рассмотрим соответствую-

щие проблемы в рамках ряда многоэлектронных мо-

¹⁾e-mail: valentin.irkhin@imp.uran.ru

делей.

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

2. Теоретические модели и представления

f_iσ - операторы рождения нейтральных фермионов

вспомогательных частиц. Для описания свойств

(спинонов), а e^†i, d^†i - заряженных бесспиновых бо-

систем с сильными корреляциями используются мно-

зонов (голонов и дублонов). При больших U мы

гоэлектронные (МЭ) модели, такие, как модель Хаб-

должны сохранить только голоны или дублоны для

барда, модель Эмери, s-d обменная модель и решет-

дырочного или электронного допирования соответ-

ка Андерсона. Они широко применяются, например,

ственно.

для купратов с высоким T_c и редкоземельных соеди-

Более сложное представление, предложенное

нений. Существуют определенные соответствия меж-

Котляром и Рукенштайном [18], использует четыре

ду этими моделями в различных областях парамет-

бозонных оператора e_i, p_iσ, d_i, так что

ров. Предельным случаем (U → ∞) модели Хаббар-

да является однозонная t-J модель, где учитыва-

c^†iσ → f^†iσz^†iσ

(5)

ется обменное взаимодействие между локализован-

ными спинами. Хотя она позволяет рассмотреть ряд

где f_iσ, f^†iσ - фермиевские операторы

экзотических фаз и успешно применяется к физике

купратов (базисных систем для высокотемператур-

z^†iσ = (1 - e^†ie_i - p^†i-σp_i-σ)^-1/2(p^†iσe_i + d^†ip_i-σ) ×

ных сверхпроводников, ВТСП) [2, 15], соответствую-

× (1 - d^†id_i - p^†iσp_iσ)^-1/2.

(6)

щие приближения трудно контролировать из-за от-

сутствия малого параметра: простота модели часто

Имеется также вращательно инвариантная вер-

не обеспечивает удобства теоретического исследова-

сия [19]

ния.

∑

†

Гамильтониан модели Хаббарда [16] с учетом пря-

c^†iσ =

f^†iσ′ z^†iσ′_σ,

zi = eⁱ LiMi^Ri pi +p

L_iM_i R_id_i,

мого обмена имеет вид

σ^′

∑

1∑

(7)

H_H = t_ijc^†iσc_jσ + U

n_i↑n_i↓ +

J_ijS_iS_j, (1)

где множители L, M, R аналогичны (6), скалярные

ijσ

и векторные бозоны p_i0 и p_i вводятся как pi =

где c^†iσ(c_iσ ) - операторы рождения (уничтожения)

=¹² (p_i0σ₀ + p_iσ) и

pi^{-обращенныйповремениопе-}

электронов, t_ij

= -t и t^′ для ближайших и сле-

ратор p_i. Эта версия подходит для магнитоупорядо-

дующих за ними соседей, U

- матричный эле-

ченных фаз, позволяя учесть поправки от спиновых

мент кулоновского взаимодействия на узле, S_i

флуктуаций. В частности, она может простым спо-

∑

=¹

c^†iσσ_σσ′ c_iσ′ .

собом описывать неквазичастичные состояния вслед-

σσ^′

Гамильтониан s - d обменной модели содержит

ствие электрон-магнонного рассеяния, которые ра-

две подсистемы коллективизированных и локали-

нее рассматривались в многоэлектронном представ-

зованных электронов:

лении операторов Хаббарда (ср. [20, 21]). В случае

∑

магнитной фазы и малой концентрации носителей

H_s-d = t_ijc^†iσc_jσ′ - I

S_ic^†iσσ_σσ′ c_iσ′ ,

(2)

тока (дырок) можно приближенно записать

ijσ

iσσ^′

где S_i - оператор локализованного спина.

√ ∑

∑

ciσ =

piσ′σfiσ′ =

√

f_iσ′ [δ_σσ′ p_i0+(p_iσ_σ′_σ)].

В пределе большого U и при заполнении полосы

σ^′

n < 1 (дырочное допирование) модель Хаббарда сво-

(8)

дится к t-J модели

Исходной моделью для описания купратов явля-

∑

1∑

ется трехзонная p-d модель

H_t-J = -

t_ijX_i(0σ)X_j(σ0) +

J_ijS_iS_j.

(3)

ijσ

∑[

H_pd =

εp^†kaσp_kaσ + Δd^†kσd_kσ +

где X_i(Γ, Γ^′) = |Γ_i〉〈Γ^′i| - X-операторы Хаббарда, дей-

kaσ

ствующие в локальном подпространстве [17], эффек-

]

∑

+ V_k(p^†kσd_kσ + d^†kσp_kσ)

+U d^†i↑d_i↑d^†i↓d_i↓,

(9)

тивное J_ij = 4t^2ij /U.

При аналитических и численных расчетах удобно

использовать представления вспомогательных слейв

где ε и Δ - положения p- и d-уровней для O- и

(slave) бозонов и фермионов. Андерсон [15], исполь-

(

)_1/2

Cu-ионов, V_k = 2V_pd

sin² k_x + sin² k_y

- матрич-

зуя идею разделения спиновых и зарядовых степеней

ные элементы p-d гибридизации (ср. [22]). В пределе

свободы электрона, ввел представление (σ = ±1):

больших U мы можем использовать представление

c^†iσ = X_i(σ, 0) + σX_i(2, -σ) → f^†iσe_i + σd^†if_i-σ,

(4)

слейв-бозонов d^†iσ → X_i(σ0) = f^†iσe_i.

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

3^∗

В.Ю.Ирхин, П.А.Игошев

При |V_pd| ≪ ε - Δ (большая щель для перено-

Хартри-Фока (HFA - Hartree-Fock approximation) с

са заряда) гамильтониан (9) снова сводится кано-

точностью до постоянных вкладов принимает вид

ническим преобразованием к t-J модели с teff =

∑

= V^2pd/(ε - Δ). Интересно, что t-J модель, полу-

H^HFAeff =

c^†iσc_jσ′ +1∑(Un-σUeff(Q)m)c†iσciσ,

ченная из однозонной модели Хаббарда, также фор-

ijσσ^′

iσ

мально сводится к аналогичной структуре в пред-

(14)

′

ставлении (6) со вспомогательными, а не физически-

где n

- электронная концентрация, t^σσij

ми частицами p_i. Таким образом, модель Хаббарда и

= exp[iQ(R_i - R_j)σ^x]_σσ′t_ij, U_eff(Q) = U - JQ/2,

∑

модель (9) могут рассматриваться параллельно [22].

J_q

(1/N)_ij J_ij exp(iqR_i). Прямое обменное

взаимодействие J_Q в HFA выступает исключительно

Для описания допированных купратов было

предложено также представление фермиевских

через посредство эффективного параметра Хаббарда

U_eff(Q).

допонов d^†iσ [23, 24],

∑

В представлении вспомогательных бозонов

ci-σ = -√ d†iσ′(1-ni-σ′)[Sδσσ′ -(Siσσ′σ)], (10)

(SBA - slave boson approach) (6) имеем

σ^′

∑

′

H^SBAeff =

t^σσij

f^†iσf_jσ′ z^†iσz_jσ′ + U

d^†id_i,

(15)

где σ = ±1, n_iσ = d^†iσ d_iσ, причем для подсистемы ло-

ijσσ^′

кализованных спинов S = 1/2 могут быть использо-

ваны как фермиевское спинонное представление, так

причем бозонное фоковское подпространство огра-

и бозонное представление Швингера. Учет гибриди-

ничено условием когерентности описаний на языке

зации между допонами и фермиевскими спинонами

фермионов и бозонов.

дает описание в рамках эффективной двухзонной мо-

Эти выражения позволяют построить приближе-

дели [23].

ние среднего поля, учитывающее разделение одно-

Переписывая (10) как

кратно занятых узлов (p_i) и дырок/двоек (e/d). Мы

имеем следующие уравнения порядка m для n и m

ciσ = (d^†i↓f^†i↑ - d^†i↑f^†i↓)fiσ

(11)

∑

и вводя голонный оператор e_i = f_i↑d_i↓ - f_i↓d_i↑, мы

f_ks,

(16)

возвращаемся к представлению Андерсона (4). При

этом, однако, возникает трудность с множителем

√

1∑

(-1)^s+1 Δ_kf_ks

2, которая обсуждается в [21].

√

(17)

Δ2

Слейв-бозонное представление SU(2) теории

+ z^2↑z^2↓e^2-(k)

[2], которое используется при описании спин-

где

Δ_k = Δ - (z^2↑ - z^2↓)e₊(k)/2, f_ks = f(E_s(k)), где

жидкостных состояний, вводит фермиевские спи-

f (E) - функция Ферми,

нонные операторы и два бозевских голонных

оператора:

E_s(k) =

(z^2↑ + z^2↓)e₊(k) + λ +

(

)

√

b^†i1f_i↑ + b^†i2f^†

ci↑ =

i↓

Δ2

+ (-1)^s

+ z^2↑z^2↓e^2-(k),

(18)

(

)

ci↓ =

√

b^†i1f_i↓ - b^†i2f^†

(12)

i↑

e_±(k)

= (t_k ± t_k+Q)/2, причем t_k

= (1/N) ×

∑

× ij^tij^exp(iQ(Ri^-Rj^{)),такчтоe}+(k)∝t′,e-^(k)∝

Соответствие с допонным представлением может

∝ t. Бозонные амплитуды получается при замене бо-

быть установлено заменой голонных операторов b_i,1

зонных полей на числа и определяются уравнениями

спинон-допонной синглетной парой f_i,↑d_i,↓ - f_i,↓d_i,↑,

а операторов b_i,2 - парой f^†i,↑d_i,↑ + f^†i,↓d_i,↓ [23].

2d² + p^2↑ + p^2↓ = n,

(19)

3. Магнитные фазовые диаграммы. Рассмот-

p^2↑ - p^2↓ = m,

(20)

рим магнитную структуру спираль в плоскости

e² + p^2↑ + p^2↓ + d² = 1,

(21)

x-y, определяемую волновым вектором Q, для ко-

торой средняя узельная намагниченность m_i = 2S_i

∑ (ep_↑ + p_↓d)(ep_↓ + p_↑d)

Φ_σ = -U,

(22)

имеет вид

edp_↑p_↓

(e² + p^2¯σ)(p^2σ + d²)

〈m_i〉 = m(x cos(QR_i) + ŷ sin(QR_i)).

(13)

ζ = p_↑p_↓ - ed,

(23)

После локального поворота в спиновом пространстве

ζ²

z^2σ = 1 -

(24)

на угол QR_i гамильтониан Хаббарда в приближении

(e² + p^2¯σ)(p^2σ + d²)

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

∑

Φ_σ =

e₊(k)f_ks +

(

)

∑

(-1)^s

-σe₊(k)Δk + e^2-(k)z^2¯σ

f_ks

√

(25)

Δ2

+ z^2↑z^2↓e^2-(k)

Параметры спектра (18), λ, Δ - множители Лагран-

жа для уравнений, ограничивающих пространство

Фока бозонов, - задаются уравнениями

∑

ep_σ + p_σd

λ=

2ed

(e² + p^2¯σ)(p^2σ + d²)

(

)

ep_σ

dp_σ

Φ_σ,

(26)

p^2σ + d²

e² + p²

J_Qm

∑

σ(ep_σ + p_σd)

Δ+

2p_↑p_↓

(e² + p^2¯σ)(p^2σ + d²)

(

)

ep_σ

p_σd

Φ_σ.

(27)

e² + p^2¯σ

p^2σ + d²

Заметим, что HFA получается дальнейшим упроще-

нием этих уравнений: (22) заменяется на ζ = 0, (26)

и (27) заменяются, соответственно, на λ = Un/2 и

Δ = U_eff(Q)m/2.

Из уравнения (24) видно, что малость параметра

ζ по сравнению с e² + p^2σ, d² + p^2σ означает несуще-

ственность различия между амплитудой двоек (ды-

рок) и однократно занятых состояний. C другой сто-

роны, из определения следует, что параметр ζ не пре-

восходит 1/2 и возможно разложение по его степе-

ням.

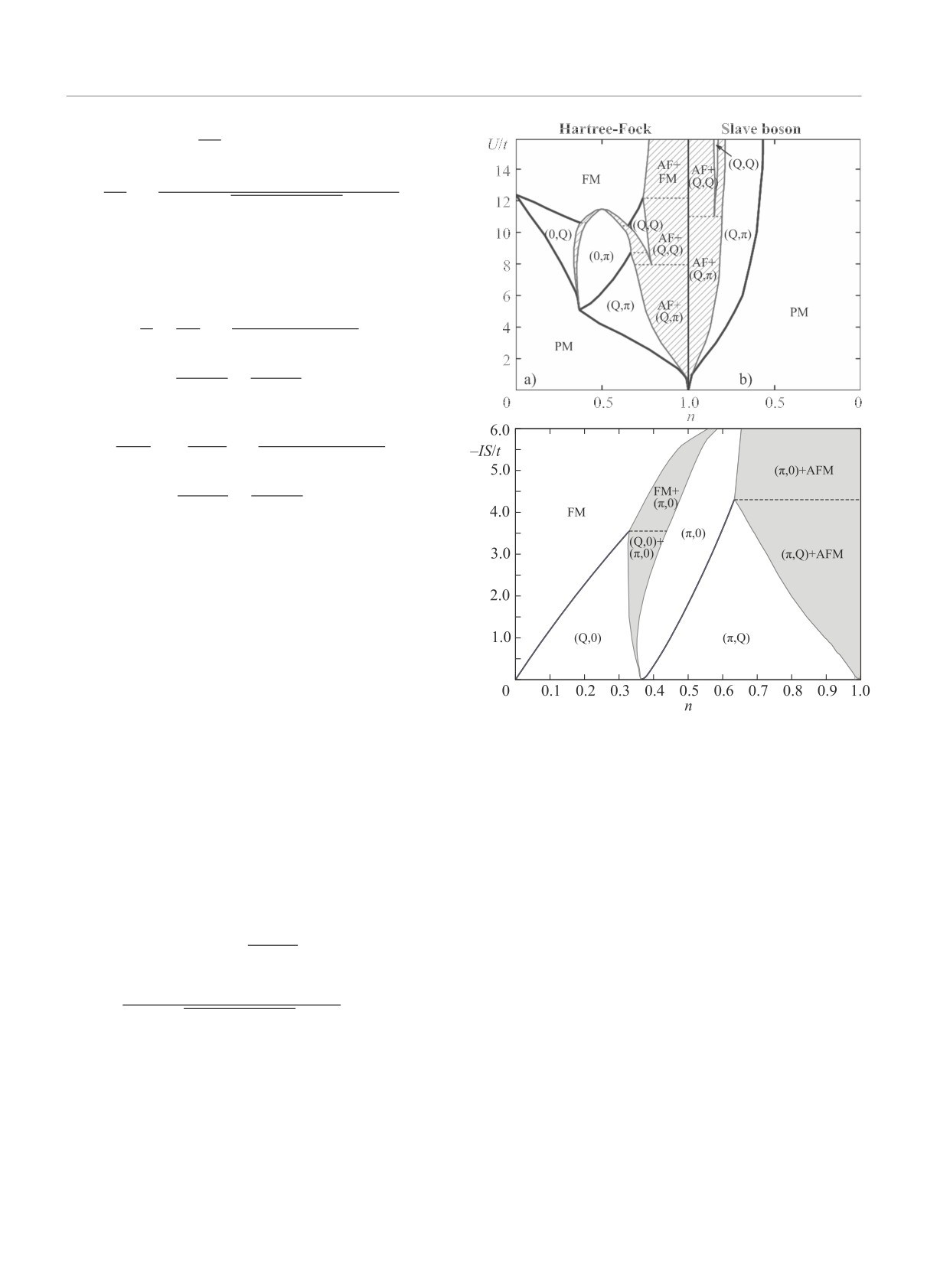
Рис. 1. (Цветной онлайн) Магнитная фазовая диаграмма

основного состояния модели Хаббарда (верхняя панель,

Рассмотрим магнитные фазовые диаграммы для

в рамках a) HFA и b) SBA) в переменных n - U и s - d

квадратной (рис. 1) и простой кубической (рис. 2) ре-

модели (нижняя панель) для квадратной решетки при

шеток в модели Хаббарда в HFA и SBA в версии сред-

n < 1. Спиральные фазы обозначаются в соответствии

него поля, а также в s-d модели в HFA (S_i → S после

с формой их волнового вектора. Заполнение показывает

локального поворота) [8, 13, 25].

области разделения фаз, пунктирными (красными) лини-

Выбор фазы для данных U, n на фазовой диа-

ями обозначены границы между различными фазовыми

грамме определяется из условия минимума свобод-

парами. Жирными (синими) линиями обозначены фазо-

ной энергии

вые переходы второго рода. Сплошные (красные) линии

(

соответствуют границам между однородной фазой и об-

∑

z^2↑ + z^2↓

ластью разделения фаз, QAFM = (π, π)

F =Ud² +

e₊(k) +



(-1)^s(z^2↑z^2↓e^2-(k) - r_z e₊(k)Δk)

удобно перейти от свободной энергии F к термодина-

√

fks,

(28)

Δ2

мическому потенциалу Ω (см. подробное изложение

+ z^2↑z^2↓e^2-(k)

методики [6]).

причем зависимость от Q неявно входит в эту фор-

Из рисунков 1, 2 видно, что подход HFA дает мно-

мулу через e_±(k).

жество магнитных фаз - спиральных, ФМ и АФМ.

При наличии перехода первого рода возникает

Учет корреляций в рамках SBA приводит к замет-

скачок концентрации, что означает формирование

ному подавлению магнитоупорядоченных состояний

фазового расслоения в межфазной области на фа-

по сравнению с HFA: соответствующие интервалы на

зовой диаграмме. Для исследования этого перехода

фазовой диаграмме сильно уменьшаются, а разнооб-

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

В.Ю.Ирхин, П.А.Игошев

ли ПМ фаза не существует; она может быть получена

при учете кондовского спаривания, см. обзор [32]).

Это приводит к невозможности прямого сравнения

свободной энергии разных фаз. Результаты оказыва-

ются близкими лишь при больших U, когда локаль-

ный момент уже сформирован и намагниченность

при данной концентрации носителей мало зависит от

выбора фазы.

В случае бесконечно большого U [12] АФМ по-

рядок формируется как результат квантового пере-

мешивания электронных состояний со спином вверх

и вниз в локальной системе координат. Эффектив-

ные зоны, спектр которых суть собственные значе-

ния (18) эффективного фермиевского гамильтониа-

на

∑

H_f =

[z_σz_σ′ (e₊(k)δ_σσ′ + e_-(k)σ^xσσ′ ) +

σσ^′

+ λδ_σσ′ - Δσ^zσσ′ ] f^†kσfkσ′ ,

(29)

сужены с факторами z^2↑ и z^2↓, соответственно. В то

время как при половинном заполнении и в ПМ фазе

z^2↑ = z^2↓, при малом дырочном допировании (δ = e²)

эти факторы существенно отличаются, z^2↓ ≪ z^2↑. В

этом случае

E₁(k) = λ - P(k) + z^2↑e₊(k),

(30)

E₂(k) = λ + P(k),

(31)

(

)

z^2↓

z^2↑e^2-

(k)

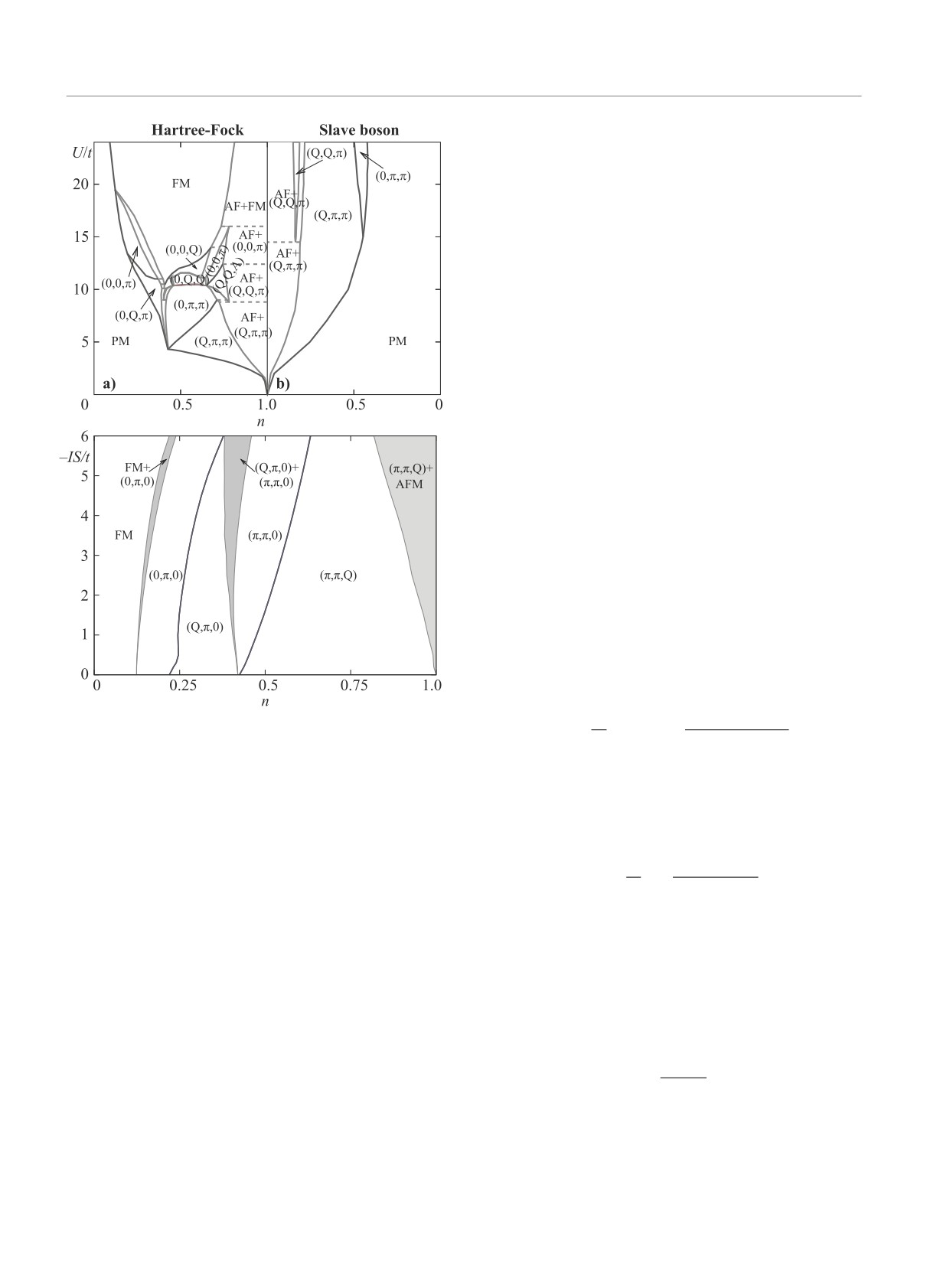
Рис. 2. (Цветной онлайн) Фазовые диаграммы для про-

P (k) = Δ +

e₊(k) +

(32)

Δ - z^2↑e₊(k)/2

стой кубической решетки в рамках модели Хаббарда

и s-d модели. Обозначения линий и фаз аналогичны

так что верхняя подзона оказывается гораздо уже,

рис. 1

чем нижняя. При этом z^2↓ ∼ δ, а поведение z^2↑ зави-

сит от решетки и параметров спектра, определяясь

величиной решеточной суммы

разие спиральных состояний исчезает. Кроме того,

в SBA возникает широкая область парамагнитного

1∑

e^2-(k)

(ПМ) состояния, что является следствием правиль-

C(ǫ) =

(33)

(ǫ - e₊(k))²

ного учета энергии двоек.

Следует подчеркнуть, что только SBA обеспечи-

при ǫ > ǫ = max_k e₊(k) (это справедливо в случае,

вает правильное описание случая большого U при

когда k-точка потолка зоны совпадает с положением

конечной плотности носителей тока δ = |1 - n|, тогда

максимума E₁(k)).

как энергия основного состояния в HFA расходится

Рассмотрим зависимость бозонных амплитуд от

при U → ∞ из-за переоценки энергии кулоновско-

величины обменного интеграла J (J_Q = -ZJ, Z - ко-

го взаимодействия, как и в приближении случайных

ординационное число). При δ → 0 имеем вид p^2↓ ∼ ωδ,

фаз (RPA) [31].

где

В приближении среднего поля по Хартри-Фоку

C_∗

гамильтонианы Хаббарда и s-d модели имеют фор-

ω=

(34)

1-C_∗

мально одинаковый вид, если положить IS = Um/2.

Тем не менее, процедура сравнения энергий различ-

где C_∗ = C(ǫ_∗), а ǫ = ǫ_∗ является решением уравне-

ных фаз и фазовые диаграммы в этих моделях суще-

ния

ственно отличаются (в частности, в рамках s-d моде-

(1 - C(ǫ))²(e - ǫ) = ZJ/2.

(35)

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

В этом случае амплитуды e² и p^2↓ сравнимы. Важное

значение имеет величина C(ǫ). Если C(ǫ) < 1, вели-

чины бозонных амплитуд лишь слабо зависят от J.

Тогда z^2↑ ∼ 1 - C_∗ > 0, величина прямой АФМ ще-

ли Δ = e_∗(1 - C_∗)/2. В этом случае доля носителей

заряда с перевернутым спином при отклонении от

половинного заполнения равна

1-m

1+C_∗

∼

(36)

1-C_∗

причем эта доля не зависит от концентрации носите-

лей.

Совершенно другая ситуация имеет место при

C(ǫ) > 1. Обозначим корень уравнения C(ǫ) = 1

как ǫ_∗0. Тогда имеем кроссовер между зависимостя-

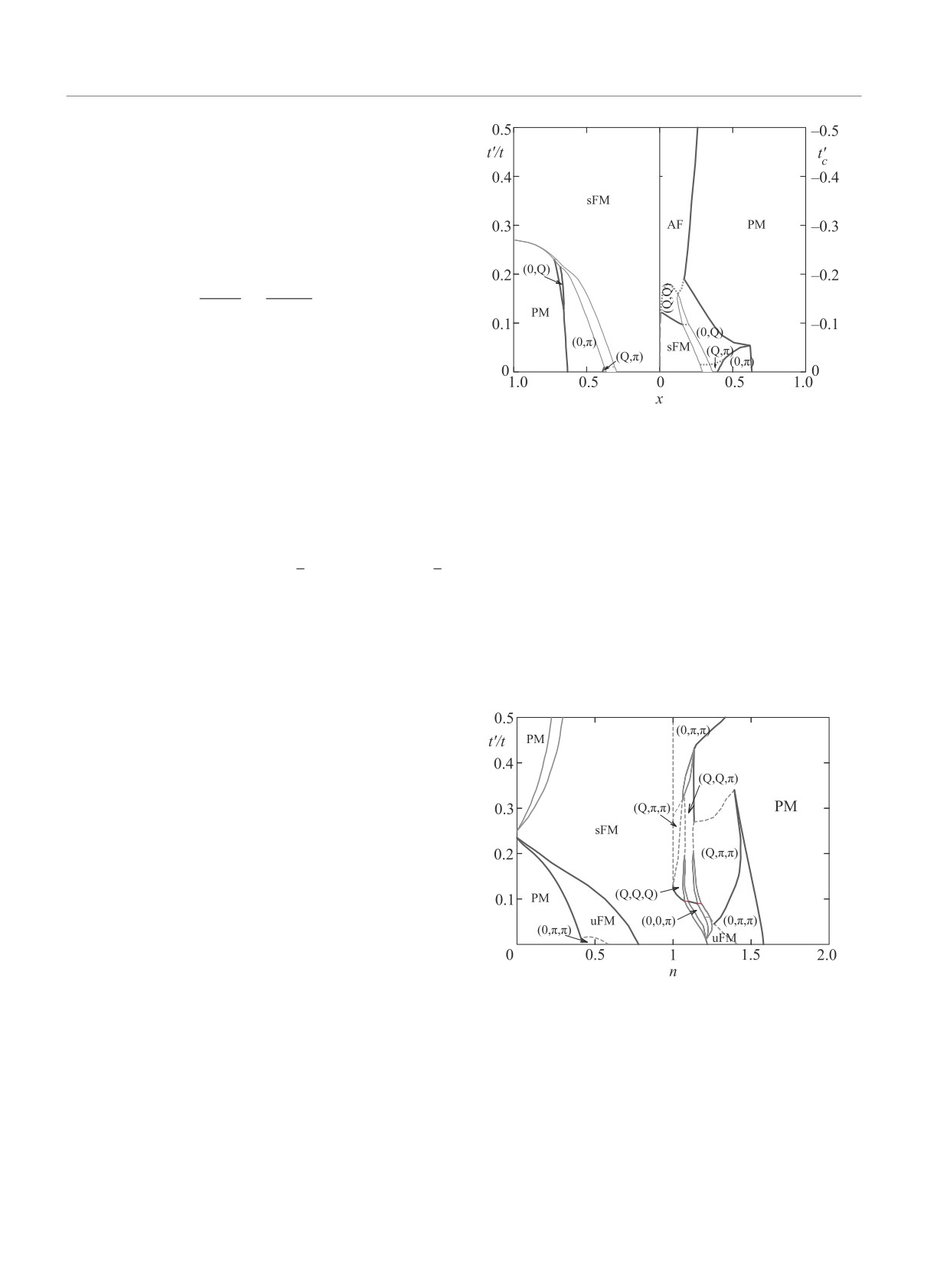
Рис. 3. (Цветной онлайн) Магнитная фазовая диаграм-

ми z^2↑ ∝ |J|^1/3, когда ǫ_∗ - ǫ_∗0 ≫ ǫ_∗0 - ǫ и z^2↑ ∝ |J|^1/2,

ма основного состояния модели Хаббарда с U = ∞ для

когда ǫ_∗ -ǫ_∗0 ≪ ǫ_∗0 -ǫ. Таким образом, в этом случае

квадратной решетки в SBA в переменных n - t^′ [12].

e² ≪ p^2↓. Оба этих случая контрастируют с ситуаци-

При t^′ = t^′c происходит смена знака C - 1 и типа АФМ

ей при половинном заполнении и больших U, когда

состояния. Остальные обозначения аналогичны рис. 1.

e² ≫ p^2↓.

АФМ область между линией n = 1 и ФМ фазой очень

Если J = 0, то аккуратное разложение уравнений

узка и ее граница показана схематически фиолетовым

(19)-(22), (26), (27) дает расходимость ω и имеет ме-

штрихом

√

сто другая асимптотика p^2↓ ∝

δ, (1 - m)/δ ∝ 1/

δ.

Описанная среднеполевая картина может изме-

В то время как для квадратной решетки ферро-

ниться при учете флуктуаций. В частности, учет вза-

магнетизм всегда насыщен благодаря влиянию лога-

имодействия со спиновыми волнами для квадратной

рифмической особенности ван Хова, магнитная фа-

решетки дает широкий некогерентный фон и узкий

зовая диаграмма ПК решетки (рис.4) содержит об-

квазичастичный пик с вычетом порядка J/t [26].

ласть ненасыщенного ферромагнетизма.

Диаграмма для квадратной решетки при беско-

нечном U содержит области ферро- и антиферромаг-

нитного упорядочения, спиральных состояний и ПМ

фазы, см. рис.3. Для t^′ = 0 картина симметрична по

отношению к линии половинного заполнения (n = 1)

в силу электронно-дырочной симметрии. АФМ состо-

яние при n = 1 сменяется насыщенным ферромагне-

тиком при малом допировании в согласии с теоре-

мой Нагаока. При умеренном допировании δ ≲ 0.3

ФМ фаза переходит в спиральную (Q, π) структуру

через фазовый переход первого рода с фазовым рас-

слоением. Эта фаза непрерывно трансформируется

в структуру (0, π), которая соответствует слоисто-

му антиферромагнетику. При большом допировании

δ ∼ 0.6 магнитный порядок подавляется и происхо-

дит фазовый переход второго рода в ПМ фазу.

Рис. 4. (Цветной онлайн) Фазовая диаграмма для ПК

Конечные t^′ нарушают электронно-дырочную

решетки [12], обозначения линий такие же, как на

симметрию и диаграмма становится существенно

рис.3. uFM обозначает область ненасыщенного ФМ со-

асимметричной. В дырочно-допированной половине

стояния, QAFM = (π, π, π)

(n < 1) диаграммы ФМ фаза постепенно вытес-

няет все остальные фазы при увеличении t^′/t. В

В пределе бесконечного U при явном введении в

электронно-допированной половине (n > 1) обла-

гамильтониан прямого антиферромагнитного обме-

сти спиральных магнитных фаз сужаются и при

на J = 0.3t (что соответствует купратным сверхпро-

t^′ ∼ 0.17t заменяются АФМ состоянием.

водникам) стабилизируется АФМ состояние, кото-

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

В.Ю.Ирхин, П.А.Игошев

рое остается основным при малом допировании для

t^′ > 0. При дальнейшем допировании происходит фа-

зовый переход первого рода в ФМ или спиральное со-

стояние, сопровождающийся широкой областью фа-

зового расслоения, которая отсутствовала при J = 0.

ФМ состояние оказывается сильно подавленным и

частично замещается спиральными фазами. В отли-

чие от обычной модели Хаббарда, при t^′ = 0 насы-

щенного ферромагнетизма не обнаруживается.

Сравнение с результатами для больших, но ко-

нечных значений U показывает, что в последнем

случае появляется достаточно широкая область фа-

зового расслоения вблизи половинного заполнения,

см. рис. 5 [12]. Ферромагнитный порядок при n > 1

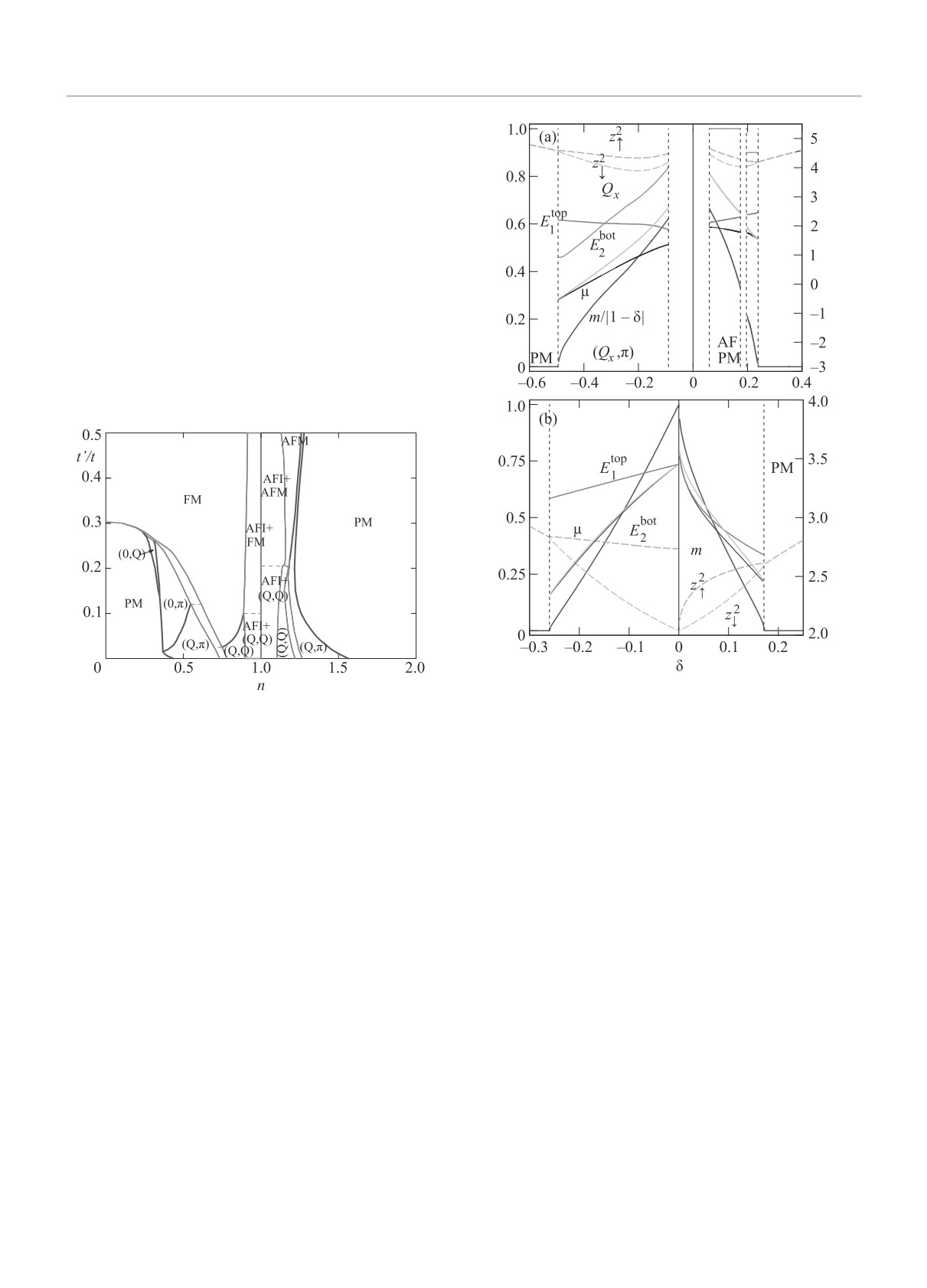
Рис. 6. (Цветной онлайн) Верхняя панель: концентра-

Рис. 5. (Цветной онлайн) Фазовая диаграмма для квад-

ционная зависимость для Qx (зеленая), µ (черная), от-

ратной решетки, аналогичная рис. 3, но при U = 50t.

носительная намагниченность r = m/(1-δ) (синяя), z^2↑

AFI - состояние АФМ изолятора при n = 1

(штрихованная фиолетовая), z^2↓ (штрихованная оран-

жевая линия) - левая ось. E^top1 (красная), E^bot2 (голу-

бая линия) - правая ось. U = 6t, t^′ = -0.2t. Нижняя

и малых t^′/t, существующий в случае U = ∞, пол-

панель: то же для U = ∞. (a) - t^′ = 0.5t, (b) - t^′ = 0.2t.

ностью уничтожается при большом, но конечном U,

Фазы отмечены в нижней части рисунков. Вертикаль-

заменяясь длинноволновым спиральным порядком с

ные штриховые линии отмечают место магнитного фа-

волновым вектором вида (Q_x, Q_x).

зового перехода, разрыв линии означает фазовое рас-

На рисунке 6 [12] представлено сравнение зависи-

слоение. Отрицательное (положительное) δ означает

мости магнитных состояний от числа носителей при

дырочное (электронное) легирование

U = 6t,t^′ = -0.2t и U = ∞ (t^′ = 0.2t и t^′ = 0.5t).

При конечных U формируется достаточно широкая

область фазового расслоения в окрестности половин-

переход с изменением магнитных свойств, определя-

ного заполнения, причем величины z^2σ лишь немно-

емый величиной решеточной суммы C_∗.

го отличаются от единицы и имеют минимум вблизи

Наши результаты для квадратной решетки да-

половинного заполнения. Вблизи половинного запол-

ют широкую область фазового расслоения в окрест-

нения АФМ зоны начинают разделяться щелью. При

ности половинного заполнения при конечных U,

U = ∞ z^2↓ стремится к нулю линейно, совпадая с чис-

что согласуется с экспериментальными данными для

лом носителей тока, а z^2↑ стремится к нулю в случае

сверхпроводящих купратов и вычислениями в рам-

t′ = 0.2t, но остается конечным при t′ = 0.5t. В слу-

ках обобщенного приближения случайных фаз (GW

чае t^′ = 0.2t возникает щель между АФМ подзонами

приближение), см. обзор [11]. Кроме того, экспери-

при приближении к половинному заполнению. Эта

ментальные результаты для квазичастичного вычета

щель отсутствует при t^′ = 0.5t. Это иллюстрирует

(рис. 33 в работе [11]) демонстрируют заметную пе-

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

ренормировку и концентрационную зависимость при

седей, когда tk+Q = -tk, АФМ щель в электрон-

промежуточных значениях U, что качественно согла-

ном спектре, а, следовательно, изоляторное состоя-

суется с нашими расчетами.

ние возникает при сколь угодно малых значениях U.

Однако при наличии переноса между вторыми со-

седями с характерной энергией D^′ неустойчивость

парамагнитного металлического состояния возника-

ет при конечном значении U. В ведущем логарифми-

ческом приближении имеем для критического значе-

ния перехода металл-изолятор (ПМИ, MIT)





ρ(0) ln(D/D^′),

ρ(E) ∼ ρ(0),

1/U_MIT =

(a/2) ln²(D/D^′), ρ(E) ∼ a ln(D/|E|),



(a^′/3) ln³(D/D^′), ρ(E) ∼ a^′ ln²(D/|E|)

(37)

соответственно, для трех решеток: простой кубиче-

ской (ПК), квадратной и объемноцентрированной

(ОЦК). Здесь D - полуширина зоны, ρ(E) - затра-

вочная плотность состояний вблизи уровня Ферми

Рис. 7. (Цветной онлайн) Магнитная фазовая диаграм-

для электронного спектра в приближении ближай-

ма основного состояния модели Хаббарда для ГЦК-

ших соседей, a, a^′ - положительные коэффициенты

решетки с t^′ = 0 в рамках SBA

при сингулярных вкладах в ρ(E). Таким образом,

сингулярности ван Хова приводят к существенному

В работе [29] в рамках SBA были построены маг-

изменению зависимости U_MIT от t^′. В этом разделе

нитные фазовые диаграммы модели Хаббарда для

удобно ввести безразмерный параметр τ = t^′/t.

ГЦК решетки при различных значениях интеграла

электронного переноса для ближайших и следующих

Конкуренция изоляторного АФМ состояния с па-

рамагнитным дает фазовую границу ПМИ первого

соседей (рис.7). Сравнение с аналогичными диаграм-

мами в HFA демонстрирует сильное подавление маг-

рода [27]. Однако учет переноса между вторыми со-

седями приводит к появлению фазы АФМ метал-

нетизма электронными корреляциями. Факторами,

препятствующими подавлению, являются близость

ла, которая может быть более энергетически выгод-

системы к половинному заполнению зоны либо к кон-

ной, чем ПМ металл. С другой стороны, наличие

центрациям, соответствующим особенностям ван Хо-

сингулярностей ван Хова внутри зоны может приве-

ва.

сти к неаналитической зависимости энергии системы

В то время как АФМ структуры I и II типов яв-

в парамагнитном (антиферромагнитном) состоянии

ляются частными случаями спирального магнитно-

от D^′ и величины АФМ щели, соответственно. Как

показывают численные расчеты для квадратной ре-

го упорядочения, АФМ порядок III типа (удвоенная

элементарная ячейка) не может быть представлен в

шетки [28,35-38], вследствие этого для нее, действи-

тельно, возможен переход первого рода.

виде спирали и требует особого подхода, который

был также разработан в [29]. Сравнение с неколлине-

Изоляторное АФМ состояние может быть

арным спиральным порядком, имеющим аналогич-

неустойчиво по отношению к переходу как в АФМ

ный волновой вектор, показало, что коллинеарный

металлическое, так и в ПМ состояние. Для первой

АФМ порядок III типа более выгоден при половин-

неустойчивости можно получить уравнение фазовой

ном заполнении зоны и вблизи него; это согласу-

границы в переменных τ-Δ путем исследования

ется с экспериментальными нейтронографическими

спектра [34].

результатами для MnS₂ [33]. Таким образом, учет

При половинном заполнении (n

= 1) уравне-

зонных эффектов приводит к снятию вырождения

ния метода вспомогательных бозонов (19)-(21), (25)-

различных магнитных структур, характерного для

(27) существенно упрощаются в силу дополнитель-

моделей локализованного магнетизма типа Гейзен-

ной симметрии между дырками и двойками: e = d.

берга и обусловленного геометрической фрустраци-

В предположении, что нижняя и верхняя АФМ под-

ей, присущей ГЦК решетке.

зоны разделены щелью, имеем уравнения, опреде-

4. Переход металл-изолятор. При половин-

ляющие m, Δ_∗ = Δ/z^2AFM (сужение спектра уже не

ном заполнении зоны в приближении ближайших со-

зависит от направления локальной проекции спина:

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

В.Ю.Ирхин, П.А.Игошев

z^2AFM ≡ z^2↑ = z^2↓ = 1 - 4ζ^2AFM/(1 - m²)) и ζ = ζ_AFM

и для ОЦК решетки

(см. определение (23)):

{

√

4τ,

τ < 2/

Δ^bccMIT(τ) =

√

(46)

m = Δ_∗Φ₁(Δ_∗),

(38)

6τ - 8τ^-1/3, τ > 2/

1-m

1+ζ_AFM

Δ_∗ -

(39)

Параметры ПМ фазы описываются уравнениями

1 - m² - 4ζ^2AFM

(1 + 2ζ_AFM)²

16ζ_AFM(1 + 2ζ_AFM)²

z^2PM = 1 - 4ζ^2PM,

(47)

Φ₂(Δ_∗) = U,

(40)

(1 - m²)((1 + 2ζ_AFM)² - m²)

U = -16ζ_PE(τ),

(48)

где

J = ZJ/8

2∑

E (τ) =

t_k(τ)f(z^2PMt_k(τ)).

(49)

∑

Φ₁(Δ) =

√

(41)

В отличие от свободной энергии АФМ изоляторной

Δ² + e^2-(k)

фазы свободная энергия ПМ фазы существенно за-

∑

e^2-(k)

висит от τ:

Φ₂(Δ) =

√

(42)

Δ² + e^2-(k)

F_PM =

(1 - ζ_PM) + E(τ).

(50)

(

)

U 1-m

Для определения рода ПМИ удобно рассмотреть

F_AFM =

Jm² +z²

AFM

- Φ₂(Δ_∗)

(43)

4 1 + 2ζ

разницу энергий фаз АФМ изолятора и ПМ метал-

ла ΔF_MIT на границе АФМ металл - АФМ изолятор

Это выражение, а также уравнения (38), (39) перехо-

(см. уравнения (44)-(46)). Величина Δ_∗ = Δ_MIT(τ),

дят в соответствующие выражения в HFA, если за-

а значит и решеточные суммы Φ₂(Δ_∗) и E(τ), будут

менить уравнение (40), определяющее ζ, на ζ = 0.

одни и те же и HFA, и в SBA. Если окажется, что сво-

Выражение (43) содержит вклады как кулонов-

бодная энергия F_PM ниже (выше), чем (43), то ПМИ

ского взаимодействия, так и межузельного обмен-

первого (второго) рода. Введем

ного взаимодействия. При этом, в отличие от HFA,

эти вклады входят различным образом: кулоновский

δΦ₂(Δ_∗) = Φ₂(Δ_∗) - Φ₂(0),

(51)

вклад в F_AFM содержит дополнительный “корреля-

δE(τ) = E(τ) + Φ₂(0).

(52)

ционный” множитель, зависящий от ζ, - таким об-

разом, выделяется вклад двоек; обменный член при

Тогда

этом лишь квадратичен по намагниченности, т.е. не

U (ζ_PM - ζ_AFM)

содержит корреляционных поправок.

ΔF_MIT =

Из уравнений (38), (39), (43) видно, что для щеле-

Um²ζ_AFM(1 + 4ζ_AFM)

вого АФМ состояния e₊(k) фактически не участвует

+ ΔFHFAMIT ,

(53)

4(1 + 2ζ_AFM)²

в определении параметров состояния. Следователь-

но, зависимость от t^′ полностью исчезает.

где явно выделен вклад в разность свободной энер-

Изоляторная АФМ фаза конкурирует с метал-

гии АФМ и ПМ фаз на границе ПМИ в HFA c J = 0

лическими фазами - парамагнитной и антиферро-

магнитной. Поскольку при половинном заполнении

Um²

ΔF^HFAMIT =

Jm² -

- δE(τ) - δΦ₂(Δ_∗).

(54)

корреляционное сужение спектра происходит равно-

мерно - в z^2AFM раз, щель, соответствующая грани-

После разложения по Δ_∗ и ζ (53) принимает вид

це перехода в состояние АФМ металла, имеет вид

Δ = z^2AFMΔ_MIT(τ) (τ = t^′/t), причем для квадратной

Uζ₀(3 - 4ζ₀)m²

(

)

ΔF_MIT =

1 - 48ζ²⁰

ΔF^HFAMIT, (55)

решетки

{

√

где

2τ,

τ < 1/

Φ^-11(Δ_∗) -

Δ^sqMIT(τ) =

√

(44)

ζ₀ =

(56)

4τ - τ^-1, τ > 1/

U_BR

U_BR = 8Φ₂(0) - критическое значение перехода ПМИ

для ПК решетки

в парафазе [30]. Критическое значение U = U_MIT на

{

√

границе ПМИ имеет вид

2τ,

τ <

3/4,

Δ^scMIT(τ) =

√

(45)

8τ - 9τ^-1/8, τ >

3/4;

U_MIT = 2(Φ^-11(Δ_∗) -

J )(1 + 3ζ₀).

(57)

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

Из выражения (55) видно, что корреляционная по-

Для исследования асимптотики зависимости ре-

правка, пропорциональная ζ₀, приводит к большему

шеточных сумм от Δ_∗ они могут быть выражены как

увеличению энергии АФМ изоляторной фазы, чем

Φ₁(Δ) = 2G(Δ) + ΔG^′(Δ),

(59)

ПМ фазы. Это означает, что корреляционные вкла-

ды расширяют область перехода первого рода либо

δΦ₂(Δ) = -Δ²(G(Δ) + ΔG^′(Δ)),

(60)

могут превратить переход второго рода в переход

через одну вспомогательную сумму

первого рода.

Перепишем разложение (55), используя уравне-

1∑

G(Δ) =

√

(61)

ния (38) и (57), и оставляя члены ведущего порядка

Δ² + e^2-(k) + |e_-(k)|

по ζ и Δ:

В общем случае логарифмические поправки проис-

ΔF_MIT = δF - δE(τ) -

JΦ²¹(Δ_∗)Δ^2∗ +

ходят от электронных состояний с малыми |e_-(k)|

3Δ^2∗

(1 -

JΦ₁(Δ_∗))²,

(58)

(

)

2U_BR

G(Δ) = D^-1 a₀ + a₁ ln

+ a2 ln²

(62)

где δF = Δ^3∗G^′(Δ_∗)/2 - ведущий вклад в изменение

энергии АФМ изоляторной фазы без учета корреля-

причем максимальная степень логарифма на еди-

ционных и обменных поправок, G определено ниже

ницу выше, чем степень логарифмического вклада

в (61). Третий член в (58) - ведущий вклад в изме-

(ρ(ǫ, τ) ∼ ln^l(D/|ǫ|)) в плотность состояний. Разло-

нение энергии от обменного взаимодействия, четвер-

жение (62) позволяет получить разложение для (59),

тый член - корреляционная поправка.

(60), а коэффициенты разложения (62) получаются

Учет прямого обменного взаимодействия в рам-

из анализа логарифмических вкладов в плотность

ках приближения Хартри-Фока приведет лишь к за-

состояний в окрестности центра зоны.

мене U на U_eff(Q), см. (14), что не может изменить

Для квадратной решетки (D_sq

4t,

род перехода. Корректный учет обменного взаимо-

U^sqBR

= 13.0t) плотность состояний в окрестно-

действия должен по-разному учитывать вклады од-

сти це(тра зоны со)ержит логарифмический вклад:

3+π²

нократно занятых состояний (p_σ) и двоек (d) и может

a^sq0 =

+ 2ln2

/π² + δg_sq, a^sq1 = (1 + 4 ln2)/π²,

изменить род перехода, см. рис. 8.

asq2 = π-2, где δgsq = 0.02805. Сингулярность ван

Хова приводит к дополнительному сингулярному

(логарифмическому) вкладу в энергию АФМ и ПМ

состояний и вкладу порядка ln²(t/Δ) в обратное

критическое значение U. Зависимость U^sqMIT и δF_sq

от τ на границе ПМИ и влияние обменных и кор-

реляционных поправок можно получить из формул

(56), (57), и (62) с учетом результата

Φ^sq1(Δ_MIT(τ)) =

ln²

(63)

2π²t

δF_sq(Δ_MIT(τ)) = -B_sq(τ)τ²t,

(64)

(

)

где B_sq(τ) =

1 + 2ln ^16τ

/(2π²). Нелинейное соотно-

шение между Δ и τ на границе перехода АФМ изо-

лятор - ПМ металл, обусловленное сингулярностью,

приводит к изменению рода перехода со второго на

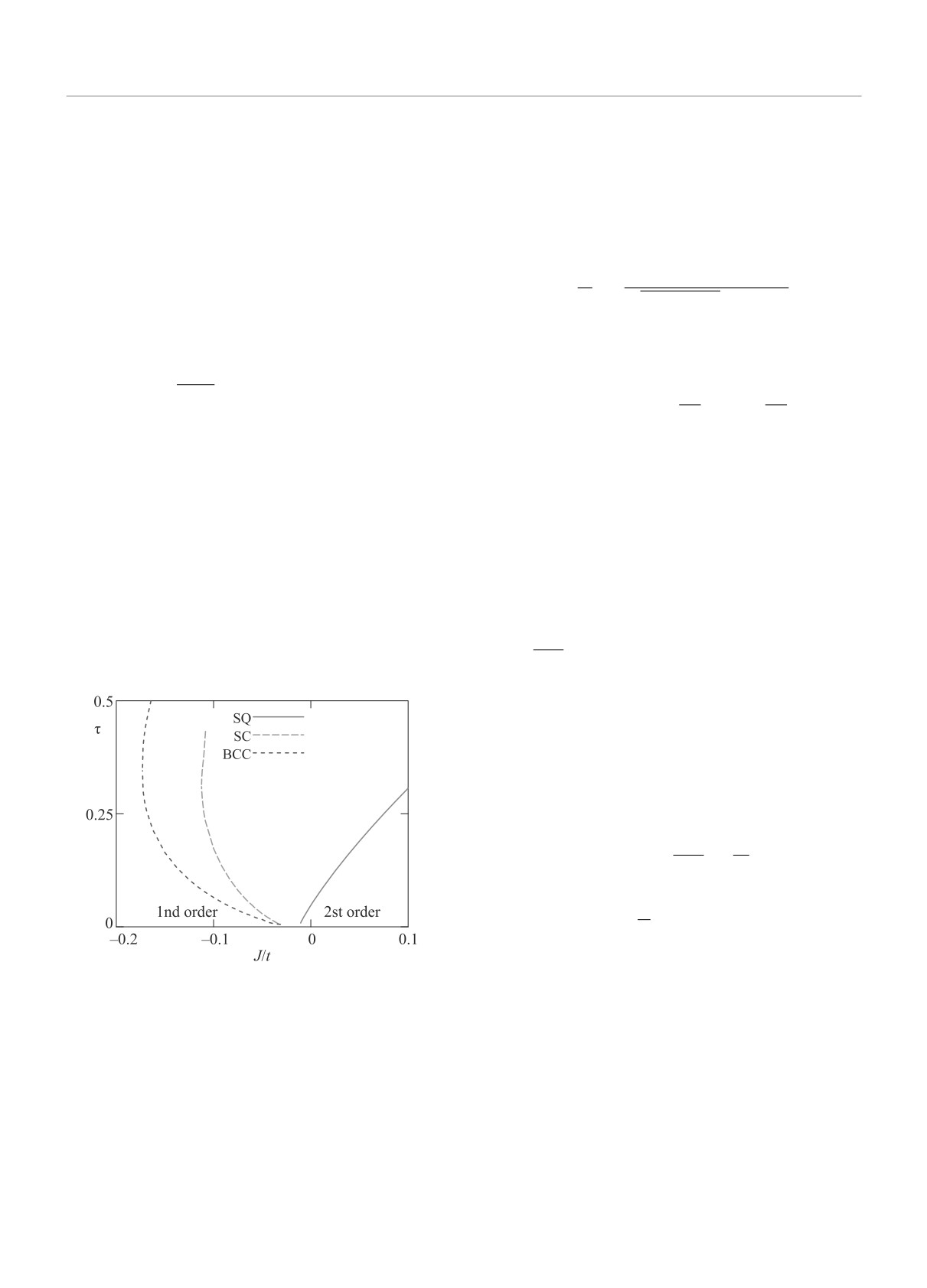
Рис. 8. (Цветной онлайн) Фазовая диаграмма, опреде-

первый при конечном τ ≃ 0.05 (в рамках HFA 0.08),

ляющая род ПМИ в переменных J - τ для квадратной

(SQ), ПК (SC) и ОЦК (BCC) решеток, J - обменный

численно этот результат был получен ранее [28, 36].

интеграл между ближайшими соседями. Слева от кри-

На границе металл-изолятор в АФМ состоянии энер-

вых имеет место переход второго рода, справа - перво-

гия АФМ изоляторной фазы очень близка к энергии

го рода

ПМ металлической фазы. Результаты по изменению

рода перехода с изменением t^′ (в частности, возник-

Роль обменной поправки зависит от знака J:

новение перехода первого рода при τ ≲ 0.2) подтвер-

J > 0 расширяет область перехода второго рода, а

ждается расчетами по методу Монте-Карло [35]. За-

ФМ обмен J < 0 - область перехода первого рода.

висимость энергии ПМ фазы от τ содержит неанали-

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

В.Ю.Ирхин, П.А.Игошев

тические вклады, происходящие от имеющейся при

любом τ сингулярности внутри зоны.

δE_sq(τ) = -A_sq(ω_F)τ²t,

(65)

где

32/π

16/π²

A_sq(ω) =

A_sq -

(66)

1 + ln(16/ω)

(1 + ln(16/ω))²

A_sq = 1.08, ω_F = E_F/t + 4τ - энергия Ферми, отсчи-

танная от положения сингулярности ван Хова.

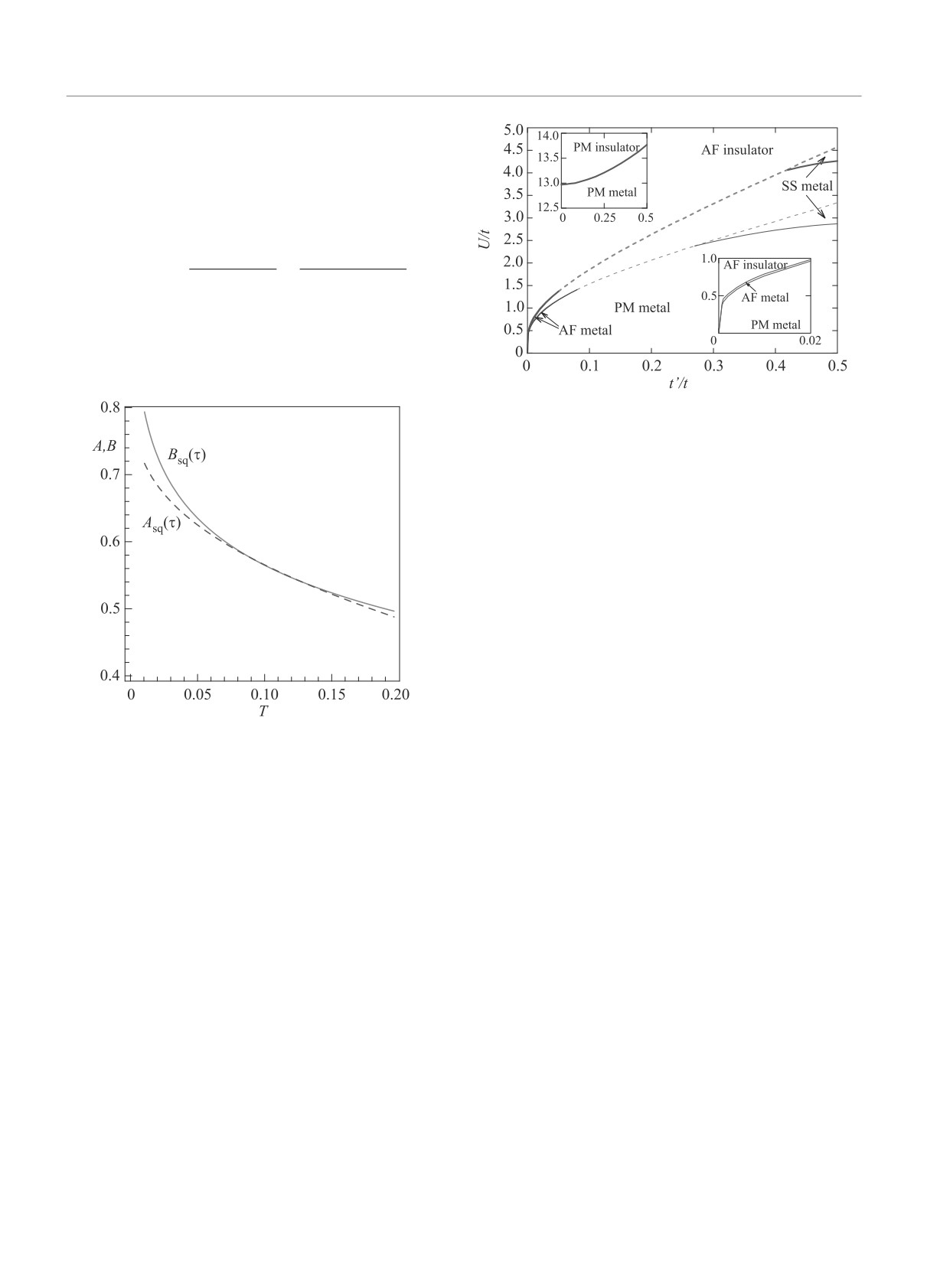
На рисунке 9 видно, что B_sq(τ)

> A_sq(τ), за

исключением малого интервала. При малых τ изо-

Рис. 10. (Цветной онлайн) Магнитная фазовая диа-

грамма основного состояния модели Хаббарда при по-

ловинном заполнении в плоскости τ -U/t для квадрат-

ной решетки. Толстые (тонкие) линии представляют

результат SBA (HFA). Сплошные (пунктирные) ли-

нии - линии перехода второго (первого) рода. Нижняя

вставка показывает фазовую диаграмму, полученную

в SBA, в частности, при малых t^′. Верхняя вставка -

результат сценария Бринкмана-Райса [30] (переход в

ПМ фазе)

= 0.143t^-1 - плотность состояний в центре зоны при

τ = 0, δg_sc = -0.346.

Φ^sc1(Δ_MIT(τ)) = (3t)^-1(D_scρ_sc(0)ln(6/τ) + δg_sc), (67)

δF_sc(Δ_MIT(τ)) = -B_scτ²t,

(68)

Рис. 9. (Цветной онлайн) Зависимость коэффициентов

где B_sc = D_scρ_sc(0)/3 = 0.285. Мы находим δE_sc(τ) =

разложения Asq(τ ), Bsq(τ ) на границе перехода металл-

= -A_scτ²t, A_sc = 0.145, так что δF_sc(τ)-δE_sc(τ) < 0.

изолятор в АФМ фазе для квадратной решетки

Таким образом, в рамках HFA мы имеем устойчивую

кривую перехода второго рода при любых τ ≲ 0.5 и

ляторная фаза выигрывает у парамагнитной из-за

область АФМ металла между областями АФМ изо-

логарифмического вклада в энергию, однако при уве-

лятора и ПМ металла на фазовой диаграмме доста-

личении Δ энергии фаз пересекаются в двух точ-

точно широка (см. рис.11a, 12).

ках τ_1,2. Пересечение при τ = τ₂ является артефак-

Как видно из рис.10, 12, моттовский сценарий

том разложения и отсутствует при численном реше-

ПМИ в ПМ фазе [30] не реализуется - такой пере-

нии уравнений: при τ > τ₁ ПМИ становится пере-

ход возможен лишь при больших U.

ходом первого рода (рис. 10). Близость коэффици-

Для ОЦК решетки, несмотря на наличие сингу-

ентов A_sq(τ) и B_sq(τ) является указанием на суще-

лярностей ван Хова, ситуация оказывается похожей:

ствование лишь узкой области АФМ металла между

всегда реализуется переход второго рода. Граница

областями АФМ изолятора и ПМ металла на фазо-

устойчивости изоляторной АФМ фазы по отноше-

вой диаграмме. Таким образом, для J = 0 мы имеем

нию к ПМ фазе в переменных τ-Δ, хотя и нелинейна

очень тонкую конкуренцию АФМ и ПМ состояний

(как и для квадратной решетки), не пересекается с

при малых значениях τ. Однако этот баланс нару-

линией перехода в АФМ металл [34].

шается даже при малых |J| - АФМ состояние вы-

Учет прямого обмена в рамках SBA существенно

игрывает для АФМ обмена, а ПМ состояние - для

меняет фазовую диаграмму (рис. 8).

ферромагнитного, см. рис.8.

Наиболее важным результатом для ГЦК решетки

Для ПК решетки (D_sc = 6t, U^scBR = 16.0t) a^sc0 =

является то, что здесь ПМИ первого рода в широкой

= D_scρ_sc(0)/2 + δg_sc, asc1 = Dscρsc(0), где ρsc(0) =

области параметров, - соответствующий магнитный

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

Магнитные состояния и переход металл-изолятор в сильно коррелированных системах...

Рис. 12. (Цветной онлайн) Фазовая диаграмма, анало-

гичная рис. 10, для простой кубической решетки; метки

фаз относятся только к результатам SBA

Рис. 11. (Цветной онлайн) (a) - Фазовая диаграмма ос-

новного состояния модели Хаббарда для ПК решетки

Рис. 13. (Цветной онлайн) Фазовая диаграмма для

в переменных τ - U. Пунктирная кривая показывает

ГЦК решетки при половинном заполнении в перемен-

неустойчивость АФМ изоляторной фазы относитель-

ных U/t и t^′/t в SBA [29]. Заштрихованная (пустая)

но АФМ металлической, сплошная кривая - относи-

область обозначает состояние изолятора (металла). На

тельно ПМ металлической фазы (последняя неустой-

вставке показан результат сценария Бринкмана-Райса

чивость не реализуется). На вставке показана фазовая

U = UBR

диаграмма в переменных τ - Δ. (b) - Граница пере-

хода АФМ металл-АФМ изолятор для различных ре-

шеток, см. формулу (57) для UMIT(τ ) в рамках HFA

свойств системы при больших U/t и переоценивает

(J = ζ0 = 0)

роль магнитных фаз. В то же время подход вспо-

могательных бозонов (SBA) дает успешное описание

парамагнитного состояния и предоставляет подроб-

переход демонстрирует прерывистое изменение маг-

ную информацию, включающую z-факторы, кото-

нитного состояния (см. рис. 13).

рые дают существенную перенормировку электрон-

5. Заключение. В данном обзоре мы предста-

ного спектра. Их концентрационная зависимость

вили картину магнитных фазовых переходов в ос-

оказывается весьма нетривиальной, особенно в пре-

новном состоянии сильно коррелированной модели

деле больших U и при включении межузельных об-

Хаббарда и s-d модели. Приближение Хартри-Фока

менных взаимодействий. Учет корреляционных эф-

не позволяет получить разумных результатов для

фектов в рамках SBA может существенно изме-

Письма в ЖЭТФ том 110 вып. 1 - 2

2019

В.Ю.Ирхин, П.А.Игошев

нить картину перехода металл-изолятор, благопри-

13.

P. A. Igoshev, M. A. Timirgazin, A. K. Arzhnikov,

ятствуя переходу первого рода.

T. V. Antipin, and V. Yu. Irkhin, J. Magn. Magn. Mater.

Таким образом, SBA позволяет учесть корре-

440, 66 (2017).

ляционные эффекты и является более простым,

14.

В. Ю. Ирхин, Ю. Н. Скрябин, ФММ 120, 563 (2019).

чем метод расцепления уравнений движения для

15.

P. W. Anderson, Int. J. Mod. Phys. B 4, 181 (1990).

Х-операторов Хаббарда [20, 39-41]: нулевое прибли-

16.

J. Hubbard, Proc. Roy. Soc. A 276, 238 (1963).

жение среднего поля здесь оказывается существенно

17.

V. Yu. Irkhin and Yu.P. Irkhin, Phys. Stat. Sol. (b) 183,

лучше, чем приближение Хаббард-I [16]. В то же вре-

9 (1994).

мя последовательный учет флуктуаций (в частности,

18.

G. Kotliar and A. E. Ruckenstein, Phys. Rev. Lett. 57,

учет некогерентных состояний) требует дальнейшей

1362 (1986).

теоретической разработки.

19.

R. Fresard and P. Wölfle, Int. J. Mod. Phys. B 6, 685

Дальнейшие исследования могут также касать-

(1992).

ся фрустрированных систем (например, треугольной

20.

V. Yu. Irkhin and M.I. Katsnelson, J. Phys.: Condens.

решетки) и описания возникающего состояния спи-

Matter. 2, 7151 (1990).

новой жидкости. При этом, по-видимому, полезными

21.

V. Yu. Irkhin, Phys. Lett. A 383, 1506 (2019).

окажутся все упомянутые представления вспомога-

22.

C. Castellani, G. Kotliar, R. Raimondi, M. Grilli,

тельных частиц.

Z. Wang, and M. Rozenberg, Phys. Rev. Lett. 69, 2009

(1992).

Работа выполнена в рамках государственного за-

23.

T. C. Ribeiro and X.-G. Wen, Phys. Rev. B 74, 155113

дания ФАНО России (тема “Квант” # AAAA-A18-

(2006).

118020190095-4) и при поддержке Программы 211

24.

В. Ю. Ирхин, Ю. Н. Скрябин, Письма ЖЭТФ 106,

Правительства Российской Федерации, соглашение

161 (2017).

02.A03.21.0006.

25.

П. А. Игошев, М. А. Тимиргазин, А. К. Аржников,

Авторы благодарны участникам проекта Россий-

В. Ю. Ирхин, Письма ЖЭТФ 98, 172 (2013).

ского Фонда Фундаментальных Исследований # 16-

26.

C. L. Kane, P. A. Lee, and N. Read, Phys. Rev. B 39,

02-00995 - своим соавторам М.А.Тимиргазину и

6880 (1989).

А. К. Аржникову.

27.

M. I. Katsnelson and V. Yu. Irkhin, J. Phys. C 17, 4291

(1984).

1. M. Ogata and H. Fukuyama, Rep. Prog. Phys. 71,

28.

M. A. Timirgazin, P. A. Igoshev, A. K. Arzhnikov, and

036501 (2008).

V. Yu. Irkhin, J. Low. Temp. Phys. 185, 651 (2016).

2. P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys.

29.

M. A. Timirgazin, P. A. Igoshev, A. K. Arzhnikov, and

78, 17 (2006).

V. Yu. Irkhin, J. Phys.: Condens. Matter 28, 505601

3. М. В. Садовский, УФН 178, 1243 (2008).

(2016).

4. Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken,

30.

W. F. Brinkman and T. M. Rice, Phys. Rev. B 2, 4302

J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe,

(1970).

T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-

31.

M. I. Auslender, V. Yu. Irkhin, and M. I. Katsnelson,

Herrero, Nature 556, 80 (2018).

J. Phys. C: Solid State Phys. 21, 5521 (1988).

5. В. Ю. Ирхин, Ю. Н. Скрябин, Письма в ЖЭТФ 107,

32.

В. Ю. Ирхин, УФН 187, 801 (2017).

684 (2018).

33.

T. Chattopadhyay, P. Burlet, and P. J. Brown, J. Phys.:

6. P. A. Igoshev, M. A. Timirgazin, A. A. Katanin,

Condens. Matter 3, 5555 (1991).

A.K. Arzhnikov, and V. Yu. Irkhin, Phys. Rev. B 81,

34.

П. А. Игошев, В. Ю. Ирхин, ЖЭТФ 155, 1072 (2019).

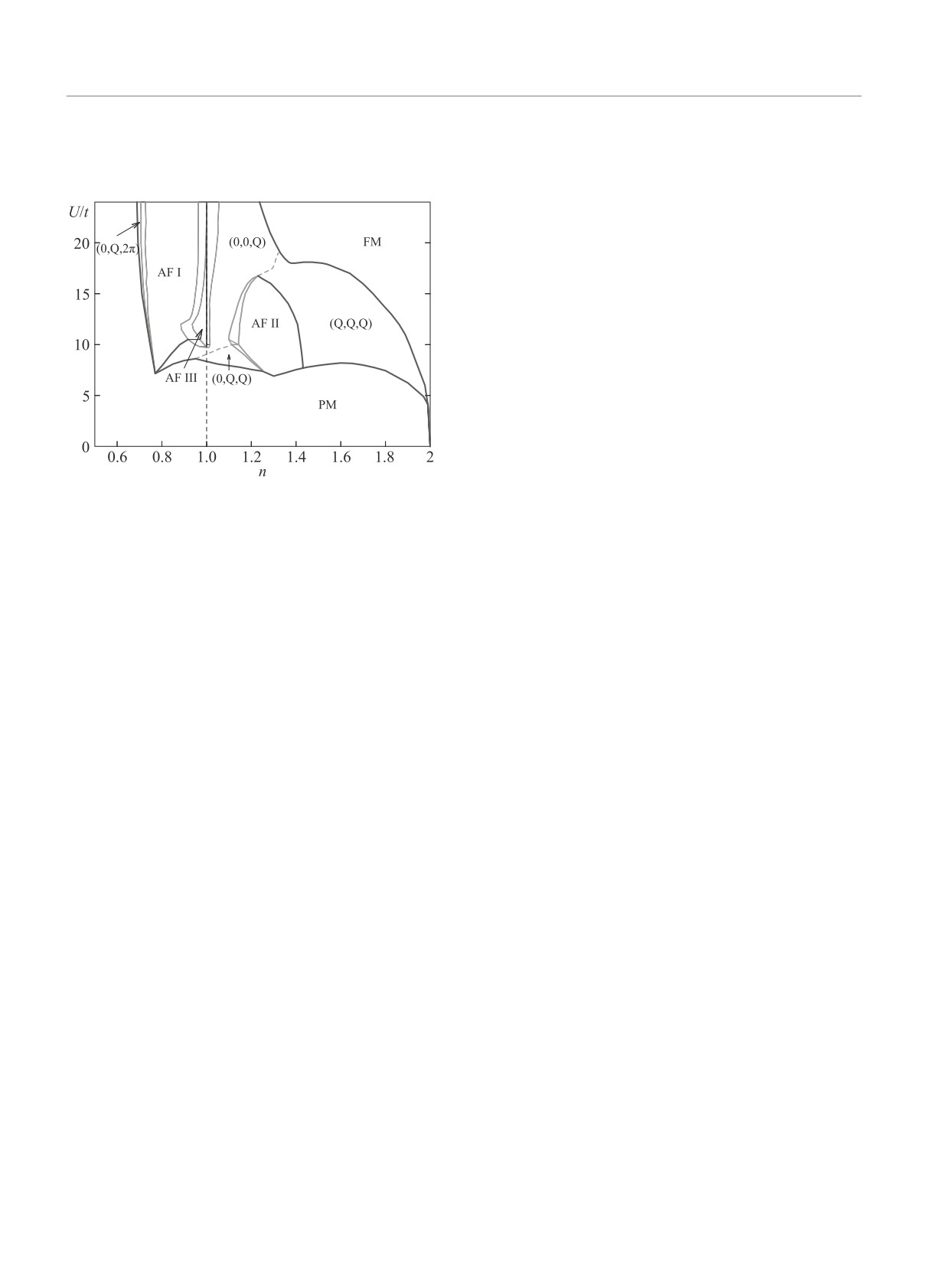
094407 (2010).

35.

D. Duffy and A. Moreo, Phys. Rev. B 55, R676 (1997).

7. P. B. Visscher, Phys. Rev. B 10, 943 (1973).

36.

Z.-Q. Yu and L. Yin, Phys. Rev. B 81, 195122 (2010).

8. M. A. Timirgazin, P. A. Igoshev, V. F. Gilmutdinov,

A.K. Arzhnikov, and V.Yu. Irkhin, J. Phys.: Condens.

37.

I. Yang, E. Lange, and G. Kotliar, Phys. Rev. B 61,

Matter 27, 446002 (2015).

2521 (2000).

9. Н. Ф. Мотт, Переходы металл-изолятор, Наука, М.

38.

М. А. Тимиргазин, А. К. Аржников, В. Ю. Ирхин,

(1979).

Письма в ЖЭТФ 98, 184 (2012).

10. M. Imada, A. Fujimori, and Y. Tokura, Rev. Mod. Phys.

39.

В. Ю. Ирхин, А. В. Зарубин, ЖЭТФ 141, 975 (2012);

70, 1039 (1998).

143, 971 (2013).

11. T. Das, R. S. Markiewicz, and A. Bansil, Adv. Phys. 63,

40.

В. Ю. Ирхин, А. В. Зарубин, ЖЭТФ 143, 971 (2013).

151 (2014).

41.

Е. И. Шнейдер, С. Г. Овчинников, М. М. Коршунов,

12. M. A. Timirgazin, P. A. Igoshev, A. K. Arzhnikov, and

С. В. Николаев, Письма ЖЭТФ 96, 381 (2012).

V.Yu. Irkhin, J. Magn. Magn. Mater. 459, 311 (2018).

Письма в ЖЭТФ том 110 вып. 1 - 2

2019