Письма в ЖЭТФ, том 110, вып. 7, с. 443 - 448

Алгоритм построения точных решений плоской нестационарной

задачи о движении жидкости со свободной границей

Е. Н. Журавлева^+∗, Н. М. Зубарев^×◦1), О. В. Зубарева^×, Е. А. Карабут^+∗

⁺Институт гидродинамики им. М. А. Лаврентьева Сибирского отделения РАН, 630090 Новосибирск, Россия

^∗Новосибирский государственный университет, 630090 Новосибирск, Россия

^×Институт электрофизики Уральского отделения РАН, 620016 Екатеринбург, Россия

^◦Физический институт им. П. Н. Лебедева РАН, 119991 Москва, Россия

Поступила в редакцию 14 августа 2019 г.

После переработки 22 августа 2019 г.

Принята к публикации 23 августа 2019 г.

Исследуются плоские потенциальные нестационарные течения идеальной несжимаемой жидкости со

свободной поверхностью в отсутствие внешних сил и капиллярности. Предложен алгоритм построения

точных решений для таких течений, основанный на анализе условий совместности уравнений движе-

ния и вспомогательного комплексного уравнения переноса. Его использование позволило радикально

расширить список известных точных нетривиальных решений рассматриваемой классической задачи,

еще несколько лет назад сводившийся к нескольким решениям Дирихле: течения, для которых гра-

ница жидкости представляет собой параболу, эллипс или гиперболу. В рамках алгоритма удается как

воспроизвести недавно найденный класс решений, задаваемый уравнением Хопфа на комплексную ско-

рость, так и найти принципиально новый широкий класс решений, для которого течения описываются

уравнением Хопфа на обратную комплексной скорости величину.

DOI: 10.1134/S0370274X19190032

1. Введение. Рассматривается классическая за-

свободной границы идеальной несжимаемой жидко-

дача о потенциальном нестационарном течении иде-

сти в пренебрежении поверхностными силами и си-

альной несжимаемой жидкости со свободной грани-

лой тяжести [2, 3]. Комплексное уравнения Хопфа в

цей. Течение считается плоским; внешние силы и ка-

форме

пиллярность не учитываются. До недавнего времени

U_t + iU_z + UU_z = O(α³)

был известен единственный класс точных решений

получалось при построении слабонелинейной тео-

этой задачи - нестационарные течения с линейным

рии развития неустойчивости Тонкса-Френкеля

полем скоростей (компоненты скорости u и v явля-

(неустойчивости границы проводящей жидкости

ются линейными функциями координат x и y), от-

во внешнем электрическом поле) [4, 5]. Наконец, в

крытый Дирихле более чем полтора века назад [1].

работе [6] было выведено уравнение

В ряде исследований динамики границы жидко-

стей, проводимых в рамках малоуглового приближе-

U_t + iU_z + e^iγUU_z = O(α³),

ния (считалось, что граница лишь незначительно от-

клоняется от плоской), задача описания ее эволюции

описывающее эволюцию поверхности раздела двух

сводилась к уравнению Хопфа на комплексную ско-

несмешивающихся жидкостей при развитии неустой-

рость (U ≡ u - iv) жидкости, которая является ана-

чивости Кельвина-Гельмгольца (здесь γ

- веще-

литической функцией пространственной переменной

ственный параметр, зависящий от отношения плот-

z = x + iy. Так, уравнение Хопфа

ностей жидкостей). Во всех указанных случаях урав-

нение Хопфа в различных модификациях описывало

U_t + UU_z = O(α³)

течение жидкости приближенно: учитывались лишь

квадратично нелинейные слагаемые в рамках теории

(здесь α - малый параметр - характерный угол на-

возмущений по малому параметру α.

клона границы) возникает при анализе динамики

Появление уравнения Хопфа на комплексную

скорость жидкости в целом ряде задач побудило ав-

¹⁾e-mail: nick@iep.uran.ru

торов недавних работ [7-9] целенаправленно иссле-

Письма в ЖЭТФ том 110 вып. 7 - 8

2019

443

444

Е. Н. Журавлева, Н. М. Зубарев, О. В. Зубарева, Е. А. Карабут

довать возможность его использования для постро-

iv(x, y, t). В отсутствие внешних сил и капиллярно-

ения точных решений (т.е. вне рамок малоуглово-

сти, не теряя общности, можно положить давление

го приближения) уравнений движения жидкости со

на свободной границе ∂Ω_t равным нулю (динамиче-

свободной границей. В итоге было продемонстриро-

ское граничное условие):

вано, что решения комплексного уравнения Хопфа

p|_∂Ω

= 0.

(6)

U_t + UU_z = 0

(1)

Кинематическое граничное условие (условие того,

описывают плоские нестационарные течения идеаль-

что граница движется со скоростью, совпадающей с

ной жидкости, особенностью которых является нуле-

нормальной компонентой скорости находящихся на

вое значение ускорения жидкости на свободной гра-

ней жидких частиц) сводится, с учетом (6), к тре-

нице: du/dt = 0 и dv/dt = 0. При этом ускорение

бованию равенства нулю на ∂Ω_t полной производной

отлично от нуля внутри жидкости.

давления:

В настоящей работе предложен алгоритм постро-



dp

ения точных решений плоской нестационарной зада-



= p_t + up_x + vp_y|

= 0.

(7)



∂Ωt

чи о движении жидкости со свободной границей, ос-

∂Ωt

нованный на предположении о том, что течение жид-

Ключевая идея настоящей работы заключается в

кости удовлетворяет комплексному уравнению пере-

том, чтобы взять комплексную скорость U не произ-

носа общего вида

вольно, а потребовать, чтобы она удовлетворяла ком-

плексному уравнению переноса (2). В разделах 3 и 4

U_t + C(U, t)U_z = 0,

(2)

мы сформулируем алгоритм выбора входящей в (2)

где C(U, t) - некоторая функция (в частном случае

функции C(U, t), позволяющий обеспечить совмест-

C(U, t) = U это уравнение сводится к (1)). Исполь-

ность интегрируемого уравнения (2) с уравнениями

зование алгоритма позволило нам открыть новый

движения (3)-(7) и, тем самым, строить их точные

класс точных решений рассматриваемой задачи, за-

решения.

даваемый нелинейным уравнением переноса

3. Условия совместности. Рассмотрим снача-

ла условия совместности переопределенной системы

U_t + U_z/U = 0.

уравнений (2)-(5). Будем использовать для давления

следующее представление:

Предложенный в работе подход может иметь важ-

ное значение для общей проблемы интегрируемости

p(x, y, t) = P (u(x, y, t), v(x, y, t), t).

(8)

уравнений движения жидкости со свободной грани-

цей [10-12].

Разбивая функцию C(U) на вещественную и мнимую

2. Постановка задачи. Выпишем уравнения

части

для плоского потенциального течения идеальной

C(U, t) = a(u, v, t) + ib(u, v, t),

(9)

несжимаемой жидкости, плотность которой равна

получим соотношения Коши-Римана, которым

единице. Предполагаем, что жидкость занимает из-

должны удовлетворять вещественные функции a

меняющуюся область Ω_t, граница которой ∂Ω_t явля-

и b:

ется свободной. В области Ω_t должны выполняться

a_u = -b_v,

a_v = b_u.

(10)

уравнения Эйлера:

Уравнение переноса (2) при разделении веществен-

u_t + uu_x + vu_y = -p_x,

(3)

ной и мнимой частей дает:

v_t + uv_x + vv_y = -p_y,

(4)

u_t = -au_x - bv_x,

v_t = bu_x - av_x.

(11)

где u(x, y, t) и v(x, y, t) - x- и y-компоненты вектора

Исключая производные по времени из уравнений Эй-

скорости, p(x, y, t) - давление. Для безвихревого те-

лера (3) и (4) при помощи (11), используя представ-

чения несжимаемой жидкости компоненты скорости

ление (8) для давления, а также избавляясь от произ-

связаны соотношениями

водных по y при помощи соотношений Коши-Римана

(5), находим

u_x = -v_y,

u_y = v_x,

(5)

- au_x - bv_x + uu_x + vv_x = -P_uu_x - P_vv_x,

которые являются соотношениями Коши-Римана

для комплексной скорости U(z, t)

= u(x, y, t) -

bu_x - av_x + uv_x - vu_x = -P_uv_x + P_vu_x.

Письма в ЖЭТФ том 110 вып. 7 - 8

2019

Алгоритм построения точных решений. . .

445

Если теперь сгруппировать члены при производных

u_x и v_x, получим:

u_x(-a + u + P_u) + v_x(-b + v + P_v) = 0,

u_x(b - v - P_v) + v_x(-a + u + P_u) = 0.

Несложно заметить, что эти уравнения превращают-

ся в тождества, если справедливо:

a = P_u + u,

b=P_v +v.

(12)

Подставляя эти выражения в условия Коши-Римана

для функций a и b (10), находим, что давление P

должно удовлетворять уравнению Пуассона в терми-

нах переменных u и v, т.е. в плоскости годографа:

P_uu + P_vv = -2.

(13)

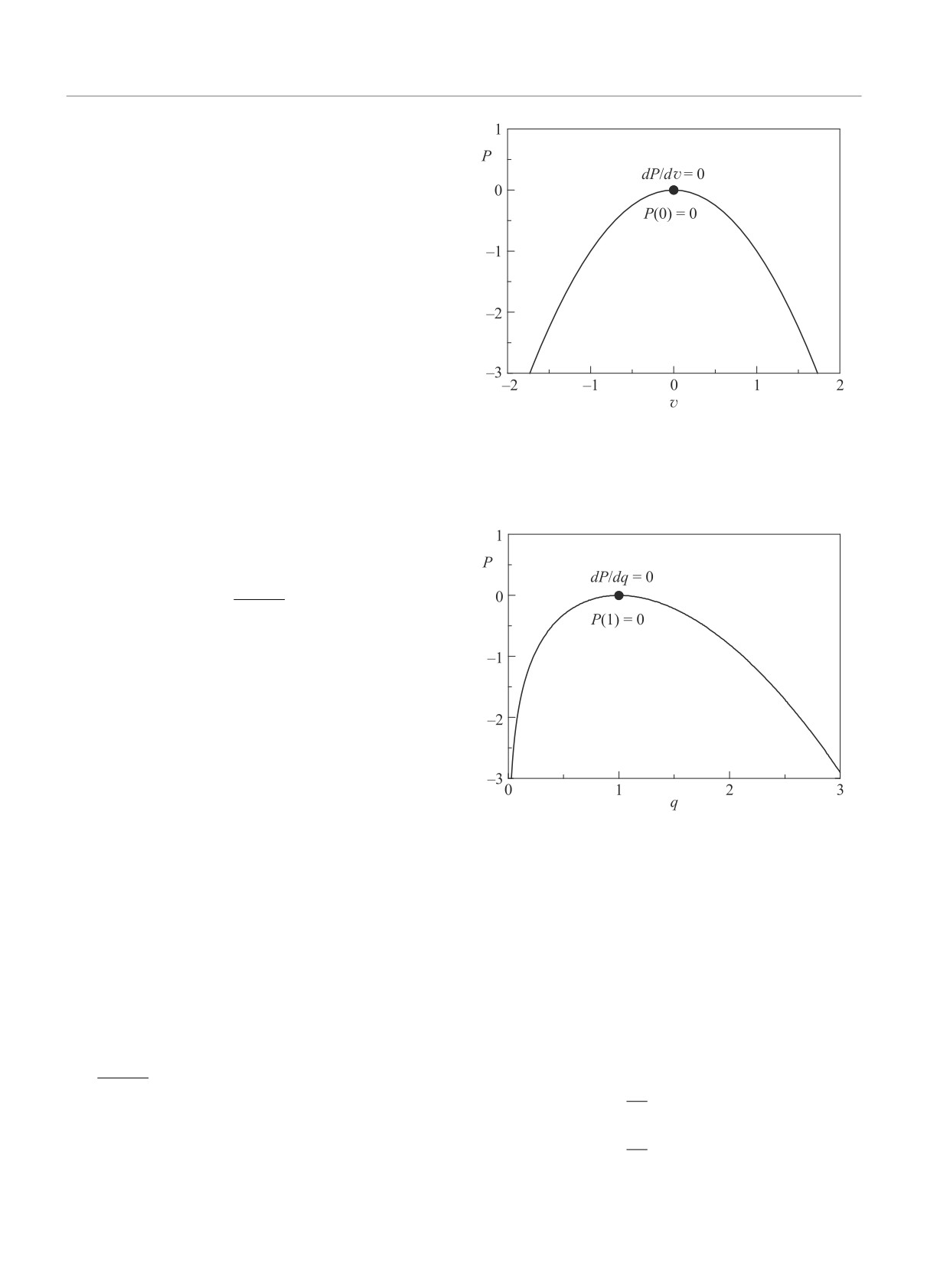
Рис. 1. Описываемая формулой (17) зависимость давле-

Его конкретное решение позволяет при помощи (12)

ния P от y-компоненты скорости v (случай I). В этой

найти функции a и b и затем, используя (9), опреде-

зависимости имеется экстремум (максимум) в точке

v = 0; ему соответствует P = 0

лить:

C = P_u + iP_v + u + iv.

(14)

Решая линейное уравнение (13), находим для дав-

ления P и для искомой функции C:

u² + v

P (u, v, t) = -

+ Re A(U, t),

(15)

C(U, t) = A_U (U, t),

(16)

где A - некоторая аналитическая функция комплекс-

ной скорости в области Ω_t.

Уравнения (13) и (14), а также их решения (15) и

(16) обеспечивают совместность уравнения переноса

(2) с уравнениями движения (3)-(5). Понятно, что

требуется также проверить совместность описывае-

мых (2) течений с динамическим (6) и кинематиче-

ским (7) граничными условиями. Этот вопрос будет

рассмотрен в следующем разделе для двух простей-

Рис. 2. Описываемая формулой (18) зависимость дав-

ших - одномерных - решений уравнения Пуассона

ления P от абсолютного значения скорости жидкости

(13).

q = |U| (случай II). В этой зависимости имеется экс-

4. Точные решения. Рассмотрим в первую оче-

тремум (максимум) в точке q = 1; ему соответствует

редь случай, когда давление зависит лишь от одной

P =0

компоненты скорости, P = P (v) (случай I). Уравне-

ние Пуассона (13) принимает тогда вид P_vv = -2,

откуда получаем для P (см. также [13]):

Зависимости давления от скорости (17) и (18) по-

казаны на рис. 1 и 2, соответственно. Видно, что в

P (v) = -v².

(17)

обоих случаях зависимость имеет единственный экс-

Другой одномерный случай соответствует ситу-

тремум (максимум), относящийся к нулевому значе-

ации, когда распределение давления в плоскости u

нию давления:

и v является осесимметричным: P = P(q), где q =

√



u² + v² - абсолютное значение скорости жидко-



P|_v=0 = 0,

(случай I),

сти (случай II). Тогда уравнение Пуассона принима-



v=0

ет вид P_qq + P_q/q = -2, откуда находим для P:



P|_q=1 = 0,



(случай II).

P (q) = ln q - q²/2 + 1/2.

(18)



q=1

Письма в ЖЭТФ том 110 вып. 7 - 8

2019

446

Е. Н. Журавлева, Н. М. Зубарев, О. В. Зубарева, Е. А. Карабут

Для случая I он соответствует условию v = 0, а для

Соответствующие течения могут быть интерпрети-

случая II - условию q = 1. В этих точках автомати-

рованы как возмущения исходного течения с линей-

чески выполняются как динамическое, так и кинема-

ным полем скоростей U = z/t, для которого занима-

тическое граничные условия. Действительно, полная

емая жидкостью область представляет собой полу-

производная давления дает в них нули:

плоскость в исходных переменных x и y (случай F =

0). Решения (21) при различном выборе F могут опи-

dP dv

= -2v

(случай I),

сывать формирование на границе точек заострения,

dv dt

(

)(

)

пузырей и капель (см. примеры течений в [13]). Отме-

dP dq

-1

(случай II).

тим, что в докладе “Are equations of deep water with a

dq dt

q²

free surface integrable?” [14] (Russian-French Workshop

Таким образом, мы доказали, что оба одномерных

“Mathematical Hydrodynamics”, Новосибирск, 2016, в

решения (17) и (18) уравнения Пуассона (13) обеспе-

соавт. с А.И.Дьяченко) ак. В.Е.Захаров указывал

чивают выполнение всех требуемых условий на дви-

на то, что уравнения на возмущения автомодельно-

жущейся свободной границе.

го течения U = z/t, рассматриваемые в конформных

Для случая I формула (14) дает C = U и, соот-

переменных, допускают широкий класс точных ре-

ветственно, течение определяется уравнением Хопфа

шений. По всей видимости, эти решения имеют связь

(1). Граница жидкости задается условием v = 0, т.е.

с решением (20) уравнения Хопфа и дают аналогич-

для описываемых (1) течений одна из компонент ско-

ные примеры течений.

рости на границе жидкости равна нулю. Таким обра-

Для случая II, когда нестационарное течение опи-

зом, мы воспроизвели результат работ [7, 8].

сывается уравнением (19), распределение поля ско-

Отметим, что если взять P = P(v, t), то решение

ростей дается выражением

(13) дает вместо (17) P = -v² + c(t)v + d(t), и тогда

z = F(U) + t/U,

(22)

входящая в уравнение переноса (2) функция C будет

зависеть от времени: C(U, t) = U + ic(t). Однако это

куда также входит произвольная комплексная функ-

не приводит к построению нового класса решений.

ция F . Свободная граница соответствует единичной

Получаемые решения отличаются от решений, соот-

окружности |U| = 1 в плоскости U (область Ω_t в

ветствующих случаю I, переходом в движущуюся с

плоскости U соответствует либо кругу единичного

ускорением систему координат.

радиуса, либо внешности такого круга), так что ее

Рассмотрение случая II приводит к новому клас-

можно параметризовать выражением U = e^iθ, где θ

су точных решений задачи. Для давления (18) фор-

- вещественный параметр. Тогда искомая эволюция

мула (14) дает C = 1/U и, соответственно, течение

границы ∂Ω_t задается параметрическими выражени-

задается нелинейным уравнением

ями

U_t + U_z/U = 0.

(19)

x = ReF(e^iθ) + tcosθ,

(23)

Граница жидкости определяется условием q ≡ |U| =

y = ImF(e^iθ) - tsinθ.

(24)

= 1, т.е. для описываемых (19) течений абсолютное

Описываемые (22)-(24) течения можно интерпрети-

значение скорости на свободной поверхности не ме-

ровать как двумерные возмущения исходного одно-

няется при ее движении - оно равно единице для всех

мерного осесимметричного течения U

= t/z (для

жидких частиц на границе. Отметим, что (19) пре-

невозмущенного течения F = 0; оно соответствует

вращается в уравнение Хопфа при введении новой

сжатию, либо расширению с постоянной скоростью

функции - обратной комплексной скорости U^-1.

круглой полости в жидкости). Различный выбор про-

5. Динамика свободной границы. Для слу-

извольной функции F позволяет строить самые раз-

чая I распределение поля скоростей дается решением

ные двумерные течения, подробный анализ которых

уравнения Хопфа (1) [7, 8, 13]:

выходит за рамки настоящей работы.

z = F(U) + tU,

(20)

Приведем здесь в качестве примера только два

√

решения. Первое - соответствует F (U) =

U. Это

куда входит произвольная комплексная функция F .

означает, что начальное поле скоростей является

Эволюция границы, которая параметризуется усло-

квадратичным: U|_t=0 = z². Тогда, согласно (23) и

вием U = u, где -∞ < v < ∞ (т.е. жидкость занима-

(24), в начальный момент t = 0 свободная грани-

ет полуплоскость в плоскости годографа U), задает-

ца представляет собой окружность |z| = 1. Исходно

ся тогда параметрическими выражениями

круглая полость в жидкости со временем деформи-

x = ReF(u) + tu,

y = ImF(u).

(21)

руется - см. рис. 3. Решение разрушается в момент

Письма в ЖЭТФ том 110 вып. 7 - 8

2019

Алгоритм построения точных решений. . .

447

Рис. 3. Описываемая формулами (23) и (24) эволюция

Рис. 4. Описываемая формулами (23) и (24) эволюция

√

полости в жидкости для F (U) =

U. Свободная гра-

полости в жидкости для задаваемой выражением (25)

ница показана в последовательные моменты времени

функции F. Свободная граница показана в последо-

t1 = 0, t2 = 0.25, t3 = 0.5

вательные моменты времени t1 = -3, t2 = -2.25,

t3 = -1.53

t = 1/2, когда на границе одновременно образует-

ся три точки заострения. Их появление связано с

шения линейного уравнения Пуассона на давление в

выходом особенностей комплексной скорости извне

плоскости годографа P_uu + P_vv = -2 и завершаю-

жидкости на ее границу (см. также [13]). Отметим,

щийся анализом зависимостей вида

что, по-видимому, на важность изучения сингуляр-

∫

ностей вне жидкости для нестационарного случая

z = F(U) + C(U,t)dt,

было впервые указано в работе [15]. Когда особая

точка приближается к свободной границе, это вызы-

вытекающих из уравнения переноса (2). Этот алго-

вает ее значительную деформацию. Подобная ситуа-

ритм позволил воспроизвести найденные в [7, 8, 13]

ция реализуется, в частности, для околопредельных

решения, а также построить новый широкий класс

волн Стокса [16].

решений, описывающий произвольные возмущения

Второе решение продемонстрировано на рис.4.

невозмущенного течения U = t/z. Если решения Ди-

Оно соответствует следующему выражению для вхо-

рихле соответствуют течениям с линейным полем

дящей в (22)-(24) функции F :

скорости U ∼ z, а решения из работ [7, 8, 13] имеют

аналогичную линейную асимптотику, то построен-

∑

F (U) = -

(25)

ный в настоящей работе новый класс решений имеет

U - 1.5exp(2ikπ/3)

k=1

иную - затухающую на бесконечности - асимптоти-

содержащему три симметрично расположенных от-

ку U ∼ z^-1, характерную для процессов сжатия или

носительно начала координат полюса. При больших

расширения полостей в несжимаемой жидкости для

|t| форма границы близка к окружности с радиусом

плоских течений. Важно, что решение (22) содержит

∼ |t|. Как видно, при сжатии полости возмущения ее

произвольную комплексную функцию F , что позво-

границы становятся более выраженными, и в момент

ляет исследовать начальные условия самого разно-

t_c ≈ -1.53 решение разрушается - происходит столк-

го вида. Возникающие из требования аналитичности

новение свободных границ, в результате чего полость

комплексной скорости в области Ω_t условия на функ-

распадается на несколько отдельных полостей.

цию F носят самый общий характер и легко выпол-

Таким образом, рис. 3 и 4 демонстрируют обра-

няются при соответствующем выборе положения ее

зование различных типов особенностей - острий и

особенностей.

пузырей.

Работа выполнена при частичной поддержке

6. Заключение. Предложен алгоритм построе-

Российского фонда фундаментальных исследований

ния точных решений задачи о двумерном течении

(проекты 19-01-00096 и 19-08-00098), Президиума

жидкости со свободной границей, стартующий с ре-

РАН (программа 2) и УрО РАН (проект 18-2-2-15).

Письма в ЖЭТФ том 110 вып. 7 - 8

2019