Письма в ЖЭТФ, том 111, вып. 1, с. 34 - 39

Фазовый переход в трехмерных неколлинеарных магнитных

системах с дополнительным двукратным вырождением

А. О. Сорокин¹⁾

Национальный исследовательский центр “Курчатовский институт”,

Петербургский институт ядерной физики, 188300 Гатчина, Россия

Поступила в редакцию 11 ноября 2019 г.

После переработки 22 ноября 2019 г.

Принята к публикации 25 ноября 2019 г.

Методом Монте-Карло исследуется критическое поведение в трехмерном фрустрированном спираль-

ном магнетике с дополнительным двукратным вырождением, реализованном в слоисто-J1-J2-J3 модели

на кубической решетке. Для случая гейзенберговских спинов (N = 3) найден переход первого рода. С

помощью ренормгруппового подхода аналогичный результат найден также для произвольного значения

числа компонент классического спина N. Из решеточной модели получен соответствующий функцио-

нал Гинзбурга-Ландау, который проанализирован в низших порядках 4 - ε разложения. Приводятся

аргументы, что при учете старших порядков разложения качественный результат не изменится.

DOI: 10.31857/S0370274X20010075

Фрустрированные магнитные системы представ-

взаимодействия в двух направлениях простой куби-

ляют значительный интерес в связи с реализацией

ческой решетки. Но на самом деле эта модель явля-

в них явлений, приводящих к возникновению новых

ется лишь частным случаем слоистой J₁-J₂-J₃ моде-

фаз и фазовых переходов. Так, в частности, фруст-

ли, в которой рассматриваются обмены первых трех

рация является одним из механизмов образования

порядков дальности в слое, с J₂ = 0. Фазовая диа-

несоизмеримых длиннопериодических модулирован-

грамма этой модели содержит две фазы с коллинеар-

ных структур типа спирали [1-3]. Другое интересное

ным спиновым упорядочением, нефрустрированную

явление, которое может наблюдаться во фрустриро-

и фрустрированную с эффектом “порядок из беспо-

ванных магнетиках, - “порядок из беспорядка”, когда

рядка”, а также две различные геликоидальные фа-

дополнительное бесконечное вырождение основного

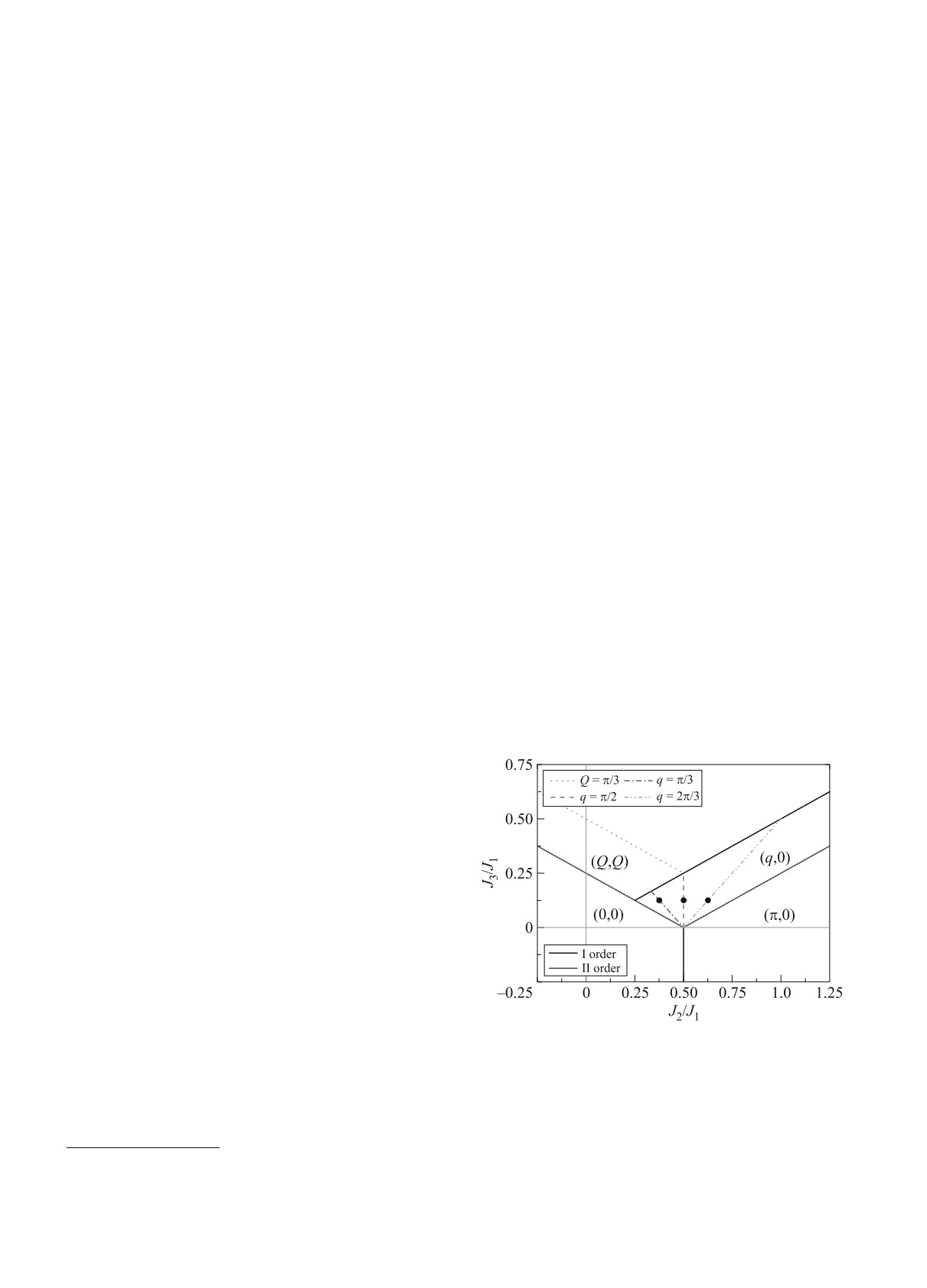
зы [13-15] (рис. 1).

состояния снимается за счет квантовых или темпера-

турных флуктуаций [4-6]. Это явление вместе с воз-

никновением неколлинеарного спинового упорядоче-

ния обеспечивают разнообразие возможных симмет-

рийных классов, реализующихся во фрустрирован-

ных системах.

Простейший (аксиальный) спиральный магнетик,

в котором конкурирующее обменное взаимодействие

присутствует только в одном направлении решетки,

соответствует, например, редкоземельным металлам

[7] и многослойным структурам [8]. Критическое по-

ведение в этом случае исследовано в работе [9]. В

данной работе рассматривается обратная ситуация,

когда спиральная структура образуется внутри сло-

ев. Этот случай оказывается более богат феномено-

Рис. 1. (Цветной онлайн) Фазовая диаграмма J1-J2-J3

логически, что особенно ярко проявляется в двумер-

модели. Точками отмечены случаи, численно рассмат-

ном и квазидвумерном случаях [10-12].

риваемые в данной работе

Очевидное обобщение аксиального спирального

магнетика — введение конкурирующего обменного

Обе фазы со спиральным порядком имеют оди-

наковые симметрийные свойства, описывающиеся

¹⁾e-mail: aosorokin@gmail.com

пространством параметра порядка G/H

= Z₂ ⊗

Письма в ЖЭТФ том 111 вып. 1 - 2

2020

Фазовый переход в трехмерных неколлинеарных магнитных системах. . .

O(N)/O(N - 2), где N — размерность классическо-

G/H = Z₂ ⊗ O(N)/O(N - 1) симметрии. Критиче-

го спина. В частности, это означает, что переходы по

ское поведение в этом случае исследовано в работах

температуре в разупорядоченную фазу должны при-

[20-24].

надлежать одному классу универсальности, причем

При J₃ > (J₁ - 2J₂)/4 и J₃ > (-J₁ + 2J₂)/4 низ-

отличающемуся от класса универсальности просто-

котемпературная фаза содержит спиральную струк-

го спирального магнетика G/H = O(N)/O(N - 2)

туру. При J₃ > J₂/2 более выгодным оказывается

или, тем более, от класса коллинеарных магнетиков

геликоидальное состояние, описываемое одной из че-

G/H = O(N)/O(N - 1). Класс O(N)/O(N - 2) по-

тырех конфигураций q₀ = (±Q, ±Q, 0), где cos Q =

дробно исследовался на протяжении нескольких де-

= J₁/(2J₂ + 4J₃). (В дальнейшем для краткости мы

сятков лет, поскольку ему же принадлежит крити-

будем называть данную фазу (Q, Q) фазой.) Остав-

ческое поведение антиферромагнетика на слоисто-

шаяся полуполоса фазовой диаграммы, ограничен-

треугольной решетке и сверхтекучего³He (для обзо-

ная условиями J₃ > (J₁ - 2J₂)/4, J₃ > (-J₁ + 2J₂)/4

ра см. [16]). Наиболее надежные результаты указыва-

и J₃ < (-J₁ + 2J₂)/4, также соответствует спираль-

ют, что при N < 6, включая физически интересные

ной структуре с четырьмя минимумами, описывае-

случаи N = 2, 3, будет наблюдаться переход первого

мыми векторами обратной решетки q₀ = (±q, 0, 0) и

рода, при N ≥ 6 - второго. Класс Z₂ ⊗ O(N)/O(N -2)

q₀ = (0, ±q, 0), где cosq = (J₁ -2J₂)/(4J₃). (Эту фазу

не исследовался ранее за исключением частного слу-

будем называть (q, 0) фазой.)

чая J₂ = 0 в J₁-J₂-J₃ модели, исследованного в ра-

Фаза (q, 0), которой мы интересуемся в данной ра-

ботах [9, 17, 18]. В данной работе будут приведены

боте, обладает рядом свойств, не встречающихся у

аргументы, основанные на ренормгрупповом анали-

других геликоидальных фаз. Так, например, в этой

зе, в пользу того, что в данном симметрийном классе

фазе могут реализоваться основные состояния и с

будет наблюдаться переход первого рода для любого

q > π/2 и с q < π/2 при фиксированных знаках

N. Мы также численно рассмотрим несколько слу-

констант обменных интегралов J_i, в то время как

чаев J₁-J₂-J₃ модели, относящихся ко второй, ранее

в простом спиральном магнетике и в (Q, Q) фазе в

не исследовавшейся геликоидальной фазе.

зависимости от знака J₁ реализуется только один

Слоисто-J₁-J₂-J₃ модель описывается гамильто-

тип основного состояния. В частности, в (q, 0) фа-

нианом

зе основным состоянием может быть конфигурация с

∑

q₀ = (π/2, 0), в то время как в (Q, Q) фазе такая кон-

H = -J S_x · Sx+e3 - J₁ S_x · Sx+eμ +

(1)

фигурация достигается лишь в пределе J₃ → ∞. На-

x,μ

конец, хотя из-за осциллирующего характера РККИ

∑

взаимодействия вполне может возникать ситуация с

+J₂

S_x ·Sx+2eμ ,

S_x ·(Sx+e1+e2 +Sx+e1-e2 )+J3

J₂ < J₃, условие J₁ > J₂ > J₃ выглядит более реа-

x,μ

листично. Поэтому фаза (q, 0) представляет особый

где μ = 1, 2, S - N-компонентный классический век-

интерес.

тор, x нумерует узлы простой кубической решетки,

Для обеих геликоидальных фаз справедливо, что

константы J выбраны положительными. Отметим,

два минимума с q₀ и -q₀, лежат на одной орбите,

что для классической модели знаки J₁ и J несуще-

связанной с группой вращений, поэтому наблюдает-

ственны, однако данная модель интенсивно исследу-

ся лишь двукратное дополнительное вырождение ос-

ется в окрестности квантовых критических точек,

новного состояния. Учитывая, что неколлинеарный

где выбирается J₁

< 0 и J < 0 (см., например,

спиновый порядок описывается параметром поряд-

[19]). При нашем выборе знака J₁ при малых значе-

ка из факторпространства G/H = O(N)/O(N - 2),

ниях фрустрирующих обменов основным состоянием

получаем полное пространство параметра порядка

является ферромагнитный порядок с q₀ = (0, 0, 0).

G/H = Z₂ ⊗ O(N)/O(N - 2).

Данная фаза существует при J₃ < (J₁ - 2J₂)/4 и

В терминах модели (1) параметр порядка может

J₂ < J₁/2. При J₂ > J₁/2 энергетически более вы-

быть сконструирован следующим образом. Для слу-

годными становятся конфигурации с q₀ = (π, 0, 0)

чая N = 3, исследуемом в данной работе, параметр

и (0, π, 0), при условии J₃ < (-J₁ + 2J₂)/4. В этой

порядка представляет собой пару взаимно ортого-

фазе возникает коллинеарный антиферромагнитный

нальных 3-векторов, плюс независимый дискретный

порядок, соответствующий одному из волновых век-

параметр изинговского типа. В случае соизмеримых

торов q₀. И поскольку одна конфигурация не мо-

спиралей одним из 3-векторов удобно взять намаг-

жет быть приведена к другой с помощью глобальных

ниченность подрешеток. Мы рассмотрели спирали с

поворотов спинов, то фазе соответствует нарушение

q = π/3, π/2, 2π/3, для которых необходимое число

Письма в ЖЭТФ том 111 вып. 1 - 2

2020

3^∗

А. О. Сорокин

подрешеток равно, соответственно, 36, 16 и 9. В ка-

(Q, Q) фазы, принадлежащей тому же симметрийно-

честве второго 3-вектора берется один из векторов

му классу [17].

киральности

∑

k^±a =

ϵ_abcSx,bSx+e1±e2,c,

(2)

L³ sinq

x,b,c

где a, b, c - индексы, нумерующие компоненты спи-

на, а L³ - объем системы. Тогда дискретный пара-

метр порядка есть просто

σ=k⁺ ·k^-.

(3)

Модель (1) исследована методом Монте-Карло,

основанном на сверх-релаксационном алгоритме [25,

26]. Для изучения типа перехода использовался ме-

тод анализа гистограмм. Термализация к равновес-

ному состоянию осуществлялась за 3 · 10⁵ шагов ал-

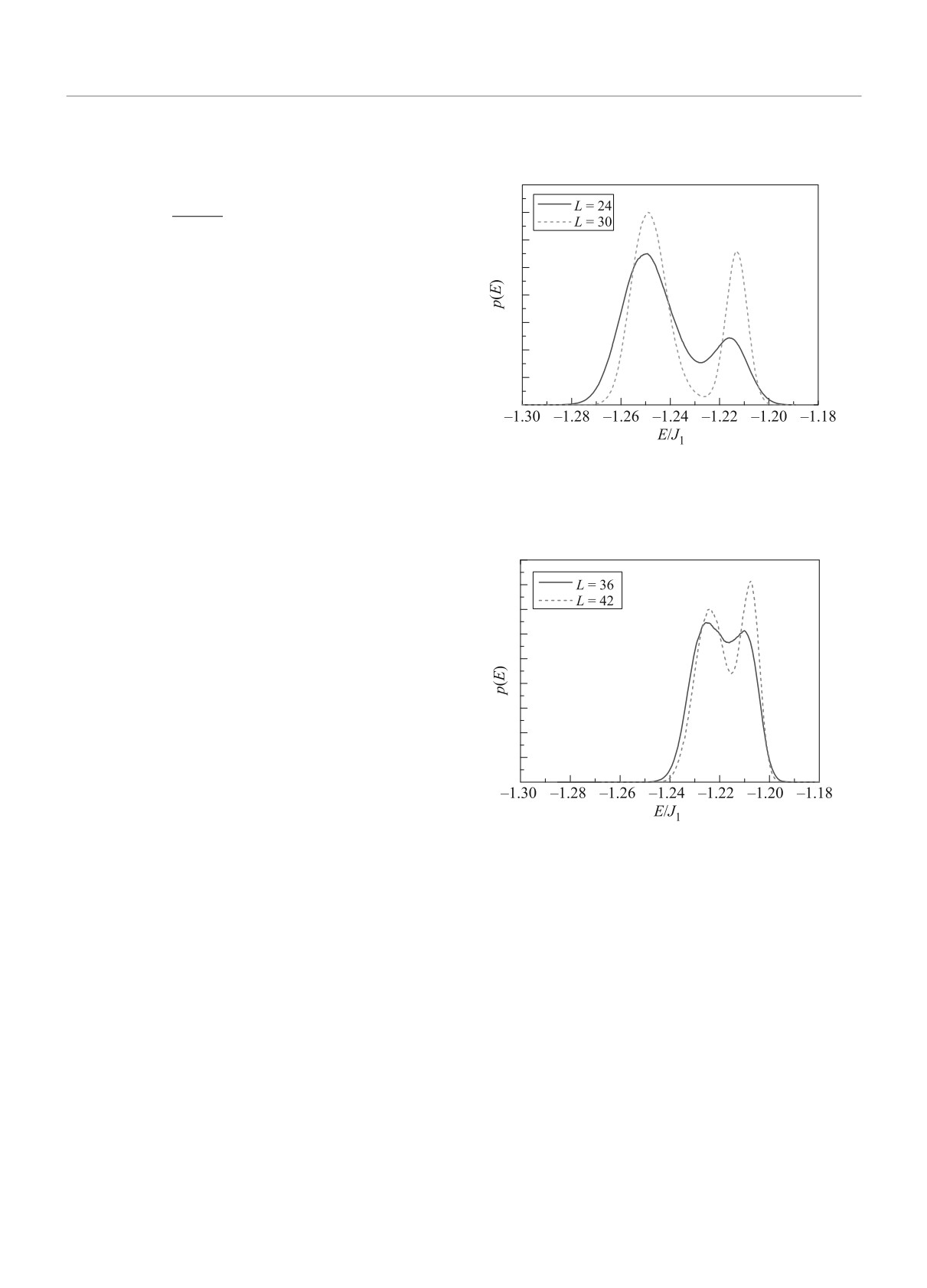
Рис. 2. (Цветной онлайн) Гистограмма распределения

горитма на спин, а набор статистики производил-

по энергии при J2/J1 = 0.5, J3/J1 = 0.125, q = π/2 и

ся за 3 · 10⁶ шагов. Каждый шаг алгоритма содер-

T /J1 = 0.605

жит один переворот спина в термостате и шесть

релаксационных поворотов. Моделирование повто-

рялось для десяти случайных стартовых конфигу-

раций, а получаемый разброс в значениях вычис-

ляемых средних использовался для оценки точно-

сти вычислений. Рассмотрение только соизмеримых

(при нулевой температуре) спиралей позволяет ис-

пользовать периодические граничные условия. Это

приводит, помимо квантования шага спирали, к до-

полнительной напряженности в системе при конеч-

ной температуре, что оказывается существенным в

окрестности точки Лифшица. Для спиралей, рас-

смотренных здесь (с q

= π/3, π/2, 2π/3), выбор

граничных условий приводит лишь к несуществен-

ному сдвигу эффективной температуры перехода

T_c(L). Во всех трех случаях выбирается J₃/J₁

= 0.125 (см. рис. 1). Для спирали q = π/3 выби-

Рис. 3. (Цветной онлайн) Гистограмма распределения

рается J₂/J₁ = 0.625, и рассматриваются решетки

по энергии при J2/J1 = 0.625, J3/J1 = 0.125, q = 2π/3.

размера L = 12, 18, 24, 30, 36. Для q

= π/2 вы-

Для L = 36 выбрана температура T/J1 = 0.64, для

бирается J₂/J1 = 0.5 и L = 12, 16, 20, 24, 32, 40.

L = 42 — T/J1 = 0.6397. В сравнении со случаем

Для q = 2π/3 выбирается J₂/J1 = 0.625 и L =

q = π/2 (рис.2) расстояние между пиками гистограм-

= 12, 15, 18, 21, 24, 30, 36, 42.

мы, отвечающее за величину внутренней теплоты пе-

Основной результат моделирования заключается

рехода, значительно меньше

в том, что в (q, 0) фазе J₁-J₂-J₃ модели наблюда-

ется переход первого рода единовременно по всем

Строго говоря, полученный результат вполне

(и непрерывному, и дискретному) параметрам по-

ожидаем. Дело в том, что для случая изотропных

рядка. Так, например, внутренняя теплота перехода,

спинов N

= 3 пространство параметра порядка

характерная для переходов первого рода, наблюда-

G/H = Z₂ ⊗ SO(3) ≡ O(3) совпадает с симметрий-

ется вблизи критической температуры для решеток

ным классом магнетиков с непланарным упорядоче-

небольшого размера L ≥ 42. На рисунках 2, 3 пока-

нием G/H = O(N)/O(N -3), реализующихся, напри-

зана двухпиковая структура распределения по энер-

мер, на решетках кагоме или структурах пирохло-

гии, отражающая наличие внутренней теплоты пере-

ра (см., например, [27]). Известно, что в этом классе

хода. Этот результат согласуется с результатами для

для N = 3 наблюдается переход ярко выраженного

Письма в ЖЭТФ том 111 вып. 1 - 2

2020

Фазовый переход в трехмерных неколлинеарных магнитных системах. . .

первого рода [28-30]. Ренормгрупповой (РГ) анализ

взаимная ориентация которых не произвольна: каж-

также показывает, что первый род перехода будет

дый вектор одной пары должен быть коллинеарен

наблюдаться при N ≤ 9 [31-33]. Разумеется, данный

одному вектору и перпендикулярен другому векто-

результат не применим к классу Z₂ ⊗ O(N)/O(N -2)

ру второй пары. Выбор одного из условий φ₁||φ₂ или

при произвольных значениях N, тем не менее, он

φ₁||ψ₂ отвечает выбору одной из четвертей простран-

оказывается полезен. В связи с этим напомним, что

ства z₁ < 0 < z₂ или z₂ < 0 < z₁. Для дальнейшего

переход из класса O(N)/O(N -P ) описывается функ-

анализа мы выберем первую альтернативу. При та-

ционалом Гинзбурга-Ландау [34, 35]

ком выборе в упорядоченной фазе r < 0 из условия

[

минимума функционала следует

∫

∑(

)

F = d³x

(∂_μφ_n)² + rφ²

w > 0,

2u+w+z₂ > 0,

2u+v+y₁+y₂+z₁ > 0, (6)

n=1

⎤

-r

(

)₂

φ2i = ψ2i =

=κ².

(7)

∑

(

2(2u + v + y₁ + y₂ + z₁)

φ²

(φ_n · φ_m)² - φ2nφ2m

)⎦_,

Более полную информацию о границах стабильности

n=1

n,m=1

выбранного нами основного состояния можно полу-

(4)

где φ_n - по-прежнему классический N-вектор.

чить из условий положительности спектра возбужде-

Чтобы получить функционал Гинзбурга-Ландау,

ний. В целом параметр порядка Ψ = (Φ₁, Φ₂) являет-

ся матрицей 4 × N. К счастью, матрица коррелятора

описывающий переход непосредственно в J₁-J₂-J₃

модели, необходимо гамильтониан (1) с дополнитель-

разбивается на N блоков размера 4 × 4, диагонали-

зация которых дает результаты:

ным потенциалом U(S) = m|S|² +λ|S|⁴, заменяющим

условие |S| = 1, рассмотреть в окрестности четырех

m21,1 = 8κ²(2u + v + y₁ + y₂ + z₁),

минимумов (±q, 0, 0) и (0, ±q, 0). (Вывод для (Q, Q)

фазы аналогичен.) Введем четыре вещественных N-

m21,2 = 8κ²(2u + v - y₁ - y₂ - z₁),

поля

φ₁ = (S|q≃(q,0,0) + S|q≃(-q,0,0))/2,

m21,3 = 8κ²(-v - y₁ + y₂ - z₁),

ψ₁ = (S|q≃(q,0,0) - S|q≃(-q,0,0))/(2i),

m21,4 = 8κ²(-v + y₁ - y₂ + z₁),

φ₂ = (S|q≃(0,q,0) + S|q≃(0,-q,0,0))/2,

m22,1 = 8κ²(w + z₂), m22,2 = 8κ²(w - z₁),

ψ₂ = (S|q≃(0,q,0) - S|q≃(0,-q,0))/(2i),

m22,3 = 8κ²(z₂ - z₁), m22,4 = 0,

в терминах которых искомый функционал записыва-

m2i,1 = m2i,2 = -8κ²z₁, m2i,3 = m2i,4 = 0,

ется в виде

где i = 3, . . . , N. Видим, что в спектре присутствуют

[

∫

2N - 3 голдстоуновских (безмассовых) мод, отвеча-

∑(

)

F = d³x

(∂_μφ_i)² + (∂_μψ_i)² + r(φ2n + φ2n)

ющих SO(N)/SO(N - 2) нарушению симметрии.

i=1

Ренормгрупповой анализ модели (5) чрезвычайно

громоздкий. К счастью, в нашем случае тип фазово-

∑(

(

)

го перехода строго определяется даже в 1-петлевом

φ4i + ψ4i

+ 2vφ2iψ2i + 2w(φ_i · ψ_i)²

приближении 4 - ε разложения. Соответствующие

i=1

(

)

(

)

РГ-уравнения можно получить из известных резуль-

+ 2y₁

φ²¹φ²² + ψ²¹ψ²²

+ 2z₁

(φ₁ · φ₂)² + (ψ₁ · ψ₂)²

татов для обобщенной N-векторной модели [36, 37]:

]

(

)

(

)

⁽ (N + 8)u² + N(v² + y²¹ + y²¹) + 2vw

+ 2y₂

φ²¹ψ²² + ψ²¹φ²²

+ 2z₂

(φ₁ · ψ₂)² + (ψ₁ · φ₂)²

β_u = -εu+

+2y₁z₁ + 2y₂z₂ + w² + z²¹ + z²

(5)

Разумеется, искомая конфигурация основного состо-

⁽ (2N + 4)uv + 2Ny₁y₂ + 4v² )

β_v = -εv +

яния остается стабильной лишь в некотором секто-

+2uw + w² + 2y₂z₁ + 2y₁z₂

ре полученного многомерного пространства парамет-

⁽ (2N + 4)uy₁ + 2Nvy₂ + 4y²¹ )

ров. На самом деле таких секторов два. Планар-

βy1 = -εy₁ +

+2uz₁ + z²¹ + 2vz₂ + 2wy₁

ное спиновое упорядочение в теории Ландау долж-

)

но описываться парой взаимно ортогональных век-

⁽ (2N + 4)uy₂ + 2Nvy₁ + 4y²²

βy2 = -εy₂ +

торов Φ = (φ, ψ). Мы имеем две таких пары Φ₁ и Φ₂,

+2uz₂ + 2vz₁ + 2wy₂ + z²

Письма в ЖЭТФ том 111 вып. 1 - 2

2020

А. О. Сорокин

(

)

можно предположить, что с ростом N скейлинг бу-

β_w = -εw +

(N + 2)w² + 4uw + 8vw + 2z₁z₂

дет становиться все более явным. Этот вопрос также

(

)

станет предметом будущих исследований.

βz1 = -εz₁ +

(N + 2)z²¹ + 4uz₁ + 8y₁z₁ + 2wz₂

Автор выражает благодарность О. И. Утесову и

(

)

А. В. Сыромятникову за полезные обсуждения. Ра-

βz2 = -εz₂ +

(N + 2)z²² + 4uz₂ + 8y₂z₂ + 2wz₁

бота выполнена при поддержке Российского фон-

да фундаментальных исследований гранта # 18-02-

Подробный анализ этих уравнений, включая слу-

00706 и гранта Фонда развития теоретической физи-

чай мультикритического поведения, будет приведен

ки и математики “БАЗИС”.

в последующих работах. Здесь мы отметим лишь

два основных результата. Во-первых, единственная

притягивающая неподвижная точка, которая может

J. Villain, J. Phys. Chem. Solids 11, 303 (1959).

описывать переход второго рода, существует (в 1-

A. Yoshimori, J. Phys. Soc. Jpn. 14, 508 (1959).

петлевом приближении) только при Nc2 ≳ 42.8. Дан-

T. A. Kaplan, Phys. Rev. 116, 888 (1959).

ная точка лежит в плоскости y₁ = y₂ = v = u - w,

J. Villain, R. Bidaux, J.-P. Carton, and R. Conte,

z₁ = z₂ = w и соответствует O(N)/O(N - 4) моде-

J. Physique 41, 1263 (1980).

ли (4) при P = 4. Учет следующих поправок, ра-

Е. Ф. Шендер, ЖЭТФ 83, 326 (1982).

зумеется, изменит оценочное значение Nc2 [31-33],

C. L. Henley, Phys. Rev. Lett. 62, 2056 (1989).

но не поменяет ситуацию качественно. В любом слу-

R. J. Elliott, Phys. Rev. 124, 346 (1961).

чае, это не влияет на другой результат: неподвиж-

D. N. Aristov, Phys. Rev. B 55, 8064 (1997).

ные точки любого типа отсутствуют в областях ста-

А. О. Сорокин, ЖЭТФ 145, 481 (2014).

бильности нашего основного состояния z₁ < 0 < z₂ и

10.

А. О. Сорокин, А.В. Сыромятников, Письма ЖЭТФ

z₂ < 0 < z₁ при всех значениях N. Таким образом,

96, 449 (2012).

в симметрийном классе G/H = Z₂ ⊗ O(N)/O(N - 2)

11.

A. O. Sorokin, Phys. Rev. B 95, 094408 (2017).

должен наблюдаться переход первого рода не только

12.

A. O. Sorokin, JMMM 479, 32 (2019).

при N = 3, что наблюдалось в данной работе мето-

13.

M. P. Gelfand, R. R. P. Singh, and D. A. Huse, Phys.

Rev. B 40, 10801 (1989).

дом Монте-Карло, но и при всех значениях N ≥ 2.

14.

A. Moreo, E. Dagotto, T. Jolicoeur, and J. Riera, Phys.

Напомним, что аналогичный результат был полу-

Rev. B 42, 6283 (1990).

чен для класса G/H = Z₂ ⊗ O(N)/O(N - 1) [20, 22],

15.

A. Chubukov, Phys. Rev. B 44, 392 (1991).

где неподвижные точки также отсутствуют в обла-

16.

B. Delamotte, D. Mouhanna, and M. Tissier, Phys.

сти стабильности исследуемого основного состояния

Rev. B 69, 134413 (2004).

для любых N. При этом единственная притягива-

17.

А. О. Сорокин, А. В. Сыромятников, ЖЭТФ 139,

ющая неподвижная точка появляется при больших

1148 (2011).

значениях N (N ≳ 6, но также для вырожденного

18.

А. О. Сорокин, А.В. Сыромятников, ЖЭТФ 140, 771

случая N = 1). Можно предположить, что аналогич-

(2011).

ный результат будет наблюдаться для многообразий

19.

D. Schmalfuss, R. Darradi, J. Richter, J. Schulenburg,

Штифеля общего вида V_N,P = O(N)/O(N -P ). Т.е. в

and D. Ihle, Phys. Rev. Lett. 97, 157201 (2006).

классе G/H = Z₂ ⊗ O(N)/O(N -P ) будет наблюдать-

20.

A. O. Sorokin, Phys. Lett. A 382, 3455 (2018).

ся переход первого рода, а в соответствующей моде-

21.

А. О. Сорокин, Письма ЖЭТФ 109, 423 (2019).

ли Гинзбурга-Ландау может присутствовать притя-

22.

А. О. Сорокин, ТМФ 200, 310 (2019).

гивающая неподвижная точка из O(N)/O(N - 2P )

23.

М. К. Рамазанов, А. К. Муртазаев, Письма ЖЭТФ

класса.

106, 72 (2017).

В заключение отметим, что при моделировании

24.

М. К. Рамазанов, А. К. Муртазаев, Письма ЖЭТФ

случаев q = π/3, 2π/3 мы наблюдали псевдоскей-

109, 610 (2019).

линговое поведение, характерное для перехода сла-

25.

F. R. Brown and T. J. Woch, Phys. Rev. Lett. 58, 2394

бого первого рода, с показателями ν = 0.39(2), β =

(1987).

= 0.12(1), γ = 0.91(5), β_k = 0.22(3), γ_k = 0.69(7), что

26.

M. Creutz, Phys. Rev. D 36, 515 (1987).

согласуется с результатами для (Q, Q) фазы [9, 17].

27.

J. N. Reimers, J. E. Greedan, and M. Björgvinsson,

Это явление трудно объяснить в рамках модели (5)

Phys. Rev. B 45, 7295 (1992).

в силу отсутствия точек с координатами Rez₁ < 0

28.

H. Kunz and G. Zumbach, J. Phys. A: Math. Gen. 26,

и Rez₂ > 0, которые могли бы приводить к замед-

3121 (1993).

лению РГ-потока и имитации скейлинга. Более того,

29.

H. T. Diep and D. Loison, J. Appl. Phys. 76, 6350

по аналогии с классом G/H = Z₂ ⊗ O(N)/O(N - 1)

(1994).

Письма в ЖЭТФ том 111 вып. 1 - 2

2020