Письма в ЖЭТФ, том 111, вып. 3, с. 203 - 208

О планковском пределе неупругой релаксации в металлах

М. В. Садовский¹⁾

Институт электрофизики Уральского отделения РАН, 620016 Екатеринбург, Россия

Поступила в редакцию 5 января 2020 г.

После переработки 5 января 2020 г.

Принята к публикации 5 января 2020 г.

Рассматривается простейшая модель линейного по температуре роста электросопротивления в ме-

таллах. Показано, что так называемый “планковский” предел для зависящей от температуры частоты

релаксации электронов является следствием определенного способа представления экспериментальных

данных по электросопротивлению и, в этом смысле, является иллюзорным.

DOI: 10.31857/S0370274X20030121

Линейный по температуре рост электросопротив-

чая совсем экзотические, основанные на аналогиях,

ления купратов и ряда других коррелированных си-

взятых из физики черных дыр, космологии и теории

стем в широком интервале температур от самых низ-

суперструн (см., например, [8-11]).

ких до достаточно высоких на протяжении уже мно-

В обычных металлах температурная зависимость

гих лет относится к числу главных загадок физики

сопротивления (проводимости) почти целиком связа-

высокотемпературных сверхпроводников. В послед-

на с процессами неупругого рассеяния на фононах.

нее время появился ряд интересных работ [1, 2], в

При достаточно высоких температурах T > 0.2Θ_D

которых, на основе анализа довольно обширного экс-

рассеяние на фононах доминирует и приводит к ли-

периментального материала по многим соединени-

нейному росту сопротивления с температурой:

ям, было показано, что в области линейного роста

сопротивления по температуре, частота рассеяния

ρ(T ) - ρ₀ = AT,

(1)

электронов (обратное время релаксации) с довольно

высокой точностью описывается зависимостью Γ =

где ρ₀ - остаточное сопротивление при T = 0, обу-

=^1τ = αkBTℏ , где α ∼ 1 и слабо меняется при перехо-

словленное статическим рассеянием на примесях.

де от одного материала к другому. В частности, для

На языке проводимости можно написать простую

систем в окрестности квантовых критических точек

формулу Друде:

(на фазовой диаграмме купратов и ряда аналогич-

ных систем) α лежит в интервале 0.7-1.1. Более того,

σ(T ) = σ₀ + σ(T ),

(2)

аналогичная зависимость довольно хорошо описыва-

где σ₀ - остаточная проводимость при T = 0, а

ет данные и для целого ряда обычных металлов (ти-

па Cu, Au, Al, Ag, Pb, Nb и т.п.) в области линейно-

ne²

го по температуре роста сопротивления (что обычно

σ(T ) =

τ (T ) =

Γ^-1(T),

(3)

реализуется при температурах T > Θ_D/5, где Θ_D -

дебаевская температура). При этом область измене-

причем m здесь и далее везде понимается как зонная

ния α охватывает заметно более широкий интервал

эффективная масса, а Γ(T) =

- зависящая от

τ (T )

от 0.7 до 2.7 [1, 2]. В связи с этими (и аналогичными)

температуры частота релаксации (рассеяния), обу-

результатами было введено [3] представление об уни-

словленная неупругим рассеянием электронов на фо-

версальном (не зависящем от силы взаимодействия)

нонах (или других аналогичных возбуждениях) и

“планковском” верхнем пределе частоты рассеяния

линейно растущая с температурой в области T

= Γ_P =kBTℏ. Для объяснения такого темпера-

τP

> 0.2Θ_D. Соответственно, для сопротивления имеем:

турного поведения сопротивления столь различных

систем, в том числе от самых низких температур,

ρ(T ) - ρ₀ =

Γ(T ).

(4)

ne²

к настоящему времени предложен целый ряд доста-

точно сложных теоретических моделей [4-7], вклю-

Представление о “планковской” релаксации мож-

но ввести из элементарных соображений [9]. При T >

¹⁾e-mail: sadovski@iep.uran.ru

> 0 работают процессы неупругого рассеяния за счет

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

203

204

М. В. Садовский

различных механизмов взаимодействия (электрон-

где ω_m = 2πmT , а спектральная плотность опреде-

фононный, взаимодействие со спиновыми флуктуа-

ляется как:

циями, квантовые флуктуации произвольной приро-

A(q, ω) =

ды). В частности, именно такие процессы ответствен-

∑

(

)

ны за установление термодинамического равновесия

=Z^-1

e^-

^T |(ρ_q)_nm

|²

1-e-ωTn

δ(ω - ω_mn), (11)

в системе электронов и формирование распределе-

ния Ферми. Проводимость металла (вырожденный

где ω_mn = E_m - E_n, (ρ_q)_nm =< n|ρ_q|m >= (ρ^+q)_mn.

случай) определяется распределением электронов в

Динамический структурный фактор флуктуаций

слое шириной ∼ k_BT вокруг уровня Ферми (химпо-

определяется как [12, 13]:

тенциала).

∑

Проведем элементарную оценку, воспользовав-

S(q, ω) = Z^-1 e^-

^T |(ρ_q)_nm|²δ(ω - ω_mn).

(12)

шись соотношением неопределенности энергия - вре-

мя:

Сравнивая (11), (12), получаем:

ΔEτ > ℏ,

(5)

[

]

где τ - время жизни квантового состояния, а ΔE -

A(q, ω) = S(q, ω)

1-e-T

(13)

неопределенность его энергии. Естественно, что в

рассматриваемой ситуации τ = τ(T ), а ΔE ∼ k_BT ,

откуда немедленно следует упомянутая выше оцен-

ка:

k_BT

Γ(T ) =

<α

≡ αΓ_P =

(6)

τ (T )

ℏ

τ_P

где α ∼ 1. Видим, что согласно такой элементарной

оценке “планковская” релаксация определяет именно

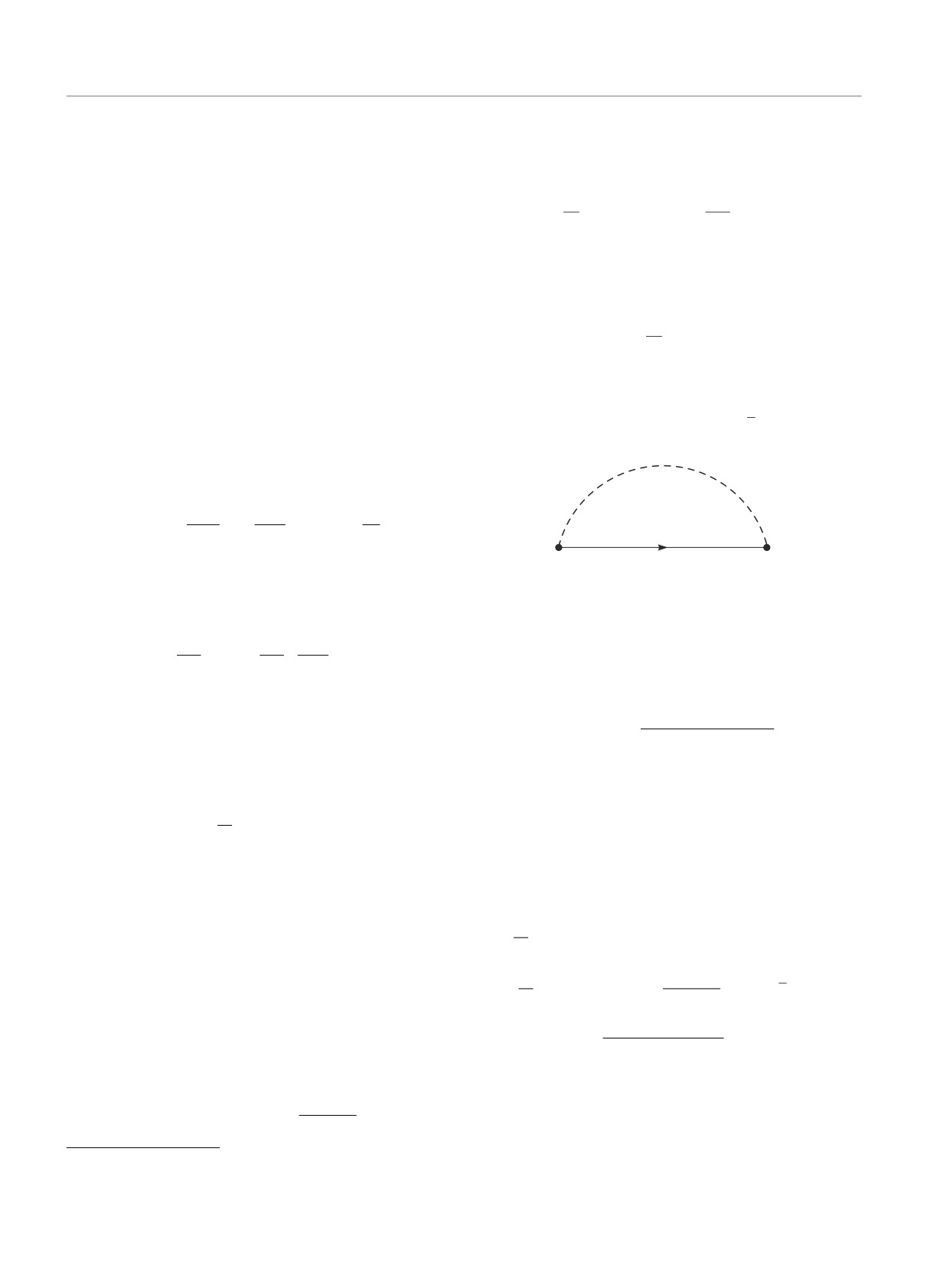
Рис. 1. Диаграмма второго порядка для собственно

верхнюю границу сопротивления за счет неупругих

энергетической части. Пунктирная линия - функция

Грина квантовых флуктуаций F , сплошная линия -

процессов рассеяния:

функция Грина электрона G

k_BT

ρ(T ) - ρ₀ =

Γ(T ) <

≡ αρ_P (T ).

(7)

ne²

ℏ

Электронная функция Грина в мацубаровском

Очевидно, что эта оценка является достаточно спеку-

представлении записывается как:

лятивной в системе многих взаимодействующих час-

тиц.

G(ε_n, p) =

(14)

iε_n - ξ_p - Σ(ε_n, p)

Рассмотрим следующий гамильтониан взаимо-

действия электронов металла с произвольными кван-

где ε_n = (2n + 1)πT , ξ_p - электронный спектр, отсчи-

товыми флуктуациями бозевского типа²⁾:

танный от уровня химпотенциала. Собственно энер-

∑

гетическую часть одноэлектронной функции Грина,

H_int =

g_qa^+p+qa_pρ_q.

(8)

предполагая справедливость теоремы Мигдала [15],

можно взять в простейшем приближении, показан-

Здесь использованы стандартные обозначения опе-

ном на диаграмме рис. 1:

раторов рождения и уничтожения электронов, ρ_q -

Σ(ε_n, p) =

оператор квантовой флуктуации “чего угодно” (плот-

T∑

∑

ности ионов, например, если речь идет о решетке),

g²

F (q, iω_m)G(ε_n + ω_m, p + q) =

g_q - соответствующая константа связи (матричный

элемент потенциала взаимодействия) [12, 13]. Введем

∫ ∞

T∑

∑

S(q, ω)

(

)

соответствующую (мацубаровскую) функцию Грина

g²

dω

1-e-T

-∞

iω_m - ω

как:

F (q, τ) = - < T_τ ρ_q(τ)ρ^+q(0) > .

(9)

(15)

iε_n + iω_m - ξ_p+q

Для нее можно выписать обычное спектральное (бо-

зевское) представление [14]:

Рассмотрим теперь случай, когда средняя частота

∫ ∞

флуктуаций 〈Ω〉 существенно ниже температуры T .

A(q, ω)

F (q, iω_m) =

dω

(10)

Тогда в (15) достаточно ограничиться лишь слагае-

iω_m - ω

-∞

мым с m = 0 и перейти, таким образом, к картине

²⁾В дальнейшем полагаем ℏ = k_B = 1.

квазиупругого рассеяния на флуктуациях:

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

О планковском пределе неупругой релаксации в металлах

205

∑

∫ ∞

S(q, ω)

Для дальнейшего упрощения модели предположим,

Σ(ε_n, p) =

g²

dω

-∞

iε_n - ξ_p+q

что спектр флуктуаций является бездисперсионным

∑

(типа эйнштейновского фонона или оптического фо-

g^2qS(q)

(16)

нона с очень слабой дисперсией), полагая ω_q = Ω₀.

iε_n - ξ_p+q

Тогда проводя все вычисления аналогично задаче об

электроне в поле случайных примесей [15], получаем:

где ввели структурный фактор флуктуаций [13]:

∫ ∞

2g²⁰

S(q) =

dωS(q, ω).

(17)

Σ(ε_n, p) = -iπsign ε_n N(0)T,

(25)

Ω₀

N -∞

Фактически, это прямой аналог известного прибли-

где N(0) - плотность состояний на уровне Ферми.

жения Займана-Эдвардса в теории жидких метал-

Соответственно, затухание записывается как:

лов. Случай S(q) = const соответствует хаотическо-

Γ(T )

2g²⁰

му распределению статических рассеивающих цен-

=π

N (0)T = πλ₀T,

(26)

Ω₀

тров [15].

Оператор флуктуации ρ_q для случая некоторой

где стандартным образом ввели безразмерную кон-

коллективной моды может быть выражен через (бо-

станту связи:

зевские) операторы уничтожения и рождения соот-

2g²⁰N(0)

λ₀ =

(27)

ветствующих квантов (например, фононов) [13]:

Ω₀

(

)

Функция Грина электрона имеет при этом обычный

ρ_q =

√

b^+q + b_-q

(18)

вид [15]:

Соответственно имеем:

G(iε_n, p) =

(28)

iε_n - ε_p +₂

Γ(T )sign ε

S(q, ω) =

∑

[

где отсутствуют какие-либо перенормировочные

=Z^-1

e-βEm

< m|b_qb^+q|m > δ(ω - ω_q) +

факторы (вычет в полюсе функции Грина Z = 1),

]

что естественно для температур, существенно

+ < m|b^+-qb_-q|m > δ(ω + ω_q)

(19)

превышающих частоты квантовых флуктуаций.

Проводя стандартные вычисления [15], получим

где ω_q - спектр соответствующих возбуждений. Вво-

электросопротивление в виде:

дя обычное бозевское распределение:

∑

ρ(T ) =

Γ(T ) = 2πλ₀ρ_P (T ),

(29)

n_q

=Z^-1

e-βEm < m|b^+qb_q|m > =

(20)

ne²

eβωq - 1

что, по существу, просто совпадает с высокотемпера-

получаем [13]

турным пределом теории Элиашберга-МакМиллана

[16] . При этом константа α, обычно используемая

S(q, ω) = [(n_q + 1)δ(ω - ω_q) + n_qδ(ω + ω_q)] =

при записи “планковского” времени релаксации в ви-

= δ(ω - ω_q) + n_q [δ(ω - ω_q) + δ(ω + ω_q)] .

(21)

де (6), выражается через параметры теории как:

В условиях, когда T ≫ ω_q, имеем:

α = 2πλ₀.

(30)

n_q =

(22)

Естественно, что она не универсальна и просто про-

ω_q

порциональна константе взаимодействия.

и, соответственно:

Все это, по сути дела, давно известно и тривиаль-

но обеспечивает линейный рост сопротивления с тем-

S(q) =

2T ,

(23)

пературой, в соответствии с многочисленными экспе-

ω_q

риментами. Для того, чтобы такой рост наблюдал-

т.е. получаем структурный фактор, линейно расту-

ся при низких температурах, достаточно выполне-

щий с температурой, импульсная зависимость ко-

ния неравенства Ω₀ ≪ T . В окрестности квантовой

торого определяется просто спектром соответствую-

критической точки (любой природы) можно ожидать

щей коллективной моды (флуктуации). Тогда:

типичного “смягчения” флуктуационной моды в духе

соотношения [17]:

∑

2g²

Σ(ε_n, p) = T

(24)

ω_q iε_n - ξ_p+q

Ω₀ ∼ |x - x_c|^zν,

(31)

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

206

М. В. Садовский

где x, например, - концентрация носителей вбли-

где

∑

зи критической x_c, а ν и z - стандартные критиче-

F (ω) = A(q, ω)

(38)

ские индексы теории квантовых фазовых переходов,

определяющие критическое поведение характерных

- плотность состояний флуктуаций. Тогда для (36)

длин:

из (35) получаем:

ξ ∼ |x - x_c|^-ν, ξ_τ ∼ |x - x_c|^-zν,

(32)

где τ обозначает мнимое (мацубаровское) время, так

Σ(ε_n) =

N (0)

что выше мы можем просто положить Ω₀ ∼ ξ^-1τ. Это

∫ ∞

dω

и обеспечивает линейное поведение по температуре в

α²(ω)F(ω)N(0)

dξ

-∞

iε_n - ξ

системах типа купратов.

∫ ∞

dω

Можно обойтись без явного введения фононов

= -iπsignε_nT

α²(ω)F(ω) =

(или других квазичастиц, связанных с флуктуаци-

-∞

ями). Из уравнения (13) при ω ≪ T следует:

Γ(T )

= -iπsignε_nλT ≡ -i

sign ε_n,

(39)

A(q, ω) ≈

S(q, ω)

(33)

где ввели безразмерную константу связи как в тео-

рии МакМиллана-Элиашберга:

или

S(q, ω) ≈

A(q, ω).

(34)

∫^∞ dω

λ=2

α²(ω)F(ω),

(40)

Подставляя это выражение в (16), получаем следу-

ющее выражение для собственно энергетической ча-

величина которой фактически определяется (усред-

сти:

ненной согласно

(37)) спектральной плотностью

∑

∫ ∞

флуктуаций A(q, ω).

dω A(p - p^′, ω)

Σ(ε_n, p) =

g²

(35)

pp^′

Итак, мы получаем:

−∞

ω iε_n - ξ_p′

p^′

Γ(T ) = 2πλT,

(41)

где определяющую роль имеет спектральная плот-

ность флуктуаций A(q, ω), которая не обязательно

что формально имеет тот же вид, что и (26) и сразу

имеет квазичастичный вид. Естественно, что для

же приводит к результату типа (29).

простейшей модели с A(q, ω) = δ(ω - Ω₀) (эйнштей-

В работах [1, 2] экспериментальные данные по со-

новская модель флуктуаций) из (35) немедленно сле-

противлению обрабатывались по формуле Друде (4),

дуют полученные выше результаты (25)-(27).

где эффективная масса определялась из низкотем-

Далее предполагаем, что флуктуации рассе-

пературных измерений (электронной теплоемкости

ивают электроны в некотором достаточно узком

или осцилляционных эффектов в сильном магнит-

слое вокруг поверхности Ферми, ширина которого

ном поле) и которая получается из зонной эффектив-

определяется их характерными частотами (〈Ω〉 ≪

ной массы простой заменой m → m = m(1 + λ), яв-

≪ T). Тогда, действуя в духе теории Элиашберга-

но учитывающей фононную перенормировку. Некор-

МакМиллана, можно ввести собственно энерге-

ректность такого подхода отмечалась в работе [18].

тическую часть, усредненную по импульсам на

Покажем, что именно такая обработка данных и со-

поверхности Ферми:

здает иллюзию универсальной планковской релакса-

∑

ции в металлах. В самом деле, выражение (29) для

Σ(ε_n) =

δ(ξ_p)Σ(ε_n, p),

(36)

высокотемпературного предела сопротивления фак-

N (0)

тически тождественно переписывается следующим

образом:

а также эффективное (усредненное по начальным и

конечным импульсам на поверхности Ферми) взаи-

m(1 + λ) Γ(T )

модействие:

ρ(T ) =

Γ(T ),

(42)

ne²

1+λ

ne²

где

g^2pp′ A(p - p^′, ω) =⇒

∑

Γ(T ) = 2π

(43)

=⇒

g^2pp′ A(p - p^′, ω)δ(ξp)δ(ξp′ )≡

1+λ

N (0)

p^′

что при λ ≫ 1 дает:

≡

α²(ω)F(ω),

(37)

Γ(T ) = 2πT

(44)

N (0)

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

О планковском пределе неупругой релаксации в металлах

207

и, таким образом, просто имитирует универсальное

В области низких температур (T < 〈Ω〉) функция

“планковское” поведение частоты релаксации (6) c

Грина имеет вид:

= 2π, не зависящее от константы взаимодей-

ствия электронов с флуктуациями (фононами). За-

G(ε_n, p) =

(47)

iε_n - Zξ_p +ⁱZΓ(T)signεn

мена m → m = m(1 + λ) в (42) вполне коррект-

на, несмотря на то, что мы имеем дело с пределом

где перенормировочный фактор Z < 1 считается для

высоких температур - при обработке эксперимен-

простоты константой. Вклад ZΓ(T ) =

Γ(T ) в зна-

тов в [1, 2] используется именно эффективная масса

менателе описывает затухание квазичастиц, для ко-

m, полученная из низкотемпературных измерений,

торого, как могло бы показаться, имеется “универ-

включающая эффекты перенормировки. Для коли-

сальный” высокотемпературный предел (44). Одна-

чественных оценок достаточно существенным оказы-

ко это не так - при высоких температурах (T > 〈Ω〉),

вается учет перенормировки массы за счет межэлек-

как видно из приведенных выше результатов, пере-

тронного взаимодействия, при котором выражение

нормировочный фактор Z → 1. Но и при низких

(43) нужно переписать как:

температурах, когда Z < 1, член Zξ_p в знаменате-

ле (47) описывает перенормированный спектр с мас-

Γ(T ) = 2π

(45)

1+λ+λ_ee

сой m = m(1 + λ), так что скорость электрона на

поверхности Ферми vF = pF/m → vF = pF/m =

где λ_ee - безразмерный параметр, определяющий пе-

= v_F/(1 + λ). Перенормировка затухания соответ-

ренормировку массы за счет межэлектронного вза-

ствует перенормировке времени свободного пробега

имодействия. Например, в теории ферми-жидкости

Γ^-1 = Γ^-1(1 + λ). Видим, что длина свободного про-

Ландау-Силина λ_ee =

, где Fs1 - соответствую-

бега не перенормируется: l = v_F Γ^-1 = v_F Γ^-1 и эф-

щий коэффициент в разложении функции Ландау

фекты многочастичной перенормировки, существен-

[13]. Прямые DMFT расчеты в модели Хаббарда да-

ные при низких температурах, вообще не влияют на

ют значения фактора перенормировки для металли-

проводимость (сопротивление) [20], так что никаких

ческой фазы Z = (1+λ_ee)^-1, монотонно меняющиеся

реальных ограничений на сопротивление системы от-

с ростом величины хаббардовского взаимодействия

сюда не возникает. Этот результат есть прямое след-

U в интервале от 1 до 0 [19]. Поэтому, для грубых

ствие общих тождеств Уорда [21].

оценок можно использовать для типичных металлов

Автор признателен Э. З. Кучинскому за много-

оценку λ_ee ∼ 1. Тогда:

численные полезные обсуждения.

2πλ

Работа выполнена при частичной поддерж-

α=

(46)

1+λ+λ_ee

ке гранта Российского фонда фундаментальных

исследований # 20-02-00011.

Тогда интервалу значений α = 0.7 - 2.7 [1, 2] при

λ_ee = 1 соответствует интервал λ = 0.25 - 1.5, что

кажется вполне разумным. Например, для Al име-

ем расчетное значение λ = 0.44 [16], что немедленно

1. J. A. N. Bruin, H. Sakai, R. S. Perry, and

дает α = 1.03 в прекрасном соответствии с “экспе-

A. P. MacKenzie, Science 339, 804 (2013).

риментальным” значением α = 1 из работы [1]. Для

2. A. Legros, S. Benhabib, W. Tabis et al. (Collaboration),

Pb, принимая λ = 1.68 [16], получаем α ∼ 2.86 в ра-

Nature Phys. 15, 142 (2019).

зумном согласии с α = 2.7 [1]. Аналогичным образом

3. J. Zaanen, Nature 430, 512 (2004).

для Nb имеем λ = 1.26 [16], и мы получаем α ∼ 2.42,

4. V. R. Shaginyan, K. G. Popov, and V. A. Khodel, Phys.

в неплохом согласии со значением α = 2.3 [1]. В це-

Rev. B 88, 115103 (2013).

лом, с учетом грубости оценки λ_ee ∼ 1 такое согласие

5. V. R. Shaginyan, M. Ya. Amusia, A. Z. Msezane,

представляется достаточно убедительным³⁾.

V. A.

Stephanovich,

G. S.

Japaridze,

and

Таким образом, “экспериментально” наблюдаемая

S. A. Artamonov, JETP Lett. 110, 290 (2019).

универсальная планковская релаксация в металлах,

6. A. A. Patel and S. Sachdev, Phys. Rev. Lett. 123,

не зависящая от величины взаимодействия, являет-

066601 (2019).

ся не более, чем иллюзией, связанной с принятой в

7. G. E. Volovik, JETP Lett. 110, 352 (2019).

работах [1, 2] процедурой представления эксперимен-

8. J. Zaanen, Nature 448, 1000 (2007).

тальных данных.

9. S. A. Hartnoll, Nature Phys. 11, 54 (2015).

³⁾Мы всюду пренебрегаем незначительным [16] отличием λ

10. C. P. Herzog, P. Kovtun, S. Sachdev, and D. T. Son,

от λtr .

Phys. Rev. D 75, 085020 (2007).

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

208

М. В. Садовский

11. S. A. Hartnoll, P. K. Kovtun, M. Muller, and S. Sachdev,

15. М. В.

Садовский,

Диаграмматика,

ИКИ-

Phys. Rev. B 76, 144502 (2007).

РХД, Москва-Ижевск

(2019)

[M. V. Sadovskii,

12. Д. Пайнс, Проблема многих тел, Мир, М. (1963)

Diagrammatics, World Scientific, Singapore (2019)].

[D. Pines, The Many Body Problem, W. A. Benjamin,

16. S. Y. Savrasov and D. Y. Savrasov, Phys. Rev. B 54,

N.Y. (1961)].

16487 (1996).

13. Д. Пайнс, Ф. Нозьер, Теория квантовых жидкостей,

17. S. Sachdev, Quantum Phase Transitions, Cambridge

Мир, М. (1967) [D. Pines and P. Nozieres, The Theory

University Press, Cambridge (1999).

of Quantum Liquids, W. A. Benjamin, N.Y. (1966), v. 1].

18. C. M. Varma, ArXiv:1908.05686.

14. А. А. Абрикосов, Л. П. Горьков, И. Е. Дзялошинский,

19. A. Georges, G. Kotliar, W. Krauth, and

Методы квантовой теории поля в статистической

M. J. Rozenberg, Rev. Mod. Phys. 68, 13 (1996).

физике, Физматгиз, М. (1963), Добросвет, М. (1998)

20. G. Grimvall, Physica Scripta 14, 63 (1978).

[A. A. Abrikosov, L. P. Gorkov, and I. E. Dzyaloshinskii,

Methods of Quantum Field Theory in Statistical Physics,

21. V. Heine, P. Nozieres, and J. W. Wilkins, Phil. Mag. 13,

Pergamon Press, Oxford (1963)].

741 (1966).

Письма в ЖЭТФ том 111 вып. 3 - 4

2020