Письма в ЖЭТФ, том 111, вып. 3, с. 209 - 212

О взаимодействии локализованных решений нелинейного уравнения

Клейна-Гордона с переменной массой

Р. К. Салимов⁺¹⁾, Е. Г. Екомасов^+∗×

⁺Башкирский государственный университет, 450076 Уфа, Россия

^∗Тюменский государственный университет, 625003 Тюмень, Россия

^×Южно-Уральский государственный университет, 454080 Челябинск, Россия

Поступила в редакцию 7 декабря 2019 г.

После переработки

20 декабря 2019 г.

Принята к публикации 20 декабря 2019 г.

Исследовалась система из материальных частиц и поля, описываемого нелинейным уравнением

Клейна-Гордона. Рассматривалось модифицированное уравнение Клейна-Гордона, сохраняющее реше-

ния уравнения Клейна-Гордона с нулевой и ненулевой массами. Частицы создают неоднородности поля

и взаимодействуют с ним. Показано, что в данной модели возможны осциллирующие устойчивые лока-

лизованные решения. Осциллирующие локализованные решения в данной системе порождают бегущие

волны, приводящие к взаимодействию этих решений на больших расстояниях.

DOI: 10.31857/S0370274X20030133

Пространственно локализованные решения нели-

гие решения - переносчики взаимодействия. Для это-

нейных полей широко используются в современной

го предлагается рассмотреть систему из взаимодей-

физике, например, в нелинейной оптике [1, 2], физи-

ствующих подвижных неоднородностей уравнений

ке конденсированных сред [3], физике частиц и кос-

Клейна-Гордона с переменной массой вида

мологии [4, 5]. Свойства некоторых из таких про-

u_xx + u_yy + u_zz - u_tt = F(u)G(u^2x + u^2y + u^2z - u^2t).

странственно локализованных уединенных волн поз-

(1)

воляют рассматривать их как классические части-

цеподобные объекты. Примером такого подхода яв-

Такие уравнения уже рассматривались ранее ав-

ляются скирмионы [6] или кинки уравнения синус-

торами [13] и интересны тем, что при условии G(0) =

Гордон [7], т.е. топологические стационарные солито-

= 0 содержат два типа решений. Для плоских волн

ны. В современной нелинейной волновой теории так-

u^2x + u^2y + u^2z - u^2t = 0 они совпадают с уравнени-

же большое внимание уделяется нахождению лока-

ем Клейна-Гордона с нулевой массой, а для случая

лизованных и периодических по времени решений [8-

u^2x + u^2y + u^2z - u^2t = 0 их можно интерпретировать

13]. В данной работе предлагается объединение этих

как уравнение Клейна-Гордона с ненулевой массой.

подходов.

Хотя уравнение (1) не допускает лагранжева форма-

Одним из свойств солитонов в строгом смысле

лизма, его можно приблизить к лагранжевым систе-

является сохранение формы при движении и вза-

мам выбором функций F и G. Действительно, взяв

имодействии с другими солитонами. При этом об-

в качестве функции G(η), например функцию вида

ласть заметного взаимодействия солитонов опреде-

tanh(η²), при решениях, достаточно сильно отличаю-

ляется пространственной областью, в которой со-

щихся от плоских волн, получим для линейной функ-

литонное решение отлично от вакуумного решения.

ции F (u) уравнение Клейна-Гордона с ненулевой по-

Например, для кинков уравнения синус-Гордон эта

стоянной массой. При этом для каждого типа реше-

область стремиться к вакуумному решению экс-

ний можно приближенно построить свою функцию

поненциально. Для более полной аналогии между

Лагранжа или Гамильтона.

взаимодействующими на больших расстояниях ча-

Далее для простоты рассмотрим одномерный слу-

стицами и солитонами интересно рассмотреть мо-

чай. Для получения частицеподобных решений в

дель, в которой кроме частицеподобных локализо-

уравнение (1) внесем слагаемое вида подвижной пря-

ванных полевых решений существовали бы и дру-

моугольной притягивающей неоднородности

u_xx - u_tt = F(u)G(u^2x - u^2t) - f(x, x_def)sin(u),

(2)

¹⁾e-mail: salemsrkk@yandex.ru

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

209

210

Р. К. Салимов, Е. Г. Екомасов

здесь x_def - координаты центра подвижной неодно-

Использовалась численная схема Абловица, Кру-

родности.

скала, Лейдика [15] для уравнения (2) и алгоритм

Зададим также уравнение движения для подвиж-

Верле для уравнения движения неоднородности.

ной неоднородности

Вначале проверялось предположение о существова-

∫

)

нии осциллирующих решений и отсутствии асимп-

∂f

m(x_def)_tt = -2

cos²

dx.

(3)

тотически устойчивых решений. Результаты числен-

∂x_def

ных экспериментов показывают, что колебания не за-

Взаимодействие поля и подвижной неоднородно-

тухают в течение всего длительного времени наблю-

сти здесь аналогично рассматриваемому ранее взаи-

дения (t = 600-800).

модействию [14]. В данном случае релятивистскими

При этом расходящиеся колебания периодически

эффектами изменения потенциала взаимодействия,

подавлялись на периферии локализованного реше-

которые вызывали нестабильность подвижной неод-

ния. Для этого решение u и его производная по вре-

нородности в модели [14], пренебрегаем. Но в дан-

мени u_t при превышении некоторого расстояния от

ной модели также возникает решение для поля, ко-

центра неоднородности (равного 6) умножались на

торое будет вызывать в общем случае нестабиль-

экспоненциально затухающую с расстоянием функ-

ность неоднородности. Для случая, когда функция

цию. На рисунке 1 видно, что, несмотря на подав-

G(η) = const, для притягивающей неоднородности f

прямоугольного вида численно можно получить ло-

кализованное решение для поля u, стремящееся со

временем к стационарному. Асимптотическая устой-

чивость локализованного решения при G(η) = const

вызвана существованием гамильтонова формализма.

Поэтому естественно предположить, что при отсут-

ствии гамильтонова формализма и минимума энер-

гии, т.е. при G(η) = const, также не будет и стремле-

ния локализованного решения к положению равнове-

сия. Таким образом, в такой системе будут возможны

некие колебания локализованных решений. Эти ко-

лебания будут в свою очередь вызывать появление

бегущих волн, которые можно интерпретировать как

переносчики взаимодействия.

Для проверки приведенных выше предположений

Рис. 1. Линии уровня функции u на больших временах

численно решалась система уравнений вида (2)-(3),

здесь θ - функция Хэвисайда и остальные функции

имеют вид

ление волн на периферии локализованного решения,

источником волн является его центральная область.

F (u) = u + u³ + αuⁿ ,

(4)

Представлен случай поведения решения при значе-

ниях параметров λ = 20, γ = 2000, m = 50, α = 0.5,

G(u^2x - u^2t) = tanh(γ(u^2x - u^2t)²),

(5)

n = 11, l = 1.

Далее исследовалось взаимодействие на расстоя-

f (x, x_def) = λ(θ(x - x_def + l) - θ(x - x_def - l)).

(6)

нии двух таких решений. Решалась система вида

Вид функции G(η) выбирался таким образом,

∑

чтобы она отличалась от константы в малом диапа-

u_xx - u_tt = F(u)G(u^2x - u^2t) -

f (x, x^idef) sin(u),

i=1,2

зоне значений η. При этом предполагалось, что и ре-

шение для поля в этом случае будет аналогичным ре-

(7)

шению при G = const. Нелинейные члены в (4) были

∫

выбраны для изучения влияния разного рода нели-

∂f

(u)

m(x^ideff)_tt = -2

cos²

dx.

(8)

нейностей на бегущие волны. Прямоугольная неод-

∂x^idef

нородность поля f(x, x_def) для существования лока-

лизованных решений должна быть достаточно про-

В качестве начальных условий для этого исполь-

тяженной и глубокой. Локализованные решения на-

зовались установившиеся решения для одной неод-

блюдались в диапазоне параметров γ = 100 - 5000,

нородности с подавленными на периферии волнами.

λ = 10-30, l = 1.

Далее расходящиеся волны не подавлялись. Одно

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

О взаимодействии локализованных решений нелинейного уравнения Клейна-Гордона...

211

из решений в некоторых численных экспериментах

умножалось на -1. В основном, при взаимодействии

двух таких неоднородностей как одного, так и раз-

ных знаков, фиксировалось отталкивание между ни-

ми. Но в некоторых случаях, для решений разных

знаков было зафиксировано притяжение, т.е. с тече-

нием времени расстояние между подвижными неод-

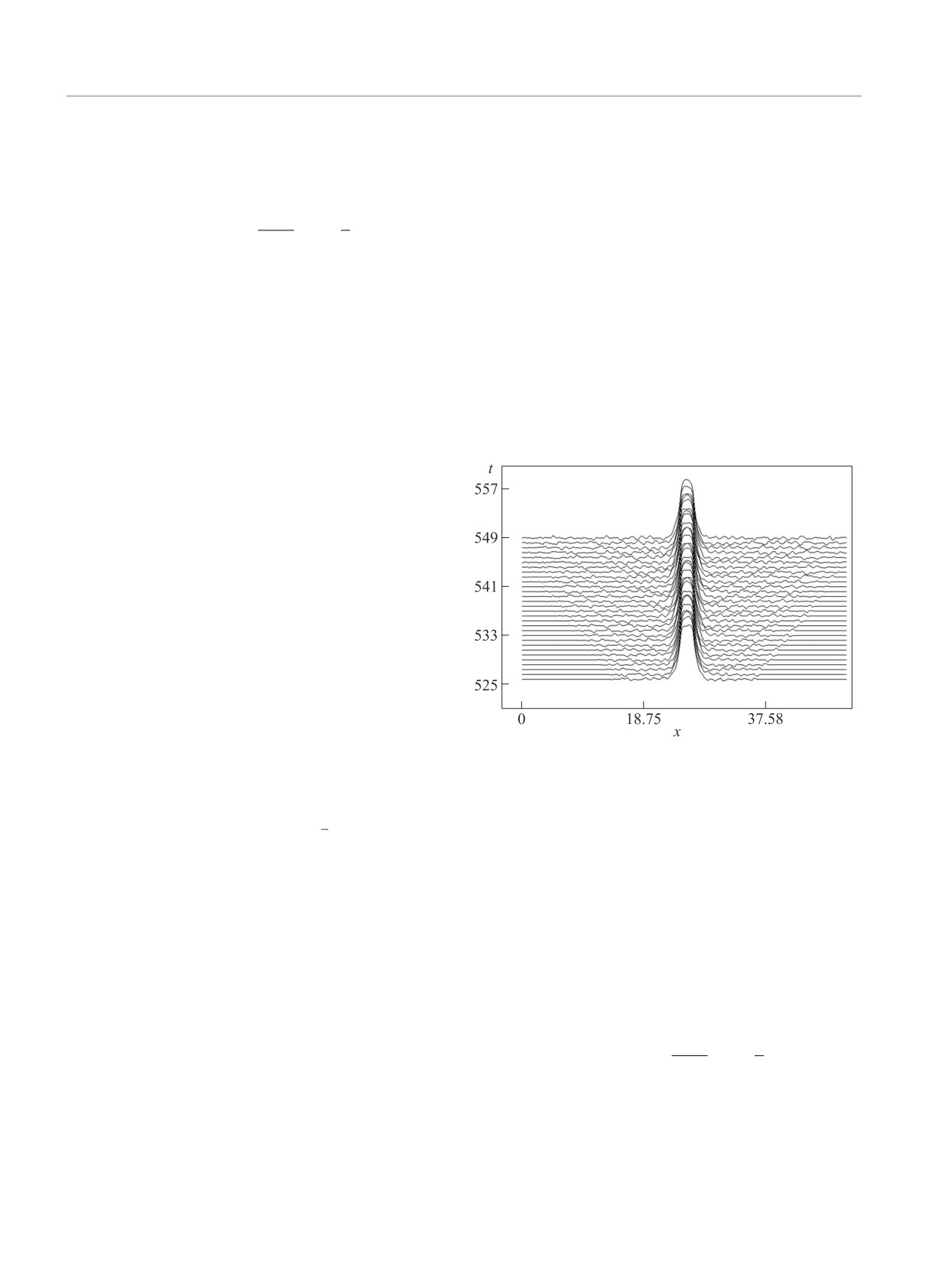
нородностями заметно уменьшалось. Например, для

параметров λ = 20, γ = 500, m = 50, α = 0, l = 1 и

первоначальном расстоянии между неоднородностя-

ми 15, расстояние между неоднородностями умень-

шается до 13.5 для времени t = 52 (см. рис.2). Такое

Рис. 3. Отталкивание локализованных решений одного

знака

движения. Хотя предложенная модель не имеет га-

мильтонова формализма, это не исключает перспек-

тивы построения подобных моделей с приближенно

сохраняющейся энергией. Но, теряя строгое сохране-

ние функции Гамильтона, в данной модели можно

получить возможность взаимодействия между соли-

тоноподобными решениями на больших расстояниях,

как было показано выше. Кроме того, представлен-

ная модель интересна с методологической точки зре-

ния, как пример системы со взаимодействием меж-

Рис. 2. Притяжение локализованных решений разных

ду солитоноподобными решениями, которую можно

знаков

легко обобщить на двумерный и трехмерный случай.

притяжение нельзя объяснить влиянием границ, так

как для решений одного знака при тех же условиях

1. A. Hasegawa and M. Matsumoto, Optical Solitons in

наблюдается отталкивание (см. рис. 3).

Fibers, Springer, Berlin, Heidelberg (1990).

Здесь нужно отметить, что такое взаимодействие

2. N. Akhmediev and A. Ankiewicz, Dissipative Solitons,

вызвано волнами-переносчиками, так как оно про-

Lecture Notes in Physics, Springer, Berlin, Heidelberg

является не сразу, а через некоторое время, срав-

(2005).

нимое со временем распространения бегущих волн

3. A. R. Bishop, J. A. Krumhansl, and S. E. Trullinger,

между локализованными решениями. Еще одним ин-

Physica D 1(1), 1 (1980).

тересным следствием этой модели является неста-

4. В. А. Рубаков, Классические калибровочные поля,

ционарность положения подвижной неоднородности

УРСС, М. (1999).

около положения равновесия, вызванная нестацио-

5. Д. С. Горбунов, В. А. Рубаков, Введение в теорию

нарностью решения для поля. В частности, для слу-

ранней Вселенной: теория горячего Большого взры-

чая λ = 20, γ = 2000, m = 50, α = 0.5, n = 11, центр

ва, УРСС, М. (2008).

неоднородности совершает колебания с амплитудой

6. G. E. Brown, Selected papers, with commentary, of Tony

порядка 10^-3. Подобное поведение может быть ин-

Hilton Royle Skyrme, World Scientific 20th Century

тересно с точки зрения построения солитонных мо-

Physics, World Scientific, Singapore (1995).

делей частиц с ненулевым собственным моментом

7. S. R. Coleman, Phys. Rev. D 11, 2088 (1975).

Письма в ЖЭТФ том 111 вып. 3 - 4

2020

5^∗