Письма в ЖЭТФ, том 111, вып. 7, с. 469 - 474

Исследование гофрированных нанотрубок нового типа, вырезанных

из бислойного графена с углом Муара Θ = 27.8^◦

В.А.Демин⁺¹⁾, А.А.Артюх⁺, В.А.Сороко^∗×, Л.А.Чернозатонский⁺

⁺Институт биохимической физики им. Н. М. Эмануэля РАН, 119334 Москва, Россия

^∗Институт ядерных проблем Белорусского государственного университета, 220030 Минск, Белоруссия

^×Центр квантовой спинтроники физического факультета Норвежского университета науки и технологии,

NO-7491, Трондхейм, Норвегия

Поступила в редакцию 5 марта 2020 г.

После переработки 5 марта 2020 г.

Принята к публикации 5 марта 2020 г.

Работа посвящена моделированию новых квазиодномерных полых наноструктур, подобных сплю-

щенным нанотрубкам. Они могут быть получены путем соединения краев нанолент, вырезанных из

бислойного графена с углом Муара Θ = 27.8^◦ . Полученные нанотрубки нехиральны и содержащат це-

почки топологических дефектов на замкнутых краях. Приведено детальное описание их структуры, а

также показана энергетическая стабильность. С помощью первопринципных методов были определены

электронные свойства, а также их изменение при деформациях. Все исследованные нанотрубки являют-

ся металлами, за исключением структуры с шириной 14Å, которая имеет запрещенную зону Eg = 0.2 эВ.

Показано, что электронные и упругие свойства таких нанотрубок существенно отличаются от свойств

образующих их нанолент и одностенных углеродных нанотрубок.

DOI: 10.31857/S0370274X20070085

Введение. Углеродные наноматериалы, такие

ширины, края которой при дальнейшем взаимодей-

как нанотрубки (УНТ) и графеновые структуры,

ствии с электронами замыкались, образуя одностен-

представляют огромный интерес для практических

ную УНТ. Таким образом были получены нанотруб-

приложений в связи с их уникальными свойствами.

ки диаметром около 1 нм, соединяющие два масси-

Одним из перспективных направлений является их

ва бислойного графена. Бислойный графен может

применение в электронике. Известно, что УНТ обла-

иметь различные типы упаковки слоев: АА, АВ, а

дают широким спектром электронных свойств - от

также иметь различные углы кристаллографической

металлических до полупроводниковых с шириной за-

ориентации - угол Муара Θ. Наиболее стабильной

прещенной зоны до 2 эВ. Структура нанотрубки опи-

является АВ упаковка, однако уже возможно полу-

сывается индексами n и m, разность которых опреде-

чать бислои с углом Муара с точностью до 0.1^◦, но

ляет ее электронные свойства. Если разность индек-

мало отличающиеся по ее энергетической стабиль-

сов n-m кратна трем, то УНТ являются металлами,

ности [3]. При повороте слоев биграфена на угол Θ

а при других значениях n- и m-полупроводниками.

образуется сверхрешетка, период трансляции кото-

Углеродные нанотрубки впервые были идентифици-

рой зависит от угла [4]. Соразмерная сверхрешетка

рованы в 1991 г. [1]. С того времени методы получе-

с Θ = 27.8^◦ (рис.1а), которая имеет относительно

ния значительно усовершенствовались, однако одной

маленькую суперячейку (количество атомов N = 52,

из важнейших проблем для практического примене-

период l = 8.9Å), наблюдалась экспериментально на

ния УНТ остается сложность синтеза УНТ опреде-

поверхности SiC [5]. В настоящее время к муаровым

ленной геометрии и, следовательно, с определенны-

бислоям приковано огромное внимание в связи с тем,

ми свойствами.

что при Θ = 1.1^◦ была обнаружена сверхпроводи-

В 2013 г. экспериментально были получены на-

мость при температуре 1.7 К [6]. Помимо изменения

нотрубки из бислойного графена в АА упаковке

угла Θ возможны различные модификации бислоя,

[2]. Используя просвечивающий электронный микро-

изменяющие свойства, такие как физические геомет-

скоп, была вырезана двуслойная нанолента заданной

рические (механические деформации) и структурные

(создание отверстий [7-11]).

¹⁾e-mail: victordemin88@gmail.com

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

469

470

В.А.Демин, А.А.Артюх, В.А.Сороко, Л.А.Чернозатонский

Рис. 1. (Цветной онлайн) (a) - Бислойный графен с углом Муара Θ = 27.8^◦ с суперячейкой из 52 атомов углерода.

(b) - Наносетка из Y -соединений, содержащая одномерную структуру 1FCNT (выделена красным). (c) - 2FCNT

Рис. 2. (Цветной онлайн) (а) - Модель структуры nFCNT. (b) - Развернутая нанолента, межслоевые связи которой

образуют по два пяти- и семиугольных дефекта (7557). Зелеными линиями показана расчетная ячейка. (c) - Зависи-

мость энергии структуры в расчете на атом от ее ширины, энергия бислойного графена с углом Θ = 27.8^◦ взята за

нуль

В данной работе мы рассматриваем структуру и

Density Approximation). Для оптимизации геометрии

свойства нехиральных нанотрубок нового типа, ко-

структур зона Бриллюена разбивалась по методу

торые основаны на нанолентах, получаемых из биc-

Монкхорст-Пака [13] с плотностью k-точек 0.08Å-1.

лойного графена с углом Муара Θ = 27.8^◦.

Расстояние между периодическими образами ква-

Метод расчета. Расчеты проводились с по-

зиодномерных структур составляло не менее 20Å

мощью программного пакета SIESTA [12], реали-

для исключения взаимодействия между ними.

зующего метод теории функционала электронной

Оптимизация геометрии структур проводилась до

плотности DFT (Density Functional Theory) в

минимизации силы, действующей на каждый атом,

приближении локальной плотности LDA (Local

до 10^-4 эВ/Å.

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

Исследование гофрированных нанотрубок нового типа, вырезанных из бислойного графена...

471

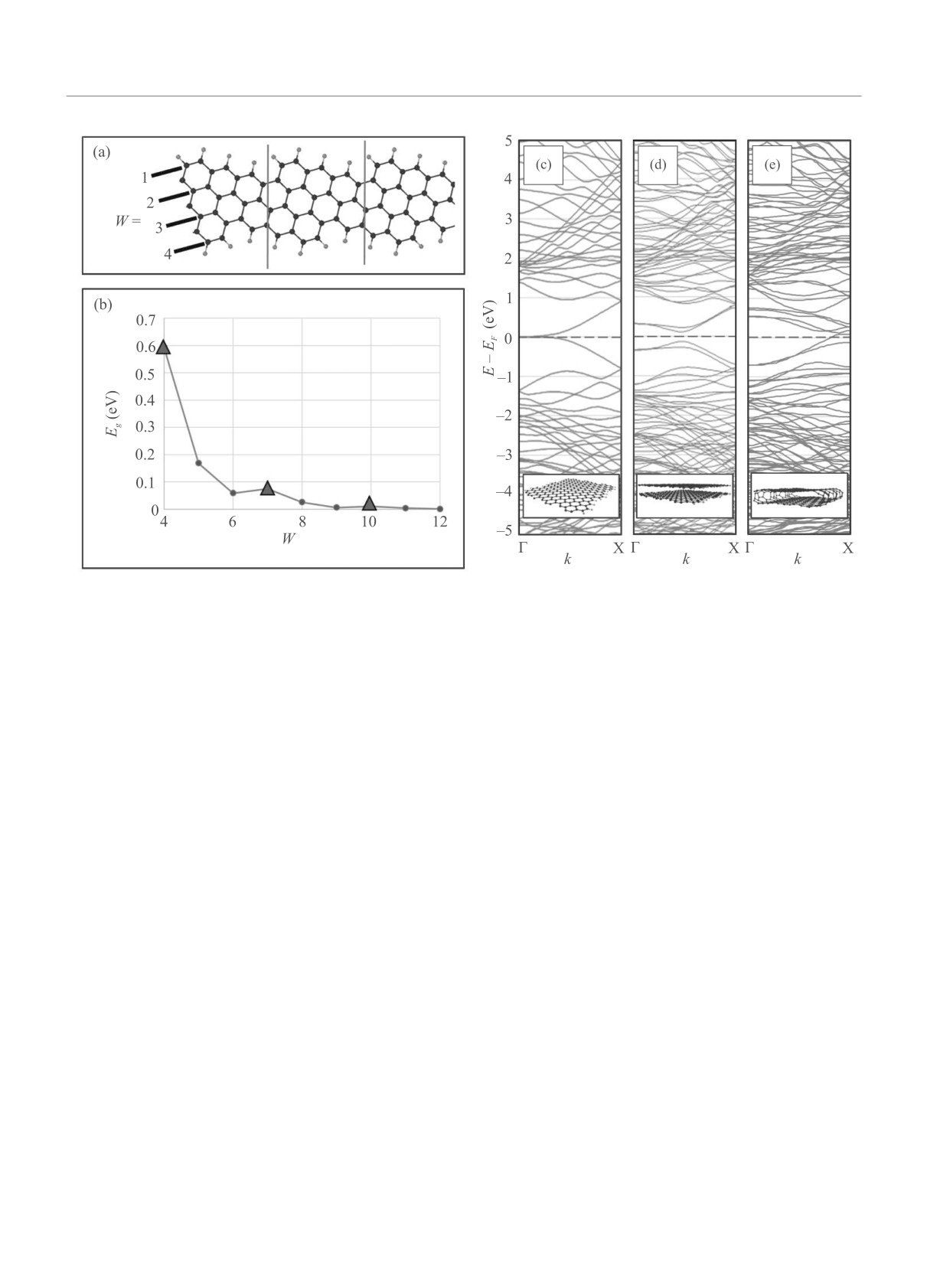
Рис. 3. (Цветной онлайн) Cтруктура 1FCNT состоит из двух нанолент с шириной w = 4 (a), зависимость запрещенной

зоны однослойных нанолент от ширины w (b), красными треугольниками показаны точки, соответствующие нано-

лентам, из которых состоят nFCNT; электронные зонные структуры монослойной наноленты с w = 7 (с), двуслойной

наноленты (d) и нанотрубки 3FCNT (e)

Результаты и обсуждение. Ранее нами были

Рассмотрим подробнее наименьшую из струк-

рассмотрены наносетки на основе такого бислоя с

тур - трубку 1FCNT (рис.2а). Она представляет

углом Муара Θ = 27.8^◦ [14]. Бислой имеет харак-

одномерную цепочку из круглых областей, каждая

терные круглые области, в которых атомы разных

из 48 атомов (выделены красным на рис. 2), соеди-

слоев находятся практически друг над другом, та-

ненных между собой перешейками из четырех ато-

ким образом, если край биграфена будет проходить

мов. Расчетная ячейка такой структуры содержит

по границе области, то возможно соединение слоев,

N = 52 атомов углерода и имеет параметр транс-

аналогично краям типа “зиг-заг” [15]. Вырезая пе-

ляции l = 8.8Å. nFCNT нанотрубка состоит из двух

риодически расположенные круглые отверстия и да-

асимметричных нанолент с краями типа “шеврон”,

лее соединяя краевые атомы разных слоев, получаем

которые при соединении образуют по два пяти- и

массив элементов Y -соединений (рис. 1b). Такая на-

семиугольных дефекта (рис.2b). Увеличение шири-

носетка может быть представлена как совокупность

ны на единицу n добавляет 52 атома к расчетной

пересекающихся квазиодномерных структур с гоф-

ячейке. Полученные нанотрубки подобны цепочкам

рированными краями, подобных сжатым нанотруб-

ковалентно-связанных фуллеренов C₆₀ или C₅₈, об-

кам (наименьшая из возможных выделена красным

разующих одномерную структуру [16].

на рис. 1b). Таким образом, возможно вырезание та-

Методом DFT была произведена оптимизация

ких гофрированных нанотрубок разной ширины, ко-

структуры набора nFCNT для n от 1 до 5. Нано-

торые содержат n возможных структур, к примеру,

трубки c n ≥ 2 содержат плоский участок, анало-

на рис. 1b показана нанотрубка с n = 1, а на рис. 1с

гично сплюснутым УНТ с диаметром более 50Å [17].

нанотрубка с n = 2. Обозначим такую нанотрубку

Расчет энергий показал, что кривая E/N(n) лежит

nFCNT (FCNT - flattened carbon nanotube - сплющен-

выше значения энергии для бислойного графена с

ная углеродная нанотрубка). При четных значениях

углом Θ = 27.8^◦ и стремится к нему с увеличени-

n края нанотрубки не симметричны.

ем n (рис.2с). Поведение зависимости связано с тем,

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

472

В.А.Демин, А.А.Артюх, В.А.Сороко, Л.А.Чернозатонский

метра: к примеру, энергия CNT(3,3) на 0.03 эВ/атом

выше, чем энергия 1FCNT.

Нанотрубка nFCNT состоит из связанных нано-

лент типа “шеврон” (рис. 3а). Подобные наноленты

синтезируются путем самосборки молекул на под-

ложке [18]. Они являются полупроводниками при

ширине, равной 7.5Å с E_g = 0.3 эВ [19]. Рассмотрен-

ные в этой работе наноленты содержат в расчетной

ячейке на 2 атома углерода меньше. Ширина таких

нанолент характеризуется параметром w, как пока-

зано на рис.3a. Результат расчета зонной структуры

методом сильной связи серии нанолент с w от 4 до 12

показан на рис. 3b. При минимальной ширине 7.5Å

также являются полупроводниками с E_g = 0.59 эВ.

Увеличение ширины приводит к быстрому уменьше-

нию значения запрещенной зоны с незначительными

осцилляциями и при значениях w ≥ 11 величина E_g

составляет менее 0.01 эВ. При наложении таких лент

друг на друга характер зонной структуры изменяет-

ся - открывается щель E_g ∼ 0.1 эВ (рис. 3d) для всех

рассмотренных бислойных лент.

DFT-LDA расчет показал, что соединение краев

бислойной наноленты приводит к исчезновению за-

прещенной зоны в nFCNT структурах. Пример эво-

люции зонной структуры - монослойная нанолента

→ бислойная нанолента → nFCNT структура - пока-

зан на рис.3с-e. Таким образом, наличие типа прово-

димости не зависит от ширины рассмотренных нано-

лент, в отличие от обычных УНТ. Однако в структу-

ре 2FCNT запрещенная зона равна E_g = 0.2 эВ. Мы

связываем это с тем, что такая структура уже содер-

жит плоский участок, сравнимый по размерам с по-

лупроводниковыми нанолентами с w ≤ 7, в отличие

от 1FCNT, которая не имеет плоских участков вооб-

ще, и от nFCNT (n ≥ 3), у которых плоский участок

не входит в область полупроводниковых нанолент.

Для расчета модулей Юнга Y были проведены

расчеты с изменением вектора трансляции от -5

до +5 % относительно значения энергетически вы-

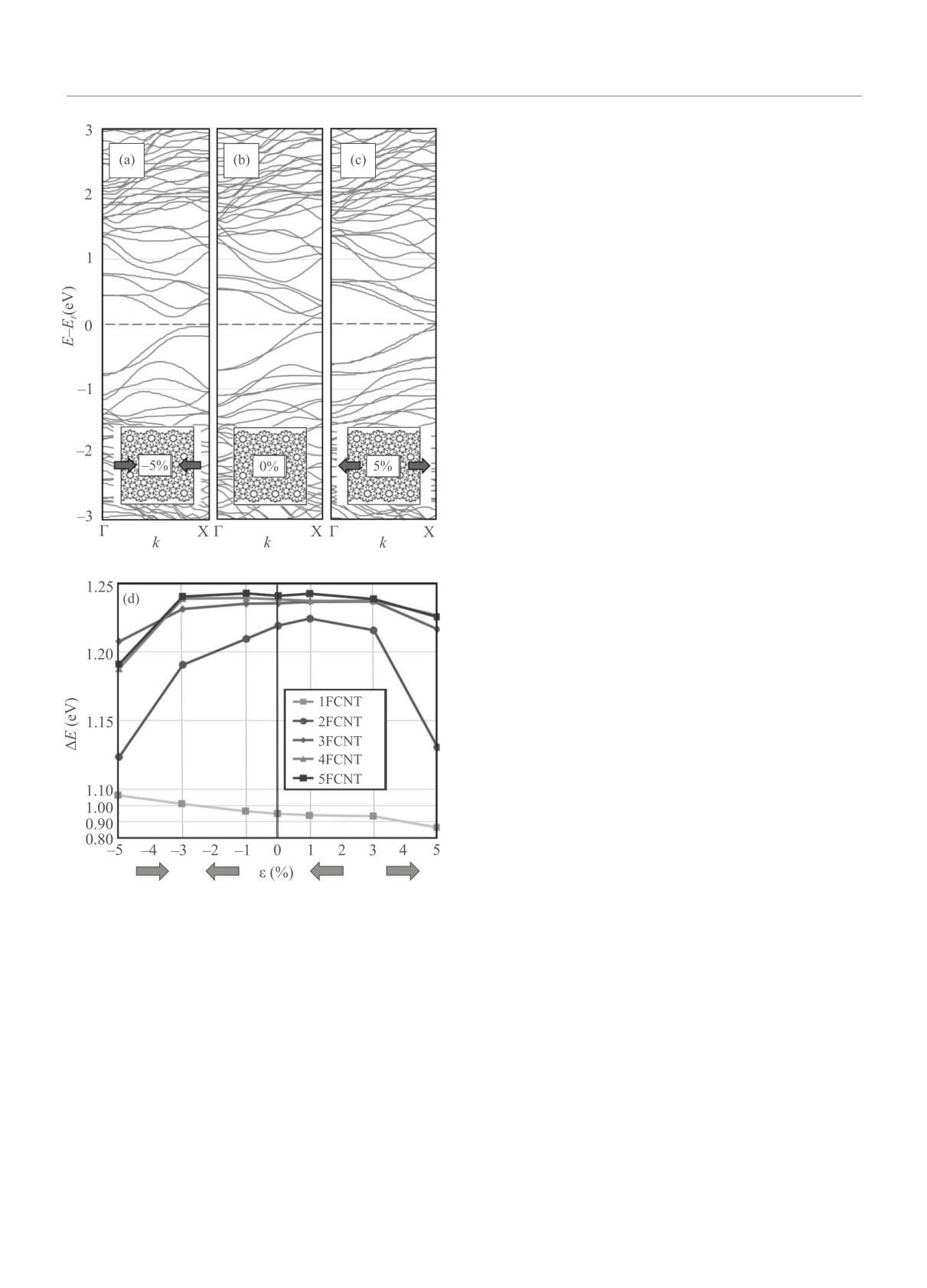
Рис. 4. (Цветной онлайн) Зонная структура нанотрубки

годного состояния. Модуль рассчитывался по стан-

4FCNT при сжатии 5 % (а), без деформаций (b) и при

растяжении 5 % (c) и зависимость разницы ΔE между

дартной формуле, используя данные об изменении

ближайшими к уровню Ферми энергетическими уров-

полной энергии системы в зависимости от деформа-

нями валентной зоны и зоной проводимости в Γ точке

ции [20]. Наличие пяти- и семиугольных дефектов в

зоны Бриллюэна от деформаций (d)

структурах на краях приводит к тому, что такие на-

нотрубки менее упруги, чем УНТ с тем же перимет-

ром. Наименьшее значение Y = 0.6 ТПа соответству-

ет структуре 1FCNT, что составляет 60 % от моду-

что отношение количества атомов плоской части на-

лей Юнга, соответствующих по периметру CNT(4,4)

нотрубки к количеству атомов, образующих пяти- и

и CNT(7,0). Далее модуль Y растет для nFCNT с уве-

семиугольные дефекты, увеличивается вместе с n.

личением индекса n и стремится к значению Y_graph

Однако, несмотря на дефектность, энергия структур

графена. Деформации сжатия/растяжения влияют

nFCNT ниже, чем у нанотрубок аналогичного пери-

на зонную структуру nFCNT нанотрубок. На рисун-

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

Исследование гофрированных нанотрубок нового типа, вырезанных из бислойного графена...

473

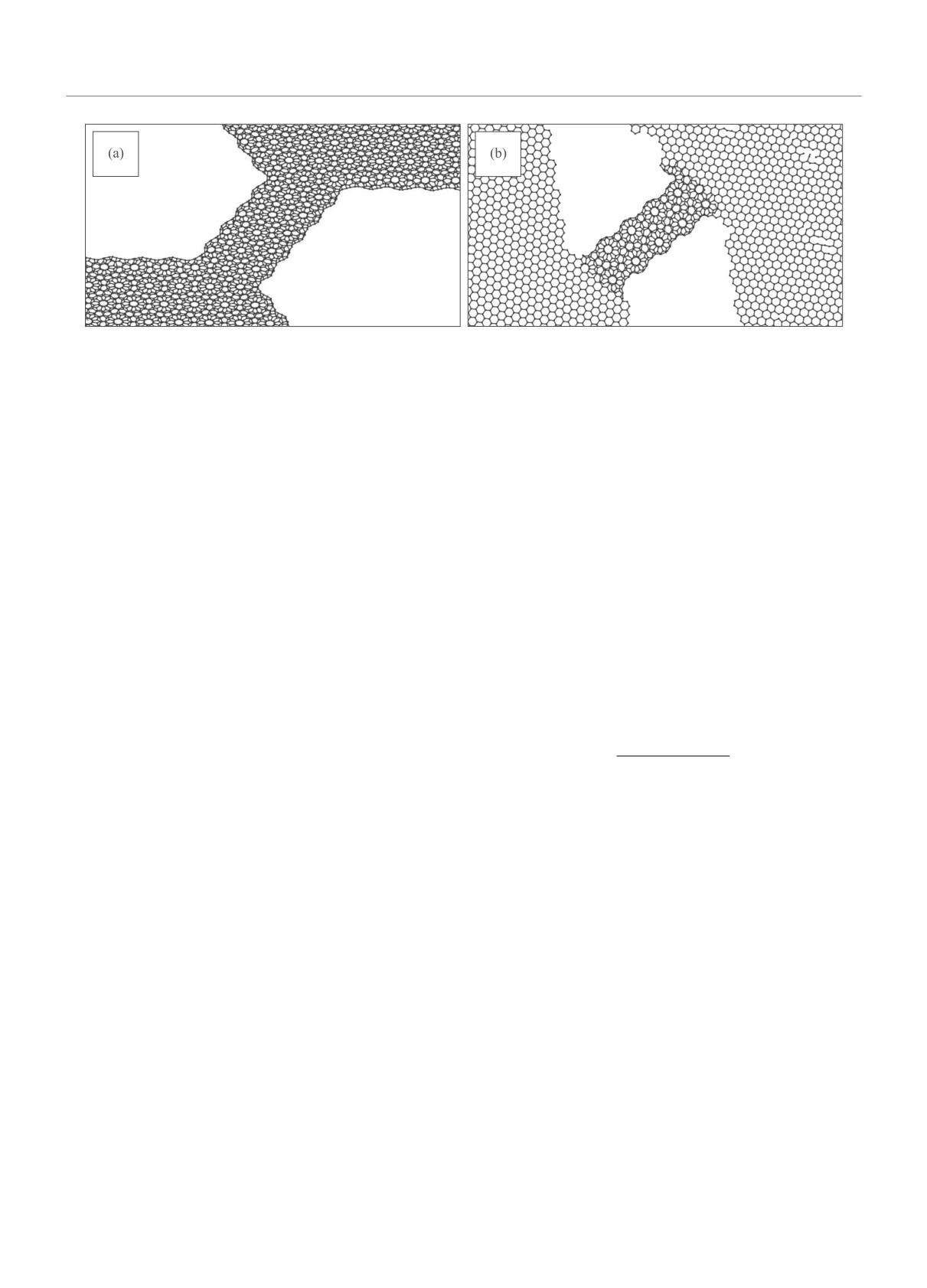
Рис. 5. (Цветной онлайн) (а) - Проводящий канал 3FCNT, соединяющий два массива биграфена с Θ = 27.8^◦ . (b) -

2FCNT, соединяющая два разориентированных монослоя графена

ке 4 приведены зонные структуры трубки 4FCNT

ного графена с углом Муара Θ = 27.8^◦. Подроб-

при деформациях -5 и +5 % в сравнении с зонной

но описана их структура, показана энергетическая

структурой недеформированной нанотрубки. При

стабильность, рассчитаны модули Юнга, которые по

сжатии в 3 % ветви зонной структуры вблизи уров-

причине наличия дефектов оказались ниже относи-

ня Ферми расходятся, образуя запрещенную зону

тельно модулей соответствующих по размеру УНТ

E_g = 0.13 эВ. Дальнейшее сжатие до 5 % увеличи-

типов “кресло” и “зиг-заг”. Показано, что при форми-

вает ее до E_g = 0.18 эВ. Растяжение также откры-

ровании такой нанотрубки путем соединения краев

вает запрещенную зону величиной менее 0.1 эВ. На

бислойной наноленты происходит существенное из-

рисунке 4d изображена зависимость от деформаций

менение ее электронной зонной структуры.

разницы ΔE между ближайшими к уровню Ферми

Работа выполнена в рамках проекта Россий-

энергетическими уровнями валентной зоны и зоной

ского фонда фундаментальных исследований

проводимости в Γ точке зоны Бриллюэна. Видно, что

#18-32-01009 и частично поддержана Research

деформации ε ≤ 3 % гофрированных нанотрубок с

Council of Norway Center of Excellence funding

индексами n ≥ 3 существенно не влияют на величину

scheme (project # 262633, “QuSpin”) с использовани-

ΔE - ее изменения лежат в интервале менее 0.01 эВ.

ем ресурсов суперкомпьютерного комплекса МГУ

Деформации ε = 5 % приводят к сближению уровней

им. М. В. Ломоносова

[22] и межведомственного

в Γ точке до 0.05эВ. Аналогично поведение ΔE для

суперкомпьютерного центра РАН.

нанотрубки 2FCNT, однако величина ΔE изменяется

сильнее и достигает 0.1 эВ при ε = ±5 %. ΔE моно-

тонно убывает от ε = -5 % до ε = 5 % для 1FCNT

1. S. Iijima, Nature 354, 56 (1991).

на 0.2 эВ. Устойчивое поведение ветвей спектра при

2. G. Algara-Siller, A. Santana, R. Onions, M. Suyetin,

n ≥ 3 связано с уменьшением влияния дефектных

J. Biskupek, E. Bichoutskaia, and U. Kaiser, Carbon

65, 80 (2013).

краев на зонную структуру гофрированных нанотру-

бок nFCNT.

3. K. Kim, M. Yankowitz, B. Fallahazad, S. Kang,

H. C. P. Movva, S. Huang, S. Larentis, C. M. Corbet,

Мы полагаем, что такие структуры могут быть

T. Taniguchi, K. Watanabe, S. K. Banerjee, B. J. LeRoy,

полезны для наноэлектроники в качестве проводя-

and E. Tutuc, Nano Lett. 16, 5968 (2016).

щих каналов между двумя массивами бислойного

4. J. M. Campanera, G. Savini, I. Suarez-Martinez, and

графена (рис. 5а). В зависимости от ширины этого

M. I. Heggie, Phys. Rev. B 75, 235449 (2007).

канала изменяются проводящие свойства, аналогич-

5. J. Hass, F. Varchon, J. E. Millan-Otoya, M. Sprinkle,

но наносвитку из работы [21], где лазером прожигал-

N. Sharma, W. A. de Heer, C. Berger, P. N. First,

ся канал в монослое графена до достижения задан-

L. Magaud, and E. H. Conrad, Phys. Rev. Lett. 100,

ного сопротивления. Также такие нанотрубки мож-

125504 (2008).

но использовать в качестве переходной области меж-

6. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi,

ду двумя разориентированными монослоями графе-

E. Kaxiras, and P. Jarillo-Herrero, Nature 556,

на (рис. 5b).

(2018).

Заключение. Таким образом, в работе был рас-

7. Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin,

смотрен новый класс гофрированных нанотрубок

A. Zettl, M. F. Crommie, Y. R. Shen, and F. Wang,

nFCNT, которые могут быть получены из бислой-

Nature 459, 820 (2009).

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

474

В.А.Демин, А.А.Артюх, В.А.Сороко, Л.А.Чернозатонский

8. L. A. Chernozatonskii, V. A. Demin, and A. A. Artyukh,

J. Lehtonen, and E. I. Kauppinen, ACS Nano 8, 9657

JETP Lett. 99, 309 (2014).

(2014).

9. D. G. Kvashnin, P. Vancsó, L. Yu. Antipina, G. I. Mark,

18. F. Schulz, P. H. Jacobse, F. F. Canova, J. van der Lit,

L. P. Biró, P. B. Sorokin, and L. A. Chernozatonskii,

D. Z. Gao, A. van den Hoogenband, P. Han,

Nano Res. 8, 1250 (2015).

R. J. M. Klein Gebbink, M.-E. Moret, P. M. Joensuu,

I. Swart, and P. Liljeroth, J. Phys. Chem. C 121, 2896

10. L. A. Chernozatonskii, V. A. Demin, and Ph. Lambin,

(2017).

Phys. Chem. Chem. Phys. 18, 27432 (2016).

19. V. A. Saroka, H. Abdelsalam, V. A. Demin, D. Grassano,

11. R. Petersen and T. G. Pedersen, J. Phys.: Condens.

S. A. Kuten, A. L. Pushkarchuk, and O. Pulci,

Matter 27, 225502 (2015).

Semiconductors 52, 1890 (2018).

12. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia,

20. A. A. Artyukh and L. A. Chernozatonskii, JETP Lett.

J. Junquera, P. Ordejón, and D. Sánchez-Portal,

109, 472 (2019).

J. Phys.: Condens. Matter 14, 2745 (2002).

21. I. Silvestre, A. W. Barnard, S. P. Roberts, P. L. McEuen,

13. H. J. Monkhorst and J. D. Pack, Phys. Rev. B 13, 5188

and R. G. Lacerda, Appl. Phys. Lett. 106,

153105

(1976).

(2015).

14. L. A. Chernozatonskii and V. A. Demin, JETP Lett.

22. Вл. В. Воеводин, С. А. Жуматий, С. И. Соболев,

107, 315 (2018).

А. С. Антонов, П. А. Брызгалов, Д. А. Ники-

15. D. Zhan, L. Liu, Y. N. Xu, Z. H. Ni, J. X. Yan, C. Zhao,

тенко, К. С. Стефанов, Вад. В. Воеводин, От-

and Z. X. Shen, Sci. Rep. 1, 00012 (2011).

крытые системы

(2012)

[Vl. V. Voevodin,

16. E. G. Gal’pern, I. V. Stankevich, A. L. Chistyakov,

S. A. Zhumatiy,

S.I. Sobolev, A.S. Antonov,

and L. A. Chernozatonskii, Fullerene Science and

P. A. Bryzgalov, D. A. Nikitenko, K. S. Stefanov,

Technology 6, 499 (1998).

and Vad. V. Voevodin, Open Systems J. 7, 36 (2012)];

17. M. He, J. Dong, K. Zhang, F. Ding, H. Jiang, A. Loiseau,

https://www.osp.ru/os/2012/07/13017641/.

Письма в ЖЭТФ том 111 вып. 7 - 8

2020