Письма в ЖЭТФ, том 111, вып. 8, с. 509 - 513

Когерентный вихрь в двумерном турбулентном потоке в

окрестности вращающегося диска

А. Б. Бузовкин⁺, С. С. Вергелес^∗1), И. В. Колоколов^∗, В. В. Лебедев^∗

⁺Национальный исследовательский университет, Высшая школа экономики, 101000 Москва, Россия

^∗Институт теоретической физики им. Л. Д. Ландау РАН, 142432 Черноголовка, Россия

Поступила в редакцию 25 марта 2020 г.

После переработки 25 марта 2020 г.

Принята к публикации 26 марта 2020 г.

Рассматривается структура когерентного вихря, образующегося вокруг твердого вращающегося дис-

ка в двумерном турбулентном потоке. Найден профиль средней скорости когерентного вихря для разных

скоростей вращения.

DOI: 10.31857/S1234567820080054

Турбулентность - хаотическое состояние, реали-

ходятся в хорошем согласии с аналитической теори-

зуемое в жидкостях при больших числах Рейнольдса

ей, разработанной для неограниченной системы [9].

Re, смотри, например, [1]. В двумерном случае на-

В частности, в обратном каскаде [2] наблюдается

блюдается тенденция к образованию все более круп-

нормальный Колмогоровский скейлинг. Нормальный

ных вихрей, что приводит к формированию так на-

скейлинг в обратном каскаде двумерной турбулент-

зываемого обратного каскада. В однородном слу-

ности контрастирует с аномальным скейлингом, на-

чае реализуется хаотическое течение со стационар-

блюдаемым в трехмерной турбулентности [10]. Неко-

ной статистикой. Однако неоднородность (скажем,

торые теоретические аргументы в пользу нормально-

наличие стенок) может привести к появлению коге-

го скейлинга в обратном каскаде были представлены

рентных структур с хорошо определенным средним

в работе [11], где эта особенность была связана с ве-

потоком. Здесь обсуждается возможность возникно-

дущей ролью сходящихся лагранжевых траекторий

вения когерентного вихря вокруг вращающегося дис-

в обратном каскаде.

ка, погруженного в двумерный турбулентный поток.

В неограниченной двумерной системе обратный

В некоторых случаях турбулентность оказывает-

каскад заканчивается на масштабе L_α, который опре-

ся эффективно двумерной [2, 3]. Уже первые теоре-

деляется балансом между потоком энергии ǫ (произ-

тические работы [4-6], посвященные двумерной тур-

водство энергии на единицу массы) в большие мас-

булентности, обнаруживают ее принципиальное от-

штабы и потерей на трение αV², где α - коэффи-

личие от трехмерной. Разница связана с существова-

циент трения о дно, а V

- характерная скорость

нием двух квадратичных величин (энергии и энстро-

на масштабе L_α. Используя Колмогоровскую оцен-

фии), сохраняемых двумерным уравнением Эйлера.

ку V ∼ (ǫL_α)^1/3 для скорости V , получаем из этого

Это приводит к двум различным каскадам, порожда-

баланса L_α = ǫ^1/2α^-3/2. Если размер ячейки L мень-

емым нелинейным взаимодействием: энстрофия пе-

ше, чем L_α, то энергия, переносимая обратным кас-

реносится от масштаба накачки к меньшим масшта-

кадом на масштабы порядка размера ячейки L, начи-

бам (прямой каскад), тогда как энергия переносится

нает там накапливаться. Сценарий реализуется, если

к более крупным масштабам (обратный каскад). Эн-

масштаб накачки l много меньше размера ячейки L,

строфия диссипирует из-за вязкости на масштабах,

l ≪ L, в противном случае нет места для обратного

меньших, чем длина накачки, а энергия диссипиру-

каскада, переносящего энергию на масштаб L.

ет из-за трения о дно на масштабах, превышающих

Накопление энергии на масштабе L приводит к

длину накачки.

появлению интенсивного крупномасштабного движе-

Статистические свойства флуктуаций скорости в

ния, включающего большие когерентные вихри. Тен-

обратном каскаде были исследованы как эксперимен-

денция к образованию вихрей была отмечена уже в

тально [7], так и численно [8]. Результаты работ на-

первых работах, посвященных двумерной турбулент-

ности, как экспериментальных [12], так и числен-

¹⁾e-mail: ssver@itp.ac.ru

ных [13-15]. В численной работе [16], где используют-

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

509

510

А. Б. Бузовкин, С. С. Вергелес, И. В. Колоколов, В. В. Лебедев

ся периодические граничные условия, было установ-

щегося диска, погруженного в двумерный турбулент-

лено, что благодаря обратному каскаду в квадрат-

ный поток при больших числах Рейнольдса Re. Та-

ной ячейке появляется устойчивая структура, кото-

кая возможность может быть реализована, если ра-

рая представляет собой вихревой диполь. Несколько

диус диска r₀ намного меньше длины L_α. Тогда из-за

иная когерентная вихревая структура генерируется

неоднородности может образоваться некоторая инте-

в лабораторных экспериментах в квадратной ячей-

гральная завихренность вокруг диска, приводящая к

ке [17, 18]. С теоретической точки зрения последний

появлению когерентного вихря. Такая ситуация мо-

случай соответствует нулевым граничным условиям

жет быть легко реализована и исследована экспери-

для скорости потока на границах ячейки.

ментально. Наша задача - теоретически исследовать

В работе [19] представлены результаты числен-

пространственную структуру когерентного вихря во-

ного моделирования двумерной турбулентности для

круг вращающегося диска.

периодических условий в квадратной ячейке с корот-

Предполагается, что профиль средней скорости,

кой по времени корреляцией накачки. Профиль сред-

возникающий вокруг вращающегося диска, являет-

ней скорости когерентного вихря оказывается изо-

ся изотропным, т.е. он может характеризоваться ис-

тропен в некотором диапазоне расстояний от центра

ключительно полярной скоростью U в системе отсче-

вихря. В той же работе был найден интервал рас-

та с началом в центре диска. Чтобы установить про-

стояний от центра вихря, где реализуется плоский

филь скорости когерентного вихря, можно использо-

профиль скорости, и были сформулированы неко-

вать уравнения, полученные в работах [19-21]. Эти-

торые теоретические аргументы в пользу плоского

ми уравнениями являются баланс углового момента

профиля. В работе [20] было показано, что плоский

αU = -(∂_r + 2/r)〈uv〉,

(1)

профиль соответствует пассивному (квазилинейно-

му) режиму турбулентных колебаний, а в работе [21]

и выражение для угловой компоненты тензора на-

мы рассчитали структурную функцию флуктуаций

пряжения Рейнольдса

скорости для этого случая.

Имеется серия работ, посвященных когерентным

〈uv〉 = ǫ/Σ,

(2)

структурам в двумерных турбулентных потоках в

полученное в квазилинейном приближении. В урав-

геометрии, отличной от квадратной. В статье [22]

нениях (1), (2) r - расстояние до центра вихря, ǫ -

в рамках подхода получены аналитические решения

скорость производства энергии на единицу массы

для двумерных средних течений, порожденных об-

(поток энергии), α - коэффициент трения о дно, u

ратным турбулентным каскадом на сфере и в плос-

и v - азимутальная и радиальная компоненты флук-

ких прямоугольных областях с различными отноше-

туирующей части скорости и

ниями сторон. В статье [23] численно показано, что

для прямоугольного прямоугольника при увеличе-

Σ = ∂_rU - U/r = r∂_r(U/r),

(3)

нии соотношения сторон формируется система сосу-

есть локальный (зависящий от r) коэффициент сдви-

ществующих струй и вихрей. В статье [24] корреля-

ционные функции скорости исследуются как анали-

га среднего течения.

Уравнения (1), (2) описывают стационарный за-

тически, так и численно для прямоугольной ячейки.

В работе [25] было численно продемонстрировано,

висящий от r профиль скорости U. Уравнения долж-

что в случае течения, поддерживаемого давлением,

ны быть дополнены граничным условием на радиусе

диска, которое фиксирует скорость течения U, рав-

появляется струя, скользящая между пристеночны-

ми вихрями.

ную скорости диска на его границе. Уравнения (1),

(2) верны, если длина накачки l много меньше r и ре-

В вышеупомянутых работах использовалась мо-

ализуется квазилинейный режим. Последнее условие

дель коротко коррелированной по времени накачки.

подразумевает, что скорость сдвига Σ среднего тече-

В статье [26] показано, что плоский профиль скоро-

ния должна быть больше, чем характерный градиент

сти должен наблюдаться в квазилинейном режиме и

скорости флуктуаций на масштабе накачки l, кото-

для статической накачки в квадратной ячейке. Это

рый был бы в случае изотропного обратного каскада

предсказание проверено в эксперименте [27], где ис-

в неограниченной ячейке:

пользовалась именно статическая накачка (на осно-

ве силы Лоренца). Таким образом, плоский профиль

Σ≫ǫ^1/3l^-2/3,

(4)

скорости весьма универсален.

В настоящей работе мы обсуждаем возможность

где мы использовали Колмогоровскую оценку для

формирования когерентного вихря вокруг вращаю-

градиента скорости на длине накачки. Уравнения

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

Когерентный вихрь в двумерном турбулентном потоке в окрестности вращающегося диска

511

(1), (2) справедливы, если r² ≫ ν/α, где ν - коэффи-

циент кинематической вязкости.

Легко найти плоский профиль скорости U

√

3ǫ/α как однородное решение уравнений (1), (2).

Однако в нашем случае следует рассмотреть про-

филь с граничным условием U = U₀ на радиусе дис-

ка r₀, где U₀ определяется угловой скоростью дис-

ка. При этом условии скорость U становится зави-

симой от r. Мы рассматриваем обе возможности:

√

U₀ >

3ǫ/α и U₀ <

3ǫ/α. Некоторое ограничение

снизу на U₀ наложено неравенством (4).

Удобно перейти к безразмерным переменным f, z,

введенным в соответствии со следующими соотноше-

ниями

√

U =

ǫ/αf, Σ = -

ǫ/α z/r.

(5)

В терминах безразмерных переменных уравнения

(1), (2) переписываются как

∂_ρf = f - z,

∂_ρz = -fz² + 3z,

(6)

где ρ = ln(r/r₀), ρ > 0. Уравнения (6) должны ре-

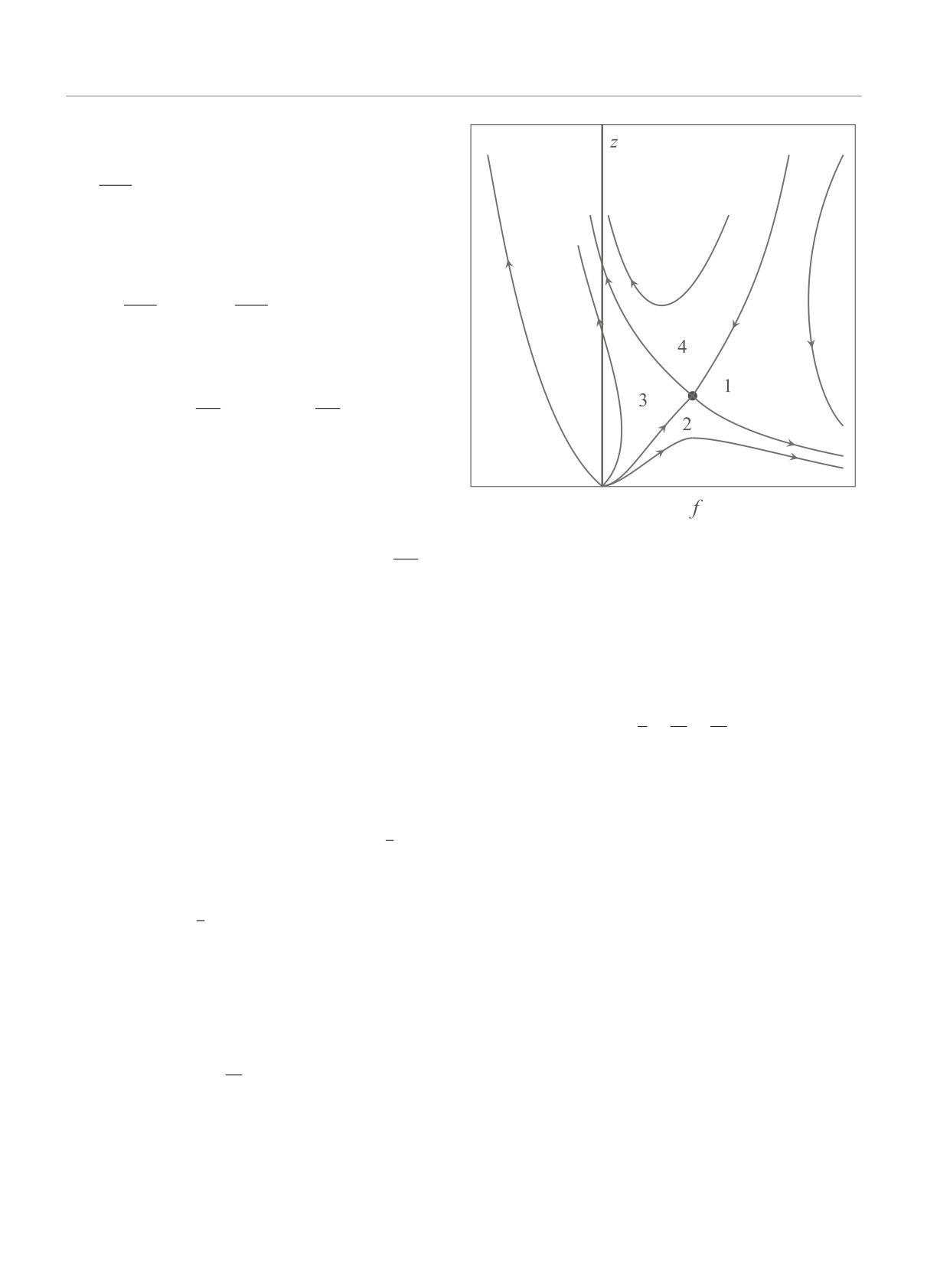
Рис. 1. (Цветной онлайн) Фазовый портрет к системе

√

уравнений (6). Траектории можно найти из уравнения

шаться с граничным условием f = f₀ = U₀

α/ǫ при

(7). Направление движения вдоль траекторий опреде-

ρ = 0.

ляется уравнениями (6)

Очевидно, что существует решение уравнений (6)

z = 0, f ∝ exp(ρ) ∝ r, соответствующее твердотель-

Траектории, начинающиеся в секторах 1, 2, в кон-

ному вращению жидкости. Траектория разделяет об-

це концов уходят в большие f. Их асимптотическое

ласти z > 0 и z < 0. Мы анализируем случай z > 0,

поведение определяется выражением

обратный случай z < 0 сводится к предыдущему,

поскольку уравнения (6) инвариантны относительно

преобразования f, z → -f, -z.

(8)

f³

f⁵

Уравнения (6) являются автономными диффе-

ренциальными уравнениями. Поэтому их решения

где C - некоторая константа. Как следует из уравне-

можно представить в виде траекторий на плоско-

ний (6), в этом случае f ∝ r с небольшими поправ-

сти f, z. Приравнивая нулю правые части уравнений

ками. Поэтому асимптотическое поведение близко к

(6), мы находим неустойчивую неподвижную точку

твердотельному вращению.

√

f = z = 0 и седловую точку f = z =

3. Имен-

Траектории, начинающиеся в секторах 3, 4 (вклю-

но эта точка соответствует универсальному плоско-

чая область f < 0), в конечном итоге уходят в боль-

му профилю скорости. Фазовый портрет системы (6)

шие z и отрицательные f с большим абсолютным

изображен на рис. 1. Траектории, идущие в седловую

значением. Асимптотически при больших |f|,

√

точку f = z =

3 и идущие из нее, разделяют по-

z ∝ exp(f²/2).

(9)

луплоскость z > 0 на четыре сектора, обозначенные

цифрами 1-4 на рис. 1.

Подставляя выражение в уравнение (6) для f, мы

Автономность системы уравнений (6) позволя-

заключаем, что |f| уходит в бесконечность при ко-

ет вывести замкнутое дифференциальное уравнение

нечном r. Таким образом, мы сталкиваемся с сингу-

для f и z, которое имеет вид

лярностью.

Оба приведенных выше случая, твердотельное

(f - z)

= -fz² + 3z.

(7)

вращение и сингулярность в решении, нас не устраи-

вают, поскольку нас интересуют решения, переходя-

Это уравнение можно использовать для установле-

щие в универсальный плоский режим при больших r.

ния геометрических характеристик траекторий на

Поэтому мы должны рассмотреть траектории, иду-

фазовом портрете, представленном на рис.1.

щие к седловой точке. В этом случае и f, и z стремят-

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

512

А. Б. Бузовкин, С. С. Вергелес, И. В. Колоколов, В. В. Лебедев

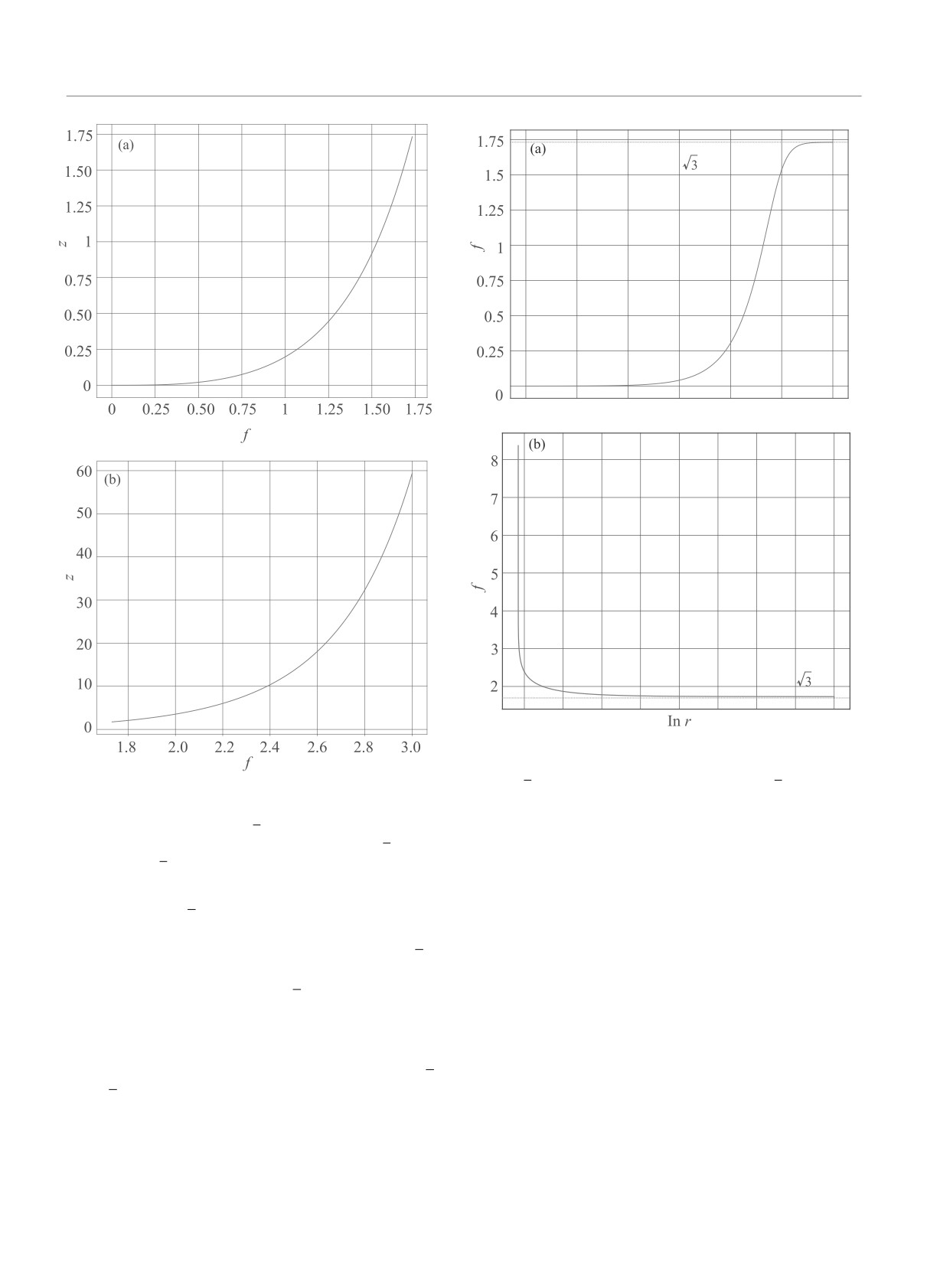
Рис. 3. (Цветной онлайн) Безразмерная полярная ско-

рость f как функция ln r. (a) - График соответствует

√

f0 <

3; (b) - график соответствует f0 >

Рис. 2. (Цветной онлайн) Зависимость z от f для ре-

шений, стремящихся к универсальному плоскому про-

√

филю скорости f = z =

3 на больших расстояниях

√

что приводит к заключению, что z = c₁f³. Числен-

r. (a) - график соответствует случаю z <

3; (b) -

√

ное решение позволяет извлечь коэффициент про-

случаю z >

порциональности, равный c₁ = 0.166. Используя за-

кон z ∼ f³ и условие применимости (4), можно найти

√

ся к значению

3, соответствующему плоскому про-

неравенство

филю скорости. Начальная точка траектории опре-

√

деляется начальным условием f₀. Если f₀ <

3, то

U₀ ≫ ǫ^4/9α^-1/3r^1/30l^-2/9,

(10)

решение определяется траекторией, ведущей в седло-

√

вую точку снизу, а если f₀ >

3, то решение опреде-

которое должно выполняться для правильности на-

ляется траекторией, идущей в седловую точку свер-

шего подхода.

ху, смотри рис. 1. Траектории можно найти численно

В пределе f₀ ≫ 1 величина f велика при малых

путем решения уравнения (7). Результаты представ-

ρ, и выполняется условие z ≫ f. Поэтому мы полу-

√

лены на рис. 2, где представлены случаи z <

3 и

чаем из уравнения (7) dz/df = fz, что приводит к

√

z = c2 exp(f²/2). Коэффициент здесь можно извлечь

В пределе f₀ ≪ 1 величина f мала при малых

из численного решения, он составляет c₂ = 0, 672. Из

ρ = 0, величина z также мала здесь. Поэтому мы по-

решения z = c₂ exp(f²/2) мы видим, что, в самом

лучаем из уравнения (7) уравнение (f -z)dz/df = 3z,

деле, z ≫ f при f ≫ 1.

Письма в ЖЭТФ том 111 вып. 7 - 8

2020

Когерентный вихрь в двумерном турбулентном потоке в окрестности вращающегося диска

513

Возвращаясь к уравнениям (6), мы можем чис-

Focus Issue: Two-Dimensional Turbulence, ed. by

ленно найти зависимости f и z от ρ. Зависимость f

G. Boffetta, G. Falkovich, and M. Shats, Physics of

√

от ρ показана на рис.3 для случаев f <

3иf >

Fluids 29(11) (2017).

Положение точки, где ρ = 0 (r = r₀), зависит от на-

R. H. Kraichnan, Phys. Fluids 10, 1417 (1967).

чального значения f₀. В пределе f ≪ 1 величина

C. E. Leith, Phys. Fluids 11, 671 (1968).

z = c₁f³ пренебрежимо мала, и из уравнений (6) мы

G. K. Batchelor, Phys. Fluids 12, 233 (1969).

находим, что f ∝ exp(ρ) ∝ r и z ∝ exp(3ρ) ∝ r³.

P. Tabeling, Phys. Rep. 362, 1 (2002).

В пределе f ≫ 1 величина z = c₂ exp(f²/2) ≫ f,

G. Boffetta, A. Celani, and M. Vergassola, Phys. Rev.

и мы находим из уравнений (6) ∂_ρf = -c₂ exp(f²/2).

E 61, R29 (2000).

Поэтому мы находим, что

R. H. Kraichnan and D. Montgomery, Rep. Prog. Phys.

∫ f0

43, 547 (1980).

c₂ρ =

dx exp(-x²/2).

(11)

10.

U. Frisch, Turbulence: The Legacy of A.N. Kolmogorov,

Cambridge University Press, Cambridge (1995).

Интеграл здесь можно записать как разницу между

11.

G. Falkovich, J. Phys. A: Math. Theor. 42, 123001

значениями функции ошибок. Поскольку интеграл в

(2009).

правой части уравнения (11) сходится при f₀ → ∞,

12.

J. Sommeria, J. Fluid Mech. 170, 139 (1986).

мы заключаем, что при большом f₀ существует по-

13.

L. M. Smith and V. Yakhot, Phys. Rev. Lett. 71, 352

граничный слой шириной 1 (порядка r₀ в терминах

(1993).

расстояний), где f переходит в значение порядка еди-

14.

L. M. Smith and V. Yakhot, J. Fluid Mech. 274, 115

ницы.

(1994).

Таким образом, мы показали, что в двумерной

15.

V. Borue, Phys. Rev. Lett. 72, 1475 (1994).

турбулентности вокруг вращающегося диска образу-

ется когерентный вихрь. Мы проанализировали слу-

16.

M. Chertkov, C. Connaughton, I. Kolokolov, and

V. Lebedev, Phys. Rev. Lett. 99, 084501 (2007).

чай, когда на больших расстояниях значение сред-

ней полярной скорости U стремится к универсальной

17.

H. Xia, M. Shats, and G. Falkovich, Phys. Fluids 21,

√

125101 (2009).

постоянной

3ǫ/α, найденной в работах [19-21]. На

границе диска средняя полярная скорость U₀ может

18.

N. Francois, Y. Xia, H. Punzmann, S. Ramsden, and

√

M. Shats, Phys. Rev. X 4, 021021 (2014).

быть больше или меньше, чем

3ǫ/α. Однако есть

условие применимости (10) нашего подхода. Такая

19.

J. Laurie, G. Boffetta, G. Falkovich, I. Kolokolov, and

установка может быть реализована эксперименталь-

V. Lebedev, Phys. Rev. Lett. 113, 254593 (2014).

но в ячейке с тонким жидким слоем, где турбулент-

20.

I. V. Kolokolov and VV. Lebedev, Phys. Rev. E 93,

ность возбуждается внешним воздействием.

033104 (2016).

Работа выполнена при поддержке гранта Ми-

21.

I. V. Kolokolov and V. V. Lebedev, J. Fluid Mech. 809,

нистерства науки и высшего образования РФ

R2-1 (2016).

#075-15-2019-1893 (С.С.Вергелес и В.В.Лебедев),

22.

G. Falkovich, Proc. R. Soc. A 472, 20160287 (2016).

гранта фонда развития теоретической физики и

23.

A. Frishman, J. Laurie, and G. Falkovich, Phys. Rev.

математики “БАЗИС” # 19-1-2-46-1 (С. С. Вергелес)

Fluids 2, 032602 (2017).

и Министерства науки и высшего образования

24.

A. Frishman and C. Herbert, Phys. Rev. Lett. 120,

Российской Федерации (в рамках госзадания)

204505 (2018).

(И. В. Колоколов).

25.

G. Falkovich and N. Vladimirova, Phys. Rev. Letters

121, 164501 (2018).

26.

I. V. Kolokolov and V. V. Lebedev, Pis’ma v ZhETF

1. A. S. Monin and A. M. Yaglom, Statistical Fluid

Mechanics, MIT Press, Cambridge, MA (1971), v. 1;

106, 633 (2017) [JETP Lett. 106, 659 (2017)].

Dover publications, Mineola (2007), v. 2.

27.

A. V. Orlov, M. Yu. Brazhnikov, and A. A. Levchenko,

2. G. Boffetta and R. E. Ecke, Annu. Rev. Fluid Mech. 44,

Pis’ma v ZhETF 107, 166 (2018) [JETP Lett. 107, 157

427 (2012).

(2018)].

Письма в ЖЭТФ том 111 вып. 7 - 8

2020