Письма в ЖЭТФ, том 111, вып. 9, с. 591 - 596
© 2020 г. 10 мая
Разности инвариантов узлов-мутантов и их дифференциальное
разложение
Л.Бишлер+∗×1), Сасвати Дхара◦1),2), Т.Григорьев∇1), А.Миронов+∗×1), А.Морозов∗×∇1),
Ан. Морозов∗×∇1), П. Рамадеви◦1),2), Вивек Кумар Сингх◦1),2), А. Слепцов∗×∇1)
+Физический институт им. П. Н. Лебедева, 119991 Москва, Россия
∗Институт теоретической и экспериментальной физики, 117218 Москва, Россия
×Институт проблем передачи информации, 127994 Москва, Россия
◦Физический факультет, Индийский Институт Технологии Бомбея, 400076 Мумбаи, Индия
∇Московский физико-технический институт, 141701 Долгопрудный, Россия
Поступила в редакцию 8 апреля 2020 г.
После переработки 8 апреля 2020 г.
Принята к публикации 8 апреля 2020 г.
Мы вычисляем разности инвариантов ХОМФЛИ-ПТ для пар узлов-мутантов, раскрашенных пред-
ставлениями SL(N), достаточно большими для того, чтобы различить эти узлы. Эти пары мутантов
включают в себя мутанты-претцели, для различения которых минимально необходимо представление,
описываемое диаграммой Юнга [4, 2]. Мы обсуждаем дифференциальное разложение для разностей,
оказывающееся нетривиальным для мутантов с ненулевыми дефектами. Наиболее эффективным техни-
ческим методом в этом случае является стандартный подход Решетихина-Тураева.
DOI: 10.31857/S1234567820090037
1. Введение. Различать разные узлы - одна из
га с помощью специальных преобразований - му-
основных целей теории узлов. Наиболее удобным и
таций (см. раздел 2). Полиномы этих узлов совпа-
универсальным способом делать это является вы-
дают во всех симметрических и даже прямоуголь-
числение и сравнение их полиномиальных инвари-
ных представлениях R [4, 5] (на самом деле это та-
антов. Достаточно сильный инвариант, который при
кие представления, разложение квадратов которых
этом можно явно вычислить, - полиномы ХОМФЛИ-
не содержит нетривиальных кратностей [6, 7]). Та-
ПТ [1, 2], которые (при правильной нормировке)
ким образом, для того чтобы различить эти узлы,
являются полиномами от двух переменных q и A.
необходимо изучать смешанные представления. Са-
С физической точки зрения, они являются наблю-
мое простое из них - представление R = [2, 1], и
даемыми (средними значениями петель Вильсона)
оно действительно позволяет различить некоторые
в трехмерной теории Черна-Саймонса. При подста-
узлы-мутанты [6, 7]. Однако, как показал Х. Мортон
новке A = qN эти полиномы описывают наблюдае-
[8] (см. также [7]), существуют мутанты, которые об-
мые (средние значения петель Вильсона) в теории
ладают еще большей степенью симметрии. Эти му-
танты не различаются представлением R = [2, 1],
Черна-Саймонса с калибровочной группой SU(N) )(
2πi
необходимо хотя бы представление R = [4, 2]. Изу-
или SL(N) и q := exp
, где κ - константа связи
κ+N
чение полиномов этих узлов и разностей между ни-
[3]. Эти полиномы также зависят от представления
ми - сложная задача, которая интересна как с точки
R калибровочной группы, бегущего вдоль вильсонов-
зрения теории узлов, так и с точки зрения теории
ской линии.
представлений. На данный момент пары мутантов,
Сложнее всего различить узлы из семейства
которые не различаются представлением R = [4, 2],
узлов-мутантов. Их можно получать друг из дру-
не найдены.
Наиболее эффективным методом вычисле-
1)mila-bishler@mail.ru; saswati123@phy.iitb.ac.in;
ния полиномов ХОМФЛИ-ПТ является подход
grigorev.ta@phystech.edu; mironov@lpi.ru; morozov@itep.ru;
Решетихина-Тураева (РТ), который впервые был
andrey.morozov@itep.ru; ramadevi@phy.iitb.ac.in;
vivek.singh@fuw.edu.pl; sleptsov@itep.ru
предложен в [9-11] и основывается на использова-
2)Saswati Dhara, P. Ramadevi, Vivek Kumar Singh.
нии R-матриц квантовой группы Uq(SL(N)). Его
Письма в ЖЭТФ том 111 вып. 9 - 10
2020
591
592
Л.Бишлер, Сасвати Дхара, Т. Григорьев и др.
современная форма, которую иногда называют
современным методом РТ, использует для R-матриц
особый базис, который не зависит от N. Этот метод
был развит в ряде статей [12-20], применялся для
вычисления полиномов большого количества узлов
и зацеплений, и оказался технически гораздо более
сильным в большинстве случаев. Однако, как мы
подчеркиваем в настоящем письме, для некоторых
задач РТ-метод в первоначальной формулировке
оказывается более прямолинейным и быстрым,
хотя и не всегда позволяет получить полиномы,
зависящие от переменных q, A. Причина этого в
том, что для применения современной РТ-техники
Рис. 1. Процедура мутации
необходимо знание матриц Рака, которые очень
сложно найти в рассматриваемых случаях. Мы
этой причине узлы-мутанты являются узлами с боль-
опишем эти подходы более подробно в разделе 3.
шим числом пересечений. Простейшие пары узлов-
Мы использовали РТ-метод для вычисления раз-
мутантов имеют, по крайней мере, 11 пересечений,
ностей между полиномами узлов-мутантов в пред-
одна из этих пар состоит из известных узлов Кон-
ставлениях R = [3, 1] и R = [4, 2] при некоторых
вея и Киношиты-Терасаки. Однако в случае узлов с
значениях N. Для [3, 1] нам удалось проделать вы-
11 пересечениями узлы-мутанты появляются только
числения вплоть до N = 7. Это позволило найти об-
парами. Мы считаем, что существует большое число
щие ответы для произвольного N в этих случаях и,
операций мутации, порождающих семейства узлов-
таким образом, вычислить соответствующие полино-
мутантов с количеством пересечений больше 11, но
мы ХОМФЛИ-ПТ. Для представления R = [4, 2] нам
они выходят за рамки нашего обсуждения.
удалось вычислить разности только для N = 3, 4.
Существует семейство узлов, которые называют
Мы изучили свойства этих разностей (см. раздел 4)
узлами-претцелями, изображенное на рис.2, и кото-
и их дифференциальных разложений.
Дифференциальное разложение [16, 21-27], кото-
рое является сравнительно новым и сильным инстру-
ментом в теории узлов, часто позволяет угадать от-
веты для полиномов узлов, изучить их различные
свойства и дает много новых идей. Оно достаточно
просто устроено для узлов с нулевым дефектом [23] и
становится менее тривиальным в других случаях. К
сожалению, узлы-мутанты обычно имеют ненулевой
дефект. Результаты, полученные нами, показывают,
что дифференциальное разложение узлов-мутантов
имеет достаточно интересные свойства, мы обсужда-
ем их в разделе 5.
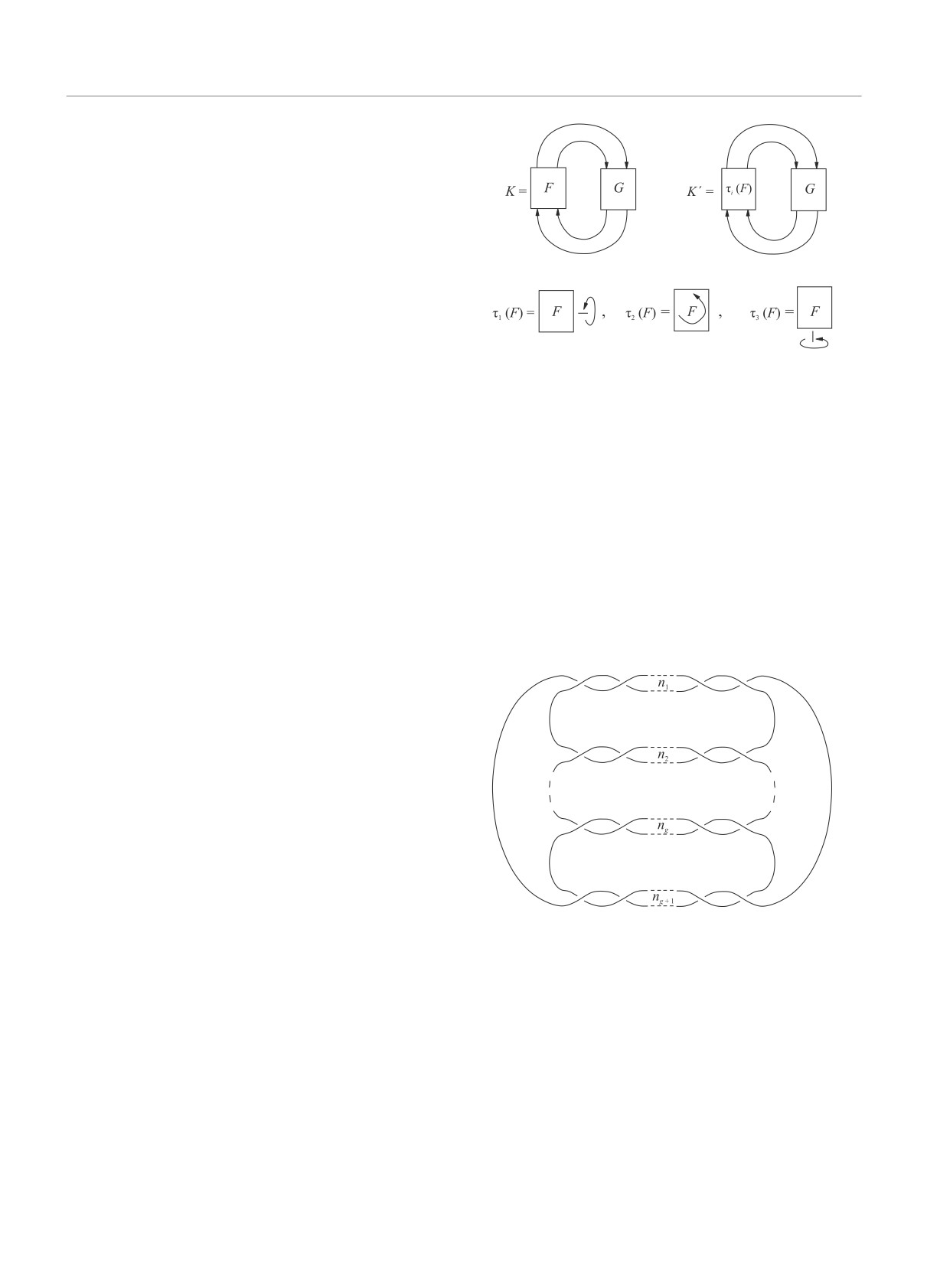
2. Узлы-мутанты. В первую очередь давайте
обсудим, что такое узлы-мутанты. Узлы-мутанты -
Рис. 2. Узлы-претцели K(n1, n2, . . . , ng , ng+1)
это семейства узлов, которые связаны друг с дру-
гом специальной операцией - мутацией (см. рис.1).
рые включают в себя много новых мутантов, полу-
Для проведения мутации необходимо вырезать часть
ченных с помощью мутаций 2-танглов. Они являются
узла с двумя входящими и двумя исходящими лини-
обобщением торических узлов, о которых многое из-
ями внутри 3-сферы. Такую вырезанную часть узла,
вестно. Узлы-претцели можно поместить на поверх-
которую технически называют 2-танглом, поворачи-
ность рода g. Однако, в отличие от торических узлов,
вают на 180 градусов и вклеивают обратно. Получив-
на одну ручку можно поместить только две нити, см.
шийся узел называют мутантом исходного узла.
рис. 2. Узлы-претцели параметризуют числом пере-
Очевидно, что, для того чтобы эти узлы были
сечений на каждой ручке.
различны, и часть узла внутри 3-сферы, и внеш-
Легко увидеть, что перестановка чисел между
няя часть узла должны быть нетривиальными. По
ручками в точности отвечает мутации. Таким обра-
Письма в ЖЭТФ том 111 вып. 9 - 10
2020
Разности инвариантов узлов-мутантов и их дифференциальное разложение
593
зом, начиная с рода 4, появляются пары мутантов.
ботает для любого представления R. Однако при ис-
Для двух и трех ручек мутация дает в точности тот
пользовании универсальной R-матрицы вычисления
же узел, однако для старших родов существуют бо-
необходимо делать отдельно для каждого N.
лее широкие наборы мутантов. Заметим, что среди
Более продвинутый современный РТ-метод [14,
этих претцелевых пар мутантов некоторые принад-
15] использует R-матрицы в базисе сплетающих опе-
лежат классу мутантов, обладающих более высокой
раторов. Когда R-матрица действует на тензорное
симметрией и различимых только представлением
произведение двух представлений V1 и V2, можно
R = [4,2] (см. рис.3 и [7]).
рассмотреть разложение произведения по неприво-
димым представлениям V1 ⊗ V2
= ⊕QMQV
· Q.
1V2
Так как R-матрица коммутирует с копроизведением
[28], на неприводимые представления она действует
умножением на число ±qC2(Q) [29], где C2(Q) - это
собственное значение второго оператора Казимира в
представлении Q.
Давайте рассмотрим R-матрицу в базисе непри-
водимых представлений, или, лучше сказать, в про-
странстве сплетающих операторов и представим узел
как замыкание n-нитевой косы. Тогда ответ для по-
линома ХОМФЛИ-ПТ HKV(A, q) узла K, раскрашен-
ного представлением V , разделяется на две части:
одна зависит от группы, другая зависит от узла
[14, 15]:
Рис. 3. Узлы-мутанты с большей степенью симметрии
∑
из [8]
HKV(A, q) =
S∗Q(A, q)BKQ(q).
(3)
Q∈V⊗n
3. R-матричный РТ-подход. Подход Решети-
хина-Тураева (РТ) возникает естественным обра-
С этого момента мы ассоциируем с представлени-
зом, если средние значения петель Вильсона [3] вы-
ем Q соответствующую ему диаграмму Юнга. S∗Q -
числяются во временной калибровке [24, 25]. То-
это квантовая размерность представления Q кванто-
гда каждое пересечение на диаграмме узла (про-
вой группы Uq(SL(N)). Квантовая размерность рав-
екции узла на двумерную плоскость) связано с R-
на полиному Шура SQ в некоторой специальной точ-
матрицей. Можно начать с универсальной квантовой
ке [30, разд. 7.1.6]. Она не зависит от узла, и зависит
R-матрицы для Uq(SL(N)) и вычислить Uq(SL(N))-
от N через переменную A = qN . С другой стороны,
матрицу в конкретных представлениях с помощью
BKQ вычисляется для конкретного узла как след про-
генераторов квантованной универсальной обертыва-
изведения R-матриц и не зависит от A или N. Важ-
ющей алгебры:
но, что оба этих фактора зависят только от диаграм-
мы Юнга Q, а вся зависимость от A скрыта в фик-
∑
-∏
(
)
hi⊗hj
сированных полиномах от A - квантовых размерно-
R=Pqi,jai,j
expq
(q - q-1)Eβ ⊗ Fβ
,
стях. Это означает, что современный РТ-подход поз-
β∈Φ+
(1)
воляет вычислить полиномы ХОМФЛИ-ПТ для всех
где Eβ , Fβ и hβ являются генераторами квантован-
N сразу, в отличие от стандартного РТ-подхода, ко-
ной универсальной обертывающей алгебры:
торый мы используем в данной работе.
Тем не менее, у современного РТ-подхода име-
[hi, Ej ] = aij Ej ,
[hi, hj] = 0,
ются большие трудности. Во-первых, необходимо ис-
(2)
qhi -q-hi
[hi, Fj ] = -aij Fj ,
[Ei, Fj ] = δij
пользовать представление узла в виде косы, которое,
q-q-1
в случае мутантов, содержит большое число нитей.
Свертка R-матриц в пересечениях на диаграмме
Во-вторых, несмотря на то, что R-матрицы в про-
узла по линиям между пересечениями и последую-
странстве сплетающих операторов устроены просто,
щее вычисление взвешенного следа [9] позволяет по-
их необходимо дополнительно вращать при переходе
лучить полином ХОМФЛИ-ПТ. В отличие от пер-
к другим парам нитей в косе [14, 15]. Это вращение
воначального определения полиномов через скейн-
производится матрицами Рака, вычисление которых
соотношения [1] этот подход одинаково хорошо ра-
является очень непростой задачей, особенно в случа-
2
Письма в ЖЭТФ том 111 вып. 9 - 10
2020
594
Л.Бишлер, Сасвати Дхара, Т. Григорьев и др.
ях больших представлений [31, 32] и большого числа
видны для группы Uq(SL(2)), так как разности исче-
нитей в косе [14], которыми мы здесь интересуемся.
зают для любых симметрических представлений, как
В вычислениях, о которых идет речь в этой ра-
было упомянуто во Введении. Это менее тривиально
боте, мы не использовали базис неприводимых пред-
для Uq(SL(3)) (см. [4]). Дифференциалы Di с поло-
ставлений для R-матриц и изучали полиномы узлов
жительными i имеют тот же смысл для транспониро-
и их разности для конкретных значений N, которые
ванного представления R. Представление R = [2, 1]
в некоторых случаях удалось продолжить на произ-
не меняется при этом преобразовании, а представле-
вольные N.
ние R = [3, 1] преобразуется в R = [2, 1, 1]. Таким об-
4. Разности полиномов узлов-мутантов. В
разом, мы заключаем, что разность для R = [2, 1, 1]
[6, 7, 20] мы использовали современный РТ-подход
исчезает для группы Uq(SL(4)).
для вычисления разностей инвариантов для узлов-
Для представления [4, 2] нам не удалось скон-
мутантов с 11 пересечениями. Мы установили, что
струировать ответ для произвольного N. Однако
эти разности очень хорошо факторизуются. Они рав-
у нас получилось вычислить ответы для мутантов-
ны
претцелей для групп Uq(SL(3)) и Uq(SL(4)).
ΔHmutant[2,1] = Aγ · f(A, q) · Mt
(q),
(4)
5. Дифференциальное разложение. Цветные
[2,1]
полиномы ХОМФЛИ-ПТ обладают дополнительной
где γ - целое число, Mt
[2,1]
(q) - функция, зависящая
структурой, которую называют дифференциальным
только от q, и
разложением (ДР) [16, 21-27]. Она связана с теорией
f (A, q) := {q}4 · [3]2D23D2D0D-2D2-3,
(5)
представлений [16, 17]. Простейший пример ДР появ-
ляется уже в фундаментальном представлении: так
где [...] обозначает q-число, {q} := q -q-1, и факторы
как для абелевой U(1) теории Черна-Саймонса, т.е.
для A = q, нормированные полиномы ХОМФЛИ-ПТ
Dk := Aqk - A-1q-k
(6)
в топологическом фрейминге тривиальны, мы полу-
чаем
называются дифференциалами. Отметим, что H
H[1](A, q) = 1 + D1D-1 · F[1](A, q)
(8)
в ур.(4) обозначает нормированные полиномы
ХОМФТИ-ПТ, при этом полные полиномы (средние
с новым, более простым полиномом Лорана F[1](A, q).
Вильсона) обозначаются H в (3).
Если продолжить эти рассуждения и обратить вни-
В данной работе, используя подход, описанный в
мание на другие N, можно получить общую структу-
предыдущем разделе и основанный на R-матрицах
ру разложения цветных полиномов по произведени-
при конкретных N, мы вычислили разности между
ям независимых от узла комбинаций ZQR различных
полиномами узлов-мутантов в представлениях [3, 1]
дифференциалов Dk:
и [4, 2]. Ответы получились достаточно громоздки,
∑
HKR(A, q) =
ZQR(A, q) · FKQ(A, q).
(9)
их можно найти как в более детальной публикации
Q∈MR
[33], так и на специальном интернет-ресурсе [34].
Для представления [3, 1] нам сначала удалось
Важным параметром дифференциального разло-
вычислить разности для нескольких значений N.
жения является дефект δK узла K. Он определяется
Это позволило построить полные ответы для произ-
как степень полинома Александера, то есть специа-
вольного N и, таким образом, получить полиномы
лизации фундаментального полинома ХОМФТИ-ПТ
ХОМФЛИ-ПТ, раскрашенные представлением [3, 1].
в точке A = 1:
Эти разности, однако, не факторизуются так же пол-
∑
но, как в случае представления [2, 1]. Тем не менее в
HK[1](A, q)
=
ajq2j.
(10)
них выделяется структура дифференциалов:
A=1
j=-δK -1
ΔHmutant[3,1] = {q}4 · [4]2[2]D4D3D0D-2 · Mt
(A, q).
Дифференциальное разложение наиболее сложно
[3,1]
(7)
устроено в случае ненулевого дефекта, к которому
Когда дифференциалы D-i появляются в качестве
относятся узлы-мутанты. Об общей теории диффе-
множителя, это значит, что разность инвариантов
ренциального разложения пойдет речь в других ра-
равна нулю для группы Uq(SL(i)). Таким образом,
ботах, здесь же мы только обсудим конкретную про-
мы видим, что разности между полиномами узлов-
блему, возникающую для пар узлов-мутантов.
мутантов для представления [2, 1] обращаются в нуль
Рассмотрим разность дифференциальных разло-
для групп Uq(SL(2)) и Uq(SL(3)), и для представле-
жений для полиномов ХОМФЛИ-ПТ пары узлов-
ния [3, 1] для группы Uq(SL(2)). Эти результаты оче-
мутантов. Мы обозначим эту разность через Δ. Мож-
Письма в ЖЭТФ том 111 вып. 9 - 10
2020
Разности инвариантов узлов-мутантов и их дифференциальное разложение
595
(
)
но предположить, что вклад в нее вносят толь-
[4]
={q}4[4]2[2]D2D-2D3D2
-3
D3D0-
D2D1
·Mt
,
ко недиагональные композитные представления, та-
[2,1]
[3][2]
|
{z
}
кие как X2
:=
([2], [1, 1]) ⊕ ([1, 1], [2]) и X3
:=
D4D-1
([3], [2, 1]) ⊕ ([2, 1], [3]). Мы, однако, допускаем так-
[3]
же дополнительное преобразование некоторых ДР-
которое делится на D4. Однако теперь возникает но-
коэффициентов, которое остается ненаблюдаемым в
вая потенциальная проблема: мы получаем D4D-1,
лидирующем порядке, но может внести вклад в стар-
а не D4D0, однако D0 с чертой может отсутство-
шие представления, это преобразование мы обозна-
вать в дифференциальном разложении для ненуле-
чим δ. В первом смешанном представлении из [7,
вого дефекта. В любом случае, еще большое количе-
ур. (106)] и [27, ур. (14)-(17)] можно получить выра-
ство других факторов должно сойтись...
жение, зависящее от двух неизвестных функций вида
Другая возможность заключается в том, чтобы
, который не участвовал
обратить внимание на F[3,1]
ΔH[2,1] =
в вышеизложенном вычислении разностей и может
(
)
отличаться для разных мутантов. В случае H[2,1] у
[3]
=
D20
+ [3]D2D-2
⊕ {q}4[3]2D2D-2
=
нас получалось ΔF[2,1] = 0, потому что эта разность
[2]2
|{z}
|
{z
}
|
{z
}
также входит в выражение для разности в прямо-
×0
×{q}4[2]2·δF[1]
×(ΔFX2 -δF[1])
угольном представлении H[2,2], которая не различа-
= {q}4 · [3]2D23D2D0D-2D2-3 · Mt
(11)
[2,1]
ет мутантов, т.е. ΔH[2,2] = 0. Однако H[3,3] содержит
вклады от двух непрямоугольных структур, таким
Величина δF1 обозначает возможное перераспреде-
образом, F[3,1] и F[3,2] могут быть ненулевыми и ком-
ление коэффициентов между разными членами диф-
пенсировать друг друга в нулевой разности в прямо-
ференциального разложения для двух мутантов, ко-
угольном представлении ΔH[3,3].
торое при этом не влияет на правую часть выраже-
6. Заключение. Это письмо является крат-
ния, однако может проявить себя в разности между
ким изложением наших результатов для полиномов
мутантами в старших представлениях. Естественно
ХОМФЛИ-ПТ узлов-мутантов. Эти полиномы и осо-
предположить, что она равна нулю, однако мы остав-
бенно разности между ними представляют большой
ляем эту возможность открытой.
Аналогично, для следующего смешанного пред-
интерес со многих точек зрения. Нам удалось скон-
ставления
струировать разности между полиномами в пред-
(
)
[4]
[4]
ставлении R = [3, 1] для всех узлов-мутантов с 11
ΔH[3,1] =
D1D0
+
D3D-2
⊕ {q}4[4]2[2]D3D-2
+
[3]
| {z }
[2]
|
{z
}
пересечениями. Они оказались менее структуриро-
0
|
{z
}
×(ΔFX
2
-δF[1])
×[2]2{q}4·δF[1]
ванными, чем ответы в случае представления [2, 1],
тем не менее зависимость от представления в них до-
(
)
[4]
+
D3D21D0
+ [4][2]D4D3D0D-2
⊕{q}4[4]2[2]D4D3D0D-2
статочно нетривиальная. Мы также изучили диффе-
[3]2
|
{z
}
|
{z
}
|
{z
}
×0
×{q}4[3]2·δF[2]
×(ΔFX
-δF[2])
ренциальное разложение этих разностей, связаное со
3
свойствами представлений, для которых они вычис-
= {q}4 · [4]2[2]D4D3D0D-2 · Mt
(12)
[3,1]
лены. В частности, мы нашли тонкое место в диффе-
ренциальном разложении мутантов, которое требует
Теперь мы сталкиваемся со следующей проблемой:
дальнейшего изучения в случае узлов с ненулевы-
все члены в последней строке делятся на D4, кроме
ми дефектами. Осталось неизученым, что происхо-
ΔFX2 = 0.
дит для старших представлений.
Существует по крайней мере два возможных вы-
Мы также вычислили разности между полинома-
хода из этой ситуации. Первая возможность заклю-
ми узлов-мутантов в представлении [4, 2], но только
чается в том, чтобы допустить δF[1] = 0. Например,
для групп Uq(SL(3)) и Uq(SL(4)), что недостаточно
пусть
для того, чтобы найти общий ответ, однако позво-
ΔFX2 = D23D0D2-3 · Mt
δF[1] = D3D2D1D2-3 ·Mt
лило нам различить узлы-мутанты. Для того чтобы
[2,1]
[2,1]
найти полные инварианты ХОМФЛИ-ПТ, необходи-
так, что ΔFX2 -δF[1] = -[2]{q}2D3D2-3 ·Mt
. Тогда
[2,1]
мо либо применить другие подходы, либо серьезно
мы получим:
оптимизировать компьютерные программы.
(
(
)
Наша работа была частично поддержана гран-
1 )
{q}4[4]2[2]D2D-2 ΔFX2 -
1-
δF[1]
=
том Фонда развития теоретической физики и
[3]
|
{z
}
математики
“БАЗИС” (Л.Бишлер, А.Миронов,
[4]
А. Морозов,
Ан. Морозов, А. Слепцов), грантом
[3][2]
Письма в ЖЭТФ том 111 вып. 9 - 10
2020
2∗
596
Л.Бишлер, Сасвати Дхара, Т. Григорьев и др.
президента Российской Федерации MK-2038.2019
14.
A. Mironov, A. Morozov, and An. Morozov, JHEP 03,
(Л. Бишлер, Ан. Морозов), грантами РФФИ
19-
034 (2012); arXiv:1112.2654.
01-00680
(А. Миронов),
19-02-00815 (А.Морозов),
15.
A. Mironov, A. Morozov, and An. Morozov, Character
20-01-00644 (Ан.Морозов, А.Слепцов),
18-31-
expansion for HOMFLY polynomials. I. Integrability
and difference equations, in Strings, Gauge Fields,
20046-мол-а-вед (А.Слепцов), совместными гран-
and the Geometry Behind: The Legacy of Maximilian
тами
19-51-50008-ЯФ-а (Л.Бишлер, А.Миронов,
Kreuzer, ed. by A. Rebhan, L. Katzarkov, J. Knapp,
Ан. Морозов),
19-51-53014-ГФЕН-а,
18-51-05015-
R. Rashkov, and E. Scheidegger (World Scientific
Арм-а, 18-51-45010-ИНД-а (Л. Бишлер, А. Миронов,
Publishins Co.Pte.Ltd. (2013), p. 101; arXiv:1112.5754.
А. Морозов, Ан. Морозов, А. Слепцов), П. Рамадеви,
16.
A. Mironov, A. Morozov, and An. Morozov, AIP Conf.
Вивек Кумар Сингх и Сасвати Дхара благодарят
Proc. 1562(1), 123 (2013); arXiv:1306.3197.
грант ДНТ-РФФИ (INT/RUS/RFBR/P-231) за под-
17.
C. Bai, J. Jiang, J. Liang, A. Mironov, A. Morozov,
держку. Работа также частично финансировалась
An. Morozov, and A. Sleptsov, Phys. Lett. B 778, 197
РФФИ и ННФБ в соответствии с исследователь-
(2018); arXiv:1709.09228.
ским проектом 19-51-18006 (А. Миронов, А. Морозов,
18.
A. Mironov, A. Morozov, and An. Morozov, JHEP
Ан. Морозов). Вивек Кумар Сингх хотел бы поблаго-
2018, 128 (2018); arXiv:1804.07278.
дарить Индийский Институт Научного Образования
19.
A. Mironov and A. Morozov, JETP Lett. 107, 728
и Исследования, Пуна (Индия), где он частично
(2018); arXiv:1804.10231.
занимался данной работой во время своего визита в
20.
A. Mironov, A. Morozov, An. Morozov, P. Ramadevi,
качестве приглашенного исследователя. А. Миронов,
Vivek Kumar Singh, and A. Sleptsov, J. Phys. A: Math.
А. Морозов и П. Рамадеви признательны Институту
Theor. 50, 085201 (2017); arXiv:1601.04199.
теоретической физики им. Кавли за гостеприимство
21.
N. M. Dunfield, S. Gukov, and J. Rasmussen,
и Национальному научному фонду за частичную
Experimental
Math.
15,
129
(2006);
arXiv:math/0505662.
поддержку по гранту NSF PHY1748958.
22.
H. Itoyama, A. Mironov, A. Morozov, and An. Morozov,
JHEP 7, 131 (2012); arXiv:1203.5978.
23.
Ya. Kononov and A. Morozov, JETP Lett. 101, 831
1. P. Freyd, D. Yetter, J. Hoste, W. B. R. Lickorish,
(2015); arXiv:1504.07146.
K. Millett, and A. Ocneanu, Bull. Amer. Math. Soc.
24.
A. Morozov and A. Smirnov, Nucl. Phys. B 835, 284
(N.S.) 12(2), 239 (1985).
(2010); arXiv:1001.2003.
2. J. H. Przytycki and P. Traczyk, J. Knot Theor. 4, 115
25.
A. Morozov and A. Smirnov, in The Most Unexpected
(1987); arXiv:1610.06679.
at LHC and the Status of High Energy Frontier,
3. E. Witten, Commun. Math. Phys. 121, 351 (1989).
Proceedings of the International School of Subnuclear
4. H. R. Morton and H. J. Ryder, Geom. Topol. Monogr.
Physics, ed. by A. Zichichi, Erice, Sicily, Italy,
29
1, 365 (1998); arXiv:math/9810197.
August-7 September 2009, World Scientific, v.47, p. 489;
5. H. R. Morton and P. R. Cromwell, J. Knot Theory
arXiv:0910.5011.
Ramif. 5, 225 (1996).
26.
S. Arthamonov, A. Mironov, and A. Morozov, Theor.
6. S. Nawata, P. Ramadevi, and Vivek Kumar Singh,
Math. Phys. 179, 509 (2014); arXiv:1306.5682.
J. Knot Theory Ramif.
26(14),
1750096
(2017);
27.
A. Morozov, arXiv:1903.00259.
arXiv:1504.00364.
28.
N. Yu. Reshetikhin, L. A. Takhtadjan, and L. D. Fad-
7. A. Mironov, A. Morozov, An. Morozov, P. Ramadevi,
deev, Algebra and Analysis 1, 178 (1989).
and Vivek Kumar Singh, JHEP 1507, 109 (2015);
29.
M. Gould and Y. Zhang, J. Math. Phys. 35(12), 6757
arXiv:1504.00371.
(1994); arXiv:hep-th/9311041.
8. H. R. Morton, Math. Proc. Cambridge Philos. Soc. 146,
30.
A. Klimyk and K. Schmüdgen, Quantum groups
95 (2009); arXiv:0705.1321.
and their representations, World Scientific
(1997);
9. V. G. Turaev, Invent. Math. 92, 527 (1988).
10. N. Yu. Reshetikhin and V. G. Turaev, Commun. Math.
31.
A. Mironov, A. Morozov, An. Morozov, and A. Sleptsov,
Phys. 127, 1 (1990).
Pisma v ZhETF 104, 52 (2016); arXiv:1605.03098.
11. N. Reshetikhin and V. G. Turaev, Invent. Math. 103,
32.
A. Mironov, A. Morozov, and A. Sleptsov, Pis’ma v
547 (1991).
ZhETF 106, 607 (2017); arXiv:1709.02290.
12. P. Ramadevi, T. R. Govindarajan, and R. K. Kaul, Mod.
33.
L. Bishler, Saswati Dhara, T. Grigoryev, A. Mironov,
Phys. Lett. A 9, 3205 (1994); hep-th/9401095.
A. Morozov, An. Morozov, P. Ramadevi, Vivek Kumar
13. S. Nawata, P. Ramadevi, and Zodinmawia, J. Knot
Singh, and A. Sleptsov, to be published.
Theory Ramif. 22, 13 (2013); arXiv:1302.5144.
34.
Письма в ЖЭТФ том 111 вып. 9 - 10
2020