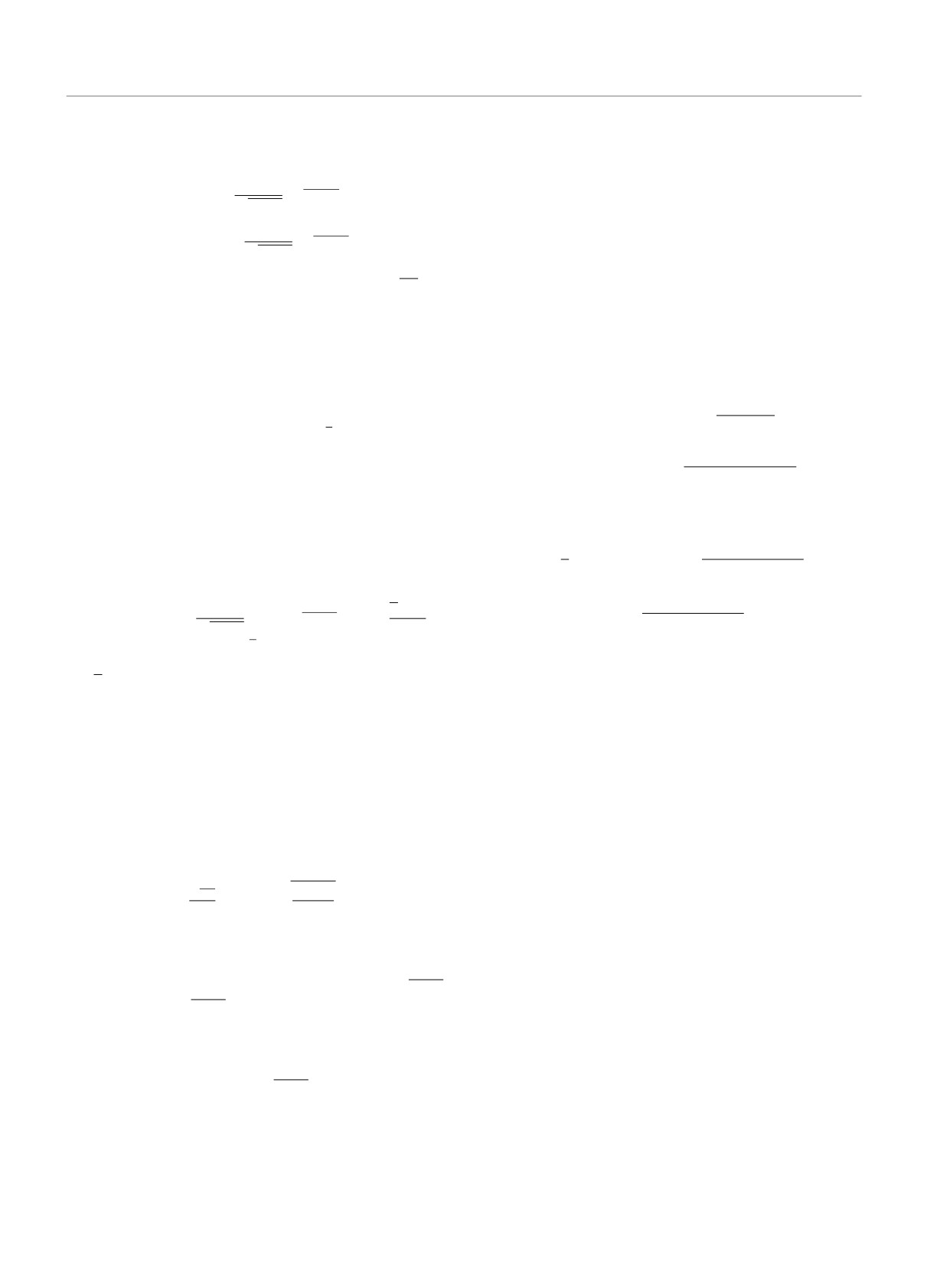Письма в ЖЭТФ, том 111, вып. 9, с. 608 - 614

О побочном квантово-классическом бинарном канале утечки

информации с гауссовским шумом

С. Н. Молотков¹⁾

Институт физики твердого тела РАН, 142432 Черноголовка, Россия

Академия криптографии Российской Федерации, 121552 Москва, Россия

Центр квантовых технологий, МГУ им. М. В. Ломоносова, 119899 Москва, Россия

Поступила в редакцию 4 апреля 2020 г.

После переработки 6 апреля 2020 г.

Принята к публикации 6 апреля 2020 г.

Детектирование побочного излучения передающей аппаратуры является дополнительным источни-

ком информации о передаваемых ключах. Детектирование побочного излучения в отличии от вторжения

в квантовый канал связи не приводит к возмущению информационных состояний и ошибкам на при-

емной стороне. Оценка величины утечки информации по побочному каналу является принципиально

необходимой для обеспечения криптографической стойкости систем квантовой криптографии. В работе

приведен простой квантовый вывод величины утечки информации по побочному квантовому каналу с

гауссовским шумом. Предложенный метод не ограничивается каналом с гауссовским шумом и применим

для других типов побочных каналов утечки информации.

DOI: 10.31857/S1234567820090062

1. Введение. Побочные каналы утечки инфор-

ней границей утечки информации к подслушивате-

мации являются одним из эффективных способов по-

лю. Структура состояний в побочном канале из-за

лучения информации, когда нет прямого доступа к

макроскопически большого числа степеней свободы

передающей и приемной аппаратуре. Применительно

аппаратуры, приводящей к побочному излучению,

к системам квантовой криптографии, кроме вторже-

точно неизвестна, поэтому невозможно обойтись без

ния в квантовый канал связи, по которому передают-

модельных предположений о структуре состояний в

ся информационные квантовые состояния, подслу-

побочном канале.

шиватель может детектировать побочное электро-

После того как побочное излучение покидает ис-

магнитное излучение, связанное с работой переда-

точник информации (например, передающую стан-

ющей аппаратуры. Побочное излучение коррелиро-

цию) и достигает подслушивателя, к исходному по-

вано с работой аппаратуры, точнее говоря, с приго-

бочному сигналу примешиваются внешние шумы, ко-

товлением состояний, отвечающих логическому биту

торые также имеют огромное число степеней свобо-

0 и логичекому биту 1, что приводит к разному по-

ды, и которые также точно неизвестны.

бочному излучению. Принципиальное отличие детек-

Далее, имея в виду приложение к квантовой

тирования побочного излучения от атаки непосред-

криптографии, будем рассматривать бинарный слу-

ственно на информационные состояния в квантовом

чай, когда передающая аппаратура - источник ин-

канале связи, состоит в том, что детектирование по-

формации приготавливает случайным образом 0 и

бочного излучения позволяет получать информацию

1. С формальной точки зрения первичный источник

о передаваемых ключах и при этом не производить

информации связан с подслушивателем через внеш-

ошибок на приемной стороне.

нюю среду, которая искажает первичный побочный

Поскольку структура квантовых состояний, по-

сигнал. Такая связь в классическом случае означа-

сылаемых с передающей станции в квантовый ка-

ет, что источник информации связан с подслушива-

нал связи известна, то при атаке непосредственно на

телем бинарным классическим каналом связи с ис-

квантовые состояния в канале связи фундаменталь-

кажениями. Из-за огромного числа степеней свобо-

ные законы квантовой механики позволяют связать

ды внешней среды, наложение множества случайных

наблюдаемую ошибку на приемной стороне с верх-

независимых величин приводит к гауссовскому рас-

пределению суммы случайных величин. По этой при-

¹⁾e-mail: sergei.molotkov@gmail.com

чине, естественным приближением для такого кана-

608

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

О побочном квантово-классическом бинарном канале утечки информации с гауссовским шумом

609

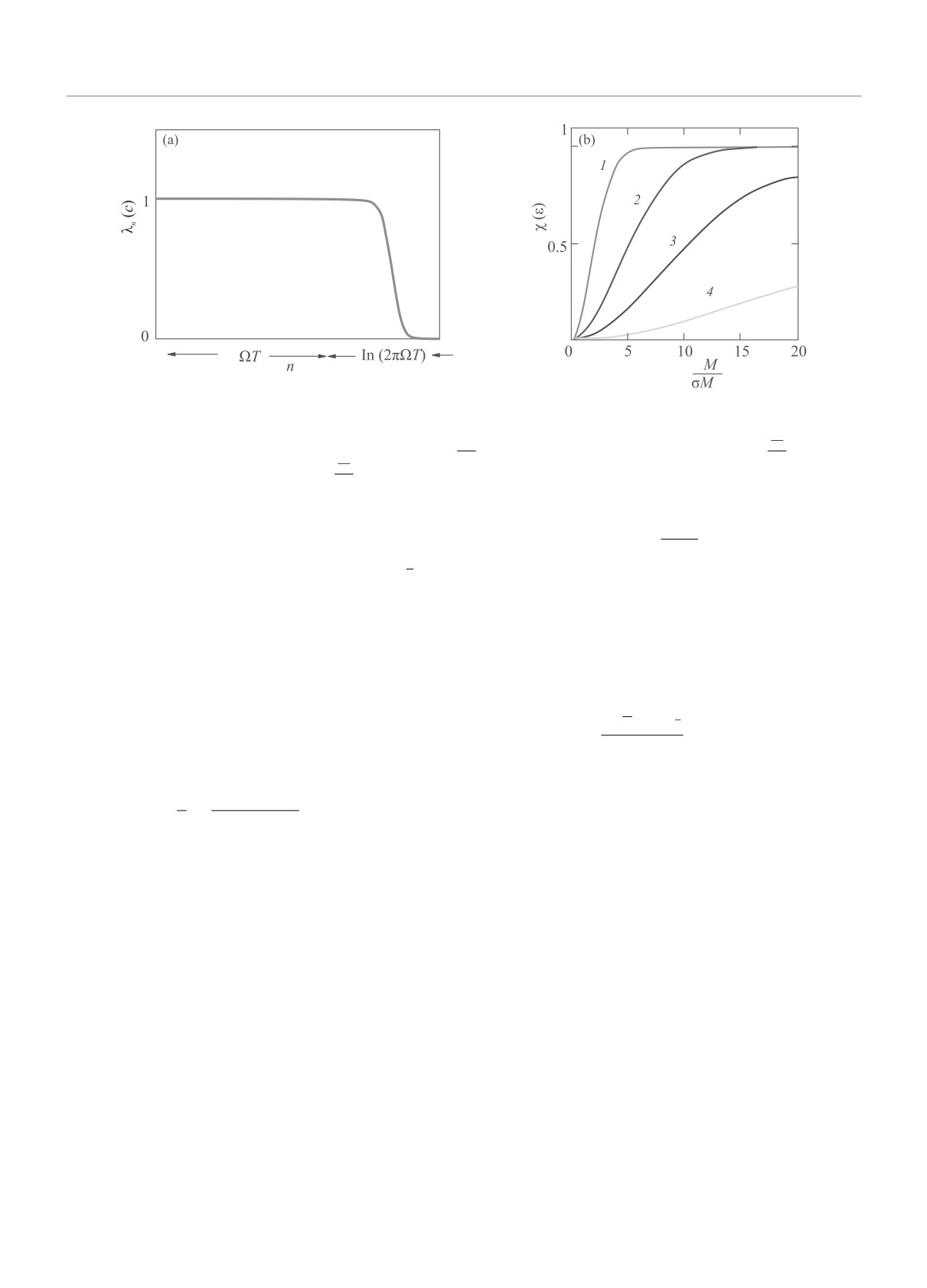
Рис. 1. (a) - Схематически показана генерация первичной информации 0 и 1. Символически показаны базичные функ-

ции вытянутого сфероида, локализованные во временном окне [0, T] наблюдения подслушивателем в каждом такте

сигнала в побочном канале. (b) - Условные вероятности при регистрации подслушивателем искаженных первичных

сигналов, отвечающих 0 и 1. Состояния различаются по принципу максимального правдоподобия. Принимается то

решение, 0 или 1, при измерении энергии сигнала, для которого вероятность при данной измеренной энергии больше.

Заштрихована область энергий, при которых приинимается решение о сигнале 0

ла с искажениями является приближение бинарно-

тектирование квантового побочного излучения, из-за

го аддитивного гауссовского канала с белым шумом

ограниченности места будет приведено в отдельном

(BAWNGC - Binary Additive White Noise Gaussian

сообщении.

Channel).

Сначала кратко напомним классическую поста-

Точную структуру побочного сигнала невозмож-

новку задачи при детектировании побочных сигна-

но контролировать, все, что возможно контролиро-

лов, а затем дадим квантовое описание, а также

вать, так это интенсивность сигнала в разных спек-

связь классического и квантового рассмотрения.

тральных диапазонах. Такой контроль достигается

2. Классический случай, канал BAWGNC.

экранированием аппаратуры. В классическом случае

Имея в виду приложение к квантовой криптографии,

побочный сигнал, который достигает подслушивате-

будем считать, что первичный источник информа-

ля, считается классическим сигналом. Применитель-

ции - аппаратура генерирует случайным образом в

но к квантовой криптографии такой подход является

каждом такте логические 0 и 1 (см. рис. 1). В ре-

недостаточным и неудовлетворительным, по крайней

альной ситуации приготовление 0 и 1 электронной

мере, двум причинам. Первая причина - искажен-

аппаратурой происходит приложением импульса на-

ный сигнал при достаточном экранировании может

пряжения разной величины на фазовый модулятор,

иметь предельно низкую интенсивность, фактически

что приводит к первичному побочному сигналу раз-

является квантовым состоянием, поэтому классиче-

ной интенсивности. После прохождения первичного

ское рассмотрение неприемлемо. Вторая причина -

сигнала через среду спектр исходного сигнала приоб-

подслушиватель может проводить совместные кол-

ретает гауссовский вид для 0 и 1 (хотя выбор гауссов-

лективные измерения как квантового состояния в по-

ского вида сигнала, как будет видно ниже, не явля-

бочном канале, так и квантовых информационных

ется ограничительным, можно выбрать любой дру-

состояний в квантовом канале связи. Как извест-

гой вид). Спектр искаженного побочного сигнала, ко-

но, теоретически возможный максимум информации

торый достигает подслушивателя, является гауссов-

- фундаментальная верхняя граница информации -

ским, центрированным в окрестности исходной энер-

информация Холево [1-3], которая может быть по-

гии сигналов для 0 и 1 (см. рис. 1b). В классическом

лучена из ансамбля квантовых состояний, достига-

случае считается, что энергия сигнала равна квад-

ется на коллективных измерениях. По этим причи-

рату амплитуды сигнала [4, 5]. Пусть амплитуда сиг-

нам требуется квантовое рассмотрение состояний в

нала есть y, тогда наблюдаемый сигнал подслуши-

побочном канале.

вателем для 0 и 1 центрирован в окрестности энер-

Цель данной работы - дать метод описания верх-

гий y₀ =

√-E_s и y₁ =√E_s. Начало отсчета энергии

ней границы утечки информации по побочному ка-

не имеет значения, важно только расстояние между

налу в зависимости от “интенсивности” состояния,

энергиями сигнала для 0 и 1 (см. ниже).

более точно, среднего числа фотонов в состоянии.

Детектирование искаженного сигнала подслуши-

Рассмотрение совместной атаки на информационные

вателем формализуется условными вероятностями.

квантовые состояния в квантовом канале связи и де-

В результате измерений подслушиватель видит рас-

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

610

С. Н. Молотков

пределение энергии сигналов. Условные вероятности

В контексте криптографии, более значимой вели-

имеют вид

чиной является не ошибка различения сигналов в по-

бочном канале, а количество информации, которую

(y-a)2

p(y|a) =

√ e^- 2σ2 ,

подслушиватель может получить из побочного кана-

2πσ²

ла. Такой величиной является взаимная информация

(1)

I(X; Y ) (см. детали в [4, 5]). Неформально взаимная

p(y| - a) =

√ e-(

2σ2

2πσ²

информация дает информацию в битах в пересчете

на каждую посылку состояний, которую может полу-

где для краткости введено обозначение a =

√E_s, σ -

чить подслушиватель о случайной величине, прини-

дисперсии сигналов для 0 и 1 после прохождения сре-

мающей значения x = -a, a, когда подслушиватель

ды, которые, для того, чтобы не загромождать вы-

имеет доступ к случайной величине y с распределе-

кладки, будем считать одинаковыми (обобщение на

ниями (1). С учетом (1) для взаимной информации

общий случай не представляет проблем). Априорные

получаем

вероятности в квантовой криптографии, с которыми

∫

(

)

∑

передающая аппаратура посылает в канал 0 и 1, счи-

p(x, y)

I(X; Y ) =

p(x, y) log

dy =

таем одинаковыми, p(a) = p(-a) =¹² .

p(x)p(y)

x=-a,a

Сигналы из-за перекрытия по спектру (см.

∫

(

)

∑

p(y|x)

рис. 1b) различаются подслушивателем с некоторой

p(y|x)p(x) log

∑

dy. (5)

p(y|x^′)p(x^′)

x=-a,a

x^′

вероятностью ошибки. Обычно в классическом слу-

чае различение сигналов происходит по максимуму

При равновероятном распределении 0 и 1 получаем

правдоподобия. При наблюдении выбирается тот

{

∫

(

)

сигнал, у которого вероятность больше (см. рис. 1b).

2p(y|0)

I(X; Y ) =

dy p(y|0) log

Для ошибки различения получаем

p(y|0) + p(y|1)

}

∞

(

)

∫

(r+a)2

(y+a)

2p(y|1)

+ p(y|1)log

(6)

P (Err|x = -a) =

√

dre^- 2σ2

p(y|0) + p(y|1)

2πσ²

(2)

Формулы (5), (6) дают утечку информации для клас-

где y - значение, при котором условные вероятности

сических сигналов. Состояния в побочном канале мо-

для сигнала y = a и y = -a сравниваются. Аналогич-

гут иметь предельно низкую интенсивность, по этой

но для ошибки различения сигнала с x = a получаем

причине классическое описание становится неприем-

лемым. Кроме того, в контексте утечки информа-

P (Err|x = a) = 1 - P (Err|x = -a).

(3)

ции в квантовой криптографии, кроме побочных ка-

налов, имеется канал утечки при атаке на кванто-

Средняя вероятность ошибки с учетом априорных

вые информационные состояния в квантовом канале.

вероятностей посылки сигналов, с учетом (1)-(3),

Для этих состояний используется квантовое описа-

равна

ние. Поскольку подслушиватель может использовать

совместную атаку на информационные состояния и

P (Err) = P (Err|x = a)p(a) + P (Err|x=-a)p(-a) =

(√

)

состояния в побочном канале, то необходимо иметь

(_√

)

E_s

(4)

квантовое описание утечки информации в побочном

2σ

N_noise

канале.

где учтено, что состояния посылаются равновероят-

3. Постановка задачи в квантовом случае.

но, и в стандартных обозначениях дисперсия сигна-

Для описания квантовых состояний в побочном ка-

нале необходимо выбрать набор базисных функций,

лов выражена через интенсивность шума σ² =Nnoise2^.

При стремленииEs

→ ∞ - энергия исходного сиг-

по которым будет раскладываться квантовое состо-

Nnoise

нала велика по отношению к шуму, ошибка различе-

яние. Таким естественным набором базисных функ-

ния состояний в побочном канале стремится к ну-

ций являются функции вытянутого сфероида. Под-

лю - состояния различаются подслушивателем до-

слушиватель измеряет состояния во временном окне

стоверно. При стремленииEs

→ 0 - малая ин-

в каждом такте (см. рис. 1a). Считаем, что длитель-

Nnoise

тенсивность сигнала по отношению к шуму, вероят-

ность τ первичного состояния в аппаратуре в каж-

ность ошибки различения стремится к вероятности

дом такте существенно меньше длительности так-

простого угадывания, в побочном канале состояния

та T , τ ≪ T. Применительно к системам кванто-

невозможно различить.

вой криптографии, это именно так, поскольку харак-

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

О побочном квантово-классическом бинарном канале утечки информации с гауссовским шумом

611

Рис. 2. (a) - Схематически показана степень локализации базисных функций вытянутого сфероида (8), (9) во времен-

ном окне наблюдения [0, T ] в зависимости от параметра ΩT . (b) - Величина утечки информации по побочному каналу

в битах в пересчете на один такт как функция отношения^M

при различных отношениях “сигнал-шум”^M

- среднего

^σM

числа фотонов к дисперсии. Параметр^M для кривых 1-4

следующий: 1 - 0.5; 2 - 0.2; 3 - 0.1; 4 - 0.05

^σM

терные времена τ ≈ 10^-9 с, а 1/T ≈ 10 ÷ 100 МГц

Для дальнейшего удобно перейти к нормированным

√

(τ/T

≈ 10^-1 ÷ 10^-2). Удобно ввести характерную

на отрезке функциям

λ_n(c)ϕ_n(t) = φ_n(t, c), пара-

ширину спектра первичного состояния Ω =^1τ , т.е.

метр c фиксирован. Уникальным свойством волно-

ΩT ≫ 1. Удобно выбрать базисные функции макси-

вых функций вытянутого сфероида является их по-

мально локализованными во временном окне [0, T ].

ведение в зависимости от величины параметра ΩT.

Условие максимальной локализации сигнала во вре-

При значении параметра ΩT ≫ 1 имеется N = ΩT

менном окне [0, T ]

функций, которые локализованы во временном окне

с субэкспоненциальной точностью [7] по параметру

∫ T

ΩT

max

x²(t)dt,

(7)

ω∈[0,Ω]

√π8ⁿcn+1

приводит к известному интегральному уравнению

λ_n(c) ∼ 1 -

e^-c, c = Ω · T.

(11)

для (см. детали в [6-8])

Имеется N = ΩT функций с вероятностью едини-

∫

sin[Ω(t - t^′)]

ца, локализованных в окне [0, T ], примерно log(ΩT )

λ_n(c)φ_n(t, c) =

ϕ_n(t^′, c)dt^′, 2c = ΩT.

t-t^′

функций в переходной области, остальные почти

равны нулю в окне [0, T ]. Принципиальным фактом

(8)

при использовании в качестве базисных функций вы-

Решением являются функции вытянутого сфероида

тянутого сфероида является следующий результат

[6-8]. При разных n и n^′ функции ортогональны как

[6-8]. Для любого ε > 0 имеет место

на конечном [0, T ], так и на бесконечном (-∞, ∞)

интервалах,

lim

λ_ΩT(1-ε) = 1,

lim

λ_ΩT(1+ε) = 0.

(12)

ΩT →∞

∫ T

φ_n(t, c)φ_n′ (t, c)dt = λ_n(c)δ_n,n′ ,

Неформально, это означает, что имеется ΩT номеров

⁰∫_∞

(9)

функций, которые почти целиком локализованы во

временном окне T . Для остальных номеров функции

φ_n(t, c)φ_n′ (t, c)dt = δ_n,n′ .

-∞

равны нулю (при этом они остаются нормированны-

ми, нормировка набирается на всем бесконечном ин-

Степень локализации во временном окне [0, T ] (6)

тервале). Переходная область по номерам имеет мас-

собственной функции (9) с номером n уравнения (8)

штаб ∼ ln(2πΩT ), т.е. является крайне узкой - лога-

дается ее собственным числом

рифмически узкой по сравнению с ΩT (см. рис. 2a).

∫ T

4. Побочный бинарный квантово-класси-

φ²ⁿ(t, c)dt = λ_n(c).

(10)

ческий канал с гауссовским шумом. В качестве

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

3^∗

612

С. Н. Молотков

базисных одночастичных состояний будем использо-

- проектор на состояния, описывающие хвосты

вать функции (9), (10), ϕ_n(ω) фурье-образ от (9).

волновых функций вытянутого сфероида вне окна

Рассмотрим квантовое состояние поля, которое со-

[0, T ]. Для вероятности исходов с учетом (13)-(15)

держит M фотонов. Число многочастичных ортого-

получаем

нальных векторов состояний с M фотонами, лока-

P_T (n₁, n₂, . . . n_N ) =

лизованных во временном окне T (таких функций

N = ΩT), равно числу способов размещения M фо-

= Tr{P_T (n₁, n₂, . . . n_N )ρ(N, M)} =

тонов по N одночастичным состояниям. Число раз-

λ_N (n₁, n₂, . . .n_N )

(16)

мещений бозе-частиц по N состояниям равно [9]

N-1+M

(N - 1 + M)!

поскольку λ_N (n₁, n₂, . . . n_N )

C^MN-1+M =

(13)

= λn11 (N)λ22(N) . . .

(N - 1)!M!

→ 1, то вероятность исходов вне

...λnMN^(N)

временного окна [0, T ] стремится к нулю:

Отметим, что бозе-статистика возникает в различ-

ных задачах квантовой криптографии, например,

P_⊥(n₁, n₂, . . . n_N ) =

при реализации квантовых генераторах случаный-

= Tr{P_⊥(n₁, n₂, . . . n_N )ρ(N, M)} =

ных чисел (см. подробности в [10]).

1 - λ_N(n₁,n₂,...n_N)

Вектор состояния, отвечающий размещению M

→ 0.

(17)

C^M

тождественных частиц по N одночастичным состо-

N-1+M

яниям - разбиению числа n₁ + n₂ + . . . + n_N = M,

Парциальная матрица плотности с заданным числом

имеет вид

фотонов, с учетом (13), (14), имеет вид

(14)

|Φn1,n2,...nN 〉 =

∫

∑

ρ_M =

|Φn1,n2,...nN 〉〈Φn1,n2,...nN |.

= ... dω₁dω2 ...dωn1 ...dωn1+1dωn1+2 ...dωn2,

M∈{n1,n2,...nN }

(18)

dωnN-1+1dωnN-1+2 . . . dωnN

Выше были получены матрицы плотности при фик-

ϕ₁(ω₁)ϕ₁(ω₂). . . ϕ₁(ωn1 )ϕ₂(ωn1+1)ϕ2(ωn1+2). . .

сированном числе фотонов M. В реальной ситуации

после прохождения первичного квантового состоя-

ϕ₂(ωn2 ). . .ϕ_N (ωnN-1+1)ϕN (ωnN-1+2). . . ϕN (ωnN )

ния из аппаратуры через среду, число фотонов не

|ω₁, ω₂, . . . ωn1 , . . . ωn1+1, ωn1+2, . . . ωn2 ,

задано, а задано лишь распределение по числу фо-

тонов. Фактически, в квантовом случае вместо клас-

ωnN-1+1, ωnN-1+2, . . .ωnN 〉.

сических распределений (1), подслушиватель видит

После прохождения через среду - максимальная эн-

не чистые состояния, а матрицы плотности, отвеча-

тропия достигается в том случае, когда подслуши-

ющие 0 и 1, - квантовый ансамбль. Получаем

вателю доступны все C^MN-1+M ортогональных раз-

личимых состояний равновероятно - все состояния с

∑

ρ_0,1 =

P_0,1(M)ρ_M ,

(19)

данным числом фотонов M равновероятны - аналог

M =0

белого шума.

Измерение над квантовыми состояниями, позво-

где P₀(M) и P₁(M) - функции распределения числа

ляющее различить все ортогональные состояния, ло-

фотонов в состояниях для 0 и 1 в побочном кана-

кализованные во временном окне [0, T ], дается сле-

ле. Матрицы плотности являются квантовыми ана-

дующим разложением единицы

логами классических сигналов. Условие нормировки

∑

вероятностей

IN,M =

P_T (n₁, n₂, . . . n_N) + I^⊥N,M,

∑

P_0,1(M) = 1.

(20)

n1+n2+...nN =M∑

M =0

I^⊥N,M =

P_⊥(n₁, n₂, . . . n_N ),

В итоге, подслушиватель имеет дело с квантовым

n1+n2+...nN =M

(15)

ансамблем E = {¹² , ρ₀;¹² , ρ₁}. Для подслушивателя

где P_T (n₁, n₂, . . . n_N )

возникает ситуация квантово-классического канала

= |Φn1,n2,...nN 〉〈Φn1,n2,...nN |

проектор на квантовое состояние, локализованное во

побочного канала с шумом. Цель подслушивателя,

временном окне [0, T ], и I^⊥N,M в (15) - дополнение до

имея в своем распоряжении квантовые состояния в

полного пространства состояний на всей временной

побочном канале, ассоцированные с классическими

оси, P_⊥(n₁, n₂, . . .n_N )

значениями бит 0 и 1, узнать, посредством измерений

= |⊥n1,n2,...nN 〉〈⊥n1,n2,...nN |

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

О побочном квантово-классическом бинарном канале утечки информации с гауссовским шумом

613

∫_∞

∑∞

квантовых состояний, классические биты, т.е. полу-

интеграл,

→

dM, а в качестве распреде-

M =0

чить классическую информацию из квантовых со-

лений взять

(M-M0,1)2

стояний. Максимум классической информации, кото-

2σ2

P_0,1(M) =

√

(26)

рую можно получить из квантового ансамбля E, да-

2πσ²

ется фундаментальной величиной Холево [1-3]. Для

где M_0,1 - среднее число фотонов в квантовом со-

информации Холево (см. [1-3]) получаем

стоянии, отвечающем первичному сигналу 0 и 1 со-

ответственно, σ_M - дисперсия числа фотонов в со-

χ(E) = H (ρ) -

H (ρ₀) -

H (ρ₁),

(21)

стояниях - аналог интенсивности шума в побочном

канале в классическом случае.

где

Для иллюстрации на рис. 2b приведены зависимо-

∑

сти информации в побочном канале при различных

ρ₀ + ρ₁

P₀(M) + P₁(M)

ρ=

отношениях среднего числа фотонов в состоянии к

2N_M

M =0

дисперсии шума^Mσ

∑

, где M =M1-M02^{.Каквидноиз}

|Φn1,n2,...nN 〉〈Φn1,n2,...nN |,

(22)

рис. 2b, чем больше отношение^M

- состояния эф-

σM

M∈{n1,n2,...nN }

фективно меньше перекрываются, тем информация,

получаемая из побочного канала оказывается боль-

здесь H(ρ) = -Tr{ρ log(ρ)} - энтропия фон Неймана.

ше.

Вычисление энтропий дает

Из-за макроскопически большого числа степеней

∑

(P₀(M) + P₁(M))

свободы и внутренних шумов аппаратуры, состояние

H (ρ) = -

в побочном канале непосредственно вблизи экрани-

M =0

(

)

рованной аппаратуры будет представлять собой за-

(P₀(M) + P₁(M))

× log

- log

(23)

шумленный сигнал, поэтому, применительно к кван-

N_M

товой криптографии спектральный состав и интен-

(

)

сивность побочного сигнала может быть измерена

∑

H (ρ_0,1) = -

P_0,1(M)log(P_0,1(M)) - log

непосредственно вблизи экранированной аппарату-

N_M

M =0

ры. Консервативно в пользу подслушивателя данный

(24)

сигнал может считаться сигналом, доступным для

Окончательно для величины Холево, с учетом (21)-

измерения подслушивателем. Таким образом может

(24), получаем

быть оценена величина утечки информации к под-

{

(

)

слушивателю. Требуемый уровень сигнала в побоч-

∑

2P₀(M)

χ(E) =

P₀(M)log

ном канале может регулироваться соответствующей

P₀(M) + P₁(M)

M =0

экранировкой.

(

)}

2P₁(M)

5. Заключение. Выше была получена верхняя

+ P₁(M)log

(25)

граница утечки информации по побочному каналу,

P₀(M) + P₁(M)

связанному с электромагнитным излучением переда-

Неформально фундаментальная величина Холево

ющей аппаратуры. Детектирование побочного излу-

равна количеству информации в битах, которую под-

чения является информационным “бонусом” для под-

слушиватель может получить из побочного канала -

слушивателя, поскольку детектирование этого излу-

квантового ансамбля в пересчете на одну посылку.

чения дает дополнительную информацию о переда-

Формула (25) по структуре аналогична формуле (6)

ваемых ключах. В отличие от вторжения в кванто-

для взаимной информации в классическом случае.

вый канал связи детектирование в данном побочном

Но в отличие от классического рассмотрения кванто-

канале не приводит к возмущению информационных

вый аналог (25) справедлив при любой интенсивно-

состояний и ошибкам на приемной стороне.

сти (числа фотонов) побочного сигнала. Кроме того,

Квантовое рассмотрение состояний в побочном

как видно по выводу (25), формула (25) не ограни-

канале необходимо для определения утечки инфор-

чена гауссовским шумом и работает при любых рас-

мации к подслушивателю при совместном измере-

пределениях P_0,1(M) числа фотонов в квантовых со-

нии информационных квантовых состояний и кван-

стояниях в побочном канале утечки информации.

товых состояний в побочных каналах. Данный ана-

Интересно сравнить (25) с классическим анало-

лиз требует существенно большего места, поэтому

гом (6), когда число фотонов становится большим. В

будет приведен в отдельном сообщении.

этом случае, считая шум в побочном канале гауссов-

Выражаю благодарность коллегам по Ака-

ским, как и в (6), сумму в (25) можно заменить на

демии криптографии Российской Федерации за

Письма в ЖЭТФ том 111 вып. 9 - 10

2020