Письма в ЖЭТФ, том 111, вып. 10, с. 646 - 652

Гиперпуассоновская статистика фотонов

Ю. И. Богданов⁺¹⁾, Н. А. Богданова⁺, К. Г. Катамадзе^+∗, Г. В. Авосопянц^∗, В. Ф. Лукичев⁺

⁺Физико-технологический институт им. К. А. Валиева РАН, 117218 Москва, Россия

^∗Центр квантовых технологий, физический факультет МГУ им. М. В. Ломоносова, 119991 Москва, Россия

Поступила в редакцию 13 апреля 2020 г.

После переработки 16 апреля 2020 г.

Принята к публикации 16 апреля 2020 г.

Получено и исследовано статистическое распределение для числа бозонов в заданной подсистеме ко-

нечномерной многоуровневой системы в условиях, когда полное число частиц является случайной вели-

чиной, имеющей распределение Пуассона. Полученное гиперпуассоновское распределение определяется

вырожденной (конфлюэнтной) гипергеометрической функцией и содержит в качестве своих частных

предельных случаев распределение Пуассона, а также одномодовое и многомодовое тепловые распреде-

ления. Разработанная модель может быть эффективно использована для описания термодинамических

свойств ограниченных квантовых систем, а также в задачах статистического восстановления оптических

квантовых состояний, процессов и детекторов.

DOI: 10.31857/S123456782010002X

1. Введение. Исследование статистики фото-

разования когерентных состояний на неоднородных

нов и фотоотсчетов является одной из базовых тех-

линейных оптических элементах, включающих вра-

нологий квантовой оптики. Часто в экспериментах

щающиеся матовые диски, диафрагмы, светодели-

статистика фотонов описывается одним из следу-

тели, линзы и т.п. Оказывается, что в результате

ющих распределений: распределение Пуассона (на-

преобразований на случайных неоднородностях ис-

пример, для когерентных состояний), распределение

ходное распределение Пуассона превращается в рас-

Бозе-Эйнштейна (для тепловых состояний) и бино-

пределение, относящееся к классу так называемых

миальное распределение (для описания преобразова-

компаунд-распределений Пуассона [7, 8]. В частно-

ния фоковских состояний на светоделителе). В то же

сти, в случае экспоненциального компаундера, когда

время, в реальных экспериментах статистика фото-

параметр среднего в распределении Пуассона ста-

нов и фотоотсчетов детекторов часто отличается от

новится случайной величиной с экспоненциальным

указанных распределений в силу разного рода экс-

распределением, когерентное состояние с пуассонов-

периментальных условий и особенностей оборудова-

ской статистикой превращается в тепловое состоя-

ния. В этой связи представляется актуальным по-

ние со статистикой Бозе-Эйнштейна. Более широкий

иск таких распределений для статистики фотонов

класс компаунд-распределений Пуассона, куда вхо-

и фотоотсчетов, которые описывали бы более широ-

дит и многомодовое тепловое состояние, возникает,

кий круг экспериментальных условий и включали бы

если вместо экспоненциального распределения в ка-

указанные выше простейшие распределения в каче-

честве компаундера выступает гамма-распределение.

стве своих частных или предельных случаев.

По сравнению с естественными источниками тепло-

Так, с 1970-х гг. прошлого века для генерации

вого излучения рассматриваемые здесь квазитепло-

квазитепловых квантовых состояний используют ла-

вые источники света часто более удобны для задач

зерное излучение, претерпевающее рассеяние на сто-

квантовой оптики, поскольку позволяют генериро-

хастических диффузорах, таких как вращающийся

вать гораздо более высокое число фотонов в расче-

матовый диск [1-5], акустооптический модулятор [6]

те на одну моду и имеют существенно более высо-

и т. п. Во всех таких системах в качестве исход-

кие времена когерентности, которыми можно управ-

ных выступают генерируемые лазерными источни-

лять в широких пределах от миллисекунд до десят-

ками когерентные квантовые состояния с пуассо-

ков секунд. С практической точки зрения рассмат-

новской статистикой. Инжиниринг других кванто-

риваемые здесь распределения важны для описания

вых состояний осуществляется посредством преоб-

статистики лазерного излучения, прошедшего через

флуктуирующие среды, например, через турбулент-

¹⁾e-mail: bogdanov_yurii@inbox.ru

646

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

Гиперпуассоновская статистика фотонов

647

ные атмосферные оптические каналы [9, 10] или че-

ское распределение описывает число бозонов в задан-

рез флуктуирующие оптические волокна [11-14].

ной подсистеме конечномерной многоуровневой си-

Еще одним важным примером является описа-

стемы в условиях, когда полное число частиц явля-

ется случайной величиной, имеющей распределение

ние отличий статистики фотоотсчетов от исходной

Пуассона. Возникающее распределение определяет-

статистики фотонов в силу неединичной квантовой

ся вырожденной (конфлюэнтной) гипергеометриче-

эффективности и темновых шумов. В простейших

ской функцией. С практической точки зрения инжи-

моделях статистика фотоотсчетов детекторов сво-

ниринга квантовых состояний важность полученно-

дится к свертке исходной статистики фотонов с би-

го распределения обусловлена тем, что оно являет-

номиальным распределением, которое определяется

эффективностью детектора и с пуассоновским рас-

ся естественным обобщением ряда хорошо известных

распределений квантовой оптики. В качестве асимп-

пределением, которое определяется действием шу-

мов. В более общих моделях статистика детекторов

тотических предельных форм гиперпуассоновского

распределения выступают, в частности, одномодовые

фотонов определяется POVM-разложением, которое

может быть довольно сложным. В частности, при

и многомодовые тепловые распределения, а также

распределение Пуассона. Будучи гибким инструмен-

использовании многопиксельных детекторов, разре-

том анализа данных по статистике фотонов и фото-

шающих число фотонов, возникает ситуация, когда

отсчетов, разработанная модель может быть эффек-

каждый отдельный пиксель имеет свои индивидуаль-

тивно использована в задачах статистической рекон-

ные значения квантовой эффективности и темновых

шумов, что приводит к различным распределениям

струкции распределений, включая задачи томогра-

фии квантовых состояний, процессов и детекторов.

по числу фотонов [15, 16]. Такие детекторы в послед-

нее время нашли применение в квантовых генерато-

2. Описание статистики бозонов с исполь-

зованием распределения Пойа. Известно, что

рах случайных чисел для задач квантовой крипто-

графии [17-20], поэтому адекватное описание стати-

общее число возможных состояний (статистический

стики фотоотсчетов в таких системах весьма важ-

вес) Ω(k, M) в системе из k бозонов и M уровней за-

дается следующей формулой [25]:

но. Заметим, что при этом система квантового рас-

пределения ключа должна непосредственно опирать-

Ω(k, M) = C^kM+k-1.

(1)

ся на фундаментальные статистические распределе-

ния квантовой статистики [21, 22]. Неоднородность

Здесь C^kM+k-1 =^{(M+k-1)!k!(M-1)!} - биномиальный коэффи-

характеристик рассматриваемых детекторов приво-

дит к тому, что их эффективность становится слу-

циент, задающий число сочетаний из M + k - 1 эле-

ментов по k элементов. На языке оптики мы можем

чайной величиной, а исходное биномиальное распре-

деление для числа отсчетов при регистрации фоков-

говорить о k фотонах, распределенных по M различ-

ным модам.

ского состояния с заданным числом фотонов превра-

щается в компаунд-распределение, аналогично то-

Рассмотрим подсистему из m мод (m ≤ M). Най-

му, как это было описано выше для квазитепловых

дем вероятность P (j|k, m, M) обнаружить ровно j

фотонов в выделенной m-модовой подсистеме, при

источников. Оказывается, что если в качестве ком-

паундера выступает бета-распределение, то биноми-

условии, что в полной M-модовой системе имеет-

ся ровно k фотонов. В соответствии с классической

альное распределение превращается в распределение

Пойа, описывающее фундаментальную статистику

формулой вероятностей имеем [23,26]:

фотонов [23,24]. Число фотонов в исходном состоя-

нии становится случайной пуассоновской величиной,

C^jm+j-1C^k-jM-m+k-j-1

P (j|k, m, M) =

(2)

когда мы переходим от регистрации труднодоступ-

C^k

M +k-1

ных фоковских состояний к регистрации когерент-

ного лазерного излучения. В этом случае распреде-

Здесь статистический вес C^kM+k-1 в системе из k фо-

ление Пойа превращается в гиперпуассоновское рас-

тонов и M мод есть величина, которая задает зна-

пределение, являющееся предметом настоящей рабо-

менатель - полное число равновозможных элемен-

ты. В то же время, как будет показано ниже, это но-

тов (исходов). Числитель (число благоприятствую-

вое статистическое распределение можно получить,

щих исходов) - это произведение двух множителей:

основываясь не только на феноменологических со-

первый - это статистический вес в системе из j фо-

ображениях, но и на общих свойствах статистики

тонов и m мод в выбранной подсистеме, второй - это

бозонов. С точки зрения фундаментальной кванто-

статистический вес в системе из k-j оставшихся фо-

вой статистической физики полученное статистиче-

тонов и M - m оставшихся мод.

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

648

Ю. И. Богданов, Н. А. Богданова, К. Г. Катамадзе, Г. В. Авосопянц, В. Ф. Лукичев

С использованием гамма-функции полученный

Второй факториальный момент непосредствен-

результат можно записать также в следующей

но позволяет нам рассчитать также дисперсию

форме:

распределения:

P (j|k, m, M) =

(3)

km(M - m)(M + k)

D = G⁽²⁾(1) + µ - µ² =

(7)

Γ(k + 1)Γ(M)Γ(m + j)Γ(M - m + k - j)

M²(M + 1)

Γ(j + 1)Γ(k - j + 1)Γ(m)Γ(M - m)Γ(M + k)

Распределение Пойа является естественным обобще-

Формула (3) является более общей по сравнению с

нием хорошо известного биномиального распределе-

формулой (2), поскольку допускает также и нецелые

ния [24]. Биномиальное распределение можно рас-

значения для параметров m и M. Это важно, в част-

сматривать как предельный случай распределения

ности, для задач квантовой томографии, поскольку

Пойа при достаточно больших M и m. Действитель-

указанные параметры могут выступать в качестве

но, пусть M → ∞, m → ∞, а θ =^mM → const. Тогда

подгоночных при обработке экспериментальных дан-

в рассматриваемом пределе возникает производящая

ных.

функция биномиального распределения, задающего

В теории вероятностей и статистике получен-

число “успехов” в серии из k независимых испыта-

ное распределение называют распределением Пойа

ний с вероятностью “успеха” в отдельном испытании,

[27, 28]. Это распределение находит применение в

равной θ:

различных областях, в том числе при описании эпи-

F (-k, m, M, (1 - z)) → (1 - θ(1 - z))^k.

(8)

демий заразных заболеваний [27], а также в задачах

обеспечения качества в микроэлектронике [24]. Из

Не менее важно, что формула (4) для производящей

приведенного выше рассмотрения мы видим также,

функции распределения Пойа позволяет нам также

что распределение Пойа имеет непосредственное от-

легко получить термодинамический предел для бо-

ношение и к фундаментальным аспектам статистики

зонов. Этот предел возникает тогда, когда рассмат-

фотонов и бозонов в целом [23,26].

ривается конечная подсистема бесконечно большой

Производящая функция распределения Пойа вы-

системы (числа M и k бесконечно велики, а число

ражается через гипергеометрическую функцию [24]

m конечно). Формально, пусть M → ∞, k → ∞,

а µ₀ =_M

→ const. Тогда в рассматриваемом пре-

G(z|k, m, M) = F (-k, m, M, (1 - z)).

(4)

деле возникает производящая функция m-модового

бозонного состояния:

Заметим, что для гипергеометрической функции

также используют обозначение₂F₁.

F (-k, m, M, (1 - z)) → (1 + µ₀(1 - z))^-m.

(9)

Мы видим, что в форме (4) рассматриваемое

Полученное многомодовое тепловое распределение

распределение выражается в наиболее простом ком-

относится к классу так называемых компаунд-

пактном виде. Такая компактная форма позволяет

распределений Пуассона и находит важные приме-

нам легко рассчитать различные моменты распреде-

нения в задачах инжиниринга квантовых состояний

ления Пойа в соответствии с известными правила-

[7, 8].

ми теории вероятностей [27, 28]. Например, вычисляя

Мы видим, что распределение Бозе-Эйнштейна,

первую производную в точке z = 1, непосредственно

один из краеугольных камней квантовой статистиче-

находим математическое ожидание распределения

ской физики, является непосредственным предель-

ным случаем более общего распределения Пойа. В

µ = G^′(1|k,m,M) =

(5)

свою очередь, распределение Пойа, будучи более об-

щим, открывает путь к описанию термодинамиче-

Аналогично, вторая производная в точке z = 1 даст

ских свойств ограниченных квантовых систем, когда

второй факториальный момент

полное число мод M и число частиц k в системе не

являются предельно большими величинами.

k(k - 1)m(m + 1)

G⁽²⁾(1) = M[k(k - 1)] =

Интересно отметить, что производящая функция

M (M + 1)

гипергеометрического распределения, описывающе-

В результате получим важную с точки зрения

го фермионы, формально получается из производя-

квантовой оптики автокорреляционную функцию

щей функции распределения Пойа, описывающего

второго порядка g⁽²⁾:

бозоны, посредством замены знака у параметров рас-

пределения: M → -M, m → -m,

G⁽²⁾(1)

M m+1k-1

g⁽²⁾ =

(6)

G(z|k, m, M) = F (-k, -m, -M, (1 - z)).

(10)

µ²

M+1

m k

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

Гиперпуассоновская статистика фотонов

649

С физической точки зрения, распределения, описы-

независимых пуассоновских случайных величин

вающие бозоны и фермионы (Пойа и гипергеомет-

тоже является пуассоновской случайной величиной.

рическое) возникают в рамках разных выборочных

При этом параметр среднего числа фотонов резуль-

схем на основе урн с шарами [23]. С математической

тирующего распределения будет суммой вкладов

же точки зрения, эти распределения можно описы-

от отдельных независимых пуассоновских величин:

вать в рамках одной и той же выборочной схемы, ес-

λ = λ₁+...+λ_m (здесь m - полное число слагаемых).

ли допустить нефизические отрицательные значения

В оптических экспериментах широко используют-

для чисел шаров в урне. Гипергеометрическое рас-

ся источники фотонов, формируемые лазерным из-

пределение можно интерпретировать в рамках схе-

лучением, проходящим через вращающийся матовый

мы Пойа (с возвращением и добавлением шаров) с

диск [2]. При этом различные неоднородности мато-

отрицательным числом шаров (в духе Дирака: имеем

вого диска порождают пуассоновские потоки с суще-

(-M) шаров, из которых (-m) - красные). Наоборот,

ственно различными интенсивностями. В результа-

распределение Пойа можно интерпретировать в рам-

те, возникающее суммарное излучение оказывается в

ках схемы без возвращения с отрицательным числом

близком соответствии с рассматриваемой здесь моде-

шаров. Формулы (4) и (10) описывают такое соответ-

лью, определяемой суммой независимых пуассонов-

ствие явно. На наш взгляд, с точки зрения кванто-

ских случайных величин. Заметим, что излучение,

вой статистической физики распределение Пойа сле-

обусловленное соседними неоднородностями матово-

дует называть гипергеометрическим распределением

го диска, может быть в той или иной степени корре-

бозонного типа, а обычное гипергеометрическое рас-

лировано, однако данный эффект может быть ниве-

пределение - гипергеометрическим распределением

лирован посредством определенного прореживания

фермионного типа.

потока фотонов [7, 8].

Мы рассмотрели случай, когда полное число час-

Известно, что излучение матового диска может

тиц k в системе является строго фиксированной ве-

служить хорошей имитацией для генерации теп-

личиной. Такие состояния, однако, весьма трудны

ловых состояний, имеющих распределение Бозе-

для практической реализации. Намного более прак-

Эйнштейна [2]. Модель, представленная в настоящем

тичной является ситуация, когда полное число час-

разделе, позволяет не только объяснить генерацию

тиц в системе не фиксировано, а само является слу-

тепловых состояний, но и описать более широкий

чайной величиной. Наиболее типичным источником

круг явлений, которые можно отнести к термодина-

фотонов в современных физических экспериментах и

мике ограниченных оптических квантовых систем.

квантовых технологиях является лазер, генерирую-

Пусть полное число фотонов n в системе есть слу-

щий когерентное излучение. Как известно, статисти-

чайная величина, имеющая распределение Пуассона

ка когерентного излучения является пуассоновской.

со средним λ. Усреднение распределения Пойа (4)

Таким образом, возникает задача о нахождении рас-

с использованием распределения Пуассона приведет

пределения вероятностей в условиях, когда полное

нас к новому распределению, производящая функ-

число частиц в бозонной системе имеет распределе-

ция которого определяется вырожденной (конфлю-

ние Пуассона. Соответствующая задача рассмотрена

энтной) гипергеометрической функцией (degenerate

в следующем разделе.

(confluent) hypergeometric function):

3. Статистика числа бозонов в подсистеме

в условиях, когда полное число частиц в си-

G(z|m, M, λ) = Φ(m, M, -λ(1 - z)).

(12)

стеме имеет распределение Пуассона. Как из-

вестно, число фотонов в когерентном состоянии опи-

сывается распределением Пуассона, которое, в свою

Заметим, что для вырожденной гипергеометри-

очередь, характеризуется следующей производящей

ческой функции также используют обозначение

функцией:

1F1. Полученное распределение будем называть

гиперпуассоновским распределением (hyper-Poisson

G(z|λ) = exp(-λ(1 - z)).

(11)

distribution). С точки зрения квантовой статисти-

Здесь λ - параметр распределения Пуассона, задаю-

ческой физики это распределение можно охаракте-

щий среднее число фотонов в квантовом состоянии.

ризовать как конфлюэнтное гипергеометрическое

Хорошо известно, что производящая функция

распределение бозонного типа (boson type confluent

суммы независимых случайных величин равна

hypergeometric distribution).

произведению отдельных производящих функций

Вывод формулы (12) основан на следующем тож-

[27, 28], поэтому, как нетрудно видеть из (11), сумма

дестве, которое можно проверить непосредственно,

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

650

Ю. И. Богданов, Н. А. Богданова, К. Г. Катамадзе, Г. В. Авосопянц, В. Ф. Лукичев

основываясь на определении гипергеометрических

Полученные формулы показывают, что эксперимен-

функций

тальное оценивание автокорреляционных функций

второго и третьего порядка позволяет приближенно

∑

λⁿ

восстановить по экспериментальным данным неиз-

F (-n, m, M, (1 - z))

exp(-λ) =

n=0

вестные параметры распределения m и M. Из фор-

мул (18) и (19) непосредственно получаем:

= Φ(m, M, -λ(1 - z)).

(13)

Производящая функция (12) порождает следующее

2[g⁽³⁾ - (g⁽²⁾)²]

(20)

распределение вероятностей:

(g⁽²⁾)² + g⁽²⁾g⁽³⁾ - 2g⁽³⁾

P (k|m, M, λ) =

2[g⁽³⁾ - (g⁽²⁾)²]

M =

(21)

2(g⁽²⁾)² - g⁽²⁾ - g⁽³⁾

Γ(M) Γ(m + k) λ

Φ(m + k, M + k, -λ). (14)

Γ(M + k) Γ(m) k!

Таким образом, гиперпуассоновское распределение -

это распределение с двумя независимыми автокорре-

Таким образом, полученное распределение задает ве-

ляционными функциями g⁽²⁾ и g⁽³⁾, что иллюстриру-

роятность обнаружить ровно k фотонов в выделен-

ют формулы (18) и (19). Заметим, что для обычно-

ной m-модовой подсистеме, при условии, что в пол-

го распределения Пуассона коэффициенты g⁽²⁾ и g⁽³⁾

ной M-модовой системе число фотонов определяется

тривиальны (оба заведомо равны 1), а для компаунд-

распределением Пуассона со средним λ.

распределения Пуассона эти коэффициенты жестко

Производящая функция (12) позволяет непосред-

связаны между собой [7,8].

ственно получить важные статистические характе-

Используя второй факториальный момент, мож-

ристики рассматриваемого распределения. Вычис-

но получить следующее выражение для дисперсии D

ляя три первые производные от производящей функ-

рассматриваемого распределения:

ции (12), получаем следующие выражения для трех

первых факториальных моментов распределения:

(

)

λ(M - m)

(22)

M (M + 1)

G⁽¹⁾(1) = M[k] = µ =

λ,

(15)

Заметим, что в реальных экспериментах и квантовых

m(m + 1)

G⁽²⁾(1) = M[k(k - 1)] =

λ²,

(16)

технологиях среднее число фотонов λ в пуассонов-

M (M + 1)

ском состоянии зачастую неизвестно априори. Одна-

G⁽³⁾(1) = M[k(k - 1)(k - 2)] =

ко, имея экспериментальную оценку среднего числа

отсчетов M[k] = µ, и вычисляя параметры распреде-

m(m + 1)(m + 2)

λ³.

(17)

ления m и M по формулам (20) и (21), легко находим:

M (M + 1)(M + 2)

Заметим, что факториальные моменты могут быть

λ=

µ.

(23)

приближенно оценены по экспериментальным дан-

ным, если рассматриваемые математические ожида-

Как уже отмечалось выше, распределение Пойа яв-

ния заменить выборочными средними. При этом пер-

ляется базовой моделью для обобщения биномиаль-

вый факториальный момент, задаваемый формулой

ного распределения. Так, в рамках простейшей мо-

(15), определяет математическое ожидание (среднее)

дели, статистика числа фотонов, регистрируемая

µ рассматриваемой случайной величины. Второй и

фазово-нечувствительным детектором, есть биноми-

третий факториальные моменты, задаваемые фор-

альная случайная величина, в которой в качестве ве-

мулами (16) и (17), служат основой для вычисления

роятности “успеха” выступает эффективность детек-

автокорреляционных функций g⁽²⁾ и g⁽³⁾ второго и

тора η [29]. В более общей модели, основанной на

третьего порядка соответственно:

распределении Пойа, эффективность детектора η са-

G⁽²⁾(1)

m+1

ма становится случайной величиной, имеющей бета-

g⁽²⁾ =

(18)

µ²

m M+1

распределение с параметрами a = m и b = M - m

[24]. В условиях тестирования такого детектора по-

G⁽³⁾(1)

средством когерентного излучения от лазерного ис-

g⁽³⁾ =

µ³

точника, статистика зарегистрированного числа фо-

(m + 1)(m + 2)

тонов описывается представленной выше моделью с

(19)

неизвестными параметрами m, M и λ, которые могут

m²

(M + 1)(M + 2)

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

Гиперпуассоновская статистика фотонов

651

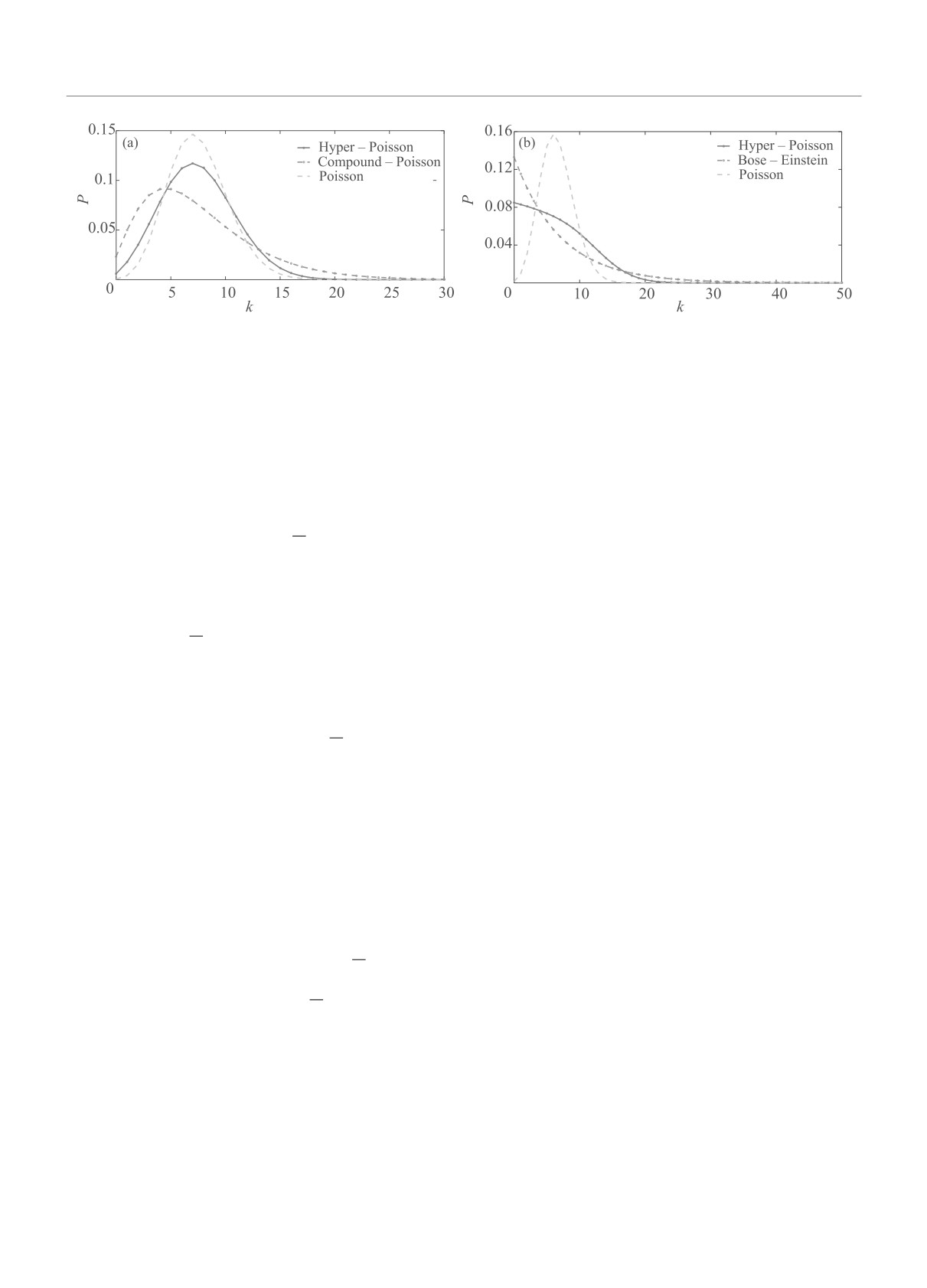
Рис. 1. (Цветной онлайн) Иллюстрация гиперпуассоновского распределения в сравнении с распределением Пуассона

и компаунд-распределением Пуассона (тепловым состоянием). Параметры задачи: (а) - m = 3, M = 4, λ = 10; (b) -

m = 1, M = 2.3, λ = 15

быть оценены по формулам (20), (21) и (23). Отме-

компаунд-распределением Пуассона (25), а также

тим также, что как параметры бета-распределения

обычное однопараметрическое распределение Пуас-

величины m и M могут быть нецелыми, выступая

сона (24).

в качестве подгоночных параметров при обработке

В качестве иллюстрации на рис. 1 представлены

экспериментальных данных.

все три рассматриваемых распределения вероятно-

Как было показано выше, в предельном случае,

стей.

когда M → ∞, m → ∞, а θ =^mM → const, распреде-

На представленных рисунках для всех трех рас-

ление Пойа превращается в биномиальное распреде-

пределений одинаковы средние значения, а, кроме

ление. В этом случае, рассматриваемое здесь гипер-

того, для теплового и гиперпуассоновского распре-

пуассоновское распределение превращается в обыч-

делений совпадают также и значения чисел выделен-

ное распределение Пуассона со средним числом от-

ных мод m. Мы видим, что визуально гиперпуассо-

счетов µ = θλ =^mM λ:

новское распределение занимает промежуточное по-

ложение между двумя своими предельными форма-

Φ(m, M, -λ(1 - z)) → exp(-µ(1 - z)).

(24)

ми, задающимися распределением Пуассона и теп-

Рассмотрим теперь термодинамический предел по-

ловым состоянием соответственно; при это рисунок

лученного гиперпуассоновского распределения (12).

(a) отвечает многомодовому тепловому состоянию, а

Пусть M → ∞, λ → ∞, а µ₀ =^λM → const. То-

рисунок (b) - одномодовому тепловому состоянию.

гда, в рассматриваемом пределе снова возникает про-

4. Выводы. Рассмотрена задача о распределе-

изводящая функция m-модового бозонного состоя-

нии числа бозонов (в частности, фотонов) в заданной

ния, отвечающего компаунд-распределению Пуассо-

подсистеме конечномерной многоуровневой системы

на [7, 8]:

в условиях, когда полное число частиц в системе яв-

ляется случайной величиной, имеющей распределе-

Φ(m, M, -λ(1 - z)) → (1 + µ₀(1 - z))^-m.

(25)

ние Пуассона.

Полученный результат вполне аналогичен предель-

Получено новое гиперпуассоновское распределе-

ному переходу (9) в распределении Пойа, только ра-

ние, которое по своей математической природе мо-

нее среднее число фотонов в расчете на одну моду

жет быть охарактеризовано как конфлюэнтное ги-

определялось фиксированным числом частиц k в си-

пергеометрическое распределение бозонного типа

стеме в соответствии с формулой µ₀ =^kM , а теперь -

и которое является естественным обобщением как

средним числом частиц λ в пуассоновском состоянии

обычного распределения Пуассона, так и известно-

в соответствии с формулой µ₀ =^λM .

го компаунд-распределения Пуассона.

Таким образом, мы можем рассматривать три ти-

Представлены возможные приложения получен-

па распределений Пуассона различной степени общ-

ного распределения для описания различных систем

ности. Наиболее общее распределение - это трех-

генерации и регистрации фотонов. Полученное новое

параметрическое гиперпуассоновское распределение

статистическое распределение будет применено нами

(12). Наряду с этим распределением, важное значе-

к задаче квантовой томографии детекторов.

ние имеют и две его предельные формы: двухпара-

Работа выполнена в рамках Государственного за-

метрическое компаунд-распределение Пуассона, за-

дания ФТИАН им. К. А. Валиева РАН Минобрна-

дающее m-модовое бозонное состояние, описываемое

уки РФ по теме # 0066-2019-0005 при поддержке

Письма в ЖЭТФ том 111 вып. 9 - 10

2020

652

Ю. И. Богданов, Н. А. Богданова, К. Г. Катамадзе, Г. В. Авосопянц, В. Ф. Лукичев

Российского фонда фундаментальных исследований

Applications, Elsevier Science, Waltham, Massachusetts

(гранты # 20-32-70153 и 19-32-90212) и Фонда разви-

(2013), 570 p.

тия теоретической физики и математики “БАЗИС”

17.

M. Ren, E. Wu, Y. Liang, Y. Jian, G. Wu,

(грант # 17-13-334-1).

and H. Zeng, Phys. Rev. A

83,

023820

(2011);

https://doi.org/10.1103/PhysRevA.83.023820.

18.

K. A. Balygin, V. I. Zaitsev, A. N. Klimov, S. P. Kulik,

C. W. Helstrom, Proc. Phys. Soc. 83, 777 (1964).

and S. N. Molotkov, JETP Lett. 106, 470 (2017).

F. T. Arecchi, Phys. Rev. Lett. 15, 912 (1965).

19.

K. A. Balygin, V. I. Zaitsev, A. N. Klimov, S. P. Kulik,

F. T. Arecchi, A. Berné, and P. Bulamacchi, Phys. Rev.

and S. N. Molotkov, JETP 126, 728 (2018).

Lett. 16, 32 (1966).

20.

K. A. Balygin, V.I. Zaitsev, A.N. Klimov, A. I. Klimov,

B. Crosignani, B. Daino, and P. Di Porto, J. Appl. Phys.

S. P. Kulik, and S. N. Molotkov, JETP Lett. 105, 606

42, 399 (1971).

(2017).

T. Gonsiorowski and J. C. Dainty, J. Opt. Soc. Am. 73,

21.

S. N. Molotkov, JETP Lett. 105, 395 (2017).

234 (1983).

22.

K. A. Balygin, V. I. Zaitsev, A. N. Klimov, S. P. Kulik,

M. V. Chekhova, S. P. Kulik, A. N. Penin, and

and S. N. Molotkov, JETP Lett. 106, 470 (2017).

P. A. Prudkovsky, Opt. Commun. 132, 15 (1996).

23.

Yu. I. Bogdanov, N. A. Bogdanova, K. G. Katamadze,

and G. V. Avosopiants, Theoretical and experimental

G. V. Avosopyants, and V. F. Lukichev, Optoelectron.

study of multi-mode thermal states with subtraction of a

Instrum. Data Process. 52, 475 (2016).

random number of photons, Proc. SPIE 11022, 110222L

Yu. I. Bogdanov, K. G. Katamadze, G. V. Avosopiants,

(15 March 2019); arXiv:1906.06384 [quant-ph].

L. V. Belinsky, N. A. Bogdanova, A. A. Kalinkin, and

S. P. Kulik, Phys. Rev. A 96, 063803 (2017).

24.

Yu. I.

Bogdanov,

N. A.

Bogdanova,

and

V. L. Dshkhunyan, Russian Microelectronics

32,

K. S. Kravtsov, A. K. Zhutov, I. V. Radchenko, and

51 (2003).

S. P. Kulik, Phys. Rev. A 98, 063831 (2018).

10.

Z. Chen, S. Cui, L. Zhang, C. Sun, M. Xiong, and J. Pu,

25.

Л. Д. Ландау, Е. М. Лифшиц, Статистическая фи-

Opt. Express 22, 18278 (2014).

зика, Наука, М. (1995), ч. 1, 608 с.

11.

J. Yammine, A. Tandjé, M. Dossou, L. Bigot, and

26.

K. G. Katamadze, G. V. Avosopiants, N. A. Bogdanova,

E. R. Andresen, APL Photonics 4, 022904 (2019).

Yu. I. Bogdanov, and S. P. Kulik, Phys. Rev. A 101,

12.

G. Nicholson and D. J. Temple, J. Light. Technol. 7,

013811 (2020).

1197 (1989).

27.

W. Feller, Introduction to Probability Theory and Its

13.

G. Rademacher, R. S. Luis, B. J. Puttnam, Y. Awaji,

Applications, 3rd ed., Wiley, N.Y., London, Sydney

and N. Wada, Opt. Express 25, 12020 (2017).

(1968).

14.

P. S. Y. Poon and C. K. Law, Phys. Rev. A 77, 032330

28.

Вероятность и математическая статистика. Эн-

(2008).

циклопедия, ред. Ю. В. Прохоров, Издательство

15.

Y. Cai, Y. Chen, X. Chen, J. Ma, G. Xu, Y. Wu, A. Xu,

“Большая Российская энциклопедия”, М.

(1999),

and E. Wu, Appl. Sci. 9, 2638 (2019).

912 с.

16.

A. Migdall, S. V. Polyakov, J. Fan, and J. C. Bienfang,

29.

M. O. Scully and M. S. Zubairy, Quantum Optics,

Single-Photon Generation and Detection: Physics and

Cambridge University Press, Cambridge (2001).

Письма в ЖЭТФ том 111 вып. 9 - 10

2020