Письма в ЖЭТФ, том 112, вып. 1, с. 3 - 8

Использование отражения частиц в изогнутых кристаллах

для коллимации пучка в больших адронных коллайдерах

М. Ю. Чесноков, Ю. А. Чесноков¹⁾, В. А. Маишеев, Ю. Е. Сандомирский, А. А. Янович, И. А. Язынин

Национальный исследовательский центр “Курчатовский институт” - Институт физики высоких энергий,

142281 Протвино, Россия

Поступила в редакцию 6 мая 2020 г.

После переработки 17 мая 2020 г.

Принята к публикации 17 мая 2020 г.

Большой адронный коллайдер (БАК) использует многоступенчатую коллиматорную систему для по-

глощения растущего гало циркулирующих пучков для защиты и обеспечения надежной работы сверхпро-

водящих магнитов. Аналогичная система запланирована и для Будущего кольцевого коллайдера (БКК).

В преддверии работы БАК с высокой светимостью проводятся исследования по совершенствованию кол-

лимационной системы. Исследования показали, что одним из решений для улучшения коллимации пучка

является использование каналирования в коротком изогнутом кристалле, который действует как пер-

вичный коллиматор, забрасывая частицы глубоко во вторичный коллиматор путем каналирования. Эта

система очень чувствительна к угловому положению кристалла и возможным вибрациям различной

природы. В настоящей работе предлагается иной подход к коллимации пучка, основанный на объем-

ном отражении частиц от изогнутых кристаллографических плоскостей в последовательности кристал-

лов. Обоснованы положительные качества этой схемы и предложено многополосковое кристаллическое

устройство, способное ее реализовать.

DOI: 10.31857/S1234567820130017

В Большом адронном коллайдере (БАК) исполь-

зуется многоступенчатая система коллиматоров для

поглощения растущего гало циркулирующих пуч-

ков для защиты и обеспечения надежной работы

сверхпроводящих магнитов [1]. Аналогичная систе-

ма планируется для Будущего кольцевого коллай-

дера (БКК) [2]. Первичные коллиматоры БАК, из-

готовленные из композитов из углеродного волокна,

отклоняют частицы гало в результате кулоновского

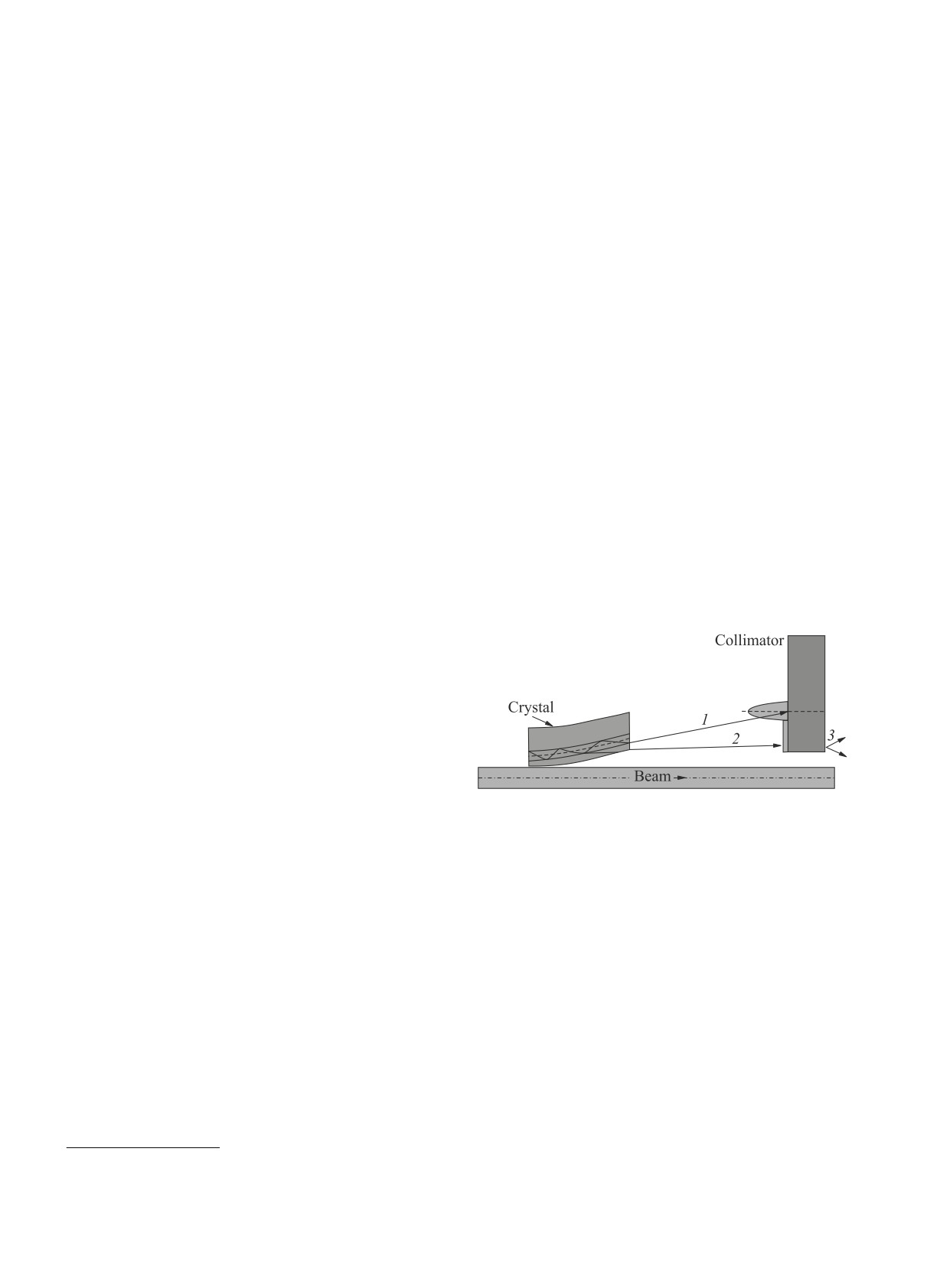
Рис. 1. Схема коллимации пучка с применением корот-

рассеяния, тем самым увеличивая их глубину забро-

кого кристалла: 1 - пик каналированных частиц, кото-

са во вторичные коллиматоры от микронных вели-

рые эффективно отклонились; 2 - фракция деканали-

чин до долей миллиметра. Взаимодействие прото-

рованных частиц; 3 - потери на коллиматоре

нов с материалом коллиматора приводит к образо-

ванию дифракционных протонов, которые могут вы-

тор (на несколько миллиметров) за счет каналирова-

летать из стенок коллиматоров и теряться в магни-

ния (рис. 1).

тах, что ограничивает эффективность очистки суще-

Поскольку критический угол каналирования до-

ствующей коллимационной системы. В преддверии

статочно мал при высоких энергиях, θ_c = 2.5 мкрад

работы БАК с большой светимостью проводятся ис-

для пучка 6.5 ТэВ в БАК и θ_c = 0.92 мкрад для пучка

следования по улучшению системы коллимации. В

50 ТэВ в БЦК, система очень чувствительна к угло-

исследованиях [3] показано, что одним из решений

вому положению кристалла и возможным вибраци-

улучшения коллимации пучка является использова-

ям разной природы. Одним из видов вибрации может

ние каналирования в коротком изогнутом кристалле,

быть явление, известное с 1980-х гг. [4], которое обу-

который выполняет роль первичного коллиматора,

словлено силой отдачи при взаимодействии сгустков

глубоко забрасывая частицы во вторичный коллима-

частиц с кристаллом в режиме каналирования. В си-

лу большой энергии каждой частицы, отклоненная

¹⁾e-mail: chesnokov@ihep.ru

за счет каналирования частица передает кристаллу

Письма в ЖЭТФ том 112 вып. 1 - 2

2020

М. Ю. Чесноков, Ю. А. Чесноков, В. А. Маишеев и др.

ощутимый поперечный импульс. По оценкам [5], да-

же 10⁶ частиц в сгустке могут создать ощутимые

амплитуды колебаний, что ухудшит эффективность

кристаллической коллимации.

В этой связи может быть полезным другой подход

к кристаллической коллимации, основанный на объ-

емном отражении частиц от изогнутых кристалло-

графических плоскостей. Это явление было открыто

недавно в экспериментах [6, 7], и оно расширяет гра-

ницы применения изогнутых кристаллов на ускори-

телях. Впервые объемное отражение было предска-

зано в [8] в компьютерном моделировании методом

Монте-Карло и позднее детально описано в аналити-

ческом виде в работе [9]. Объемное отражение обу-

словлено взаимодействием налетающей релятивист-

ской частицы с потенциалом изогнутой атомной ре-

шетки и происходит на малой длине кристалла в

области, где траектория частицы выходит на каса-

тельную к изогнутой атомной плоскости, приводя к

отклонению частицы в сторону, противоположную

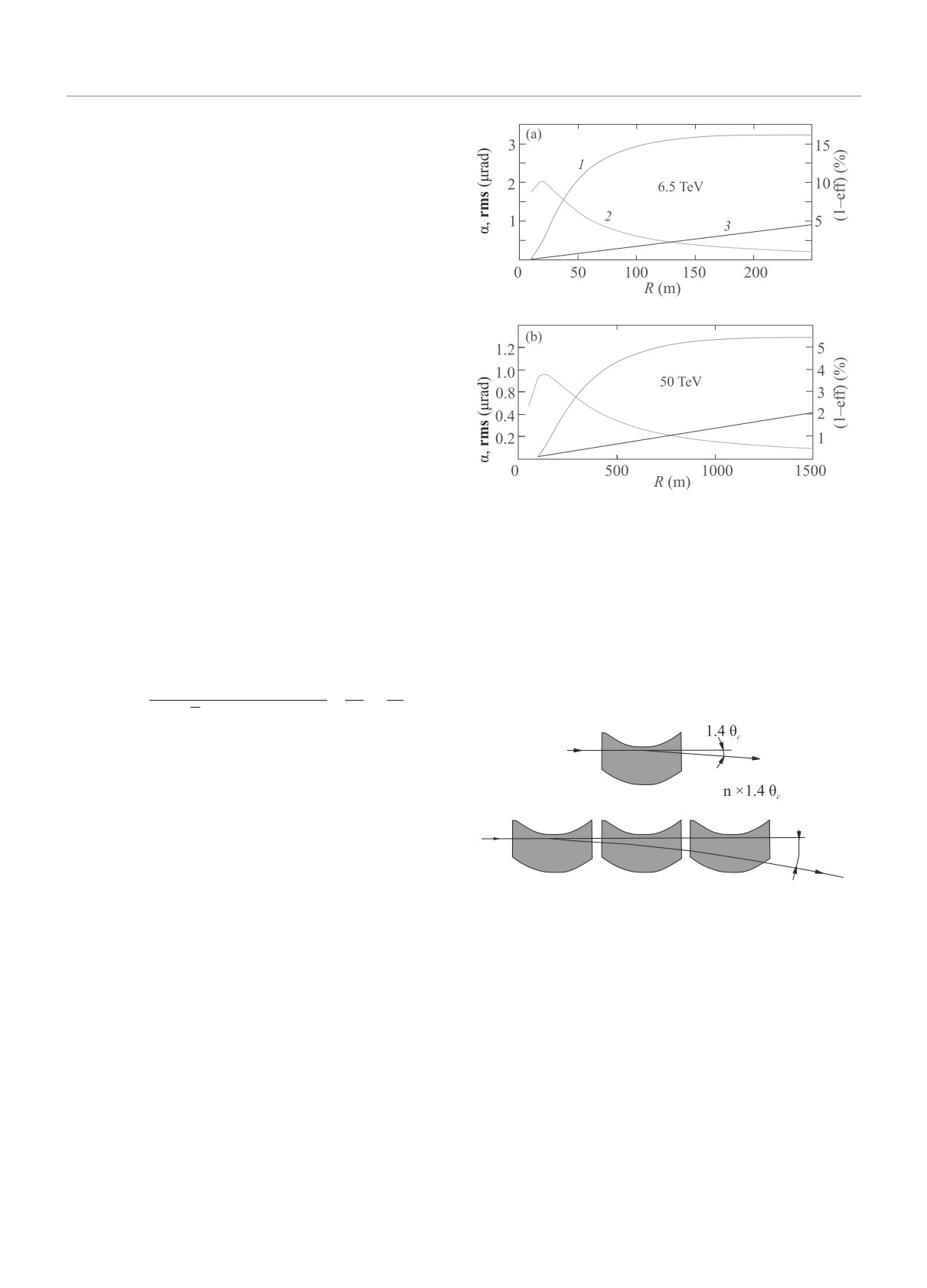
Рис. 2. (Цветной онлайн) Зависимость параметров от-

изгибу. Вероятность эффекта отражения eff велика

ражения от радиуса изгиба кристалла: 1 - средний угол

и для положительно заряженных частиц с энергией

отражения α, 2 - среднеквадратичное значение углово-

го распределения rms; 3 - величина (1 - eff)

несколько ТэВ близка к единице. В [10, 11] показа-

но, что эффективность процесса отражения ограни-

чена величиной альтернативного процесса, называе-

периментальными данными при энергиях частиц до

мого объемным захватом, вероятность которого рав-

400 ГэВ (см. подробное сравнение в работах [10,11]).

на:

Отражение в одном кристалле, как это видно из

1/4

)

рис. 2, мало, около 1.4 θ_c, но может быть усилено в по-

1.39AU₀

J_p

κ₁

P_vc(R) =

≃

следовательности кристаллов (рис. 3). В рамках UA9

R_c

κ_c

2^7/4

√πE^1/40ε_maxd1/2X^1/20

≃ 1 - eff,

(1)

где R - это радиус изгиба, E₀ - энергия частицы,

U₀ - плоскостной потенциальный барьер, ε_max - мак-

симальное значение плоскостного электрического по-

ля, d обозначает межплоскостное расстояние, X₀ -

радиационная длина, R_c - критический радиус ка-

налирования и константы A = 11 МэВ, J_p = 1.49,

κ_c = 0.186, κ₁ = 0.13 для кремния.

Рис. 3. Усиление угла отклонения частиц при последо-

Для определения значений U₀, ε_max, R_c мы ис-

вательном отражении на цепочке хорошо ориентиро-

пользовали функцию потенциала из рентгеновских

ванных кристаллов. Разориентация кристаллов в це-

измерений [9]. В частности, R_c = 10.83 и 83.33 м для

почке относительно друг друга должна быть много

E₀ = 6.5 и 50 ТэВ соответственно. Для этих энергий

меньше угла изгиба каждого из кристаллов

частиц уравнение (1) справедливо для R/R_c менее,

чем 40-50.

активности в ЦЕРН исследовались различные ва-

Параметры отражения частицы с энергией 6.5 и

рианты мультикристаллических систем [12-15] для

50 ТэВ, средний угол отражения α, среднеквадратич-

кратного увеличения отклонения частиц. Одним из

ное значение углового распределения при отраже-

удачных вариантов для ультравысоких энергий мо-

нии rms и эффективность процесса, рассчитанные

жет быть разработанное в ИФВЭ устройство [16],

по модели [9, 10] с учетом уравнения (1), показаны

проверенное на пучке 400 ГэВ протонов [15].

на рис. 2a, b. Следует отметить, что расчеты, выпол-

Принципиальная схема кристаллического де-

ненные по данной модели, хорошо согласуются с экс-

флектора и его фотография приведены на рис. 4a, b.

Письма в ЖЭТФ том 112 вып. 1 - 2

2020

Использование отражения частиц в изогнутых кристаллах для коллимации пучка...

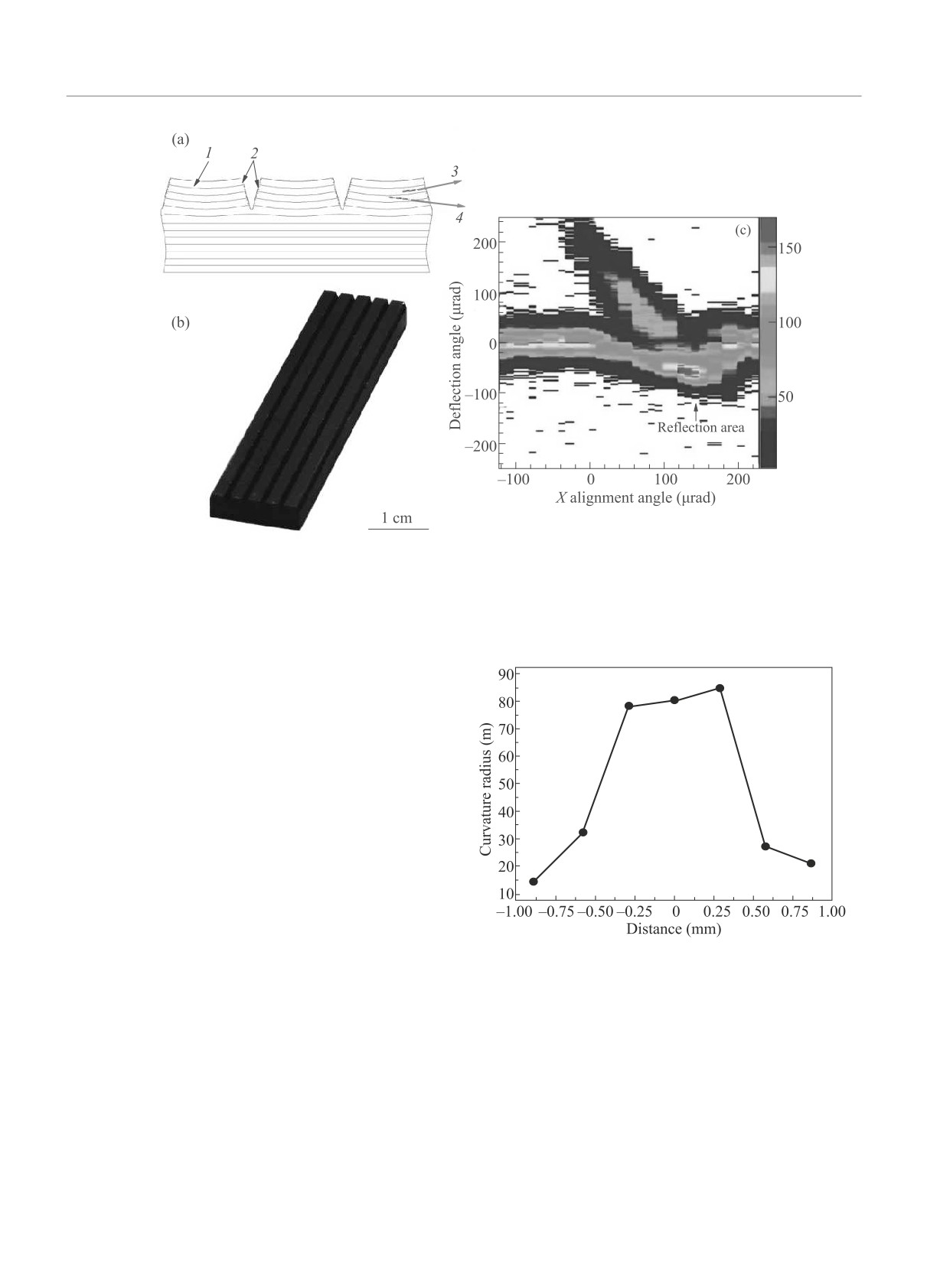
Рис. 4. (Цветной онлайн) (а) - Схематическое представление изогнутого многополоскового кристалла, образованного

периодическими канавками на поверхности толстого кристалла. 1 - Изогнутые кристаллографические плоскости; 2 -

шероховатые поверхности канавок; 3 - частица, отклоненная вследствие каналирования; 4 - частица, кратно отражен-

ная изогнутыми плоскостями. (b) - Фотография кремниевой кристаллической пластины с периодическими канавками.

(с) - Эффективное отклонение протонов 400 ГэВ за счет кратного отражения в изогнутых полосках, согласно [15]

Дефлектор был изготовлен из кремниевой пластины

размерами 70 × 15 × 5 мм. Большие грани кристал-

лической пластины были параллельны плоскостям

кристалла (111), в то время как входная грань

была перпендикулярна оси

〈110〉. В отличие от

метода, основанного на использовании внешней

силы, создаваемой держателем, предложенный

метод использует внутренние напряжения, со-

здаваемые механически нанесенными канавками

на поверхности толстой кристаллической пла-

стины. Глубина треугольных канавок в нашем

случае составляла около

1.1 мм. Изгиб отдель-

ных полос длиной

2 мм, образующихся между

канавками, производился деформацией поверх-

ностных слоев за счет эффекта Тваймана

[17].

Рис. 5. Радиус изгиба кристаллической полоски вдоль

Из-за толстого общего основания кристаллическо-

ее длины, согласно измерениям [18]

го дефлектора взаимное положение полосок на

поверхности, как угловых, так и пространствен-

ных, значительно лучше, чем при использовании

новского пучка были проведены исследования изги-

внешнего изгибающего устройства. На рисунке 4c

ба отдельных полосок и их взаимной ориентации [18].

показано эффективное (свыше

90 %) отклонение

Исследования показали, что эта конструкция - серия

протонного пучка этим кристаллом по результа-

изогнутых полосок, образованная между крупными

там [15].

канавками на толстой пластине - настолько хорошо

На Курчатовском источнике синхротронного из-

взаимно ориентирована, что подходит для коллима-

лучения (КИСИ) с помощью параллельного рентге- ции пучка протонов БАК и даже планируемого уско-

Письма в ЖЭТФ том 112 вып. 1 - 2

2020

М. Ю. Чесноков, Ю. А. Чесноков, В. А. Маишеев и др.

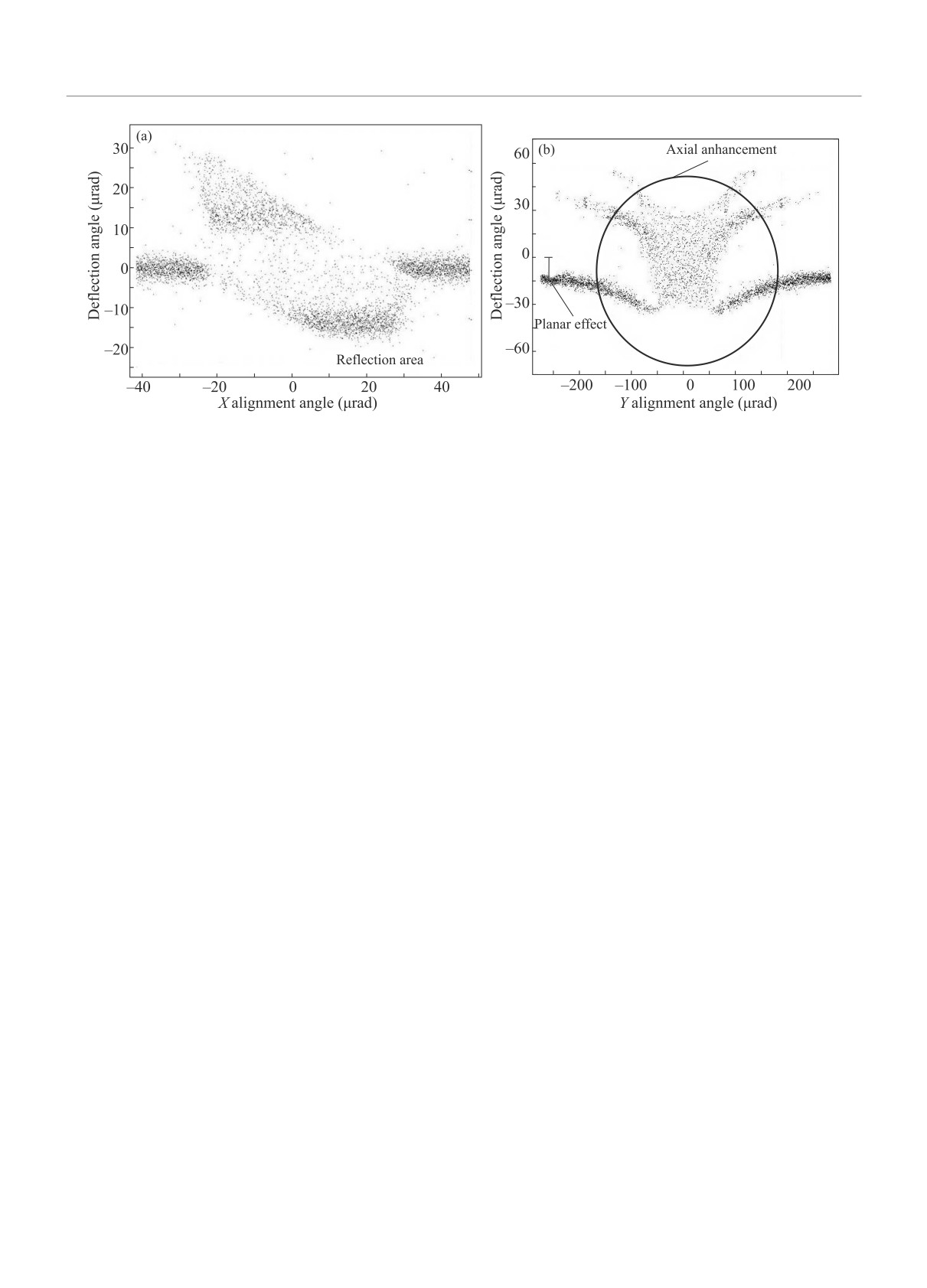
Рис. 6. (а) - Отклонение частиц с энергией 6.5 ТэВ многополосковым устройством в режиме плоскостного отражения

частиц. (b) - Усиление угла отражения в осевой ориентации кристалла

рителя БКК на энергию 50 ТэВ с помощью кратного

нии на пяти полосках равен 15 и 5 мкрад, и он может

отражения частиц. На рисунке 5 показан радиус из-

быть увеличен за счет осевой ориентации прибора,

гиба каждой кремниевой полоски по длине кристал-

как это продемонстрировано в [15]. На рисунке 6b по-

ла. В центре полоски, где происходит отражение, ра-

казан эффект расчета осевого отклонения при отра-

диус изгиба постоянный, около 100 м, что оптималь-

жении для энергии 6.5 ТэВ. При осевой ориентации

но для энергии БАК. Это утверждение поясняется

кристалла средний угол рассеяния и угловая ширина

данными на рис. 2. Для энергии БАК средний угол

пучка увеличиваются в несколько раз, по сравнению

отражения сначала растет с радиусом изгиба кри-

с плоскостным случаем. Это свойство очень важно

сталла, а затем выходит на плато в районе 100 м,

для снятия радиационных нагрузок на стенки вто-

это и есть оптимальный радиус изгиба кристалла.

ричных коллиматоров. В этом случае кристалл не

Для энергии БКК (нижний график рис. 2) выход уг-

только улучшает эффективность коллимации, но и

ла отражения на плато происходит при радиусе из-

хорошо защищает дорогостоящие вторичные колли-

гиба 800 м. Оптические измерения кривизны крем-

маторы от разрушений.

ниевой полоски с помощью метода автоколлиматора

Отметим дополнительные положительные каче-

(см. [19], с. 85) показали, что такой радиус изгиба по-

ства использования кратного отражения, в сравне-

лучается, если увеличить длину каждой кремниевой

нии с использованием каналирования:

полоски до 5 мм, а глубину канавок уменьшить до

◦ Широкий рабочий диапазон по углам, равный

0.5 мм.

углу изгиба каждого кристалла в последовательно-

С использованием программы СКРЕПЕР [20]

сти. Эта величина равна 30 мкрад для БАК и 6 мкрад

методом Монте-Карло проведен расчет отклонения

для БКК. Это значит, что нет сильной чувстви-

частиц с энергиями 6.5 и 50 ТэВ в системе из несколь-

тельности к вибрации, как при каналировании. Так-

ких кристаллических полосок. Для энергии 6.5 ТэВ

же меньше требования к гониометрическому устрой-

был выбран кристалл с пятью полосками, каждая 3

ству. Нет необходимости подстраивать кристалл по

мм длиной, радиусом изгиба 100 м и углом изгиба

углу для каждого цикла накопления. Достаточно на-

30 мкрад. Для энергии 50 ТэВ кристалл имеет пять

строить угол один раз и дальше двигать кристалл

полосок по 5 мм длиной, радиусом изгиба 800 м и уг-

только линейно, как обычные коллиматоры.

лом изгиба 6 мкрад. Результаты расчетов для энер-

◦ Меньше требования к совершенству кристалла,

гии 6.5 ТэВ показаны на рис. 6а. Видно, что в широ-

так как отражение происходит в центре кристалла

ком интервале углов (все 30 мкрад) кристалл эффек-

на малой длине порядка 1.2R × θ_c, доли миллимет-

тивно отклоняет пучок за счет кратного отражения.

ра (рис. 7), в то время как при каналировании час-

Эффективность кратного отражения на нескольких

тицы совершают десятки колебаний вдоль всей дли-

изогнутых полосках высока, около 92 % для энергии

ны изогнутого кристалла. Поэтому и радиационная

БАК 6.5 ТэВ и 95 % для энергии 50 ТэВ в БКК. Соот-

стойкость будет выше и выше, долговременная ста-

ветствующий угол отклонения при кратном отраже-

бильность - как результат. Эти аргументы говорят

Письма в ЖЭТФ том 112 вып. 1 - 2

2020

Использование отражения частиц в изогнутых кристаллах для коллимации пучка...

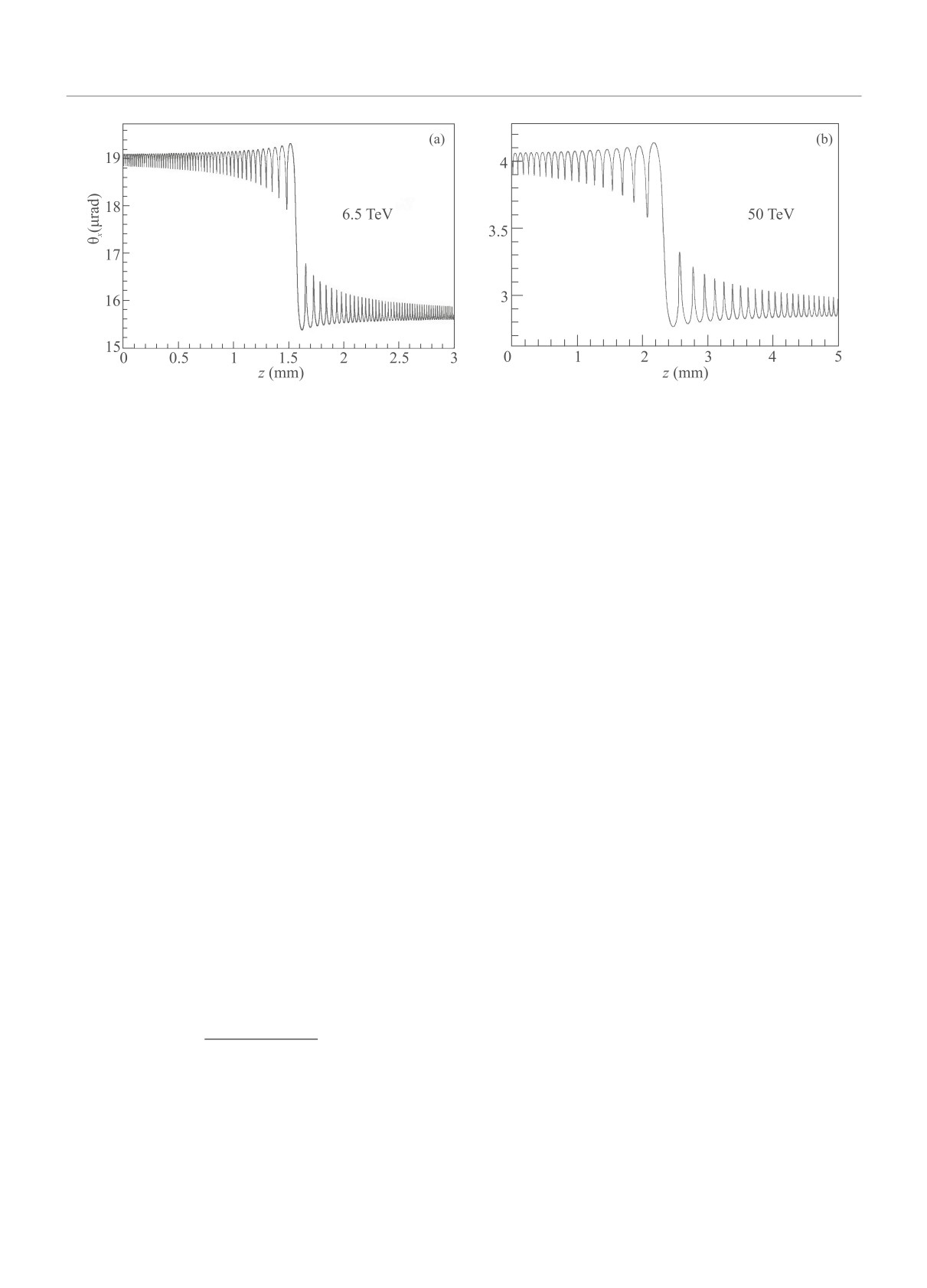
Рис. 7. (Цветной онлайн) Зависимость угла θx частицы от длины пути в коротком изогнутом кристалле при объемном

отражении

о перспективности этого метода коллимации пучка

R. Bruce, A. Abramov, A. Bertarelli et al.

при ультравысоких энергиях.

(Collaboration), J. Phys. Conf. Ser. 1350(1), 012009

Следует отметить, режим отклонения пучка за

(2019).

счет кратного объемного отражения в многополос-

W. Scandale, G. Arduini, M. Butcher et al.

(Collaboration), Phys. Lett. B 758, 129 (2016).

ковых кристаллических устройствах использовался

А. Н. Алейник, С. Г. Афанасьев, С. А. Воробьев,

для коллимации пучка в ускорителях при меньших

В. Н. Забаев, С. И. Ильин, Б. Н. Калинин, А. П. По-

значениях энергии, на ускорителе У70 при энергии

тылицын, ЖТФ 59, 191 (1989).

70 ГэВ в ИФВЭ [21,22] и при энергии 1 ТэВ на уско-

Ф. П. Денисов, А. П. Потылицын, С. И. Ильин, Ма-

рителе Тэватрон в Фермилаб [23]. Эти исследования

териалы совещания “Проблемы применения эффек-

показали, даже при меньших значениях энергии кол-

тов каналирования частиц кристаллами в физике

лимация на объемном отражении происходит не ху-

высоких энергий”, ИФВЭ, Протвино (1991), с. 56;

же, чем при каналировании в коротких кристаллах.

https://inis.iaea.org/collection/NCLCollectionStore/

В заключение отметим, что кристаллы кремния

_Public/24/060/24060554.pdf#page=57.

в качестве первичного коллиматора обладают до-

Yu. M. Ivanov, A. A. Petrunin, V. V. Skorobogatov et al.

статочной радиационной и тепловой стойкостью. В

(Collaboration), Phys. Rev. Lett. 97, 144801 (2006).

штатной работе потери частиц на коллиматорах в

W. Scandale, D. A. Still, A. Carnera et al.

больших коллайдерах не превышают 10⁸ частиц в

(Collaboration), Phys. Rev. Lett. 98, 154801 (2007).

секунду [1,2], с учетом малых размеров пучка плот-

A. M. Taratin and S. A. Vorobiev, Phys. Lett. A 119,

ность потока на кромке коллиматора составляет

425 (1987).

≃ 10¹¹ см^-2 c^-1. В экспериментах ИФВЭ [24] по вы-

V. A. Maisheev, Physical Review Special Topics-

воду циркулирующего пучка показано, что кристал-

Accelerators and Beams 10, 084701 (2007).

лы кремния длительное время выдерживают потоки

10.

S. Bellucci, Yu.A. Chesnokov, V.A. Maisheev,

≃ 10¹² см^-2 c^-1, а радиационный предел для канали-

and I. A. Yazynin, Physical Review Special Topics-

Accelerators and Beams 18, 114701 (2015).

рования составляет 10²⁰ см^-2 частиц. Это значит, что

кристаллический коллиматор простоит около одного

11.

V. A. Maisheev, Coherent Processes in Bent Single

Crystals, Proceedings of 51st Workshop “Charged and

года в коллайдере (вполне приемлемый срок).

Neutral Particles Channeling Phenomena” Erice, Italy,

Работа выполнена при поддержке Российского

October 2008, World Scientific Publishing Co Pte Ltd,

научного фонда, грант # 17-12-01532.

The Science and Culture Series - Physics, Singapore

(2010); doi:10.1142/9789814307017_0009.

12.

W. Scandale, A. Carnera, G. Della Mea et al.

1. R. W. Assmann I. S. Baishev, M. Brugger et

al. (Collaboration), Requirements for the LHC

(Collaboration), Phys. Lett. B 658, 109 (2008).

collimation system, LHC-PROJECT-REPORT-599,

13.

W. Scandale, A. Vomiero, S. Baricordi et al.

in 8th European Particle Accelerator Conference: A

(Collaboration), Phys. Rev. Lett. 102, 084801 (2009).

Europhysics Conference, La Vilette, Paris, France, 3-7

14.

W. Scandale, A. Vomiero, E. Bagli et al.

Jun 2002, JACOW publishing, CERN, Geneva (2002).

(Collaboration), Phys. Lett. B 688, 284 (2010).

Письма в ЖЭТФ том 112 вып. 1 - 2

2020

М. Ю. Чесноков, Ю. А. Чесноков, В. А. Маишеев и др.

15. W. Scandale, G. Arduini, M. Butcher et al.

20. I. I. Degtyarev, O. A. Liashenko, and I. A. Yazynin, Proc.

(Collaboration), Nucl. Instrum. Methods Phys.

Eur. Particle Accelerator Conf. (EPAC_2000), Vienna,

Res. B 338, 108 (2014).

Austria (2000), p. 2506.

21. A. G. Afonin, V. T. Baranov, V. N. Gorlov, V. I. Kotov,

16. A. G. Afonin, V. T. Baranov, V. A. Maisheev,

V. A. Maisheev, V. I. Terekhov, V.N. Chepegin,

D. A. Savin, Yu.E. Sandomirskiy, Yu.A. Chesnokov,

Yu. A. Chesnokov, and I. A. Yazynin, Atomic Energy

and I. A. Yazynin, Instruments and Experimental

106(6), 409 (2009).

Techniques 56(6), 617 (2013).

22. A. G. Afonin, I. A. Yazynin, E. A. Syshchikov et al.

17. J. C. Lambropoulos, S. Xu, T. Fang, and D. Golini,

(Collaboration), JETP Lett. 93, 187 (2011).

Appl. Opt. 35, 5704 (1996).

23. N. V. Mokhov, G. E. Annala, A. Apyan et al.

18. A. A. Kaloyan, S. A. Tikhomirov, K. M. Podurets,

(Collaboration), Int. J. Mod. Phys. A 25(supp01), 98

V.A.

Maisheev,

Yu. E.

Sandomirskiy,

and

(2010).

Yu. A. Chesnokov, Crystallography Reports

62(3),

24. A. G. Afonin, V. T. Baranov, E. V. Barnov,

370 (2017).

G. I. Britvich, Yu. A. Chesnokov, P. N. Chirkov,

19. V. M. Biryukov, Yu. A. Chesnokov, and V. I. Kotov,

V. A. Kalinin, V. A. Maisheev, S. F. Reshetnikov,

Crystal channeling and its application at high-energy

D. A. Savin, and V. I. Terekhov, Int. J. Mod. Phys. A

accelerators, Springer, Berlin, Germany (1997), 219 p.

33, 1850138 (2018).

Письма в ЖЭТФ том 112 вып. 1 - 2

2020