Письма в ЖЭТФ, том 113, вып. 4, с. 267 - 273

Влияние электронной делокализации на поглощение “без отдачи”

γ-квантов в варвиките Fe_1.75V_0.25BO₄

Ю. В. Князев⁺¹⁾, О. А. Баюков⁺, М. С. Шустин⁺, Д. В. Балацкий^∗, Н. А. Бельская^×, С. А. Громилов^◦,

А. С. Сухих^◦, В. В. Руденко⁺, Н. В. Казак⁺¹⁾

⁺Институт физики им. Л. В. Киренского Федеральный исследовательский центр

“Красноярский научный центр Сибирского отделения РАН”, 660036 Красноярск, Россия

^∗Институт химии Дальневосточного отделения РАН, 690022 Владивосток, Россия

^×СибГУ им. М. Ф. Решетнева, 660037 Красноярск, Россия

^◦Институт неорганической химии им. А. В. Николаева Сибирского отделения РАН, 630090 Новосибирск, Россия

Поступила в редакцию 25 декабря 2020 г.

После переработки 12 января 2021 г.

Принята к публикации 13 января 2021 г.

Метод мессбауэровской спектроскопии использован для исследования динамических особенностей

кристаллической решетки порошка монокристаллов варвикита Fe1.75V0.25BO4 в температурном интер-

вале 4.2-505 К. По температурной зависимости вероятности эффекта Мессбауэра в приближении тон-

кого поглотителя определена температура Дебая (ΘD = 260 К). Обнаружено, что в области температур

260-505 К происходит электронная делокализация, которая обусловлена быстрым электронным обме-

ном между соседними катионами Fe³⁺ и Fe²⁺. В результате образуются катионы железа со смешанной

валентностью (Fe^2.5+). Этот процесс коррелирует с изменением упругих свойств решетки. Такая кор-

реляция приводит к резкому уменьшению эффекта поглощения без отдачи γ-квантов кристаллической

решеткой в области 260-400 К.

DOI: 10.31857/S1234567821040091

I. Введение. В первые десятилетия после от-

быть использована для анализа структурных фазо-

крытия Р. Мессбауэром эффекта поглощения гамма-

вых переходов различного рода.

квантов без отдачи [1, 2] проводилось большое число

Наиболее известным примером применения месс-

экспериментов по изучению динамики кристалличе-

бауэровской спектроскопии для анализа локальных

ской решетки твердых тел [3-7]. Прямая взаимосвязь

динамических процессов является исследование

фононного спектра вещества и вероятности поглоще-

вблизи сегнетоэлектрического перехода в BaTiO₃

ния без отдачи гамма-квантов кристаллической ре-

со структурой перовскита [9]. Было показано, что

шеткой описывается моделью Дебая и может быть

резкое изменение вероятности процесса без отдачи

выражена с помощью известного соотношения [8]:

вблизи температуры фазового перехода происходит

[

в результате небольшого смещения атомов Ti внутри

E^2γ

кислородного октаэдра, которое приводит к появле-

f = exp

4Mc²k_BΘ_D

нию поперечных фононных мод, энергия которых

(

)₂ ∫ ΘD

)]

аномально мала. Рост вероятности возбуждения та-

xdx

× 1+4

(1)

ких фононных колебаний и приводит к уменьшению

Θ_D

e^x - 1

вероятности эффекта Мессбауэра [3, 10].

M - масса атома⁵⁷Fe, c - скорость света в вакуу-

Несколько меньшее распространение получили

ме, k_B - постоянная Больцмана, E_γ - энергия гамма-

работы, посвященные изучению явления поглощения

излучения (14.4 кэВ для⁵⁷Fe), Θ_D - температура Де-

без отдачи в области магнитного перехода [11-13].

бая, x = hω/k_BT (h - постоянная Планка, ω - час-

Благодаря использованию эффекта Мессбауэра в ме-

тота упругих колебаний). С учетом того, что в вы-

таллическом железе [11] удалось впервые показать,

ражение вероятности эффекта входит температура

как магнитные взаимодействия между атомами же-

Дебая (Θ_D), мессбауэровская спектроскопия может

леза приводят к уменьшению среднеквадратичного

смещения атомов и резкому увеличению вероятности

¹⁾yuk@iph.krasn.ru; nat@iph.krasn.ru

поглощения без отдачи.

Письма в ЖЭТФ том 113 вып. 3 - 4

2021

267

268

Ю. В. Князев, О. А. Баюков, М. С. Шустин и др.

Несмотря на вышесказанное, в недавней работе

[14] авторами было отмечено, что “мессбауэровская

спектроскопия на волне развития других методов

изучения локальной структуры вещества оказалась

незаслуженно забытой при изучении динамических

процессов кристаллической решетки в твердом те-

ле”. Дальнейшее развитие методики ядерного гамма-

резонанса связано с появлением источников синхро-

тронного излучения [15, 16]. Например, неупругое

ядерное рассеяние позволяет детально изучить упру-

гие свойства вещества путем прямого измерения фо-

нонных спектров [17-19].

В данной работе мы исследовали особенности

динамики кристаллической решетки порошка моно-

кристаллов Fe_1.75V_0.25BO₄ со структурой варвикита

методом мессбауэровской спектроскопии в интерва-

ле температур 4.2-505 К. Особенностью этого мате-

риала является наличие двух кристаллографически

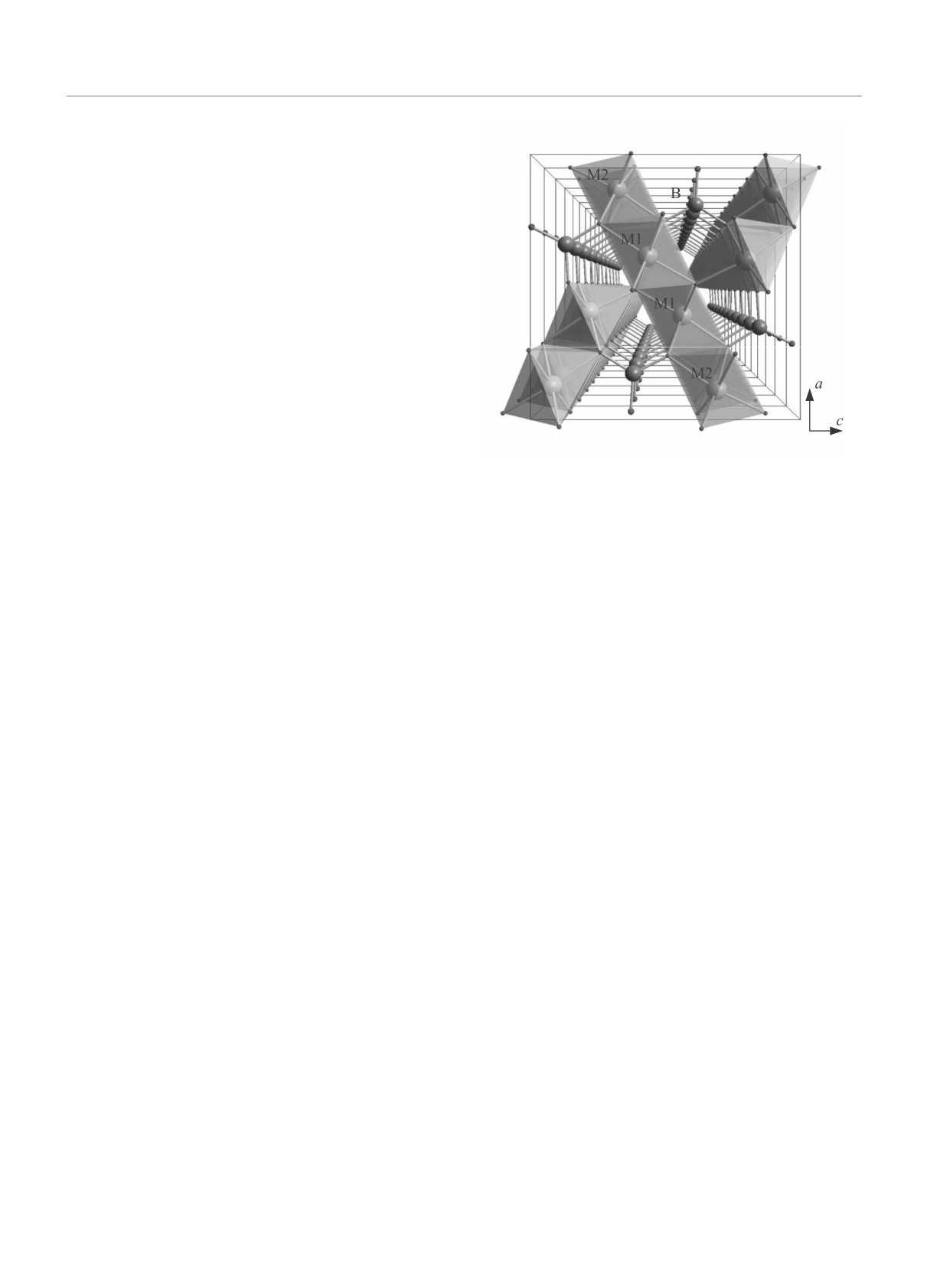
Рис. 1. (Цветной онлайн) Кристаллическая структура

неэквивалентных позиций, занятых атомами пере-

варвикита Fe1.75V0.25BO4 в проекции на ac-плоскость.

ходных металлов. Поскольку степень искажения ло-

Неэквивалентные кристаллографические узлы М1 и

кального окружения в этих позициях различна, их

М2 и атомы бора обозначены. Атомы кислорода на-

вклады в упругие свойства кристалла могут сильно

ходятся в вершинах октаэдров

отличаться.

С прикладной точки зрения исследуемый обра-

зец имеет перспективу использования в накопителях

II. Образцы и методы. Монокристаллы

энергии. Изучение электрохимических свойств пока-

варвикита Fe_1.75V_0.25BO₄ были получены раствор-

зало высокую эффективность композитов на осно-

расплавным методом. Синтез подробно описан в

ве FeVBO₄ для применения в качестве анода [20]. В

работе [21]. Рентгеноструктурный анализ проведен

работе [21] проведена характеризация магнитных и

на дифрактометре BRUKER X8 (МоКa-излучение,

электрических свойств монокристаллов с малой сте-

графитовый монохроматор, CCD-детектор ApexII)

пенью замещения Fe_1.91V_0.09BO₄. С помощью месс-

при температурах 100 и 390 К. Температура образца

бауэровской спектроскопии при комнатной темпера-

контролировалась при помощи потокового азотного

туре обнаружены катионы железа со смешанным за-

криостата Cryostream 800Plus (Oxford Cryosystems).

рядовым состоянием Fe^2.5+, аналогично Fe₂BO₄ [22].

Стратегия съемки состояла из стандартных 0.5^◦ φ- и

Здесь важно отметить, что незамещенный Fe₂BO₄

ω-сканов. Сбор первоначальных данных, уточнение

изучен достаточно подробно [22-27] и обладает весь-

параметров элементарной ячейки, интегрирование и

ма интересными электронными и магнитными свой-

введение поправки на поглощение были выполнены

ствами. Ниже T = 317 К в Fe₂BO₄ электроны лока-

в пакете программ Bruker Apex 2 V.2013.6-2 (Bruker

лизуются на катионах железа с формированием двух

Advanced X-ray Solutions, Madison, Wisconsin, USA).

зарядовых состояний Fe³⁺ и Fe²⁺. При этом катио-

Полученный массив данных обрабатывался в про-

ны Fe²⁺ предпочитают кристаллографические пози-

грамме Olex2 v.1.2.10 [29] с использованием SHELXT

ции сжатого октаэдра (М2), а катионы Fe³⁺ распо-

2014/5 [30] для расшифровки и SHELXL 2018/3 [30]

лагаются в позициях М1 (рис. 1). Это предпочтение

для уточнения кристаллической структуры.

разновалентных катионов к неэквивалентным пози-

Мессбауэровские спектры измерены на порошке

циям рассматривается как зарядовое упорядочение

монокристаллов варвикита Fe_1.75V_0.25BO₄ с плотно-

[22, 25]. В результате формируется несоразмерная

стью 7-10 мг/см² по содержанию железа. Измере-

сверхструктура, состоящая из электрических дипо-

ния в интервале 4.2-300 К выполнены на спектро-

лей [25, 26]. Поскольку известно, что зарядовое упо-

метре МС-1104Ем (НИИ физики ЮФУ) в геометрии

рядочение при определенных условиях может яв-

пропускания с радиоактивным источником⁵⁷Co(Rh)

ляться причиной сегнетоэлектричества [28], то дина-

(АО “Ритверц”) с использованием криостата CFSG-

мика кристаллической решетки подобных материа-

311-MESS с образцом в обменном газе на базе

лов заслуживает более тщательного исследования.

криорефрижератора замкнутого цикла Гиффорда-

Письма в ЖЭТФ том 113 вып. 3 - 4

2021

Влияние электронной делокализации на поглощение “без отдачи”. . .

269

МакМагона. Съемка мессбауэровских спектров в

высокотемпературной области (350-505 К) выполне-

на на спектрометре Wissel MB-550 (Германия), в

геометрии пропускания с источником γ-излучения

⁵⁷Co(Rh). В качестве нагревательного элемента вы-

ступала печь Wissel MBF-1100. Контроль темпера-

туры осуществлялся с помощью контроллера TR-

55. Запрессованный образец помещался между дву-

мя керамическими пластинами (BN) и располагался

в стеклянной трубке печи.

Обработка спектров была выполнена в два эта-

па. На первом этапе определялись возможные неэк-

вивалентные позиции железа в образце с помощью

расчета распределений вероятностей квадрупольных

расщеплений и сверхтонких полей. В соответствии

с полученными результатами формировался предва-

рительный модельный спектр. На следующем этапе

модельный спектр подгонялся к экспериментально-

му при варьировании всего набора сверхтонких пара-

метров методом наименьших квадратов в линейном

приближении. Величины химических сдвигов приве-

дены относительно металлического железа (αFe).

III. Результаты. Кристаллическая решетка об-

разца показана на рис. 1. Параметры решетки и

объем элементарной ячейки приведены в табл.1.

Полный набор кристаллографических данных де-

Таблица 1. Параметры элементарной ячейки монокристалла

Fe_1.75V_0.25BO₄ при температурах 100 и 390 К

T, K

100

390

a,Å

9.2410 (11)

9.255 (10)

b,Å

3.1672 (3)

3.1786 (14)

c,Å

9.3833 (12)

9.401 (4)

V,Å3

274.63 (5)

276.6 (2)

Пространственная

Pnma

группа

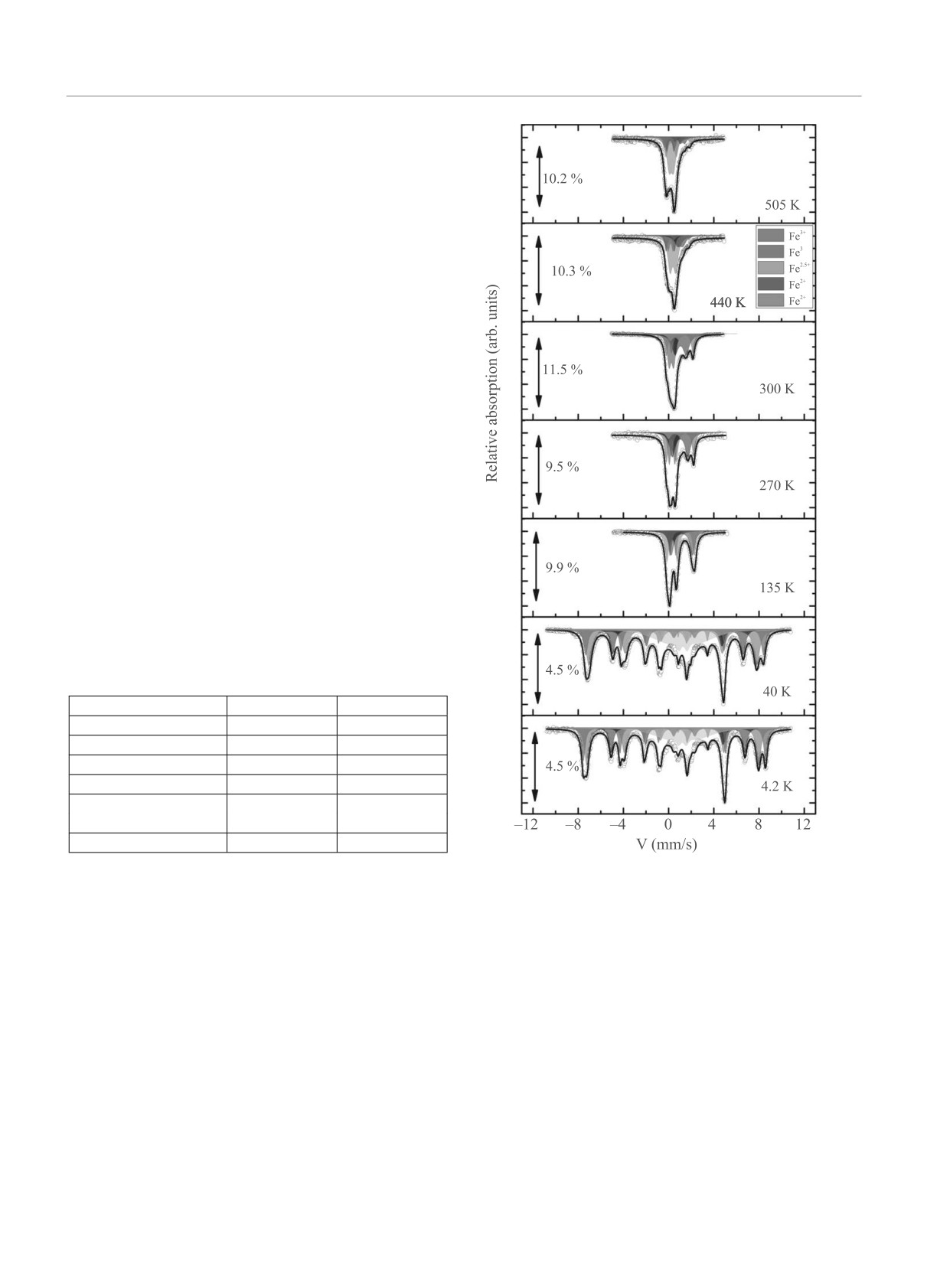
Рис. 2. (Цветной онлайн) Мессбауэовские спектры

понирован в Кембриджской базе структурных дан-

Fe1.75V0.25BO4 в интервале 4.2-505 К. Кружками по-

ных (https://www.ccdc.cam.ac.uk/structures), номера

казаны экспериментальные данные. Сплошной линией

CCDC 2051305 (100 К) и CCDC 2051306 (390 K).

показан результат обработки спектров

Здесь отметим, что Fe_1.75V_0.25BO₄ не испытывает

структурных переходов, и ромбическая симметрия

(пространственная группа Pnma(62)) сохраняется в

ки. Однако сначала рассмотрим некоторые аспекты

интервале 390-100 К. Уточнение заселенностей пока-

тонкой структуры образца.

зало, что узлы М1 и М2 совместно заняты катио-

Зеемановские секстеты, обусловленные магнит-

нами железа и ванадия в следующих соотношениях:

ным упорядочением, сохраняются в интервале 4.2-

M1(0.87Fe+0.13V) и М2(0.88Fe+0.12V).

125 К. Это согласуется с температурой ферримаг-

Мессбауэровские спектры Fe_1.75V_0.25BO₄, полу-

нитного упорядочения (T_N = 130 K), определенной

ченные в интервале 4.2-505 К, показаны на рис. 2.

по данным магнитометрических измерений [21]. При

Измерения в широком интервале температур позво-

T = 4.2К спектр состоит из четырех секстетов, по-

ляют исследовать динамику кристаллической решет-

парно относящихся к двух- (IS ≈ 1.2 мм/с) и трех-

Письма в ЖЭТФ том 113 вып. 3 - 4

2021

270

Ю. В. Князев, О. А. Баюков, М. С. Шустин и др.

валентным катионам железа (IS ≈ 0.5 мм/с), зани-

мающих две кристаллографически неэквивалентные

позиции [31]. Кроме этого, наблюдается секстет двух-

валентного железа с сильно уширенными линиями и

низкой величиной сверхтонкого поля H_hf = 140 кЭ.

Подобное значение сверхтонкого поля наблюдалось

в незамещенном Fe₂BO₄ [22, 32]. Состояние железа

с такой низкой величиной сверхтонкого поля может

быть как проявлением сильных ковалентных эффек-

тов [33], так и следствием геометрической фруст-

рации, которой сильно подвержена структура вар-

викита [34]. Фрустрация является свойством самой

кристаллической структуры варвикита и может при-

водить к потере дальнего магнитного порядка при

определенных условиях [31, 35].

Далее мы сосредоточимся на взаимосвязи зарядо-

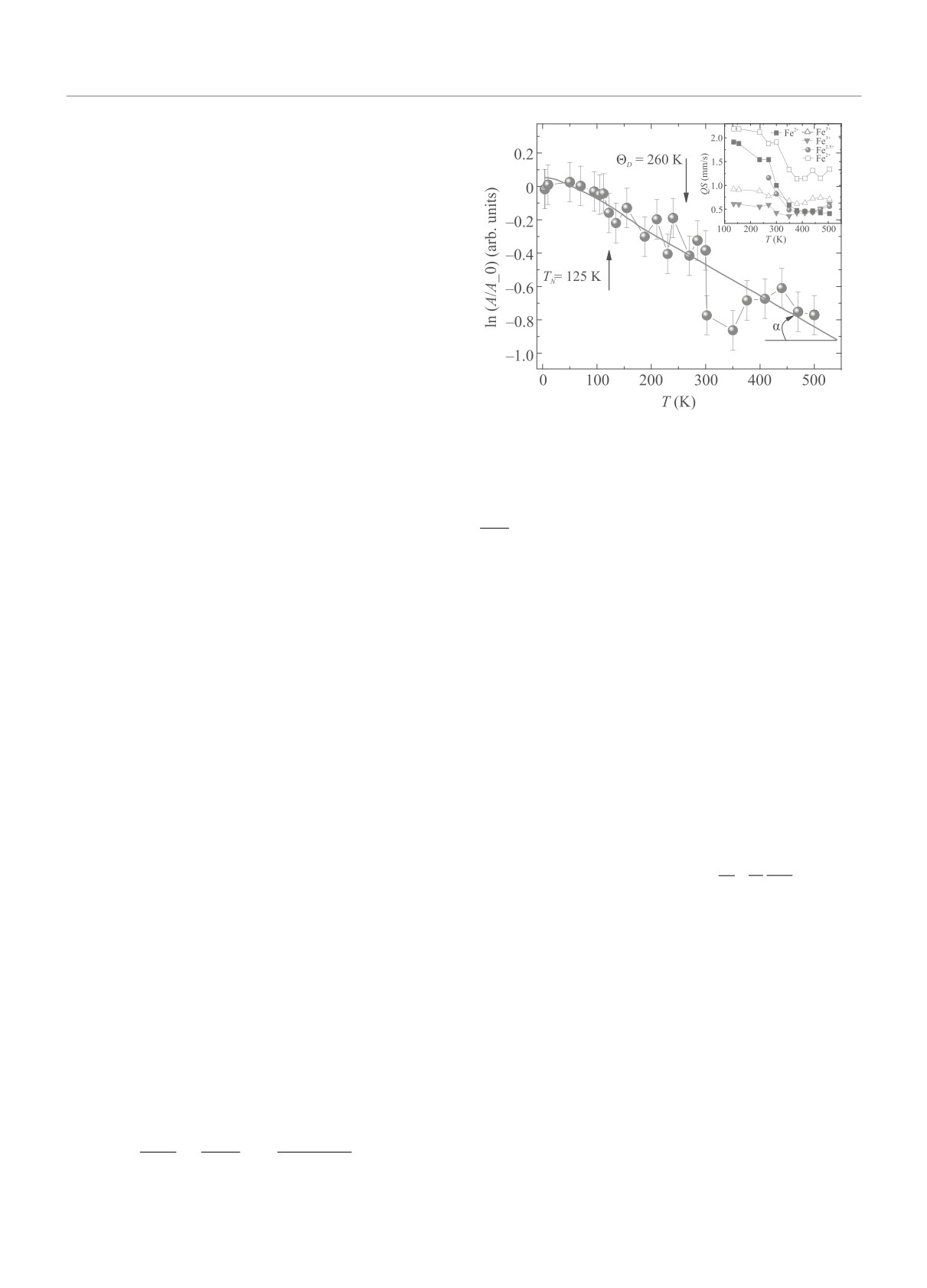
Рис. 3. (Цветной онлайн) Температурная зависимость

вой и колебательной подсистем Fe_1.75V_0.25BO₄. Вы-

вероятности эффекта Мессбаэура в логарифмическом

ше 135 К вид мессбауэровских спектров указывает

масштабе. Сплошная линия показывает зависимость

на парамагнитное состояние вещества. В интерва-

в соответствии с моделью Дебая. Значение ΘD опре-

делено по углу наклона сплошной линии tg(α)

ле 135-260 К спектры состоят из четырех дублетов,

d ln A

= 0.00201. На вставке показана температурная

которые по величине химического сдвига соответ-

зависимость квадрупольного расщепления спектраль-

ствуют двух- и трехвалентным катионам железа в

ных компонент

октаэдрическом кислородном окружении. Дальней-

ший рост температуры приводит к возникновению

Тогда температура Дебая, полученная согласно

состояния железа со смешанной валентностью Fe^2.5+

(2), составляет Θ_D = 260 К. Эта величина несколь-

(IS ≈ 0.5-0.7 мм/с). Это объясняется коллективиза-

ко меньше Θ_D для других кристаллов со структурой

цией электрона между двумя соседними катионами

варвикита [39, 40]. Таким образом, происходит неко-

железа в позициях М1 и М2. По нашим данным, та-

торое “размягчение” решетки, в отличие, например,

кое состояние существует во всем интервале темпе-

от замещения Se атомами серы в FeSe_0.91S_0.09, кото-

ратур выше 260 К. Если сравнивать это явление с

рое привело к двукратному росту Θ_D [41].

переходом Вервея в магнетите [36] и с “зарядовым

Используя значение Θ_D, можно оценить неко-

упорядочением” в Fe₂BO₄ [22, 32], то можно отме-

торые параметры, характеризующие упругие свой-

тить, что переход Вервея и “зарядовое упорядочение”

ства кристалла. Так, по определению Θ_D максималь-

в Fe₂BO₄ сопровождаются аномалиями электропро-

ная частота фононных колебаний составляет ω_m =

водности, что в замещенном варвиките не было об-

= k_BΘ_D/h = 3.62 · 1013 Гц. Оценка скорости упру-

наружено [21].

гих колебаний в среде, V_m, может быть выполнена

Площадь спектра при данной температуре эк-

[

]_1/3

NAρ

вивалентна величине эффекта Мессбауэра, поэтому

с помощью выражения Θ_D =^h

· V_m

4π

для оценки ее величины использовано интегриро-

[42]. Здесь q - количество атомов в элементарной

вание накопленного сигнала резонансных γ-квантов

химической формуле (для Fe_1.75V_0.25BO₄ q

= 7),

по всем каналам анализатора мессбауэровского спек-

N_A- постоянная Авогадро, ρ - плотность среды (для

трометра с учетом спектрального фона. Нормируя

Fe_1.75V_0.25BO₄ по данным рентгеновской дифракции

полученные значения на значение площади при 4.2 К

ρ = 4.448г/см³), M- молярная масса (186г/моль).

(A₀), мы получили температурную зависимость от-

Для рассматриваемого образца скорость распростра-

носительной величины эффекта A/A₀, которая пока-

нения упругих колебаний составляет 1880 м/с, что

зана в виде кружков на рис.3. Логарифмируя выра-

несколько меньше, чем в веществах с ромбической

жение (1) в области температур T > Θ_D/2, получа-

кристаллической решеткой [42].

ем выражение для определения температуры Дебая

В высокотемпературной области наблюдается

[37, 7, 38]:

сильное уменьшение поглощения без отдачи с даль-

нейшим возвращением на линейную зависимость.

d ln f

d ln A

3E^2γ

Этот процесс проявляется в области 260-505 К и

∝

(2)

Mc²k_BΘ2

может быть разделен на два температурных интер-

Письма в ЖЭТФ том 113 вып. 3 - 4

2021

Влияние электронной делокализации на поглощение “без отдачи”. . .

271

вала:

260-400 К, когда степень делокализации

при температурах 260-400 К связаны с перестрой-

электрона растет медленно, и коррелирует с пове-

кой колебательных спектров. Качественное понима-

дением зависимости QS (T), показанной на вставке

ние особенностей перестройки фононных спектров

к рис. 3;

400-505 К с резким ростом степени

можно получить, аппроксимируя различные темпе-

делокализации общего для атомов железа элек-

ратурные области интервала 260-505 К линейными

трона. Это хорошо иллюстрируется температурной

зависимостями, которые бы характеризовали упру-

зависимостью заселенности компонент спектров с

гие параметры системы на каждом интервале. В та-

разными зарядовыми состояниями на рис. 4.

ком подходе, увеличение угла наклона (α) функ-

ции ln (A/A₀) (T ) в области 260-400 К указывает

на уменьшение жесткости решетки. Таким образом,

вклад быстрого электронного обмена имеет призна-

ки фазового перехода без изменения симметрии ре-

шетки и требует дополнительного изучения. По всей

видимости, электронная делокализация приводит к

увеличению заселенности низкоэнергетических фо-

нонных мод, которые определяют упругие свойства

решетки на этом интервале.

Отметим, что в процессе взаимной перестройки

электронной структуры и колебательных характе-

ристик в температурном интервале 260-505 К воз-

можно влияние электронной и фононной подсистем

друг на друга. С одной стороны, делокализация

электрона может приводить к изменению упругих

свойств решетки. С другой стороны, колебания (в

Рис. 4. (Цветной онлайн) Температурная зависимость

том числе ангармонические) катионов могут при-

заселенности зарядовых состояний катионов железа в

водить к выравниванию энергий электрона на со-

Fe1.75V0.25BO4. На вставке показана температурная за-

седних катионах и способствовать коллективизации

висимость изомерного сдвига спектральных компонент

электронов.

IV. Заключение. Таким образом, по данным

В первом интервале наблюдается существенное

мессбауэровской спектроскопии определена темпе-

отклонение зависимости ln(A/A₀)(T) от линейной,

ратура Дебая для монокристаллов Fe_1.75V_0.25BO₄

предсказываемой в рамках модели Дебая. Подобное

Θ_D = 260 К. Наблюдаемое увеличение степени де-

поведение величины эффекта Мессбауэра характер-

локализации электрона между соседними катионами

но для сегнетоэлектриков в области сегнетоэлектри-

железа, вероятно, связано с температурным умень-

ческого перехода вследствие появления мягких фо-

шением порога возбуждения быстрого электронно-

нонных мод и ангармонизма колебаний атомов в ре-

го обмена. Обнаруженная взаимосвязь электронной

шетке [9, 14]. Поскольку в Fe_1.75V_0.25BO₄ структур-

и колебательной подсистем может быть обусловле-

ный переход в интервале 100-390 К не наблюдает-

на, как изменением упругих связей пар катионов

ся, то причиной резкого уменьшения вероятности по-

железа при обобществлении электрона, так и силь-

глощения без отдачи γ-квантов, возможно, является

ным электрон-фононным взаимодействием в систе-

сильная связь электронной и фононной подсистем.

ме. В первом случае изменение спектра фононных

По всей видимости, в этой области происходит пе-

мод происходит исключительно за счет особенно-

рестройка спектра колебательных мод совместно с

стей локализованных электронных состояний, че-

изменением электронной структуры при коллекти-

го, как уже было отмечено, не наблюдалось, то-

визации электронов и образования состояний Fe^2.5+.

гда как второй случай затрагивает зонные состо-

Во втором выделенном интервале соответствие

яния электронов и, как ожидается, должен приво-

между экспериментальной и теоретической зависи-

дить к модификации проводящих свойств соедине-

мостями поглощения без отдачи восстанавливает-

ния. Поэтому мы считаем, что сильная связь элек-

ся. По всей видимости, в этом интервале происхо-

тронной и фононной подсистем в интервале темпера-

дит возбуждение всех колебательных мод в систе-

тур T = 260-400 К обусловлена изменением упругих

ме. Это позволяет предположить, что существенные

свойств решетки, вследствие делокализации электро-

отклонения зависимости ln(A/A₀)(T) от линейной

нов. Отметим, что возможно и обратное влияние:

Письма в ЖЭТФ том 113 вып. 3 - 4

2021

272

Ю. В. Князев, О. А. Баюков, М. С. Шустин и др.

возбужденные колебания в решетке (в том числе ан-

H. Winkelmann, and M. Abd-Elmeguid, Phys.

гармонические) могут способствовать уменьшению

Rev. B 58, 254 (1998).

энергетического барьера между разными электрон-

19.

R. Pradip, P. Piekarz, D. G. Merkel, J. Kalt, O. Waller,

ными состояниями и выравниванию энергий двух

A. I. Chumakov, R. Rüffer, A.M. Oles, K. Parlinski,

соседних узлов и, как следствие, коллективизации

T. Baumbach, and S. Stankov, Nanoscale 11, 10968

электронов.

(2019).

Работа выполнена при финансовой поддержке

20.

M. Dong, Q. Kuang, X. Zeng, L. Chen, J. Zhu, Q. Fan,

Совета по грантам Президента Российской Фе-

Y. Dong, and Y. Zhao, J. Alloys Compd. 812, 152165

дерации (проект МК-2339.2020.2) и Российского

(2020).

фонда фундаментальных исследований (проект

21.

A. Balaev, O. Bayukov, A. Vasilev, D. Velikanov,

РФФИ-20-02-00559-а).

N. Ivanova, N. Kazak, S. Ovchinnikov, M. Abd-Elmigid,

and V. Rudenko, ZhETF 124, 1103 (2003).

22.

A. Douvalis, V. Papaefthymiou, A. Moukarika,

T. Bakas, and G. Kallias, J. Phys. Condens. Matter 12,

R.L. Mössbauer, Naturwissenschaften 45, 538 (1958).

177 (2000).

R.L. Mössbauer, Z. Phys. 151, 124 (1958).

23.

N. Suda, K. Kohn, and S. Nakamura, Ferroelectrics 286,

Č. Muzikář, V. Janovec, and V. Dvořák, Physica Status

155 (2003).

Solidi B. Basic Solid State Physics 3, К9 (1963).

24.

M. Sánchez-Andújar, J. Mira, B. Rivas-Murias,

V.A. Bokov and V.P. Romanov, and V. V. Chekin,

S. Yáñez-Vilar, N. Biskup, J. Rivas, and M. A. Señarıs-

Fizika Tverdogo Tela 7, 1886 (1965).

Rodr´ıguez, IEEE Transactions on Magnetics 44, 2989

V. Chekin, V. Romanov, B. Verkin, and V. Bokov,

(2008).

Pis’ma v ZhETF 2, 186 (1965).

25.

M. Angst, P. Khalifah, R. Hermann, H. Xiang,

T. Kobayashi and K. Fukumura, Nuclear Instruments

M.-H. Whangbo, V. Varadarajan, J. W. Brill,

and Methods 180, 549 (1981).

B. C. Sales, and D. Mandrus, Phys. Rev. Lett.

R.D. Ernst, D. R. Wilson, and R. Herber, J. Am. Chem.

99, 086403 (2007).

Soc. 106, 1646 (1984).

26.

S. Bland, M. Angst, S. Adiga, V. Scagnoli, R. Johnson,

M. Eibschüutz, S. Shtrikman, and D. Treves, Phys. Rev.

J. Herrero-Martin, and P. Hatton, Phys. Rev. B 82,

156, 562 (1967).

115110 (2010).

V. Bhide and M. Multani, Physical Review 139, A1983

27.

H. Yang, H. Tian, Y. Song, Y. Qin, Y. Zhao, C. Ma,

(1965).

and J. Li, Phys. Rev. Lett. 106, 016406 (2011).

10.

A. Jain, S. Shringi, and M. Sharma, Phys. Rev. B 2,

28.

J. van Den Brink and D. I. Khomskii, J. Phys. Condens.

2756 (1970).

Matter 20, 434217 (2008).

11.

B. Kolk, A. Bleloch, and D. Hall, Hyperfine Interactions

29.

O. Dolomanov, L. Bourhis, R. Gildea, J. Howard, and

29, 1377 (1986).

H. Puschmann, J. Appl. Crystallogr. 42, 339 (2009).

12.

J. Fontcuberta, Physica Status Solidi (b) 139,

379

30.

G. M. Sheldrick, Acta Crystallogr. A 71, 3 (2015).

(1987).

31.

I. Lyubutin, N. Y. Korotkov, K. Frolov, N. Kazak,

13.

K. Sharma, V. R. Reddy, A. Gupta, S. Kaushik, and

M. Platunov, Y. V. Knyazev, L. Bezmaternykh,

V. Siruguri, J. Phys. Condens. Matter 24,

376001

S. Ovchinnikov, A. Arauzo, and J. Bartolomé, J. Alloys

(2012).

Compd. 642, 204 (2015).

14.

M. Podgórna, J.

Żukrowski, I. Jankowska-Sumara,

32.

A. Douvalis, V. Papaefthymiou, A. Moukarika, and

A. Majchrowski, and K. Berent, Physica Status Solidi

T. Bakas, Hyperfine Interactions 126, 319 (2000).

(b) 254, 1700137 (2017).

33.

G. Abramova, Y. Knyazev, O. Bayukov, and S. Kubrin,

15.

I. S. Lyubutin, S. Starchikov, A.G. Gavriliuk, I. Troyan,

Fizika Tverdogo Tela 63, 69 (2021).

Y.A. Nikiforova, A. Ivanova, A. Chumakov, and

34.

A. Akrap, M. Angst, P. Khalifah, D. Mandrus,

R. Rüffer, JETP Lett. 105, 26 (2017).

B. C. Sales, and L. Forró, Phys. Rev. B 82, 165106

16.

Y.V. Knyazev, A. Chumakov, A. Dubrovskiy,

(2010).

S. V. Semenov, S.S. Yakushkin, V. Kirillov,

35.

Y. V. Knyazev, N. Kazak, M. Platunov, N. Ivanova,

O. N. Martyanov, and D. A. Balaev, JETP Lett.

L. Bezmaternykh, A. Arauzo, J. Bartolomé, and

110, 613 (2019).

S. Ovchinnikov, J. Alloys Compd. 642, 232 (2015).

17.

V. Belyakov, Pis’ma v ZhETF 67, 9 (1998).

36.

E. Verwey, Nature 144, 327 (1939).

18.

A. Chumakov, A. Barla, R. Rüffer, J. Metge,

37.

R. H. Herber and D. Johnson, Inorg. Chem. 18, 2786

H. Grünsteudel, H. Grünsteudel, J. Plessel,

(1979).

Письма в ЖЭТФ том 113 вып. 3 - 4

2021